Электрической цепи формулы – Закон Ома для участка цепи. Закон Джоуля – Ленца. Работа и мощность электрического тока. Виды соединения проводников.

Формулы и расчеты в электрике и электротехнике – раздел, категория сайта

Формулы Расчёты Вычисления

Категория «Электрические расчёты» является разделом который содержит в себе все те материалы и статьи, что связаны с непосредственными вычислениями конкретных величин, характеристик, параметров, относящиеся к сфере электричества.  В нём вы найдёте все те расчёты, формулы, определения, что могут пригодится для точных нахождений токов, напряжений, сопротивлений, мощности, частоты и прочих электрофизических величин.

 

P.S. — Приятного времяпровождения на сайте Электро Хобби

 

 

Как известно во всем нужна своя мера, которая позволяет делать точные системы, устройства, механизмы, схемы. Мера множественная, имеет свои конкретные величины. В сфере электротехники основными величинами являются напряжение, ток, сопротивление, мощность, частота (для переменного и импульсного тока). Величины между собой связаны определенными формулами …

Подробнее…

Электрическая мощность является одной из наиболее важных и значимых характеристик, которая показывает величину, силу той электротехники, систем, цепей, что работают, выполняя ту или иную функцию. Естественно, как и любая другая физическая величина электрическая мощность должна иметь свою меру, благодаря которой …

Подробнее…

В сфере электрики и электроники такая вещь (и понятие) как сопротивление встречается повсеместно. Хоть может и показаться, что электрическое сопротивление это плохо, так как она препятствует свободному течению электрических зарядов по проводникам, но это не совсем так. Возможно вы уже сталкивались с тем, что во всем нужна своя мера. Любой вид энергии (в …

Подробнее…

Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного …

Подробнее…

Электрический ток, это именно та сила, которая течет во всей электротехники заставляя ее работать. Но сводить все к простому течению электротока по электрическим цепям в схемах неразумно, должна быть какая-то мера, определенная величина этой силы тока. Ведь если в электрической схеме пойдет слишком большой ток по проводникам, которые на него не рассчитаны, то просто эта …

Подробнее…

Рекомендуемый материал

electrohobby.ru

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ОНЛАЙН – ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ, ТОКА, МОЩНОСТИ И СЕЧЕНИЯ ПРОВОДНИКА

Наверное, каждый кто делал или делает ремонт электрики сталкивался с проблемой определения той или иной электрической величины. Для кого-то это становится настоящим камнем преткновения, а для кого-то все предельно ясно и каких-либо сложностей при определении той или иной величины нет. Данная статья посвящена именно первой категории – то есть для тех, кто не очень силен в теории электрических цепей и тех показателей, которые для них характерны.

Итак, для начала вернемся немного в прошлое и постараемся вспомнить школьный курс физики, касательно электрики. Как мы помним, основные электрические величины определяются на основании всего одного закона – закона Ома. Именно этот закон является базой проведения абсолютно для любых расчетов и имеет вид:

Отметим, что в данном случае речь идет о расчете самой простейшей электрической цепи, которая выглядит следующим образом:

Подчеркнем, что абсолютно любой расчет ведется именно посредством этой формулы. То есть путем не сложных математических вычислений можно определить ту или иную величину зная при этом два иных электрических параметра. Как бы там ни было, наш ресурс призван упростить жизнь тому кто делает ремонт, а поэтому мы упростим решение задачи определения электрических параметров, вывив основные формулы и предоставив возможность произвести

расчет электрических цепей онлайн.

Как узнать ток зная мощность и напряжение?

В данном случае формула вычисления выглядит следующим образом:

Расчет силы тока онлайн:

(Не целые числа вводим через точку. Например: 0.5)

Как узнать напряжение зная силу тока?

Для того, чтобы узнать напряжение, зная при этом сопротивление потребителя тока можно воспользоваться формулой:

Расчет напряжения онлайн:

Если же сопротивление неизвестно, но зато известна мощность потребителя, то напряжение вычисляется по формуле:

Определение величины онлайн:

Как рассчитать мощность зная силу тока и напряжения?

Здесь необходимо знать величины действующего напряжения и действующей силы тока в электрической цепи. Согласно формуле предоставленной выше, мощность определяется путем умножения силы тока на действующее напряжение.

Расчет цепи онлайн:

Как определить потребляемую мощность цепи имея тестер, который меряет сопротивление?

Этот вопрос был задан в комментарие в одном из материалов нашего сайта. Поспешим дать ответ на этот вопрос. Итак, для начала измеряем тестером сопротивление электроприбора (для этого достаточно подсоединить щупы тестера к вилке шнура питания). Узнав сопротивление мы можем определить и мощность, для чего необходимо напряжение в квадрате разделить на сопротивление.

Онлайн расчет:

Формула расчета сечения провода и как определяется сечение провода

Довольно много вопросов связано с определением сечения провода при построении электропроводки. Если углубиться в электротехническую теорию, то формула расчета сечения имеет такой вид:

Конечно же, на практике, такой формулой пользуются довольно редко, прибегая к более простой схеме вычислений. Эта схема довольно проста: определяют силу тока, которая будет действовать в цепи, после чего согласно специальной таблице определяют сечение. Более детально по этому поводу можно почитать в материале – «Сечение провода для электропроводки»

Приведем пример. Есть бойлер мощностью 2000 Вт, какое сечение провода должно быть, чтобы подключить его к бытовой электропрводке? Для начала определим силу тока, которая будет действовать в цепи:

I=P/U=2000/220В = 9А

Как видим, сила тока получается довольно приличной. Округляем значение до 10 А и обращаемся к таблице:

Таким образом, для нашего бойлера потребуется провод сечением 1,7 мм. Для большей надежности используем провод сечением 2 или 2,5 мм.

Рекомендуем ознакомиться:

 — БЛОК ПИТАНИЯ ДЛЯ СВЕТОДИОДНЫХ ЛЕНТ

 — ЗАЩИТНОЕ ЗАНУЛЕНИЕ

 — СВЕТОДИОДНЫЕ СВЕТИЛЬНИКИ — ЛУЧШЕ НЕ ПРИДУМАЕШЬ!

 — АЛМАЗНАЯ РЕЗКА БЕТОНА И ЖБ КОНСТРУКЦИЙ

 Автор — Антон Писарев

---

moydomik.info

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью

эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований

типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R₁ = R₂ = 0,5 Ом, R₃ = 8 Ом, R₄ = R₅ = 1 Ом, R₆ = 12 Ом, R₇ = 15 Ом, R₈ = 2 Ом, R₉ = 10 Ом, R₁₀= 20 Ом.

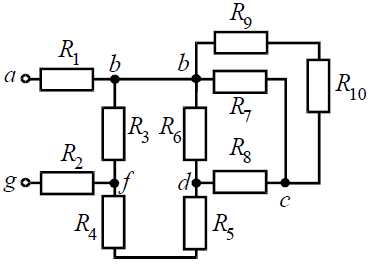
Рис. 1

Решение

Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

---

Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R₁ = R₂ = R₃ = R₄= 40 Ом.

Рис. 2

Решение

Исходную схему можно перечертить относительно входных зажимов (рис. 2,

б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:

где R – величина сопротивления, Ом;

n – количество параллельно соединенных сопротивлений.

---

Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = 10 Ом (рис. 3, а).

Рис. 3

Решение

Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):

По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:

И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

---

Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R₁ = 4 Ом, R₂ = 8 Ом, R₃ =4 Ом, R₄ = 8 Ом, R₅ = 2 Ом, R₆ = 8 Ом, R₇ = 6 Ом, R₈ =8 Ом.

Решение

Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

Рис. 4

Ветвь a−b разрывают, и т.к. сопротивление R_a–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):

Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

---

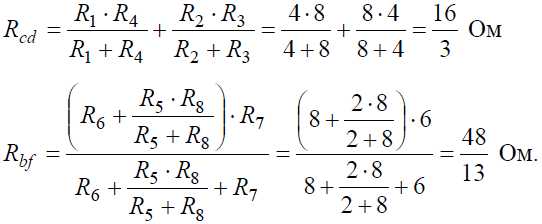
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I₁, I₂, I₃ и составить баланс мощностей, если известно: R₁ = 12 Ом, R₂ = 20 Ом, R₃ = 30 Ом, U = 120 В.

Рис. 5

Решение

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

Баланс мощностей:

---

Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R₁ = 2 Ом, R₂ = 20 Ом, R₃ = 30 Ом, R₄ = 40 Ом, R₅ = 10 Ом, R₆ = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.

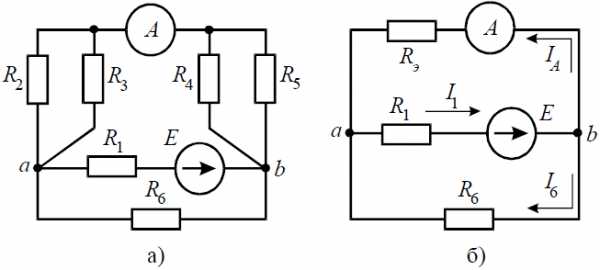
Рис. 6

Решение

Если сопротивления R₂, R₃, R₄, R₅ заменить одним эквивалентным сопротивлением R_Э, то исходную схему можно представить в упрощенном виде (рис. 6, б).

Величина эквивалентного сопротивления:

Преобразовав параллельное соединение сопротивлений R_Э и R₆ схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:

откуда ток I₁:

Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э и R₆:

Тогда амперметр покажет ток:

---

Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R₁ = R₂ = R₃ = R₄ = 3 Ом, J = 5 А, R₅ = 5 Ом.

Рис. 7

Решение

Преобразуем «треугольник» сопротивлений R₁, R₂, R₃ в эквивалентную «звезду» R₆, R₇, R₈ (рис. 7, б) и определим величины полученных сопротивлений:

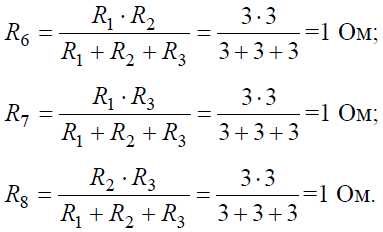
Преобразуем параллельное соединение ветвей между узлами 4 и 5

Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

И теперь можно определить токи I₄ и I₅:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

---

Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

---

Метод эквивалентных преобразований 

02.09.2011, 221630 просмотров.

rgr-toe.ru

формулы тоэ продолжение 2 | энергетик

    Пассивные элементы цепи (резистор, катушка индуктивности и конденсатор), их основные характеристики и параметры.

   Напомним, что все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия (не способные производить электрическую энергию). К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их как линейных, что существенно упрощает математическое описание и анализ процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются параметрами элемента.

1. Резистивный элемент (резистор)

   Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением r (Ом´ м) или обратной величиной – удельной проводимостью G=1/R (См/м), условное графическое изображение резистора на рис. 1:

2. Индуктивный элемент (катушка индуктивности)

   Протекание тока в электрической цепи сопровождается возникновением магнитного поля в окружающей среде. Магнитному полю присуща энергия, равная работе, совершаемой электрическим током i в процессе создания поля и численно равная W_м =
L · i²/2 . Коэффициент L, определяющий энергию магнитного поля называется индуктивностью. Условное графическое изображение катушки индуктивности приведено на рис. 2. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.

3. Емкостный элемент (конденсатор)

   Электрические заряды в цепи могут не только перемещаться по её элементам, но также накапливаться в них, создавая запас энергии W_э  = C · u²/2, где u – напряжение на элементе электрической цепи, а C – коэффициент, определяющий запас энергии и называемый электрической ёмкостью или просто ёмкостью. Условное графическое изображение конденсатора приведено на рис. 3. Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними.

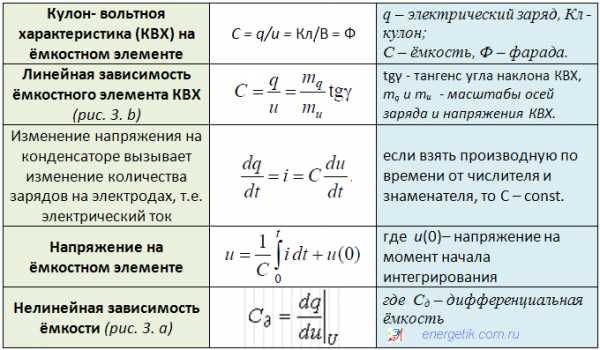
Основные формулы пассивных элементов электрической цепи (из выражений 1 — 3):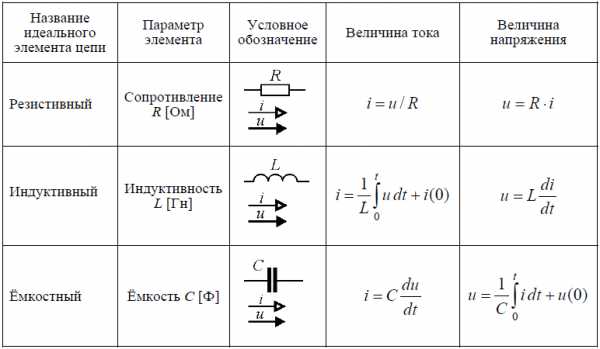

   При этом следует отметить, что все рассмотренные элементы электрической цепи (резистор, катушка индуктивности и конденсатор) обладают всем набором параметров (R, L и C), из трёх рассмотренных элементов цепи только резистивный элемент связан с необратимым преобразованием электрической энергии. Индуктивный и ёмкостный элементы соответствуют процессам накопления энергии в магнитном и электрическом полях с последующим возвратом её в источник в том же количестве, в котором она была накоплена.

 Вернутся  →       Формулы ТОЭ

energetik.com.ru

правила расчета для определения силы тока

На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.

Пример сложных электрических цепей

Пути вычисления электрических схем

Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.

Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.

Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.

Все элементы и устройства подразделяются на три категории:

1. Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
2. Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
3. Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.

Также к основным понятиям электрической схемы относятся:

• Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
• Узел электрической схемы – точка соединения трех и более ветвей схемы;
• Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.

Обозначение ветвей, узлов и контуров на схеме

Метод расчета по законам Ома и Кирхгофа

Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.

Закон Ома для участка цепи

По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:

UR=RI.

Исходя из этой формулы, найти силу тока можно по выражению:

I=UR/R, где:

• UR – напряжение или падение напряжения на резисторе;
• I – ток в резисторе.

Закон Ома для полной цепи

В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:

I=E/Rэ = E/r0+R, где:

• E – ЭДС источника питания;
• rо – внутреннее сопротивление источника питания.

Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.

Первый закон Кирхгофа

Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:

∑mIk=0, где m – число ветвей, подведенных к узлу.

Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».

Второй закон Кирхгофа

Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:

∑nEk=∑mRkIk=∑mUk, где:

• n – число источников ЭДС в контуре;
• m – число элементов с сопротивлением Rk в контуре;
• Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.

Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:

1. Указать относительно положительные направления ЭДС, токов и напряжений;
2. Указать направление обхода контура, описываемого уравнением;
3. Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.

Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:

∑EI=∑RI2.

Метод преобразования электрической цепи

Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.

Последовательное и параллельное соединение элементов

Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.

Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:

• R1=R12R31/R12+R31+R23,
• R2=R12R23/R12+R31+R23,
• R3=R31R23/R12+R31+R23.

Треугольник и звезда соединений

Дополнительные методы расчета цепей

Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:

1. Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
2. Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
3. Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
4. Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.

Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.

Видео

Оцените статью:

elquanta.ru

Мощность тока в электрических цепях :: SYL.ru

Одним из параметров, характеризующих поведение электронов в электрической цепи, кроме напряжения и тока, выступает мощность. Она является мерой количества работы, которую можно совершить за единицу времени. Работу обычно сравнивают с подъёмом веса. Чем больше вес и высота его подъёма, тем больше работы выполнено. Мощность определяет быстроту совершения единицы работы.

Единицы измерения

Мощность автомобилей исчисляют в лошадиных силах – единице измерения, придуманной изготовителями паровых двигателей с целью измерения работоспособности своих агрегатов в обычном источнике энергии того времени. Мощность автомобиля не говорит, как высоко он может заехать на холм или сколько веса он может перевезти, а только показывает, как быстро он это сделает.

Мощность двигателя зависит от его скорости и вращающего момента выходного вала. Скорость измеряют в оборотах в минуту. Вращающий момент – это момент силы двигателя, который измерялся первоначально в фунт-футах, а сейчас в ньютон-метрах или джоулях.

Тракторный двигатель в 100 л. с. вращается медленно, но с большим крутящим моментом. Мотоциклетный двигатель равной мощности вращается быстро, но с небольшим крутящим моментом. Уравнение расчёта мощности имеет вид:

P = 2π S T / 33000, где S – скорость вращения, об/мин, а T – момент вращения.

Переменными здесь являются момент и скорость. Иначе говоря, мощность прямо пропорциональна ST: P~ST.

Мощность постоянного тока

В электроцепях мощность находится в функциональной зависимости от напряжения и тока. Неудивительно, что она похожа на вышеприведённое уравнение P=IU.

Но тут P не пропорциональна току, умноженному на напряжение, а равняется ему. Исчисляется в ваттах, сокращённо Вт.

Важно знать, что ток и напряжение отдельно мощность не определяют, лишь их совокупность. Напряжение является работой на единицу электрического заряда, а ток – скоростью движения зарядов. Напряжение (эквивалент работы) подобно работе при подъёме веса в противодействие силе гравитации. Ток (эквивалентен скорости) подобен скорости подъёма веса. Их произведение и составляет мощность.

Как тракторный и мотоциклетный моторы, цепь с высоким напряжением и небольшим током способна быть одинаковой мощности с цепью невысокого напряжения и большим током. Напряжение и ток вне взаимосвязи не могут характеризовать мощность электроцепи.

Разомкнутая цепь с напряжением и нулевой силой тока работы не совершает, вне зависимости от высоты напряжения. Ведь, согласно формуле, что угодно, умноженное на 0, даёт 0: P = 0 U = 0. В замкнутой цепи из сверхпроводящего провода с нулевым сопротивлением можно достичь тока при напряжении, равном нулю, что также не приведёт к рассеиванию энергии: P = I 0 = 0.

Лошадиные силы и ватты обозначают одно и то же: количество работы, которую можно совершить за единицу времени. Эти единицы взаимосвязаны соотношением

1 л. с. = 745,7 Вт

Пример расчёта

Итак, мощность тока электроцепи в ваттах равняется произведению напряжения на ток.

Чтобы определить, например, мощность нагрузки сопротивлением 3 Ом, в цепи с батареей питания напряжением 12 В, необходимо, применив закон Ома, найти ток

I = U/R = 12/3 =4 А

Умножение полученной силы тока на напряжение и даст искомый результат:

P = I U = 4 А 12 В = 48 Вт

Таким образом, лампа потребляет 48 Вт.

Что же произойдёт при увеличении напряжения?

При напряжении 24 В и сопротивлении 3 Ом ток

I= U/R = 24/3 =8 А

При удвоении напряжения удвоилась и сила тока.

P = IU = 8 А 24 В = 192 Вт

Мощность также увеличилась, но больше. Почему? Потому что это функция произведения напряжения на ток, напряжение и ток увеличились в 2 раза, следовательно, мощность возросла в 4 раза. Это можно проверить делением 192 ватт на 48, частное от которого равно 4.

Варианты формулы

Применив алгебру для преобразования формулы, можно взять исходное уравнение и преобразовать его для случаев, когда неизвестен один из параметров.

Если даны напряжение и сопротивление:

P = (U/R) U или P = U²/R

При известной силе тока и сопротивлении:

P = I (I R) или P = I² R

Исторический факт: отношение между рассеиваемой мощностью и силой тока через сопротивление открыл Джеймс Прескотт Джоуль, а не Георг Симон Ом. Оно было опубликовано в 1841 г. в виде уравнения P = I² R и носит название закона Джоуля–Ленца.

Уравнения мощности:

Переменный ток

Закон Ома и Джоуля–Ленца были установлены для постоянного тока, но они справедливы и для мгновенных значений изменяющегося тока и напряжения.

Мгновенное значение P равно произведению мгновенных значений силы тока и напряжения с учётом их смещения по фазе на угол φ:

P(t) = U(t)I(t) = U_m cosωt I_m cos(ωt-φ) = (1/2)U_m I_m cosφ + (1/2) U_m I_m cos(2ωt-φ).

Из уравнения следует, что у мгновенной мощности есть постоянная составляющая, и она совершает колебательные движения вокруг среднего значения с частотой, которая вдвое превышает частоту тока.

Среднее значение P(t), представляющее практический интерес, равно:

P = (U_mI_m/2) cosφ

С учётом того, что cos φ=R/Z, где Z=(R² + (ωL – 1/ω C)²)^1/2 и U_m/Z = I_m,

P = (R I_m²)/2

Здесь I = I_m 2^-1/2 = 0,707 I_m – эффективное значение силы тока, А.

Аналогично U = U_m2^-1/2 = 0,707 U_m – эффективное напряжение, В.

Средняя мощность через эффективное напряжение и ток определяется

P = U I cos φ, где cos φ – коэффициент мощности.

P в электроцепи переходит в тепловую или другой вид энергии. Наибольшей активной мощности можно достичь при cosφ=1, то есть при отсутствии сдвига фаз. Она носит название полной мощности

S = U I = Z I² = U²/Z

Её размерность совпадает с размерностью P, но с целью отличия S измеряется вольт-амперами, ВА.

Степень интенсивности обмена энергией в электроцепи характеризуется реактивной мощностью

Q = U I sinφ = U I_p = U_p I = X I² = U²/X

Она имеет размерность активной и полной, но с целью различения её выражают вольт-амперами реактивными, ВАр.

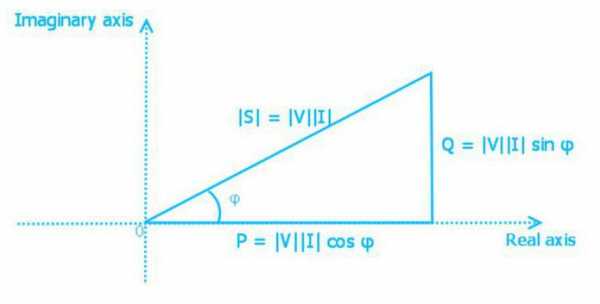
Треугольник мощностей

Мощность активная, реактивная и полная взаимосвязаны выражением

S = (P ²+ Q²)^1/2

Мощность представляют в виде стороны прямоугольного треугольника. Используя законы тригонометрии, можно найти длину одной стороны (количество мощности любого типа) по двум известным сторонам или по длине одной и углу. В таком треугольнике активная мощность является прилежащим катетом, реактивная – противолежащим, а полная мощность – гипотенузой. Угол между катетом активной мощности и гипотенузой равен углу фазы импеданса Z электрической цепи.

Комплексная форма записи этой взаимосвязи следующая:

S = P+jQ = U I cosφ + j U I sinφ= U I e^jφ = U I*, где

S – комплексная мощность;

I* – комплексное сопряжённое значение тока.

Вещественная составляющая комплекса – активная, а мнимая – реактивная.

Мгновенная полная мощность всегда остаётся постоянной величиной.

Мощность трёхфазного тока

Нагрузка каждой фазы трёхфазной электроцепи преобразует энергию или обменивается ею с источником питания. Вследствие этого P и Q цепи равняются суммарной мощности всех фаз:

P = P_r+ P_y+ P_b; Q = Q_r+ Q_y+ Q_b – соединение «звезда»;

P = P_ry+ P_yb+ P_br; Q = Q_ry+ Q_yb+ Q_br – соединение «треугольник».

Активные и реактивные мощности каждой фазы определяются, как в однофазной цепи.

Полная мощность трёхфазной цепи:

S = (P²+Q²)^1/2,

что в комплексной форме имеет вид

S = P+jQ = (P_r + P_y + P_b) + j(Q_r + Q_y + Q_b )= S_r + S_y + S_b= U_r I_r + U_y I_y + U_b I_b

Симметричная нагрузка фаз имеет следствием равенство их мощностей. Вот почему мощность тока равна утроенной активной и реактивной мощности фазы:

P = 3P_ф = 3 I_ф U_фcosφ_ф = 3 R_ф I_ф²

Q = 3 Q_ф = 3 I_ф U_ф sinφ_ф = 3 X_ф I_ф²

S = 3 S_ф = 3 I_ф U_ф

I_ф и U_ф здесь можно заменить их линейными значениями, учитывая, что для звезды U_ф=U_л; I_ф=I_л, а для треугольника U_ф=U_л; I_ф=I_л3^-1/2:

P = 3^1/2 I_л U_лcosφ_ф;

Q = 3^{1/2 I_л U_л}sinφ_ф;

S = 3^{1/2 I_л U_л}.

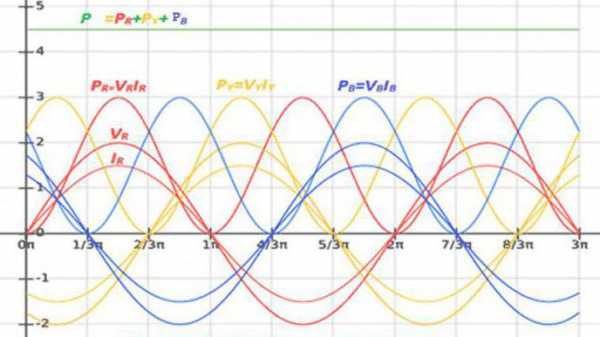
Ток несинусоидальной формы

Определение P в цепи несинусоидального тока аналогично её определению в цепи тока синусоидального, так как за период T средняя мгновенная мощность

P = 1/T∫u i dt

Активная мощность тока определяется суммой P гармонических составляющих, в том числе и постоянной, являющейся гармоникой нулевой частоты.

Реактивная мощность тока подобным образом является результатом сложения Q каждой гармоники.

Q = ∑U_k I_k sinφ_k = ∑ Q_k

Полная мощность определяется произведением эффективного тока и напряжения:

S = I U.

www.syl.ru

Закон Ома для участка цепи. Закон Джоуля – Ленца. Работа и мощность электрического тока. Виды соединения проводников.

Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток:

Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. N При последовательном соединении общее сопротивление увеличивается (больше большего).

Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+…

2. Напряжение на всех параллельно соединенных участках цепи одинаково:     U1=U2=U3=…=Un=…  3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то:  При параллельном соединении общее сопротивление уменьшается (меньше меньшего).

4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+…   т.к.  A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+…   6. Т.к. силы тока во всех участках одинаковы, то:       U1:U2:…:Un:…  = R1:R2:…:Rn:… Для двух резисторов:  – чем больше сопротивление, тем больше напряжение.

4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+…    т.к.     .   5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+…   6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов:  – чем больше сопротивление, тем меньше сила тока.

www.eduspb.com