Энтропия в термодинамике – Энтропия в классической термодинамике — Википедия. Что такое Энтропия в классической термодинамике

Энтропия в термодинамике, теория и примеры

Понятие энтропии в термодинамике

Понятие энтропии ввел в XIX веке Р. Клаузиус. Энтропия () – это функция состояния, в обратимом процессе дифференциалом которой является величина :

   

где – количество теплоты, полученное термодинамической системой в ходе обратимого процесса; – термодинамическая температура системы.

В любом обратимом круговом процессе изменение энтропии равно нулю:

   

Энтропия системы, которая совершает необратимый цикл, растет:

   

Выражения (2) и (3) относятся только к замкнутым системам, в том случае, если система обменивается теплотой с внешней средой, то энтропия может вести себя как угодно. Формулы (2) и (3) в единстве представляют собой неравенство Клаузиуса:

   

которое говорит о том, что в замкнутых системах при обратимых процессах, энтропия остается постоянной, а в необратимых процессах она растет.

В случае равновесного перехода из одного состояния в другое, в соответствии с определением энтропии (1), имеем:

   

где по первому началу термодинамики. – изменение внутренней энергии термодинамической системы; – работа выполняемая системой. В формуле (5) подынтегральное выражение и пределы интегрирования следует выразить, используя параметры, которые характеризуют процесс, происходящий в термодинамической системе. Выражение (5) определяет энтропию с точностью до аддитивной постоянной. Физический смысл несет изменение энтропии, а не сама энтропия.

Свойство энтропии

Энтропия имеет свойство аддитивности: Энтропия совокупности тел равна сумме энтропий каждого тела, которое входит в систему.

Глубинный смысл энтропии открывает статистическая физика. Больцман установил, что энтропия системы связана с термодинамической вероятностью ():

   

где – постоянная Больцмана.

Напомним, что термодинамической вероятностью называют число способов, при помощи которых можно реализовать макросостояние термодинамической системы, или количество микросостояний, которые реализуют данное макросостояние.

В соответствии с (6) энтропия — это мера вероятности состояния термодинамической системы. Иногда, исходя из статистического толкования энтропии, говорят, что энтропия – мера неупорядоченности системы.

Примеры решения задач

ru.solverbook.com

Энтропия в термодинамике — это что такое? Описание, теория и примеры

Понятие об энтропии в термодинамике — это достаточно важный и в то же время непростой вопрос, поскольку существуют различные точки зрения для ее интерпретации. Опишем энтропию подробно в статье, а также приведем примеры процессов, где она играет ключевую роль.

Значение понятия

Разговор об энтропии логичнее всего начать с ее определения. Итак, энтропия в термодинамике — это экстенсивная физическая величина, которая отражает число возможных микросостояний описываемой макросистемы. Иными словами, энтропия отражает уровень организации: чем более неоднородной является система, тем меньше ее энтропия.

Важно понимать два основных свойства энтропии:

1. Экстенсивность. То есть эта величина зависит от размеров системы и массы вещества, которая в ней присутствует. Например, если посчитать количество энтропии для каждого из двух сосудов с водородом объемами V₁ и V₂, в которых газ находится при некотором давлении P и имеет температуру T, то в результате соединения этих сосудов между собой общая энтропия будет равна их сумме.
2. Энтропия в термодинамике — это функция состояния системы. Это означает, что говорить об этой величине можно только тогда, когда система находится в термодинамическом равновесии. При этом энтропия не зависит от истории эволюции этой системы, то есть совершенно не важно, каким способом она пришла к этому термодинамическому состоянию.

Что определяет энтропия?

Другими словами, для чего она была введена в физику? Чтобы ответить на этот вопрос, достаточно рассмотреть простой эксперимент: всем известно, что если взять холодный прут металла и привести его в контакт с таким же прутом, но нагретым до некоторой температуры, то с течением времени горячее тело будет охлаждаться, а холодное – нагреваться. Никто никогда не наблюдал обратный процесс. Направление протекания рассмотренного явления описывается с использованием концепции “энтропия”.

Любая изолированная система, предоставленная самой себе, всегда стремится занять наиболее вероятное состояние. Это состояние характеризуется хаотичным и однородным распределением элементов, составляющих систему, и понимается как состояние с максимальным значением энтропии.

Статистическая интерпретация

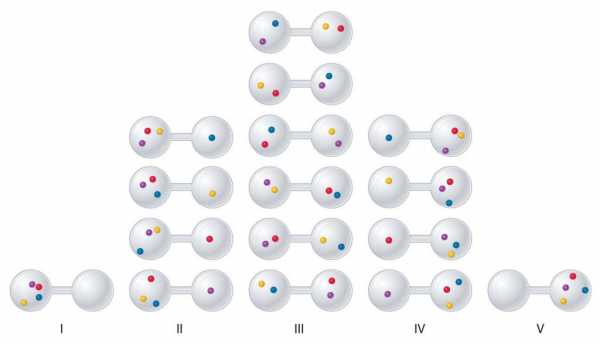
В конце XIX — начале XX века австрийский физик Людвиг Больцман развил новое направление в физике, получившее название статистическая механика. В этой новой науке он ввел понятие об абсолютной энтропии, которую ученый представил в виде: S = k*ln(Ω), где k — константа Больцмана, Ω — количество возможных состояний в системе.

Отметим, что в физике абсолютное значение энтропии мало кого интересует, поскольку все математические формулы, которые учитывают рассматриваемую физическую величину, включают в себя именно ее изменение.

Обратимые процессы в термодинамике

Еще одно определение энтропии в термодинамике — это связь с энергией, которая никаким способом не может быть переведена в полезную работу, например, в механическую. Известно, что эта энергия существует в виде тепла в данной системе, но для практического использования она непригодна.

Например, двигатель внутреннего сгорания работает с некоторым КПД (многие люди, возможно, об этом никогда не задумывались, но коэффициент полезного действия двигателей, которые находятся внутри их автомобилей, составляет всего около 20-25 %), который никогда не будет равен 100 %, какими бы совершенными ни были технологии. Это происходит потому, что в результате термодинамического процесса сгорания топлива часть энергии (большая часть в рассматриваемом случае) теряется на разогрев деталей и на трение. Процесс сгорания топлива — яркий пример увеличения энтропии.

В середине XIX века немецкий ученый Рудольф Клаузиус, анализируя разные термодинамические процессы, ввел понятие “энтропия системы” и смог математически его выразить в виде следующего выражения: dS = δQ/T, здесь dS — изменение энтропии системы, δQ — изменение энергии, которое произошло в результате данного процесса, T — абсолютная температура. Отсюда получаем, что единицей измерения dS в СИ является Дж/К.

Приведенная формула энтропии в термодинамике справедлива только для обратимых процессов, то есть таких переходов, которые могут происходить как в прямом, так и обратном направлении, если изменить внешние условия. Например, если сжать газ, находящийся в герметичном цилиндре с помощью внешней силы, а затем прекратить действие этой силы, то газ восстановит свой первоначальный объем (состояние).

Таким образом, согласно уравнению Клаузиуса, изменение энтропии во время обратимого процесса равно отношению изменения энергии между начальным и конечным состояниями к абсолютной температуре.

Изотермический и адиабатический обратимые процессы

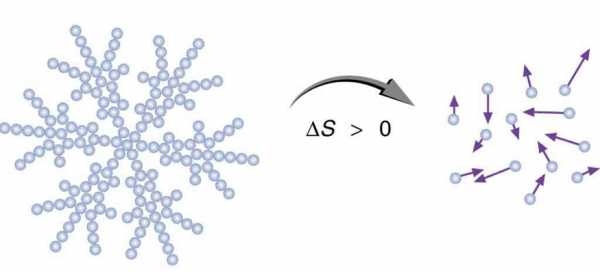
Изотермический процесс — это частный случай, который предполагает, что конечное и начальное состояния системы имеют одинаковую температуру. Согласно формуле Клаузиуса, в результате обратимого изотермического процесса изменение энтальпии системы будет точно равно количеству тепла, которым она обменялась с окружающей средой, деленному на температуру.

Примером такого процесса является расширение идеального газа за счет подвода к нему теплоты извне. Вся подводимая энергия в этом случае тратится на выполнение механической работы (расширение), а температура газа при этом остается постоянной.

Рассматривая концепцию энтропии, интересно также вспомнить об адиабатическом процессе, под которым понимают любой переход в изолированной системе, то есть в ней сохраняется внутренняя энергия. Если этот процесс является обратимым, то согласно формуле dS = δQ/T = 0, поскольку δQ = 0 (нет обмена теплом с окружающей средой).

Необратимые процессы

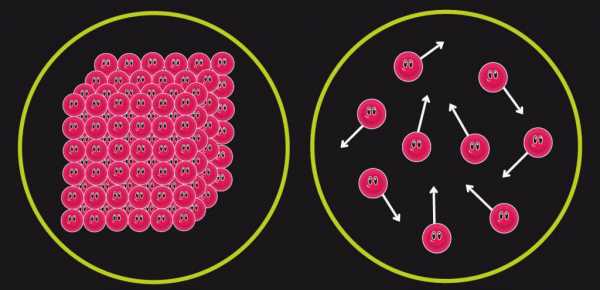
Рассмотренные примеры разных процессов могут только в грубом приближении считаться обратимыми, поскольку в них всегда существуют различные тепловые потери. В нашей Вселенной практически все процессы являются необратимыми. Для них сформулирован 2 закон термодинамики, и энтропия играет важную роль. Приведем формулу: dS≥δQ/T. О чем говорит это выражение: согласно второму закону термодинамики, энтропия в результате абсолютно любого необратимого процесса всегда увеличивается (см. знак “>” в выражении).

Таким образом, подобно факту, что энергия не может быть создана из ничего и не может исчезать бесследно, второй закон термодинамики свидетельствует, что энтропия может быть создана, но не может быть уничтожена (постоянно увеличивается).

Историческая справка

Как было выше сказано, об энтропии физики стали задумываться только в середине XIX века. Причиной этому послужил тот факт, что первые паровые машины обладали чрезвычайно низким КПД (в начале XVIII века типичным значением КПД для этих машин было 2 %). То есть энтропия изначально понималась как “распыление” тепловой энергии во время термодинамического процесса.

Само слово “энтропия”, введенное Клаузиусом, с древнегреческого языка означает “эволюция, преобразование”, тем самым подчеркивается ее важность для описания протекающих процессов.

Энтропия и тепловая смерть Вселенной

Согласно 2-му началу термодинамики, энтропия в нашей Вселенной постоянно увеличивается. Это означает, что в конце концов она достигнет своего максимального значения, когда вещество однородно распределится и температура выровняется во всем пространстве. Такая гипотеза была выдвинута тем же Клаузиусом и получила название тепловой смерти Вселенной.

Реализуется ли она в действительности, зависит от области применимости термодинамики. Дело в том, что на микроуровне, когда рассматриваются отдельные молекулы и атомы, энтропия в термодинамике — это бессмысленная величина, так как сами законы этой ветви физики перестают работать. Предполагается, что аналогичные ограничения их применимости существуют, когда масштабы системы достигают бесконечных значений, то есть размеров Вселенной.

fb.ru

Энтропия (в термодинамике) | Наука

Термодинами́ческая энтропи́я S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Термодинамическое определение энтропии Править

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:

$ \Delta S = \frac{\Delta Q}{T}. $

Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή

, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

$ dS = \frac{\delta Q}{T} $,

где $ dS $ – приращение (дифференциал) энтропии, а $ \delta Q $ – бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому $ \delta Q $ считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана Править

В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются. Больцман постулировал, что:

$ S = k (\ln \Omega) \,\!, $

где константу k=1,38•10^–23 Дж/К мы знаем теперь как постоянную Больцмана, а Ω является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (

S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как Ω может быть только натуральным числом (1,2,3,…), то энтропия Больцмана должна быть положительной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка Править

Существует мнение, что мы можем смотреть на Ω и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах, как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный “беспорядок”, т.к. при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка Править

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

• когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
• когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[1].

Рассмотрим оба пункта более подробно.

Рассмотрим пример термодинамической системы – распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример – учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим максимуму энтропии, будет упорядоченное кристаллическое состояние, а совсем не “хаос”. (Термин “хаос” здесь понимается в смысле беспорядка – в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель – совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, т.е. – беспорядок согласно вышеуказанному определению. Но данный “беспорядок” вовсе не соответствует “беспорядку” в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из “хаотичной” жидкости идёт параллельно с увеличением энтропии.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т.н. “демона Максвелла”. Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т.н. “демон”. “Демон” мог измерять скорость отдельных летящих молекул, и т.о. избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные – в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы “демон” должен был бы получить информацию о её скорости. Но всякое получение информации – материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ, проведённый, например, в ^[2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспрелением молекул “демоном”.

Однако многие учёные стали отождествлять информацию с “отрицательной энтропией” ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер ^[3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Рассмотрим, например, набор 10 монет, каждая из которых может находиться либо в состоянии «орёл», либо в состоянии «решка». Наиболее «упорядоченным» макроскопическим состоянием будет являться или 10 «орлов», или 10 «решек»; для каждого результата в каждом случае имеется только одна возможная конфигурация. И наоборот, наиболее «неупорядоченное» состояние содержит 5 «орлов» и 5 «решек», и здесь ¹⁰C₅ = 252 способов для получения этого результата (см. комбинаторика.)

Безусловно, этот пример также некорректен, т.к. система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах Править

В силу второго начала термодинамики, энтропия $ S_i $ замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: $ dS_i \ge 0 $, индекс $ i $ обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла $ \delta Q_1 $ при температуре $ T_1 $ и уходит количество тепла $ \delta Q_2 $ при температуре $ T_2 $. Приращение энтропии, связанное с данными тепловыми потоками, равно:

$ dS_o = \frac{\delta Q_1}{ T_1}- \frac{\delta Q_2}{ T_2}. $

В стационарных системах обычно $ \delta Q_1 = \delta Q_2 $, $ T_1 > T_2 $, так что $ dS_o <0 $. Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как обратная величина энтропии. Суммарное изменение энтропии открытой системы будет равно:

$ dS = dS_i + dS_o . $

Если всё время $ dS >0 $, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если $ dS =0 $, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру $ T_1 $ внешнего потока тепла в температуру $ T_2 $ уходящего из системы потока тепла.

Измерение энтропии Править

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

$ C_X = T \left(\frac{\partial S}{\partial T}\right)_X $

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

$ \Delta S = \int \frac{C_X}{T} dT $

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

$ S(P,V) = S(P, V_0) + \int^{T(P,V)}_{T(P,V_0)} \frac{C_P(P,V(T,P))}{T} dT $

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии Править

Основная статья: адиабатический процесс

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P-V:

$ S = n R \ \ln (1 + P^{C_V \over R} V^{C_P \over R}) $

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что C_V и C_P постоянные, что на самом деле не так.

• Fermi, E., Thermodynamics, Prentice Hall (1937)
• Reif, F., Fundamentals of statistical and thermal physics, McGraw-Hill (1965)
• Шамбадаль П. Развитие и приложение понятия энтропии. – М.: Наука, 1967. – 280 с.
• Волькенштейн М.В. Энтропия и информация. – М.: Наука, 1986. – 192 с.
1. ↑ http://www.entropysite.com/
2. ↑ Бриллюэн Л. Наука и теория информации. – М., 1960.
3. ↑ Винер Н. Кибернетика. – М.: Советское радио, 1958.

---

---

• Страница 0 – краткая статья
• Страница 1 – энциклопедическая статья
• Разное – на страницах: 2 , 3 , 4 , 5
• Прошу вносить вашу информацию в «Энтропия (в термодинамике) 1», чтобы сохранить ее

ru.science.wikia.com

Термодинамическая энтропия | Cybernetics Wiki

Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Термодинамическое определение энтропии Править

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла $ \Delta Q $ к величине абсолютной температуры $ T $:

$ \Delta S = \frac{\Delta Q}{T} $.

Рудольф Клаузиус дал величине $ S $ имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

$ dS = \frac{\delta Q}{T} $,

где $ dS $ — приращение (дифференциал) энтропии, а $ \delta Q $ — бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому $ \delta Q $ считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана Править

В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются. Больцман постулировал, что:

$ S = k (\ln \Omega) \,\!, $

где константу $ k= $1,38 · 10⁻²³ Дж/К мы знаем теперь как постоянную Больцмана, а $ \Omega $ является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы ($ \Omega $) с одним из её термодинамических свойств (S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как $ \Omega $ может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка Править

Существует мнение, что мы можем смотреть на $ \Omega $ и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах, как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», так как при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка Править

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

• когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
• когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[1].

Рассмотрим оба пункта более подробно.

Рассмотрим пример термодинамической системы — распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример — учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим максимуму энтропии, будет упорядоченное кристаллическое состояние, а совсем не «хаос». (Термин «хаос» здесь понимается в смысле беспорядка — в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель — совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, то есть — беспорядок согласно вышеуказанному определению. Но данный «беспорядок» вовсе не соответствует «беспорядку» в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из «хаотичной» жидкости идёт параллельно с увеличением энтропии.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т. н. «демона Максвелла». Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т. н. «демон». «Демон» мог измерять скорость отдельных летящих молекул, и т.о. избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные — в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы «демон» должен был бы получить информацию о её скорости. Но всякое получение информации — материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ, проведённый, например, в ^[2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспрелением молекул «демоном».

Однако многие учёные стали отождествлять информацию с «отрицательной энтропией» ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер ^[3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Рассмотрим, например, набор 10 монет, каждая из которых может находиться либо в состоянии «орёл», либо в состоянии «решка». Наиболее «упорядоченным» макроскопическим состоянием будет являться или 10 «орлов», или 10 «решек»; для каждого результата в каждом случае имеется только одна возможная конфигурация. И наоборот, наиболее «неупорядоченное» состояние содержит 5 «орлов» и 5 «решек», и здесь $ ^{10}C_5 = 252 $ способов для получения этого результата (см. комбинаторика.)

Безусловно, этот пример также некорректен, так как система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах Править

В силу второго начала термодинамики, энтропия $ S_i $ замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: $ dS_i \ge 0 $, индекс $ i $ обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла $ \delta Q_1 $ при температуре $ T_1 $ и уходит количество тепла $ \delta Q_2 $ при температуре $ T_2 $. Приращение энтропии, связанное с данными тепловыми потоками, равно:

$ dS_o = \frac{\delta Q_1}{ T_1}- \frac{\delta Q_2}{ T_2}. $

В стационарных системах обычно $ \delta Q_1 = \delta Q_2 $, $ T_1 > T_2 $, так что $ dS_o <0 $. Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как обратная величина энтропии.

Суммарное изменение энтропии открытой системы будет равно:

$ dS = dS_i + dS_o . $

Если всё время $ dS >0 $, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если $ dS =0 $, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру $ T_1 $ внешнего потока тепла в температуру $ T_2 $ уходящего из системы потока тепла.

Измерение энтропии Править

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

$ C_X = T \left(\frac{\partial S}{\partial T}\right)_X $

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

$ \Delta S = \int \frac{C_X}{T} dT $

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

$ S(P,V) = S(P, V_0) + \int^{T(P,V)}_{T(P,V_0)} \frac{C_P(P,V(T,P))}{T} dT $

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии Править

Основная статья: адиабатический процесс

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P—V:

$ S = n R \ \ln (1 + P^{\frac{C_V}{R}} V^{\frac{C_P}{R}}) $

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что $ C_V $ и $ C_P $ постоянные, что на самом деле не так.

• Осипов А.И., Уваров А.В. Энтропия и ее роль в науке // Сетевой образовательный журнал. — 2004. — Т. 8. — № 1. — С. 70-79.
• Fermi, E., Thermodynamics, Prentice Hall (1937)
• Reif, F., Fundamentals of statistical and thermal physics, McGraw-Hill (1965)
• Шамбадаль П. Развитие и приложение понятия энтропии. – М.: Наука, 1967. – 280 с.
• Волькенштейн М.В. Энтропия и информация. – М.: Наука, 1986. – 192 с.
1. ↑ http://www.entropysite.com/
2. ↑ Бриллюэн Л. Наука и теория информации. — М., 1960.
3. ↑ Винер Н. Кибернетика. — М.: Советское радио, 1958.

ru.cybernetics.wikia.com

Энтропия в термодинамике.

Величина, равная отношению теплоты, полученной телом при изотермическом процессе, к температуре, при которой происходит теплопередача, т.е. Q/T, называется приведённой теплотой.

Алгебраическая сумма приведённых теплот для обратимого цикла Карно равна нулю.

Функция, характеризующая направление протекания самопроизвольных процессов в замкнутой термодинамической системе, называется энтропией: .

Каждому состоянию тела соответствует одно определённое значение энтропии. Поэтому энтропия является однозначной функцией состояния.

31. Энтропия в термодинамике.

Величина, равная отношению теплоты, полученной телом при изотермическом процессе, к температуре, при которой происходит теплопередача, т.е. Q/T, называется приведённой теплотой.

Алгебраическая сумма приведённых теплот для обратимого цикла Карно равна нулю.

Функция, характеризующая направление протекания самопроизвольных процессов в замкнутой термодинамической системе, называется энтропией: .

Каждому состоянию тела соответствует одно определённое значение энтропии. Поэтому энтропия является однозначной функцией состояния.

35. Реальные газы.

Силы взаимодействия, проявляющиеся на расстоянии порядка 10^-9-10^-10 м, называют ван-дер-ваальсовыми.

Внутренняя энергия реального газа.

Внутренняя энергия реального газа определяется суммой потенциальной энергии взаимодействия молекул и кинетической энергии их движения.

Так как потенциальная энергия взаимодействия молекул зависит от их взаимного расположения, то она должна изменяться при изменении объёма газа. Потенциальную энергию взаимодействия молекул 1 моль газа можно вычислить по формуле: Eп=интг(_внdV), где _вн=-a/V² – добавочное внутренне давление, входящее в уравнение Ван-дер-Ваальса.

Эта энергия имеет отрицательный знак, т.к. молекулярные силы, создающие внутреннее давление, являются силами притяжения.

Использую закон Джоуля, можно вычислить внутреннюю энергию реального газа: U=C_VT-a/V_M – для одного моля.

Внутренняя энергия  моль газа определяется по формуле U=C_VT-a/V, где a=²a, V=V_M.

Внутренняя энергия реального газа зависит как от температуры, так и от объёма.

studfiles.net

Энтропия в классической термодинамике — WiKi

В термодинамике энтропию вводят, обосновывая её существование, перечисляя её свойства и строя для неё шкалу измерения на основании первого, второго и третьего начал термодинамики.

В термодинамических формализмах Клаузиуса^[1] и Каратеодори^[2] энтропию вводят одновременно с абсолютной термодинамической температурой. Математический аппарат термодинамики Гиббса^[3] основан на использовании энтропии в качестве независимой термодинамической переменной, тогда как температура — естественный кандидат на эту роль, вводится как функция внутренней энергии и энтропии. Наконец, в рациональной термодинамике энтропию выражают через внутреннюю энергию и температуру, которые рассматривают как основные неопределяемые переменные теории.

Энтропия простой системы

Первое начало (закон) термодинамики устанавливает связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые их можно было бы подвести^[4]. Термодинамика заимствует понятия энергии и работы из других разделов физики^[5][6], тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. Согласно Клаузиусу теплоту Q{\displaystyle Q}  определяют через внутреннюю энергию U{\displaystyle U}  и работу W{\displaystyle W} ^[7][8]. При использовании термодинамического правила знаков^[9] математическое выражение для первого начала термодинамики в формулировке Клаузиуса имеет вид^[10]:

Q≡ΔU−W.{\displaystyle Q\equiv \Delta U-W.}

(Дефиниция теплоты по Клаузиусу)

Первое начало в этой формулировке вводит теплоту как физическую характеристику процесса, поведение которой определяется законом сохранения энергии, но не определяет её как математический объект. Детализировать дефиницию теплоты проще всего для равновесного процесса, когда работу, а следовательно и теплоту, можно выразить через переменные состояния. Для бесконечно малого^[11]равновесного процесса в простой системе^[12] возможен единственный вид работы — работа расширения/сжатия Wv{\displaystyle W_{v}} :

δWv=−PdV,{\displaystyle \delta W_{v}=-PdV,}

(Работа расширения/сжатия для равновесного процесса в простой системе)

где P{\displaystyle P}  — давление, V{\displaystyle V}  — объём; символ δ{\displaystyle \delta }  означает, что соответствующая величина относится к бесконечно малому процессу. Таким образом, для первого начала термодинамики в формулировке Клаузиуса получаем^[13][14]:

δQ=dU+PdV,{\displaystyle \delta Q=dU+PdV,}

(Первое начало для равновесного процесса в простой системе)

где δQ{\displaystyle \delta Q}  — элементарная (бесконечно малая) теплота процесса.

Это выражение, определяющее элементарную теплоту как математический объект, есть линейная дифференциальная форма (форма Пфаффа) для двух независимых переменных. Для данной пфаффовой формы условие интегрируемости Эйлера не выполняется, то есть δQ{\displaystyle \delta Q}  есть функционал^[15], а не полный дифференциал несуществующей функции Q(U,V){\displaystyle Q(U,V)} ^[14]. Из теории дифференциальных форм известно, однако, что если выполняется условие Фробениуса^[16], то пфаффова форма имеет интегрирующий множитель/делитель, превращающий эту форму в полный дифференциал и представляющий из себя функцию тех же независимых переменных, которые входят в форму Пфаффа^[17]. Пфаффовы формы, имеющие интегрирующий множитель/делитель называют голономными; пфаффова форма двух переменных всегда голономна (теорема Коши)^[18][19]. Поэтому для простых равновесных систем существует функция состояния S(U,V){\displaystyle S(U,V)} , полный дифференциал которой равен

dS ≡ δQT = 1TdU + PTdV,{\displaystyle dS~\equiv ~{\frac {\delta Q}{T}}~=~{\frac {1}{T}}dU~+~{\frac {P}{T}}dV,}

(Дефиниция энтропии простой равновесной системы)

где

T=T(U,V){\displaystyle T=T(U,V)} 

есть интегрирующий делитель для формы Пфаффа. Клаузиус назвал функцию состояния S{\displaystyle S}  энтропией (от греческого ἐντροπία — изменение, превращение, преобразование). Второе начало термодинамики утверждает, что энтропия существует для любых равновесных систем, а не только простых, и что интегрирующий делитель T{\displaystyle T}  есть абсолютная термодинамическая температура^{[20][21][22][19]}. Неравновесная термодинамика распространяет представление о локальной энтропии и локальной температуре на любые термодинамические системы.

Интегрирование уравнения для энтропии приводит к появлению в выражении для функции S(U,V){\displaystyle S(U,V)}  произвольной постоянной, зависящей от выбора начальной точки отсчёта энтропии. Произвол в выборе начального состояния для энтропии устраняет третий закон термодинамики.

Энтропия закрытой системы

Помимо работы расширения/сжатия система может выполнять и другие виды работ, например работу изменению площади поверхности раздела фаз, работу перемещения в поле тяготения, работу поляризации диэлектрика в электрическом поле и т. д. Объединяет все эти виды работ, включая работу расширения/сжатия, формальная структурная идентичность расчётных формул друг с другом и с выражением для работы расширения/сжатия^[23][24][25]:

δWi=Xidxi,{\displaystyle \delta W_{i}=X_{i}dx_{i},}

где δWi{\displaystyle \delta W_{i}}  — элементарная работа i{\displaystyle i} -го типа, xi{\displaystyle x_{i}}  — обобщенная координата, сопряжённая с обобщенной силой Xi.{\displaystyle X_{i}.}  Каждой обобщенной координате соответствует своя обобщённая сила; физические переменные, соответствующие обобщённым координатам и силам, конкретизируют применительно к решаемой задаче^[26][27].

Если однородная система одновременно совершает несколько различных видов работ, то они суммируются и полная работа системы δW{\displaystyle \delta W}  равна^[23][28][29]

ru-wiki.org

Термодинамическая энтропия | Virtual Laboratory Wiki

Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Термодинамическое определение энтропии Править

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла $ \Delta Q $ к величине абсолютной температуры $ T $:

$ \Delta S = \frac{\Delta Q}{T} $.

Рудольф Клаузиус дал величине $ S $ имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

$ dS = \frac{\delta Q}{T} $,

где $ dS $ — приращение (дифференциал) энтропии, а $ \delta Q $ — бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому $ \delta Q $ считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.


Недоразумения в представлениях об энтропии

Основные недоразумения в понимании проблем возникновения жизни, эволюции с позиции физики и физической химии, как правило, связаны с неверными представлениями об энтропии. Этот термин ввел Рудольф Клаузиус. Свое «модельное» представление о мире (Вселенной) он представил в виде высказывания: «Энергия мира постоянна. Энтропия мира стремиться к максимуму». В дальнейшем это высказывание Дж. У. Гиббс выбрал в качестве эпиграфа к работе «О равновесии гетерогенных веществ». Упомянутые ученые сделали приведенное высказывание применительно к своей модели Вселенной. Эта модель соответствует простой изолированной системе идеального газа, т.е. изолированной системе идеального газа, энергия и объем которой постоянны и в которой не совершается никакой работы, или совершается только работа расширения. Энтропия такой системы может только возрастать!

Следует заметить, что если говорить о подобной модели, которая соответствовала бы реальной Вселенной, необходимо было бы принять недоказуемое предположение о том, что все виды энергии реальной Вселенной перейдут в тепловую энергию. Только в этом случае, к тому же при дополнительных нереальных предположениях, Вселенная могла бы превратиться в «модельную систему» Клаузиуса – Гиббса.

Однако любители науки и дилетанты распространили рассматриваемое утверждение на системы других типов, в которых имеют место взаимодействия различной природы между частицами (молекулами или объектами других иерархий) и которые (системы) взаимодействуют с окружающей средой. Подобных ошибок не избежали некоторые ученые, не являющиеся профессионалами в соответствующих областях знания. Это привело к невообразимой путанице и затормозило, более чем на столетие, развитие науки. Появились сотни тысяч публикаций в научных журналах и популярной литературе, содержащие отмеченные недоразумения. К этим недоразумениям прибавились некорректные представления о негоэнтропии и «диссипативных структурах в живом мире».

Возникновение жизни и ее эволюция легко объяснимы с позиции иерархической термодинамики близких к равновесию сложных динамических систем. Эта термодинамика создана на прочном фундаменте классической (равновесной) термодинамики – термодинамики Рудольфа Клаузиуса, Дж. У. Гиббса и других великих творцов. http://www.membrana.ru/particle/17266

http://www.eoht.info/page/Entropy+%28misinterpretations%29 http://www.youtube.com/watch?v=CYr1G5TZO50

Статистическое определение энтропии: принцип Больцмана Править

В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются. Больцман постулировал, что:

$ S = k (\ln \Omega) \,\!, $

где константу $ k= $1,38 · 10⁻²³ Дж/К мы знаем теперь как постоянную Больцмана, а $ \Omega $ является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы ($ \Omega $) с одним из её термодинамических свойств (S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как $ \Omega $ может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка Править

Существует мнение, что мы можем смотреть на $ \Omega $ и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах, как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», так как при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка Править

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

• когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
• когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[1].

Рассмотрим оба пункта более подробно.

Рассмотрим пример термодинамической системы — распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример — учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим максимуму энтропии, будет упорядоченное кристаллическое состояние, а совсем не «хаос». (Термин «хаос» здесь понимается в смысле беспорядка — в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель — совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, то есть — беспорядок согласно вышеуказанному определению. Но данный «беспорядок» вовсе не соответствует «беспорядку» в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из «хаотичной» жидкости идёт параллельно с увеличением энтропии.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т. н. «демона Максвелла». Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т. н. «демон». «Демон» мог измерять скорость отдельных летящих молекул, и т.о. избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные — в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы «демон» должен был бы получить информацию о её скорости. Но всякое получение информации — материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ, проведённый, например, в ^[2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспрелением молекул «демоном».

Однако многие учёные стали отождествлять информацию с «отрицательной энтропией» ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер ^[3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Рассмотрим, например, набор 10 монет, каждая из которых может находиться либо в состоянии «орёл», либо в состоянии «решка». Наиболее «упорядоченным» макроскопическим состоянием будет являться или 10 «орлов», или 10 «решек»; для каждого результата в каждом случае имеется только одна возможная конфигурация. И наоборот, наиболее «неупорядоченное» состояние содержит 5 «орлов» и 5 «решек», и здесь $ ^{10}C_5 = 252 $ способов для получения этого результата (см. комбинаторика.)

Безусловно, этот пример также некорректен, так как система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах Править

В силу второго начала термодинамики, энтропия $ S_i $ замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: $ dS_i \ge 0 $, индекс $ i $ обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла $ \delta Q_1 $ при температуре $ T_1 $ и уходит количество тепла $ \delta Q_2 $ при температуре $ T_2 $. Приращение энтропии, связанное с данными тепловыми потоками, равно:

$ dS_o = \frac{\delta Q_1}{ T_1}- \frac{\delta Q_2}{ T_2}. $

В стационарных системах обычно $ \delta Q_1 = \delta Q_2 $, $ T_1 > T_2 $, так что $ dS_o <0 $. Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как обратная величина энтропии.

Суммарное изменение энтропии открытой системы будет равно:

$ dS = dS_i + dS_o . $

Если всё время $ dS >0 $, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если $ dS =0 $, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру $ T_1 $ внешнего потока тепла в температуру $ T_2 $ уходящего из системы потока тепла.

Измерение энтропии Править

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

$ C_X = T \left(\frac{\partial S}{\partial T}\right)_X $

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

$ \Delta S = \int \frac{C_X}{T} dT $

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

$ S(P,V) = S(P, V_0) + \int^{T(P,V)}_{T(P,V_0)} \frac{C_P(P,V(T,P))}{T} dT $

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии Править

Основная статья: адиабатический процесс

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P—V:

$ S = n R \ \ln (1 + P^{\frac{C_V}{R}} V^{\frac{C_P}{R}}) $

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что $ C_V $ и $ C_P $ постоянные, что на самом деле не так.

• Осипов А.И., Уваров А.В. Энтропия и ее роль в науке // Сетевой образовательный журнал. — 2004. — Т. 8. — № 1. — С. 70-79.
• Fermi, E., Thermodynamics, Prentice Hall (1937)
• Reif, F., Fundamentals of statistical and thermal physics, McGraw-Hill (1965)
• Шамбадаль П. Развитие и приложение понятия энтропии. – М.: Наука, 1967. – 280 с.
• Волькенштейн М.В. Энтропия и информация. – М.: Наука, 1986. – 192 с.
1. ↑ http://www.entropysite.com/
2. ↑ Бриллюэн Л. Наука и теория информации. — М., 1960.
3. ↑ Винер Н. Кибернетика. — М.: Советское радио, 1958.

ru.vlab.wikia.com