Что такое предел функции как его найти
Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.
Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть . Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле
Величина, которую нам требуется найти, будет записана так:
Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.
Теперь вычислим предел, присвоив переменной
С рассмотренной последовательностью окружностей свяжем другую переменную величину – последовательность сумм их диаметров:
Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.
Предел функции при
Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :
(1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
и можно ставить вопрос о существовании её предела.
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится
Пример 1. Найти предел функции при .
Решение. Подставляем вместо x значение 0. Получаем:
.
Итак, предел данной функции при равен 1.
Предел функции при , при и при
Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.
Определение 2. Число A называется пределом функции f(x)
при ,
если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2)
значений функции сходится к
Символически это записывается так: .
Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: ().
Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо
Пример 2. Найти предел функции при .
Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
.
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.
Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
(5)
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.
Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке , то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида – самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Освоим эти приёмы на примерах.
Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.
Неопределённость вида
Пример 12. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или “супермалому числу”.
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Пример 13. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем “икс” под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо “икса”.
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Неопределённость вида
Пример 14. Раскрыть неопределённость и найти предел .
Решение. В числителе – разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе – квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Пример 15. Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 16. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Продолжение темы “Предел”
Поделиться с друзьями
function-x.ru
Первый замечательный предел, примеры решения
Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.
Формула первого замечательного предела
Формула первого замечательного предела имеет вид:
Замечаем, что при получается , тем самым в числетеле и в знаменателе имеем нули. Таким образом формула первого замечательного предела нужна для раскрытия неопределенностей .
Для применения формулы необходимо, чтобы были соблюдены два условия:
- Выражения, содержащиеся в синусе и знаменателе дроби совпадают
- Выражения, стоящие в синусе и знаменателе дроби стремятся к нулю
Внимание! Хотя выражения под синусом и в знаменателе одинаковые, однако , при . Не выполнено второе условие, поэтому применять формулу НЕЛЬЗЯ!
Следствия первого замечательного предела
Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.
Примеры решения первого замечательного предела
Рассмотрим первый замечательный предел, примеры решения которого на вычисление пределов содержащих тригонометрические функции и неопределенность
| Пример 1 |
| Вычислить |
| Решение |
| Рассмотрим предел и заметим, что в нём присутствует синус. Далее подставим в числитель и знаменатель и получим неопределенность нуль делить на нуль: Уже два признака того, что нужно применять замечательный предел, но есть небольшой нюанс: сразу применить формулу мы не сможем, так как выражение под знаком синуса отличается от выражения стоящего в знаменателе. А нам нужно, чтобы они были равны. Поэтому с помощью элементарных преобразований числителя мы превратим его в . Для этого мы вынесем двойку из знаменателя дроби отдельным множителем. Выглядит это так: Обратите внимание, что в конце получилось по формуле. |
| Ответ |
| Пример 2 |
| Найти |
| Решение |
Как всегда сначала нужно узнать тип неопределенности. Если она нуль делить на нуль, то обращаем внимание на наличие синуса: Данная неопределенность позволяет воспользоваться формулой первого замечательного предела, но выражение из знаменателя не равно аргументу синуса? Поэтом “в лоб” применить формулу нельзя. Необходимо умножить и разделить дробь на аргумент синуса: Теперь по свойствам пределов расписываем: Второй предел как раз подходит под формулу и равен единице: Снова подставляем в дробь и получаем неопределенность . Для её устранения достоточно вынести за скобки и сократить на него: |
| Ответ |
| Пример 3 |
| Определить |
| Решение |
Подставляя в аргумент синуса обращаем внимание на то, что сам аргумент стремится к нулю, как и синус: Выполняем решение, используя первый замечательный предел: |
| Ответ |
| Пример 4 |
| Вычислить |
| Решение |
Вычисление начнём с подстановки . В результате получаем неопределенность . Предел содержит синус и тангенс, что намекает на возможное развитие ситуации с использованием формулы первого замечательного предела. Преобразуем числитель и знаменатель дроби под формулу и следствие: Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей |
| Ответ |
В статье: “Первый замечательный предел, примеры решения” было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.
xn--24-6kcaa2awqnc8dd.xn--p1ai
Первый и второй замечательный предел
Найти замечательные пределы трудно не только многим студентам первого, второго курса обучения которые изучают теорию пределов, но и некоторым преподавателям.
Формула первого замечательного предела
Следствия первого замечательного предела запишем формулами
1. 2. 3. 4. Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.
Пример 1. Найти предел функции sin(7*x)/(5*x)
Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7
Некоторым такая детализация покажется лишней, но большинству студентов которым трудно даются пределы поможет лучше понять правила и усвоить теоретический материал.
Также, если есть обратный вид функции – это также первый замечательный предел. А все потому, что замечательный предел равен единице
Это же правило касается и следствий 1 замечательного предела. Поэтому если Вас спросят “Чему равен первый замечательный предел?” Вы без колебаний должны ответить, что это – единица.
Пример 2. Найти предел функции sin(6x)/tan(11x)
Решение: Для понимания конечного результата распишем функцию в виде
Чтобы применить правила замечательного предела умножим и разделим на множители
Далее предел произведения функций распишем через произведение пределов
Без сложных формул мы нашли предел часки тригонометрических функций. Для усвоения простых формул попробуйте придумать и найти предел на 2 и 4 формулу следствия 1 замечательного предела. Мы рассмотрим более сложные задачи.
Пример 3. Вычислить предел (1-cos(x))/x^2
Решение: При проверке подстановкой получим неопределенность 0/0. Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу
При этом предел преобразится к понятному виду
Нам удалось свести функцию к квадрату замечательного предела.
Пример 4. Найти предел
Решение: При подстановке получим знакомую особенность 0/0. Однако переменная стремится к Pi, а не к нулю. Поэтому для применения первого замечательного предела выполним такую замену переменной х, чтобы новая переменная направлялась к нулю. Для этого знаменатель обозначим за новую переменную Pi-x=y
Таким образом использовав тригонометрическую формулу, которая приведена в предыдущем задании, пример сведен к 1 замечательному пределу.
Пример 5. Вычислить предел
Решение: Сначала неясно как упростить пределы. Но раз есть пример, значит должен быть и ответ. То что переменная направляется к единице дает при подстановке особенность вида ноль умножить на бесконечность, поэтому тангенс нужно заменить по формуле
После этого получим нужную неопределенность 0/0. Далее выполняем замену переменных в пределе, и используем периодичность котангенса
Последние замены позволяют использовать следствие 1 замечательного предела.
Второй замечательный предел равен экспоненте
Это классика к которой в реальных задачах на пределы не всегда легко прийти.
В вычислениях Вам понадобятся пределы – следствия второго замечательного предела:
1. 2. 3. 4.
Благодаря второму замечательному пределу и его последствиям можно исследовать неопределенности типа ноль разделить на ноль, единица в степени бесконечность, и бесконечность разделить на бесконечность, да еще и в таком же степени
Начнем для ознакомления с простых примеров.
Пример 6. Найти предел функции
Решение: Напрямую применить 2 замечательный пределу не получится. Сначала следует превратить показатель, чтобы он имел вид обратный к слагаемому в скобках
Это и есть техника сведения к 2 замечательному пределу и по сути – вывода 2 формулы следствия предела.
Пример 7. Найти предел функции
Решение: Имеем задания на 3 формулу следствия 2 замечательного предела. Подстановка нуля дает особенность вида 0/0. Для возведения предела под правило превратим знаменатель, чтоб при переменной был тот же коэффициент что и в логарифм
Это также легко понять и выполнить на экзамене. Трудности у студентов при исчислении пределов начинаются с следующих задач.
Пример 8. Вычислить предел функции [(x+7)/(x-3)]^(x-2)
Решение: Имеем особенность типа 1 в степени бесконечность. Если не верите, можете везде вместо “икс” подставить бесконечность и убедиться в этом. Для возведения под правило поделим в скобках числитель на знаменатель, для этого предварительно выполним манипуляции
Подставим выражение в предел и превратим к 2 замечательному пределу
Предел равен экспоненте в 10 степени. Константы, которые являются слагаемыми при переменной как в скобках так и степени никакой “погоды” не вносят – об этом следует помнить. А если Вас спросят преподаватели – “Почему не превращаете показатель?” (Для этого примера в x-3), то скажите что “Когда переменная стремится к бесконечности то к ней хоть добавляй 100 хоть отнимай 1000, а предел останется такой как и был!”.
Есть и второй способ вычислять пределы такого типа. О нем расскажем в следующем задании.
Пример 9. Найти предел
Решение: Теперь вынесем переменную в числителе и знаменателе и превратим оду особенность на другую. Для получения конечного значения используем формулу следствия 2 замечательного предела
Пример 10. Найти предел функции
Решение: Заданный предел найти под силу не каждому. Для возведения под 2 предел представим, что sin (3x) это переменная, а нужно превратить показатель
Далее показатель запишем как степень в степени
В скобках описаны промежуточные рассуждения. В результате использования первого и второго замечательного предела получили экспоненту в кубе.
Пример 11. Вычислить предел функции sin(2*x)/ln(3*x+1)
Решение: Имеем неопределенность вида 0/0. Кроме этого видим, что функцию следует превращать к использованию обеих замечательных пределов. Выполним предыдущие математические преобразования
Далее без труда предел примет значение
Вот так свободно Вы будете чувствовать себя на контрольных работах, тестах, модулях если научитесь быстро расписывать функции и сводить под первый или второй замечательный предел. Если заучить приведенные методики нахождения пределов Вам трудно, то всегда можете заказать контрольную работу на пределы у нас.
Для этого заполните форму, укажите данные и вложите файл с примерами. Мы помогли многим студентам – сможем помочь и Вам!
yukhym.com
Второй замечательный предел, примеры решения
Данная статья: «Второй замечательный предел: примеры решения» посвящена раскрытию в пределах неопределенностей вида:
и .
Так же такие неопределенности можно раскрывать с помощью логарифмирования показательно-степенной функции, но это уже другой метод решения, о котором будет освещено в другой статье.
Формула второго замечательного предела и его следствия
Формула второго замечательного предела записывается следующим образом:
Из формулы вытекают следствия, которые очень удобно применять для решения примеров с пределами:
Стоить заметить, что второй замечательный предел можно применять не всегда к показательно-степенной функции, а только в случаях когда основание стремится к единице. Для этого сначала в уме вычисляют предел основания, а затем уже делают выводы. Всё это будет рассмотрено в примерах решений.
Примеры решений второго замечательного предела
Рассмотрим примеры решений с использованием прямой формулы и её следствий. Так же разберем случаи, при которых формула не нужна. Достаточно записать только готовый ответ.
| Пример 1 |
| Найти предел |
| Решение |
Подставим бесконечность в предел и посмотрим на неопределенность: Найдем предел основания: Получили основание равное единице, а это значит уже можно применить второй замечательный предел. Для этого подгоним основание функции под формулу путем вычитания и прибавления единицы: Смотрим на второе следствие и записываем ответ: |
| Ответ |
| Пример 2 |
| Определить предел |
| Решение |
Замечаем, что основание степени стремится к единице , при , а показатель . Поэтому можно применить второе следствие. Но сперва, разберемся с показателем и приведем его в нужный вид – сделаем равным знаменателю основания. Для этого умножим его на и разделим на него же. Получаем: Уже теперь применяем формулу и получаем: |
| Ответ |
| Пример 3 |
| Вычислить предел |
| Решение |
Получаем неопределенность . Для её раскрытия воспользуемся вторым замечательным пределом. Но у нас . Как быть? Выполняем замену , тогда , при . Из замены следует, что . |
| Ответ |
| Пример 4 |
| Решить предел |
| Решение |
Находим предел основания и видим, что , значит можно применить второй замечательный предел. Стандартно по плану прибавляем и вычитаем единицу из основания степени: Подгоняем дробь под формулу 2-го замеч. предела: Теперь подгоняем степень. В степени должна быть дробь равная знаменателю основания . Для этого умножим и разделим степень на неё, и продолжим решать: Предел, расположенный в степени при равен: . Поэтому продолжая решение имеем: |
| Ответ |
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
| Пример 5 |
| Найти |
| Решение |
Начинаем с проверки равен ли предел основания единице. Имеем: А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как Продолжаем вычисление предела: |
| Ответ |
| Пример 6 |
| Найти |
| Решение |
Начинаем с проверки равен ли предел основания единице. Имеем: А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как Продолжаем вычисление предела: |
| Ответ |
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
xn--24-6kcaa2awqnc8dd.xn--p1ai
Определение предела функции на бесконечности
Конечный предел функции на бесконечности
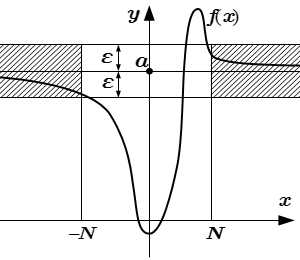
Предел функции на бесконечности:
|f(x) – a| < ε при |x| > N
Определение предела по Коши
Пусть функция f(x) определена в некоторой окрестности бесконечно удаленной точки, при |x| > K, где K – положительное число. Число a называется пределом функции f(x) при x стремящемся к бесконечности (), если для любого, сколь угодно малого положительного числа ε > 0, существует такое число Nε> K, зависящее от ε, что для всех x, |x| > Nε, значения функции принадлежат ε – окрестности точки a:
|f(x) – a| < ε.
Предел функции на бесконечности обозначается так:
.
Или при .
Также часто используется следующее обозначение:
.
Запишем это определение, используя логические символы существования и всеобщности:
.
Здесь подразумевается, что значения принадлежат области определения функции.
Односторонние пределы
Левый предел функции на бесконечности:
|f(x) – a| < ε при x < –N
Часто встречаются случаи, когда функция определена только для положительных или отрицательных значений переменной x (точнее в окрестности точки или ). Также пределы на бесконечности для положительных и отрицательных значений x могут иметь различные значения. Тогда используют односторонние пределы.
Левый предел в бесконечно удаленной точке или предел при x стремящемся к минус бесконечности () определяется так:
.
Правый предел в бесконечно удаленной точке или предел при x стремящемся к плюс бесконечности ():
.
Односторонние пределы на бесконечности часто обозначают так:
; .
Бесконечный предел функции на бесконечности
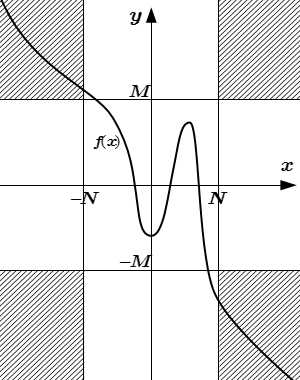
Бесконечный предел функции на бесконечности:
|f(x)| > M при |x| > N
Определение бесконечного предела по Коши
Пусть функция f(x) определена в некоторой окрестности бесконечно удаленной точки, при |x| > K, где K – положительное число. Предел функции f(x) при x стремящемся к бесконечности (), равен бесконечности, если для любого, сколь угодно большого числа M > 0, существует такое число NM> K, зависящее от M, что для всех x, |x| > NM, значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x)| > M.
Бесконечный предел при x стремящемся к бесконечности обозначают так:
.
Или при .
С помощью логических символов существования и всеобщности, определение бесконечного предела функции можно записать так:
.
Аналогично вводятся определения бесконечных пределов определенных знаков, равных и :
.
.
Определения односторонних пределов на бесконечности.
Левые пределы.
.
.
.
Правые пределы.
.
.
.
Определение предела функции по Гейне
Пусть функция f(x) определена на некоторой окрестности бесконечно удаленной точки x0, где или или .
Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в точке x0:
,
если для любой последовательности {xn}, сходящейся к x0: ,
элементы которой принадлежат окрестности , последовательность {f(xn)} сходится к a:
.
Если в качестве окрестности взять окрестность бесконечно удаленной точки без знака: , то получим определение предела функции при x стремящемся к бесконечности, . Если взять левостороннюю или правостороннюю окрестность бесконечно удаленной точки x0: или , то получим определение предела при x стремящемся к минус бесконечности и плюс бесконечности, соответственно.
Определения предела по Гейне и Коши эквивалентны.
Примеры
Пример 1
Используя определение Коши показать, что
.
Решение
Введем обозначения:
.
Найдем область определения функции . Поскольку числитель и знаменатель дроби являются многочленами, то функция определена для всех x кроме точек, в которых знаменатель обращается в нуль. Найдем эти точки. Решаем квадратное уравнение. ;
.
Корни уравнения:
; .
Поскольку , то и .
Поэтому функция определена при . Это мы будем использовать в дальнейшем.
Выпишем определение конечного предела функции на бесконечности по Коши:
.
Преобразуем разность:
.
Разделим числитель и знаменатель на и умножим на –1:
.
Пусть .
Тогда
;
;
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при , и .
Поскольку всегда можно увеличить, то возьмем . Тогда для любого ,
при .
Это означает, что .
Пример 2
Пусть .
Используя определение предела по Коши показать, что:
1) ;
2) .
1) Решение при x стремящемся к минус бесконечности
Поскольку , то функция определена для всех x.
Выпишем определение предела функции при , равного минус бесконечности:
.
Пусть . Тогда
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что для любого положительного числа M, имеется число , так что при ,
.
Это означает, что .
2) Решение при x стремящемся к плюс бесконечности
Преобразуем исходную функцию. Умножим числитель и знаменатель дроби на и применим формулу разности квадратов:
.
Имеем:
.
Выпишем определение правого предела функции при :
.
Введем обозначение: .
Преобразуем разность:
.
Умножим числитель и знаменатель на :
.
Пусть
.
Тогда
;
.
Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
при и .
Поскольку это выполняется для любого положительного числа , то
.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Пределы
0)Постоянная величина (число) сама себе служит пределом:.
1а)Величина, обратная бесконечно
большой, есть бесконечно малая величина,
т.е. еслих → ∞, то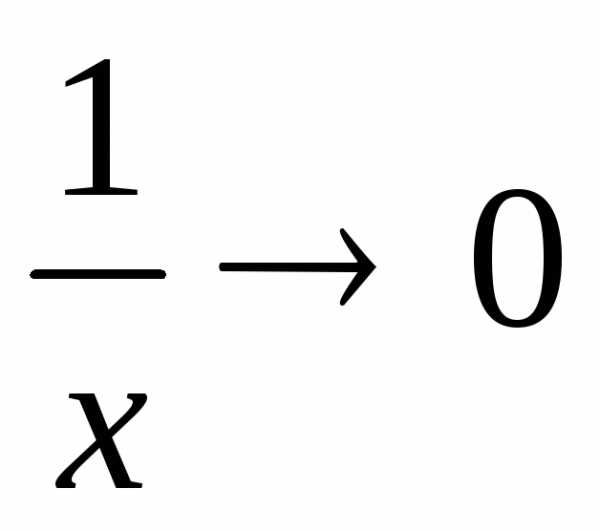
.
1b)Величина, обратная бесконечно
малой, есть бесконечно большая величина,
т.е. еслих → 0, то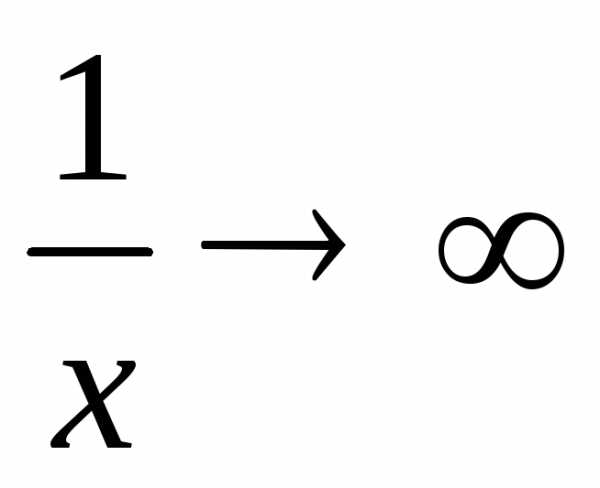
.
2a)Если две переменные стремятся к одному и тому же пределу, а третья переменная заключена между ними, то и она стремится к этому же пределу. Еслиxn < yn < zn, причемxn → pиzn → p, тоyn → p.
2b)Если две функцииF(x)иФ(х)стремятся к одному и тому же пределуAприх→ p, а значения функцииf(x)заключены между значениямиF(x)иФ(х), тоf(x)стремится к этому же пределуAприх→ p.
Если F(x)≤f(x)≤Ф(х)и
,
то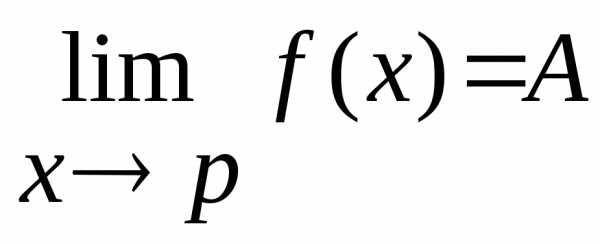
.
3) Предел суммы (разности) конечного числа слагаемых равен сумме (разности) пределов этих слагаемых:
lim (u ± v ± … ± t) = lim u ± lim v ± … ± lim t.
4) Предел произведения конечного числа множителей равен произведению пределов этих множителей:
lim (u · v · … · t) = lim u ·lim v · … · lim t.
Постоянный множитель можно выносить за знак предела lim c·u = с · lim u.
5) Предел частного равен частному
пределов, если только предел делителя
(знаменателя) не равен нулю:
,
если lim v ≠ 0.
6)Если предел числителя не равен нулю, а предел знаменателя равен нулю, то предел дроби является бесконечно большой величиной (см. п.1b):
Если lim u ≠ 0, а lim v = 0, то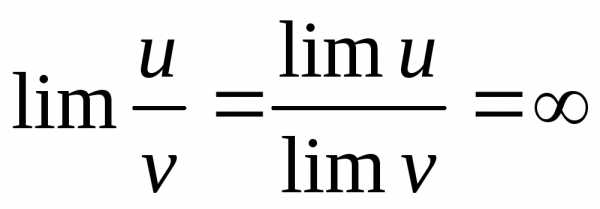 
.
Если же lim u =0 и lim v =0, то для нахождения
предела необходимы дополнительные
исследования.
0)Постоянная величина (число) сама себе служит пределом:.
1а)Величина, обратная бесконечно
большой, есть бесконечно малая величина,
т.е. еслих → ∞, то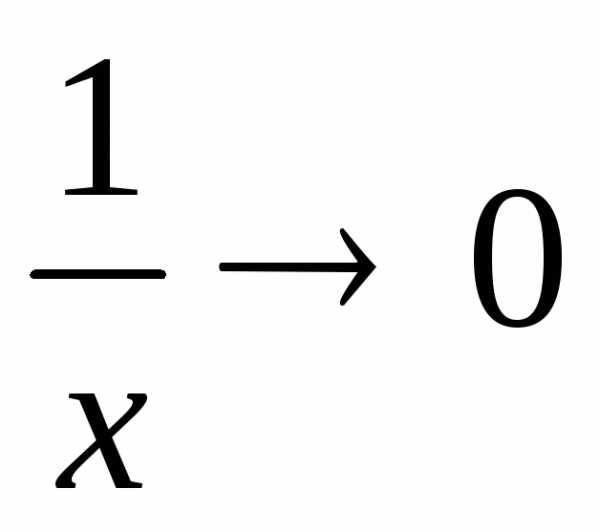
.
1b)Величина, обратная бесконечно
малой, есть бесконечно большая величина,
т.е. еслих → 0, то
.
2a)Если две переменные стремятся к одному и тому же пределу, а третья переменная заключена между ними, то и она стремится к этому же пределу. Еслиxn < yn < zn, причемxn → pиzn → p, тоyn → p.
2b)Если две функцииF(x)иФ(х)стремятся к одному и тому же пределуAприх→ p, а значения функцииf(x)заключены между значениямиF(x)иФ(х), тоf(x)стремится к этому же пределуA
при х→ p. ЕслиF(x)≤f(x)≤Ф(х)и
,
то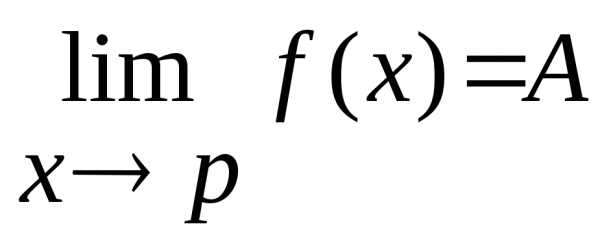
.
3) Предел суммы (разности) конечного числа слагаемых равен сумме (разности) пределов этих слагаемых:
lim (u ± v ± … ± t) = lim u ± lim v ± … ± lim t.
4) Предел произведения конечного числа множителей равен произведению пределов этих множителей:
lim (u · v · … · t) = lim u ·lim v · … · lim t.
Постоянный множитель можно выносить за знак предела
lim c·u = с · lim u.
5) Предел частного равен частному
пределов, если только предел делителя
(знаменателя) не равен нулю:
,
если lim v ≠ 0.
6)Если предел числителя не равен
нулю, а предел знаменателя равен нулю,
то предел дроби является бесконечно
большой величиной (см. п.1b): Если lim u ≠
0, а lim v = 0, то
.
Если же lim u =0 и lim v =0, то для нахождения
предела необходимы дополнительные
исследования.
Раскрытие некоторых типов неопределённостей.
7)Чтобы раскрыть неопределенность
вида
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
8)Чтобы раскрыть неопределенность
вида
,
заданную в форме:,
надо и в числителе и в знаменателе
выделить критический множитель (х –
а) и сократить на него дробь.
9)Чтобы раскрыть неопределенность
вида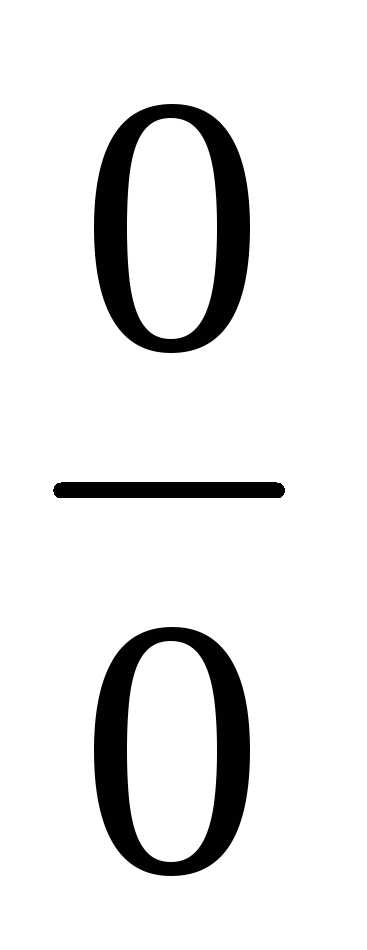
,
в которой числитель или знаменатель
иррациональны, следует надлежащим
образом избавиться от иррациональности.
Первый замечательный предел:
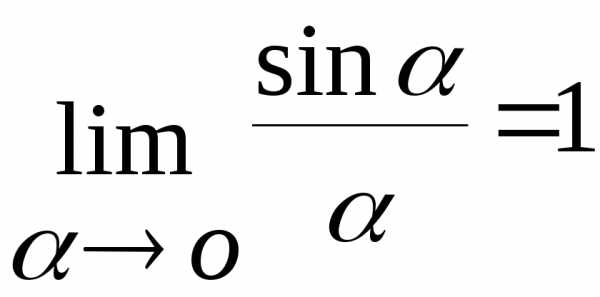
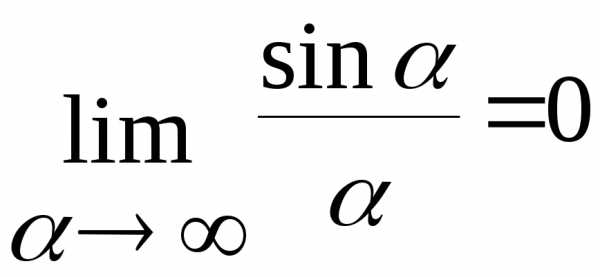
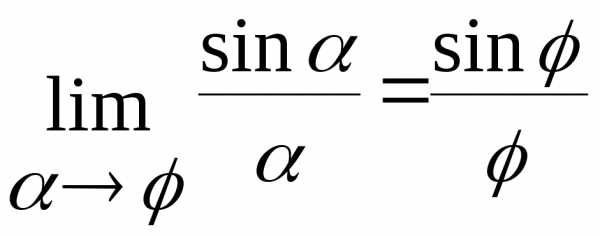
Второй замечательный предел:
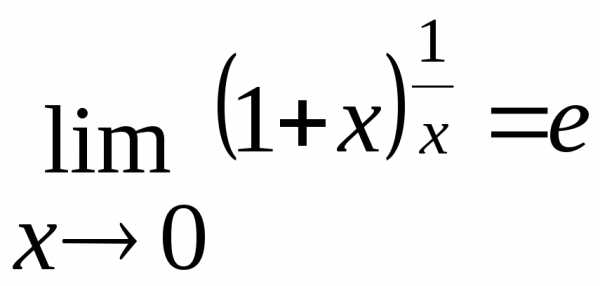
Другие замечательные пределы
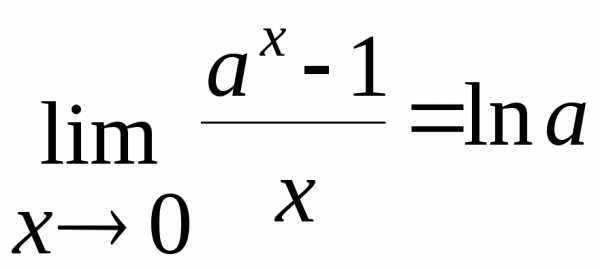
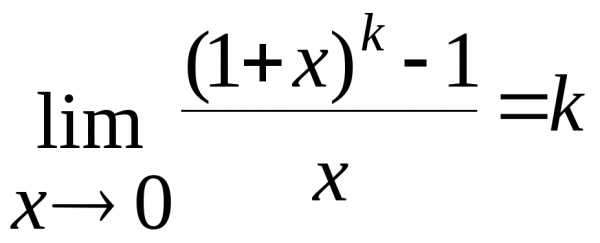
Понижение степени
Раскрытие некоторых типов неопределённостей.
7)Чтобы раскрыть неопределенность
вида
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
8)Чтобы раскрыть неопределенность
вида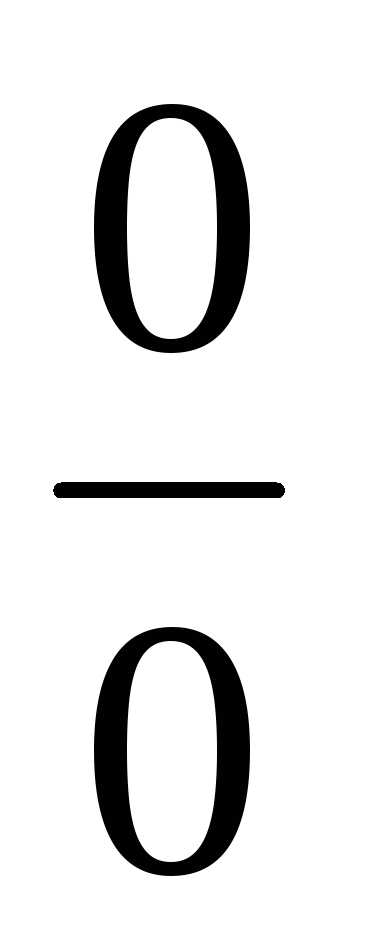
,
заданную в форме:,
надо и в числителе и в знаменателе
выделить критический множитель (х –
а) и сократить на него дробь.
9)Чтобы раскрыть неопределенность
вида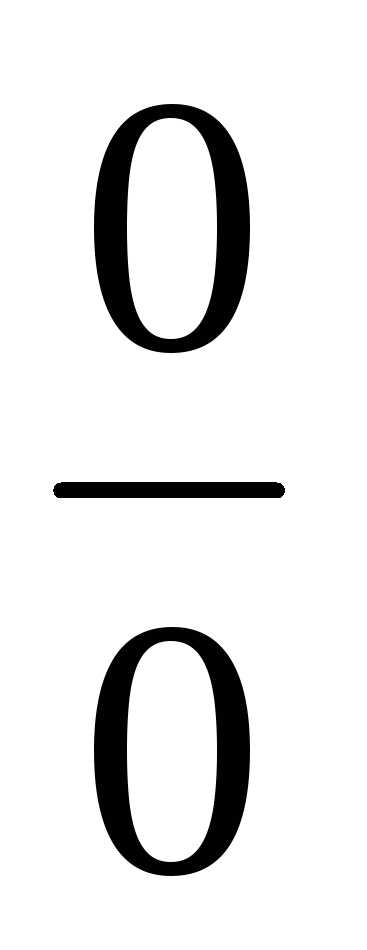
,
в которой числитель или знаменатель
иррациональны, следует надлежащим
образом избавиться от иррациональности.
Первый замечательный предел:
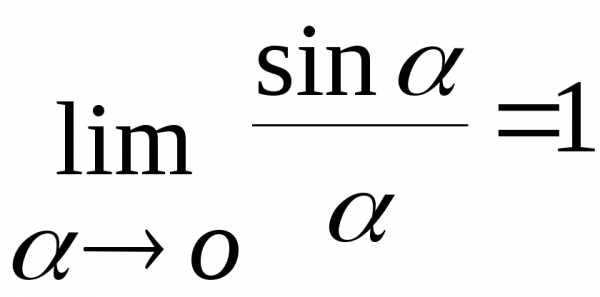
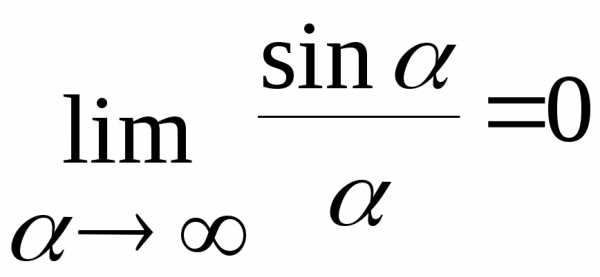
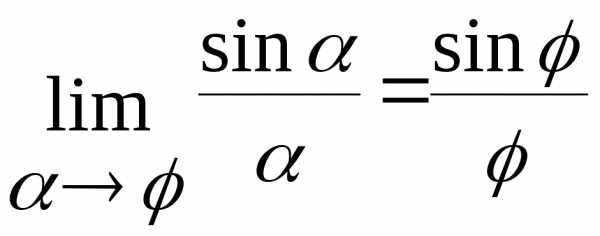
Второй замечательный предел:
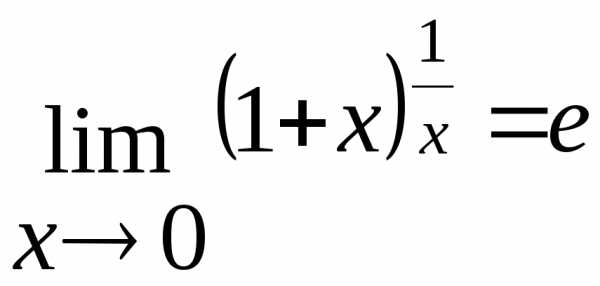
Другие замечательные пределы
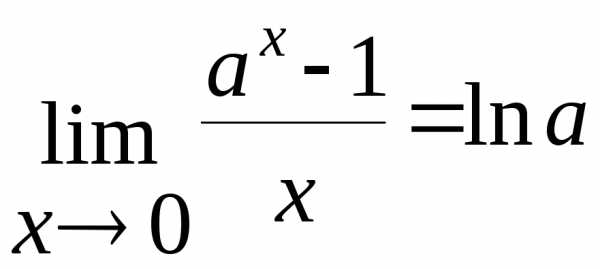
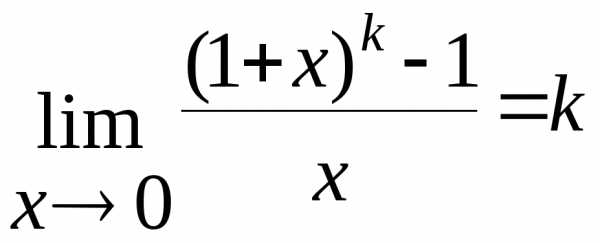
Понижение степени
studfiles.net
Второй замечательный предел. Примеры решения.
Обычно второй замечательный предел записывают в такой форме:
\begin{equation} \lim_{x\to\infty}\left(1+\frac{1}{x}\right)^x=e\end{equation}Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $e\approx{2{,}718281828459045}$. Если сделать замену $t=\frac{1}{x}$, то формулу (1) можно переписать в следующем виде:
\begin{equation} \lim_{t\to{0}}\biggl(1+t\biggr)^{\frac{1}{t}}=e\end{equation}Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $\frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^\infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+\infty$ или $-\infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Пример №1
Вычислить предел $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}$.
Решение
Сразу отметим, что основание степени (т.е. $\frac{3x+1}{3x-5}$) стремится к единице:
$$ \lim_{x\to\infty}\frac{3x+1}{3x-5}=\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{3+\frac{1}{x}}{3-\frac{5}{x}} =\frac{3+0}{3-0} =1. $$При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $\lim_{x\to\infty}(4x+7)=\infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^\infty$. Применим формулу (1) для раскрытия этой неопределённости. Для начала отметим, что в основании степени формулы (1) расположено выражение $1+\frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $\frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $\frac{3x+1}{3x-5}$ под вид $1+\frac{1}{x}$. Для начала прибавим и вычтем единицу:
$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} $$Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
$$ \frac{3x+1}{3x-5}-1 =\frac{3x+1}{3x-5}-\frac{3x-5}{3x-5} =\frac{3x+1-3x+5}{3x-5} =\frac{6}{3x-5}. $$Так как $\frac{3x+1}{3x-5}-1=\frac{6}{3x-5}$, то:
$$ \lim_{x\to\infty}\left(1+ \frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right )^{4x+7} $$Продолжим «подгонку». В выражении $1+\frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+\frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
$$ 1+\frac{6}{3x-5} =1+\frac{1}{\frac{3x-5}{6}} $$Таким образом,
$$ \lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right )^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{4x+7} $$Итак, основание степени, т.е. $1+\frac{1}{\frac{3x-5}{6}}$, подогнано под вид $1+\frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $\frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $\frac{6}{3x-5}$. Итак, имеем:
$$ \lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} $$Выражение $\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}$ полностью соответствует записи второго замечательного предела согласно формуле (1). Следовательно, $\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}}=e$. Учитывая это, получим:
$$ \lim_{x\to\infty}\left (1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =e^{\lim_{x\to\infty}\left(\frac{6}{3x-5}\cdot(4x+7)\right)} $$Отдельно рассмотрим предел в степени:
$$ \lim_{x\to\infty}\left(\frac{6}{3x-5}\cdot(4x+7)\right) =6\cdot\lim_{x\to\infty}\frac{4x+7}{3x-5}=\left|\frac{\infty}{\infty}\right| =6\cdot\lim_{x\to\infty}\frac{4+\frac{7}{x}}{3-\frac{5}{x}} =6\cdot\frac{4}{3} =8 $$Учитывая то, что степень стремится к 8, будем иметь:
$$ e^{\lim_{x\to\infty}\left(\frac{6}{3x-5}\cdot(4x+7)\right)} =e^8 $$Ответ получен, $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}=e^8$. Полное решение без пояснений и промежуточных выкладок выглядит так:
$$ \lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}=\left|1^\infty\right| =\lim_{x\to\infty}\left(1+\frac{3x+1}{3x-5}-1\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{6}{3x-5}\right)^{4x+7}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{4x+7} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}\cdot\frac{6}{3x-5}\cdot(4x+7)} =e^{\lim_{x\to\infty}\left(\frac{6}{3x-5}\cdot(4x+7)\right)} =e^8. $$Ответ: $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}=e^8$.
Пример №2
Найти предел $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}$.
Решение
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $x\to{1}$, т.е. $\lim_{x\to{1}}(7-6x)=7-6\cdot1=1$. Для показателя степени, т.е. $\frac{x}{3x-3}$, получаем: $\lim_{x\to{1}}\frac{x}{3x-3}=\infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $x\to{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $x\to{1}$, то ${x-1}\to{0}$, т.е. $y\to{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $y\to{0}$, получим:
$$ \lim_{x\to{1}}\biggl(7-6x\biggr )^{\frac{x}{3x-3}} =\left|\begin{aligned}&y=x-1;\;x=y+1\\&y\to{0}\end{aligned}\right|=\\ =\lim_{y\to{0}}\biggl(7-6\cdot(y+1)\biggr)^{\frac{y+1}{3\cdot(y+1)-3}} =\lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y} =\lim_{y\to 0}\biggl(1+(-6y)\biggr)^\frac{y+1}{3y} $$Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $\frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $\frac{1}{-6y}$. Домножим показатель степени на выражение $\frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $\frac{-6y}{1}=-6y$:
$$ \lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y}=\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{-\frac{1}{6y}\cdot(-6y)\cdot\frac{y+1}{3y}}=\\ =e^{\lim_{x\to{0}}\left((-6y)\cdot\frac{y+1}{3y}\right)} =e^{\lim_{t\to{0}}\left((-2)\cdot(y+1)\right)} =e^{-2\cdot(0+1)} =e^{-2} =\frac{1}{e^2}. $$Итак, $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}=\frac{1}{e^2}$. Полное решение без пояснений таково:
$$ \lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}} =\left|\begin{aligned}&y=x-1;\;x=y+1\\&y\to{0}\end{aligned}\right| =\lim_{y\to{0}}\biggl(7-6\cdot(y+1)\biggr)^{\frac{y+1}{3\cdot(y+1)-3}} =\lim_{y\to{0}}\biggl(1-6y\biggr)^\frac{y+1}{3y}=\\ =\lim_{y\to{0}}\biggl(1+(-6y)\biggr)^{-\frac{1}{6y}\cdot(-6y)\cdot\frac{y+1}{3y}} =e^{\lim_{x\to{0}}\left((-6y)\cdot\frac{y+1}{3y}\right)} =e^{\lim_{t\to{0}}\left((-2)\cdot(y+1)\right)} =e^{-2\cdot(0+1)} =e^{-2} =\frac{1}{e^2}. $$Ответ: $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}=\frac{1}{e^2}$.
Пример №3
Найти предел $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}$.
Решение
Так как $\lim_{x\to{0}}(\cos{2x})=1$ и $\lim_{x\to{0}}\frac{1}{\sin^2{3x}}=\infty$ (напомню, что $\sin{u}\to{0}$ при $u\to{0}$), то мы имеем дело с неопределённостью вида $1^\infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
$$ \lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}} =|1^\infty| =\lim_{x\to{0}}\biggl(1+\cos{2x}-1\biggr)^{\frac{1}{\sin^2{3x}}} $$Так как $\sin^2x=\frac{1-\cos{2x}}{2}$, то $\cos{2x}-1=-2\sin^2x$, поэтому:
$$ \lim_{x\to{0}}\biggl(1+\cos{2x}-1\biggr)^{\frac{1}{\sin^2{3x}}} =\lim_{x\to{0}}\biggl(1+\left(-2\sin^2x\right)\biggr)^{\frac{1}{-2\sin^2x}\cdot(-2\sin^2x)\cdot\frac{1}{\sin^2 3x}}=\\ =e^{\lim_{x\to{0}}\left(\left(-2\sin^2x\right)\cdot\frac{1}{\sin^2{3x}}\right)} =e^{-2\cdot\lim_{x\to{0}}\frac{\sin^2x}{\sin^2{3x}}} =e^{-2\cdot\frac{1}{9}} =e^{-\frac{2}{9}} $$Подробное описание того, как находить предел $\lim_{x\to{0}}\frac{\sin^2x}{\sin^2{3x}}$ дано в соответствующей теме.
Ответ: $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}=e^{-\frac{2}{9}}$.
Пример №4
Найти предел $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)$.
Решение
Так как при $x>0$ имеем $\ln(x+1)-\ln{x}=\ln\left(\frac{x+1}{x}\right)$, то:
$$ \lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) $$Раскладывая дробь $\frac{x+1}{x}$ на сумму дробей $\frac{x+1}{x}=1+\frac{1}{x}$ получим:
$$ \lim_{x\to+\infty}\left(x\cdot\ln\left(\frac{x+1}{x}\right)\right) =\lim_{x\to+\infty}\left(x\cdot\ln\left(1+\frac{1}{x}\right)\right) =\lim_{x\to+\infty}\left(\ln\left(\frac{x+1}{x}\right)^x\right) =\ln{e} =1. $$Ответ: $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)=1$.
Пример №5
Найти предел $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}$.
Решение
Так как $\lim_{x\to{2}}(3x-5)=6-5=1$ и $\lim_{x\to{2}}\frac{2x}{x^2-4}=\infty$, то мы имеем дело с неопределенностью вида $1^\infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=x-2;\;x=t+2\\&t\to{0}\end{aligned}\right| =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{2t+4}{t^2+4t}}=\\ =\lim_{t\to{0}}\biggl(1+3t\biggr)^{\frac{1}{3t}\cdot 3t\cdot\frac{2t+4}{t^2+4t}} =e^{\lim_{t\to{0}}\left(3t\cdot\frac{2t+4}{t\cdot(t+4)}\right)} =e^{\lim_{t\to{0}}\left(3\cdot\frac{2t+4}{t+4}\right)} =e^3. $$Можно решить данный пример и по-иному, используя замену: $t=\frac{1}{x-2}$. Разумеется, ответ будет тем же:
$$ \lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}} =\left|\begin{aligned}&t=\frac{1}{x-2};\;x=\frac{2t+1}{t}\\&t\to\infty\end{aligned}\right| =\lim_{t\to\infty}\biggl(1+\frac{3}{t}\biggr)^{t\cdot\frac{4t+2}{4t+1}}=\\ =\lim_{t\to\infty}\biggl(1+\frac{1}{\frac{t}{3}}\biggr)^{\frac{t}{3}\cdot\frac{3}{t}\cdot\frac{t\cdot(4t+2)}{4t+1}} =e^{\lim_{t\to\infty}\left(\frac{3}{t}\cdot\frac{t\cdot(4t+2)}{4t+1}\right)} =e^{\lim_{t\to\infty}\left(\frac{3\cdot(4t+2)}{4t+1}\right)} =e^3. $$Ответ: $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}=e^3$.
Пример №6
Найти предел $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} $.
Решение
Выясним, к чему стремится выражение $\frac{2x^2+3}{2x^2-4}$ при условии $x\to\infty$:
$$ \lim_{x\to\infty}\frac{2x^2+3}{2x^2-4} =\left|\frac{\infty}{\infty}\right| =\lim_{x\to\infty}\frac{2+\frac{3}{x^2}}{2-\frac{4}{x^2}} =\frac{2+0}{2-0}=1. $$Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела:
$$ \lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} =|1^\infty| =\lim_{x\to\infty}\left(1+\frac{2x^2+3}{2x^2-4}-1\right)^{3x} =\lim_{x\to\infty}\left(1+\frac{7}{2x^2-4}\right)^{3x}=\\ =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{3x} =\lim_{x\to\infty}\left(1+\frac{1}{\frac{2x^2-4}{7}}\right)^{\frac{2x^2-4}{7}\cdot\frac{7}{2x^2-4}\cdot 3x} =e^{\lim_{x\to\infty}\frac{21x}{2x^2-4}} =e^0 =1. $$Ответ: $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x}=1$.
math1.ru