Куда направлено ускорение?
Ускорение – это быстрота изменения скорости. Эта величина векторная, она имеет свое направление и измеряется в м/с 2 (в СИ).
Для того чтобы понять, куда направлен вектор ускорения, необходимо сначала определить, какой вид движения имеет точка, за которой мы следим.
Виды движения
Если это движение по прямой и скорость увеличивается.
Ускорение будет направлено туда же, куда направлена скорость. Их векторы будут совпадать.
Если это движение по прямой и скорость уменьшается.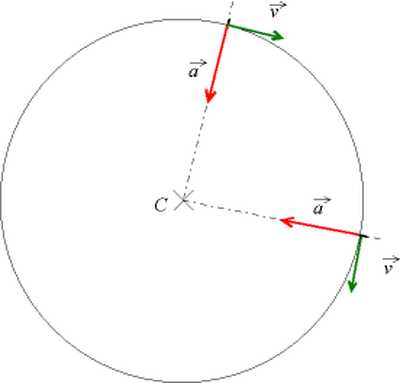
Вектор ускорения будет противоположен вектору скорости.
Если это движение по прямой, скорость не меняется.
Ускорение будет равно нулю и никуда не будет направлено.
Движение по окружности с равномерной скоростью.
Если точка движется по кругу и скорость не меняется, то ускорение здесь называется центростремительным (или нормальным) и его вектор направлен к центру окружности.
Движение по окружности с меняющейся скоростью.
В таком случае появляется еще одно ускорение – касательное (или тангенциальное). Оно 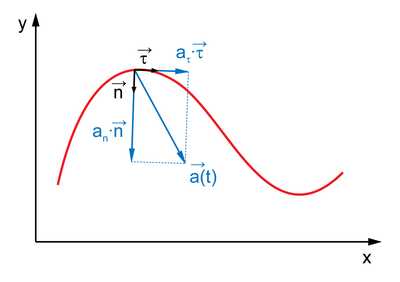
Обратите внимание, что в каждой точке движения по окружности вектор полного ускорения будет менять свое направление.
Кроме направления, ускорение имеет еще и свою величину. О том, какие формулы использовать для того, чтобы рассчитать ускорение, узнайте здесь: Как найти ускорение?
Вектор – касательное ускорение – Большая Энциклопедия Нефти и Газа, статья, страница 1
Вектор – касательное ускорение
Cтраница 1
Вектор касательного ускорения а м направлен по скорости, а вектор нормального ускорения апм направлен по радиусу к центру О. [1]
Вектор касательного ускорения а ( м будет действовать по направлению скорости, а вектор нормального ускорения апм направлен по радиусу к центру О. [2]
Заметим, что вектор касательного ускорения проектируется только на касательную к траектории в натуральную величину со знаком плюс или минус. Вектор нормального ускорения проектируется только на главную нормаль к траектории и только со знаком плюс. [3]
Q, то – векторы касательного ускорения и скорости направлены в одну сторону, и движение будет ускоренным. [4]
В ускоренном движении направления векторов касательного ускорения и скорости совпадают, в замедленном – не совпадают. [6]
Следовательно, в этот момент времени вектор касательного ускорения Wt направлен по касательной к траектории в сторону, противоположную движению точки. [7]
Чтобы определить направление этого ускорения, необходимо вектор касательного ускорения nta9 перенести в точку А3 кулисы. В положении 5 механизма угловое ускорение направлено в сторону, противоположную вращению часовой стрелки. За его положительное значение принято направление ускорения, совпадающее с направлением вращения часовой стрелки. [8]
Если at – – jr §, то векторы касательного ускорения и скорости направлены в одну сторону и движение будет ускоренным. [9]
Если же модуль скорости уменьшается с течением времени, то ее производная по времени отрицательна ( ат 0), и вектор касательного ускорения ат направлен по касательной к траектории в сторону против движения. Такое движение называют замедленным. [10]
В криволинейном переменном движении ( рис. 2.25, б) вектор нормального ускорения / норм направлен по радиусу круга кривизны к центру, вектор касательного ускорения / нас и вектор скорости V направлены в одну сторону, если движение ускоренное, и в противоположные стороны – если замедленное. [11]
Векторы нормальных ускорений направлены по нормали к центру кривизны соответствующей траектории относительного движения точек.
Вычисление работы сил тяжести и сил инерции грузов не требует пояснений. Умножая вектор касательного ускорения гг каждой частицы блока на массу т частицы и изменив направление на обратное, получим силы инерции частиц. [13]
Он направлен по касательной к траектории. Если скорость ( модуль) увеличивается с течением времени, то производная dv / dt положительна ( ат0), и вектор касательного ускорения – ат направлен по вектору скорости. Такое движение называют ускоренным. [14]
Напомним, что знак направляющего косинуса определяется знаком числителя. Если ш и Е имеют одинаковые знаки ( как в данной задаче), то тело вращается ускоренно и направление касательных ускорений его точек совпадает с направлением их скоростей, если же знаки со и е различны, то вращение замедленное и векторы касательных ускорений и скоростей точек направлены в противоположные стороны. [15]
Страницы: 1
8.3. Вектор скорости точки
Одной из кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Скорость точки – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Введем сначала понятие о средней скорости
точки за какой-нибудь промежуток времени.
Пусть движущаяся точка находится в
момент времени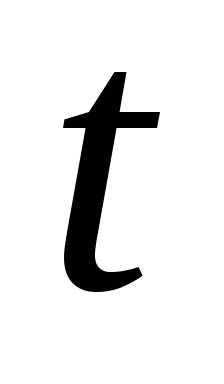
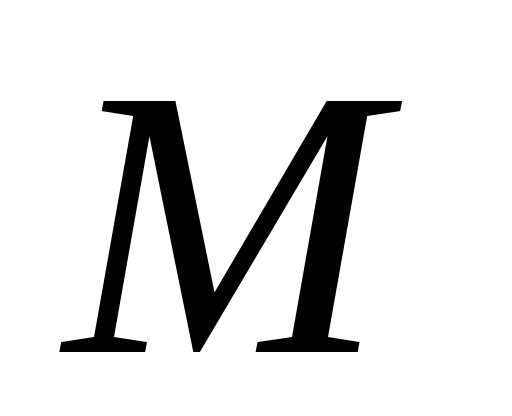 (рис.
1.3), определяемом радиус-вектором
(рис.
1.3), определяемом радиус-вектором ,
а в момент
,
а в момент приходит в положение
приходит в положение ,
определяемое вектором
,
определяемое вектором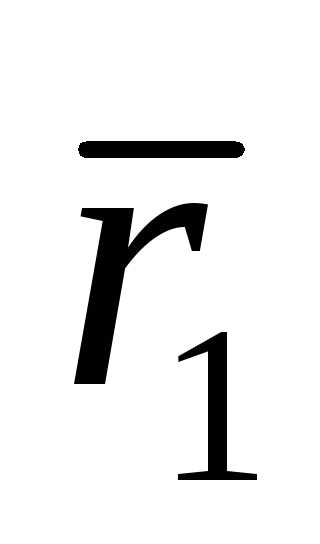 .
Тогда перемещение точки за промежуток
времени
.
Тогда перемещение точки за промежуток
времени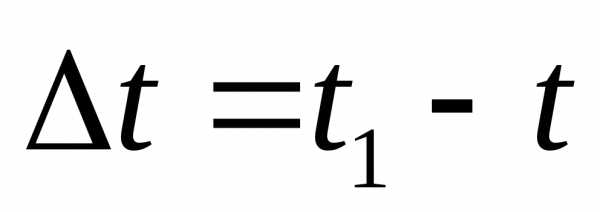
 ,
который будем называтьвектором
перемещения точки.Этот вектор
направлен по хорде, если точка движется
криволинейно (рис. 1.3,а), и вдоль самой
траектории
,
который будем называтьвектором
перемещения точки.Этот вектор
направлен по хорде, если точка движется
криволинейно (рис. 1.3,а), и вдоль самой
траектории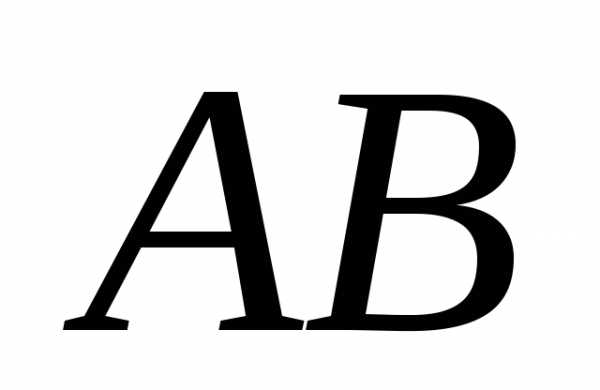 ,
когда движение является прямолинейным
(рис. 1.3,б).
,
когда движение является прямолинейным
(рис. 1.3,б). 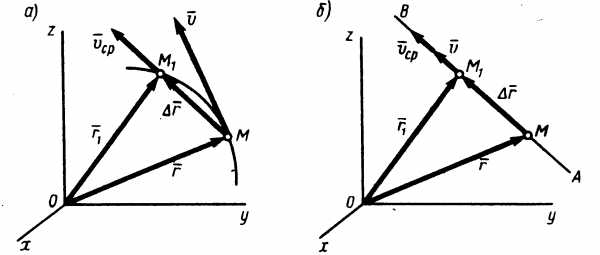
Рисунок 1.3
Из треугольника 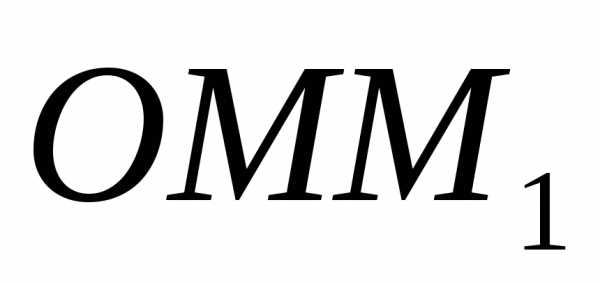 ,
видно, что,
следовательно,
,
видно, что,
следовательно,
.
Отношение вектора перемещения точки к
соответствующему промежутку времени
дает векторную величину, называемую
средней по модулю и направлению скоростью
точки за промежуток времени  :
:
| (7) |
Направлен вектор 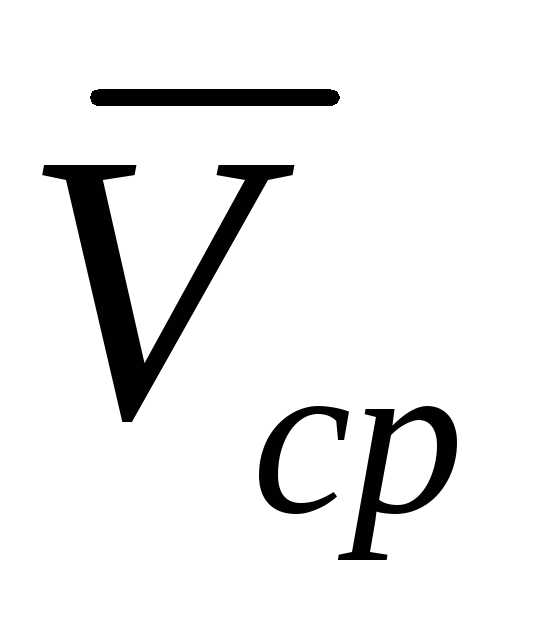 так
же, как и вектор
так
же, как и вектор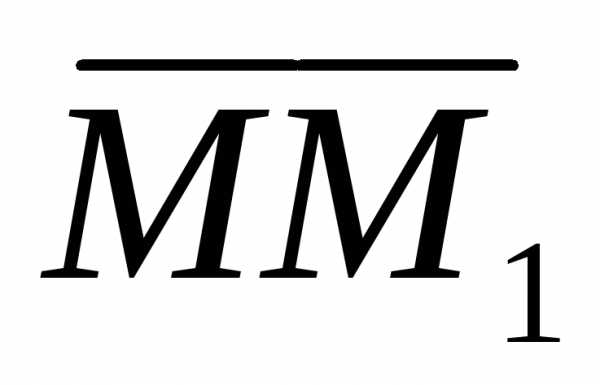 ,
т.е. при криволинейном движении вдоль
хорды
,
т.е. при криволинейном движении вдоль
хорды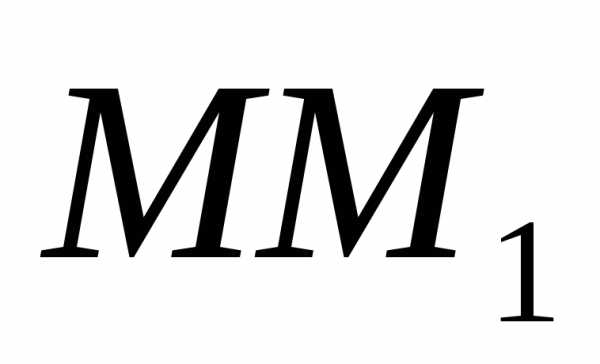 ,
в сторону движения точки, а при
прямолинейном движении – вдоль самой
траектории.
,
в сторону движения точки, а при
прямолинейном движении – вдоль самой
траектории.
Очевидно, что чем меньше промежуток
времени 
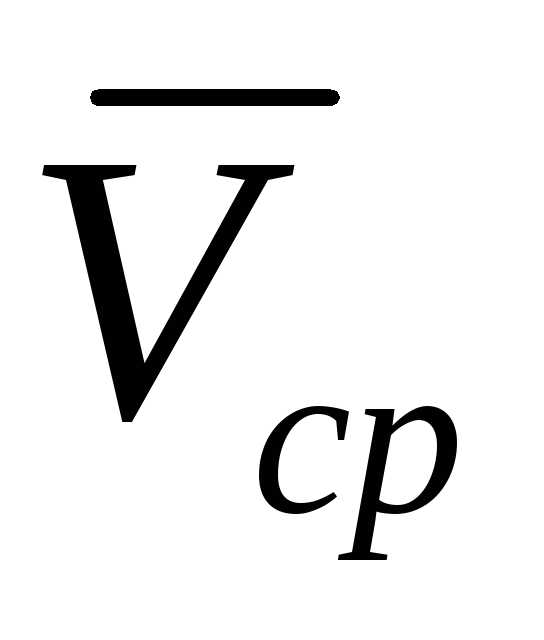 будет точнее характеризовать движение
точки.
будет точнее характеризовать движение
точки. Поэтому скоростью точки  в данный момент времени
в данный момент времени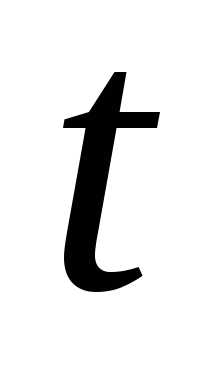 называется векторная величина
называется векторная величина ,
к которой стремится скорость
,
к которой стремится скорость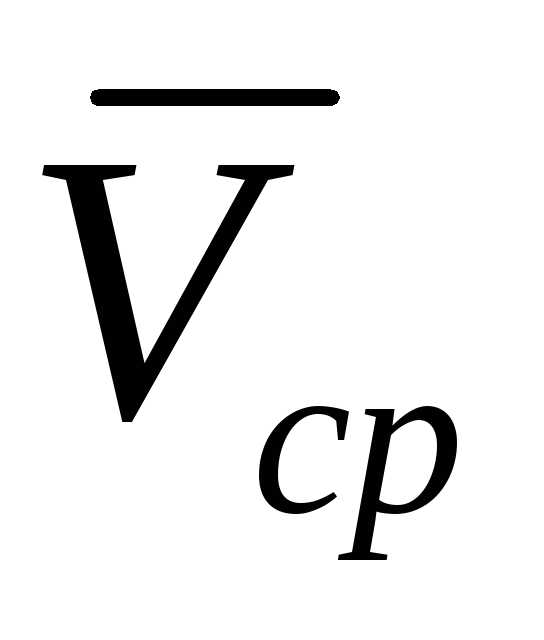 при
стремлении промежутка времени
при
стремлении промежутка времени к нулю.
к нулю.
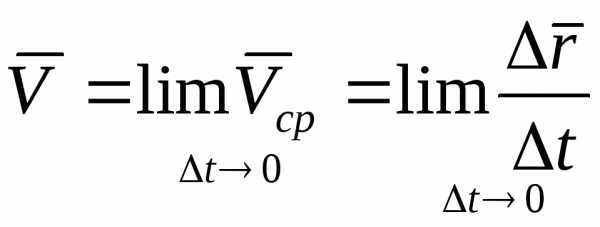 .
.
Предел отношения 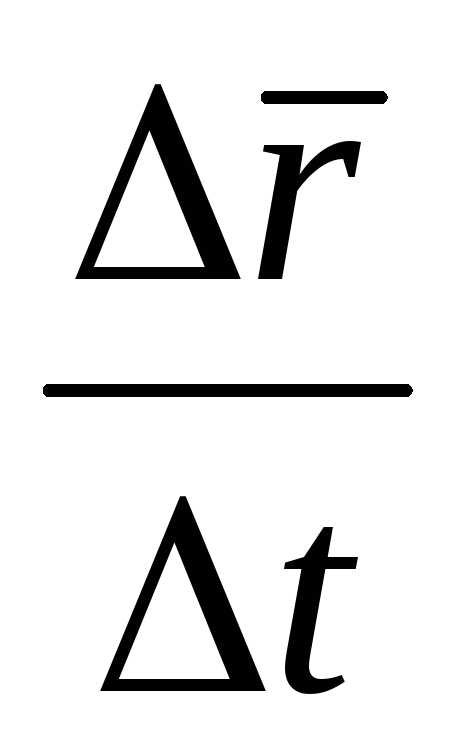 при
при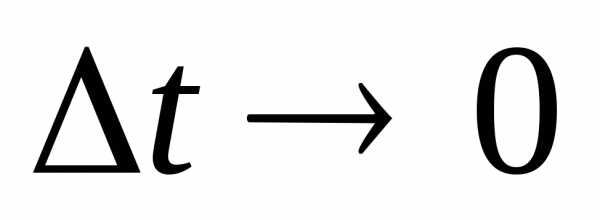 представляет собой первую производную
от вектора
представляет собой первую производную
от вектора по аргументу
по аргументу 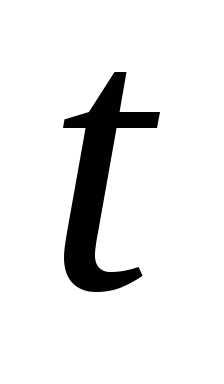 и обозначается
и обозначается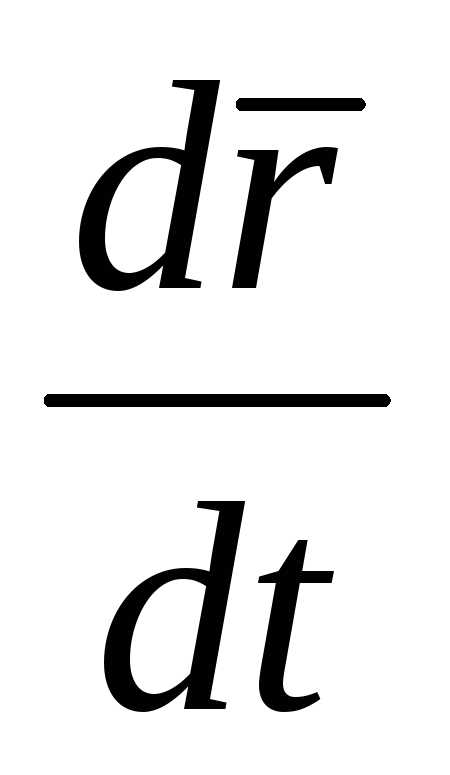 ,
тогда
,
тогда
| (8) |
Итак, вектор скорости точки в данный
момент времени равен первой производной
от радиус-вектора точки по времени. Так
как предельным направлением секущей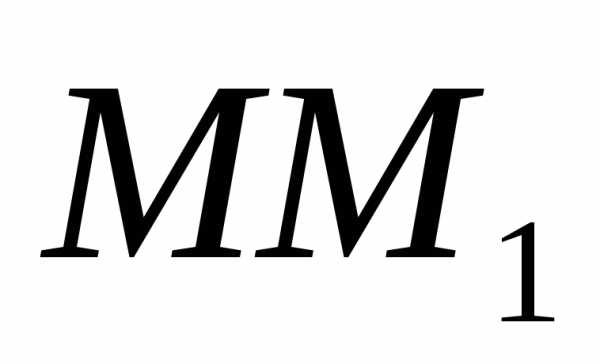 является
касательная, то вектор скорости в данный
момент времени направлен по касательной
к траектории точки в сторону движения.
является
касательная, то вектор скорости в данный
момент времени направлен по касательной
к траектории точки в сторону движения.
Размерность
скорости  ,
т.е..
Единицы измерения
,
т.е..
Единицы измерения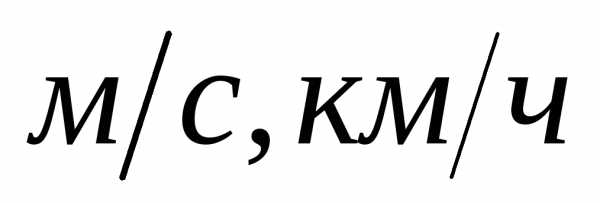 .
.
8.4. Вектор ускорения точки
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости.
Пусть в некоторый момент времени 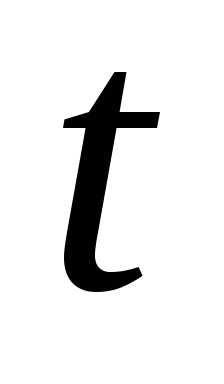 движущаяся
точка находится в положении
движущаяся
точка находится в положении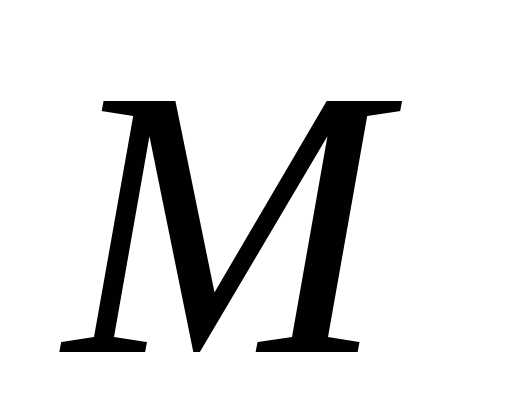 и имеет скорость
и имеет скорость (рис.1.4),
а в момент времени
(рис.1.4),
а в момент времени приходит
в точку
приходит
в точку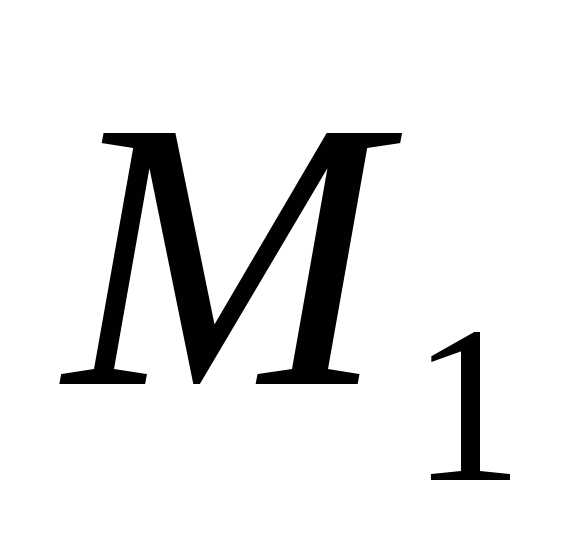 и
имеет
и
имеет
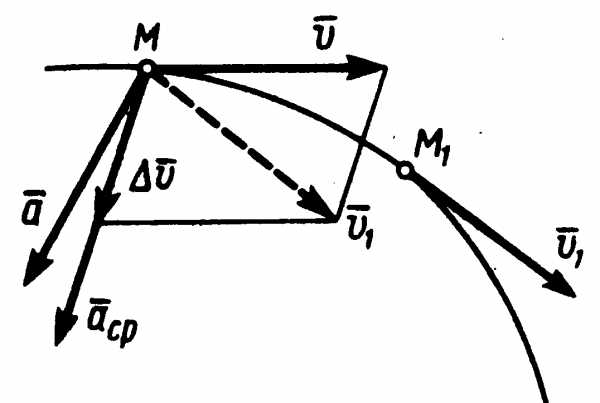
Рисунок 1.4
скорость  .
Тогда за промежуток времени
.
Тогда за промежуток времени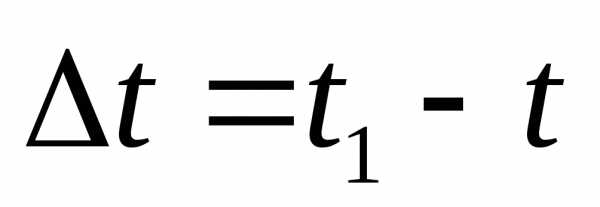 скорость изменится на.
Для построения вектора
скорость изменится на.
Для построения вектора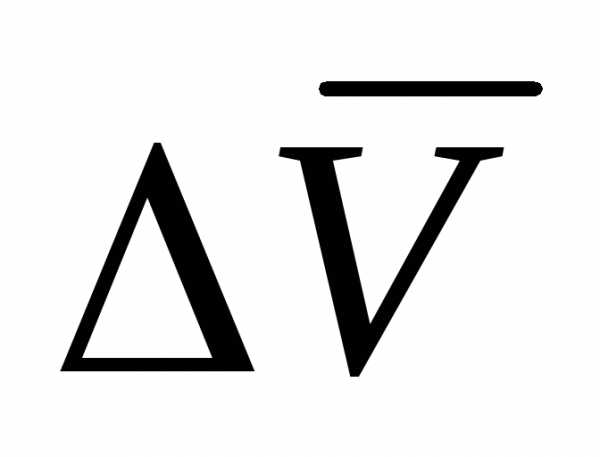 отложим
от точки
отложим
от точки вектор,
равный
вектор,
равный ,
и построим параллелограмм, в котором
диагональю будет
,
и построим параллелограмм, в котором
диагональю будет , а одной из сторон
, а одной из сторон .
Тогда, очевидно,
.
Тогда, очевидно,
вторая сторона и будет изображением
вектора 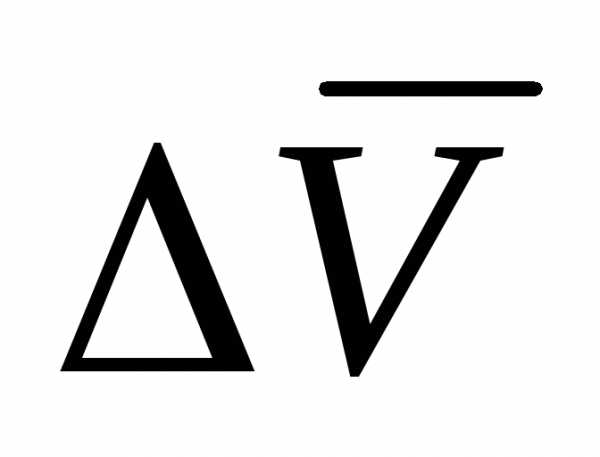 .
Заметим, что вектор
.
Заметим, что вектор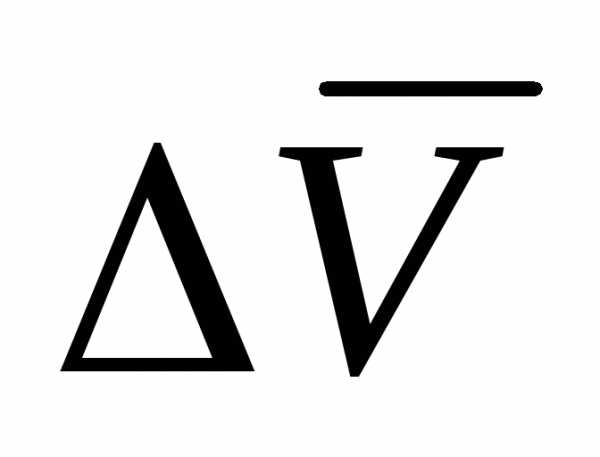 всегда
направлен в сторону вогнутости траектории.
всегда
направлен в сторону вогнутости траектории.
Отношение 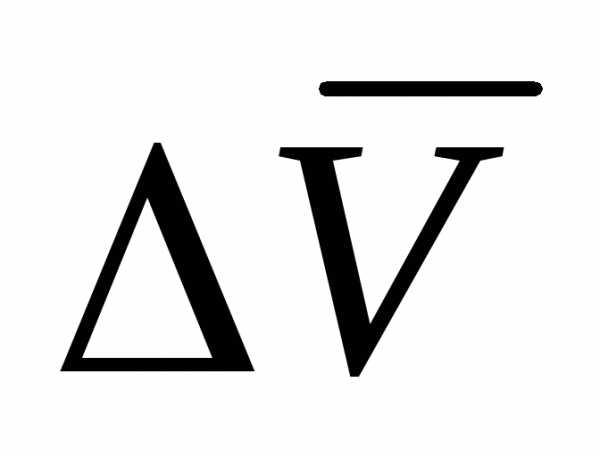 к
к определяет вектор среднего ускорения
точки за промежуток времени
определяет вектор среднего ускорения
точки за промежуток времени .
.
| (9) |
Вектор среднего ускорения имеет то же
направление, что и вектор 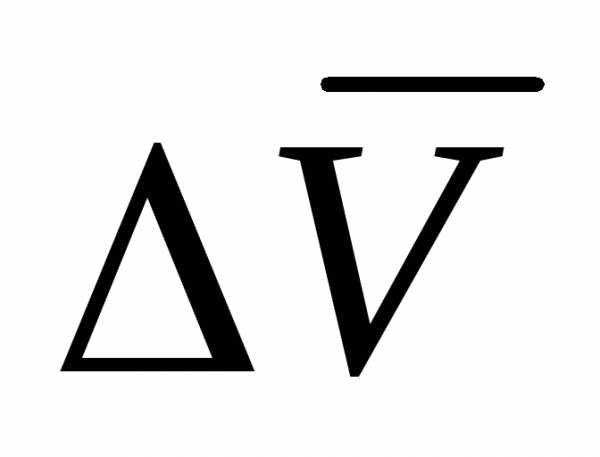 ,
т.е. направлен в сторону вогнутости
траектории. Тогда
,
т.е. направлен в сторону вогнутости
траектории. Тогда
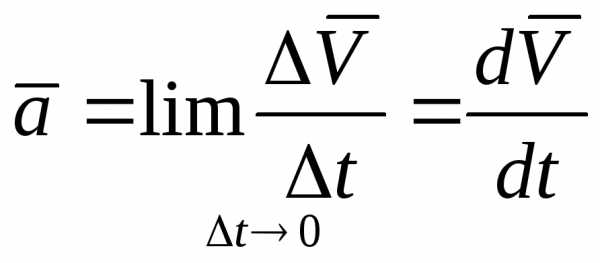
или с учетом равенства (8),
| (10) |
Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.
Размерность 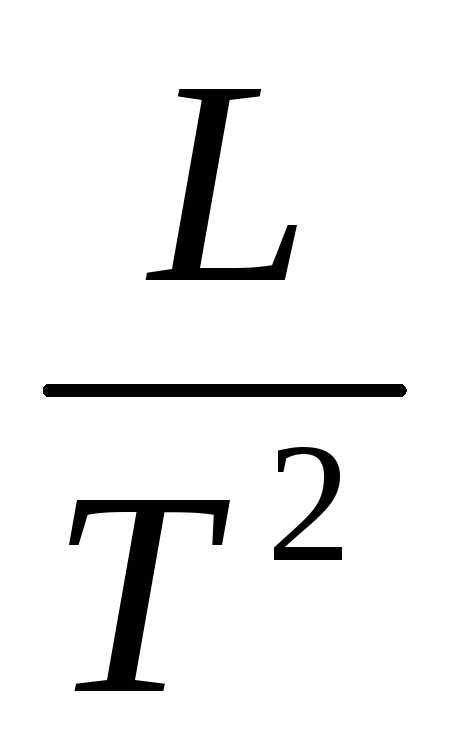 ,
т.е.
,
т.е.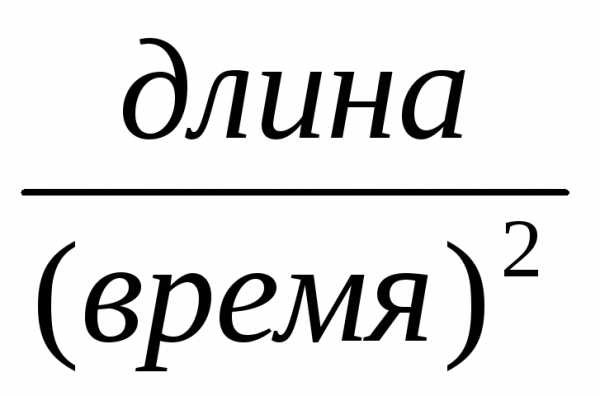 .
Единица измерения
.
Единица измерения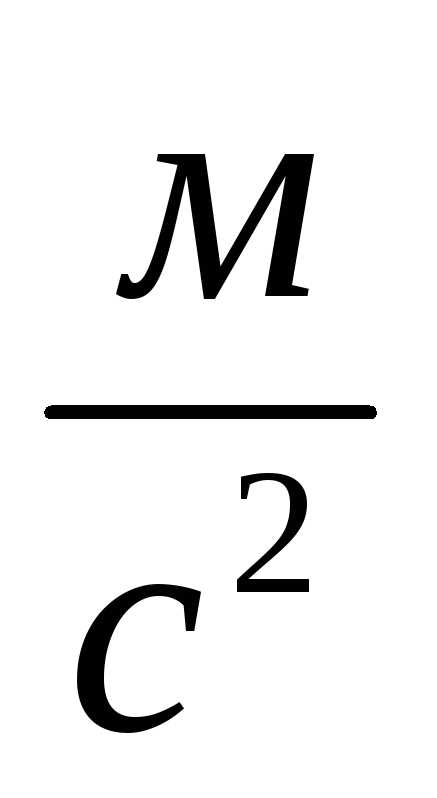 .
.
Вектор  направлен, также как и вектор
направлен, также как и вектор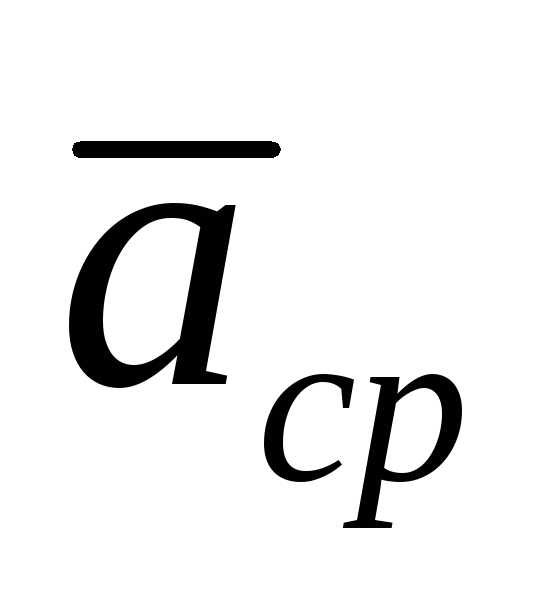 ,
лежит в плоскости этой кривой и направлен
в сторону её вогнутости.
,
лежит в плоскости этой кривой и направлен
в сторону её вогнутости.
studfiles.net

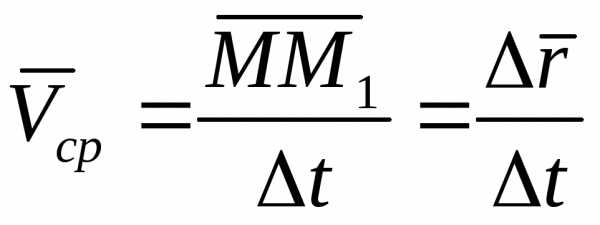
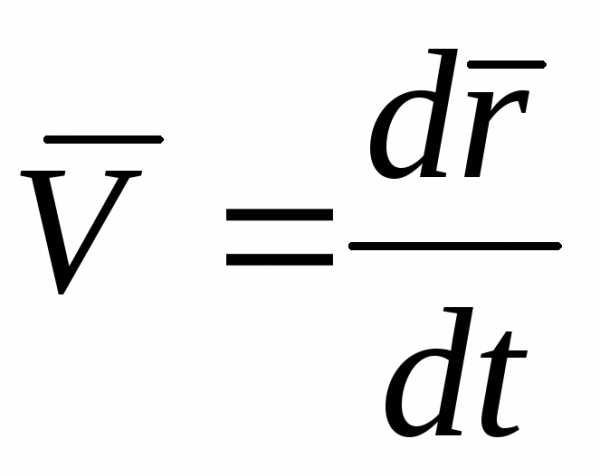 .
.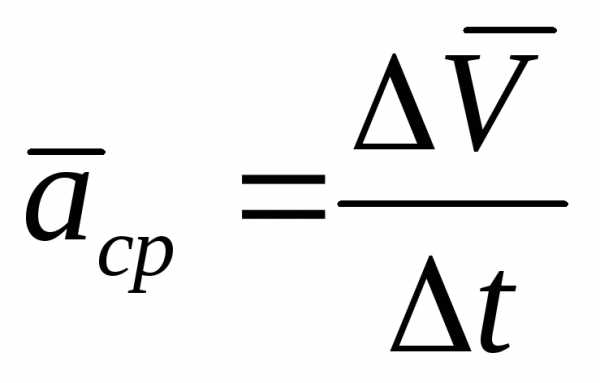 .
.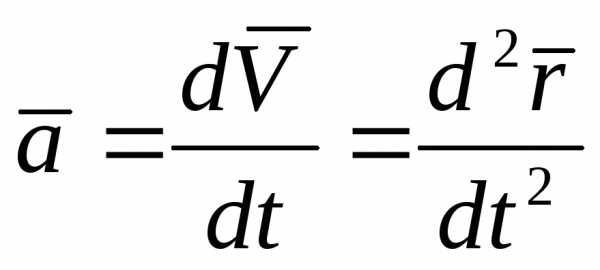 .
.