физические уравнения — с русского на английский
См. также в других словарях:
Уравнения Эйлера — Лагранжа — Уравнения Эйлера Лагранжа (в физике также уравнения Лагранжа Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти… … Википедия
Уравнения Прока — Уравнения Прока обобщение уравнений Максвелла, призванное описывать массивные частицы со спином 1. Уравнения Прока обычно записываются в виде , где антисимметричный тензор электромагнитного поля … Википедия
Уравнения Рауса — Уравнения Рауса дифференциальные уравнения движения механической системы в переменных Рауса. Предложены Э. Раусом (англ.)русск. в 1867 г. Для системы с s степенями свободы, находящейся под действием потенциальных сил, уравнения… … Википедия
Физические постоянные — физические константы, фундаментальные постоянные, мировые постоянные, численные коэффициенты, входящие в уравнения физических законов и являющиеся в ряде случаев масштабными характеристиками физических процессов и микрообъектов. К Ф. п.… … Большая советская энциклопедия
Уравнения Максвелла — Классическая электродинамика … Википедия
Уравнения мелкой воды — Механика сплошных сред … Википедия
Уравнения Навье — Механика сплошных сред … Википедия
Уравнения Гамильтона — (также называемые каноническими уравнениями) в физике и математике система дифференциальных уравнений: где точкой над p и q обозначена производная по времени. Система состоит из 2N дифференциальных уравнений первого порядка (j = 1, 2, …, N) … Википедия
Уравнения Эйлера (механика) — У этого термина существуют и другие значения, см. Список объектов, названных в честь Леонарда Эйлера#Уравнения. В физике, Уравнения Эйлера описывают вращение твердого тела в системе координат, связанной с самим телом. Вывод В системе отсчёта… … Википедия
Уравнения Аппеля — В классической механике уравнения Аппеля рассматривают как альтернативную формулировку общих уравнений движения, предложенных Ньютоном. Выписаны Полем Аппелем в 1900 [1]. Несмотря на то, что эти уравнения полностью эквивалентны уравнениям,… … Википедия
Уравнения Эйлера — У этого термина существуют и другие значения, см. Список объектов, названных в честь Леонарда Эйлера#Уравнения. В физике, Уравнения Эйлера описывают вращение твердого тела в системе координат, связанной с самим телом. Вывод В системе отсчёта… … Википедия
Книги
- Неголономные, фрактальные и связанные структуры в релятивистских сплошных средах, электродинамике, квантовой механике и космологии. Книга 2, Подосенов С.А.. В книге, состоящей из трех томов, рассмотрено взаимодействие голономных, неголономных, фрактальных и связанных структур с различными полями, используемыми в современных задачах физики. Во… Подробнее Купить за 757 руб
- Неголономные, фрактальные и связанные структуры в релятивистских сплошных средах, электродинамике, квантовой механике и космологии. Книга 2. Силовые поля в связанных и неголономных структурах, С. А. Подосенов, А. А. Потапов, Дж. Фоукзон, Е. Р. Менькова. В книге, состоящей из трех томов, рассмотрено взаимодействие голономных, неголономных, фрактальных и связанных структур с различными полями, используемыми в современных задачах физики. Во… Подробнее Купить за 607 грн (только Украина)
- Физика. Кванты. Строение и физические свойства вещества, Юрий Рахштадт. Настоящее пособие соответствует программе учебного курса «Физика» факультета информатики и экономики. Оно призвано помочь студентам освоить теоретический курс, выработать навыки решения задач… Подробнее Купить за 576 руб электронная книга
translate.academic.ru
Физические уравнения связи напряжений и деформаций
Основная задача: дать физические уравнения связи напряжений и деформаций и замкнуть систему дифференциальных и конечных уравнений теории пластичности.
1. Начальные сведения о механических свойствах деформируемых материалов
1. Гипотеза об изотропии
Достаточно крупные изделия из металла, которые подвергаются обработке пластической деформацией, состоят из множества мелких зерен – кристаллов, которые, как правило, имеют различную ориентацию кристаллографических плоскостей. Механические свойства таких изделий, несмотря на анизотропию (различие) свойств в отдельном зерне, примерно одинаковы в различных направлениях (статистически усреднены), поэтому такие тела можно назвать квазиизотропными. Квазиизотропия сохраняется по мере уменьшения размера рассматриваемого элементарного объема до тех пор, пока этот элементарный объем содержит достаточное количество различным образом ориентированных кристаллов.
В прикладной теории пластичности, рассматривающей технологические задачи деформации металлов, принимается, условно, что материал на любом уровне размера элементарного объема обладает изотропными механическими свойствами. Это условие называется гипотезой об изотропии сплошной среды.
Конечно, результаты расчета НДС будут справедливы лишь на макроскопическом уровне: механические переменные будут, строго говоря, найдены при достаточно точном решении задачи не в каждой точке деформируемого металла, а будут найдены усредненные значения для элементарного (в макросмысле) объема. Этот объем настолько мал, чтобы имели смысл операции дифференцирования, но и настолько велик, чтобы содержал, по крайней мере, несколько различным образом ориентированных кристаллов.
Гипотеза об изотропии существенно упрощает математический аппарат расчета НДС при решении технологических задач, однако в ряде случаев она неприемлима.
2. Инвариантное представление физических уравнений связи
напряжений и деформаций
Тензор
скорости деформации 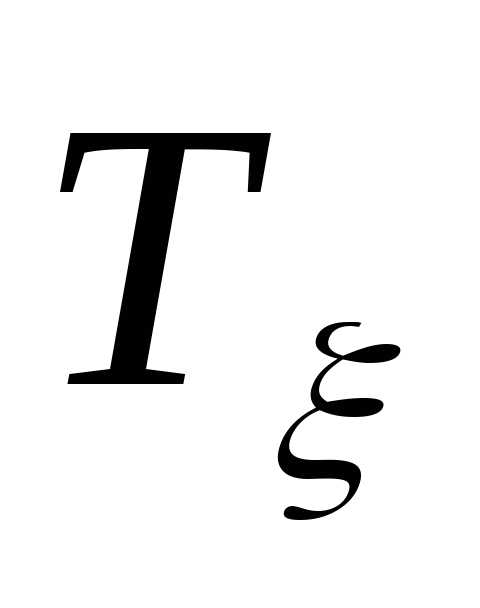 и
тензор напряжений
и
тензор напряжений 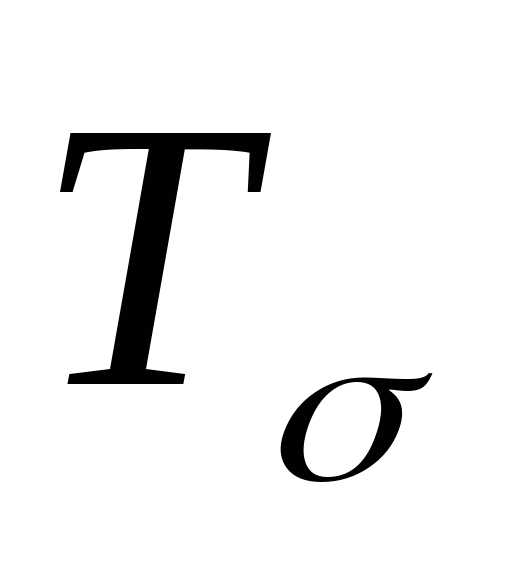 были разложены на шаровой тензор и
девиатор. Шаровой тензор напряжений
содержит одну существенную величину
– среднее ( гидростатическое ) напряжение
.
были разложены на шаровой тензор и
девиатор. Шаровой тензор напряжений
содержит одну существенную величину
– среднее ( гидростатическое ) напряжение
.
Аналогично, шаровой тензор скорости деформации и шаровой тензор приращения деформации имеют также по одной существенной величине и d (скорость относительного изменения объема и приращение относительного изменения объема).
Девиатор
напряжений 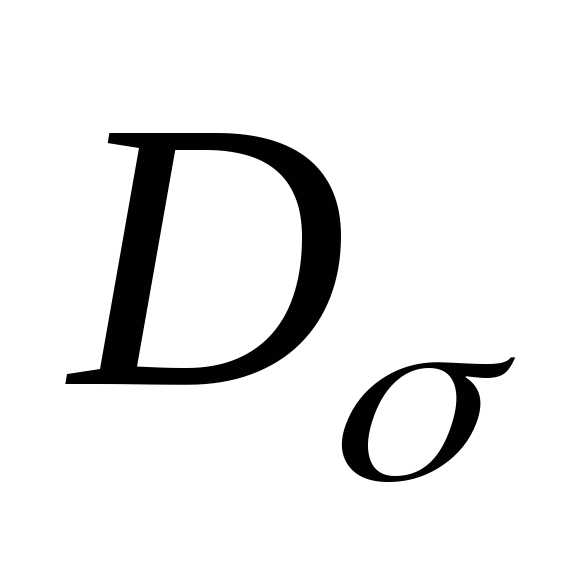 и
девиатор скорости деформации
и
девиатор скорости деформации  или девиатор приращения деформации
или девиатор приращения деформации 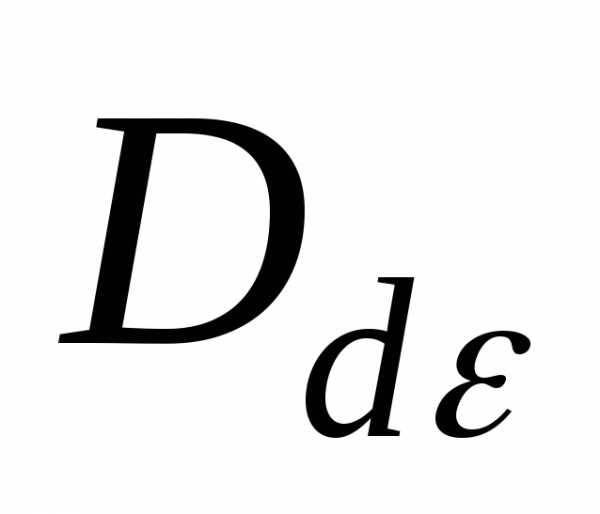 имеют два отличных от нуля инварианта.
имеют два отличных от нуля инварианта.
Вторые инварианты, как уже отмечалось, можно представить в виде интенсивности касательных напряжений
Итак, задача состоит в том, чтобы, основываясь на опыте и фундаментальных положениях термодинамики, установить зависимости между , или d ; Т , Н или d ; .
studfiles.net
Геометрическое физическое уравнение – Большая Энциклопедия Нефти и Газа, статья, страница 1
Геометрическое физическое уравнение
Cтраница 1
Решая совместно статические, геометрические и физические уравнения, находим неизвестные усилия. [2]
Приводятся уравнения статики, геометрические и физические уравнения. На основе общих уравнений моментной теории получены уравнения для расчета тонких торсовых оболочек. [3]
Тогда необходимость в привлечении геометрических и физических уравнений отпадет и достаточно рассмотреть одну только статическую сторону задачи. Так именно и будет обстоять дело с выводом формулы для т при изгибе. [4]
Тогда необходимость в привлечении геометрических и физических уравнений отпадет и достаточно рассмотреть одну только статическую сторону задачи. Так именно и будет обстоять дело с выводом формулы для т при изгибе. [5]
Использование одной группы из множества статических, геометрических и физических уравнений в качестве дополнительных условий, накладываемых на полный функционалЭ м ( р, а, е), можно проиллюстрировать схемой, аналогичной рис. 3.3, заменив на нем и на ф, е на а и а на е и поменяв местами геометрические и статические уравнения. [6]
Для решения этой задачи могут быть использованы приведенные выше системы статических, геометрических и физических уравнений теории упругости. [7]
Как известно, общие уравнения механики сплошной среды включают в себя статические, геометрические и физические уравнения. [8]
Для составления граничных условий в верхнем узле сопряжения корпуса с упругим кольцом жесткости необходимо иметь уравнения равновесия, геометрические и физические уравнения криволинейного стержня. [9]
Решение уравнений (21.3) и (21.5) относится к статической задаче безмоментной теории оболочек вращения при осесимметричной нагрузке, Чтобы найти деформации и перемещения в оболочке, к этим уравнениям следует добавить геометрические и физические уравнения. [10]
Это уравнение отличается от уравнения равновесия (16.1), полученного при расчете толстостенного цилиндра, только слагаемым ( У / е) и. Геометрические и физические уравнения не отличаются от уравнений (16.2) – (16.4), полученных для толстостенного цилиндра. [11]
В данной главе построена и рассмотрена полная система уравнений строительной механики стержневых систем. Эта система состоит из статических, геометрических и физических уравнений. Показано, что расчет, любой стержневой системы, как статически определимой, так и статически неопределимой, сводится к решению системы уравнений, которая строится по двум матрицам, одна из которых получается путем вырезания узлов, а вторая является квазидиагональной и строится по готовым формулам. [12]
Реакциями конструкции являются усилия Л в стержнях и угол поворота ф жесткого бруса. Для их определения, как обычно, рассмотрим статические, геометрические и физические уравнения. [13]
Решение системы уравнений (10.1) и (10.2) относится к статической задаче безмоментной теории оболочек вращения при осесимметричной нагрузке. Чтобы найти деформации и перемещения в оболочке, к этим уравнениям следует добавить геометрические и физические уравнения. [15]
Страницы: 1 2
www.ngpedia.ru
Физические уравнения, реферат — allRefers.ru
Физические уравнения – раздел Физика, ШАРНИРНО-СТЕРЖНЕВЫХ СИСТЕМ
Физические уравнения для шарнирно-стержневой системы устанавливают взаимосвязь между удлинениями стержней и внутренними усилиями. Для линейно упругого материала физические уравнения имеют форму линейных алгебраических уравнений и основываются на законе Гука s = Еe, где s – нормальное напряжение при одноосном растяжении (сжатии), Е – модуль Юнга, e – относительная линейная деформация. Умножая записанное равенство на площадь F поперечного сечения стержня и учитывая, что e = , получаем:
, (5)
где константу k можно назвать коэффициентом жесткости стержня.
Запишем уравнение (5) для каждого стержня:
N1 = k1 D1, N2 = k2 D2, …, Nm = km Dm.
Объединение m равенств в одно векторное уравнение дает физическое уравнение
N =d, (6)
в котором матрица называется матрицей «внутренней» жесткости системы; она имеет диагональный вид:
, (i = 1, 2, …, m). (7)
Уравнение (6) может быть записано в обратной форме d =N,
где матрица обратна матрице (=) и называется матрицей «внутренней» податливости системы:
. (8)
7 Полная система уравнений и методы её решения
Полная система уравнений состоит из уравнений равновесия узлов, геометрического и физического уравнений. Запишем физическое уравнение первым:
Объединим три уравнения в одно с вектором неизвестных [d,q,N]:
. (9)
Получили уравнение с симметричной матрицей порядка 2m + n. Порядок полной системы можно понизить, исключая вектор деформаций d из первого уравнения с помощью геометрического (третьего) уравнения. В результате получим систему с неизвестными векторами перемещений q и усилий N:
(10)
Матрица системы (10) имеет порядок m + n.
Формирование и решение систем (9) или (10) составляет суть смешанного метода. В этих системах в качестве неизвестных фигурируют векторы, имеющие различный физический смысл.
Исключение неизвестных можно продолжить. Если в качестве основных неизвестных принять вектор усилий N и из системы (10) исключить вектор перемещений q, то такой способ решения полной системы уравнений называется методом сил. Если же, наоборот, за вектор основных неизвестных принять вектор перемещений q, а из системы (10) исключить вектор усилий N, то такой способ решения полной системы называется методом перемещений.
Аналогами методов сил и перемещений в теории упругости являются решения задач в напряжениях и в перемещениях.
Наиболее просто получается разрешающее уравнение метода перемещений. Выразим вектор N из первого уравнения системы (10) и подставим его выражение во второе уравнение:
Kq = p. (11)
Матрица уравнения (11) является квадратной порядка n и определяется по формуле
. (12)
Матрицу К называют матрицей “внешней” жёсткости системы, или просто матрицей жёсткости системы (МЖС).
Следует особо отметить, что в случае геометрически изменяемых систем, а также систем с недостаточным числом опорных связей, ранг матрицы А меньше n, что приводит к вырожденности матрицы К и невозможности однозначного определения перемещений из уравнения (11). В дальнейшем будем считать, что такой ситуации не возникает. Решая уравнение (11), получаем вектор узловых перемещений q. Затем, используя геометрическое уравнение (3), находим вектор деформаций d и, наконец, с помощью физического уравнения (6) определяем вектор внутренних усилий N.
Уравнение (11) позволяет получить явную зависимость узловых перемещений от внешней нагрузки:
. (13)
Матрица D обратна матрице К (D = K-1) и называется матрицей влияния перемещений; её также называют матрицей “внешней” податливости системы. Элемент матрицы D представляет собой перемещение узла системы по направлению qi от единичной силы, приложенной в узле по направлению qj .
С помощью уравнений (10) и (13) нетрудно получить явную зависимость внутренних усилий от внешней нагрузки:
.
Матрица называется матрицей влияния усилий.
Для статически определимых геометрически неизменяемых систем, для которых А является квадратной невырожденной матрицей, выражение для матрицы влияния усилий упрощается:
.
Опорные реакции определяются по уравнению (2) и могут быть выражены через нагрузку: r = RN = RZp.
Матрица Zr = RZ называется матрицей влияния опорных реакций.
– Конец работы –
Эта тема принадлежит разделу:
ШАРНИРНО-СТЕРЖНЕВЫХ СИСТЕМ
На сайте allrefs.net читайте: ШАРНИРНО-СТЕРЖНЕВЫХ СИСТЕМ…
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Физические уравнения
allrefers.ru
Физические уравнения теории упругости – Энциклопедия по машиностроению XXL
ФИЗИЧЕСКИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ [c.37]В каждой точке г П справедливы уравнения равновесия, геометрические соотношения Коши и физические уравнения теории упругости. К точкам поверхности S приложим усилия —Sf, такие что вызванные ими перемещения —и граничных точек обеспечат совпадение конфигураций поверхностей S и S. [c.117]
Физические уравнения теории упругости для изотропного тела. Обобщенный закон Гука [c.194]
Закон наследственной упругости для общего случая пространственного напряженного состояния можно получить, если в физических уравнениях теории упругости заменить упругие константы соответствующими операторами. [c.361]
Для решения задач прикладной геомеханики используются физические уравнения теории упругости (линейной и нелинейной),, пластично-вязких течений и др. Кратко остановимся иа основных уравнениях состояния, связывающих напряжения и деформации-Для описания поведения изотропного однородного упругого тела необходимо знать модуль Юнга и коэффициент Пуассона. Кроме этих двух констант, используются две другие упругие константы, которые непосредственно связаны с шаровой и девиатор-ной составляющими тензора напряжений модуль объемной деформации К и модуль сдвига (перекоса) О. [c.55]
Выпишем еще раз в сокращенной форме основные уравнения теории упругости, а именно I — статические, II — геометрические и III — физические [c.43]
Остановимся вкратце на случае, когда среда несжимаема (о = 0,5). Будем рассматривать этот вопрос только с позиций интегральных уравнений. Дело здесь усложняется тем, что значение а = 0,5 является вырожденным для дифференциальных уравнений. Интегральные уравнения теории упругости для несжимаемой среды совпадают (с точностью до физического смысла) с уравнениями линеаризованного течения вязкой жидкости [230]. Эти уравнения являются регулярными, и в дополнение к полюсу резольвенты в точке к = —1 возникает еще полюс в точке Я. = 1. Это обстоятельство очевидно, поскольку для несжимаемой среды постановка задачи 1+ возможна лишь при условии [c.565]
Таким образом, все точки прямолинейной границы имеют постоянное перемещение, направленное в сторону начала координат. Мы можем считать такое перемещение физически возможным, если припомним, что вокруг точки приложения силы Р мы мысленно удалили часть материала, ограниченную цилиндрической поверхностью малого радиуса (рис. 53), в пределах которой уравнения теории упругости теряют силы. В действительности, конечно, произойдет пластическая деформация этого материала в силу этого можно допустить существование вдоль прямолинейной границы перемещений, определяемых формулами (70). Вертикальные перемещения на прямолинейной границе получаются из второго выражения (ж). Учитывая, что перемещение v считается положительным, если оно направлено в сторону увеличения 0, и что деформация симметрична относительно оси х, найдем вертикальные перемещения, направленные вниз, на расстоянии гот начала координат в виде [c.118]
Наиболее эффективным из приближенных методов в теории пластичности следует считать метод последовательных приближений А. А. Ильюшина, именуемый методом упругих решений [3] в нем для первого приближения принимается решение аналогичной задачи теории упругости (со сходственными граничными и другими условиями), благодаря чему в первом приближении выясняются границы между упругими и пластическими зонами как по длине стержня (пластинки и др.), так и по высоте сечения. Это позволяет в первом приближении вычислить для каждой точки такого сечения значение числа ш, входящего в основной физический закон пластичности (4.13). Зная величину ш, можно в порядке первого уточнения исправить ранее вычисленные компоненты напряжения, внести поправки в первоначальные основные уравнения теории упругости, что определит новые границы между упругой и пластическими зонами, [c.193]
Итак, исходные основные уравнения теории упругости, статические, геометрические и физические, заданы приведенными выше соотношениями. [c.52]
Наряду с теоремой, указанной в названии параграфа, имеется еще и теорема о существовании решения задачи теории упругости. Доказательство этой последней теоремы является далеко не простым в математическом отношении. Вместе с тем, если исходить из физических соображений, то факт существования решения задачи теории упругости является достаточно очевидным. Все уравнения теории упругости, приведенные выше, получены из принципов механики, не вызывающих сомнения, вследствие чего они, эти уравнения, не могут быть в противоречии с природой — сплошное тело (сохраняющее свою сплошность) определенным образом нагруженное и надлежащим способом закрепленное, должно иметь хотя бы одно положение равновесия. Поскольку теорема о существовании решения задачи теории упругости (в том числе и нелинейной), представляя большую математическую сложность, с точки зрения механики не вызывает сомнения в смысле ее справедливости, на доказательстве этой теоремы мы не останавливаемся и будем исходить из предположения о существовании решения отмеченной выше задачи. Что касается теоремы о единственности решения линейной задачи теории упругости, то ее ниже докажем. [c.624]
Задача теории упругости неоднородного тела формулируется и решается аналогично задаче теории упругости однородного изотропного или анизотропного тела. Различие между ними состоит лишь в том, что в физических уравнениях (законе упругости) механические характеристики являются заданными непрерывными функциями координат. Здесь необходимо еще раз подчеркнуть, что при этом деформации тела считаются малыми и предполагается выполнение обобщенного закона Гука. Очевидно, что в случае неоднородного тела остаются справедливыми общие уравнения механики сплошной среды соотношения Коши между деформациями и перемещениями и т. д. Подробное изложение теории напряжений и деформаций приводится в многочисленных книгах [11, 100, 138 и др.], поэтому ниже они даются без вывода в прямоугольной системе координат х, у, z) в объеме, необходимом для дальнейшего изложения. Эти же уравнения в других системах координат (цилиндрической, сферической) можно найти в указанных выше и других изданиях. [c.32]
Как и в теории упругости, математический аппарат теории пластичности состоит из трех групп уравнений. Это уравнения теории напряжений, теории деформаций и физические уравнения. Уравнения первых двух групп совпадают с соответствующими уравнениями теории упругости. [c.219]
Равенства (22.41) no своей сути существенно отличаются от уравнений закона Гука тем, что содержат не постоянные упругости материала, а переменные параметры и v , которые в свою очередь зависят от секущего модуля Е . Поскольку секущий модуль зависит от напряжений и деформаций в данной точке тела (рис. 22.7), то Е и v являются функциями координат, и, таким образом, равенства (22.41) как бы являются физическими соотношениями теории упругости для неоднородного тела. Задача дополнительно осложняется тем, что законы изменения У, z) и Vn(x, у, z) могут быть найдены лишь [c.515]
Физические уравнения (соотношения упругости) для оболочек имеют такую же структуру, как и для пластин, поскольку в технической теории пластин и оболочек рассматривается плоское напряженное состояние. [c.196]
Уравнения теории упругости для процесса статического нагружения, происходящего в натуре (параметры натуры отмечены далее индексом 2), отличаются от уравнений (5.1), (5.2) только индексами у соответственных физических величин. Выпишем эти уравнения в сокращенном виде- [c.85]
Физические уравнения для упругого тела представляют собой обобщенный закон Гука и имеют тот же вид, что и в геометрически линейных задачах теории упругости (5.2). [c.97]
Используемые здесь гипотезы необычны, хотя в сущности они мало отличаются от гипотез Кирхгофа—Лява. Автор отдает себе отчет, что его предположения не обладают такой физической наглядностью, как предположения Кирхгофа—Лява, но они имеют и свои преимущества, которые выявляются в части VI. В ней показано, что соответствующая этим гипотезам теория заслуживает названия итерационной в том смысле, что ее можно рассматривать как исходное приближение итерационного процесса интегрирования уравнений теории упругости. При обсуждении и сопоставлении возможных гипотез теории оболочек автор стремился подчеркнуть, что, если не принимать в расчет вопросы обоснования и уточнения теории оболочек, то выбор гипотез не играет существенной роли (конечно, если не выходить за разумные рамки). Поэтому читатель, питающий вполне объяснимую симпатию к гипотезам Кирхгофа—Лява, найдет в книге все вытекающие из них соотношения. [c.11]
Задача построения математически непротиворечивой теории оболочек, являющейся корректно разрешимой и обеспечивающей выполнение всех независимых физических краевых условий, связана с необходимостью отказа от всех упрощающих физических и геометрических гипотез и использованием математически строгих методов редукции уравнений теории упругости. Сюда можно отнести проекционный метод уменьшения размерности дифференциальных уравнений в частных производных, основанный на том, что любую непрерывную функцию можно равномерно приблизить полиномами (теорема Вейерштрасса). Он представляет собой обобщение классических приближенных методов (метода моментов, метода Бубнова—Галеркина и др.) в рамках функционального анализа [75]. [c.8]
Однако сперва мы пойдем по пути, использованному самим Сен-Вена-ном, который исходил из основных уравнений теории упругости, и сперва будем искать только точные решения. Конечно, мы должны тотчас же предостеречь читателя от переоценки точности этих решений. Хотя математическая задача о нахождении интеграла основных уравнений, удовлетворяющего требуемым граничным условиям, в некоторых случаях может быть решена совершенно строго, но из этого еще не следует, что такое решение безусловно надежно н с физической точки зрения. Это было бы действительно так, если бы предположения, на которых основан вывод основных уравнений, выполнялись строго. Однако обычно об этом не может быть и речи мы предполагаем, что материал изотропен, но материал, из которого изготовляют рассчитываемые стержни, обычно обнаруживает в разных направлениях разные упругие свойства, что как раз может быть довольно отчетливо замечено при испытании на кручение ). Это видно уже из того, что значение модуля сдвига G, найденное из опытов над кручением, не особенно точно согласуется со значением, выражаемым через упругие постоянные и /и по формуле (29) 2, как это должно было бы иметь место для изотропного тела. Точно так же и предположение об однородности материала или об одинаковости свойств его в разных точках оправдывается не всегда, например в двутавровых балках часто можно заметить довольно резко выраженную разницу между внутренней частью и наружным слоем. [c.51]
Система уравнений квазистатической линейной тбо-рин вязкоупругости для случая малых деформаций аналогична системе определяющих уравнений теории упругости, за исклю- чением физического соотношения между напряжениями и деформациями, рассмотренного выше. Мы имеем следующие уравнения [c.35]
Общая постановка плоских контактных задач для полупространства и слоя, подверженных одновременному воздействию сил тяжести и однородных, ориентированных вдоль границы, начальных напряжений дана в работе В. М. Александрова и Н. X. Арутюняна [1]. Предполагалось, что материал среды является несжимаемым и описывается либо уравнениями физически нелинейной (геометрически линейной) теории установившейся ползучести, либо уравнениями геометрически нелинейной (физически линейной) теории упругости. В предположении, что силы трения в области контакта отсутствуют, изучена проблема эллиптичности линеаризованных уравнений (внутренней устойчивости среды), исследованы явления поверхностной неустойчивости среды. В качестве иллюстрации проведен анализ влияния механических свойств и начального напряженного состояния среды на контактную жесткость. Для потенциала Муни обнаружены значения начальных напряжений, при которых упругий континуум начинает работать как основание Винклера. [c.236]
Замечание. В окрестностях точек приложения сосредоточенных сил компоненты напряжения и смещения перестают быть ограниченными, что, очевидно, не допустимо с физической точки зрения помимо этого, сами уравнения теории упругости перестают быть справедливыми для этих окрестностей. [c.200]
Следовательно, если физические уравнения теории малых упругопластических деформаций (5.5) и (5.6) заменить соответствующими уравнениями (5.41) и (5.43), то решение задачи теории пластичности сводится к решению задачи теории упругости с переменными параметрами упругости, определяемыми по формулам (5.42) и (5.42а). Этот метод впервые предложен И. А. Биргером [9,11 , Согласно (5.42) зависимость между переменными параметра-ми упругости имеет тот же вид, что и для упругих постоянных Я, О, п, а именно О = [c.147]
Решение задач теории пластичности с помощью теории пластического течения представляет значительные трудности, обусловленные тем, что физические уравнения теории пластического течения (см. (5.9)) содержат не только компоненты напряжения, но и их приращения. Не представляется возможным данные уравнения решить относительно напряжений следовательно, нельзя составить систему уравнений в перемещениях. Во многих частных задачах обычно применяют численное интегрирование, прослеживая шаг за шагом развитие пластической деформации. На каждом этапе внешняя нагрузка получает приращения, по которым затем вычисляют соответствующие приращения напряжений и деформаций [224]. На каждом этапе, как указано в работах И. А. Биргера [9,11], необходимо решать некоторую задачу для упругого анизотропного тела с переменными параметрами упругости. [c.148]
Для нашей задачи физические уравнения теории малых упругой ласти чес ких деформаций при == О с учетом (8.79) принимают вид [c.204]
Постановка вопроса. Из опыта известно, что твердые тела под влиянием внешних сил претерпевают некоторые изменения формы, исчезающие при постепенном прекращении действия сил внезапное же прекращение действия сил вызывает колебательные движения. Задачей математической теории упругости является точный количественный учет возникших таким путем изменений геометрической формы и механического состояния тела. Пред нами стоит, таким образом, вопрос об определении деформаций и напряженного состояния твердого тела, если известны как действующие на него внешние силы так и те условия закрепления, которым оно подчинено. Метод, которым мы руководствуемся, приступая к ре шению этих задач, есть обычный метод математической физики. В первую очередь определяются механические величины, характеризующие физическую картину напряженного состояния материала затем, геометрические величины, определяющие деформацию тела. Зависимость между механическими и геометрическими величинами определяется из опыта их математическая формулировка приводит нас к так называемым основным уравнениям теории упругости, иными словами, к уравнениям с часТными производными, интегрирование которых отвечает в каждом отдельном случае на поставленные выше вопросы. Кроме составления этих основных уравнений, главным содержанием математической теории упругости является еще теория их интегрирования. [c.5]
Основные уравнения теории упругости для общего случая (см. гл. 3) соответствующим образом упрощаются для плоской задачи, причем различие между плоским деформированным состоянием и плоским напряженным состоянием становится заметным только в физическом законе >. [c.191]
Граничные условия. Статические (1.3), физические (1.6) и геометрические (1.11) соотношения образуют полную систему уравнений теории упругости анизотропного тела, содержащую 15 уравнений и столько же искомых функций — шесть напряжений, шесть относительных деформаций и три перемещения. Решение этой системы должно удовлетворять заданным граничным условиям, которые характеризуют условия закрепления и нагружения тела. Если на границе заданы перемещения, то найденные в результате решения перемещения приравниваются к заданным. Если на граничной поверхности задаются распределенные по этой поверхности нагрузки, то ставятся статические граничные условия [c.307]
При простом нагружении интенсивность приращения деформаций равна дифференциалу интенсивности деформаций йе,р, и поэтому физические уравнения теории упруго-пластпческих деформаций и теории течения совпадают. Совпадают при этом и результаты решения по обеим теориям. [c.294]
В предыдущих главах были рассмотрены статические ус-“яовия (условия равновесия) внутри и на поверхности тела (уравнения (1.16), (1.18)), геометрические уравнения, устанавливающие связь между деформациями и перемещениями (уравнения Коши (1.19)) и между деформациями (условия неразрывности Сен-Венаиа (1.29)), и, наконец, физические уравнения, устанавливающие связь между напряжениями и деформациями в точке тела (обобщенный закон Гука, уравнения (2.8) и (2.10)). Составим сводку основных уравнений теории упругости. [c.51]
Отнесем к физическим свойствам имеющиеся экспериментальные зависимости, связывающие изменение основных физических свойств смазки (д, р, с, X. ai,p) и материалов тел с температурой и давлением, а также выражаемую классическими уравнениями теории упругости связь напряжений, деформаций тел с характерисгиками контакта и упругими свойствами материалов. [c.167]
Эти уравнения называются уравнениями Ламе. Они объединяют статические, геометрические и физические предпосылки теории упругости, рассмотренные н предыдущих главах. Действительно, в них содержатся условия разновесин каждого зле.мента тела, геометрические характеристики деформации и, г и., G и физические характеристики материала л и и. [c.43]
Рассматриваемая в данной главе стохастическая краевая задача теории упругости является основой статистической механики композитов со случайной структурой. Начало систематическому изучению этой задачи положено работой И.М. Лифшица и Л.Н. Розенцвейга [160] применительно к поликристаллам, в дальнейшем многочисленные результаты были обобщены в монографиях [62, 130, 162, 172, 247, 296, 320 и др.]. При единой практически для всех работ в этом направлении постановке задачи, связанной с представлением упругих модулей микронеоднородной среды как случайных статистически однородных функций координат и выбором граничных условий в виде, обеспечивающим однородность макроскопических деформаций, а также общности подхода к решению с использованием метода функции 1 ина уравнений теории упругости в перемещениях для неограниченной изотропной или анизотропной среды существуют различия в получаемых результатах для эффективных свойств композитов и, в большей мере, для оценки полей напряжений и деформаций в компонентах композитов. Это обусловлено статистической нелинейностью исследуемой задачи и построением приближенных решений, которые неодинаково адекватны физической модели композита, в частности, его структуре. [c.39]
Это решение, полученное из уравнений теории упругости, само имеет органичение при опрсании практических физических задач, состоящее главным образом в том, 4lfo п и удовлетворении заданных условий да результирующие силы и моменты на концах, действительное распределение сил по концам не такое, какое можно было бы встретить в практической задаче Из выражений (3.22) на концах при х а имеем. [c.159]
В своём выводе основных уравнений теории упругости Навье (см. стр. 129) исходил из предположения, что идеально упругое тело состоит из молекул, между которыми при его деформировании возникают силы взаимодействия. При этом принималось, что силы эти пропорциональны изменениям расстояний между молекулами и действуют по направлениям соединяющих их прямых линий. Таким путем Навье удалось установить соотношения между деформациями и упругими силами для изотропных тел с введением лишь одной упругой константы. Коши (см. стр. 135) первоначально ввел две константы в зависимости между напряжением и деформацией в случае изотропии. В самом же общем случае анизотропного тела Пуассон и Коши допускали, что каждая из шести компонент напряжения может быть представлена однородной линейной функцией шести компонент деформации (обобщенный закон Гука). В эти функции входило 36 постоянных. Положив в основу физического истолкования явления упомянутую выше молекулярнуро теорию, они снизили число постоянных для общего случая до 15. Они показали, что изотропия допускает дальнейшее снижение этого числа, так что окончательно для записи соотношений между компонентами напряжения и деформации необходима лишь одна постоянная, которую и ввел Навье. [c.262]
Введенные выше потенциалы простого слоя, двойного слоя и их производные, как показано в 1, удовлетворяют тождественно дифференциальным уравнениям теории упругости внутри тела при отсутствии объемных сил. Частное решение, соответствующее действию объемных сил, выражается объемным потенциалом с плотностью, равной объемной силе. В связи с этим решение тон или иной краевой задачи теории упругости можно попытаться искать в виде суммы одного или нескольких граничных потенциалов и объемного потенциала. Плотности граничных потенциалов должны содержать достаточно неизвестных, чтобы можно было удовлетворить граничные условия. Для нахождения этих неизвестных строятся интегральные уравнения на границе тела —граничные интегральные уравнения (ГИУ). Если при заданных краевых условиях доказано существование решения построенного интегрального уравнения, то тем самым обоснована использованная формула представления решения. Вопрос обоснования формулы представления решения не возникает, если в качестве ее используется формула Сомильяны, справедливая дл любого регулярного, т. е. принадлежащего классу ( (Q) n (Q)) , поля перемещений, а также для более общих классов перемещений, для которых имеет место формула Бетти. Поскольку плотности потенциалов простого и двойного слоя, входящих в формулу Сомильяны, имеют прямой физический смысл, то соответствующую формулировку метода граничных элементов (МГЭ) называют прямой формулировкой МГЭ. В противоположность этому формулировку МГЭ, использующую другие формулы представления, называют непрямой формулировкой МГЭ. [c.62]
Выводом уравнений изгиба пластинок, на основании молекулярной модели и обпщх уравнений теории упругости, занимались Пуассон, Навье и Коши. У Навье мы находим вполне строгое уравнение для статического изгиба пластинки как для случая нормальной нагрузки, так и для случая выпучивания пластинки под действием сил на контуре, лежащих в плоскости пластинки В случае свободно опертой прямоугольной пластинки Навье получил правильное решение, использовав двойные тригонометрические ряды. Общим анализом условий на контуре пластинки занимался Пуассон , однако он сформулировал одно лишнее условие на контуре в случае задания на нем внеш-58 них сил. Правильное число условий было указано позже Г. Кирхгофом и ясно интерпретировано физически В. Томсоном . Кирхгофу принадлежит общая теория изгиба стержней, а также теория пластинок, основанная на четких гипотезах, близких к гипотезе плоских сечений в элементарной теории изгиба, и вполне строгий вывод известных уже уравнений малых прогибов пластинок при помощи принципа виртуальных перемещений. Позже Кирхгоф и Клебш развили теорию для не слишком малых прогибов пластинок. [c.58]
В основу вывода уравнений движения вязкой жидкости Пуассон положил своеобразный анализ деформации частиц среды за бесконечно малые промежутки времени, представляя каждую элементарную деформацию состоящей из двух процессов — упругой деформации согласно уравнениям теории упругости и последующего перераспределения (выравнивания) давлений в жидкости. Применение этих рассуждений привело Пуассона к прспорцио-нальности касательных напряжений скоростям деформации частиц. Однако в результате он получил уравнения движения, содержащие формально не две, а три физические характеристики жидкости (помимо плотности). Причиной этого было отсутствие достаточно строгого определения равновесного давления в потоке вязкой жидкости. Впрочем для малосжимаемой капельной ншдкости и адиабатического движения газа Пуассон свел число независимых физических характеристик жидкости к двум, в результате чего его уравнения движения приняли форму, близкую к точным уравнениям движения вязкой жидкости. [c.67]
В случаях, когда тело ограничено многосвязным контуром, доказательство однозначности решения уравнений теории упругости, основанное на представлении о естественном состоянии упругого тела теряет силу, и мы будем, вообще говоря, получать многозначные решения. Физический смысл этого заключения выясним на простейшем примере. Возьмем случай кольца. Одним плоским разрезом мы можем обратить кольцо в тело с односвязным контуром. В таком теле при определенных внешних силах возникают вполне определенные напряжения и деформации. Если мы удалим внешние силы, напряжения и деформации пропадут, тело вернется к своему естественному состоянию. Удалим посредством плоского сечения тонкий слой материала кольца у места разреза. Тогда концы разрезанного кольца не будут совпадать друг с другом при отсутствии внешних сил мы сможем привести их к соприкасанию, лишь приложив внешние силы. Предположим, что мы достигли таким путем соприкасания и скрепили (склеили, спаяли) между собой поверхности, соответствующие месту разреза, тогда по удалении внешних сил в кольце останутся напряжения, величина которых будет зависеть от того, какая часть материала кольца была удалена у места разреза. Напряжения эти, возникающие, как мы видим, в телах с многосвязным контуром, при изготовлении называют самонапряжениями или начальными напряжениями. Они именно и обусловливают многозначность решений уравнений теории упругости в случае многосвязных контуров [c.55]
Проделанный выше переход от среднего напряжения по площадке к напряжению в точке связан с воображаемым процессом уменьшения размеров площадки ДР до нуля, необходимым для п )и-менения анализа бесконечно малых. Законность и обоснованность такого формального процесса, как уже указывалось выше, долгое время были под сомнением и являлись предметом дискуссий среди ученых однако приложение полученных основных уравнений теории упругости к решению задач физики довольно быстро показало эффективность разработанных Методов и дало ряд замечательных результатов, подтвержденных опытом это относится прежде всего к области изучения колебаний и распространения волн (например, звуковых) в упругих телах некоторые более простые задачи этого рода освещены в главах IV и IX настоящей книги. Середина XIX века была особенно богата достижениями в смысле развития теории упругости и получения решений задач, важных для физики и техники здесь главную роль сыгралк работы крупнейшего французского исследователя Сен-Венана и его учеников. В этих условиях постепенно исчезли сомнения в физической обоснованности метода теории упругости, оперирующего как бы с непрерывной, сплошной средой с этой точки зрения иногда говорят, что теория упругости основывается на гипотезе сплошного строения твердых тел. При этом, конечно, нельзя забывать, что такая гипотеза является только рабочей гипотезой-, она диктуется принятым математическим методом исследования и не вторгается в те области физики, которые непосредственно занимаются вопросами строения тел. [c.12]
Отметим одно важное обстоятельство. Вообхце говоря, в случае осесимметричной задачи можно было бы отвлечься от соображепий, использованных при выводе формул (6.8), и рассматривать эти формулы как первичные выражения (см. [32]). Основные уравнения теории упругости (1.8) — (1-13) при этом были бы удовлетворены (в предположении отсутствия объемных сил и изменения температуры). Однако использованный выше способ вывода придает этим формулам определенный физический смысл. [c.54]
Задача решения интегрального уравнения Фредгольма первого рода является некорректной [370]. Понятие корректности постановки задач математической физики впервые сформулировано Ж. Адамаром при изучении задачи Коши для уравнения Лапласа [4]. Некорректность решения интегральных уравнений Фредгольма первого рода заключается в том, что их решен 1я неустойчивы к малым изменениям исходных данных. Долгое время считалось, что некорректно поставленные задачи не имеют физического смысла и поэтому они не изучались. Однако в последнее время были разработаны эффективные методы решения таких задач и показано, что практические задачи сводятся к ин-Т5гральным уравнениям первого рода [370]. В частности, классическая задача Дирихле для уравнения Лапласа, если ее решение искать в виде потенциала простого слоя, сводится к интегральному уравнению первого рода [56, 208]. Аналогичная ситуация имеет место и для уравнений теории упругости [298, 299]. Контактные задачи теории упругости и теории оболочек также могут быть сведены к интегральным уравнениям Фредгольма первого рода (см. параграф 3.5 настоящей работы н [144, 156]). Заметим, что задача численного обращения преобразова- [c.103]
Вывод физических уравнений теории оболочек осуществляется так. Определяются, напряжения Оц, и х — х 1 исходя из уравнения обобщенного закона ГуКа в случае пространственной задачи теории упругости [уравнения (131)]. Согласно этим уравнениям СТц и Стаа выражаются через и 3(2) [c.107]
mash-xxl.info
Физические уравнения теории оболочек – Энциклопедия по машиностроению XXL
Физические уравнения теории оболочек можно представить в упрощенной форме, считая коэффициент Пуассона v = 0. Тогда из формул (10.18) находим [c.235]ФИЗИЧЕСКИЕ УРАВНЕНИЯ ТЕОРИИ ОБОЛОЧЕК [c.100]
Уравнения (10.18) представляют собой упрощенные физические уравнения теории тонких оболочек. Они выражают зависимость между усилиями и деформациями в тонкой круговой цилиндрической оболочке. [c.225]
Для связи между усилиями и деформациями воспользуемся упрощенными физическими уравнениями теории тонких оболочек (10.18), которые в данном случае будут иметь вид [c.241]
Приведенные выше соотношения явились основой вычислительных программ численного решения задач о напряженных, деформированных и предельных состояниях оболочечных конструкций, подверженных длительным статическим и малоцикловым воздействиям в условиях повышенных температур [8, 3, 15]. Разработанная в [15] программа исследования прочности сильфонов основана на линеаризованных уравнениях теории оболочек и уравнениях состояния (8.17). Для учета физической нелинейности материала оболочки используется метод переменных параметров упругости [10]. [c.160]
Выражения для обобщенных параметров НДС оболочки выводятся из геометрических и физических уравнений теории пологих оболочек с помощью процедуры метода Канторовича-Власова, когда соответствующее уравнение моментного состояния умножается на Xi x) и безмоментного состояния – на Х2 х) И интегрируется в пределах оболочки. В этом случае через функции R y) и Г у) можно выразить статические и кинематические параметры оболочки. Для этого необходимо построить 7 производных фундаментальных функций (см. таблицу 7.17) и использовать соотношения (7.154)-(7.156). Получается 8 уравнений. Система 8 уравнений при у=0 в силу свойств фундаментальных функций ФДо), ЖДо) распадается на две системы 4-го порядка [c.495]
Основные. результаты исследования контактных задач получены прп такой постановке, когда учитывалась лишь конструктивная нелинейность — следствие ограничений (неравенств), отражающих неотрицательность контактной реакции. Решения строились на основе линейных кинематических, статических и физических соотношений теории оболочек. Классически ” подход, заключающийся в построении интегрального уравнения относительно контактного давления, существенно опирается на линейность теории, поскольку базируется на принципе суперпозиции. [c.3]
Под расчетными уравнениями моментной теории тонких оболочек будем подразумевать полную систему уравнений теории оболочек, которая включает в себя дифференциальные уравнения равновесия, геометрические уравнения (формулы деформации — смещения ) и физические уравнения (уравнения закона Гука, или уравнения состояния). [c.159]
Существует огромное разнообразие уравнений теории оболочек, отличие которых связано с исходными физическими гипотезами, на которых построена частная теория, областью ее применимости, геометрией оболочки и используемой системой координат. Для выявления и анализа некоторых эффектов гидроупругого взаимодействия достаточно ограничиться случаем малых перемещений оболочки, в других случаях необходимо рассматривать весьма большие формоизменения среды с учетом геометрически и физически нелинейных свойств оболочки. Из всех существующих вариантов здесь приведем уравнения нелинейной теории пологих оболочек, а также уравнения, описывающие сильные формоизменения осесимметричных оболочек. Такой выбор определяется характером рассматриваемых далее задач. Исчерпывающее изложение приводимых ниже материалов можно найти в работах [39, 40, 67, 83, 161]. [c.25]
Решение системы уравнений (ЮЛ) и (10.2) относится к статической задаче безмоментной теории оболочек вращения при осесимметричной нагрузке. Чтобы найти деформации и перемещения в оболочке, к этим уравнениям следует добавить геометрические и физические уравнения. Здесь ограничиваемся исследованием только статической стороны задачи. [c.207]
При решении задач ползучести и устойчивости гибких оболочек используем физические зависимости теории течения в сочетании с гипотезами течения и упрочнения, Анизотропию при ползучести следует учитывать исходя из основных положений анизотропной теории пластичности [9, 69], в частности из модифицированных уравнений изотропной ползучести при сложном напряженном состоянии. Эти модификации состоят во введении параметров анизотропии, что эквивалентно замене интенсивности скоростей деформаций и напряжений на соответствующие квадратичные формы, в которые входят параметры анизотропии, а также в формулировке определенных условий и гипотез. [c.15]
Формулы (10.13) могут быть получены из формул (10,11), если в них принять V = 0. Поэтому при рассмотрении приближенных решений в теории оболочек пользуются упрощенной системой физических уравнений (10.11), полагая в них v = 0. [c.190]
Физические уравнения (соотношения упругости) для оболочек имеют такую же структуру, как и для пластин, поскольку в технической теории пластин и оболочек рассматривается плоское напряженное состояние. [c.196]
Используемые здесь гипотезы необычны, хотя в сущности они мало отличаются от гипотез Кирхгофа—Лява. Автор отдает себе отчет, что его предположения не обладают такой физической наглядностью, как предположения Кирхгофа—Лява, но они имеют и свои преимущества, которые выявляются в части VI. В ней показано, что соответствующая этим гипотезам теория заслуживает названия итерационной в том смысле, что ее можно рассматривать как исходное приближение итерационного процесса интегрирования уравнений теории упругости. При обсуждении и сопоставлении возможных гипотез теории оболочек автор стремился подчеркнуть, что, если не принимать в расчет вопросы обоснования и уточнения теории оболочек, то выбор гипотез не играет существенной роли (конечно, если не выходить за разумные рамки). Поэтому читатель, питающий вполне объяснимую симпатию к гипотезам Кирхгофа—Лява, найдет в книге все вытекающие из них соотношения. [c.11]
Структуре разрешающих уравнений теории пологих оболочек можно дать простую физическую интерпретацию. Отбросив в (10.22.5) члены, содержащие оператор Ад, получаем два самостоятельных уравнения. Одно из них имеет вид [c.144]
Как правило, любые полезные упрощения оказываются приемлемыми только в определенных границах их приложения, потому-то и существуют различные типы теорий оболочек для соответствующих областей применения. Наибольшая трудность в теории оболочек состоит в том, чтобы выяснить, какие упрощения являются приемлемыми для соответствующих областей применения, а также указать границы их применимости. Границы применимости и точность различных представленных теорий обсуждаются в конце глав 3, 5. и 7. Понимание физического смысла аппроксимаций и значение отбрасываемых членов уравнений являются, очевидно, первым шагом в попытке прийти к некоторым разумным заключениям. [c.12]
Для того чтобы избежать как этих трудностей, так неупомянутого выше формального математического подхода, в начале главы 6 приводится использующая минимум аппроксимаций общая теория оболочек, которая может быть применена к любым частным случаям, если сделать те пренебрежения, которые представятся подходящими в конкретном случае. Таким образом, вместо того чтобы опираться на весьма смутные представления о введенных аппроксимациях, читатель может рассмотреть все представленные прямо перед его глазами члены уравнений и безошибочно разглядеть, что будет отбрасываться и каков физический смысл как оставленных, так и опущенных членов уравнений. Возможно, это вызовет удивление, но оказалось, что воспроизвести такую общую теорию в. скалярной форме, не делая попыток упростить ее уменьшением числа неизвестных по срав- [c.14]
Для получения разрешающей системы уравнений теории физически нелинейной слоистой оболочки теперь достаточно к найденным ранее уравнениям (VI.22) добавить слагаемые [c.111]
Шестая глава. посвящена моментной теории расчета тонких упругих оболочек. Приводятся уравнения статики, геометрические и физические уравнения. На основе общих уравнений моментной теории получены уравнения для расчета тонких торсовых оболочек. [c.3]
При выводе уравнений равновесия (6.11) не учитывались физические свойства материала оболочки и картина деформации. Такую независимость теории равновесия от теории деформации оболочки возможно допустить при условии малости перемещений оболочки по сравнению с ее толщиной и рассматривать равновесие оболочки в недеформированном состоянии. [c.167]
В классической теории оболочек кинематические соотношения (2.43), в свою очередь, исключают применение уравнений из (1.4) для Охг и Оуг- Указанные напряжения вычисляются статически из условий равновесия для элемента оболочки (см., например, [8, 32]). По отношению к физическим соотношениям напряжения бесконечно больших значений соответствующих жесткостей материала оболочки, а именно [118] [c.99]
Сформулируем соответствующие упрощенные уравнения теории слоистых оболочек. Ясно, что на физических уравнениях (2.1.1) допущение о пологости оболочки никак не сказывается и они сохраняют свою форму. Соотношения [c.57]
При разработке классической теории оболочек исследователи ориентировались на методы, требующие максимального упрощения разрешающих уравнений и устранения из них величин, существенно не влияющих на окончательные результаты. Однако это сужает класс исследуемых оболочек и исключает из поля зрения некоторые важные механические и физические эффекты. [c.3]
Задача построения математически непротиворечивой теории оболочек, являющейся корректно разрешимой и обеспечивающей выполнение всех независимых физических краевых условий, связана с необходимостью отказа от всех упрощающих физических и геометрических гипотез и использованием математически строгих методов редукции уравнений теории упругости. Сюда можно отнести проекционный метод уменьшения размерности дифференциальных уравнений в частных производных, основанный на том, что любую непрерывную функцию можно равномерно приблизить полиномами (теорема Вейерштрасса). Он представляет собой обобщение классических приближенных методов (метода моментов, метода Бубнова—Галеркина и др.) в рамках функционального анализа [75]. [c.8]
Отметим некоторые варианты теории оболочек, основанные на введении физических гипотез более общего характера, чем гипотеза прямой нормали. Достаточно эффективной и в то же время вполне приемлемой представляется гипотеза о несжимаемости материала по толщине оболочки. Уравнения пологих слоистых оболочек получены на основе этого предположения в работах 45, 46, 47]. Построению и некоторым приложениям теории слоистых плит и стержней посвящены работы [15, 16, 19, 93, 95]. [c.87]
Приведем уравнения нелинейной безмоментной теории оболочек, обобщающие уравнения (1.37)—(1.39) и учитывающие изменение радиусов кривизны в процессе нагружения. Физические и геометрические соотношения этой теории по-прежнему определяются равенствами (1.37), (1.39), а уравнения равновесия следуют из [c.327]
Пологие оболочки. Оболочкой называется тело, один размер которого — толщина к — мал по сравнению с двумя другими. Ее можно назвать пологой, если кривизна любого участка оболочки невелика. Приведем основные соотношения геометрически и физически нелинейной теории пологих оболочек, основываясь на уравнениях монографии [39] и теории пластического течения. В качестве координатных линий X, у используются линии кривизны срединной (равноудаленной от лицевых) поверхности, ось направлена вдоль нормали к срединной поверхности, к центру ее кривизны. [c.25]
Вывод физических уравнений теории оболочек осуществляется так. Определяются, напряжения Оц, и х — х 1 исходя из уравнения обобщенного закона ГуКа в случае пространственной задачи теории упругости [уравнения (131)]. Согласно этим уравнениям СТц и Стаа выражаются через и 3(2) [c.107]
Равенства (20) являются физическими зависимостями теории оболочек и позволяют записать фумкнионал (16) в форме, представленной в табл. 4.1. Физические константы совпадают с коэффициентами квадратичной формы (18). Из (16) следует, что они зависят от кривизн бар- Однако обычно их упрощают, пренебрегая (в соответствии с точностью уравнений теории оболочек) величинами такого же порядка малости, как hba , по сравнению с единицей в (5). Выражения для упрощенных таким образом физических коэффициентов не содержат крнвизн бая из (16) —(19) следует h, [c.104]
В. В, Понятовского (1962). Анализ выведенных систем показывает, что с увеличением порядка системы дифференциальных уравнений выше восьмого в решениях появляются краевые эффекты типа Сен-Венана более того, увеличение порядка системы уравнений (физически это соответствует увеличению числа степеней свободы) порождает только новые интегралы с большим показателем изменяемости — краевые эффекты типа Сен-Венана. Итак, если нужно выделить краевые эффекты Сен-Венана, соответствуюш,ие краевому кручению и краевой плоской деформации в первом приближении, то система дифференциальных уравнений теории оболочек должна быть 14-го порядка. Однако пока не имеется опубликованных результатов по анализу таких расширенных систем уравнений теории оболочек. [c.263]
Анализируя различные подходы к решению геометрически и физически нелинейных задач теории оболочек, выбираем вариационный подход. При построении вариационного уравнения термоползучести используем допущения технической теории гибких оболочек, успещ-но применяемой в расчетах упругих пологих оболочек, и физические соотношения в форме связи тензоров скоростей изменения деформаций и напряжений с учетом ползучести материала. Вариационное уравнение смешанного типа, в котором независимому варьированию подвергаются скорости изменения прогиба и функции усилий в срединной поверхности, позволяет использовать для описания реологических свойств материала хорошо обоснованные теории ползучести типа течения и упрочнения. Задачи мгновенного деформирования решаем методом последовательных нагружений, а задачи ползучести — методом шагов по времени. [c.13]
Решение системы уравнений (10.1) относится к статической задаче безмоментной теории оболочек. Чтобы найти деформации и перемещении Б оболочке, к этим уравнения , следует добавить геометрические и физические уравнения Здесь ограничиваемся исследованием только статической сторокы задачи и рассмотрим основные уравнения дл двух частных случаев [c.176]
Для выяснения характера этих ограничений необходимые критерии статического подобия пластин при аффинном соответствии модели и натуры получим, минуя процедуру масштабных преобразований физических уравнений. С этой целью преобразуем имеющиеся критериальные уравнения теории пологих оболочек ( 6.2) путем исключения характерного радиуса R в формулах (6.29) с помощью определяющего критерия подобия [b/ Rh) = idem (6.28). Такой прием равносилен предельному переходу в исходных уравнениях теории пологих оболочек (6.14)— (6,17) к уравнениям изгиба пластин при Ri- оо, R – оо. [c.127]
Переход от тензорной формы. чаписи к развернутой. В задачах теории упругости и теории оболочек физические компоненты векторов и тензоров (представляющие практический интерес) можно получить двумя путями 1) решить соответствующую краевую или вариационную задачу в обычных компонентах и затем по формлам (28) перейти к физическим 2) записать в физических компонентах все необходимые уравнения и функционалы н получить решение. Ниже приведены правила, которые можно использовать при реализации второго пути. [c.215]
Переход от общей теории оболочек к безмоментной теории сопровождается понижением порядка уравнений. Поэтому необходимо условиться, какие краевые задачи должны ставиться для безмоментных уравнений, чтобы их решение представляло определенный физический интерес. Напрашивающийся ответ на этот вопрос заключается в том, что безмоментные уравнения надо интегрировать с учетом таких граничных условий и таких условий сопряжения, которые связаны с тангенциальными (параллельными касательной плоскости) направлениями, т. е. что в безмоментной теории, должны быть сохранены только тангенциальные граничные условия и условия тангенциальной непрерывности. Эта точка зрения и будет принята в настоящем разделе книги. Она оправдана результатами, полученными в части П. Во всех рассмотренных там примерах оказалось, что решение сфорл улиро-ванной таким образом безмоментной краевой задачи определяет в первом приближении напряженно-деформированное состояние оболочки с точностью [c.211]
Выше указана только часть публикаций по нелинейным-проблемам эластомерного слоя и конструкций. Перечень работ можно бы продолжить, но это не меняет общей оценки состояния вопроса. Если создание линейной теории слоя можно считать завершенным и ее значение можно сравнить со значением классической теории оболочек для соответствующих краевых задач, то создание общей нелинейной теории слоя находится в-началь-. ной стадии. Опубликованных результатов мало, и они не достоверны даже в отношении интегральных упругих характеристик констукций, не говоря уже о полях перемещений и напряжений, В то же время только теоретические исследования и расчеты с последующей экспериментальной проверкой позволяют пороз11ь оценить влияние геометрической и физической нелинейности и решить такие важные вопросы, как пределы применения закона-Гука и выбор упругого потенциала. Лелать упор на физическую нелинейность при умеренных деформациях формулы Коши, связывающие деформации с перемещениями, уравнения равновесия и закон упругости, которые, вообще говоря, независимы. [c.23]
В заключение обсуждения метода гипотез остановимся на подходе В.В. Пикуля [228, 229], который занимает в этом методе несколько обособленное положение. Уравнения теории слоистых оболочек строятся им по следующей [229] схеме. Принимаются физически обоснованные” гипотезы [c.10]
Применение методов асимптотического интегрирования для решения проблемы приведения находится в целом в начальной стадии развития. Ярким примером этого утверждения является постановка А. Л. Гольденвейзером задачи о напряженных состояниях замкнутой оболочки типа полной сферы (всюду положительной кривизны ). Такую задачу считают наиболее благоприятной в отношении классической теории оболочек. Результаты анализа решения этой задачи весьма интригуюш ие Гольденвейзер показал, что некоторыми изменениями в физических соотношениях можно увеличить точность уравнений классической теории оболочек. Однако эти соотношения не могут быть выведены на базе гипотез Кирхгофа — Лява поэтому можно лишь сказать, что в рассматриваемом случае новое содержание удалось представить в старой форме, что не всегда возможно или целесообразно. [c.264]
mash-xxl.info
Физическое уравнение – Большая Энциклопедия Нефти и Газа, статья, страница 3
Физическое уравнение
Cтраница 3
Для того чтобы исходные физические уравнения можно было решать на АВМ, их необходимо запрограммировать. [31]
Уравнения (10.18) представляют собой упрощенные физические уравнения теории тонких оболочек. Они выражают зависимость между усилиями и деформациями в тонкой круговой цилиндрической оболочке. [32]
Такая замена шести физических уравнений одним не позволяет однозначно определять деформации для тела, полностью находящегося в пластическом состоянии. [33]
Эти зависимости называют физическими уравнениями. [34]
Эта связь дается физическими уравнениями теории пластичности или уравнениями состояния. Однако до сих пор еще не создано универсальной теории, которая бы связывала напряжения, деформации, время и температуру так, чтобы было хорошее соответствие с опытом в самых сложных случаях нагружения. [35]
Поэтому они называются физическими уравнениями механики сплошной среды. [36]
Теория пластического течения устанавливает физические уравнения связи между компонентами напряжений и компонентами скоростей пластических деформаций. [37]
Рассмотрим второй вариант получения физических уравнений. [38]
Для пояснения техники нормализации физических уравнений рассмотрим пример изгиба пологой цилиндрической оболочки при действии на поверхности нормального давления интенсивностью Рп (, У) – На рис. 4 2 представлены необходимые обозначения, схема нагружения и размеры оболочки. В качестве граничных условий рассматривается случай защемления краев оболочки на жестком контуре при сохранении возможности аксиальных перемещений одного из торцовых сечений. [40]
Наконец, определим видоизмененную форму физического уравнения для каждой внутренней нерегулярной точки. [41]
Перейдем к изучению подобных преобразований физических уравнений, содержащихг-дифференциальные операторы и переменные под знаком интеграла. Особенности анализа подобия явлений, описываемых дифференциальными и интегральными уравнениями, связаны с масштабными Преобразованиями – указанных операторов. [42]
В главе VII, посвященной физическим уравнениям механики сплошной среды, были даны некоторые общие сведения о реологии. Ниже более подробно обсуждаются отдельные реологические модели. [43]
Таким образом, если в физическом уравнении (2.1) имелась величина Ар, зависящая от шести размерных величин, то в уравнение (2.8) входит параметр Эйлера, определяемый тремя безразмерными величинами. [44]
В результате все члены в физическом уравнении должны иметь одну и ту же размерность. [45]
Страницы: 1 2 3
www.ngpedia.ru
