Теплоёмкость идеального газа | ЭТО ФИЗИКА
сли в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
Во многих случаях удобно использовать молярную теплоемкость C:
где M – молярная масса вещества.
Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.
Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов:
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
Qp = ΔU + p (V2 – V1) = CV ΔT + pΔV, |
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на Δ
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
где R – универсальная газовая постоянная. При p = const
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
Молярная теплоемкость
|
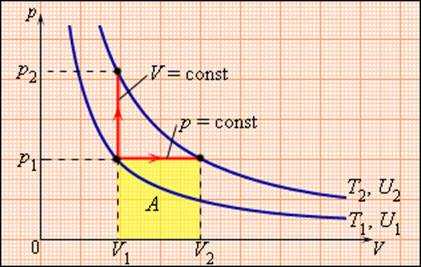
Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT = T2 – T1. При p = const газ совершает работу A = p1(V2 – V1). Поэтому Cp > CV |
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
В частности, это отношение входит в формулу для адиабатического процесса.
Между двумя изотермами с температурами T1 и T2 на диаграмме (p, V) возможны различные пути перехода. Поскольку для всех таких переходов изменение температуры ΔT = T2 – T1 одинаково, следовательно, одинаково изменение ΔU внутренней энергии. Однако, совершенные при этом работы
Следует отметить, что «теплоемкость», как и «количество теплоты» – крайне неудачные термины. Они достались современной науке в наследство от теории
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией поступательного движения молекул и абсолютной температурой T:
Внутренняя энергия 1 моля идеального газа равна произведению на число Авогадро NА:
При изменении температуры на ΔT внутренняя энергия изменяется на величину
Коэффициент пропорциональности между ΔU и ΔT равен теплоемкости CV при постоянном давлении:
Это соотношение хорошо подтверждается в экспериментах с газами, состоящими из одноатомных молекул (гелий, неон, аргон). Однако, для двухатомных (водород, азот) и многоатомных (углекислый газ) газов это соотношение не согласуется с экспериментальными данными. Причина такого расхождения состоит в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию не только поступательного, но и вращательного движения молекул.
|
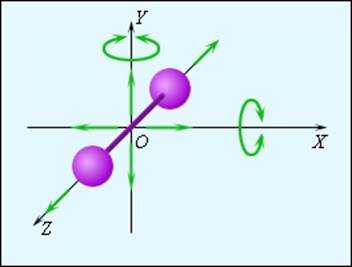
Рисунок 3.10.2. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы |
На рис. 3.10.2 изображена модель двухатомной молекулы. Молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y. Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси
В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:
Если система молекул находится в тепловом равновесии при температуре
Из этой теоремы следует, что молярные теплоемкости газа Cp и CV и их отношение γ могут быть записаны в виде
где i – число степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i = 3)
Для газа, состоящего из
Для газа, состоящего из многоатомных молекул (i = 6)
Экспериментально измеренные теплоемкости многих газов при обычных условиях достаточно хорошо согласуются с приведенными выражениями. Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле.
Теорему о равномерном распределении энергии по степеням свободы можно применить и к тепловому движению частиц в твердом теле. Атомы, входящие в состав кристаллической решетки, совершают колебания около положений равновесия. Энергия этих колебаний и представляет собой внутреннюю энергию твердого тела. Каждый атом в кристаллической решетке может колебаться в трех взаимно перпендикулярных направлениях. Следовательно, каждый атом имеет 3 колебательные степени свободы. При гармонических колебаниях средняя кинетическая энергия равна средней потенциальной энергии. Поэтому в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. Внутренняя энергия 1 моля твердого вещества равна:
Поэтому молярная теплоемкость вещества в твердом состоянии равна:
C = 3R = 25,12 Дж/моль·К. |
Это соотношение называется законом Дюлонга–Пти. Для твердых тел практически не существует различия между Cp и CV из-за ничтожно малой работы при расширении или сжатии.
Опыт показывает, что у многих твердых тел (химических элементов) молярная теплоемкость при обычных температурах действительно близка к 3R. Однако, при низких температурах наблюдаются значительные расхождения между теорией и экспериментом. Это показывает, что гипотеза о равномерном распределении энергии по степеням свободы является приближением. Наблюдаемая на опыте зависимость теплоемкости от температуры может быть объяснена только на основе квантовых представлений.
www.its-physics.org
Определение отношения cp/cv для воздуха методом клемана-дезорма
Цель работы: изучение различных изопроцессов, протекающих в газах, экспериментальное определение CP/CV для воздуха.
Приборы и принадлежности: прибор Клемана-Дезорма, манометр, насос, секундомер.
Элементы теории и метод эксперимента
Теплоемкостью CM какого-либо тела называется величина, численно равная количеству теплоты dQ, которое нужно сообщить этому телу, чтобы повысить его температуру на один кельвин:
. (1)
Теплоемкость единицы массы вещества C называется удельной теплоемкостью, теплоемкость единицы количества вещества (одного моля) C называется молярной теплоемкостью. Удельная и молярная теплоемкости связаны соотношением
, (2)
Где M – молярная масса.
Теплоемкость зависит от условий, при которых происходит нагревание тела. В частности, когда нагревание происходит при постоянном объеме, мы имеем дело с теплоемкостью при постоянном объеме (обычно обозначается как CV). Аналогично в случае нагревания при постоянном давлении имеем дело с теплоемкостью при постоянном давлении CP.
Выведем выражения для СV и CP для одного моля идеального газа.
Изохорный процесс. Выражение для Cv
В соответствии с первым началом термодинамики количество теплоты dQ, переданное системе (например, газу), расходуется на приращение внутренней энергии DU системы и совершение системой работы dA над внешними телами
. (3)
Если нагревание происходит при постоянном объеме, то газ не совершает работы (dA=0) и вся теплота, подводимая к нему, идет на увеличение его внутренней энергии. Тогда на основе (3) и исходя из определения теплоемкости (1) можно записать, что
, (4)
Где DU – изменение внутренней энергии одного моля газа. Выражение (4) определяет молярную теплоемкость газа при постоянном объеме.
Изобарный процесс. Выражение для Cp
Если нагревание проводится при постоянном давлении P, то совершенная системой элементарная работа над внешними телами может быть определена как dA=PdV, где DV – изменение объема одного моля газа. Тогда на основе (1) и (3) можем записать, что
. (5)
Из уравнения Менделеева-Клапейрона, записанного для одного моля газа PV=RT, следует, что
.
Так как P=Const, то Dp=0 и, следовательно, PdV=RdT. Подставляя полученное выражение в (5) и учитывая (4), получаем выражение для молярной теплоемкости газа при постоянном давлении
. (6)
Из (4) и (6) следует, что всегда СP > CV.
Число степеней свободы I и его связь с теплоемкостями Cp и СV
Важным параметром идеального газа является число степеней свободы его молекулы – I, определяющее минимальное количество координат, с помощью которых можно однозначно задать положение молекулы в пространстве. Экспериментально установлено, что при определении числа степеней свободы молекул атомы нужно рассматривать как материальные точки. Для одноатомных газов, например He, положение молекулы (а точнее, атома) в пространстве может быть задано тремя координатами: x, y,z. Соответственно и число степеней свободы молекулы такого газа I=3. Двухатомные газы, такие как N2, O2 и другие, имеют I=5. Действительно, если рассматривать молекулы таких газов как два жестко связанных атома, то для полного определения положения молекулы в пространстве необходимо помимо трех координат, определяющих положение ее центра масс, задать также два угла (j и q), определяющих ориентацию молекулы в пространстве. Степени свободы в такой молекуле можно разделить на поступательные (x, y,z) и вращательные (j и q). Вообще, число степеней свободы молекулы определяется формулой
I=νПост+νВращ+2·νКолеб,
Где VПост – число поступательных степеней свободы, νВращ – число вращательных степеней свободы, νКолеб – число колебательных степеней свободы.
Молекулярно-кинетическая теория позволяет установить связь между числом степеней свободы молекулы газа I и его теплоемкостями CP и CV. Согласно закону равнораспределения На каждую степень свободы (поступательную, вращательную и колебательную) в среднем приходится одинаковая кинетическая энергия, равная. Таким образом, энергия одной молекулы может быть записана в виде
. (7)
Внутренняя энергия одного моля идеального газа соответственно равна
. (8)
Тогда из (4) и (6) получим, что
, . (9)
Адиабатический процесс.
Уравнение Пуассона. Постоянная адиабаты γ
Процесс, протекающий без теплообмена с внешней средой, называется адиабатическим. Для вывода уравнения адиабаты идеального газа, то есть уравнения, связывающего параметры состояния идеального газа при адиабатическом процессе, воспользуемся уравнением (3) первого начала термодинамики, записывая при этом элементарную работу dA в виде PdV и элементарное изменение внутренней энергии DU в виде , где M – масса газа. Получим
. (10)
При адиабатическом процессе DQ = 0 и выражение (10) приводится к виду
. (11)
Для дальнейшего вывода возьмем дифференциал от обеих частей уравнения Менделеева-Клапейрона
. (12)
Уравнения (11) и (12) можно привести к виду
, (13)
Где .
Левую часть этого уравнения можно представить в виде D(ln(PVγ)), откуда следует, что
PVγ=Const. (14)
Полученное уравнение адиабаты идеального газа в переменных P, V называют уравнением Пуассона.
Описание экспериментального макета.
Методика определения постоянной адиабаты γ
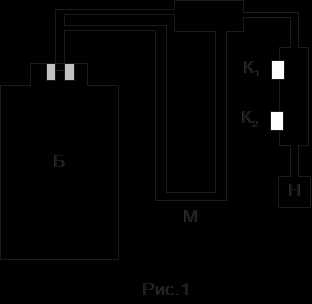
Экспериментальная установка состоит из баллона Б (см. рис. 1) емкостью 25 л, к которому через резиновую пробку подсоединены последовательно U-образный манометр М, краны коммутации газовых потоков К1 и К2 и насос Н, включаемый в сеть ~220 В. Положения кранов на различных этапах проведения эксперимента приведены в табл. 1.
Принцип определения постоянной адиабаты состоит в следующем. В баллон насосом нагнетается воздух до давления немного больше атмосферного (разность давлений контролируется манометром M). Затем производится выдержка воздуха в баллоне в течение некоторого промежутка времени (2…3 минуты).
При этом температура воздуха в баллоне за счет теплообмена становится равной температуре окружающей среды.
Таблица 1
№ | Насос | Операция | Положение кранов К2 К1 |
1 | Включен | Накачка воздуха В баллон | |
2 | Выключен | Выдержка 2-3 минуты | |
3 | Выключен | Сброс давления В баллоне. Выдержка 4, 8, 12, 16 c | |
4 | Выключен | Изолирование баллона От атмосферы. Выдержка 2-3 минуты |
Поскольку масса газа в ходе эксперимента меняется, то расчеты удобно вести для одного моля газа.
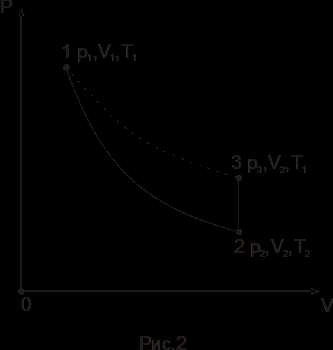
После выравнивания температур молярный объем газа будет V1, давление P1 и температура T1 (точка 1 на рис. 2).
Сообщим на короткое время полость баллона с атмосферой, установив соответствующим образом краны К1 и К2. Как только давление в баллоне станет равным атмосферному (уровни воды в коленах манометра выровняются), закроем краны, прерывая сообщение полости баллона с атмосферой. Молярный объем теперь станет равным V2, а температура T2, что соответствует точке 2 на рис. 2. Поскольку процесс 1-2 протекает в течение короткого промежутка времени, можно пренебречь потерями теплоты за счет теплообмена через стенку баллона. Тогда переход газа из состояния 1 в состояние 2 происходит адиабатически и на участке 1-2 справедливо уравнение Пуассона
P1V1γ = P2V2γ. (15)
После 2-3 минут выдержки при закрытых кранах воздух в баллоне изохорно нагревается до первоначальной температуры T1. Давление при этом повысится вследствие нагрева до величины P3, что соответствует точке 3 на рис. 2. Кривая 1-3, таким образом, является изотермой, и для нее справедлив закон Бойля-Мариотта
P1V1=P3V2. (16)
Из (15) и (16) следует, что . Логарифмируя это выражение, найдем, что
. (17)
В условиях эксперимента давление P2 равно атмосферному. Давление P1 может быть определено по формуле
P1=P2+ρGH,
Где ρ – плотность жидкости в манометре, H – разность уровней жидкости в манометре при давлении P1, G – ускорение свободного падения. Аналогично можно определить и давление P3 по формуле P3=P2+ρGh, где H – разность уровней жидкости в трубках манометра при измерении P3. Так как давления P1, P3 мало отличаются от атмосферного P2, то формулу (17) можно упростить, используя приближенное равенство ln(1+x)≈x, выполняющееся для всех x<<1. Тогда
. (18)
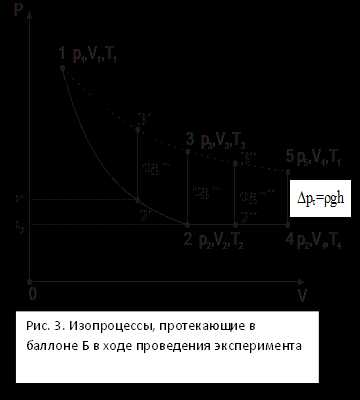Величина H в выражении (18) получена в предположении, что краны К1 и К2 закрываются в момент окончания адиабатического процесса 1-2 (рис. 2).
В случае если краны были закрыты до окончания процесса 1-2, давление в баллоне снизится до величины p2′ (см. рис. 3). При этом разность уровней жидкости в коленах манометра после расширения и затем изохорного нагревания H′ окажется завышенной. Значение γ, определенное по (18), окажется больше истинного.
Если кран закрыть спустя некоторое время после завершения адиабатного процесса 1-2, то за это время температура воздуха в баллоне за счет теплообмена с окружающей средой немного повысится (процесс 2-2′′ на рис. 3). Соответствующая разность уровней H″ окажется заниженной, что приведет к уменьшению γ.
Закрыть краны точно в момент, когда газ находится в состоянии 2, на практике не представляется возможным. Поэтому определять H приходится косвенным путем.
Рассмотрим процесс адиабатного расширения 1-2 при открытом кране с учетом теплообмена с окружающей средой во время протекания процесса 2-4 (рис. 3). Допустим, что газ находится в состоянии 1. Откроем краны и произведем сообщение полости баллона с атмосферой. По окончании адиабатического процесса 1-2 температура воздуха в баллоне станет равной T2 и будет меньше комнатной, давление станет равным атмосферному P2.
Если теперь оставить краны открытыми на время τ, то температура воздуха в баллоне вследствие теплообмена возрастет до величины T4 (изобарный процесс 2-4). Закроем после этого краны и оставим их в таком положении до тех пор, пока температура внутри баллона не станет равной температуре окружающей среды T1 (изохорный процесс 4-5). При этом давление газа в сосуде повысится на некоторую величину DPτ, определяемую по соответствующей разности уровней жидкости в коленах манометра M. При уменьшении времени выдержки τ величина Hτ возрастает и при τ→ 0 приближается к истинному значению H. Таким образом, величину H можно определить, имея график зависимости Hτ=F(τ), полученный в ходе эксперимента. Можно показать, что в условиях нашего опыта имеет место соотношение
Ln(Hτ)=ln(H)-aτ, (19)
Где a – некоторая константа. Получив на опыте ряд значений ln(Hτ), соответствующих различным длительностям расширения τ, и построив график зависимости ln(Hτ)=F(τ), можно, продлив полученную прямую до пересечения с осю ln(Hτ), получить логарифм искомой величины H (рис. 4).
Порядок выполнения работы
1. Перед началом работы проверить наличие жидкости в манометре. В случае недостаточного уровня сообщить об этом преподавателю или лаборанту. При наличии разности уровней в коленах манометра установить краны в положение 3, сбросив лишнее давление в баллоне. Перевести краны К1 и К2 в положение 1 (см. таблицу приложения).
2. Включить насос (при этом давление в баллоне начнет увеличиваться) и добиться разности уровней в коленах манометра H2-H1=20-25 см. Занести показания манометра H=H2-H1 в таблицу.
При проведении последующих серий измерений придерживаться выбранного значения H.
3. Установить краны в положение 2 и выключить насос.
4. Выдержать воздух в баллоне в течение не менее 2-3 минут.
5. Установить кран К2, а затем К1 в положение 3 и сбросить давление в баллоне до атмосферного (при этом разность уровней в коленах манометра станет равной нулю).
6. Выдержать в таком положении баллон в течение времени τ=16 с.
7. Перевести краны в положение 4, изолировав таким образом баллон от атмосферы, и выждать не менее 2-3 минут, после чего вновь измерить разность уровней в коленах манометра Hτ и занести показания в таблицу.
8. Повторить пункты 1-7 не менее трех раз.
9. Повторить измерения по пунктам 1-8, устанавливая время выдержки τ по пункту 6 сначала 12, затем 8 и 4 с. Данные занести в таблицу.
10. Используя методику, описанную в методических указаниях получить значение ln(H), рассчитать значение H, по формуле (18) рассчитать γ.
11. Рассчитать погрешность результата измерений Dγ, принимая точность шкалы манометра DH=1мм. Погрешность ln(H) следует взять соответствующей 1 мм на графике. Сравнить полученное значение γ с теоретическим, считая воздух смесью двухатомных газов.
Вопросы и задания для самоконтроля
1. Дайте определение теплоемкости тела (удельной, молярной). От чего она зависит?
2. Перечислите виды изопроцессов в газе. Сформулируйте условия их протекания.
3. Сформулируйте первое начало термодинамики. Примените его к различным изопроцессам.
4. Дайте определение адиабатного процесса. Выведите уравнение Пуассона. Запишите его в переменных V, T и P, T.
5. Дайте определение числа степеней свободы. Как распределяется энергия молекулы по степеням свободы?
6. Покажите связь теплоемкости газа с числом степеней свободы его молекулы.
7. Запишите выражения для работы в изохорном, изобарном процессах. Выведите выражение для работы газа в изотермическом процессе.
8. Выведите выражение для работы газа в адиабатном процессе.
Таблица экспериментальных данных
Н=…мм DН=…мм DH=…мм
T, с | Значение Hτ, мм | <Hτ>, мм | Ln<Hτ> | ||
1 | 2 | 3 | |||
16 | |||||
12 | |||||
8 | |||||
4 |
Формулы для расчета погрешности
, P=0,95, TСт=1,96 .
, , , .
Записи по теме
naparah.com
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ CP_CV
Таврический национальный университет им. В.И. Вернадского
Кафедра экспериментальной физики
Лабораторная работа № 1
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ
CP /CV ДЛЯ ВОЗДУХА МЕТОДОМ
КЛЕМЕНА И ДЕЗОРМА И
Методом стоячей волны
Симферополь 2002
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ CP /CV ДЛЯ ВОЗДУХА
МЕТОДОМ КЛЕМЕНА И ДЕЗОРМА
Оборудование: стеклянный сосуд с кранами, насос, манометр.
Теоретическая часть работы.
Удельная
теплоемкость вещества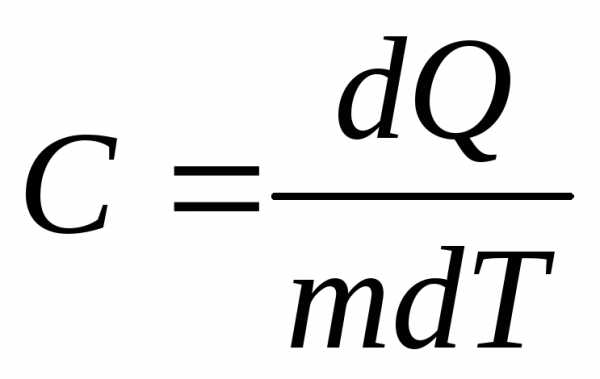 
,
гдеdQ – количество теплоты, необходимое для
изменения температуры массы m вещества на dT градусов.
Молярная
теплоемкость вещества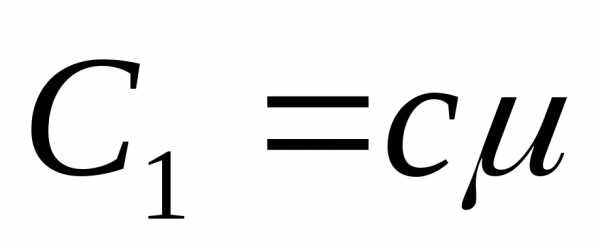 
,
гдеμ – молекулярный вес.
У газов необходимо различать удельную теплоемкость при постоянном давлении СР и при постоянном объеме – СV. Для определения отношения CP/CV в данной работе используется прибор изображенный на рис.1.
стеклянный сосуд соединенный с открытым U-образным манометром. Краны позволяют соединить сосуд с манометром, атмосферой и насосом.
В сосуд накачивают воздух до тех пор, пока разность уровней воды в коленах манометра не станет равной 25-35см. По прошествии 1-2 минут температура воздуха в сосуде становится равной температуре окружающей среды.
Пусть удельный объем V1, давление Р1 и температура Т1 (комнатная). Быстро откачивают и сейчас же закрывают кран, на мгновение соединив сосуд с окружающей средой. Практически сразу давление в сосуде станет равным атмосферному, так как кран имеет большое отверстие, процесс происходит быстро и его можно назвать адиабатическим.
Новый удельный объем V2 , давление Р2 (атмосферное) и температура Т2. Через 1-2 минуты воздух в сосуде нагревается до комнатной тямпературы Т3=T1, его давление будет P3, а удельный объем V3=V1 (ни масса, ни объем не меняется). Переход из первого состояния во второе (адиабатический) подчинен уравнению Пуассона:
(1)
Сравнивая конечное, третье состояние газа с первым, мы видим, что газ в первом и третьем состояниях имеет одну и ту же температуру.
Рис.1. Прибор для определения отношения CP /CV методом Клемена и Дезорма.
Следовательно, к этому переходу применим закон Бойля-Мариотта:
(2)
Решая систему двух уравнений, можно определить γ. Возведем это второе уравнение в степень γ и разделим его на первое уравнение:
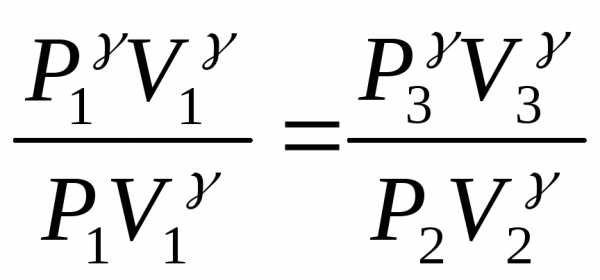(3)
так
как V2=V3,
то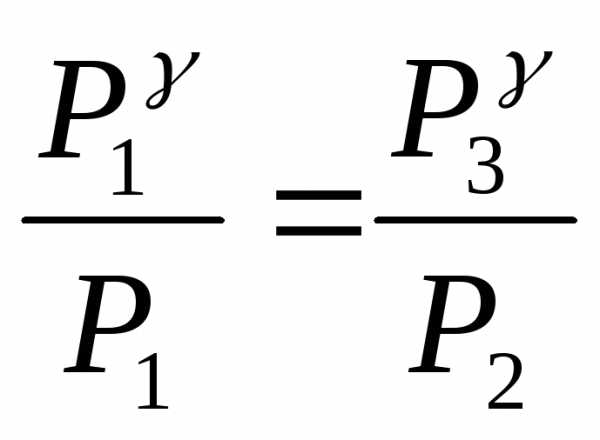 
или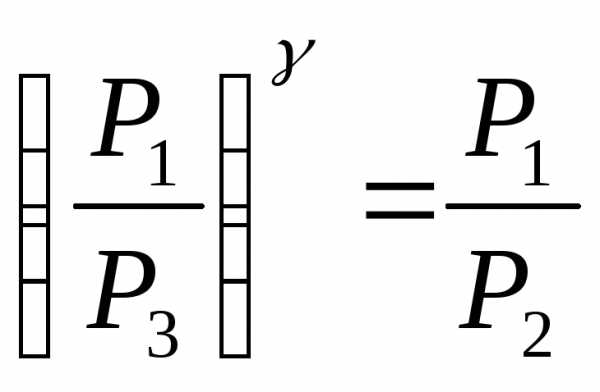
Логарифмируя последнее уравнение находим:
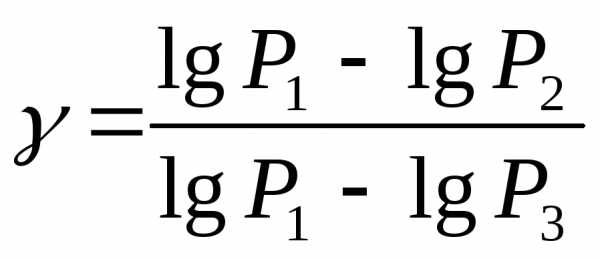(4)
Обозначим разность уровней жидкости в манометре в первом состоянии через h1, а в третьем через h2, тогда:
(5)
(d – удельный вес жидкости в манометре). Подставим это выражение в формулу (4) для γ:
(6)
В нашем случае P1 и Р2 мало отличаются от Р3, то есть h1d и h2d малы по сравнению Р1, Р2, Р3, поэтому отношение разности логарифмов в последнем выражении можно заменить отношением разностей чисел, то есть:
(7)
Это дает расчетную формулу для нашего опыта:
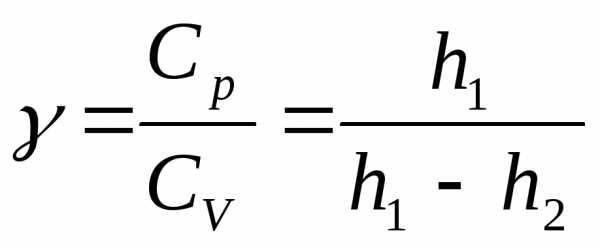(8)
ВЫПОЛНЕНИЕ РАБОТЫ
Накачивают в сосуд воздух.
Закрывают кран К и выжидают, пока температура внутри сосуда станет равна температуре окружающей среды, то есть пока уровни жидкости в манометре не установятся. Это происходит через 1-2 минуты.
Отсчитывают разность уровней в манометре h1 (отсчет производится по нижним краям мениска).
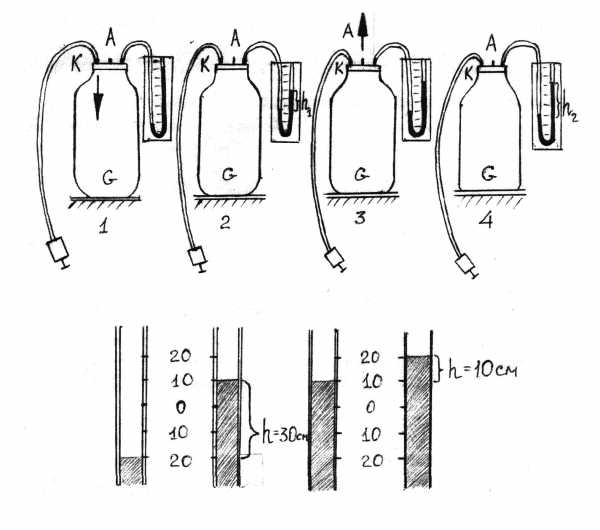
Быстро полностью открывают кран А и сейчас же его закрывают, соединив на мгновение воздух в сосуде с атмосферой.
Подождав еще 1-2 минуты пока температура воздуха в сосуде не станет постоянной, отсчитывают показания манометра h2
Вычисляют γ.
Пункты 1-6 повторяют не меннее 10 раз.
Расчитывают γ среднее.
Оценку погрешности произвести самостоятельно.
ВОПРОСЫ, КОТОРЫЕ НЕОБХОДИМО ЗНАТЬ
ДЛЯ ВЫПОЛНЕНИЯ РАБОТЫ
Почему Ср>Сv?
Вывод уравнения Майера
Вывод уравнения Пуассона.
Связь теплоемкости газа с числом степеней свободы молекул.
Как посчитать число степеней свободы?
Метод определения Ср/Cv.
ЛИТЕРАТУРА
И.К.Кикоин, Л..К.Кикоин. Молекулярная физика. -М.: 1976,
гл. 6,§§ 73, 74. 75, 77, 78.
Д.В. Сивухин. Курс Общей физики .- М.: Наука, 1979,
гл. II, §5 10-16, 18-21, 23, 24.
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ СP/СV МЕТОДОМ
СТОЯЧЕЙ ВОЛНЫ.
Оборудование: звуковой генератор, осциллограф, труба.
Задачей работы является определение скорости звука в воздухе методом стоячей волны и определение отношений удельных теплоемкостей.
Скорость распространения продольных волн в сплошной среде
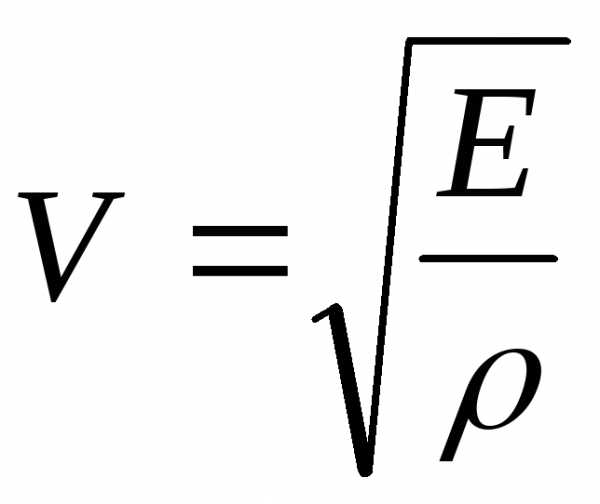
где Е – модуль Юнга среды, ρ – ее плотность.
Процесс распространения акустических волн можно считать адиабатическим, поэтому формула для скорости звука записывается в виде:
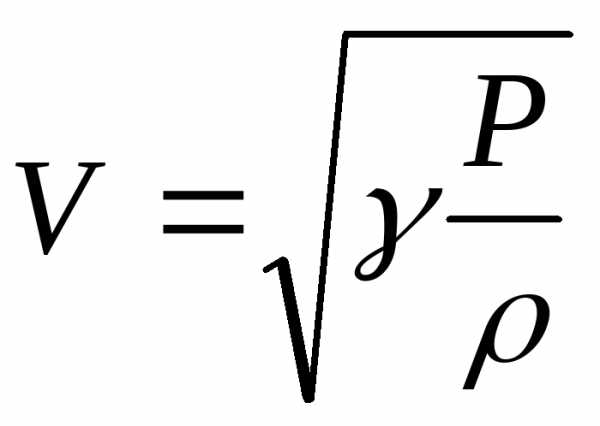
где γ =СP/СV – отношение удельных теплоемкостей газа, Р – атмосферное давление.
ОПИСАНИЕ УСТАНОВКИ
Установка состоит из трубы, звукового генератора, осциллографа. Внутри трубы могут перемещаться стержни, на которых помещены телефоны Т2 и Т1, один из которых является передатчиком колебаний, а другой – приемником. Телефон Т1 возбуждается звуковым генератором, сигнал воспринимается телефоном Т2 и подается на осциллограф.
ЗАДАНИЕ 1.
Определение скорости звука методом стоячей волны.
Включить питание осциллографа и генератора от сети переменного тока. После прогрева (5 мин) поставить лимб звукового генератора на ν=1050 Гц, а ручку выходного напряжения в крайнее правое положение. Выдвигая телефон Т1, фиксируют и находят расстояние между двумя последовательными положениями стержня, при которых устанавливается стоячая волна. Установлению стоячих волн соответствует резкое увеличение амплитуды электрических колебаний, наблюдаемых на экране осциллографа. Каждое измерение необходимо провести 3 раза и взять среднее значение.
Зная расстояние между максимумами амплитуды, найти длину звуковой волны и по формуле V = λν найти скорость звука.
Произведя измерения скорости звука при данной температуре, вычислить по известной формуле:
, 
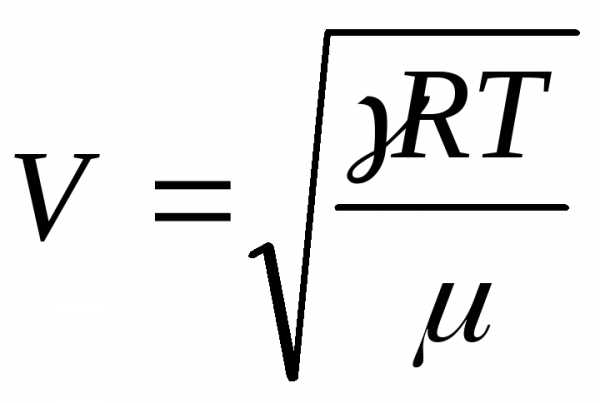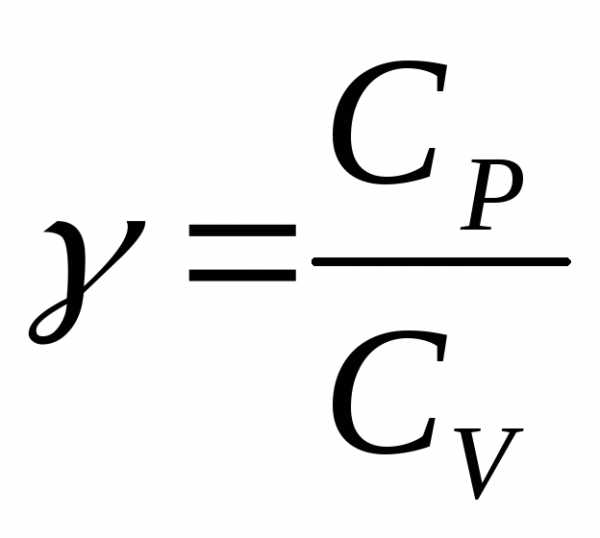
Сравнить полученный результат с результатом, полученным в методе Клемена и Дезорма.
2
studfiles.net
Теплоёмкость идеального газа – это… Что такое Теплоёмкость идеального газа?
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
Молярная теплоемкость
Молярная теплоемкость — теплоемкость 1 моля идеального газа.
Теплоемкость идеального газа в изопроцессах
Адиабатический
В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть . Однако, объём, давление и температура меняются, то есть .
Следовательно, теплоемкость идеального газа в адиабатическом процессе равна нулю: .
Изотермический
В изотермическом процессе постоянна температура, то есть . При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности:
Изохорный
В изохорном процессе постоянен объем, то есть . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (). Первое Начало Термодинамики для изохорного процесса имеет вид:
А для идеального газа
Таким образом,
где — число степеней свободы частиц газа.
Изобарный
В изобарном процессе ():
CP=δQ/νΔT=CV+R=((i+2)/2)*R
Вывод формулы для теплоемкости в данном процессе
Согласно 1 началу термодинамики существует 2 способа изменить внутреннюю энергию тела (в нашем случае идеального газа): передать ему тепло или совершить над ним работу.
dU=δQ+δA, где δA — работа окр. среды над газом.
δAокр.среды=-δAгаза
δQ=dU+δAгаза
В расчете на 1 моль:
С=δQ/ΔT=(ΔU+pΔV)/ΔT
ΔU=CV*ΔT
C=CV+(pΔV/ΔT)в данном процессе
См. также
dic.academic.ru
ФИЗИКА – Молекулярная физика и термодинамика. Учебное пособие
дифференциал. Это означает, что ни количество переданного тепла δQ , ни
работа не тождественны с энергией. Они имеют только тот смысл, что их сумма определяет изменение энергии (разд. Д1, 2).
На рис. 5, б работа, совершаемая газом, положительна, на рис. 5, в – отрицательна. Итоговая работа (работа цикла) на рис. 5, а – положительна.
Равновесное состояние системы – это такое состояние, при котором все параметрысистемы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Процесс, состоящий из непрерывной последовательности равновесных
состояний, называется равновесным, иликвазистатическим.Из сказанного следует, что равновесным может быть только бесконечно медленный процесс. При достаточно медленном протекании реальные процессы могут приближаться к равновесному сколь угодно близко.
Равновесный процесс может быть проведен в обратном направлении, причем система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности.Поэтому равновесные процессы
называют также обратимыми (разд. Д1).
Процесс, при котором система после ряда изменений возвращается в исходное состояние, называется круговым процессом, или циклом (рис. 5, а). Графически цикл изображается замкнутой кривой.
Внутренняя энергия идеального газа равна сумме кинетических энергий отдельных молекул этого газа (взаимодействием между молекулами в схеме идеального газа пренебрегают).
Внутренняя энергия − это функция состояния системы. Всякий раз, как система возвращается в данное состояние, ее внутренняя энергия приобретает одно и то же значение, присущее этому состоянию.
5. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
[1, с. 267–270;2; 6]
Количество тепла1 Q, сообщенное системе, идет на приращение ее внутренней энергии∆U и на совершение системой работы (А) над внешними телами:
Количество теплоты функцией состояния не является, оно зависит от пути перехода системы из одного состояния в другое.
Первое начало термодинамики означает, что невозможен процесс,
единственным результатом которого было бы производство работы без каких-либоизменений в других телах. Механизм, в котором осуществляется такой процесс, называется перпетум мобиле I рода (вечный двигатель).
1 Отметим, что в дальнейшем количество тепла, полученное системой, будем обозначать какQ, или как ∆Q, а соответствующую малую величину −δQ .
studfiles.net
3.3. Явление переноса Понятия о физической кинематике. Время релаксации. Физическая кинетика – это микроскопическая теория процессов в неравновестных системах. Физическая кинетика исходит из представления о молекулярном строении рассматриваемой среды и силы взаимодействия между частицами. Физическая кинетика включает в себя кинетическую теорию газов, основанную на следующих общих положениях классической статистичекой физики: 1. В системе частиц выполняются законы сохранения энергии, импульса, момента импульса, электрического заряда и числа частиц. 2. Все частицы являются “меченными”, т.е. тождественные частицы отличны друг от друга. 3. Все физические процессы в системе протекают непрерывно в пространстве и времени (не квантуются). 4. Каждая частица системы может иметь произвольное значение координат и компонент скорости, независимо от других частиц. Рассмотрим систему, находящуюся в неравновесном состоянии. Если эту систему изолировать от внешних воздействий. которые и вывели ее из равновесного состояния, то через некоторое время она самопроизвольно перейдет в равновесное состояние. Этот процес называется релаксацией. Переход в равновесное состояние обусловлен хаотическим тепловым движением частиц. Время, за которое первоначальное отклонение какой-лтбо величины от ее равновесного значения уменьшается в e раз называется временем релаксации. Эффективное сечение. Длина свободного пробега. Молекулы газа при своем хаотическом движении сталкиваются друг с другом, в результате этих столкновений изменяется направление движения и модуль скорости молекул. Между двумя столкновениями молекул проходит некоторый путь λ, который называется длинной свободного пробега. В дальнейшем линной свободного пробега будем называеть среднее значение < λ >. Эффективный диаметр молекулы – минимальное расстояние, на которое сближаются центры двух молекул в момент соударения. Эффективный диаметр слабо зависит от температуры, уменьшаясь с ее увеличением < λ > = <v> t / <z> ; z – число молекул, с которыми она столнется за время t ; Ясно, что молекула при своем движении столкнется со всеми молекулами, центр которых находится внутри цилиндра радиусом d, а длинна образующей <v> t. <z> = nTd (ст.2) <v> ПИ ; < λ > = <v> t / ПИ d (ст.2) n <v> t = 1/ ПИ d (ст.2) n Эта формула получена нами в предположении, что движется только одна молекула, а все остальные заморожены. Если учесть движения других молекул, то это выражение имеет вид: < λ > = 1 / (корень из 2) ПИ d (ст.2) n ; P = nkT ; n = P / kT; < λ > = kT / (корень из 2) ПИ d (ст.2) P Явление переноса. В термодинамической неравновесной системе возникают особые неравновесные процессы, называемые явлением переноса., в результате которых происходит перенос в пространстве энергии, массы и импульса. К явлениям переноса относятся: 1) теплопроводность (перенос энергии) ; 2) диффузия (перенос массы) ; 3) внутренние трение или вязкость (перенос импульса) ; | 1. Теплопроводность. Если в некоторой области газа средняя кинетическая энергия молекул больше, чем в остальных областях, то за счет хаотического движения молекул и соударений между ними происходит постоянное вырабатывани кинетической энергии молекул по всему объему газа. Энергия переносится из областей, где температура газа выше в те области, где она ниже. Рассмотрим одномерный случай: если T1 > T, то dQ = – æ (dT / dx) S dt ; æ = 1/3 c p <v> <ЛЯМДА> ; c – теплоемкость, p – плотность. Диффузия – это обусловленное тепловым движением выравнивание концентрации смеси нескольких веществ. Этот процес наблюдается в газах, жидкостях и твердых телах. Рассмотрим двухкомпонентную смесь. Будем считать, что молекулы обеих компонент обладают близкими массами и близкими значениями эффективных диаметров. В этом случае можно считать, что <v> и <ЛЯМДА> у молекул обеих компонент одинаковы. Эмпирическое уравнение диффузии имеет вид: dmi = Д (dpi / dx) dS dt. Д – коэффициент диффузии. Д = (1/3) <v> <ЛЯМДА> ; dpi / dx – градиент плотности ; Т.к. <v> и <ЛЯМДА> для обеих компонент смеси примерно одинаковы, то и коэффициент диффузии для них будет одинаков. Вязкость или внутреннее трение. В потоке газа молекулы участвуют одновременно в двух видах движений – хаотическом тепловом и упорядоченном направленном движении. Пусть <v> – скорость хаотического теплового движения, а <u> – скорость упорядоченного движения молекул ; u значительно меньше v ; В результате движения молекул, молекулы из слоя газа, двигающегося с одной поступательной скоростью u будут перемешиваться с молекулами из другого слоя. В результате столкновеня молекул между собой молекулы из быстрого слоя будут передавать часть своего импульса молекулам из медленного слоя и таким образом тормозиться. По этой причине в газе возникает своеобразная сила внутреннего трения, которая замедляет движение быстрых слоев и ускоряет движение медленных слоев. Fтр = η | du / dx| S ; При увеличении температуры газа возрастает скорость теплового движения молекул и следовательно частота соударений между ними. Следствием этого является увеличение переноса импульса от одного слоя газа к другому, поэтому при увеличении температуры газа, его вязкость возрастает. Иная картина наблюдается в жидкостях. В жидкостях основной причиной возникновения внутреннего трения являются межмолекулярные взаимодействия (которые в газе практически отсутствуют). С увеличением температуры жидкости возрастает скорость теплового движения молекул и их кинетической энергии оказывается достаточно для разрыва межмолекулярных связей. Это приводит к ослаблению взаимодействия между молекулами и как следствие уменьшению вязкости жидкости. | 3.4. Основы термодинамики Термодинамический процесс – это переход термодинамической системы из одного состояния в другое. Термодинамический процесс называется обратимым, если после него можно возвратить систему в исходное состояние, при этом в исходное состояние должны вернуться и все тела, взаимодействующие с системой. Процесс, который не удовлетворяет этим условиям называется необратимым. Необходимым условием обратимого процесса является его равновестность, однако не всякий равновестный процесс обратим. Работа газа при изменении объема. dA = Fdl ; при этом сила постоянна ; dA = PS dl ; Sdl = dV ; dA = p dV ; A = (интеграл V1 – V2) P dV ; (рисунок – график, на нем правая часть гиперболы, оси – V, P ; dA – отрезок на этом графике). Графики зависимости термодинамических параметров друг от друга мы имеем право рисовать только для равновесного процесса, т.к. только для равновестного процесса значения этих параметров можно приписать всей термодинамической системе. Для неравновестного процесса, например P может быть разным для различных точек термодинамической системы. Чем медленнее протекает процесс, тем он ближе к равновестному. Эквиваленты теплоты и работы. Обмен энергией между термодинамической системой и внешними телами может осуществляться 2мя качественно различными способами: путем совершения работы и путем теплообмена. В отсутствии внешних полей работа совершается при изменении объема или формы системы. Работа A’, совершаемая внешнми телами над системой численно равна и противоположна по знаку работе, совершаемой самой системой. Первое начало термодинамики или первый закон термодинамики. dQ = dU + dA ; Теплота, подводимая к термодинамической системе идет на изменение внутренней энергии и на совершение работы. Внутренняя энергия U определяется только состоянием термодинамической системы, а Q и A являются характеристиками процесса при котором система переходит из одного состояния в другое. Переход системы из одного состояния в другое может осуществляться различными путями, поэтому Q и A зависят от способа перехода системы из одного состояния в другое, в то время, как внутренняя энергия U определяется только состоянием системы и не зависит от того, каким путем система перешла в это состояние. Теплоемкость многоатомных газов. C = Q / m delta T ; C = dQ/ dTm ; Cm = dQ / dT МЮ – молярная теплоемкость. В газе различают теплоемкости при постоянном давлении и теплоемкость при постоянном объеме. 1) V=const ; dV=0 ; dA=PdV=0 ; dQ=dU ; Ev = dQm / dT ; Eт = dUm / dT ; Um = i k T Na/ 2 = i R T / 2 ; где i – число степеней свободы ; dUm = i R dT / 2 ; Ev = i R / 2 – теплоемкость при постоянном V ; 2) P = const ; dAm = dm + dA ; dA= pdV ; PV=RT ; PdV= RdT ; dQm = Cv dT + RdT = Cv + RdT ; Cp = dQm / dT= Cv +R ; Cp= Cv +R – уравнение Майера ; Cp = (iR / 2) + R = ((i +2)/ 2) R ; Cp = ((i+2) / 2) R ; γ = Cp / Cv = (i+2) / i – коэффециент Пуассона Из полученной формулы видно, что теплоемкость газа не зависит от температуры. Эксперементально было установленно, что этот закон соблюдается в достаточно широком интервале температур только для одноатомных газов. Уже для простых молекул – молекул h3 зависимость Cv от температуры имеет вид: Cv = i R / 2 (рисунок – график, ступеньки; оси T, Cv). Такая зависимость теплоемкости от температуры обусловлена тем, что в случае простейшей молекулы нарушается принцип равновестного распределения энергии по степеням свободы. Вращательное и колебательное движение молекул квантуются, т.е. энергия вращательных и колебательных движений не может принимать любые значения, а может иметь только вполне определенные дискретные значения. При низких температурах энергии не достаточно, чтобы возбудить вращательное и колебательное движения молекул, поэтому вращательные и колебательные степени свободы “выморожены” и не участвуют в создании теплоемкости, поэтому при низких температурах молекулы h3 имеют только 3 степени свободы (поступ.) и Cv= 3R / 2. При увеличении температуры возбуждается сначало вращательное движение (i = 5, Cv = 5 R / 2), а затем при достаточно высокой температуре и колебательном движении (i =7, Cv = 7R / 2), т.е. число степеней свободы зависит от температуры. Применение 1-го начала термодинамики к изопроцессам и адиабатическому процессу. 1) V = const изохорный => dV=0 ; d = PdV=0 ; dQ=dU ; dU = МЮ dUмол = МЮ Cv dT ; dQ= МЮ Cv dT ; Q = (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T2 – T1) – m Cv (T2 – T1)/ μ 2) T = const изотермический => dT= 0 ; dQ= МЮ Cv dT = 0 ; dQ = dA ; dA = PdV ; PV = МЮ RT ; P= МЮ RT / V ; dA = МЮ RT dV / V ; A = (интеграл V1 – V2) МЮ RTdV / V = МЮ RT (интеграл V1 – V2) dV/ V = МЮ RT ln (V2/ V1) = МЮ RT ln (P1/ P2) ; P1 V1 = P2 V2 ; | 3) P = const изобарический => dQ = PdV ; A = (интеграл V1 – V2) PdV = P (V2 – V1) ; A = P (V2 – V1) ; dU = МЮ Cv dT ; PdV = МЮ RdT ; dQ = МЮ Cv dT + МЮ Rdt = МЮ (Cv + R) dT ; Q = МЮ Cp (T2 – T1) ; 4) Q = const Адиабатный dA = dU ; dA = МЮ Cv dT ; PdV = – МЮ Cv dT ; PV = МЮ RT – продифференцированное уравнение Менделеева-Клайперона ; PdV + VdP = МЮ R dT ; … ; lnP = – γ lnP + const ; γ – коэффициент Пуассона ; lnP + lnV (ст. γ) = const ; PV (ст. γ) = const ; (график такой же как и изотермический, только чуть выше вверх). dA = – dU = – МЮ Cv dT ; A = – (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T1 – T2) ; Энтропия. Помимо внутренней энергии, которая является только функциональной составляющей термодинамической системы, в термодинамике используется еще ряд других функций, описывающих состояние термодинамической системы. Особое место среди них занимает энтропия. Пусть Q – теплота, полученная термодинамической системой в изотермическом процессе, а T – температура, при которой произошла эта передача теплоты. Величина Q/ T называется приведенной теплотой. Приведенное количество теплоты, сообщаемое термодинамической системе на бесконечно малом участке процесса будет равно dQ / T. В термодинамике доказывается, что в любом обратимом процессе сумма приведенных количеств теплоты, передаваемая системе на бесконечно малых участках процесса равна нулю. Математически это означает, что dQ/T – есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от того, каким путем перешла система в такое состояние. Функция, полученный дифференциал которой равен dS= dQ/ T – называется энтропией. Энтропия определяется только состоянием термодинамической системы и не зависит от способа перехода системы в это состояние. S – энтропия. Для обратимых процессов delta S = 0. Для необратимых delta S > 0 – неравенство Клаудио. Неравенство Клаудио справедливо только для замкнутой системы. Только в замкнутой системе процессы идут так, что энтропия возрастает. Если система незамкнута и может обмениваться теплотой с окружающей средой, ее энтропия может вести себя любым образом ; dQ = T dS ; При равновестном переходе системы из одного состояния в другое dQ = dU + dA ; delta S = (интеграл 1 – 2) dQ / T = (интеграл) (dU + dA) / T. Физический смысл имеет не сама энтропия, а разность энтропий при переходе системы из одного состояния в другое. Связь энтропии с вероятностью состояния системы. Более глубокий смысл энтропии скрывается в статической физике. Энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы. Иными словами W – это число микросостояний, которые реализовывают данные макросостояния. Больцман методами статистической физики показал, что энтропия S системы и термодинамическая вероятность связаны соотношением: S= k ln (W) ; где k – постоянная Больцмана. Термодинамическая вероятность W не имеет с математической вероятностью ничего общего. Из этого соотношения видно, что энтропия может рассматриваться как мера вероятности состояния термодинамической системы, энтропия является мерой неупорядоченной системы. Чем больше число микросостояний, реализующих данное макросостояние, тем больше ее энтропия. Второй закон термодинамики. Количество теплоты, полученное от нагревателя, не может быть целиком преобразовано в механическую работу циклически действующей тепловой машиной. Это и есть 2ой закон: в циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от источника энергии – нагревателя. (by Кельвин Copyright 1851). Второй закон связан с необратимостью процессов в природе. Возможна другая формулировка: невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от холодного тела к горячему. Второй закон имеет вероятный характер. В отличие от закона сохранения энергии, второй закон применим лишь к системам, состоящим из очень большого числа частиц. Для таких систем необратимость процессов объясняется тем, что обратный переход должен был бы привести систему в состояние ничтожно малой вероятностью, практически не отличимой от невозможности. Самопроизвольные процессы в изолированной системе всегда проходят в направлении перехода от маловероятного состояния в более вероятное. |
studfiles.net
Теплоемкость идеального газа
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
Во многих случаях удобно использовать молярную теплоемкость C:
где M – молярная масса вещества. Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом.
В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры. Такая неоднозначность определения теплоемкости характерна только для газообразного вещества.
При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp – молярная теплоемкость в изобарном процессе (p = const). В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры. Для процесса при постоянном давлении первый закон термодинамики дает:
|
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
где R – универсальная газовая постоянная. При p = const
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
Молярная теплоемкость Cp газа в процессе с постоянным давлением всегда больше молярной теплоемкости CV в процессе с постоянным объемом (рис. 3.10.1).
| 1 |
| Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT = T2 – T1. При p = const газ совершает работу A = p1(V2 – V1). Поэтому Cp > CV. |
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
В частности, это отношение входит в формулу для адиабатического процесса (см. §3.9). Между двумя изотермами с температурами T1 и T2 на диаграмме (p, V) возможны различные пути перехода. Поскольку для всех таких переходов изменение температуры ΔT = T2 – T1 одинаково, следовательно, одинаково изменение ΔU внутренней энергии. Однако, совершенные при этом работы A и полученные в результате теплообмена количества теплоты Q окажутся различными для разных путей перехода.
Отсюда следует, что у газа имеется бесчисленное количество теплоемкостей. Теплоемкости Cp и CV – это лишь частные (и очень важные для теории газов) значения теплоемкостей. Термодинамические процессы, в которых теплоемкость газа остается неизменной, называются политропическими.
Все изопроцессы являются политропическими. В случае изотермического процесса ΔT = 0, поэтому CT = ∞. В адиабатическом процессе ΔQ = 0, следовательно, Cад = 0. Следует отметить, что «теплоемкость», как и «количество теплоты» – крайне неудачные термины.
Они достались современной науке в наследство от теории теплорода, господствовавшей в XVIII веке. Эта теория рассматривала теплоту как особое невесомое вещество, содержащееся в телах. Оно не может быть ни создано, ни уничтожено. Нагревание тел объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Теория теплорода несостоятельна.
Она не может объяснить, почему одно и то же изменение внутренней энергии тела можно получить, передавая ему разное количество теплоты в зависимости от работы, которую совершает тело. Поэтому лишено физического смысла утверждение, что «в данном теле содержится такой-то запас теплоты». В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией поступательного движения молекул и абсолютной температурой T:
Внутренняя энергия 1 моля идеального газа равна произведению на число Авогадро NА:
При изменении температуры на ΔT внутренняя энергия изменяется на величину
Коэффициент пропорциональности между ΔU и ΔT равен теплоемкости CV при постоянном давлении:
Это соотношение хорошо подтверждается в экспериментах с газами, состоящими из одноатомных молекул (гелий, неон, аргон). Однако, для двухатомных (водород, азот) и многоатомных (углекислый газ) газов это соотношение не согласуется с экспериментальными данными. Причина такого расхождения состоит в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать не только энергию поступательного движения, но и энергию вращательного движения молекул.
| 2 |
| Рисунок 3.10.2. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы. |
На рис. 3.10.2 изображена модель двухатомной молекулы. Молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y. Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси Z не происходит, так же как не вращается одноатомная молекула.
Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные). В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы: Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна Из этой теоремы следует, что молярные теплоемкости газа Cp и CV и их отношение γ могут быть записаны в виде
где i – число степеней свободы газа. Для газа, состоящего из одноатомных молекул (i = 3)
Для газа, состоящего из двухатомных молекул (i = 5)
Для газа, состоящего из многоатомных молекул (i = 6)
Экспериментально измеренные теплоемкости многих газов при обычных условиях достаточно хорошо согласуются с приведенными выражениями. Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле. Теорему о равномерном распределении энергии по степеням свободы можно применить и к тепловому движению частиц в твердом теле.
Атомы, входящие в состав кристаллической решетки, совершают колебания около положений равновесия. Энергия этих колебаний и представляет собой внутреннюю энергию твердого тела. Каждый атом в кристаллической решетке может колебаться в трех взаимно перпендикулярных направлениях. Следовательно, каждый атом имеет 3 колебательные степени.
При гармонических колебаниях средняя кинетическая энергия равна средней потенциальной энергии. Поэтому в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. Внутренняя энергия 1 моля твердого вещества равна:
Поэтому молярная теплоемкость вещества в твердом состоянии равна:
|
Это соотношение называется законом Дюлонга–Пти. Для твердых тел практически не существует различия между Cp и CV из-за ничтожно малой работы при расширении или сжатии. Опыт показывает, что у многих твердых тел (химических элементов) молярная теплоемкость при обычных температурах действительно близка к 3R. Однако, при низких температурах наблюдаются значительные расхождения между теорией и экспериментом. Это показывает, что гипотеза о равномерном распределении энергии по степеням свободы является приближением. Наблюдаемая на опыте зависимость теплоемкости от температуры может быть объяснена только на основе квантовых представлений.
fizika.ayp.ru