Скорость при РПД
Известно что, для того чтобы найти положение тела в какой-то момент времени, нужно знать вектор перемещения, потому что именно он связан с изменением координат движущегося тела. Как же найти вектор перемещения? Ответ на этот вопрос зависит от того, какое движение совершает тело.
Рассмотрим равномерное движение тела.
Равномерное движение — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Стоит отметить, что равномерное движение может быть как прямолинейным, когда траекторией движения тела является прямая линия, так и криволинейным, когда траекторий является любая кривая.
Равномерное прямолинейное движение – самый простой вид движения, так как траекторией является прямая линия.
При движении тела вдоль прямой в одном направлении перемещение тела непрерывно возрастает. Чтобы найти перемещение за некоторый промежуток времени, надо знать, как быстро оно возрастает. Быстроту этого возрастания определяют отношением перемещения к значению промежутка времени, в течение которого оно произошло. Это отношение называют
Таким образом, скорость равномерного прямолинейного движения тела — это физическая векторная величина, равная отношению перемещения тела к промежутку времени, в течение которого это перемещение произошло.
Т.е. скорость показывает, какое перемещение тело совершает в единицу времени.
Важно помнить, что единицей скорости в системе СИ является м/с.
Значит, для того чтобы найти перемещение тела заданное время t, надо знать его скорость υ. Тогда перемещение тела можно вычислить по формуле:
По формулам, написанным в векторной виде, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия. Тогда, в проекциях на ось х уравнение примет вид:
s
Это уравнение называют уравнением перемещения.
Остановимся более подробно на определении знака проекции скорости и перемещения.
– Проекция скорости и перемещения будет положительной, если тело движется в положительном направлении оси координат (х >x0).
– Проекция скорости и перемещения будет отрицательной, если тело движется в отрицательном направлении оси координат (х<x0).
– Проекция скорости и перемещения будет равна нулю, если тело покоится или движется в направлении, перпендикулярном оси координат
Получим формулу для вычисления координаты тела х в любой момент времени.
Пусть в момент времени t0= 0 с координата тела была х0, в момент времени t — х. Тогда за промежуток времени Δt = t – t0 = t координата тела изменилась на величину Δх = х – х0. Проекция скорости тела в этом случае будет равна
Тогда
x – x0= υх
Или
х = х0+ υхt
Это уравнение называют кинематическим уравнением равномерного движения.
Полученная формула может видоизменяться в зависимости от знака проекции скорости и значения начальной координаты.
Если тело движется вдоль оси х в положительном направлении, то формула принимает вид
x = х1+ υ1t
Если тело движется вдоль оси х в отрицательном направлении, то формула принимает вид:
если начальная координата равна нулю
х = –υ2t
или
х
Так как, при равномерном прямолинейном движении направление скорости тела не изменяется, то путь равен модулю перемещения.
Тогда
s = |υx|t
Это выражение называют уравнением пути.
Если же направление движения тела меняется, то пройденный путь окажется больше модуля вектора перемещения.
Основные выводы:
· Равномерное прямолинейное движение — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
· Основной характеристикой равномерного движения является скорость.
· Единицей скорости в системе СИ является м/с.
· Скорость показывает, какое перемещение тело совершает в единицу времени.
· х = х0+ υхt — кинематическое уравнение равномерного движения
· Проекция скорости на ось х будет положительной, если тело движется вдоль оси х в положительном направлении. При этом проекция вектора перемещения так же будет положительной.
· Проекция скорости на ось х будет отрицательной, если тело движется вдоль оси х в отрицательном направлении. При этом проекция вектора перемещения так же будет отрицательной.
· Скорость тела и перемещение будут равны нулю, если тело покоится или движется в направлении, перпендикулярном оси координат.
videouroki.net
Уравнение РПД
Мы знаем, что в каждый момент времени, положение точки задаётся радиус-вектором. Пусть в момент времени
Исходя из определения скорости равномерного прямолинейного движения, запишем:
Как правило, начальный момент времени — это точка отсчёта, поэтому примем t0 = 0. Если мы теперь выразим из полученного выражения, то получим функцию зависимости радиус-вектора от времени:
Это и есть уравнение равномерного прямолинейного движения. То есть, если нам известно начальное положение точки и скорость её движения, то мы сможем найти радиус-вектор в каждый момент времени.
Вместо векторного уравнения можно использовать уравнение для каждой из координат:
Поскольку пройденный путь — это изменение координаты х в данном случае, мы можем найти его, используя модуль скорости. Заметим, что числовые значения пройденного пути и перемещения будут совпадать при прямолинейном движении. Только не стоит забывать, что пройденный путь — это скалярная величина, которая не может быть отрицательной.
Перемещение же, легко может быть отрицательным, если точка двигается в направлении, противоположном направлению координатной оси.
Итак, мы выяснили, что для описания равномерного прямолинейного движения достаточно получить уравнение для одной координаты. Давайте рассмотрим, как будут выглядеть графики функций зависимости скорости и координаты от времени. Начнём с простого: при равномерном движении скорость постоянна. Поэтому график зависимости скорости от времени будет представлять собой прямую горизонтальную линию.
Иными словами, при равномерном движении скорость не зависит от времени, так как является константой. Заметим, что если мы рассмотрим конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением координаты
Рассмотрим теперь несколько графиков зависимости координаты от времени. На рисунке вы видите три прямых, каждая из которых описывается одним и тем же уравнением.
Точки пересечения этих графиков с осью х соответствуют значениям начального положения х0. Как видно из графика, для зелёной прямой х0 = 0, для синей прямой х0 > 0, а для красной — х0 < 0. На графике видно, что скорость для красной и зелёной прямых больше нуля. Действительно, ведь значение координаты
Примеры решения задач.
Задача 1. Точка, равномерно двигаясь вдоль оси X, переместилась из координаты в координату за 5 с. Определите модуль и направление скорости этой точки.
Задача 2. Две машины равномерно двигаются по одной прямой. Опишите условия, при которых столкновение невозможно.
Движения и того, и другого автомобиля описываются одним и тем же общим уравнением. Обозначим одну машину за грузовик, а другую за легковую. На графике обозначим грузовик синей точкой, а легковую машину — красной точкой. Итак, рассмотрим первый случай: машины двигаются в разные стороны. Тогда, скорость одной машины должна быть положительной, а скорость другой — отрицательной (например, легковая машина будет двигаться в положительном направлении). Чтобы машины не столкнулись, начальная координата машины с отрицательной скоростью, должна быть меньше, чем начальная координата машины с положительной скоростью. В противном случае, они будут двигаться навстречу друг другу и столкнуться. Графически это можно изобразить так:
Скорость красного графика положительная, поскольку координата х увеличивается с течением времени, а скорость синего графика — отрицательная, поскольку координата х уменьшается с течением времени. Эти графики никогда не пересекутся, поэтому столкновения не произойдёт. Заметим, что при таком раскладе, скорости не имеют значения. Имеет значение только знак (то есть направление движения). Конечно, вы можете сказать, что если мы продолжим графики, то они всё же пересекутся. Но для этого машинам нужно переместиться в прошлое, потому что координата времени, соответствующая точке пересечения, отрицательная.
Рассмотрим теперь второй случай: когда машины двигаются в одном направлении, и при этом, машина, идущая впереди, едет быстрее. Что значит, машина, идущая впереди? Это значит, что её начальная координата должна быть больше.
То есть условие таково: машина, начальная координата которой больше, должна двигаться со скоростью не меньше, чем скорость второй машины. Опять же, если мы изобразим это графически, то увидим, что графики не пересекаются.
Начальная координата красного графика больше и скорость тоже больше. Если же скорости будут одинаковы, то это будет означать одинаковый наклон синей и красной линий по отношению к оси времени. В этом случае, графики будут представлять собой параллельные прямые, а такие прямые, как известно, не пересекаются.
videouroki.net
Графики зависимости кинематических величин от времени при РПД и РУД
Механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.
В свою очередь механическое движение бывает двух видов — равномерным, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.
Вспомним основные формулы для равномерного и неравномерного движения.
Если движение равномерное, то:
Скорость тела не меняется с течением времени. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени
Это уравнение называется уравнением перемещения.
Это уравнение называется кинематическим уравнением равномерного движения.
Для равноускоренного движения:
Ускорение тела не изменяется с течением времени. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло.
Уравнение скорости для равноускоренного движения имеет вид:
Это уравнение называется уравнением перемещения для равноускоренного движения.
Кинематическое уравнение равноускоренного движения имеет вид:
Для большей наглядности движение можно описывать с помощью графиков.
Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, то полученный график будет выражать зависимость ускорения тела от времени.
Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.
Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, или под осью времени, если тело движется замедленно.
Если же по оси ординат откладывать значение не ускорения, а скорости тела, то можно получить график скорости.
Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. График скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.
Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта зависимость состоит в том, что скорость с течением временине меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.
По графику скорости можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади закрашенного прямоугольника: верхнего, если тело движется в сторону положительного направления, или нижнего — в случае движения тела в отрицательном направлении.
Действительно, площадь прямоугольника равна произведению его сторон:
где a и b стороны прямоугольника.
Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, или отрицательным, если проекция вектора скорости отрицательна.
При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле
Т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненных к оси времени. Причем, чем больше угол наклона, тем большую скорость имеет тело. На представленном графике прямая 1 соответствует движению с положительным ускорением и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением и начальной скоростью равной нулю.
По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника для второго тела. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В представленном случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости. При этом проекция перемещения для первого тела будет положительной.
Для второго тела, прямоугольного треугольника, проекция перемещения равна половине произведения его катетов. Т.е. это время и конечная скорость тела. Проекция перемещения — отрицательна.
Теперь рассмотрим зависимость пройденного пути от времени.
Как и в предыдущих случаях, по оси абсцисс будем откладывать время, с момента начала движения, а по оси ординат — путь.
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.
При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем большая скорость движения тела.
При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.
Теперь перейдем к рассмотрению зависимости перемещения от времени.
Рассмотрим равномерное движение. Т.к. при равномерном движении перемещение линейно зависит от времени, то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго. А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения тела.
Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю. Для 2-го тела ускорение и начальная скорость тела больше нуля. Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля. У 4-го тела начальная скорость и ускорение меньше нуля. Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю. Шестое тело двигается замедленно с некоторой начальной скоростью.
Рассмотрим зависимость координаты тела от времени.
Если по оси абсцисс откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по оси ординат — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения). Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.
График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.
В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).
С помощью графика движения можно определить:
– координаты тела в любой момент времени;
– путь, пройденный телом за некоторый промежуток времени;
– время, за которое пройден какой-то путь;
– кратчайшее расстояние между телами в любой момент времени;
– момент и место встречи и т.д.
По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).
При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.
Основные выводы:
– Механическое движение для большей наглядности можно описывать с помощью графиков:
– Зависимости скорости от времени
– Ускорения от времени
– Координаты тела от времени
– И зависимости перемещения тела от времени, в течении которого это перемещение произошло.
videouroki.net
Графическое представление рпд. График зависимости координаты тела от времени
Графическое представление РПД.График зависимости координаты тела от времени
Для построения этого графика (который иначе называют графиком движения) на оси абсцисс откладывают время движения, а на оси ординат – координату движущегося тела.
Тело движется равномерно вдоль оси Ох системы координат, связанной с телом отсчета. Тогда уравнение движения тела имеет вид х = x0+vx·t.
Из этой формулы видно, что зависимость х от t линейная, следовательно, график этой зависимости представляет собой прямую линию. Эта прямая пересекает ось ординат в точке х = х0. Угол наклона этой прямой к оси абсцисс зависит от скорости движения тела.
График координаты – зависимость координаты тела от времени:
График координаты при равномерном прямолинейном движении – прямые (1, 2, 3).
Если с течением времени координата увеличивается (1, 2), то тело движется по направлению оси ОХ; если координата уменьшается (3), то тело движется против направления оси ОХ.
Чем больше тангенс угла наклона (1), тем больше модуль скорости.
Если графики координат двух тел пересекаются, то из точки пересечения следует опустить перпендикуляры на ось времени и ось координат – так мы узнаем, в какое время тела встретились и координату точки встречи.
Зачем нужна координата, спросите вы. Ведь можно выбрать икс нулевое = 0, это естественно. И формула упростится, будет совпадать с перемещением.
Представьте, соревнуются байкер и велосипедист. Естественно, мотоциклист должен дать фору велосипедисту. Например, 200 метров. Стартуют одновременно по звуку выстрела. Тогда начальная координата байкера 0, а велосипедиста 200. Очень удобно. Чертите график и задача решена! Скорость байкера больше, он обязательно догонит велосипедиста, но это может произойти позже, чем велосипедист успеет доехать до финиша.
График перемещения.
Для выражения зависимости проекции перемещения тела от времени его движения строят график пути. Для этого на оси абсцисс откладывают время, а на оси ординат – пройденный проекцию перемещения. В отличие от графика координаты график проекции перемещения начинается только от нуля.
График проекции перемещения от времени.
График проекции перемещения при равномерном прямолинейном движении – прямая, выходящая из начала координат (1, 2, 3).
Если прямая (1) лежит над осью времени, то тело движется по направлению оси ОХ, а если под осью (2, 3), то против оси ОХ.
Чем больше тангенс угла наклона графика, тем больше модуль скорости (1).
График пути
Для выражения зависимости пути, проходимого телом, от времени его движения строят график пути. Для этого на оси абсцисс откладывают время, а на оси ординат – пройденный телом путь. Зависимость пути от времени линейная, следовательно, график этой зависимости является прямой линией. Эта прямая начинается там же где и начало координат и всегда идет только вверх, ведь путь может только увеличиваться!
Угол наклона этой прямой к оси времени тем больше, чем больше скорость тела. На рис. изображены графики 1 и 2 пути двух тел. Из этого рисунка видно, что за одно и то же время t тело 1, имеющее большую скорость, чем тело 2, проходит больший путь (s1>s2).
Примеры решения задач.
Написать уравнения движения тел, графики которых даны на рисунке.
Обратите внимание, что время для нахождения координаты x выбирается произвольно – то, которое на ваш взгляд удобнее всего!!!
1 тело.
За 2 секунды тело не изменило своего положения, значит скорость тела vx=0, т.е. тело стоит. Тогда уравнение движения будет иметь вид
2 тело
За 2 секунды тело оказалось в точке с координатой
Найдем скорость vx:
Тогда уравнение движения будет иметь вид
3 тело
За 4 секунды тело оказалось в точке с координатой
Найдем скорость vx: (тело движется против выбранной оси!!!)
Тогда уравнение движения будет иметь вид
Решите задачи письменно:
-
Написать уравнения движения тел, графики которых даны на рисунке.
-
Написать уравнения движения тел, графики которых даны на рисунке.
-
Даны уравнения движения: х1=4+0,5t и х2=8-2t. Найти место и время встречи. Задачу решить двумя способами -
Даны уравнения движения: х1=20-4t и х2=10+t. Найти место и время встречи. Задачу решить двумя способами
www.takya.ru
1.1.6 Равноускоренное прямолинейное движение
Видеоурок 1: Равноускоренное движение – Физика в опытах и экспериментахВидеоурок 2: Уравнения равноускоренного движения
Лекция: Равноускоренное прямолинейное движение
Равноускоренное прямолинейное движение
Равноускоренным можно назвать то движение, при котором на протяжении всего наблюдаемого участка пути значение и направление ускорения остается неизменной величиной.

Траектория РПД: прямая линия.
При равноускоренном движении тело за одинаковые интервалы времени изменяет значение своей скорости на постоянную величину.
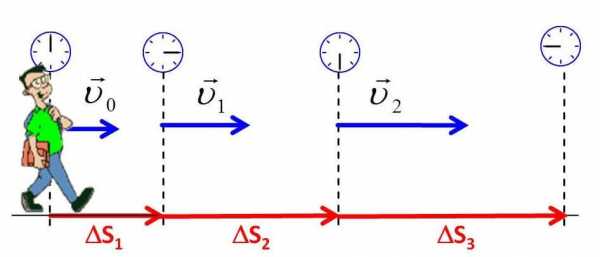 Уравнения движения при РПД
Уравнения движения при РПДДля определения положения тела в любой момент времени следует пользоваться основным уравнением движения.
Уравнение движения для перемещения несколько отличается от уравнения движения для изменения координаты, поскольку начального перемещения быть не может:
Кроме положения тела можно определить и скорость, которую будет иметь тело на отдельном участке пути:
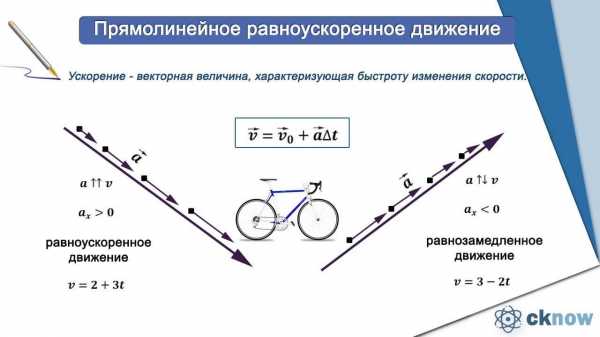
Если тело начинает двигаться с начала координат, то х0=0, если тело двигается вдоль оси ОХ, то значение скорости будет положительным, а если против оси – отрицательным. Если тело двигается равноускоренно, то в основном уравнении ускорение будет иметь положительное значение, если же движение равнозамедленное, то значение ускорения – отрицательное.
Из основных уравнений равноускоренного движения вытекают дополнительные. Если тело двигается из начала координат с нулевой начальной скоростью, то перемещение тела можно определить по формуле:
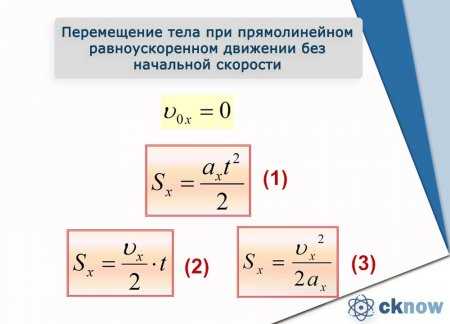 Графики равноускоренного движения
Графики равноускоренного движения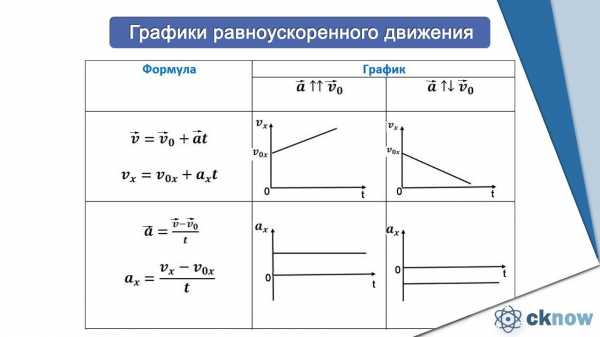
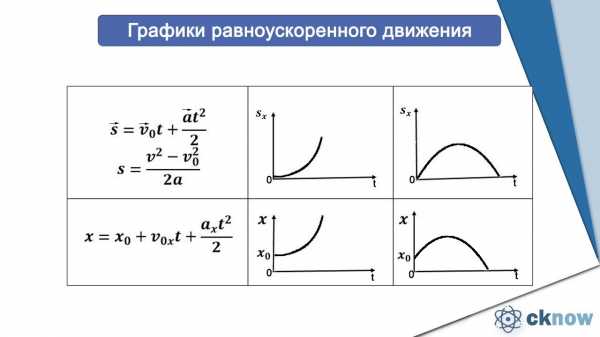
Решать задачи на РП движение можно графическим и аналитическим способом.
cknow.ru
Основное кинематическое уравнение для РПД. — КиберПедия
• Кинематическое уравнение равнопеременного движения()вдоль оси x
где v0 —начальная скорость; t— время.
Скорость точки при равнопеременном движении
Графики скорости и ускорения.
При большем ускорении график скорости изображается прямой, наклоненной к оси времени под большим углом (линия II на рис. 30).
|
Точки пересечения этих графиков с осью времени — это точки перемены знака скорости, т. е. перемены направления движения.
|
Билет №3
Движение тела по окружности с постоянной по модулю скорости.
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.
Положение тела на окружности определяется радиусом-вектором , проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).

Рис. 1
За время Δt тело, двигаясь из точки А в точку В, совершает перемещение , равное хорде АВ, и проходит путь, равный длине дуги l.
Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.
Скорость движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:
Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:
В СИ единицей угловой скорости является радиан в секунду (рад/с).
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.
Положение тела можно определить, если известен модуль радиуса-вектора и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t0 = 0 угловая координата равна φ0, а в момент времени t она равна φ, то угол поворота Δφ радиуса-вектора за время равен . Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:
Оно позволяет определить положение тела в любой момент времени t. Учитывая, что , получаем:
— формула связи между линейной и угловой скоростью.
Промежуток времени Τ, в течение которого тело совершает один полный оборот, называется периодом вращения:
где N — число оборотов, совершенных телом за время Δt.
За время Δt = Τ тело проходит путь . Следовательно,
Величина ν, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:
Следовательно,
Билет №4
Взаимодействие тел.
Взаимодействие тел. Опыт показывает, что при сближении тел (или систем тел) характер их поведения меняется. Поскольку эти изменения носят взаимный характер, говорят, что тела взаимодействуют друг с другом. При разведении тел на очень большие расстояния (на бесконечность) все известные на сегодняшний день взаимодействия исчезают. Галилей первым дал правильный ответ на вопрос, какое движение характерно для свободных (т.е. не взаимодействующих тел). Вопреки существующему тогда мнению, что свободные тела стремятся к состоянию покоя, он утверждал, что при отсутствии взаимодействия тела находятся в состоянии равномерного движения, включающего покой как частный случай. Инерциальные системы отсчета. В рамках формального математического подхода, реализуемого в кинематике, утверждение Галилея выглядит бессмысленным, поскольку равномерное в одной системе отсчета движение может оказаться ускоренным в другой, которая ничем не хуже исходной. Наличие взаимодействия позволяет выделить особый класс систем отсчета, в которых свободные тела движутся без ускорения (в этих системах большинство законов природы имеют наиболее простую форму). Такие системы называются инерциальными. Все инерциальные системы эквивалентны друг другу, в любой из них законы механики проявляются одинаково. Это свойство было также отмечено Галилеем в сформулированном им принципе относительности: никаким механическим опытом в замкнутой (т.е. не сообщающейся с внешним миром) системе отсчета невозможно установить покоится ли она или равномерно движется. Любая система отсчета, равномерно движущаяся относительно инерциальной тоже является инерциальной. Между инерциальными и неинерциальными системами отсчета существует принципиальное отличие: находящийся в замкнутой системе наблюдатель способен установить факт движения с ускорением последних, не выглядывая наружу(напр. при разгоне самолета пассажиры ощущают, что их вдавливает в кресла).
Принцип суперпозиции сил.
Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые, подчеркнём, полностью эквивалентны приведённой выше:
Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя;
Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.
Законы динамики Ньютона.
Билет №5
Силы в природе.
В настоящее время, когда говорят о единстве природы, обычно имеют в виду единство в строении вещества: все тела построены всего лишь из нескольких сортов элементарных частиц. Однако в этом проявляется только одна сторона единства природы. Не менее существенно и другое.
Несмотря на удивительное разнообразие взаимодействий тел друг с другом, взаимодействий, сводящихся в конце концов к взаимодействию элементарных частиц, в природе по современным данным имеется совсем немного типов сил. О четырех из них: о силах тяготения, электромагнитных силах, ядерных силах и слабых взаимодействиях*) мы можем говорить с уверенностью. Из них только два первых типа сил можно рассматривать в смысле ньютоновой механики. С проявлениями всех четырех типов сил мы встречаемся, изучая то, что происходит в безграничных просторах Вселенной, на нашей планете, исследуя любой кусок вещества, живые организмы, атомы, атомные ядра, взаимные превращения элементарных частиц. Еще вчера казалось, что этими четырьмя типами сил исчерпываются все имеющиеся в природе взаимодействия. Сегодня картина представляется уже более сложной. Изучение «интерьера» элементарных частиц приоткрыло новые глубины. Мы уже не можем с прежней уверенностью утверждать, что все известные нам процессы в природе объясняются действием лишь этих сил, что в недрах элементарных частиц не проявляются какие-то новые взаимодействия. Каковы они, эти взаимодействия? Какова их природа? Об этом мы пока почти ничего не знаем.
cyberpedia.su

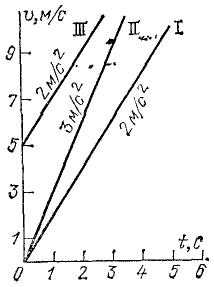 Рис. 30. Графики скорости различных равномерно-ускоренных движений.
Рис. 30. Графики скорости различных равномерно-ускоренных движений.
 Рис. 31. Графики скорости равномерно-ускоренных (I, III) и равномерно-замедленных (II, IV) движений.
Рис. 31. Графики скорости равномерно-ускоренных (I, III) и равномерно-замедленных (II, IV) движений.