Физика формулы ускорения – Равноускоренное движение, вектор ускорения, направление, перемещение. Формулы, определение, законы

Формула ускорения

ОПРЕДЕЛЕНИЕ Ускорение – это величина, показывающая, как быстро изменяется скорость тела.

Ускорение равно разности между конечной и начальной скоростью тела, делённой на время, в течение которого тело меняло скорость.

   

Условное обозначение —

Единицы измерения ускорения м/с

Формула верна только для тел, ускоряющихся равномерно. Если в начальный момент времени тело покоилось, то есть его начальная скорость была равна нулю, то формула упрощается:

   

Где – ускорение, — скорость тела, – время прошедшее с начала движения.

Примеры решения задач по теме «Ускорение»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Все главные формулы по физике – Физика – Теория, тесты, формулы и задачи

Оглавление:

 

Кинематика

К оглавлению…

Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты

h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v₀, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):

Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

 

Динамика

К оглавлению…

Второй закон Ньютона:

Здесь: F – равнодействующая сила, которая равна сумме всех сил действующих на тело:

Второй закон Ньютона в проекциях на оси

(именно такая форма записи чаще всего и применяется на практике):

Третий закон Ньютона (сила действия равна силе противодействия):

Сила упругости:

Общий коэффициент жесткости параллельно соединённых пружин:

Общий коэффициент жесткости последовательно соединённых пружин:

Сила трения скольжения (или максимальное значение силы трения покоя):

Закон всемирного тяготения:

Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:

Где: g – ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:

Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:

Скорость спутника на круговой орбите:

Первая космическая скорость:

Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:

 

Статика

К оглавлению…

Момент силы определяется с помощью следующей формулы:

Условие при котором тело не будет вращаться:

Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):

 

Гидростатика

К оглавлению…

Определение давления задаётся следующей формулой:

Давление, которое создает столб жидкости находится по формуле:

Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:

Идеальный гидравлический пресс:

Любой гидравлический пресс:

КПД для неидеального гидравлического пресса:

Сила Архимеда (выталкивающая сила, V – объем погруженной части тела):

 

Импульс

К оглавлению…

Импульс тела находится по следующей формуле:

Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):

Общий импульс системы тел (важно то, что сумма векторная):

Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:

Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

 

Работа, мощность, энергия

К оглавлению…

Механическая работа рассчитывается по следующей формуле:

Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):

Мгновенная механическая мощность:

Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:

Формула для кинетической энергии:

Потенциальная энергия тела поднятого на высоту:

Потенциальная энергия растянутой (или сжатой) пружины:

Полная механическая энергия:

Связь полной механической энергии тела или системы тел и работы внешних сил:

Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):

 

Молекулярная физика

К оглавлению…

Химическое количество вещества находится по одной из формул:

Масса одной молекулы вещества может быть найдена по следующей формуле:

Связь массы, плотности и объёма:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Определение концентрации задаётся следующей формулой:

Для средней квадратичной скорости молекул имеется две формулы:

Средняя кинетическая энергия поступательного движения одной молекулы:

Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:

Следствия из основного уравнения МКТ:

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):

Газовые законы. Закон Бойля-Мариотта:

Закон Гей-Люссака:

Закон Шарля:

Универсальный газовый закон (Клапейрона):

Давление смеси газов (закон Дальтона):

Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

 

Термодинамика

К оглавлению…

Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:

Теплоемкость (С – большое) тела может быть рассчитана через удельную теплоёмкость (c – маленькое) вещества и массу тела по следующей формуле:

Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:

Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:

При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:

При сгорании топлива выделяется количество теплоты равное:

Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):

Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:

Работа идеального газа:

Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:

Изменение внутренней энергии рассчитывается по формуле:

Первый закон (первое начало) термодинамики (ЗСЭ):

Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):

Изобарный процесс (p = const):

Изотермический процесс (T = const):

Адиабатный процесс (Q = 0):

КПД тепловой машины может быть рассчитан по формуле:

Где: Q₁ – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q₂ – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:

Наибольший КПД при заданных температурах нагревателя T₁ и холодильника T₂, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:

Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):

Относительная влажность воздуха может быть рассчитана по следующим формулам:

Потенциальная энергия поверхности жидкости площадью S:

Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:

Высота столба жидкости в капилляре:

При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:

При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.

 

Электростатика

К оглавлению…

Электрический заряд может быть найден по формуле:

Линейная плотность заряда:

Поверхностная плотность заряда:

Объёмная плотность заряда:

Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):

Где: k – некоторый постоянный электростатический коэффициент, который определяется следующим образом:

Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):

Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):

Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:

Напряженность электрического поля, которую создает заряженная плоскость:

Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

Определение потенциала задаётся выражением:

Потенциал, который создает точечный заряд или заряженная сфера:

Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):

Для диэлектрической проницаемости вещества верно следующее:

Определение электрической ёмкости задаётся формулой:

Ёмкость плоского конденсатора:

Заряд конденсатора:

Напряжённость электрического поля внутри плоского конденсатора:

Сила притяжения пластин плоского конденсатора:

Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):

Объёмная плотность энергии электрического поля:

 

Электрический ток

К оглавлению…

Сила тока может быть найдена с помощью формулы:

Плотность тока:

Сопротивление проводника:

Зависимость сопротивления проводника от температуры задаётся следующей формулой:

Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):

Закономерности последовательного соединения:

Закономерности параллельного соединения:

Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:

Закон Ома для полной цепи:

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Сила тока короткого замыкания:

Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:

Мощность электрического тока:

Энергобаланс замкнутой цепи

Полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

Где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

 

Магнетизм

К оглавлению…

Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:

educon.by

Формула скорости

   

Здесь – скорость, – пройденный путь, – время, за которое был пройден этот путь.

Единица измерения скорости – м/с (метр в секунду).

Скорость – это мера того, какое расстояние проходит тело за единицу времени. Формула верна только тогда, когда скорость не менялась на всём протяжении пути. Если происходило равноускоренное движение, то:

   

Где – ускорение тела, – начальная скорость. Равноускоренное движение – такое, в котором ускорение не меняется.

Примеры решения задач по теме «Скорость»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Ускорение | Физика для всех

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

 

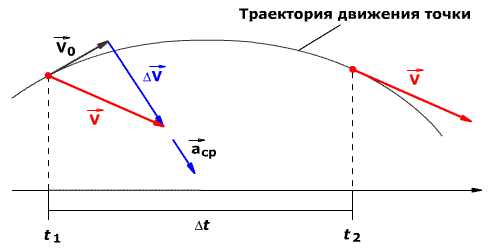Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости 

Если скорость тела по модулю уменьшается, то есть

v2 < v1

то направление вектора ускорения противоположно направлению вектора скорости  Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

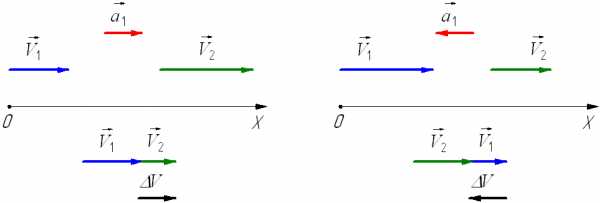
Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

av-mag.ru

Что называют ускорением в физике: основные формулы

Отвечая на вопрос о том, что называют ускорением в физике, следует сказать, что это векторная величина, которая показывает, как изменяется скорость за единицу времени. В ньютоновской векторной механике ускорение обычно обозначают a^→ и измеряют в системе международных единиц в м/с².

Что называют ускорением?

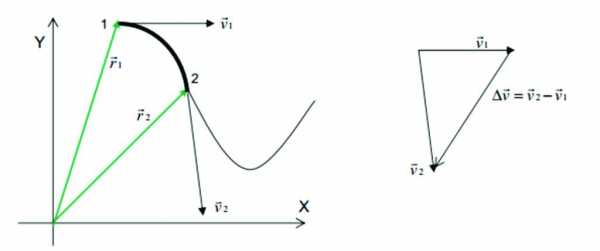
Согласно постулатам механики Ньютона, частица (тело) не может двигаться по искривленной траектории, если на нее не действует никаких внешних сил, то есть такая частица будет прямолинейно двигаться. В то же время, движущаяся по прямой траектории частица, может увеличить свою скорость или уменьшить ее, если вектор силы, действующей на нее, параллельно вектору ее скорости.

В классической механике ответом на вопрос, что называют ускорением, является изменение скорости за данный промежуток времени, то есть a = dv/dt, что математически интерпретируется, как производная скорости по времени.

Ускорение и второй закон Ньютона

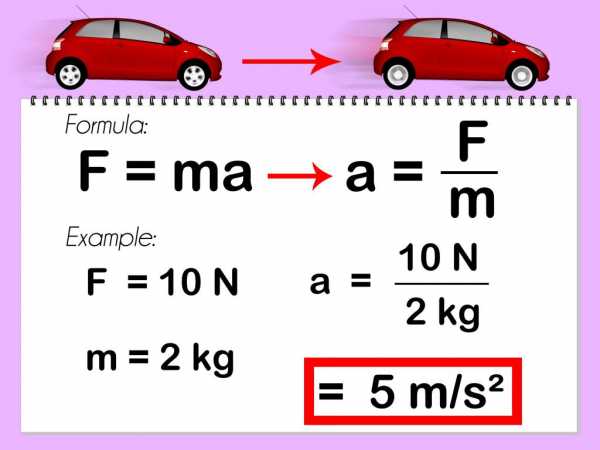
Ускорение тела a массой m, в соответствии со вторым закон Ньютона, пропорционально результирующей F силе, которая действует на это тело, то есть F = ma. Данное выражение действительно для любой инерциальной системе отсчета, то есть такой системе, которая находится в состоянии покоя, либо прямолинейно движется и равномерно.

Приведем следующие примеры использования этой формулы нахождения ускорения или действующей на тело силы.

1. Ускорение при свободном падении на нашей планете своим существованием обязано силе тяжести, действующей на все без исключения объекты, имеющие какую-либо отличную от нуля массу. Оно обозначается g и равно 9,8 м/с² недалеко от поверхности земли. Это означает, что если в гравитационном поле Земли какое-либо тело в состоянии свободного падения находится, то оно будет увеличивать свою скорость за каждую секунду полета на 9,8 м/с. После начала такого падения скорость в каждый момент времени для тела определяется по формуле: v = at = gt = 9,8t. При этом сила тяжести, действующая на данное тело, равна F = mg. Отметим, что в действительности при свободном падении на тело действует еще и сопротивление воздуха, сила которая зависит от скорости, а при ее определенном значении становится равной по модулю силе тяжести. В таком случае движение тела происходит с постоянной скоростью.
2. Другой пример, когда можно пользоваться вторым законом Ньютона, это процесс торможения или ускорения автомобиля.

Среднее и мгновенное ускорение

Когда тело движется, то вектор скорости и его модуль в общем случае меняются со временем, но вектор скорости направлен к траектории по касательной всегда. Например, пусть в t₁момент времени тело двигалось с v₁^→скоростью, а в t₂момент времени со скоростью v₂^→. Отвечая на вопрос, что называют ускорением средним, скажем, что эта физическая величина определяется по формуле: a^→= Δv^→/Δt, в которой Δt = t₂– t₁ и Δv^→= v₂^→-v₁^→. Заметим, что вектор ускорения направлен так же, как и вектор изменения скорости Δv^→.

Мгновенное ускорение в физике определяется как по времени производная скорости для конкретного момента времени, то есть a^→ = dv^→/dt. Учитывая, что скорость является производной по времени координаты тела, можно получить ускорение, если взять от координаты тела второй раз производную по времени, то есть a = d²r/dt², где r – координата тела в t момент времени.

Круговое равномерное движение

Равномерное и круговое представляет собой такое движение, тело или частица при котором движется по окружности некоторого постоянного радиуса R с постоянным модулем скорости V, то есть это тело или частица проходит одинаковый путь за одинаковые промежутки времени. Так как тело движется по траектории окружности, то оно постоянно изменяет направление скорости.

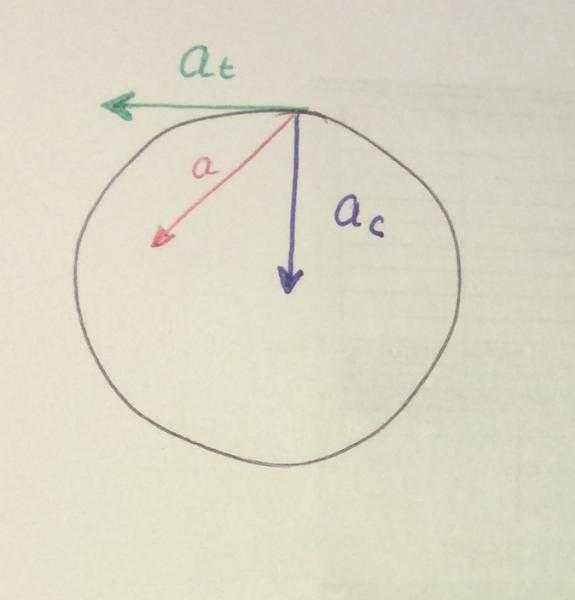
Если вектор ускорения разложить на пару компонентов так, что один из них будет направлен к траектории движения по касательной, а второй к центру окружности вдоль радиуса R, тогда первый компонент называется тангенциальным, а второй нормальным. Учитывая, что движение является равномерным, тангенциальный компонент ускорения равен нулю, а нормальный – постоянная величина, которая является ответом на вопрос, что называют центростремительным ускорением. Это ускорение направлено на изменение траектории движения объекта и не изменяет само значение скорости. Центростремительное ускорение в физике вычисляется по формуле a = v²/R.

Прямолинейное равномерно ускоренное движение

Если рассмотреть прямолинейное движение тела, то есть при этом движении вектор скорости не изменяет своего направления, а меняется лишь ее модуль, тогда формулу в любой момент t времени для скорости можно записать так: v = v0+∫^t₀a(t)dt, где v₀ – начальная ненулевая скорость. В данном выражении присутствует зависимость ускорения от времени. Если действующая на тело сила является постоянной, тогда и ускорение не будет меняться с течением времени, в этом случае мы получаем простое выражение в t момент времени для скорости: v = v₀+at.

Интегральное выражение для скорости можно проинтегрировать еще раз, тогда мы получим выражение для пути, который проходит данное тело за время t. Учитывая, что ускорение является постоянным, получаем формулу: x – x₀ = v₀t+at²/2, в которой x – x₀ – разница конечной и начальной координат тела, которая показывает пройденный им путь.

fb.ru

Ускорение тела в физике

Важно помнить, что ускорение – величина векторная. Говорить об ускорении можно, когда скорость изменяется как по величине, так и по направлению.

Единицей измерения ускорения в системе СИ является м/с .

Примеры ускоренного движения – разгон, торможение, падение, различные маневры.

Если скорость всегда направлена по касательной к траектории движения, и направление вектора скорости совпадает с направлением движения, то вектор ускорения в общем случае может составлять любой угол с вектором скорости. Так, при разгоне по прямолинейному участку пути направления векторов скорости и ускорения совпадают (угол между векторами скорости и ускорения ) (рис.1,а). При торможении на прямолинейном участке шоссе вектора скорости и ускорения противоположно направлены (угол между векторами скорости и ускорения ) (рис.1,б).

При равномерном движении по окружности вектор ускорения перпендикулярен вектору скорости (угол между векторами скорости и ускорения ) (рис.1,в). В более общем сложном случае движения по криволинейной траектории угол между векторами скорости и ускорения зависит от кривизны траектории и интенсивности разгона/торможения, т.е. может принимать любое значение (рис.1,г).

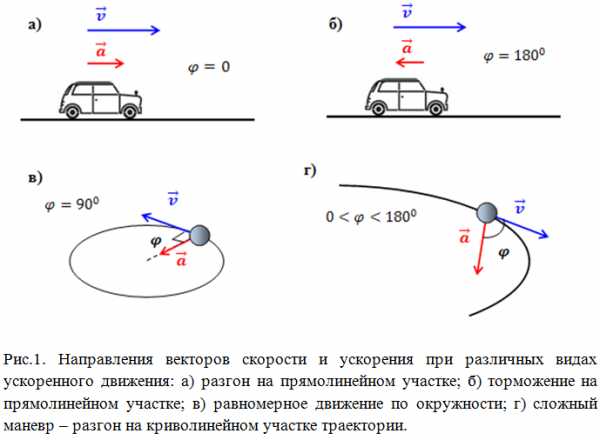
Ускорение может быть как положительным, так и отрицательным. Если , говорят об ускоренном движении, если , движение замедленное.

Примеры решения задач по теме «Ускорение»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Равномерно ускоренное движение без начальной скорости | Формулы и расчеты онлайн

Перемещение выраженное через скорость и время

Тело начинает двигаться равноускоренно из состояния покоя.

На графике скорости перемещение равно площади треугольника \[s = \frac{ut}{2}\] Здесь: u — скорость тела через промежуток времени t, s — перемещение тела за время t, t — время движения,

График скорости – Равномерно ускоренное движение без начальной скорости

Скорость выраженная через ускорение и время

Поскольку движение начинается из состояния покоя, то изменение скорости равно величине скорости, достигнутой к моменту времени t, и скорость вычисляется по следующей формуле: \[u = at\]

График ускорения – Равномерно ускоренное движение без начальной скорости

Перемещение выраженное через ускорение и время

Из формул (1) и (2) получается следующая формула пройденного пути: \[s = \frac{at^2}{2}\] Здесь: a — ускорение тела, постоянное в течение времени t, s — перемещение тела за время t, t — время движения,

График перемещения – Равномерно ускоренное движение без начальной скорости

В помощь студенту

Равномерно ускоренное движение без начальной скорости	стр. 397

www.fxyz.ru