3. Производная суммы, произведения и частного от деления двух функций
Используем свойства предела для доказательства правил дифференцирования.
1.
. (1)
2.
. (2)
3.
(3)
4.
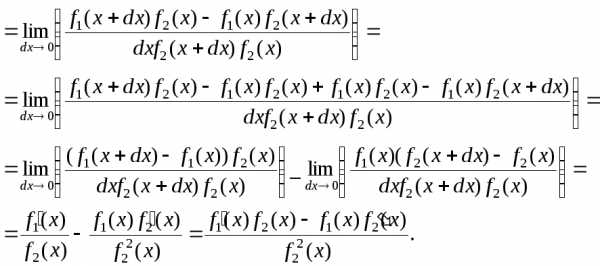 (4)
(4)
4. Производная сложной и обратной функций.
Пусть функция 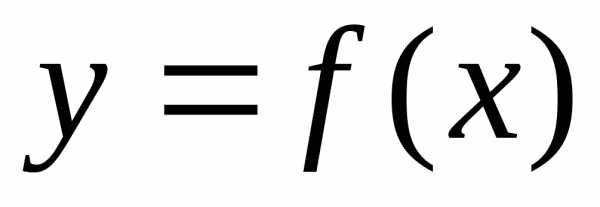 в некоторой окрестности точки
в некоторой окрестности точки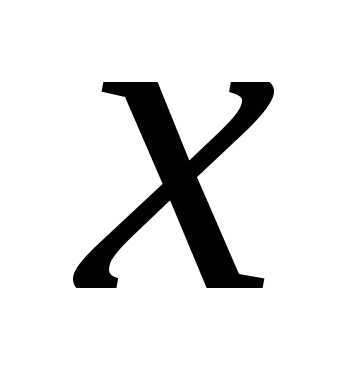 является непрерывной, монотонной, а в
самой точке
является непрерывной, монотонной, а в
самой точке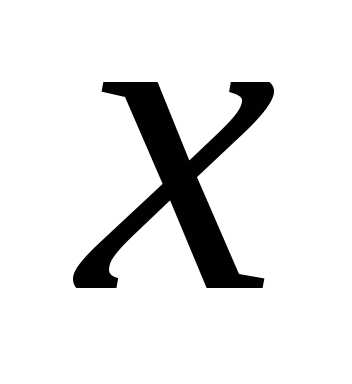 – дифференцируемой. Тогда по теореме о
непрерывных функциях она имеет обратную
– дифференцируемой. Тогда по теореме о
непрерывных функциях она имеет обратную
. (1)
Формулу (1) следует
понимать так, что производные в ее левой
и правой части вычисляются при значениях
аргументов, связанных между собой
соотношениями 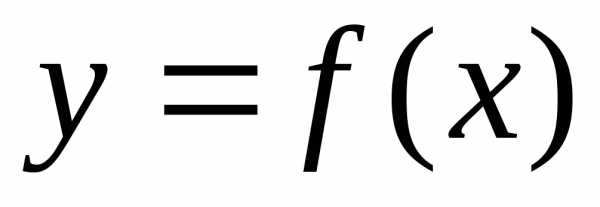 или
или .
.
Определение.Сложнойназывается функция, которая зависит от своего аргумента, таким образом, что эту зависимость можно представить посредством как минимум одного промежуточного аргумента.
Например, пусть 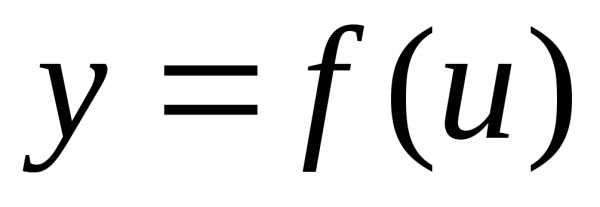
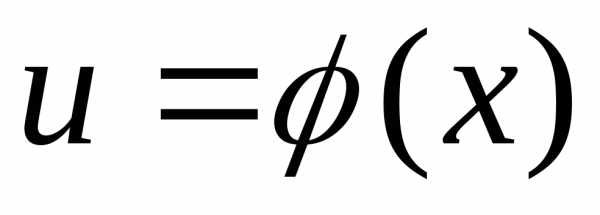 .
Тогда- сложная функция с промежуточным
аргументом
.
Тогда- сложная функция с промежуточным
аргументом и независимым аргументом
и независимым аргументом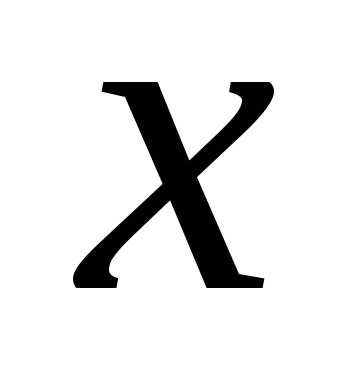 .
. Теорема.
Если функция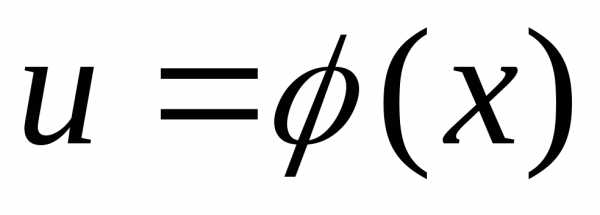 имеет производную
имеет производную в точке
в точке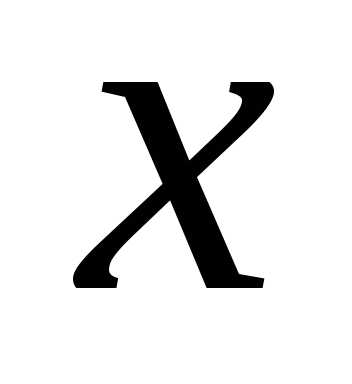 ,
а функция
,
а функция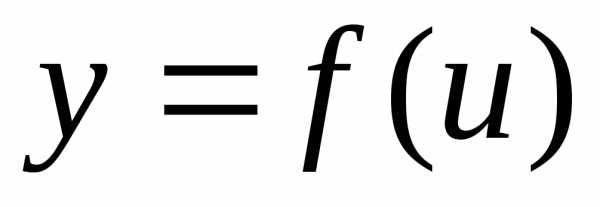 имеет производную
имеет производную
 ,
соответствующей точке
,
соответствующей точке ,
то сложная функцияимеет производную
,
то сложная функцияимеет производную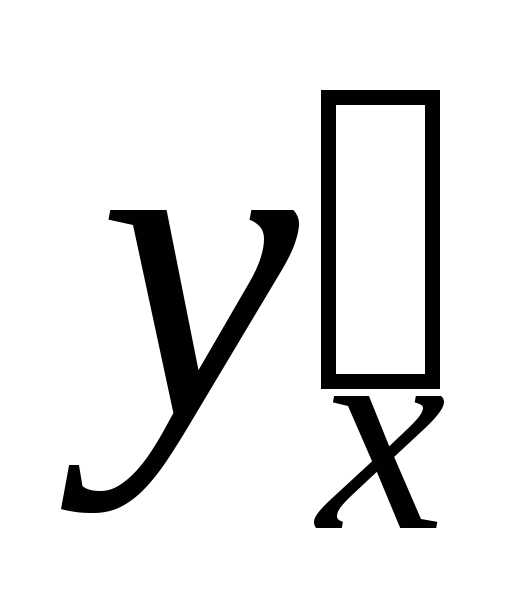 в точке
в точке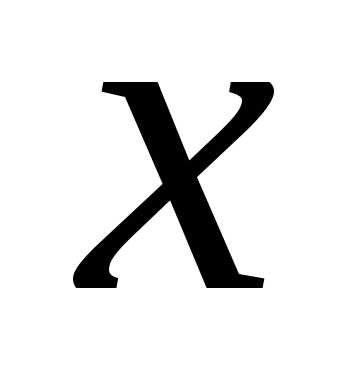 ,
которая находится по формуле
,
которая находится по формуле. (2)
Доказательство
В окрестности
точки 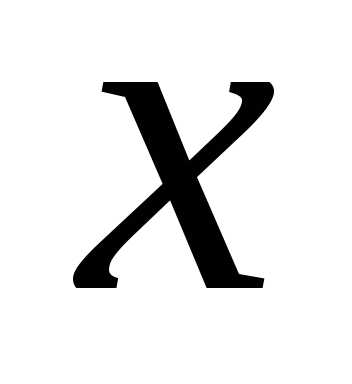 дадим приращение
дадим приращение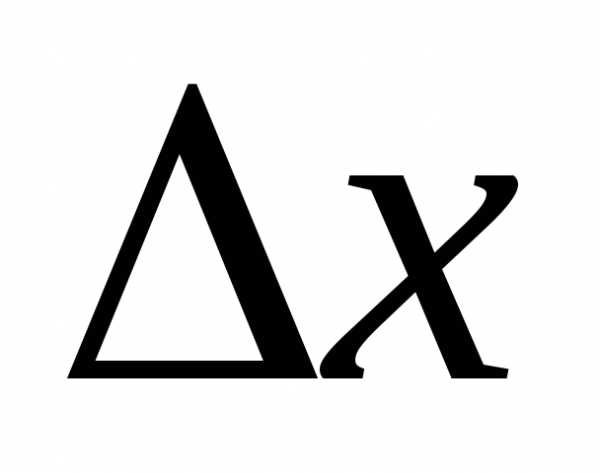 аргументу
аргументу
 получит приращение
получит приращение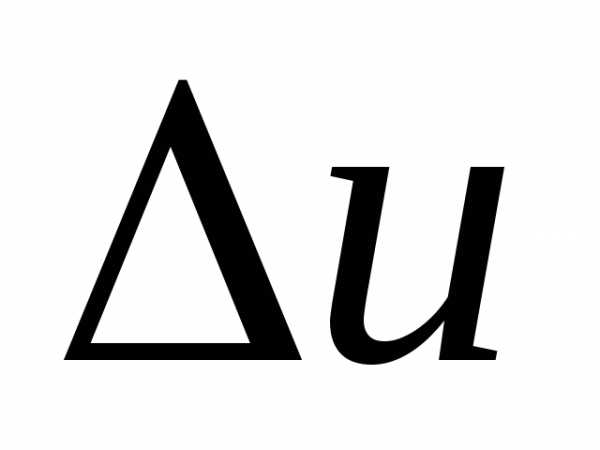 ,
а функция
,
а функция – приращение
– приращение .
..
Поскольку в силу
существования производной  функция
функция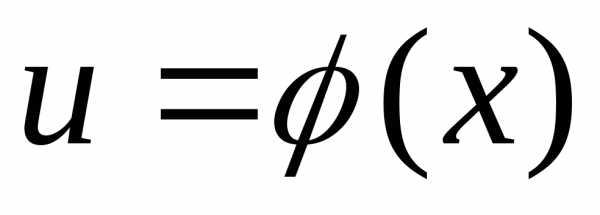 является непрерывной в рассматриваемой
точке, то при
является непрерывной в рассматриваемой
точке, то при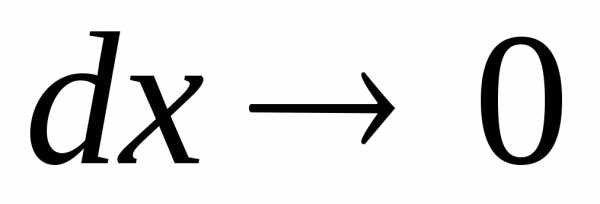
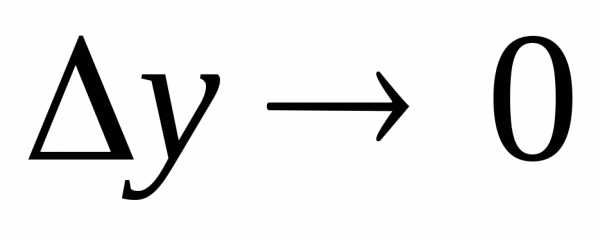 .
Тогда продолжая выкладки, получаем
.
Тогда продолжая выкладки, получаем.
5. Таблица производных
Получим сейчас формулы для дифференцирования основных элементарных функций. Знание этих формул совместно с ранее полученными правилами дифференцирования позволит нам выполнять дифференцирование элементарных функций.
Пусть . Применяя формулу (1) получим
. (1)
Пусть
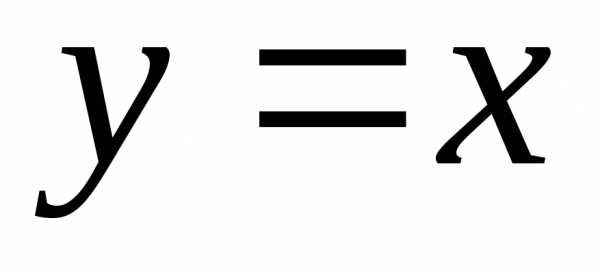 .
Тогда
.
Тогда
. (2)
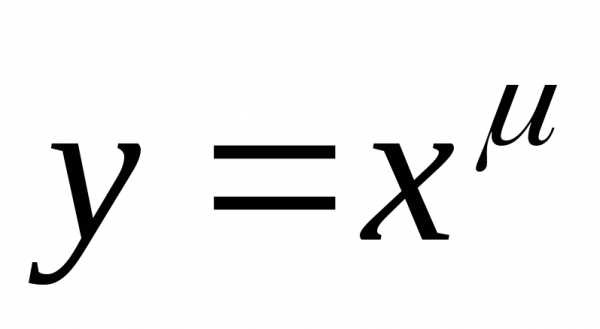 с вещественным показателем степени
с вещественным показателем степени .
При этом воспользуемся таблицей
эквивалентных бесконечно малых величин.
.
При этом воспользуемся таблицей
эквивалентных бесконечно малых величин.. (3)
В частном случае,
когда  = целое число
= целое число
. (4)
4. Для получения
формулы дифференцирования показательной
функции 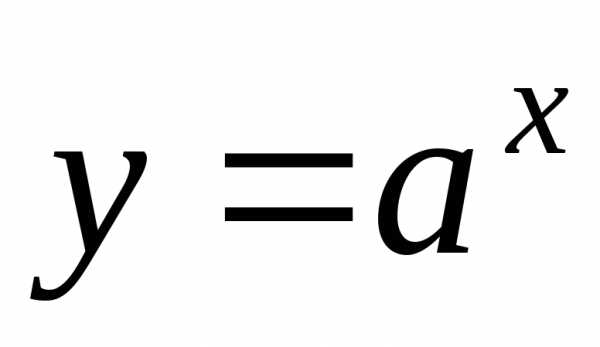 (также воспользуемся таблицей эквивалентных
бесконечно малых величин
(также воспользуемся таблицей эквивалентных
бесконечно малых величин
В частном случае,
когда 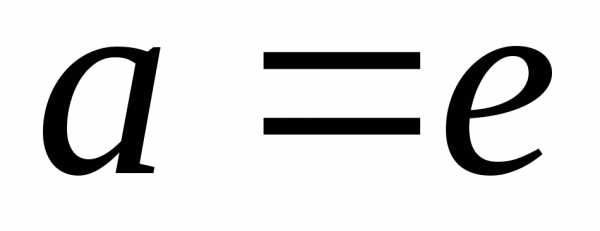
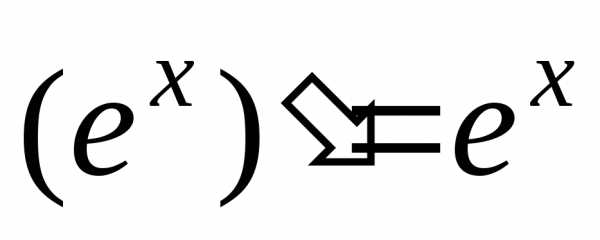 . (6)
. (6)
5. Для получения формулы дифференцирования логарифмической функции (также воспользуемся таблицей эквивалентных бесконечно малых величин. В результате получим
. (1)
В частном случае,
когда 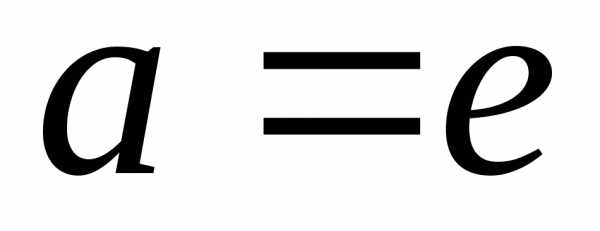
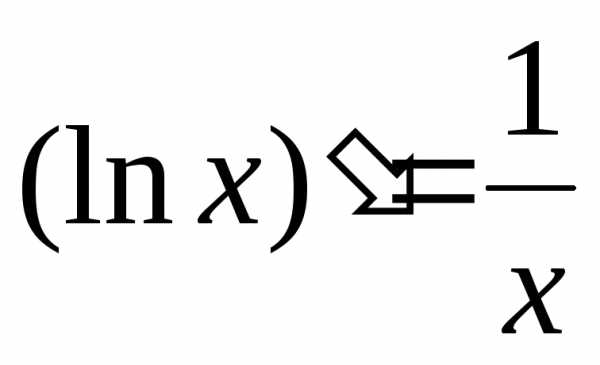 . (2)
. (2)
Перейдем теперь к вычислению производных тригонометрических функций.
6. Найдем производную
функции 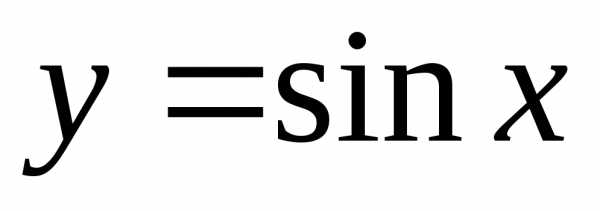 .
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
.
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
. (9)
7. Найдем производную функции . Пользуясь таблицей эквивалентных бесконечно малых величин, получим
. (10)
8. Найдем производную
функции 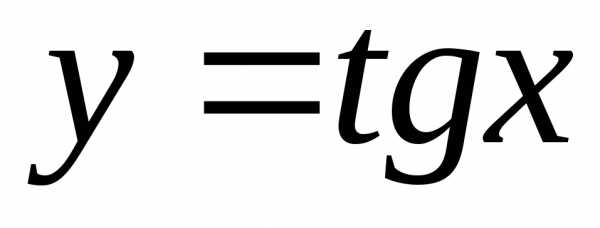 .
Пользуясь правилами дифференцирования,
получим
.
Пользуясь правилами дифференцирования,
получим
. (11)
9. Найдем производную функции . Пользуясь правилом дифференцирования частного от деления двух функций, получим
. (12)
10. Найдем производную
функции
,
где,
а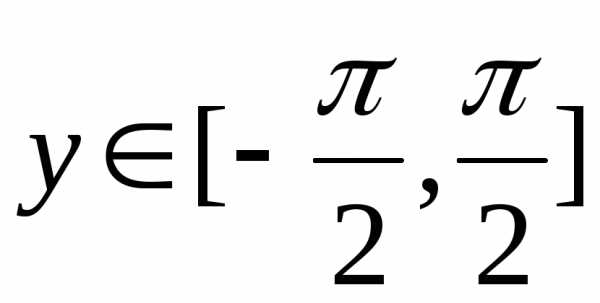 .
Очевидно
.
Очевидно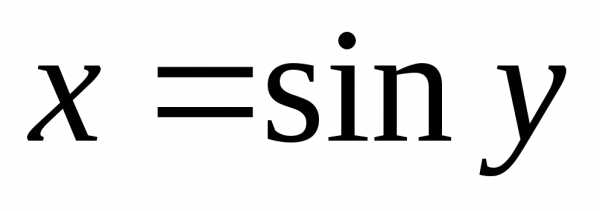 ,
тогда пользуясь формулами (3.1) и (9),
получим
,
тогда пользуясь формулами (3.1) и (9),
получим
. (13)
Здесь было
использовано свойство функции 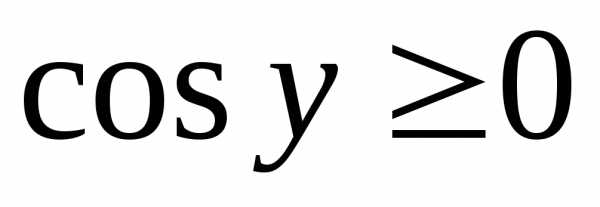 на промежутке
на промежутке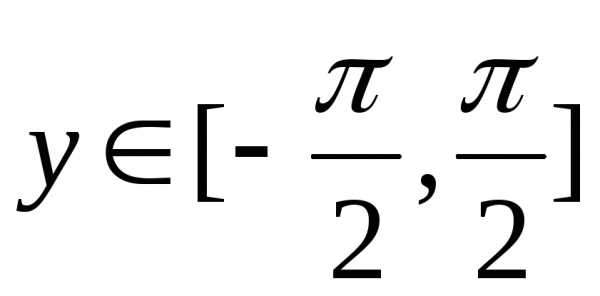 .
.
11. Найдем производную
функции
,
где,
а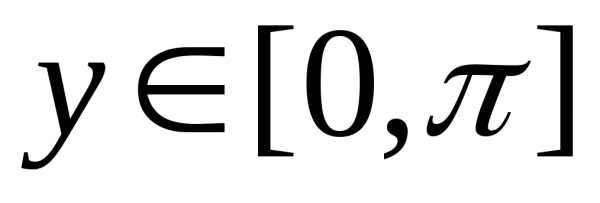
. (14)
Здесь было
использовано свойство функции  на промежутке
на промежутке .
.
12. Найдем производную
функции
,
где,
а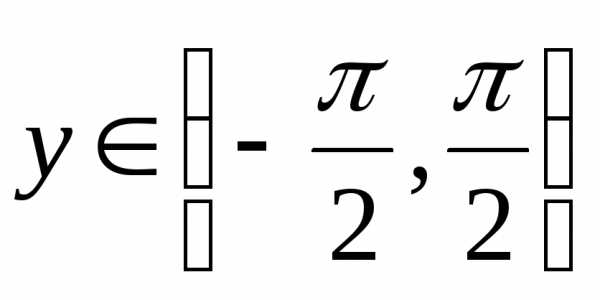 .
Очевидно
.
Очевидно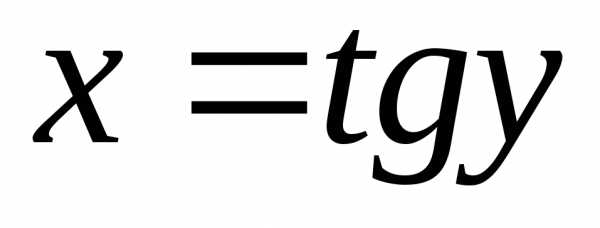 ,
тогда пользуясь формулами (3.1) и (11),
получим
,
тогда пользуясь формулами (3.1) и (11),
получим
. (15)
13. Найдем производную функции , где, а. Очевидно, тогда пользуясь формулами (3.1) и (12), получим
14. Так как гиперболический синус определяется соотношением
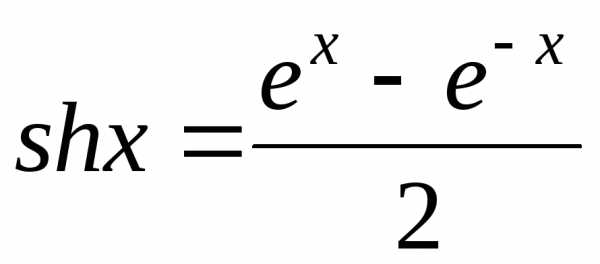 ,
то
,
то
. (17)
15. Так как гиперболический косинус определяется соотношением
 ,
то
,
то
. (18)
Графики гиперболического синуса и косинуса представлены на рис. 1.
Рис. 1. Синус и косинус гиперболические1
16. Так как гиперболический тангенс определяется соотношением
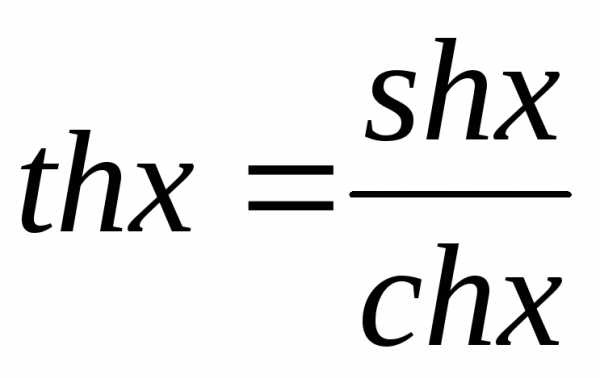 ,
то
,
то. (19)
17. Так как гиперболический котангенс определяется соотношением
 ,
то
,
то
. (20) Графики гиперболического тангенса и котангенса представлены на рис. 2.
Рис. 2. Тангенс и котангенс гиперболические2
Результаты вычисления производных представлены в таблице.
Таблица
Полная производная функции, формула и примеры
Функция где называется сложной функцией переменных и
В случае, когда функции и зависят только от переменной то есть то производная рассматриваемой функции по независимой переменной задается соотношением:
Если же а то формула (1) принимает вид:
В формулах (1), (2) выражение называется полной производной функции
ПРИМЕР 1| Задание | Найти полную производную функции если |
| Решение | Находим частные производные:
Тогда, согласно формуле (1), имеем:
|
| Ответ |
| Задание | Найти полную производную функции если |
| Решение | Искомую производную будем находить по следующей формуле:
Находим частные производные:
Итак, имеем:
|
| Ответ |
ru.solverbook.com
Внеклассный урок – Формулы и правила дифференцирования (нахождения производной)
Формулы и правила дифференцирования (нахождения производной)
Дифференцирование – это вычисление производной.
1. Формулы дифференцирования.
Основные формулы дифференцирования – в таблице. Их необязательно зазубривать. Поняв некоторые закономерности, вы сможете из одних формул самостоятельно выводить другие.
1) Начнем с формулы (kx + m)′ = k.
Ее частными случаями являются формулы x′ = 1 и C′ = 0.
Поясним.
В любой функции вида у = kx + m производная равна угловому коэффициенту k.
Например, дана функция у = 2х + 4. Ее производная в любой точке будет равна 2:
(2х + 4)′ = 2.
Производная функции у = 9х + 5 в любой точке равна 9. И т.д.
А давайте найдем производную функции у = 5х. Для этого представим 5х в виде (5х + 0). Мы получили выражение, похожее на предыдущее. Значит:
(5х)′ = (5х + 0)′ = 5.
Наконец, выясним, чему равна x′.
Применим прием из предыдущего примера: представим х в виде 1х + 0. Тогда получим:
x′ = (1х + 0)′ = 1.
Таким образом, мы самостоятельно вывели формулу из таблицы:
x′ = 1.
Идем дальше. Пусть k = 0. Мы знаем, что производная равна коэффициенту. То есть:
(0 · x + m)′ = 0.
Но тогда получается, что m′ тоже равна 0. Пусть m = C, где C – произвольная постоянная. Тогда мы приходим к еще одной истине: производная постоянной равна нулю. То есть получаем еще одну формулу из таблицы:
C′ = 0.


raal100.narod.ru
Как осуществить деление производных? :: SYL.ru
При работе с функциями часто приходится учитывать их специфику, производя сложение, умножение или деление производных. Последнее из действий чаще всего вызывает вопросы у обучающегося, поэтому этот аспект стоит рассмотреть подробнее.
Производная частного
Когда выполняется деление производных, формула для преобразования выглядит как разность производной числителя, помноженного на знаменатель, и производной знаменателя, умноженного на числитель, и поделённое на квадрат знаменателя. При этом необходимо учитывать, что значение в нижней части дроби должно быть не равным нулю. При решении первых примеров преобразование производной частного нередко возникает проблема, поэтому лучше всего иметь перед глазами эту формулу:

Благодаря этой формуле удаётся привести пример в более простую форму, которую можно разделить на табличные функции производных, после чего решить данную задачу не составит большого труда.
Пример решения
В качестве примера, демонстрирующего ход решения, где выполняется деление производных, стоит рассмотреть следующий:
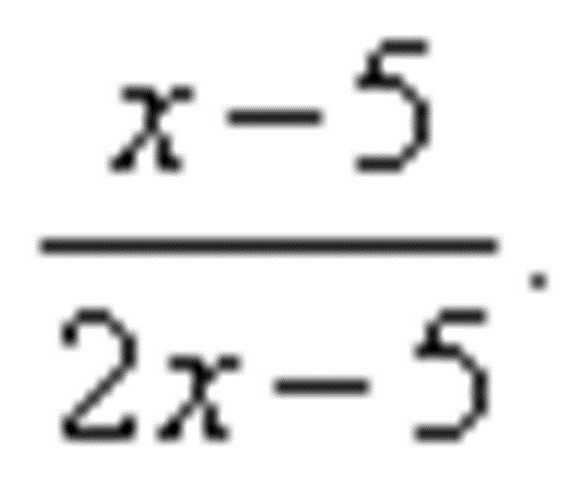
Согласно заданию, необходимо найти производную данного выражения. Воспользовавшись формулой, упрощающей деление производных, преобразуем исходный пример к следующему виду:
В результате в числителе оказалось две производные табличного вида, значения которых можно вычислить без дополнительных преобразований. В первом случае результатом будет единица, во втором – двойка. Подставив вычисленные данные в пример, получим дробь, в которой останется лишь произвести несложные вычисления в числителе, получив итоговый результат:
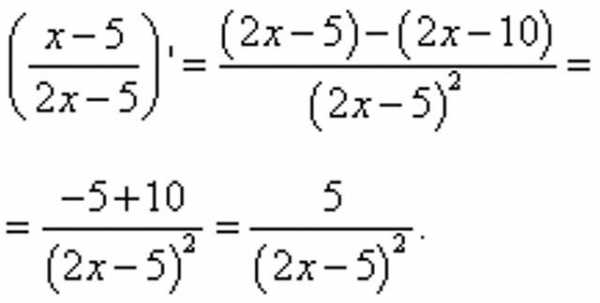
Маленькие хитрости
Перед применением формулы стоит внимательно посмотреть на деление производных. В некоторых случаях дробь можно упростить, благодаря чему приведенная в начале формула может оказаться ненужной или станет более простой. Упрощение дроби можно выполнить несколькими способами, включая деление числителя на знаменатель с целью определения целой части, а также домножением обеих частей дроби на одно и то же ненулевое число – этот приём часто применяется при наличии иррациональности под знаком производной.
Стоит отметить, что перед вначале необходимо проверить пример на наличие решения. Для этого нужно найти область допустимых значений (ОДЗ), и если она будет существовать, не создавая неопределённостей различного вида, можно приступать к вычислениям.
www.syl.ru
