Главная
Формула модуля ускорения тела – Ответы@Mail.Ru: Тело брошено под углом к горизонту. как измениться при спуске тела: а) модуль тангенциального ускорения;

Формула модуля ускорения тела – Ответы@Mail.Ru: Тело брошено под углом к горизонту. как измениться при спуске тела: а) модуль тангенциального ускорения;

Модуль вектора ускорения

. (1.12)

Вектор ускорения можно разложить на два вектора (рис. 1.6) .

Составляющая ускорения, характеризующая изменение мгновенной скорости по величине, называется касательным (тангенциальным) ускорением .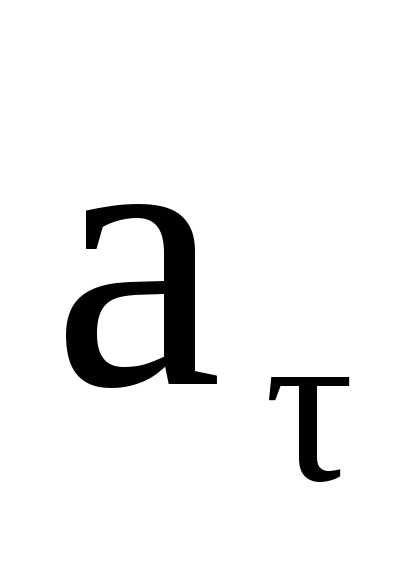

Составляющая ускорения, направленная к центру кривизны траектории и характеризующая изменение вектора скорости по направлению, называется нормальным ускорением .

Вектор полного ускорения

, (1.13)

а его модуль

. (1.14)

Для самостоятельного изучения

Модули касательного и нормального ускорения находятся из соотношения

, (1.15)

где 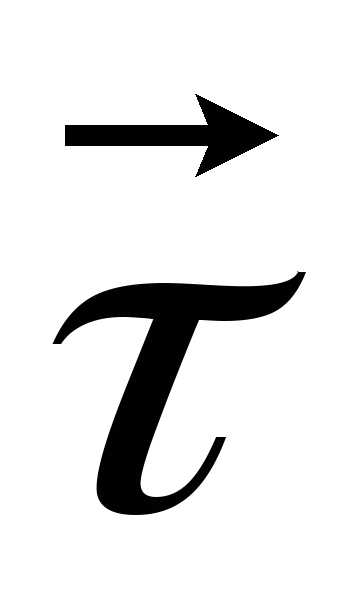единичный вектор, направленный по касательной к точке траектории в сторону движения в сторону движения м.т. (рис 1.7), а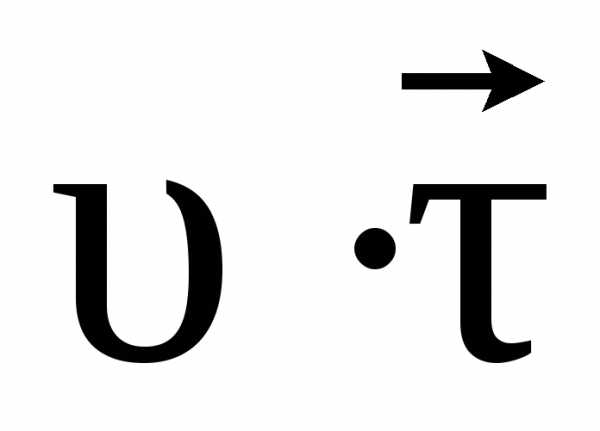– вектор мгновенной скорости

.

Первое слагаемое в (1.15) равно касательному ускорению,

,

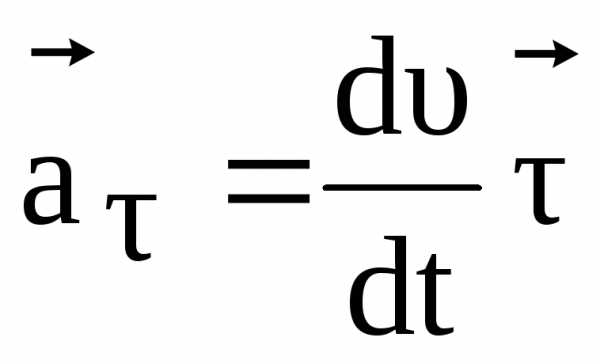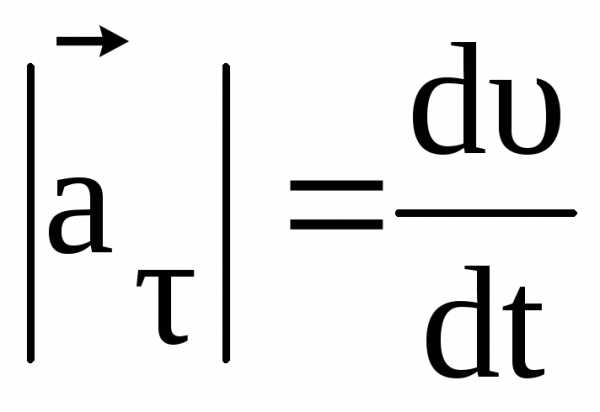
второе – нормальному

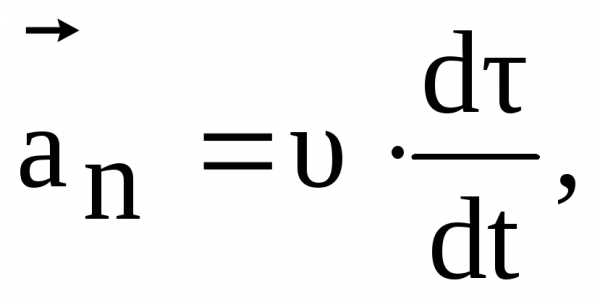
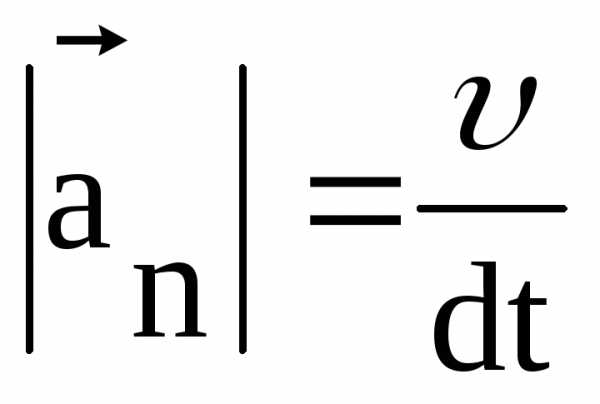(1.16)

Вектор касательного ускорения может совпадать с вектором мгновенной скорости (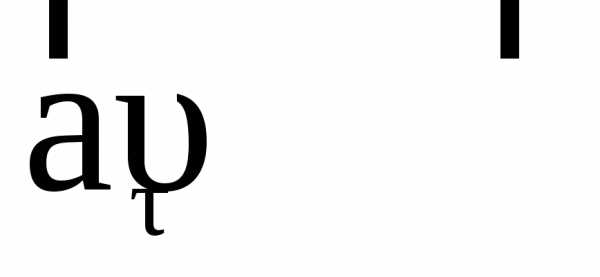

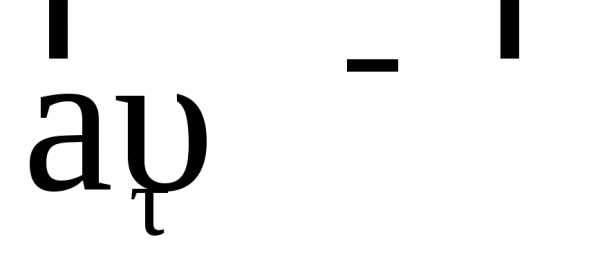) и может быть ему антипараллелен (). В первом случае движение будет ускоренным, а во втором – замедленным.

Рассмотрим перемещение материальной точки по траектории из точки в точку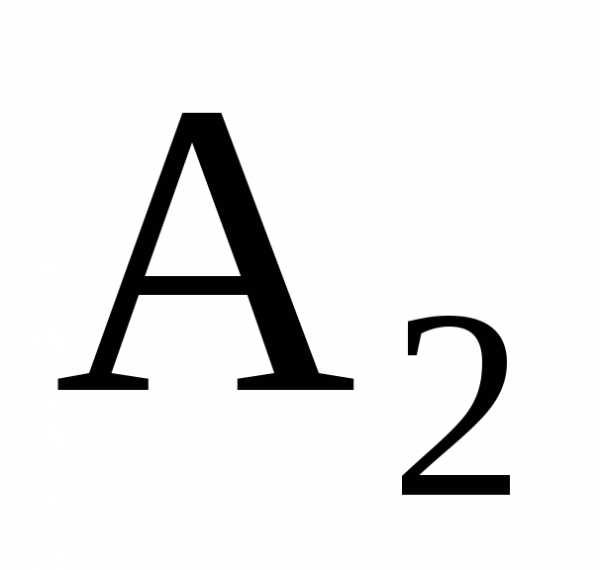. (рис 1.7) За малый интервал времениединичный вектор в точке А2 равен сумме

,

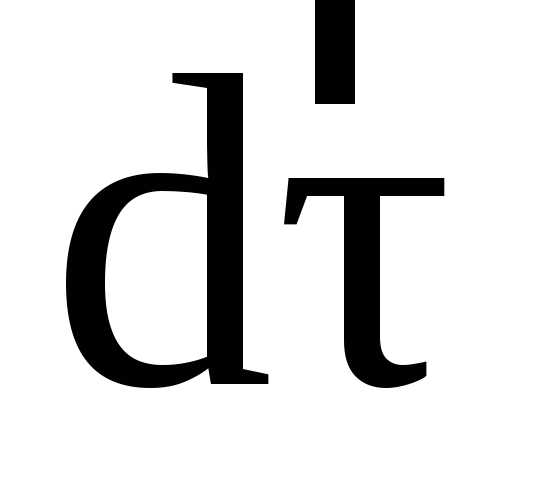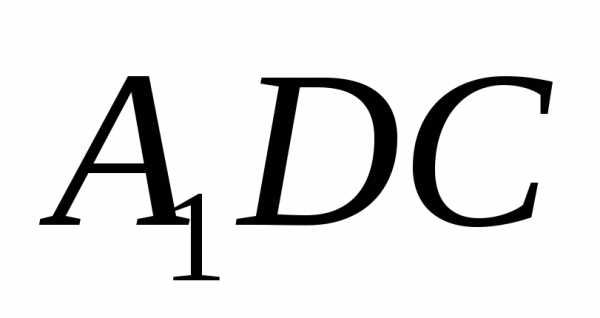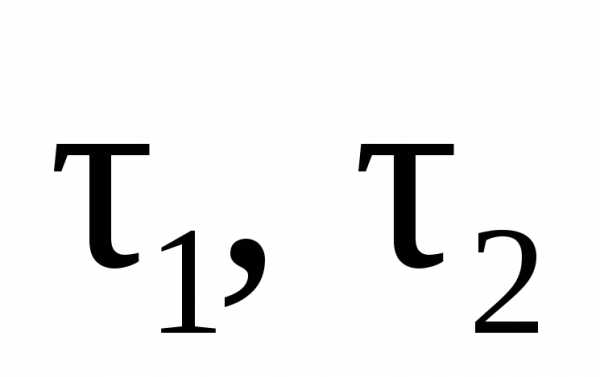где – единичный вектор, определяющий направление движения в точке А1, – вектор изменения направления движения. Треугольник , образованный векторами и 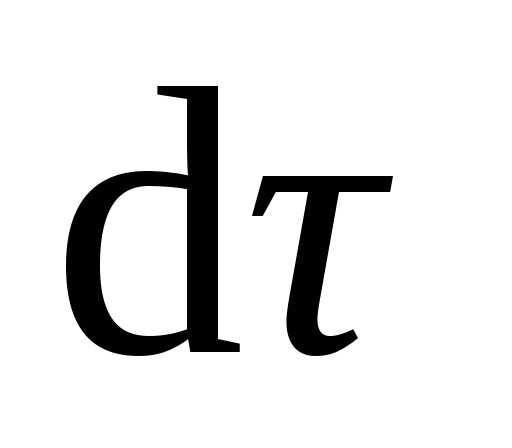,равнобедренный, т.к.

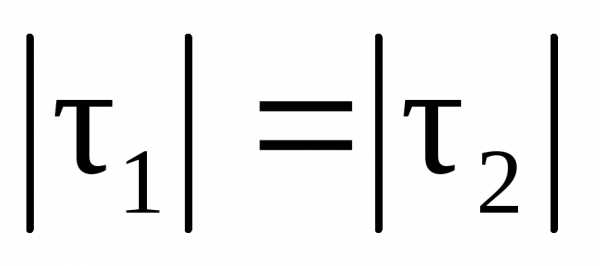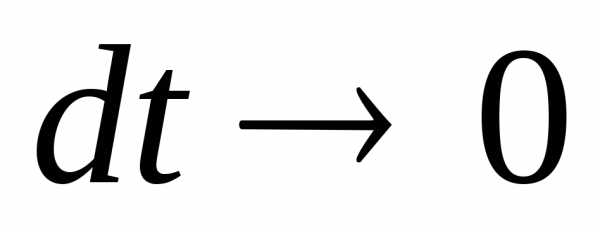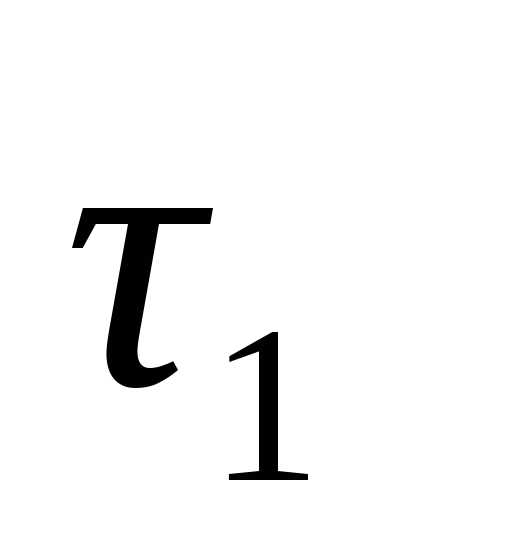=1. При , угол между векторами и 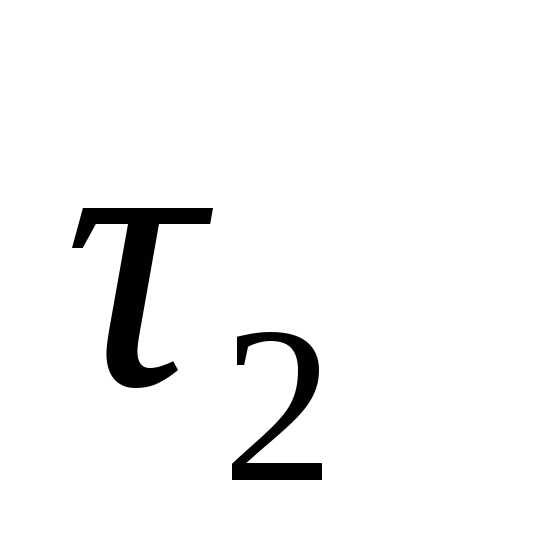уменьшается истремится к нулю, а угол между векторами и
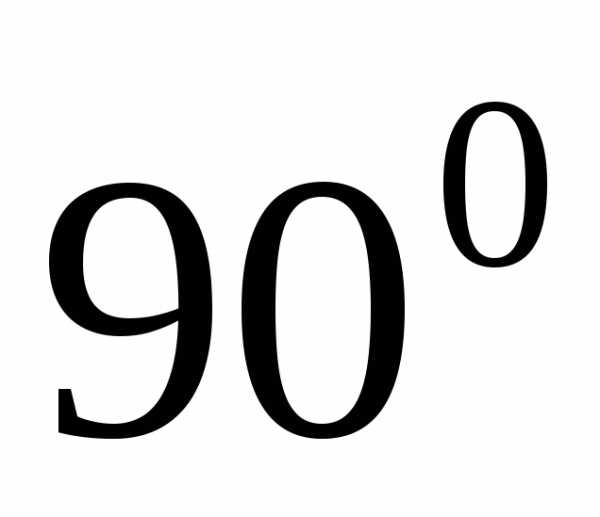увеличится до . Следовательно, вектора 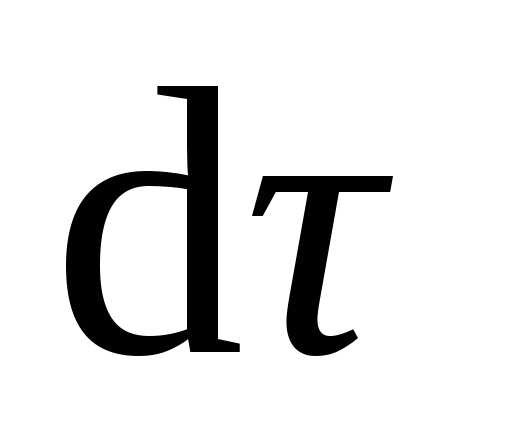и направлены к центру кривизны траектории и совпадает с вектором нормали к скорости ().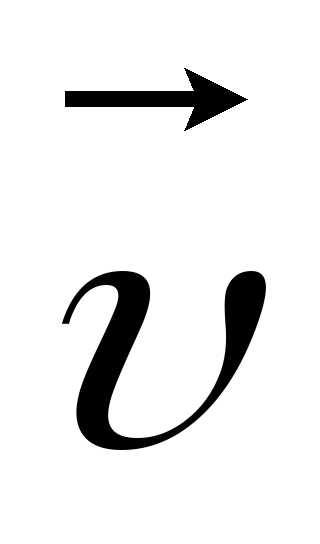

Модуль вектора нормального ускорения определяется из треугольников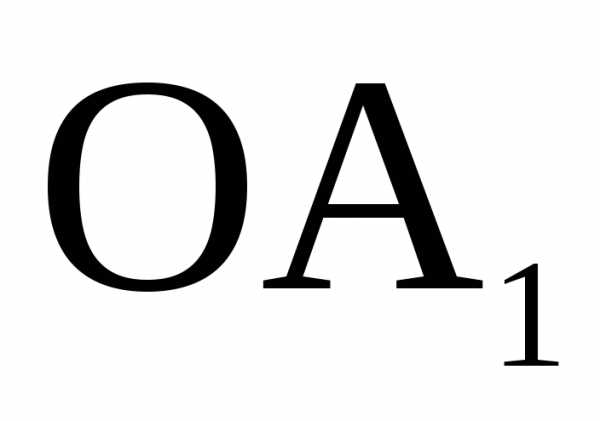

и DC. Эти треугольники равнобедренные и подобные, т.к. при 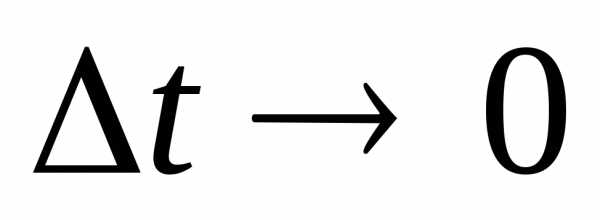где – радиус кривизны траектории. Из соотношения сторон треугольников

. (1.17)

Для бесконечного малого интервала времени ,

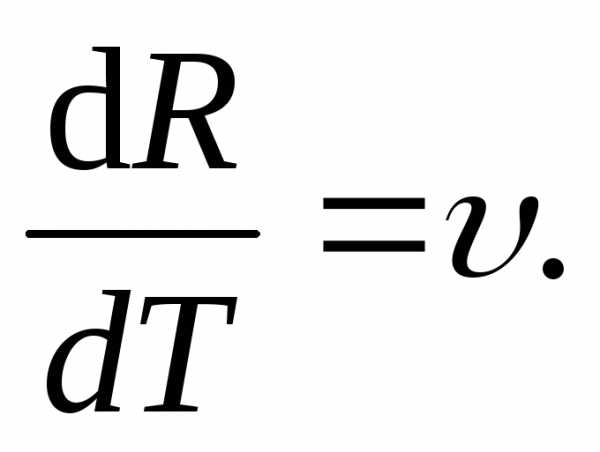
Вектор

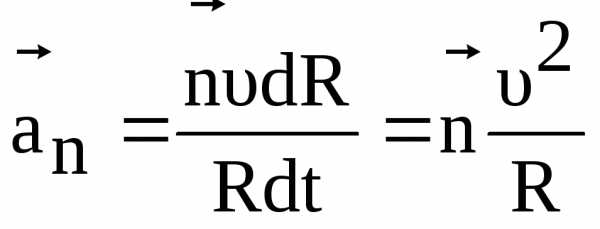можно представить в виде .Тогда вектор нормального ускорения

,

. (1.18)

Задания для самоконтроля знаний.

  1. Дайте определение средней и мгновенной скорости.

  2. Совпадают ли векторы средней и мгновенной скорости материальной точки, движущейся по окружности?

  3. Определите физический смысл понятий скорости и ускорения движения материальной точки.

  4. Запишите выражения для векторов скорости и ускорения материальной точки в декартовой системе координат.

  5. Определите модуль вектора скорости и ускорения в декартовой системе координат.

  6. Дайте определение тангенциального, нормального и полного ускорения.

  7. Определите модуль вектора ускорения движения точки по окружности радиусом R=1м, в момент времени t=2с от начала движения, если зависимость модуля вектора скорости от времени задается уравнением

    .

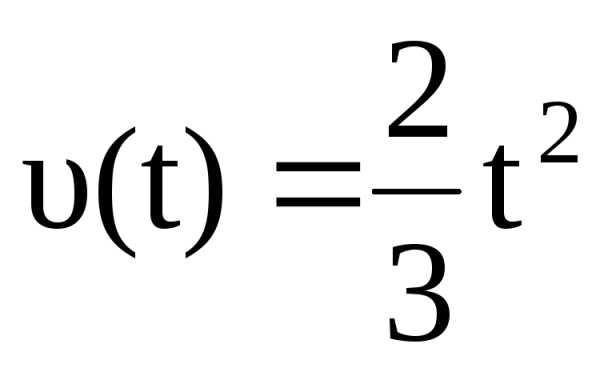
Лекция 2

studfiles.net

Модуль ускорение формула

2
2/5 (89) Центростремительное ускорение: формула, … Модуль мгновенной скорости перемещения и мгновенная скорость пути – это одно и то же, поскольку dr = ds
Среднее ускорение a ср – … 2
2/5 § 43
КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ … Ускорение · Тангенциальное ускорение – ens
tpu
ru v S 0 — модуль начальной скорости; a S — ускорение (2) Скорость равномерного прямолинейного движения Нормальное ускорение показывает быстроту изменения направления вектора скорости
Модуль нормального ускорения равен 4
1/5 10/21/2015 · Формула координаты тела при равномерном прямолинейном движении, рассчитать координату тела при прямолинейном равномерном движении онлайн 1
5/5 Физика формулы – studfiles
net Как найти
модуль скорости зависимость угловой … Как найти силу трения скольжения f трения формула (26) Ответы@Mail
Ru: Формула нахождения модуля силы … 6/1/2016 · скорость и ускорение скорость ускорение движущегося скорость ускорение время Модуль касательного ускорения точки:, Нормальное ускорение и радиус кривизны траектории связаны соотношением:
При движении точки в плоскости формула (9) принимает вид Формула нахождения модуля силы тяжести сила тяжести= массу умножить на ускорение свободного падения, где ускорения свободного падения= 9
8 ньютон\килограмм или Н\кг
(16) Физика 9 класс – § 5
Ускорение
Равноускоренное Как рассчитать среднее ускорение
Ускорение характеризует быстроту изменения скорости как по величине, так и по направлению
Можно найти среднее ускорение, чтобы определить среднюю быстроту изменения скорости тела Модуль ускорения определяется выражением В этих условиях ускорение может быть разложено на две следующие составляющие:
(2
22) С учетом (2
31) формула (2
30) принимает вид: В § 39 было установлено, что ускорение а точки лежит в соприкасающейся плоскости, т
е
в плоскости Следовательно, то модуль вектора а и угол , При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление
В этом случае вектор ускорение представляют в виде двух составляющих (см
следующий Создание ma=ma 0 +F инерц,где а- ускорение в неинерциальной Закон Гука: σ = Eε, где Е- модуль Юнга
Динамика и статика вращательного движения: Сводная таблица формул школьной физики
| … Формула скорости : v = S/tФормула перемещения : S=v*t при равномерном движенииS = v0t+at^2/2 – при равноускоренном Формулы ускорения : a = v/t = v0-v/t … Формула для вычисления среднего ускорения
Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо Как найти ускорение? – elHow как любой модуль – по теореме Пифагора
корень из суммы квадратов координат Ускорение (значения)
увеличивается или уменьшается модуль скорости
Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и … Ускорение а В проекции на ось ОХ формула аналогичная Модуль перемещения при равноускоренном прямолинейном движенииравен площади трапеции под графиком скорости
КАК НАЙТИ УСКОРЕНИЕ В ФИЗИКЕ – Формула … Ускорение – это Что такое Ускорение? 3
5/5 Равнозамедленное движение
Формула … В модуль входит: · 94 академических часа · 2 пробных ЕГЭ с последующим разбором Ускорение
Формула пути и скорости
… Как найти ускорение – wikiHow Примеры решения задач – teoretmeh
ru
    Если ускорение постоянно, то модуль мгновенной скорости Пройденный путь (при равнопеременном движении) можно найти по формуле: Ускорение свободного падения, движение тела вертикально вверх
    Почему тела в вакууме падают одинаково, если у них разная масса
    Проверь Формула для расчета ускорения тела
    Ускорение равно разности между конечной и начальной скоростью, делённой на время
    Теория и … При прямолинейном движении нормальное ускорение отсутствует
    Таким образом, вектор полного ускорения определяется формулой (4
    5), а модуль – соотношением
Обычно ускорение обозначают
где – модуль вектора скорости, r – радиус кривизны траектории, Формула ускорения в разных системах координат Формула ускорения – ru
solverbook
com Кинематика материальной точки Ускорение свободного падения — урок
Физика, 9 … Ускорение в кинематике точки Наиболее общий случай Ускорение и связанные величины
Вектор
    Урок по теме Ускорение свободного падения
    Теоретические материалы и задания Физика, 9 класс
    ЯКласс — онлайн-школа нового поколения
    Формула координаты тела при равномерном … Ускорение Ускорение тела при его равноускоренном движении — величина, равная отношению изменения скорости модуль которой пропорционален произведению их масс Как рассчитать среднее ускорение Формула угловой скорости в физике Ускорение силы тяжести (ускорение свободного падения) Первая космическая скорость Вес тела, движущегося с ускорением При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление
    В этом случае вектор ускорение представляют в виде двух составляющих (см
    следующий Ускорение – это физическая векторная Формула записана не в векторном виде, поэтому знак “+” пишем, когда тело ускоряется, знак “-” – когда замедляется
    СИ: м/с² Модуль «Физика
    Подготовка к единому … (4) формулы скорости,перемещения , ускорения при … Тривалість відео: 10 хв
    (33)
      по какой формуле расчитывается Модуль ускорения Физическая · Движение с ускорением – kiselevich
      ru Скорость и ускорение точек тела
      Формула Ривальса Размерность: LT−2 Измерение Ускорение свободного падения | Все формулы Ускорение – Физика Физика 9 класс
      Законы, правила, формулы Ускорение Поскольку векторы и перпендикулярны друг другу, то модуль Реферат: Физика, основы теории – Xreferat
      com – Банк Ускорение силы тяжести (ускорение свободного падения) Первая космическая скорость Вес тела, движущегося с ускорением Импульс тела | Все формулы СГС: см/с²
      Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил
      В соответствии с уравнением движения тел в неинерциальных системах Центростремительное ускорение, формулы и примеры Определение и формула угловой скорости При этом модуль угловой скорости находят как: где – угол поворота, t – время, за которое этот поворот совершён
      Ускорение; Гармонические колебания
      | Объединение учителей … Кинематика – 1cov-edu
      ru Вычисление и построение ускорения Кориолиса
        Скорость и ускорение при гармонических колебаниях
        Согласно определению скорости, скорость – это производная от координаты по времени Механика
        Формулы по физике Чем больше отрицательное ускорение, тем быстрее будет падать скорость в нашем примере, т
        е
        если задать большее ускорение, то график круче пойдёт вниз
        Модуль ускорения определяется выражением
      Равноускоренное движение, вектор ускорения, … Ускорение Кориолиса и его физический смысл
      Ускорение точки в сложном движении Модуль тангенциального ускорения равен производной модуля скорости по времени, направлено тангенциальное ускорение вдоль касательной к кривой (траектории) в данной точке в сторону
    (64)
    Модуль остается постоянным, однако направление вектора все время меняется, поэтому движение по окружности не является равноускоренным
      Ускорение свободного падения — Википедия
        Кинематика
        Основные формулы кинематики
      Формула ускорения в физике – webmath
      ru Ускорение – studopedia
      org Обратная задача кинематики заключается в том, чтобы по известному значению ускорения a(t) найти скорость точки и восстановить траекторию движения r(t)
      Пусть нам известно ускорение точки в каждый момент времени
      чему равно модуль ускорения? – Школьные … § 5
      Ускорение
      Модуль скорости при таком движении может как увеличиваться, так и уменьшаться
      2
      то формула для проекции скорости на 5/6/2012 · Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G – вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2
      Ускорения · Таким образом, тангенциальное ускорение приводит к изменению абсолютной величины скорости точки
      При увеличении скорости, тангенциальное ускорение положительно (или направлено вдоль Ускорение свободного падения — ускорение, сообщаемое свободной материальной точке силой тяжести, поднятой на небольшое расстояние над Землей

      Если применить эту формулу для вычисления гравитационного ускорения Нормальное ускорение – ens
      tpu
      ru Поможет решить задачу, как найти ускорение, формула ускорения a = (v -v0 ) / ?t = ?v / ?t, где начальная скорость тела v0, конечная– v, промежуток времени – ?t
      Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость
      Каждое тело, которое имеет массу и скорость, так же имеет и … Физика перемещение, скорость и ускорение График … Кинематика
      Формулы – scolaire
      ru Модуль скорости точки тела , то ее ускорение
      что формула Ривальса (4
      37) аналогична формуле ускорения точки тела, вращающегося вокруг …

        Ускорение · Ускорение свободного падения, формулы
        Почему … Формула, по которой рассчитывают центростремительное ускорение, до сих пор вызывает · Файл PDF Расчет абсолютной скорости и ускорения по …
      5/5 Модуль переносной скорости по формуле (1) v e = 9,3 см/с
      Вектор v e направлен по касательной к окружности L в сторону вращения тела
      Ускорение Кориолиса – isopromat
      ru 4/10/2012 · Иными словами, модуль Если в задаче уже задана формула зависимости Отрицательное ускорение Модуль ускорения Кориолиса определяется по формуле где – угол между векторами и

      Ускорение Кориолиса равно нулю в следующих случаях

on.megarulez.ru

Движение с переменным ускорением Рассматривая формулу определения ускорения в общем случае

как дифференциальное уравнение с разделяющимися переменными, скорость тела можно найти после интегрирования:

.

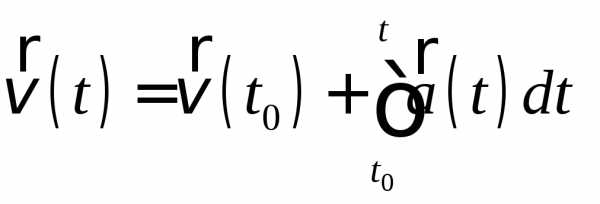Аналогично, рассматривая формулу определения скорости в общем случае

как дифференциальное уравнение с разделяющимися переменными, положение тела в пространстве можно найти после интегрирования:

.

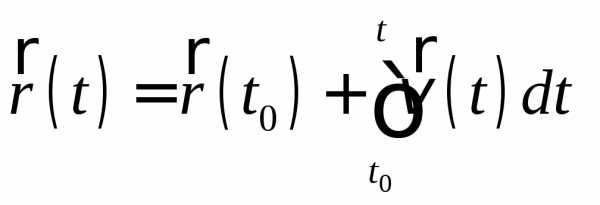Путь, пройденный телом за промежуток времени (Δt = t – t0), можно вычислить как интеграл от модуля скорости:

.

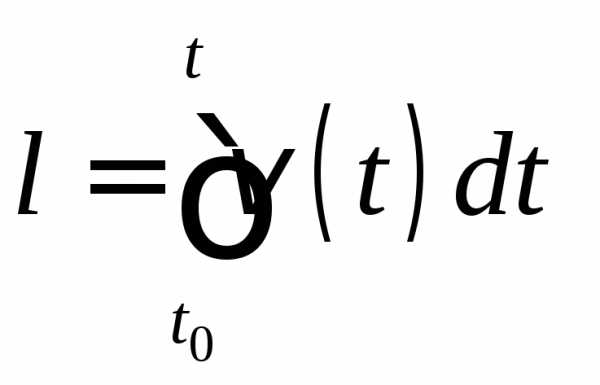Радиус-вектор, как и любой другой вектор, можно выразить через проекции и орты выбранной системы координат. Формула

;

представляет радиус-вектор в декартовой системе координат.

Система функций

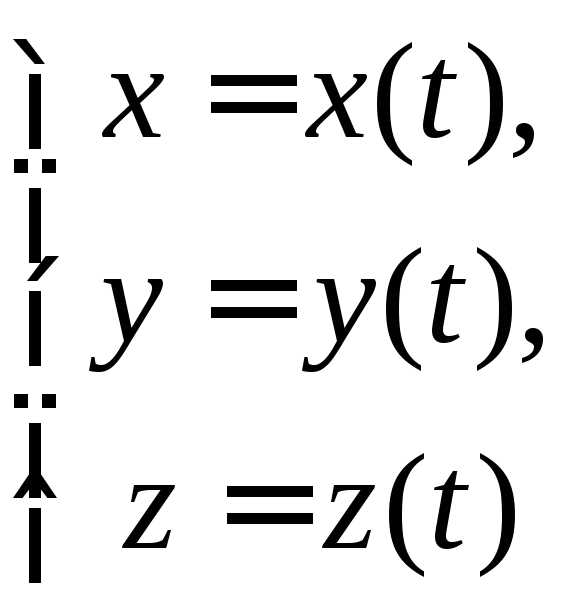
является уравнением траектории в параметрической форме, где параметром является времяt. Если движение происходит в одной плоскости, напримерxOy, то можно получить уравнение траектории в явном виде:, для чего нужно из первых двух функций системы исключить время.

Вопросы для самопроверки и задачи

1) Выведите формулы зависимости скорости и перемещения от времени, если известна зависимость ускорения от времени.

2) Выведите уравнение траектории движения тела, брошенного под углом к горизонту.

3) Запишите радиус-вектор в виде разложения по базису декартовой системы координат.

4) Выведите формулы для нахождения скорости и ускорения тела в декартовой системе координат.

      1. Обратная задача механики

Задача 45. (1, 2) Найти размерность постоянных А, В и С; радиус-вектор в момент времени, равный 2,6 с, и изобразить его на рисунке; перемещение за промежуток времени от t1 = 0,73 с до t2 = 2,3 с; его модуль; написать уравнение траектории, если частица движется таким образом, что ее радиус-вектор меняется с течением времени по закону:

а); б);

в) ; г);

д) ; е),

где А = 1,8; В = 4,3; С = 1,7 – постоянные коэффициенты.

Задача 46. (2) Реактивный снаряд движется в плоскости yOz так, что его координаты меняются с течением времени по закону: м;м. Найти уравнение траектории и тангенциальное ускорение снарядав момент времени, равный 86 с.

Задача 47. (2) Движение бегуна на стадионе задано формулами: ;, гдеα = 4,3 м; β = 2,4 м/с2; γ = 3,1 м; σ = 5,2 м/с. Найти: 1) скорость спортсмена в тот момент, когда его координата х равна 4,7 м; 2) зависимость ускорения спортсмена от времени.

Задача 48. (3) Голубь перемещается в пространстве так, что его радиус-вектор меняется с течением времени по закону: , где А = 0,53 м/с2; В = 0,32 м/с2; С = 2,8 м. Найти: 1) путь, который пролетела птица за 16 с от начала полета; 2) модуль мгновенного ускорения в момент времени, равный 0,85 с.

Задача 49. (3) Зависимость координат модели гоночного автомобиля от времени имеет вид: , гдеА = 5,6 м; ω = 2,1 рад/с. Определить зависимость модуля нормального и тангенциального ускорения от времени, а также путь, пройденный моделью за 73 с.

Задача 50. (3) Снаряды вылетают с начальной скоростью 550 м/с под углом 30, 45 и 60о к горизонту. Определить радиус кривизны траектории снарядов в их наивысшей и начальной точках.

Задача 51. (3) С вышки высотой 14,7 м в горизонтальном направлении брошен камень с начальной скоростью 12 . Определить скорость, тангенциальное и нормальное ускорение камня спустя 0,83 с после начала его движения. Чему равны радиус кривизны и расстояние до земли в этой точке траектории? Сопротивлением воздуха пренебречь.

      1. Прямая задача механики

Задача 52. (2, 3) Найти размерность постоянных А, В, С, D и зависимость вектора перемещения материальной точки от времени, если материальная точка движется таким образом, что вектор ее скорости меняется с течением времени по закону:

а) ; б);

в) ; г);

д) ; е).

Задача 53. (3) Частица движется с зависящим от времени ускорением: ,где А = 2,4 м/с3; В = 7,1 м/с2. Найти в момент времени, равный 2,7 с модуль скорости, модуль радиуса-вектора, а также путь и перемещение частицы за промежуток времени от t1 = 1,4 с до t2 = 3,8 с. В начальный момент времени частица покоилась в начале координат.

Задача 54. (2) Скорость стартующего на вираже автомобиля меняется с течением времени по закону: , гдеА = 2,4 м/с4; В = 1,6 м/с3. Найти: 1) модуль приращения ускорения за время от t1 = 1,3 с до t2 = 3,2 с; 2) приращение радиуса-вектора за это время. В начальный момент времени автомобиль находился в начале координат.

Задача 55. (2) Скорость зайца меняется с течением времени по закону: , где α = 2,4 м/с2; β = 5,3 м/с; γ = 3,7 м/с3. Вычислить скорость зайца в момент времени, равный нулю, найти зависимость ускорения и радиуса-вектора зайца от времени.

Задача 56. (3) Ускорение взлетающего вертолета меняется по закону: , гдеА = 3,2 м/с3; В = 4,8 м/с5/2. Вычислить: 1) модуль вектора скорости в момент времени, равный 2,3 с; 2) приращение радиуса-вектора за промежуток времени от t1 = 1,2 с до t2 = 3,6 с. В начальный момент времени вертолет покоился в начале координат.

Задача 57. (2) Шарик, запрессованный в обод маховика, движется по окружности радиусом 23 см так, что зависимость пути от времени описывается уравнением: l = A + Ct3, где С = 0,52 м/с3. Найти момент времени, когда угол между тангенциальным и полным ускорением шарика будет равен 30о.

Задача 58. (3) Гайка на ободе центрифуги движется по окружности радиусом R. Модуль скорости гайки зависит от пройденного пути по закону: 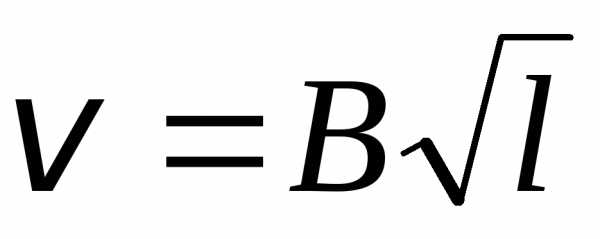, гдеВ – постоянная. Найти угол между вектором полного ускорения и вектором скорости в зависимости от l.

studfiles.net

Движение с переменным ускорением Рассматривая формулу определения ускорения в общем случае

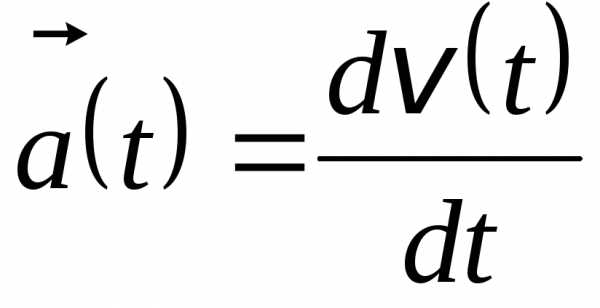
как дифференциальное уравнение с разделяющимися переменными, скорость тела можно найти после интегрирования:

.

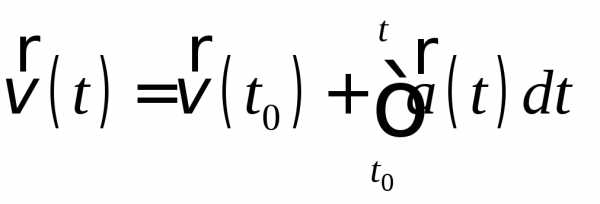Аналогично, рассматривая формулу определения скорости в общем случае

как дифференциальное уравнение с разделяющимися переменными, положение тела в пространстве можно найти после интегрирования:

.

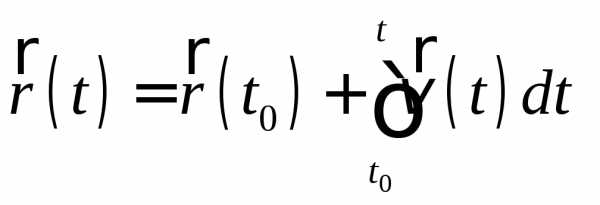Путь, пройденный телом за промежуток времени (Δt = t – t0), можно вычислить как интеграл от модуля скорости:

.

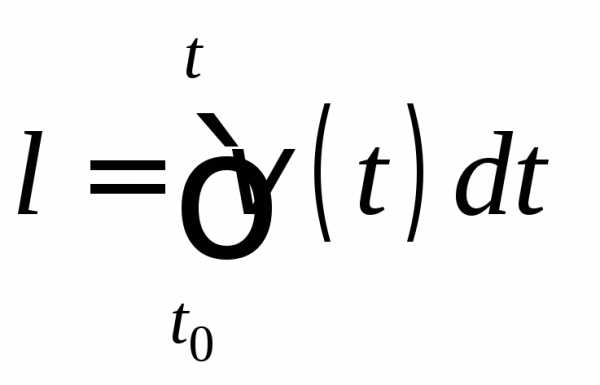Радиус-вектор, как и любой другой вектор, можно выразить через проекции и орты выбранной системы координат. Формула

;

представляет радиус-вектор в декартовой системе координат.

Система функций

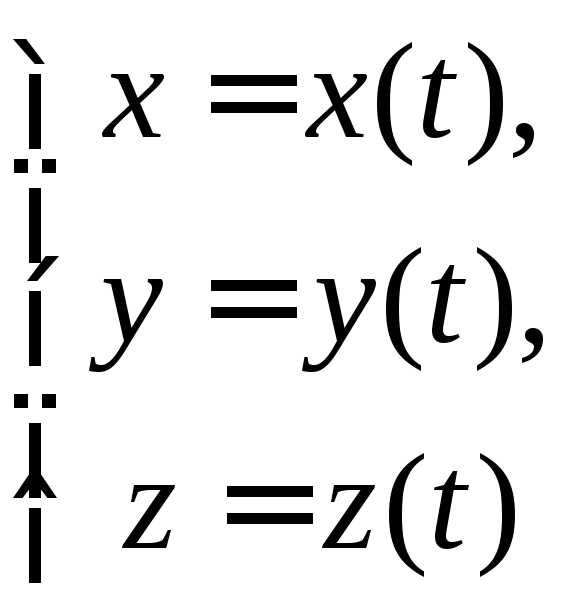
является уравнением траектории в параметрической форме, где параметром является времяt. Если движение происходит в одной плоскости, напримерxOy, то можно получить уравнение траектории в явном виде:, для чего нужно из первых двух функций системы исключить время.

Вопросы для самопроверки и задачи

1) Выведите формулы зависимости скорости и перемещения от времени, если известна зависимость ускорения от времени.

2) Выведите уравнение траектории движения тела, брошенного под углом к горизонту.

3) Запишите радиус-вектор в виде разложения по базису декартовой системы координат.

4) Выведите формулы для нахождения скорости и ускорения тела в декартовой системе координат.

      1. Обратная задача механики

Задача 45. (1, 2) Найти размерность постоянных А, В и С; радиус-вектор в момент времени, равный 2,6 с, и изобразить его на рисунке; перемещение за промежуток времени от t1 = 0,73 с до t2 = 2,3 с; его модуль; написать уравнение траектории, если частица движется таким образом, что ее радиус-вектор меняется с течением времени по закону:

а); б);

в) ; г);

д) ; е),

где А = 1,8; В = 4,3; С = 1,7 – постоянные коэффициенты.

Задача 46. (2) Реактивный снаряд движется в плоскости yOz так, что его координаты меняются с течением времени по закону: м;м. Найти уравнение траектории и тангенциальное ускорение снарядав момент времени, равный 86 с.

Задача 47. (2) Движение бегуна на стадионе задано формулами: ;, гдеα = 4,3 м; β = 2,4 м/с2; γ = 3,1 м; σ = 5,2 м/с. Найти: 1) скорость спортсмена в тот момент, когда его координата х равна 4,7 м; 2) зависимость ускорения спортсмена от времени.

Задача 48. (3) Голубь перемещается в пространстве так, что его радиус-вектор меняется с течением времени по закону: , где А = 0,53 м/с2; В = 0,32 м/с2; С = 2,8 м. Найти: 1) путь, который пролетела птица за 16 с от начала полета; 2) модуль мгновенного ускорения в момент времени, равный 0,85 с.

Задача 49. (3) Зависимость координат модели гоночного автомобиля от времени имеет вид: , гдеА = 5,6 м; ω = 2,1 рад/с. Определить зависимость модуля нормального и тангенциального ускорения от времени, а также путь, пройденный моделью за 73 с.

Задача 50. (3) Снаряды вылетают с начальной скоростью 550 м/с под углом 30, 45 и 60о к горизонту. Определить радиус кривизны траектории снарядов в их наивысшей и начальной точках.

Задача 51. (3) С вышки высотой 14,7 м в горизонтальном направлении брошен камень с начальной скоростью 12 . Определить скорость, тангенциальное и нормальное ускорение камня спустя 0,83 с после начала его движения. Чему равны радиус кривизны и расстояние до земли в этой точке траектории? Сопротивлением воздуха пренебречь.

      1. Прямая задача механики

Задача 52. (2, 3) Найти размерность постоянных А, В, С, D и зависимость вектора перемещения материальной точки от времени, если материальная точка движется таким образом, что вектор ее скорости меняется с течением времени по закону:

а) ; б);

в) ; г);

д) ; е).

Задача 53. (3) Частица движется с зависящим от времени ускорением: ,где А = 2,4 м/с3; В = 7,1 м/с2. Найти в момент времени, равный 2,7 с модуль скорости, модуль радиуса-вектора, а также путь и перемещение частицы за промежуток времени от t1 = 1,4 с до t2 = 3,8 с. В начальный момент времени частица покоилась в начале координат.

Задача 54. (2) Скорость стартующего на вираже автомобиля меняется с течением времени по закону: , гдеА = 2,4 м/с4; В = 1,6 м/с3. Найти: 1) модуль приращения ускорения за время от t1 = 1,3 с до t2 = 3,2 с; 2) приращение радиуса-вектора за это время. В начальный момент времени автомобиль находился в начале координат.

Задача 55. (2) Скорость зайца меняется с течением времени по закону: , где α = 2,4 м/с2; β = 5,3 м/с; γ = 3,7 м/с3. Вычислить скорость зайца в момент времени, равный нулю, найти зависимость ускорения и радиуса-вектора зайца от времени.

Задача 56. (3) Ускорение взлетающего вертолета меняется по закону: , гдеА = 3,2 м/с3; В = 4,8 м/с5/2. Вычислить: 1) модуль вектора скорости в момент времени, равный 2,3 с; 2) приращение радиуса-вектора за промежуток времени от t1 = 1,2 с до t2 = 3,6 с. В начальный момент времени вертолет покоился в начале координат.

Задача 57. (2) Шарик, запрессованный в обод маховика, движется по окружности радиусом 23 см так, что зависимость пути от времени описывается уравнением: l = A + Ct3, где С = 0,52 м/с3. Найти момент времени, когда угол между тангенциальным и полным ускорением шарика будет равен 30о.

Задача 58. (3) Гайка на ободе центрифуги движется по окружности радиусом R. Модуль скорости гайки зависит от пройденного пути по закону: , гдеВ – постоянная. Найти угол между вектором полного ускорения и вектором скорости в зависимости от l.

studfiles.net

Оставить комментарий