Модуль ускорения определяется выражением
. (2.21)
Выше
было отмечено, что вектор  ускорения
материальной точки характеризует
изменение скорости
ускорения
материальной точки характеризует
изменение скорости 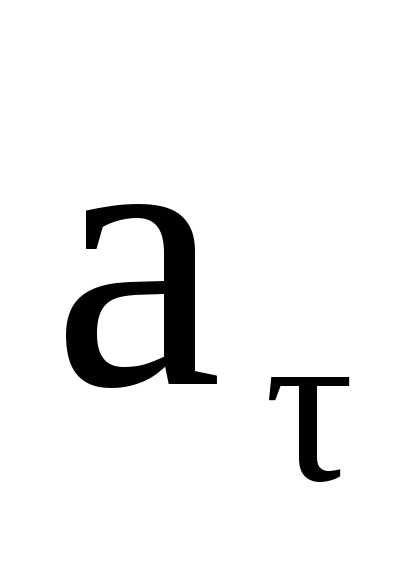 по модулю и направлению. Оказывается,
что вектор
по модулю и направлению. Оказывается,
что вектор можно разложить на две составляющие,
одна из которых характеризует изменение
только модуля скорости, а другая – только
его направления. Такое разложение
возможно при любом виде движения
материальной точки. В качестве примера
покажем это для случая плоского движения
точки по произвольной криволинейной
траектории.
можно разложить на две составляющие,
одна из которых характеризует изменение
только модуля скорости, а другая – только
его направления. Такое разложение
возможно при любом виде движения
материальной точки. В качестве примера
покажем это для случая плоского движения
точки по произвольной криволинейной
траектории.
Пусть материальная точка M совершает неравномерное плоское движение по криволинейной траектории (рис. 2.6). Проведем в точке М
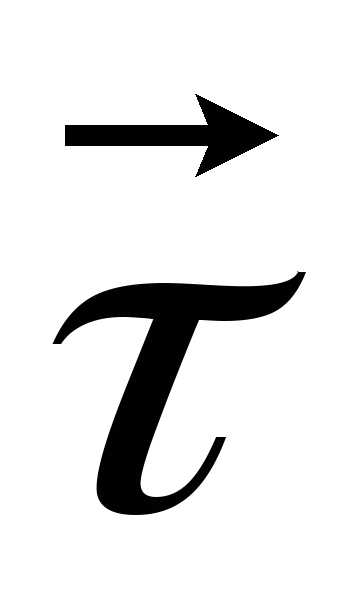 и
и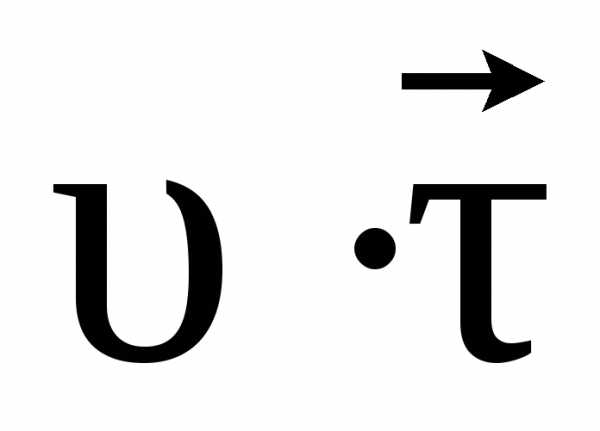 лежащих в плоскости траектории. Вектор
лежащих в плоскости траектории. Вектор направлен по касательной к траектории
в сторону движения материальной точки,
то есть в направлении ее скорости
направлен по касательной к траектории
в сторону движения материальной точки,
то есть в направлении ее скорости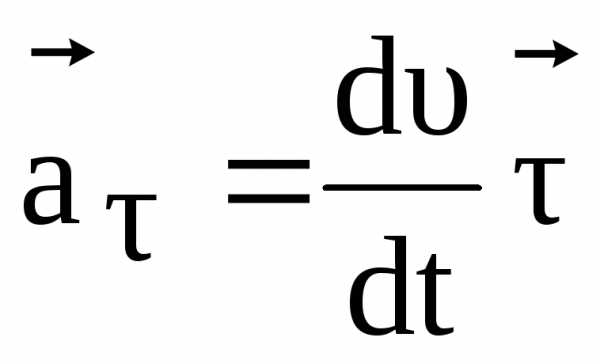 .
Вектор
.
Вектор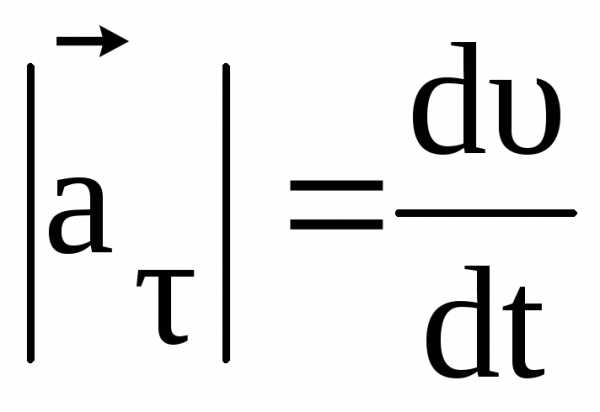 , проведен
в сторону вогнутости траектории по
линии, соединяющей точку M с
центром О кривизны
траектории для данной ее точки.
, проведен
в сторону вогнутости траектории по
линии, соединяющей точку M с
центром О кривизны
траектории для данной ее точки.В
этих условиях ускорение 
. (2.22)
В
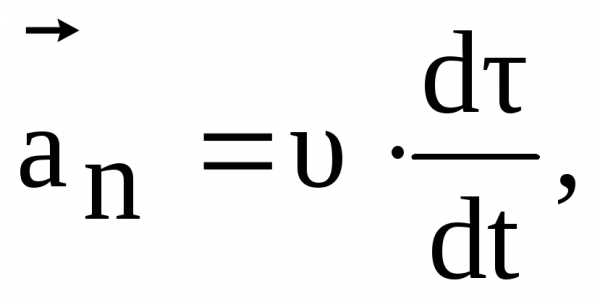
Рис. 2.7
качестве примера рассмотрим неравномерное движение точки М по окружности (рис 2.7). В момент времени t точка М находится в положении 1 и имеет скорость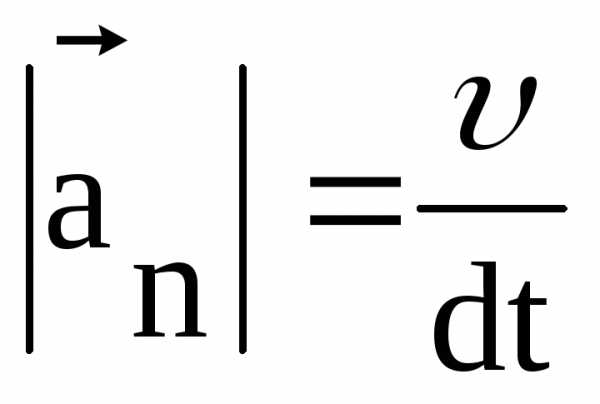 .
Через малый промежуток времениt
точка переместится в положение 2 и будет
иметь скорость
.
Через малый промежуток времениt
точка переместится в положение 2 и будет
иметь скорость 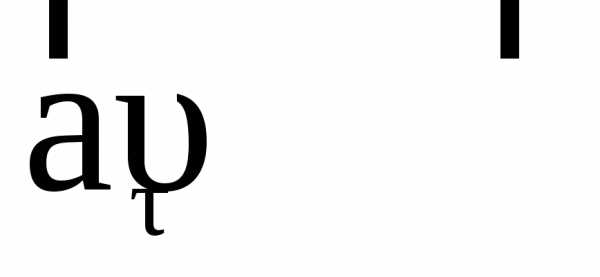 .
Найдем приращение вектора скорости
.
Найдем приращение вектора скорости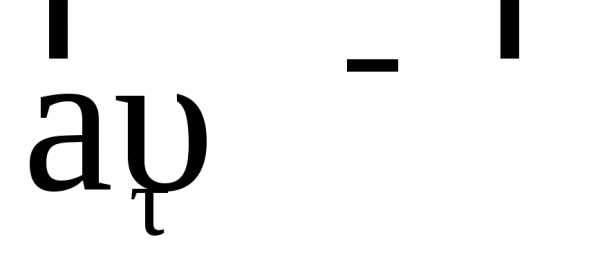
 без изменения его направления так, чтобы
его начало совпало с началом вектора
без изменения его направления так, чтобы
его начало совпало с началом вектора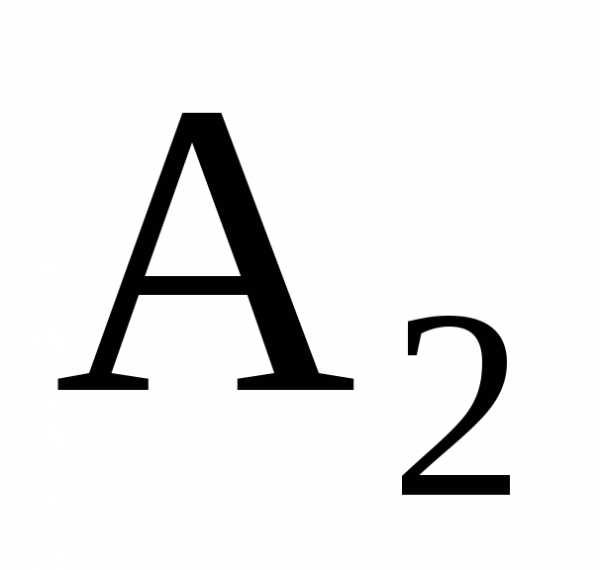 (рис. 2.8). Вектор
(рис. 2.8). Вектор изображен направленным отрезком,
проведенным из конца вектора
изображен направленным отрезком,
проведенным из конца вектора в конец вектора
в конец вектора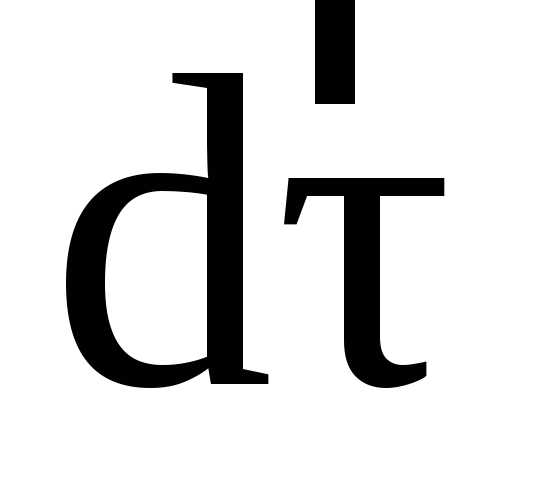 .
Разложим вектор
.
Разложим вектор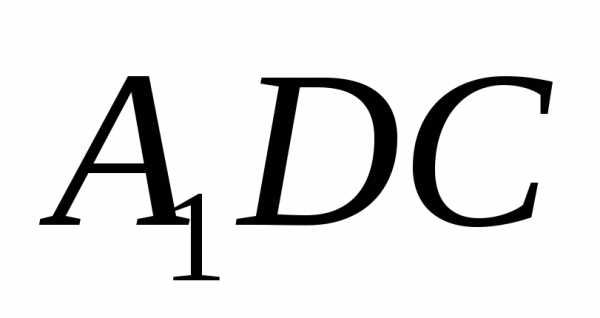
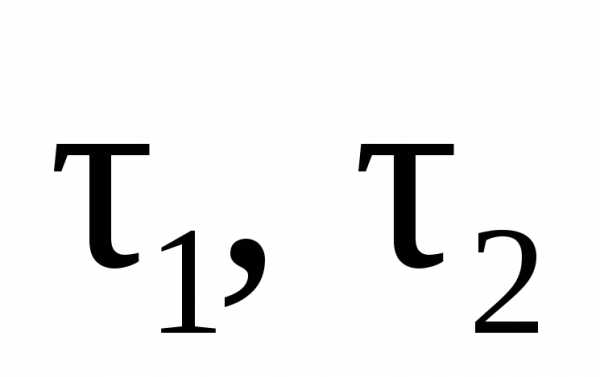 n и
n и 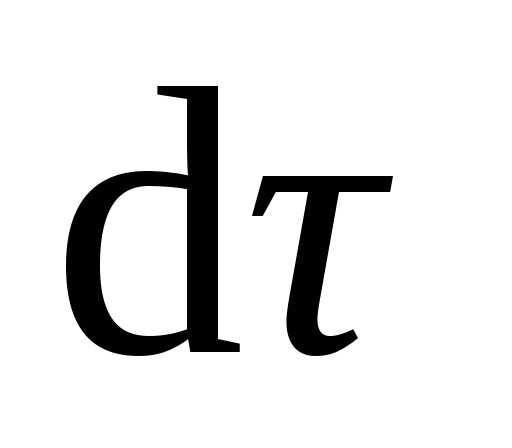 .
Составляющую
.
Составляющую 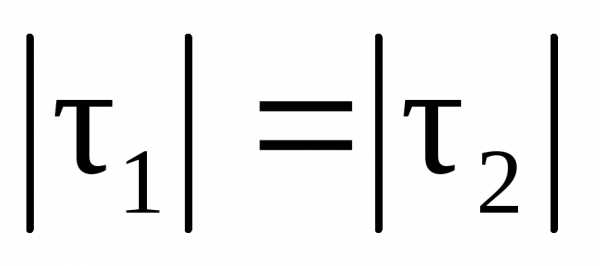 n выберем так, чтобы расстояние от точки
1 до конца вектора
n выберем так, чтобы расстояние от точки
1 до конца вектора 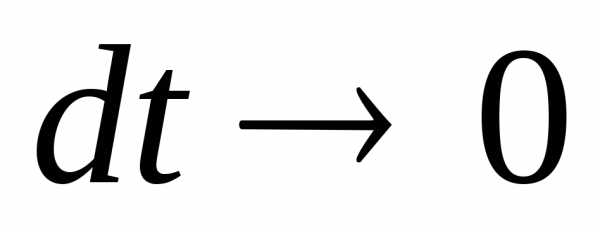 было равно
было равно .
При таком выборе
.
При таком выборе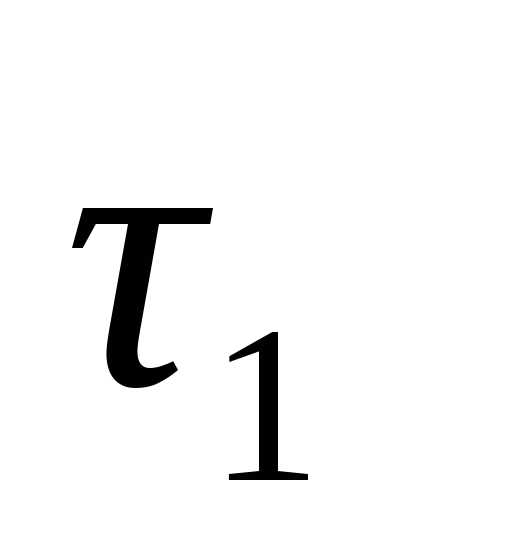 n,
составляющая
n,
составляющая 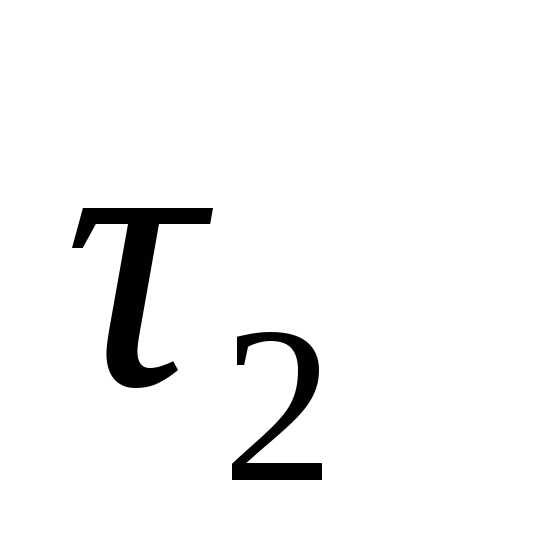
| |=|
|=| |.
(2.27)
|.
(2.27)
Введем
единичный вектор  ,
совпадающий по направлению с вектором,
тогда его можно будет представить в
виде
,
совпадающий по направлению с вектором,
тогда его можно будет представить в
виде
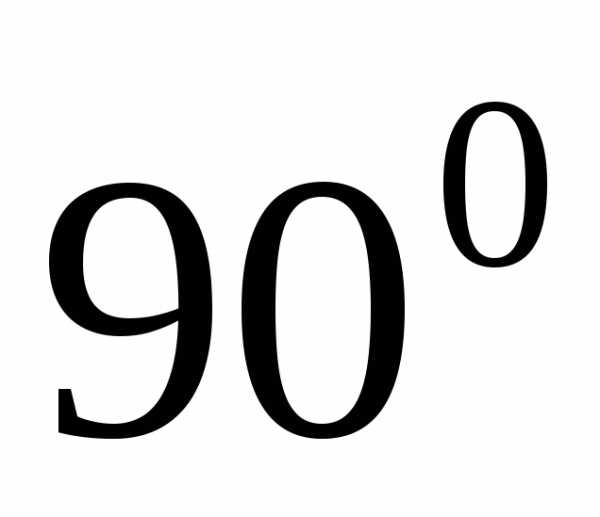 =
=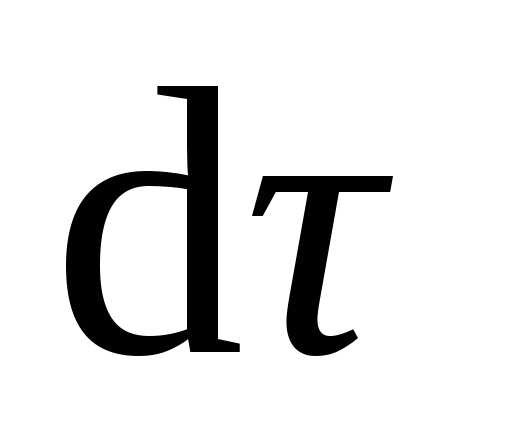

Вектор 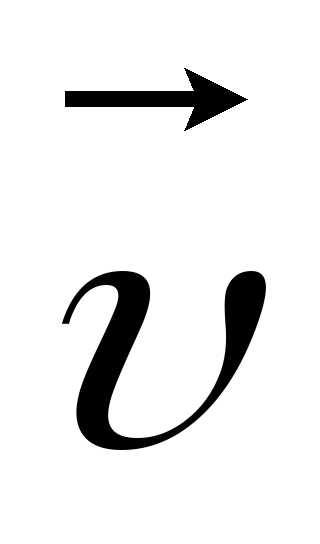 n также можно представить в виде произведения
его модуля на единичный вектор
n также можно представить в виде произведения
его модуля на единичный вектор 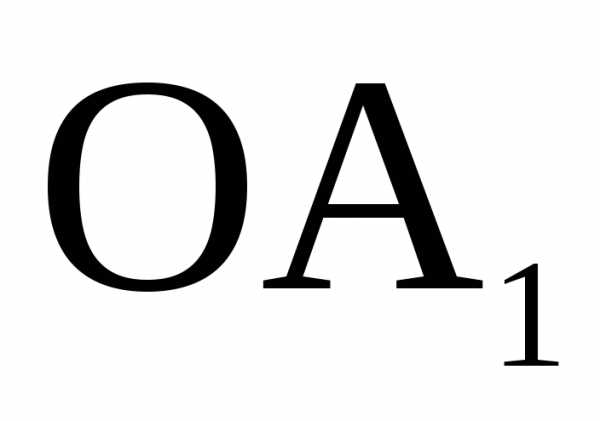 ,
задающий его направление
,
задающий его направление
 n =|
n =| n |
n |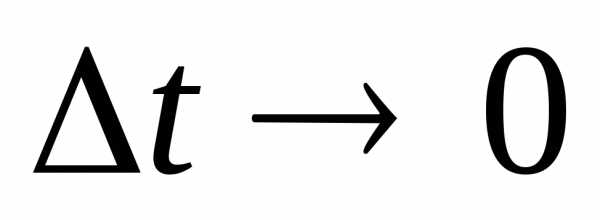 .(2.29)
.(2.29)
Угол
между векторами 
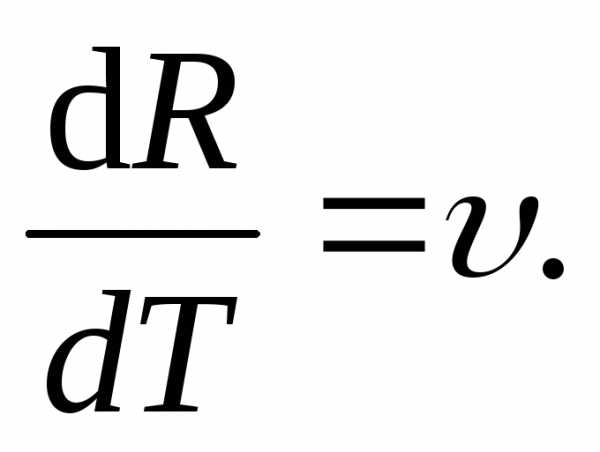 )
равен,
то есть углу между векторами
)
равен,
то есть углу между векторами  и (
и (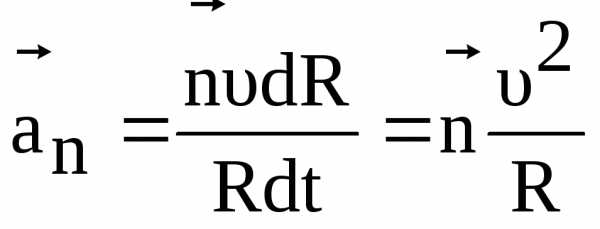 )
(рис 2.7 и 2.8). При малыхt
модуль вектора
)
(рис 2.7 и 2.8). При малыхt
модуль вектора  n можно приближенно заменить дугой
окружности радиуса |
n можно приближенно заменить дугой
окружности радиуса |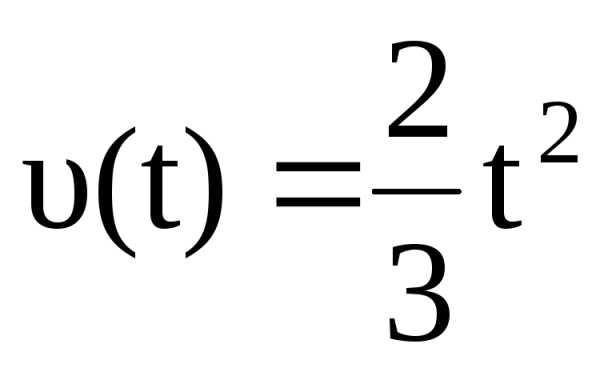 |
(рис. 2.8):
|
(рис. 2.8):  n
n
Угол можно выразить через радиус окружности и пройденный точкой М путь S за время t (рис. 2.7) с помощью известного из геометрии соотношения
=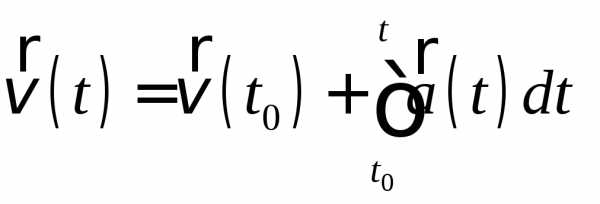 . (2.31)
. (2.31)
С учетом (2.31) формула (2.30) принимает вид:
 n
n 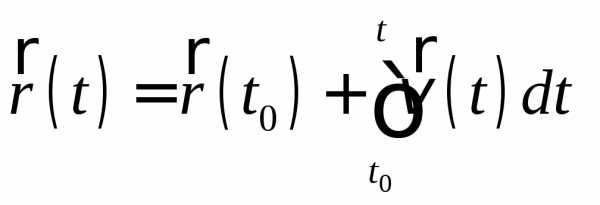
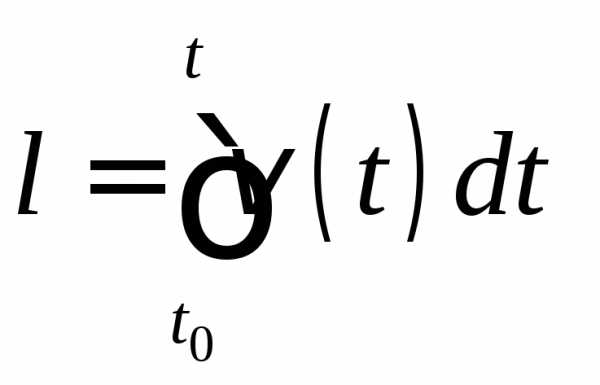
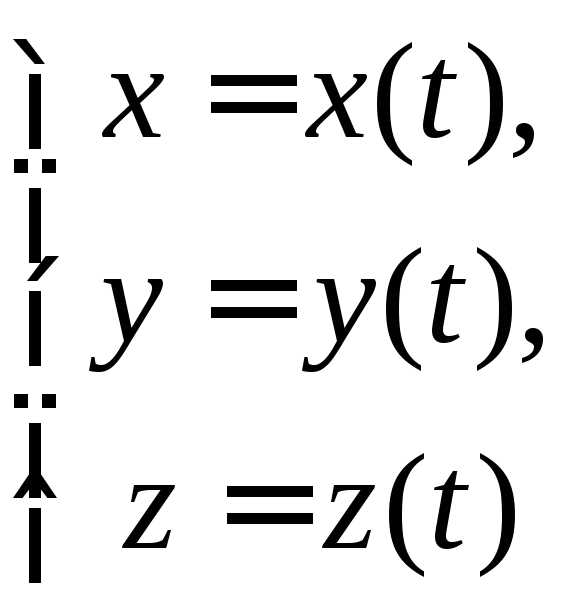 .
(2.32)
.
(2.32)
Найдем
ускорение точки М в положении 1 (рис.
2.7). Для этого учтем, что  =
= n +
n +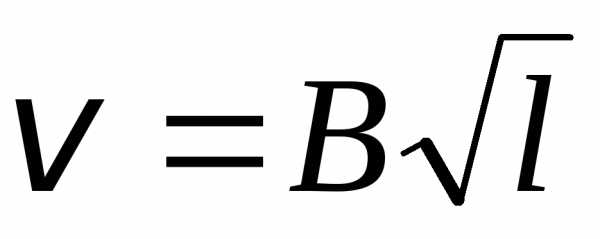 ,
и воспользуемся формулой (2.21)
,
и воспользуемся формулой (2.21)
(2.33)
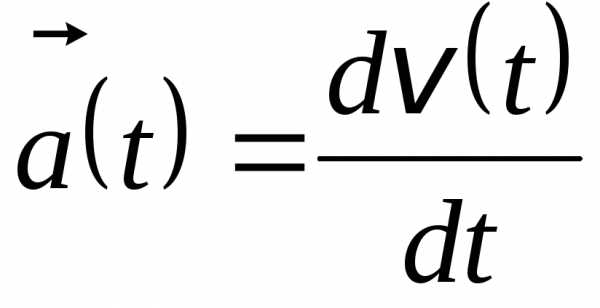
Рис 2.8
С учетом выражения (2.32) первый предел справа принимает вид:. (2.34)
В
точке 1 траектории V и 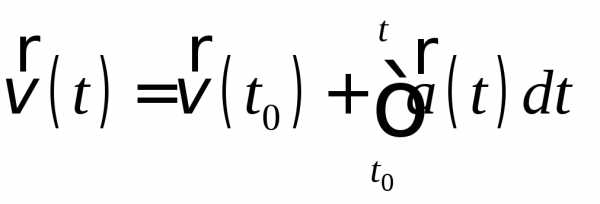
 .
Кроме того, приt0
вектор
.
Кроме того, приt0
вектор 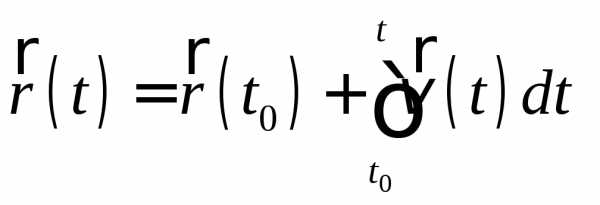 переходит в вектор
переходит в вектор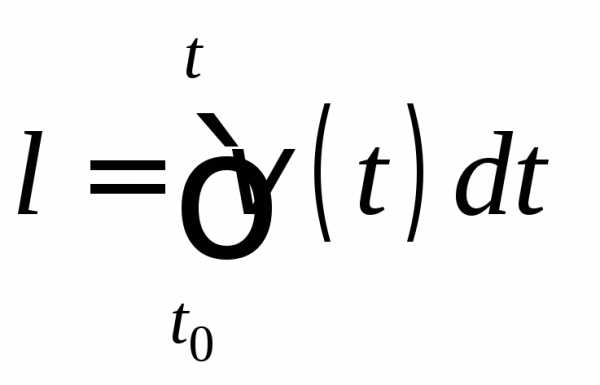 –
вектор главной нормали к траектории в
точке 1 (рис. 2.8). Таким образом, вычисляя
предел в (2.34) и обозначая его через
–
вектор главной нормали к траектории в
точке 1 (рис. 2.8). Таким образом, вычисляя
предел в (2.34) и обозначая его через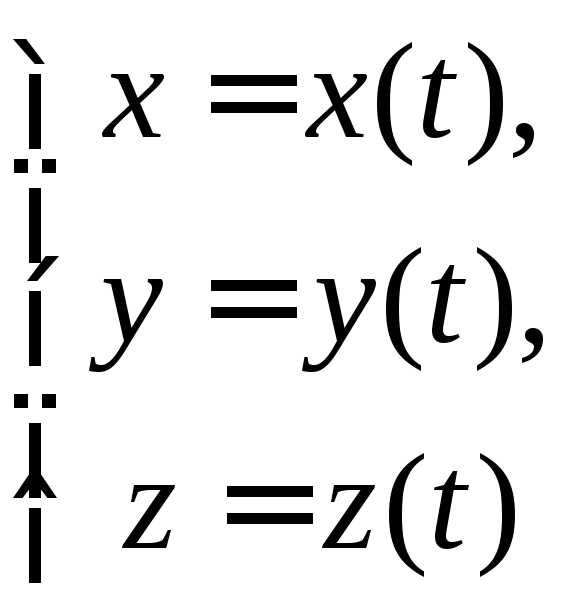 ,
получим
,
получим  . (2.35)
. (2.35)
Второй
предел в выражении (2.33) обозначим через 
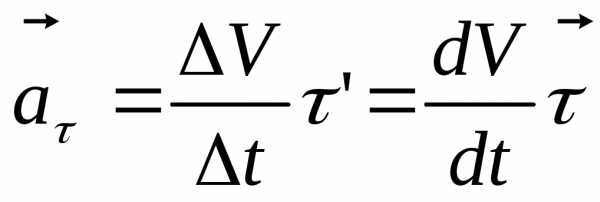 . (2.36)
. (2.36)
При
вычислении предела в (2.36) учтено, что
при t0 вектор  переходит в вектор
переходит в вектор –
единичный вектор касательной к траектории
в точке 1 (рис. 2.8).
–
единичный вектор касательной к траектории
в точке 1 (рис. 2.8).
Таким образом, вектор ускорения точки в любой момент времени может быть представлен в виде суммы двух векторов:
. (2.37)
Вектор 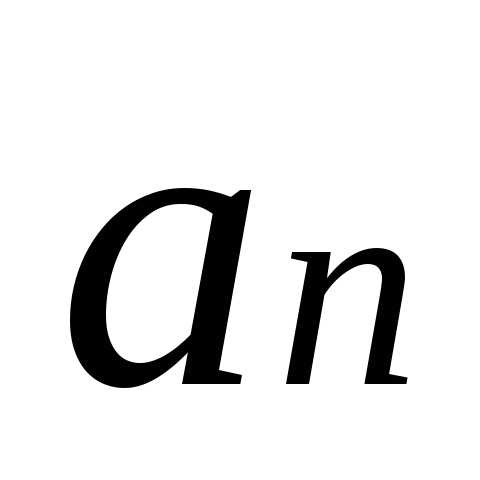
Вектор 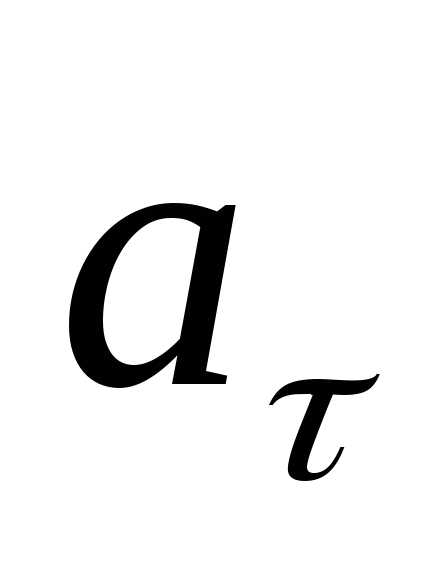 –
называется тангенциальным (касательным)
ускорением и характеризует изменение
скорости по величине.
–
называется тангенциальным (касательным)
ускорением и характеризует изменение
скорости по величине.
Модуль полного ускорения в соответствии с выражениями (2.35), (2.36) и (2.37) равен:
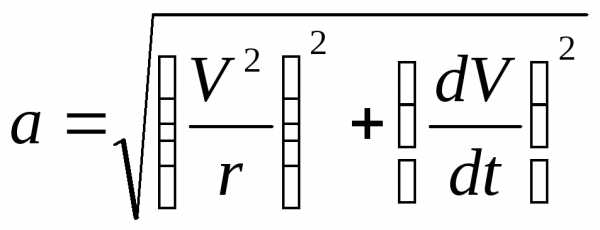 . (2.38)
. (2.38)
Если
траектория не окружность, а произвольная
кривая, то в формуле (2.38) 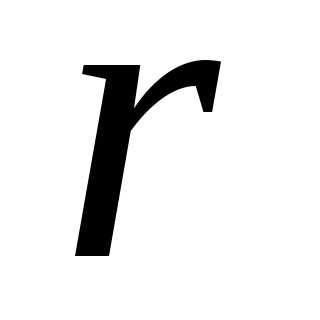 представляет собой радиус кривизны
траектории в точке, для которой
определяется полное ускорение.
представляет собой радиус кривизны
траектории в точке, для которой
определяется полное ускорение.
studfiles.net
Модуль нормального ускорения
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса – ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший “Салат из свеклы с чесноком”
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека – Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков – Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) – В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Кинематика. Основные формулы
Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров. Именно для этого абстрактного образа (модели) и справедливы все представленные ниже определения и формулы. Однако для краткости я в дальнейшем буду часто говорить о движении тела,объектаили частицы. Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.
Радиус-вектор точки – это вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой. Радиус-вектор обозначается, как правило, буквой r.
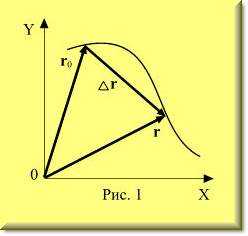
Вектор перемещения (часто говорят просто – перемещение) – это вектор, начало которого совпадает с той точкой траектории, где было тело, когда мы начали изучать данное движение, а конец этого вектора совпадает с той точкой траектории, где мы это изучение закончили. Будем обозначать этот вектор как Δr. Использование символа Δ очевидно: Δr – это разность между радиус-вектором rконечной точки изучаемого отрезка траектории и радиус-вектором r0 точки начала этого отрезка (рис. 1), то есть Δr =r − r0.
Траектория – это линия, вдоль которой движется тело.
Путь – это сумма длин всех участков траектории, последовательно проходимых телом при движения. Обозначается либо ΔS, если речь идет об участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают и другой буквой, например, L (только не обозначайте его как r). Запомните! Путь – это положительный скаляр! Путь в процессе движения может только увеличиваться.
Средняя скорость перемещения vср – это вектор, определяемый выражением
vср = Δr/Δt.
Мгновенная скорость перемещения v– это вектор, определяемый выражением
v = dr/dt.
Средняя скорость путиvср – это скаляр, определяемый выражением
vср = Δs/Δt.
Часто встречаются и другие обозначения, например, <v>.
Мгновенная скорость пути v – это скаляр, определяемый выражением
v = ds/dt.
Модуль мгновенной скорости перемещения и мгновенная скорость пути – это одно и то же, поскольку dr = ds.
Среднее ускорениеaср – это вектор, определяемый выражением
aср = Δv/Δt.
Мгновенное ускорение(или просто, ускорение) a – это вектор, определяемый выражением
a =dv/dt.
Касательное (тангенциальное) ускорение aτ (нижний индекс – это греческая строчная буква тау) – это вектор, являющийсявекторной проекцией мгновенного ускорения на касательную ось.
Нормальное (центростремительное) ускорение an – это вектор, являющийсявекторной проекцией мгновенного ускорения на ось нормали.
Модуль касательного ускорения
| aτ | = dv/dt,
то есть это – производная модуля мгновенной скорости по времени.
Модуль нормального ускорения
| an | = v2/r,
где r – величина радиуса кривизны траектории в точке нахождения тела.
Важно! Хочу обратить внимание на следующее. Не путайтесь с обозначениями, касающимися касательного и нормального ускорений! Дело в том, что в литературе по этому поводу традиционно наблюдается полная чехарда.
Запомните!
aτ – это вектор касательного ускорения,
an – это вектор нормального ускорения.
aτ и an являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,
aτ – это проекция (скалярная!) касательного ускорения на касательную ось,
an – это проекция (скалярная!) нормального ускорения на ось нормали,
| aτ |- это модульвектора касательного ускорения,
| an | – это модульвектора нормального ускорения.
Не зная азов векторной алгебры или пренебрегая ими, очень легко полностью запутаться при изучении и анализе физических процессов. Поэтому знание векторной алгебры является наиглавнейшим условием успеха в изучении механики. И не только механики. В дальнейшем, при изучении других разделов физики, Вы неоднократно в этом убедитесь.
Мгновенная угловая скорость(или просто, угловая скорость) ω– это вектор, определяемый выражением
ω = dφ/dt,
где dφ– бесконечно малое изменение угловой координаты (dφ– вектор!).
Мгновенное угловое ускорение(или просто, угловое ускорение) ε– это вектор, определяемый выражением
ε= dω/dt.
Связь между v, ω и r:
v =ω ×r.
Связь между v, ω и r:
v = ω · r.
Связь между | aτ |, ε и r:
| aτ | = ε · r.
Теперь перейдем ккинематическим уравнениям конкретных видов движения. Эти уравнения надо выучить наизусть.
Кинематическое уравнение равномерного и прямолинейного движенияимеет вид:
r = r0 + v t,
гдеr– радиус-вектор объекта в момент времени t, r0 – то же в начальный момент времени t0 (в момент начала наблюдений).
Кинематическое уравнение движения с постоянным ускорениемимеет вид:
r = r0 + v0 t + at2/2, где v0 скорость объекта в момент t0 .
Уравнение для скорости тела при движении с постоянным ускорениемимеет вид:
v= v0 + a t.
Кинематическое уравнение равномерного движения по окружности в полярных координатахимеет вид:
φ = φ0 + ωz t,
где φ – угловая координата тела в данный момент времени, φ0 – угловая координата тела в момент начала наблюдения (в начальный момент времени), ωz – проекция угловой скорости ωна ось Z (обычно эта ось выбирается перпендикулярно плоскости вращения).
megapredmet.ru
Кинематика материальной точки (средняя школа)
Кинематика материальной точки
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Скорость равномерного движения определяется по формуле:
|
Рис. 1. Перемещение, скорость и ускорение при равномерном прямолинейном движении |
|
Рис. 2. Перемещение, скорость и ускорение при равноускоренном прямолинейном движении |
Равноускоренным прямолинейным движением называется движение, при котором скорость и ускорение направлены вдоль одной прямой и ускорение остается неизменным по модулю. В этом случае модуль ускорения определяется по формуле:
Перемещение, в свою очередь, равно:
где x0 – значение перемещения в момент времени t = 0.
Также используется формула:Примером равноускоренного движения является свободное падение тела с небольшой (по сравнению с радиусом Земли) высоты h в безвоздушном пространстве. Ускорение свободного падения тела не зависит от самого тела и всегда направлено вертикально вниз. Высота тела при этом определяется формулой (при условии, что начальная скорость равна нулю). Время падения с высоты h равно
При равномерном движении со скоростью υ по окружности радиуса R ускорение (центростремительное ускорение) постоянно по модулю:
|
Рис. 3. Равномерное движение по окружности |
Период обращения T – это промежуток времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Модуль скорости движения тела при этом можно записать как:
Частота обращения ν – это число оборотов, совершаемых материальной точкой при равномерном движении по окружности за единицу времени:
Часто используется понятие круговой (или циклической) частоты:
В этом случае центростремительное ускорение записывается в виде:Если модуль скорости движения материальной точки при движении по окружности изменяется, то помимо центростремительного появляется тангенциальное (касательное) ускорение aτ. Оно направлено по касательной к окружности и равно по модулю Полное ускорение в этом случае будет равно:
|
Рис. 4. Нормальное и тангенциальное ускорение |
files.school-collection.edu.ru
Ускорение – Класс!ная физика
Ускорение
Как изменяются показания спидометра в начале движения и при торможении автомобиля?
Какая физическая величина характеризует изменение скорости?
При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо жеодновременно как по модулю, так и по направлению.
Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает. Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис 1.26). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.
Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении).
Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.
Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае её скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени t точка занимает положение М и имеет скорость (рис. 1.27). Спустя промежуток времени Δt точка займёт положение М1 и будет иметь скорость 1. Изменение скорости за время Δt1 равно Δ1 = 1 – . Вычитание вектора можно произвести путём прибавления к вектору 1 вектора (-):
Δ1 = 1 – = 1 + (-).
Согласно правилу сложения векторов вектор изменения скорости Δ1 направлен из начала вектора 1 в конец вектора (-), как это показано на рисунке 1.28.
Поделив вектор Δ1 на промежуток времени Δt1 получим вектор, направленный так же, как и вектор изменения скорости Δ1. Этот вектор называют средним ускорением точки за промежуток времени Δt1. Обозначив его через cр1, запишем:
По аналогии с определением мгновенной скорости определим мгновенное ускорение. Для этого найдём теперь средние ускорения точки за всё меньшие и меньшие промежутки времени:
При уменьшении промежутка времени Δt вектор Δ уменьшается по модулю и меняется по направлению (рис. 1.29). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени Δt к нулю отношение изменения скорости к изменению времени стремится к определённому вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени или просто ускорением и обозначают .
Ускорение точки — это предел отношения изменения скорости Δ к промежутку времени Δt, в течение которого это изменение произошло, при стремлении Δt к нулю.
Ускорение направлено так, как направлен вектор изменения скорости Δ при стремлении промежутка времени Δt к нулю. В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения точки при прямолинейном и криволинейном движениях.
В общем случае ускорение направлено под углом к вектору скорости (рис. 1.30). Полное ускорение характеризует изменение скорости и по модулю, и по направлению. Часто полное ускорение считается равным векторной сумме двух ускорений — касательного (к) и центростремительного (цс). Касательное ускорение к характеризует изменение скорости по модулю и направлено по касательной к траектории движения. Центростремительное ускорение цс характеризует изменение скорости по направлению и перпендикулярно касательной, т. е. направлено к центру кривизны траектории в данной точке. В дальнейшем мы рассмотрим два частных случая: точка движется по прямой и скорость изменяется только по модулю; точка движется равномерно по окружности и скорость изменяется только по направлению.
Единица ускорения.
Движение точки может происходить как с переменным, так и с постоянным ускорением. Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени. Поэтому, обозначив через Δt некоторый произвольный промежуток времени, а через Δ — изменение скорости за этот промежуток, можно записать:
Так как промежуток времени Δt — величина положительная, то из этой формулы следует, что если ускорение точки с течением времени не изменяется, то оно направлено так же, как и вектор изменения скорости. Таким образом, если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени. Это позволяет установить единицы модуля ускорения и его проекций.
Запишем выражение для модуля ускорения:
Отсюда следует, что:
модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости изменяется на единицу.
Если время измерено в секундах, а скорость — в метрах в секунду, то единица ускорения — м/с2 (метр на секунду в квадрате).
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика – Физика, учебник для 10 класса – Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
class-fizika.ru
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости Δ = – 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – 0. Тогда определить ускорение можно так:
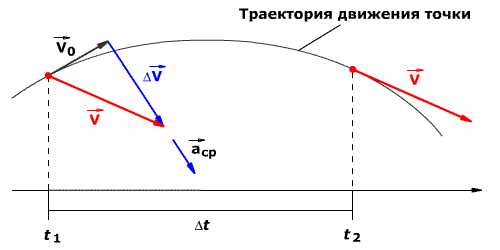
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1а направление вектора ускорения совпадает с вектором скорости 2.
Если скорость тела по модулю уменьшается, то есть
v21то направление вектора ускорения противоположно направлению вектора скорости 2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а
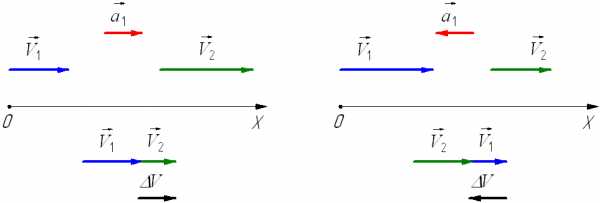
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
= τ + n
av-physics.narod.ru
Ускорение в кинематике формула. Ускорение в кинематике определение
Ускорение
Ускорение в кинематике формула. Ускорение в кинематике определение.
Что такое ускорение?
Скорость может изменяться во время движения.
Скорость является векторной величиной.
Вектор скорости может изменяться по направлению и по модулю, т.е. по величине. Для учёта таких изменений скорости используют ускорение.
Ускорение определение
Определение ускорения
Ускорение служит мерой любых изменений скорости.
Ускорение, его ещё называют полным ускорением, является вектором.
Вектор ускорения
Вектор ускорения есть сумма двух других векторов. Один из этих других векторов называется тангенциальным ускорением, а другой называется нормальным ускорением.
Тангенциальное ускорение описывает изменение модуля вектора скорости.
Нормальное ускорение описывает изменение направления вектора скорости.
При прямолинейном движении направление скорости не меняется. В этом случае нормальное ускорение равно нулю, а полное и тангенциальное ускорения совпадают.
При равномерном движении модуль скорости не меняется. В этом случае тангенциальное ускорение равно нулю, а полное и нормальное ускорения совпадают.
Если тело совершает прямолинейное равномерное движение, то его ускорение равно нулю. А это значит, что и составляющие полного ускорения, т.е. нормальное ускорение и тангенциальное ускорение, тоже равны нулю.
Вектор полного ускорения
Вектор полного ускорения равен геометрической сумме нормального и тангенциального ускорений, как показано на рисунке:
Формула ускорения:
a = an + aт
Модуль полного ускорения
Модуль полного ускорения:
Угол альфа между вектором полного ускорения и нормальным ускорением (он же угол между вектором полного ускорения и радиус-вектором):
Обратите внимание, что вектор полного ускорения не направлен по касательной к траектории.
По касательной направлен вектор тангенциального ускорения.
Направление вектора полного ускорения определяется векторной суммой векторов нормального и тангенциального ускорений.
www.sbp-program.ru
Равноускоренное движение, формулы и примеры
Равноускоренное прямолинейное движение
Траектория движения в данном случае — прямая линия.
Основные формулы и кинематические характеристики
Ускорение (по модулю и по направлению).
Скорость тела меняется по закону
где начальная скорость движения.
Закон движения в случае равноускоренного движения имеет вид:
где радиус-вектор точки в момент времени , радиус-вектор начального положения точки, начальная скорость, ускорение.
В одномерном случае закон движения запишется в виде:
Для двумерного случая (движения по плоскости) закон движения в случае равноускоренного движения запишется в виде системы двух уравнений:
Также справедлива так называемая формула для определения пути «без времени»:
Графическое изображение зависимости кинематических характеристик от времени представлено на рисунках 1-3.
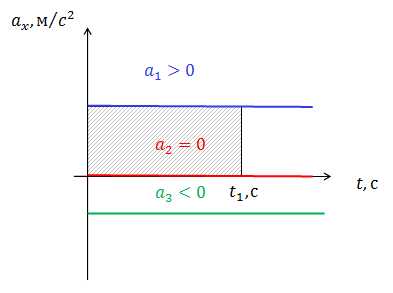
Рис.1. Зависимость ускорения от времени при равноускоренном движении
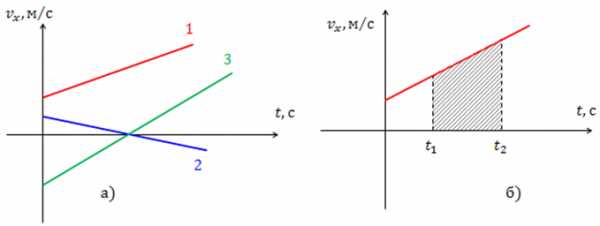
Рис.2. Зависимость скорости от времени при равноускоренном движении: а) закон изменения скорости для различных случаев; б) определение перемещения с помощью графика скорости.
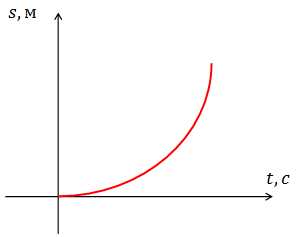
Рис.3. Зависимость перемещения от времени при равноускоренном движении.
На рис.1 изображен график зависимости ускорения от времени при равноускоренном движении. Случай соответствует равноускоренному движению, случай — равнозамедленному движению, случай — равномерному движению. Площадь заштрихованного прямоугольника численно равна средней скорости движения тела.
На рис.2 представлена зависимость скорости от времени при равноускоренном движении. Рис.2 (а) демонстрирует разные случаи движения: 1- тело двигалось в направлении оси равноускоренно; 2 — тело двигалось равнозамедленно в направлении оси , затем остановилось и поменяло направление движения; 3- тело двигалось равноускоренно в направлении, противоположном оси , затем остановилось и стало двигаться в противоположном направлении. Во всех трех случаях тело имело начальные скорости.
По графику скорости можно определить ускорение движущегося объекта как тангенс угла наклона прямой зависимости к оси
Площадь заштрихованной трапеции (рис.2 (б)) численно равна пути, пройденному телом за время
Зависимость перемещения от времени при равноускоренном движении — это квадратичная функция (рис.3). Положение вершины параболы зависит от направлений начальной скорости и ускорения.
Примеры решения задач
ru.solverbook.com
