Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW – считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн – построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW – эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции – теория, практика, задачи… Примеры решения задач Справочная информация – ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги – разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Базовый курс лекций по сопромату, теория, практика, задачи.::Оглавление:: 1. Геометрические характеристики сечений. 1.3. Моменты инерции простых сечений.  1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию. За dA примем площадь бесконечно тонкого слоя dA = bdy.
Тогда Аналогично, получим 2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга За dA принимаем площадь бесконечно тонкого кольца толщиной dp тогда Следовательно, Теперь легко найдем Ixo. Действительно, для круга согласно формуле (1.9.), имеем Iр = 2Iхо = 2Iуо, откуда 2. Кольцо (рис. 1.5,в). Осевой момент инерции в этом случае равен разности моментов инерции внешнего и внутреннего кругов Аналогично полярный момент инерции 2. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника: dA = bydy, где by – длина прямоугольника. Легко получить из подобия треугольников by = yb/h; тогда Определим момент инерции относительно центральной оси; для этого используем формулу (1.10) Определим момент инерции относительно оси, проходящей через основание: ::Оглавление:: |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME |
www.sopromat.org
Осевой момент инерции круга. — МегаЛекции
Осевой момент инерции фигуры – этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси.
Подсчитываем сначала полярный момент инерции круга. Для этого выделим в сечении окружностями радиусами ЭЛЕМНЕТАРНОЕ КОЛЬЦО ПЛОЩАДЬЮ и вычислим по формуле:
Обычно размеры круглого сечения выражают через диаметр d и подсчитывают по формуле
Осевой момент инерции тела является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Метод начальных параметров.
Прогиб (y) – смещение центра тяжести балок по направлению, перпендикулярному к её оси;
Угол поворота сечения (φ) – угол, на который сечение поворачивается относительно своего первоначального положения (или угол между касательной к упругой линии и первоначальной осью балки)
Суть метода начальных параметров применительно к расчету собственных колебаний стержневой системы заключается в том, что по известным значениям перемещений ( прогиб, угол поворота) и внутренних сил ( поперечная сила, изгибающий момент) в начале участка в соответствии с определенным алгоритмом находят значения этих переменных в конце участка.
Позволяет при любом числе участков балки свести решение к отысканию всего двух констант – прогиба и угла по ворота в начале координат. Для реализации метода начальных параметров необходимо при составлении уравнении моментов по участкам и интегрировании этого уравнения придерживаться следующих правил:
1. Начало координат необходимо выбирать общим для всех участков в крайней левой точке балки;
2. Все составляющие уравнения моментов на предыдущем участке должны сохраняться неизменными в уравнении моментов последующих участков;
3. В случае обрыва распределенной нагрузки её продлевают до конца балки, а для восстановления действительных условий нагружения вводят “компенсирующую” нагрузку обратного направления;
4. Интегрировать уравнения на всех участках следует, не раскрывая скобок.
Окончательные универсальные уравнения метода начальных параметров:
;
;
;
;
Величина – угол поворота в промежуточном (подвесном) шарнире, при этом – координата шарнира.
– угол поворота и прогиб балки в начале координат;
– координаты точек приложения внешнего момента, силы или начало распределенной нагрузки.
При решении задач удобно записать универсальные уравнения для сначала для наиболее удаленного от начала координат участка, тогда уравнение для предыдущих участков легко получить, вычеркивая из полученного уравнения члены, учитывающие нагрузку на последующий участок.
Билет 10.
Осевой момент инерции кольца.
Осевой момент инерции фигуры – этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси.
Осевой момент инерции кольца с внешним диаметром D и внутренним d относительно любой центральной оси может быть найден как разность моментов инерции большого и малого кругов:
≈ 0,05
где – коэффициент полости.
Осевой момент инерции тела является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Момент инерции кольца, теория и примеры
Если тело, которое нельзя считать материальной точкой, совершает вращение вокруг неподвижной оси, то момент инерции служит мерой инертности тела в этом движении. Для вычисления момента инерции такого тела его разбивают на частицы, которые можно принять за материальные точки массы материальных точек), измеряют расстояния от каждой такой точки до оси вращения (), момент инерции тела находят как:
где – количество материальных точек, на которое разбито тело.
Если тело можно считать непрерывным ) , то
в выражении (3) интегрирование проводят по всему объему тела. Параметр – функция расположения точки в пространстве; – плотность тела; – элемент объема.
Момент инерции бесконечно тонкого кольца
Рассмотрим бесконечно тонкое кольцо имеющее радиус , массу , вращающееся вокруг оси, проходящей через его центр нормально плоскости кольца (рис.1) (ось X). Считаем, что масса распределена по кольцу равномерно.

Для вычисления момента инерции воспользуемся формулой:
где расстояния от любого элемента кольца равно его радиусу, то есть:
В таком случае момент инерции тонкого кольца равен:
Момент инерции тонкого кольца относительно оси параллельной оси найдем, используя теорему Штейнера:
условием применения теоремы Штейнера является параллельность осей и , что выполняется в нашем случае. Расстояние между осями равно радиусу кольца. Получаем:
Момент инерции толстого кольца
Рассмотрим однородное кольцо внешний радиус которого, равен , внутренний радиус — , масса этого кольца

Разобьем это кольцо на тонкие кольца. Одно из таких колец показано на рис. 2 пунктиром, его радиус . Момент инерции этого кольца относительно оси X равен:
где (h — высота кольца, если диск представляем как цилиндр малой высоты), тогда выражение (8) принимает вид:
Момент инерции всего нашего толстого кольца найдем как:
в формуле (10) мы учли, что объем нашего кольца равен:
соответственно масса кольца:
И так, получили, что момент инерции толстого кольца относительно оси вращения, проходящей через его центр, перпендикулярно плоскости кольца равен:
Примеры решения задач
ru.solverbook.com
Формула момента инерции диска, J
Момент инерции тела, которое можно представить в виде совокупности дискретных частиц, относительно оси вращения равен:
где – масса i-ой материальной точки тела; – расстояние от материальной точки i до оси вращения. При рассмотрении твердого тела как сплошной среды с непрерывным распределением массы определение момента инерции заменяют следующим:
где – элемент массы тела; – плотность тела; – элементарный объем.
Момент инерции однородного диска
Рассмотрим, как находится момент инерции однородного диска, если его радиус равен R, а масса m. Ось вращения пусть проходит через центр инерции данного диска (точку О) и будет перпендикулярна его плоскости (рис.1).
Диск можно заменить совокупностью бесконечно тонких колец, радиусы которых изменяются от нуля до R. На рис.1 выделено одно из таких колец. Рассмотрим это кольцо. Радиус его обозначим как Момент инерции данного кольца (обозначим его равен (см. формулу момента инерции тонкого кольца):
Массу данного кольца (а точнее цилиндра) можно представить как:
где – высота цилиндра. Подставим выражение для в формулу (3) и проведем интегрирование:
где – масса диска.
Если диск можно считать абсолютно тонким или он является частью цилиндра, то формула для вычисления момента инерции диска относительно оси, проходящей через его центр масс, и перпендикулярной плоскости диска, имеет вид:
В случае плоского распределения масс выполняется равенство:
где оси вращения совпадают с осями декартово системы координат. И если мы будем считать, что ось Z проходит через центр инерции диска и перпендикулярна его плоскости, то моменты инерции относительно осе X и Y будут равны:
Иногда величины моментов инерции называют моментами инерции диска относительно его диаметров.
Примеры решения задач по теме «Момент инерции диска»
ru.solverbook.com
Моменты инерции простейших фигур (вывод формул для круга, прямоугольника, треугольника)
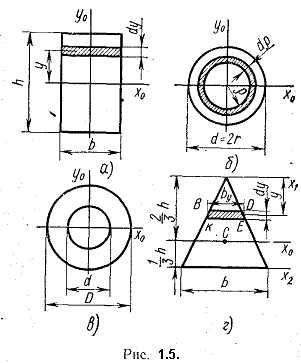
1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию.
За dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда
(1.11)
Аналогично получим
(1.12)
2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга
За dA принимаем площадь бесконечно тонкого кольца толщиной dp
Тогда
Следовательно
(1.13)
Теперь легко найдем Ixo. Действительно, для круга имеем Iр = 2Iхо = 2Iуо, откуда
(1.14)
3. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника
За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника:
dA = bydy,
где by – длина прямоугольника.
Легко получить из подобия треугольников
by = yb/h;
тогда (1.15)
Определим момент инерции относительно центральной оси
(1.16)
Определим момент инерции относительно оси, проходящей через основание:
(1.17)
studopedia.net
Калькулятор моментов инерции и моментов сопротивления сечений
Моменты инерции и моменты сопротивления применяются при расчете прочности и деформаций в стержнях, балках, валах и т.д.
Их значения могут быть вычислены: для простых фигур (круг, прямоугольник и т.д.) – по формулам, для стандартных профилей – по специальным таблицам ГОСТов (так называемые сортаменты).
Здесь собраны онлайн-калькуляторы площади, моментов инерции и моментов сопротивления простых фигур.
Момент инерции круга
Диаметр d = Рассчитать
Площадь круга $$A = \frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 22^2}{4} = 380$$
Осевые моменты инерции круга $$J_x = J_y = \frac{\pi \cdot d^4}{64} = \frac{\pi \cdot 22^4}{64} = 11500$$
Осевые моменты сопротивления круга $$W_x = W_y = \frac{\pi \cdot d^3}{32} = \frac{\pi \cdot 22^3}{32} = 1045$$
Полярный момент инерции круга $$J_{\rho} = \frac{\pi \cdot d^4}{32} = \frac{\pi \cdot 22^4}{32} = 23000$$
Полярный момент сопротивления круга $$W_{\rho} = \frac{\pi \cdot d^3}{16} = \frac{\pi \cdot 22^3}{16} = 2091$$
Моменты инерции прямоугольника
Моменты инерции треугольника равнобедренного
Моменты инерции треугольника прямоугольного

Ширина b = Высота h = Рассчитать
Площадь прямоугольника $$A = \frac{b \cdot h}{2} = \frac{ 20 \cdot 36 }{2} = 360$$
Осевые моменты инерции $$J_x = \frac{b \cdot h^3}{36} = \frac{ 20 \cdot 36^3 }{36} = 25920$$ $$J_y = \frac{b^3 \cdot h}{48} = \frac{ 20^3 \cdot 36 }{36} = 8000$$
Центробежный момент инерции $$J_{xy} = \frac{b^2 \cdot h^2}{72} = \frac{ 20^2 \cdot 36^2 }{72} = 7200$$
Осевые моменты сопротивления $$W_x = \frac{b \cdot h^2}{24} = \frac{ 20\cdot 36^2 }{24} = 1080$$ $$W_y = \frac{b^2 \cdot h}{24} = \frac{ 20^2 \cdot 36 }{24} = 600$$
Для составных сечений моменты инерции определяются как сумма (разница) моментов инерции составных частей.
Момент инерции кольцевого сечения
Внешний диаметр D =
Внутренний диаметр d =
Рассчитать
Ответ: $A = 126$, $J_x = 6350$, $J_{\rho} = 12700$, $W_x = 577$, $W_{\rho} = 1155$
А теперь поподробнее:
Площадь сечения $$A = \frac{\pi \cdot D^2}{4}-\frac{\pi \cdot d^2}{4} = \frac{\pi \cdot (22^2-18^2)}{4} = 126$$
Отношение диаметров $$\alpha = \frac{ d }{ D } = \frac{ 18 }{ 22 } = 0.818$$
Осевые моменты инерции кольцевого (трубчатого) сечения $$J_x = J_y = \frac{\pi \cdot D^4}{64}(1-\alpha^4) = \frac{\pi \cdot 22^4}{64}(1-0.818^4) = 6350$$
Осевые моменты сопротивления $$W_x = W_y = \frac{\pi \cdot D^3}{32}(1-\alpha^4) = \frac{\pi \cdot 22^3}{32}(1-0.818^4) = 577$$
Полярный момент инерции $$J_{\rho} = \frac{\pi \cdot d^4}{32}(1-\alpha^4) = \frac{\pi \cdot 22^4}{32}(1-0.818^4) = 12700$$
Полярный момент сопротивления $$W_{\rho} = \frac{\pi \cdot d^3}{16}(1-\alpha^4) = \frac{\pi \cdot 22^3}{16}(1-0.818^4) = 1155$$
sopromat.xyz
момент инерции сечения – это сумма всех элементарно малых площадей dF, составляющих это сечение, умноженных на квадрат расстояния от этих площадей до выбранной оси:I = ∑ri2dFi =∫r2dF (1.1) В принципе и определение и формула, его описывающая, не сложные и запомнить их намного легче, чем вникнуть в суть. Но все-таки попробуем разобраться, что же такое момент инерции и откуда он взялся. Понятие момент инерции пришло в сопромат и строительную механику из другого раздела физики, изучающего кинематику движения, в частности вращательное движение. Но все равно начнем издалека. Я точно не знаю, упало ли Исааку Ньютону на голову яблоко, упало оно рядом, или вообще не падало, теория вероятности допускает все эти варианты (к тому же в этом яблоке слишком много от библейской легенды о древе познания), однако я уверен, что Ньютон был наблюдательным человеком, способным делать выводы из своих наблюдений. Так наблюдательность и воображение позволили Ньютону сформулировать основной закон динамики (второй закон Ньютона), согласно которому масса тела m, умноженная на ускорение a, равна действующей силе Q (вообще-то более привычным для силы является обозначение F, но так как дальше мы будем иметь дело с площадью, которая также часто обозначается как F, то я использую для внешней силы, рассматриваемой в теоретической механике как сосредоточенная нагрузка, обозначение Q, сути дела это не меняет): Q = ma (1.2) По мне величие Ньютона именно в простоте и понятности данного определения. А еще, если учесть, что при равноускоренном движении ускорение а равно отношению приращения скорости ΔV к периоду времени Δt, за который скорость изменилась: a = Δv/Δt = (v – vо)/t (1.3.1) при Vо = 0 a = v/t (1.3.2) то можно определить основные параметры движения, такие как расстояние, скорость, время и даже импульс р, характеризующий количество движения: p = mv (1.4) Например, яблоко, падающее с разной высоты под действием только силы тяжести, будет падать до земли разное время, иметь разную скорость в момент приземления и соответственно разный импульс. Другими словами, яблоко, падающее с бóльшей высоты, будет дольше лететь и сильнее треснет по лбу незадачливого наблюдателя. И все это Ньютон свел к простой и понятной формуле. А еще Ньютон сформулировал закон инерции (первый закон Ньютона): если ускорение а = 0, то в инерциальной системе отсчета невозможно определить, находится ли наблюдаемое тело, на которое не действуют внешние силы, в состоянии покоя или движется прямолинейно с постоянной скоростью. Это свойство материальных тел сохранять свою скорость, пусть даже и нулевую, называется инертностью. Мерой инертности является инерционная масса тела. Иногда инерционная масса называется инертной, но сути дела это не меняет. Считается, что инерционная масса равна гравитационной массе и потому часто не уточняется, какая именно масса имеется в виду, а упоминается просто масса тела. Не менее важным и значимым является и третий закон Ньютона, согласно которому сила действия равна силе противодействия, если силы направлены по одной прямой, но при этом в противоположные стороны. Не смотря, на кажущуюся простоту, и этот вывод Ньютона гениален и значение этого закона трудно переоценить. Об одном из применений этого закона чуть ниже. Однако данные положения справедливы только для тел, движущихся поступательно, т.е. по прямолинейной траектории и при этом все материальные точки таких тел двигаются с одинаковой скоростью или одинаковым ускорением. При криволинейном движении и в частности при вращательном движении, например, когда тело вращается вокруг своей оси симметрии, материальные точки такого тела перемещаются в пространстве с одинаковой угловой скоростью w, но при этом линейная скорость v у различных точек будет разная и эта линейная скорость прямо пропорциональна расстоянию r от оси вращения до этой точки: v = wr (1.5) при этом угловая скорость равна отношению приращения угла поворота Δφ к периоду времени Δt, за который угол поворота изменился: w = Δφ/Δt = (φ – φо)/t (1.6.1) при φо = 0 w = φ/t (1.7.2) соответственно нормальное ускорение аn при вращательном движении равно: an = v2/r = w2r (1.8) И получается, что для вращательного движения мы не можем прямо использовать формулу (1.2), так как при вращательном движении одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться (в данном случае речь идет о приложении силы в одной и той же точке). К тому же при вращении тела более удобно рассматривать не действующую силу, а вращающий момент, так как при вращательном движении точка приложения силы также имеет большое значение. Поразительные свойства момента нам известны со времен Архимеда и если применить понятие момента к вращательному движению, то значение момента М будет тем больше, чем больше расстояние r от оси вращения до точки приложения силы F (в строительной механике внешняя сила часто обозначается как Р или Q): М = Qr (1.9) Из этой также не очень сложной формулы выходит, что если сила будет приложена по оси вращения, то никакого вращения не будет, так как r = 0, а если сила будет приложена на максимальном удалении от оси вращения, то и значение момента будет максимальным. А если мы подставим в формулу (1.9) значение силы из формулы (1.2) и значение нормального ускорения и формулы (1.8), то получим следующее уравнение: М = mw2r·r = mw2r2 (1.10) В частном случае когда тело является материальной точкой, имеющей размеры намного меньше, чем расстояние от этой точки до оси вращения, уравнение (1.10) применимо в чистом виде. Однако для тела, вращающегося вокруг одной из своих осей симметрии, расстояние от каждой материальной точки составляющей данное тело, всегда меньше одного из геометрических размеров тела и потому распределение массы тела имеет большое значение, в этом случае требуется учесть эти расстояния отдельно для каждой точки: M = ∑ri2w2mi (1.11.1) Мс= w2∫r2dm (1.11.2) – при вращении тела вокруг оси симметрии И тогда получается, что согласно третьему закону Ньютона в ответ на действие вращающего момента будет возникать так называемый момент инерции I. При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. В итоге формула момента инерции примет следующий вид: [- М] = I = ∑ri2mi (1.12.1) Ic = ∫r2dm (1.11.2) – при вращении тела вокруг оси симметрии где I – общепринятое обозначение момента инерции, Ic – обозначение осевого момента инерции тела, кг/м2. Для однородного тела, имеющего одинаковую плотность ρ по всему объему тела V формулу осевого момента инерции тела можно записать так: Ic = ∫ρr2dV (1.13) Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении. Все круг замкнулся. И тут может возникнуть вопрос, какое отношение все эти законы динамики и кинематики имеют к расчету статических строительных конструкций? Оказывается, что ни на есть самое прямое и непосредственное. Во-первых потому, что все эти формулы выводились физиками и математиками в те далекие времена, когда таких дисциплин, как “Теоретическая механика” или “Теория сопротивления материалов” попросту не существовало. А во-вторых потому, что весь расчет строительных конструкций и построен на основе указанных законов и формулировок и пока ни кем не опровергнутом утвержении о равенстве гравитационной и инертой масс. Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит. А проще потому, что при решении определенных задач может рассматриваться не все тело, а только его поперечное сечение, а при необходимости несколько поперечных сечений. Но в этих сечениях действуют такие же физические силы, правда имеющие несколько иную природу. Таким образом, если рассматривать некое тело, длина которого постоянна, а само тело является однородным, то если не учитывать постоянные параметры – длину и плотность (l = const, ρ = const) – мы получим модель поперечного сечения. Для такого поперечного сечения с математической точки зрения будет справедливым уравнение: Iр = ∫r2dF (2.1) → (1.1) где Ip – полярный момент инерции поперечного сечения, м4. В итоге мы получили формулу, с которой начинали (а вот стало ли понятнее, что такое момент инерции сечения, не знаю). Так как в теории сопротивления материалов часто рассматриваются прямоугольные сечения, да и прямоугольная система координат более удобна, то при решении задач обычно рассматриваются два осевых момента инерции поперечного сечения: Iz = ∫y2dF (2.2.1) Iy = ∫z2dF (2.2.2)
Рисунок 1. Значения координат при определении осевых моментов инерции. Тут может возникнуть вопрос, почему использованы оси z и у, а не более привычные х и у? Так уж сложилось, что определение усилий в поперечном сечении и подбор сечения, выдерживающего действующие напряжения, равные приложенным усилиям – две разные задачи. Первую задачу – определение усилий – решает строительная механика, вторую задачу – подбор сечения – теория сопротивления материалов. При этом в строительной механике рассматривается при решении простых задач достаточно часто стержень (для прямолинейных конструкций), имеющий определенную длину l, а высота и ширина сечения не учитываются, при этом считается, что ось х как раз и проходит через центры тяжести всех поперечных сечений и таким образом при построении эпюр (порой достаточно сложных) длина l как раз и откладывается по оси х, а по оси у откладываются значения эпюр. В то же время теория сопротивления материалов рассматривает именно поперечное сечение, для которого важны ширина и высота, а длина не учитывается. Само собой при решении задач теории сопротивления материалов, также порой достаточно сложных используются все те же привычные оси х и у. Мне такое положение дел кажется не совсем правильным, так как не смотря на разницу, это все же смежные задачи и потому будет более целесообразным использование единых осей для рассчитываемой конструкции. Значение полярного момента инерции в прямоугольной системе координат будет: Iр = ∫r2dF = ∫y2dF + ∫z2dF (2.3) Так как в прямоугольной системе координат радиус – это гипотенуза прямоугольного треугольника, а как известно квадрат гипотенузы равен сумме квадратов катетов. А еще существует понятие центробежного момента инерции поперечного сечения: Ixz = ∫xzdF (2.4) Среди осей прямоугольной системы координат, проходящих через центр тяжести поперечного сечения, есть две взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значение, при этом центробежный момент инерции сечения Izy = 0. Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерцииКогда в теории сопротивления материалов речь заходит о моментах инерции, то как правило в виду имеются именно главные центральные моменты инерции поперечного сечения. Для квадратных, прямоугольных, круглых сечений главные оси будут совпадать с осями симметрии. Моменты инерции поперечного сечения также называют геометрическими моментами инерции или моментами инерции площади, но суть от этого не изменяется. В принципе самому определять значения главных центральных моментов инерции для поперечных сечений наиболее распространенных геометрических форм – квадрата, прямоугольника, круга, трубы, треугольника и некоторых других – большой необходимости нет. Такие моменты инерции давно определены и широко известны. А при расчете осевых моментов инерции для сечений сложной геометрической формы справедлива теорема Гюйгенса-Штейнера: I = Ic + r2F (2.5) таким образом, если известны площади и центры тяжести простых геометрических фигур, составляющих сложное сечение, то определить значение осевого момента инерции всего сечения не составит труда. А для того, чтобы определить центр тяжести сложного сечения, используются статические моменты поперечного сечения. Более подробно статические моменты рассматриваются в другой статье, здесь лишь добавлю. Физический смысл статического момента следующий: статический момент тела – это сумма моментов для материальных точек, составляющих тело, относительно некоторой точки (полярный статический момент) или относительно оси (осевой статический момент), а так как момент – это произведение силы на плечо (1.9), то и определяется статический момент тела соответственно: S = ∑M = ∑rimi = ∫rdm (2.6) и тогда полярный статический момент поперечного сечения будет: Sр = ∫rdF (2.7) Как видим, определение статического момента сходно с определением момента инерции. Но есть и принципиальная разница. Статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если опора приложена к центру тяжести тела. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение = 0. А еще с чисто математической точки зрения статический момент может быть равен нулю по той простой причине, что при определении статического момента необходимо учитывать направление действия момента. Например относительно осей координат, проходящих через центр тяжести прямоугольника, площади верхней части и нижней части прямоугольника будут положительными так как символизируют силу тяжести, действующую в одном направлении. При этом расстояние от оси до центра тяжести можно рассматривать как положительное (условно: момент от силы тяжести верхней части прямоугольника пытается вращать сечение по часовой стрелке), а до центра тяжести нижней части – как отрицательное (условно: момент от силы тяжести нижней части прямоугольника пытается вращать сечение против часовой стрелки). А так как такие площади численно равны и равны расстояния от центров тяжести верхней части прямоугольника и нижней части прямоугольника, то сумма действующих моментов и составит искомый 0. Sz = ∫ydF = 0 (2.8) А еще этот великий ноль позволяет определять опорные реакции строительных конструкций. Если рассматривать строительную конструкцию, к которой приложена например сосредоточенная нагрузка Q в некоторой точке, то такую строительную конструкцию можно рассматривать, как тело с центром тяжести в точке приложения силы, а опорные реакции в этом случае рассматриваются, как силы приложенные в точках опор. Таким образом зная значение сосредоточенной нагрузки Q и расстояния от точки приложения нагрузки до опор строительной конструкции, можно определить опорные реакции. Например для шарнирно опертой балки на двух опорах значение опорных реакций будет пропорционально расстоянию до точки приложения силы, а сумма реакций опор будет равна приложенной нагрузке. Но как правило при определении опорных реакций поступают еще проще: за центр тяжести принимается одна из опор и тогда сумма моментов от приложенной нагрузки и от остальных опорных реакций все равно равна нулю. В этом случае момент от опорной реакции относительно которой составляется уравнение моментов, равен нулю, так как плечо действия силы = 0, а значит в сумме моментов остаются только две силы: приложенная нагрузка и неизвестная опорная реакция (для статически определимых конструкций). Таким образом принципиальная разница между статическим моментом и моментом инерции в том, что статический момент характеризует сечение, которое сила тяжести как бы пытается сломать пополам относительно центра тяжести или оси симметрии, а момент инерции характеризует тело, все материальные точки которого перемещаются (или пытаются переместиться в одном направлении). Возможно, более наглядно представить себе эту разницу помогут следующие достаточно условные расчетные схемы для прямоугольного сечения:
Рисунок 2. Наглядная разница между статическим моментом и моментом инерции. А теперь вернемся еще раз к кинематике движения. Если проводить аналогии между напряжениями, возникающими в поперечных сечениях строительных конструкций, и различными видами движения, то в центрально растягиваемых и центрально сжатых элементах возникают напряжения равномерные по всей площади сечения. Эти напряжения можно сравнить с действием некоторой силы на тело, при котором тело будет двигаться прямолинейно и поступательно. А самое интересное, это то, что поперечные сечения центрально-растянутых или центрально сжатых элементов действительно движутся, так как действующие напряжения вызывают деформации. И величину таких деформаций можно определить для любого поперечного сечения конструкции. Для этого достаточно знать значение действующих напряжений, длину элемента, площадь сечения и модуль упругости материала, из которого изготовлена конструкция. У изгибаемых элементов поперечные сечения также не остаются на месте, а перемещаются, при этом перемещение поперечных сечений изгибаемых элементов подобно вращению некоего тела относительно некоторой оси. Как вы уже наверное догадались, момент инерции позволяет определить и угол наклона поперечного сечения и перемещение Δl для крайних точек сечения. Эти крайние точки для прямоугольного сечения находятся на расстоянии, равном половине высоты сечения (почему – достаточно подробно описано в статье “Основы сопромата. Определенение прогиба” ). А это в свою очередь позволяет определить прогиб конструкции. А еще момент инерции позволяет определить момент сопротивления сечения. Для этого момент инерции нужно просто разделить на расстояние от центра тяжести сечения до наиболее удаленной точки сечения, для прямоугольного сечения на h/2. А так как исследуемые сечения не всегда симметричны, то значение момента сопротивления может быть разным для разных частей сечения. А началось все с банального яблока… хотя нет, начиналось все со слова. |
doctorlom.com


