Скорость и путь равноускоренного движения
17. Скорость и путь равноускоренного движения
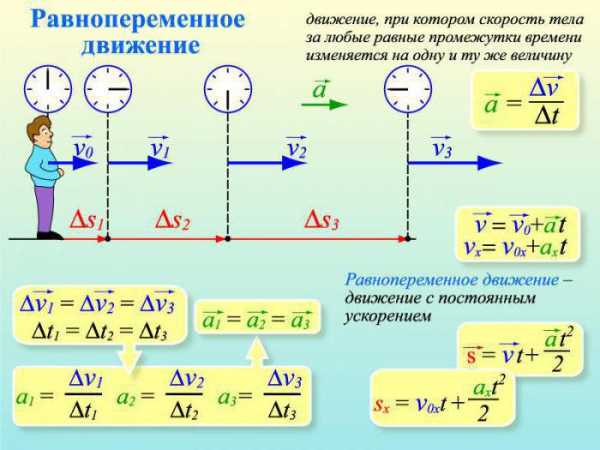
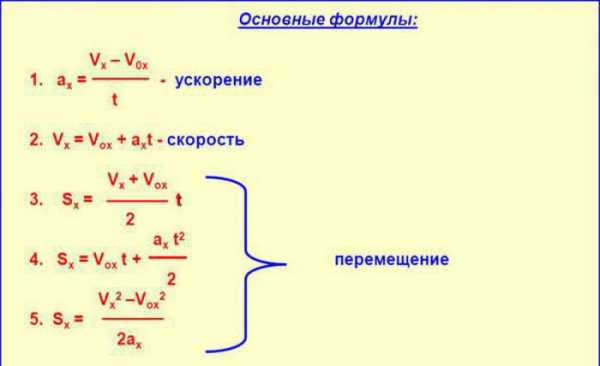
При равноускоренном движении скорость предмета v в каждую секунду увеличивается на постоянную величину; эта величина – ускорение a. Зависимость скорости v от ускорения a и продолжительности движения t следующая:
v = a * t .
Если перед началом ускорения предмет уже имел некоторую скорость v0, то последующая скорость v определится как
v = v0 + a t .
Средняя скорость предмета vСР при начале движения с нуля будет в два раза меньше:
Путь s, пройденный предметом за продолжительность движения t , равен произведению средней скорости vСР на эту продолжительность:
s = vсрt .
В случае начала движения с нуля путь s определится как
Если перед началом ускорения был уже пройден некоторый путь s0, то зависимость примет вид
Наиболее характерный случай равноускоренного движения – падение тяжёлых предметов с некоторой высоты. Тяжёлые предметы, такие как, например, камни, при падении с большой высоты не испытывают большого сопротивления воздуха, и поэтому в расчётах их движений ускорение можно считать постоянным.
Пример. С отвесной скалы падает камень. Требуется определить скорость падения и путь падения через одну секунду и через 10 секунд.
Ускорение свободного падения определяется земным тяготением и равно 9,8 ускоров.
Через 1 секунду:
v1 = a t = 9,8*1 = 9,8 ск;
Через 10 секунд:
v2 = a t =
russkaja-fizika.ru
Путь, пройденный при равнопеременном движении
Воспользуемся графическим способом нахождения пройденного пути для случая равноускоренного движения. Пусть график скорости равноускоренного движения изображен прямой (рис. 36). Путь, пройденный за время , численно равен площади трапеции :
Рис. 36. Графическое нахождение формулы пути, пройденного при равноускоренном движении
Но (начальная скорость), (скорость в момент при ускорении ). Значит,
| (22.1) |
Эта формула справедлива как для равноускоренного, так и для равнозамедленного движения; в первом случае и одинаковы по знаку, а во втором — противоположны.
Для движения с начальной скоростью, равной нулю, на графике вместо трапеции получается прямоугольный треугольник с катетами и , так что площадь, выражающая пройденный путь, оказывается равной
| (22.2) |
Эту формулу можно было бы получить и непосредственно из предыдущей формулы, полагая .
На рис. 37 дан график пути равноускоренного движения с начальной скоростью, равной нулю. График построен по формуле (22.2) для значения . Он изображается кривой линией, поднимающейся вверх все круче и круче. Расстояния точек графика от оси времени пропорциональны квадратам расстояний от оси пути. Такая кривая называется параболой.
Рис. 37. График пути при равноускоренном движении
Из формулы (22.2) видно, что при начальной скорости, равной нулю, путь, пройденный при равноускоренном движении за первую секунду движения ( ) численно равен половине ускорения. Если известен путь, пройденный без начальной скорости за время , то ускорение можно найти по формуле
| (22.3) |
Если начальная скорость равна нулю, можно выразить путь , пройденный к моменту , через скорость и в этот момент или скорость — через пройденный путь. Действительно, в этом случае и . Исключая из этих выражений , найдем
| (22.4) |
| (22.5) |
Наконец, зная пройденный путь и ускорение, можно, воспользовавшись формулой (22.2), найти время движения:
| (22.6) |
22.1. Напишите формулы, аналогичные (22.4) и (22.5), для случая начальной скорости \(v_0\), не равной нулю.
22.2. Покажите, пользуясь формулой (22.1), что для равноускоренного движения пути, проходимые точкой за любые равные промежутки времени, следующие друг за другом, получают одинаковое приращение.
22.3. Покажите, пользуясь формулой (22.2), что для равноускоренного движения без начальной скорости приращения пути за любые равные промежутки времени, следующие друг за другом, равны двойному пути, проходимому точкой за первый такой промежуток времени.
22.4.
Электровоз подходит по горизонтальному пути к уклону, имея скорость 8 м/с, затем движется по уклону вниз с ускорением 0,2 м/с2. Определите длину уклона, если электровоз проходит его за 30 с. 22.5. Электровоз начинает двигаться равноускоренно в тот момент, когда с ним поравнялся мальчик, бегущий равномерно со скоростью 2 м/с. Определите скорость электровоза в тот момент, когда он догонит мальчика.
22.6. Автомобиль, пройдя с постоянным ускорением некоторое расстояние от остановки, достиг скорости 20 м/с. Какова была его скорость на половине этого расстояния?
22.7. Какой путь прошло тело за время, в течение которого скорость его увеличилась с 4 до 12 м/с, если ускорение равно 2 м/с2?
sfiz.ru
Равноускоренное движение. Задачи и формулы :: SYL.ru
Важнейшей характеристикой при движении тела является его скорость. Зная ее, а также некоторые другие параметры, мы всегда можем определить время движения, пройденное расстояние, начальную, конечную скорость и ускорение. Равноускоренное движение же является только одним из типов движения. Обычно оно встречается в задачах по физике из раздела кинематики. В подобных задачах тело принимают за материальную точку, что существенно упрощает все расчеты.
Скорость. Ускорение
Прежде всего, хотелось бы обратить внимание читателя на то, что эти две физических величины являются не скалярными, а векторными. А это значит, что при решении определенного рода задач необходимо обращать внимание на то, какое ускорение имеет тело в плане знака, а также каков вектор самой скорости тела. Вообще в задачах исключительно математического плана подобные моменты опускают, но в задачах по физике это достаточно важно, поскольку в кинематике из-за одного неверно поставленного знака ответ может получиться ошибочным.
Примеры
В качестве примера можно привести равноускоренное и равнозамедленное движение. Равноускоренное движение характеризуется, как известно, разгоном тела. Ускорение остается постоянным, но скорость непрерывно увеличивается в каждый отдельный момент времени. А при равнозамедленном движении ускорение имеет отрицательное значение, скорость тела непрерывно снижается. Эти два вида ускорения заложены в основу многих физических задач и достаточно часто встречаются в задачах первой части тестов по физике.
Пример равноускоренного движения

Равноускоренное движение мы встречаем ежедневно повсеместно. Ни один автомобиль не движется в реальной жизни равномерно. Даже если стрелка спидометра показывает ровно 6 километров в час, следует понимать, что это на самом деле не совсем так. Во-первых, если разбирать данный вопрос с технической точки зрения, то первым параметром, который будет давать неточность, станет прибор. Вернее, его погрешность.
Их мы встречаем во всех контрольно-измерительных приборах. Те же самые линейки. Возьмите штук десять хоть одинаковых (по 15 сантиметров, например) линеек, хоть разных (15, 30, 45, 50 сантиметров). Приложите их друг к другу, и вы заметите, что есть небольшие неточности, а их шкалы не совсем совпадают. Это и есть погрешность. В данном случае она будет равна половине цены деления, как и у других приборов, выдающих определенные значения.
Вторым фактором, который будет давать неточность, является масштаб прибора. Спидометр не учитывает такие величины, как половина километра, одна вторая километра и так далее. Заметить на приборе это глазом достаточно тяжело. Практически невозможно. Но ведь изменение скорости есть. Пускай на такую маленькую величину, но все же. Таким образом, это будет равноускоренное движение, а не равномерное. То же самое можно сказать и про обычный шаг. Идем, допустим, мы пешком, и кто-то говорит: наша скорость – 5 километров в час. Но это не совсем так, а почему, было рассказано немного выше.
Ускорение тела

Ускорение может быть положительным и отрицательным. Об этом говорилось ранее. Добавим, что ускорение – это векторная величина, которая числено равна изменению скорости за определенный промежуток времени. То есть через формулу его можно обозначить следующим образом: a = dV/dt, где dV – изменение скорости, dt – промежуток времени (изменение времени).
Нюансы

Сразу может возникнуть вопрос о том, как ускорение при таком раскладе может быть отрицательным. Те люди, которые задают подобный вопрос, мотивируют это тем, что даже скорость не может быть отрицательной, не то что время. На самом деле время отрицательным быть действительно не может. Но очень часто забывают о том, что скорость принимать отрицательные значения вполне может. Это же векторная величина, не следует забывать об этом! Все дело, наверное, в стереотипах и некорректном мышлении.
Так вот, для решения задач достаточно уяснить одну вещь: ускорение будет положительным в том случае, если тело разгоняется. И оно будет отрицательным в том случае, если тело тормозит. Вот и все, достаточно просто. Простейшее логическое мышление или способность видеть между строк уже будет, по сути дела, частью решения физической задачи, связанной со скоростью и ускорением. Частный случай – это ускорение свободного падения, и оно не может быть отрицательным.
Формулы. Решение задач
Следует понимать, что задачи, связанные со скоростью и ускорением, бывают не только практического, но и теоретического характера. Поэтому мы будем разбирать их и по возможности постараемся объяснить, почему тот или иной ответ правильный или, наоборот, неправильный.
Теоретическая задача

Очень часто на экзаменах по физике в 9 и 11 классах можно встретить подобные вопросы: “Как будет вести себя тело, если сумма всех действующих на него сил равна нулю?”. На самом деле формулировка вопроса может быть самой разной, но ответ все равно один. Здесь первым делом в ход нужно пускать поверхностные здания и обыкновенное логическое мышление.
На выбор ученика предоставляется 4 ответа. Первый: “скорость будет равна нулю”. Второй: “скорость тела убывает в течение некоторого периода времени”. Третий: “скорость тела постоянна, но она точно не равна нулю”. Четвертый: “скорость может иметь любое значение, но в каждый момент времени она будет постоянной”.
Правильным ответом здесь будет, конечно же, четвертый. Сейчас разберемся, почему именно так. Давайте попробуем рассмотреть все варианты по очереди. Как известно, сумма всех сил, действующих на тело, есть произведение массы на ускорение. Но масса у нас остается величиной постоянной, ее мы отбросим. То есть если сумма всех сил равна нулю, ускорение тоже будет равно нулю.
Итак, предположим, что скорость будет равна нулю. Но этого не может быть, поскольку нулю у нас равно ускорение. Чисто физически это допустимо, но только не в данном случае, поскольку сейчас речь идет о другом. Пускай скорость тела убывает в течение некоторого периода времени. Но как она может убывать, если ускорение постоянно, и оно равно нулю? Никаких причин и предпосылок для убывания или возрастания скорости нет. Поэтому второй вариант мы отметаем.
Предположим, что скорость тела постоянна, но она точно не равна нулю. Она действительно будет постоянной в силу того, что ускорение просто-напросто отсутствует. Но нельзя однозначно сказать, что скорость будет отлична от нулевой. А вот четвертый вариант – прямо в яблочко. Скорость может быть любой, но, поскольку ускорение отсутствует, она будет постоянной во времени.
Практическая задача
Определите, какой путь был пройден телом в определенный период времени t1-t2 (t1 = 0 секунд, t2 = 2 секунды), если имеются следующие данные. Начальная скорость тела на отрезке от 0 до 1 секунды равна 0 метров в секунду, конечная – 2 метра в секунду. Скорость тела по состоянию на время 2 секунды равна также 2 метрам в секунду.
Решить подобную задачу достаточно просто, нужно лишь уловить ее суть. Итак, требуется найти путь. Ну что же, начнем искать его, предварительно выделив два участка. Как легко заметить, первый участок пути (от 0 до 1 секунды) тело проходит равноускоренно, о чем свидетельствует увеличение его скорости. Тогда найдем это ускорение. Его можно выразить как разность скоростей, разделенную на время движения. Ускорение будет равно (2-0)/1 = 2 метра на секунду в квадрате.
Соответственно, расстояние, пройденное на первом участке пути S будет равно: S = V0t + at^2/2 = 0*1 + 2*1^2/2 = 0 + 1 = 1 метр. На втором же участке пути в период от 1 секунды до 2 секунд тело движется равномерно. Значит, расстояние будет равно V*t = 2*1 = 2 метра. Теперь суммируем расстояния, получаем 3 метра. Это и есть ответ.
www.syl.ru
как найти время если известно расстояние ускорение и начальная скорость?
Равноускоренное движение описывается формулой: x(t) = x0 + v0*t + at^2/2 x0 обычно = 0, потому что мы берем начало пути за начало координат, и получаем: x(t) = v0*t + at^2/2 at^2/2 + v0*t – х = 0 Получили квадратное уравнение относительно времени t. Решаем и находим 2 значения, нужное подбираем по смыслу задачи. Например, отрицательное значение отбрасываем.
S = V0*t + a*(t^2)/2 – пройденное расстояние, выраженное через начальную скорость, время и ускорение. Очевидно, нужно решить квадратное уравнение относительно времени.
Дима странное что-то написал Вообще уравнение равноускоренного движения x = x0 + v0 * t + a * t^2 / 2 Отсюда и найдёшь
touch.otvet.mail.ru
