Формула давления
ОПРЕДЕЛЕНИЕДавление столба жидкости (гидростатическое давление) равно плотности этой жидкости, умноженной на высоту столба жидкости и ускорение свободного падения.
Здесь – давление, – плотность жидкости, – ускорение свободного падения ( м/с), – высота столба жидкости (глубина, на которой находится сдавливаемое тело).
Единица измерения давления – Па (паскаль).
Это векторная величина. В каждой точке жидкости давление одинаково во всех направлениях. Чаще всего в задачах требуется найти давление столба воды. Её плотность – 1000 кг/м. Формула верна не только для жидкости, но и для идеального газа. Есть ещё одна формула давления:
Где – сила тяжести, действующая на жидкость (её вес), – площадь поверхности, на которую оказывается давление.
Примеры решения задач по теме «Давление»
ПРИМЕР 1| Задание | Высота воды в аквариуме 1 м. Найти давление на дно аквариума. |
| Решение | Напоминаем, плотность воды кг/м, а м/с. Таким образом:
(Па) |
| Ответ | Давление воды составляет 9800 Паскаль. |
| Задание | Закрытый сосуд устроен так, что его крышка подвижна (см. рисунок). Сосуд наполнен жидкостью, плотность которой известна. На крышку сосуда действует сила . Найти давление на дно сосуда, если известны площадь дна и крышки и объём жидкости в сосуде. |
| Решение | Пусть:
– площадь крышки – площадь дна – объём жидкости Крышка подвижна, значит она давит на жидкость с той силой, с которой внешние силы давят на неё сверху. Очевидно: Попробуем найти давление жидкости: Соберём всё вместе: |
| Ответ |
Все формулы по физике
Формула силы выталкивания
Формула напряжённости магнитного поля
Формула силы Ампера
Формула силы Лоренца
Формула ЭДС
Формула длины волны
ru.solverbook.com
Работа газа
Для сложения тучи чего-то маленького в то, что можно пощупать или увидеть, существует интеграл:. Геометрический смысл определенного интеграла – это площадь криволинейной трапеции (площадь под кривой). Если объем газа в цикле сначала растет (работа положительна), а потом уменьшается (работа отрицательна), то в итоге газ совершает работу, которая пропорциональна площади фигуры, ограниченной линиями цикла (см. рисунок)Здесь газ переходит сначала из состояния 1 в состояние 2, не совершая работы (изохорно), затем он переходит в сосотояние 3 изобарно, работа, которую он при этом совершает, равна площади голубого прямоугольника. Работа положительна, так как объем газа растет. Затем следует переход в точку 4, и снова работа газом не совершается. Из точки 4 газ возвращается в первоначальное состояние, работа, совершаемая им отрицательна (объем становится меньше, то есть газ сжимают внешние силы, работа которых как раз положительна). Отрицательная работа газа показана фиолетовым прямоугольником Таким образом, вся работа, совершенная в этом цикле – это площадь прямоугольника 1-2-3-4.
Немного обобщим и подведем итог:
При изохорном процессе, так как объем не меняется, то работа равна нулю.
При изобарном процессе давление постоянно, вытащим его за знак интеграла:. А при изотермическом процессе происходит как изменение давления, так и объема. Выразим давление через объем с помощью уравнения Клапейрона -Менделеева: : Подставим в наш интеграл: .1. При переходе из состояния 1 в состояние 3 температура газа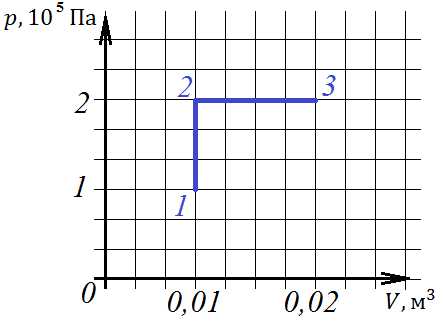
1) увеличилась в 2 раза; 2) уменьшилась в 2 раза; 3) увеличилась в 4 раза; 4) уменьшилась в 4 раза.
С помощью уравнения Клапейрона -Менделеева: заключаем, что температура газа прямо зависит от произведения его давления и объема. В состоянии 1 это произведение равно 0,01, а в состоянии 3 – 0,04, что больше в 4 раза, значит, и температура газа больше в 4 раза в третьем состоянии, чем в первом.
Ответ: 3
2. При переходе из состояния 1 в состояние 3 газ совершает работу
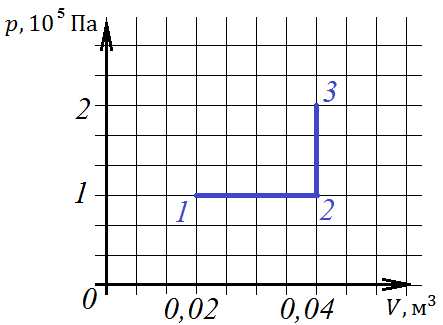 1) 2 кДж; 2) 4 кДж; 3) 6 кДж; 4) 8 кДж.
1) 2 кДж; 2) 4 кДж; 3) 6 кДж; 4) 8 кДж.
На рисунке процесс 1-2 – изобарный, выше мы записали, как рассчитать работу газа в таком процессе: Дж, или 2 кДж. Из состояния 2 в состояние 3 газ переходит изохорно, его объем не меняется, поэтому работа не совершается.
Ответ: 1.
3. В каком из процессов перехода идеального газа из состояния 1 в состояние 2 газ совершает наибольшую работу?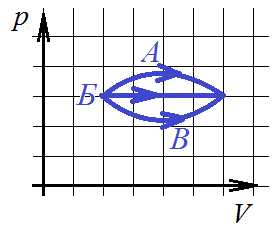
1) А 2) Б 3) В 4) Во всех трех процессах совершаемая работа одинакова
Вспоминаем, что работа газа в осях p-V есть интеграл, а интеграл – это площадь криволинейной трапеции. Площадь такой трапеции максимальна при переходе газа из начального состояния в конечное по траектории А.
Ответ: 1.
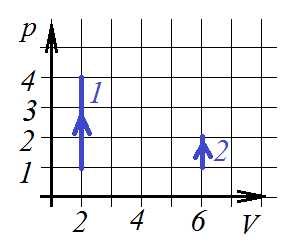
4. В двух сосудах находится одинаковое количество азота. С газами в сосудах происходят процессы, показанные на pV-диаграммах 1 и 2. Сравните работы, совершенные над газами в сосудах.
1)
2)
3)
4)
Так как ни в первом, ни во втором случае объем газа не меняется (тип газа нам тоже не важен), то работы никакой газы не совершают.
Ответ:4.
5. Какую работу совершил одноатомный газ в процессе, изображенном на диаграмме?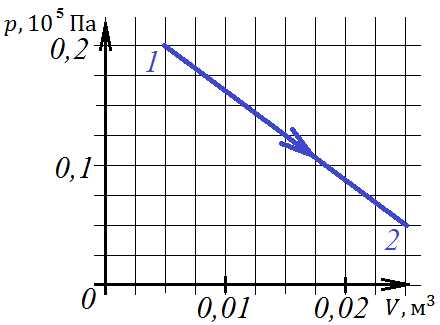
1) 250 Дж 2) 150 Дж 3) 300 Дж 4) 400 Дж
Решить задачу можно, определив площадь трапеции по формуле: . При этом за основания трапеции примем величины давлений в состояниях 1 и 2, а высота – изменение объема. Тогда:
Ответ: 1.
easy-physic.ru
11.2. Элементарная работа. Работа идеального газа при изопроцессах
Принято считать, что если система совершает работу против действия внешних сил, то эта работа положительная.
Если внешние силы совершают работу над системой, то работа отрицательная.
Рассмотрим идеальный
газ, находящийся под поршнем в цилиндре
(рис. 11.6). Газ расширяется, и поршень
поднимается на бесконечно малую высоту 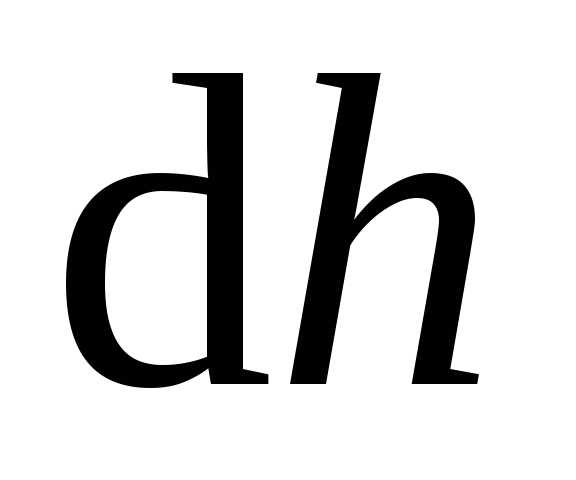
 ,
действующую со стороны газа на поршень,
находим по формуле
,
действующую со стороны газа на поршень,
находим по формуле,
где  – давление газа на поршень;
– давление газа на поршень;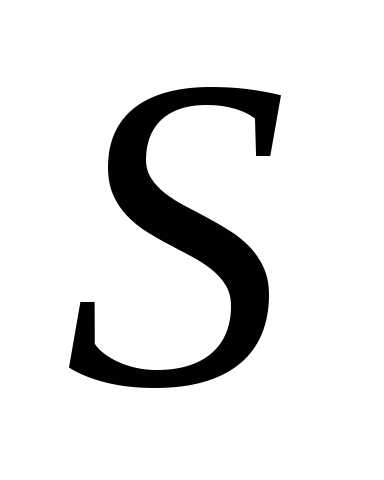 – площадь поршня. Бесконечно малую
работу, совершаемую газом, можно найти
по формуле
– площадь поршня. Бесконечно малую
работу, совершаемую газом, можно найти
по формуле
,
где 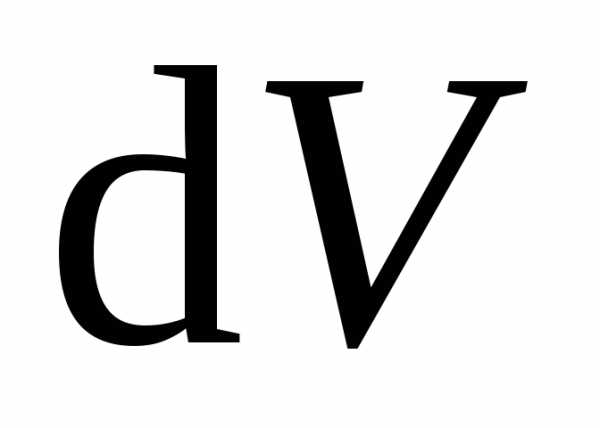 – бесконечно малое изменение объёма
газа. Окончательно
– бесконечно малое изменение объёма
газа. Окончательно
(11.6)
Рис. 11.6 |
Элементарной работой газа называется величина
. (11.7)
Это выражение остается справедливым для элементарной работы произвольной физически однородной и изотропной термодинамической системы в равновесном процессе.
Работа A12 термодинамической системы в равновесном процессе перехода из начального состояния с объёмом V1 в конечное состояние с объёмом
При конечном
изменении объёма газа от  до
до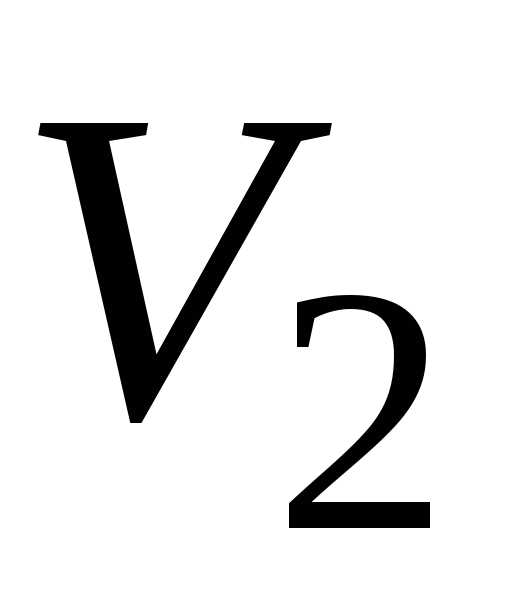 работа
работа
 .
(11.8)
.
(11.8)
Изобразим процесс перехода системы из начального состояния 1 в конечное состояние 2, построив график зависимости P(V). Элементарная работа численно равна площади прямоугольника с длинами сторон P и d
 до
до ,
работа равна площади фигуры, ограниченной
отрезком
,
работа равна площади фигуры, ограниченной
отрезком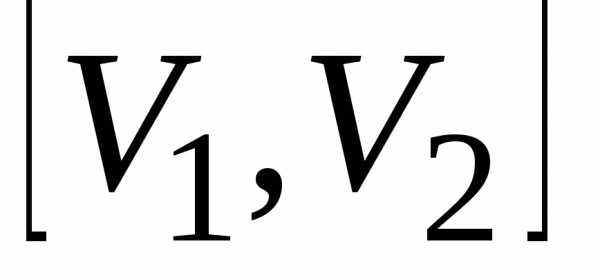 оси абсцисс, соответствующим этому
отрезку участком графика функцииP(V)
и проходящими через концы отрезка
оси абсцисс, соответствующим этому
отрезку участком графика функцииP(V)
и проходящими через концы отрезка 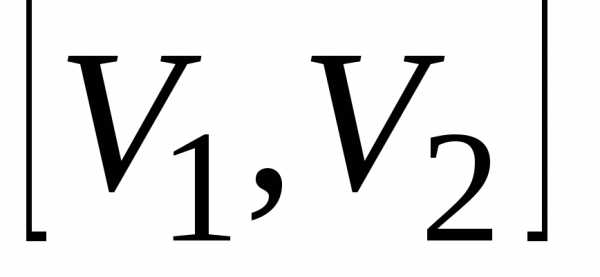 параллельными оси ординат прямыми.
параллельными оси ординат прямыми.Рис. 11.7 | Работа – это мера изменения внутренней энергии системы в процессе совершения работы. Работа является функцией процесса, но не является функцией состояния. |
Работа идеального газа при изопроцессах
В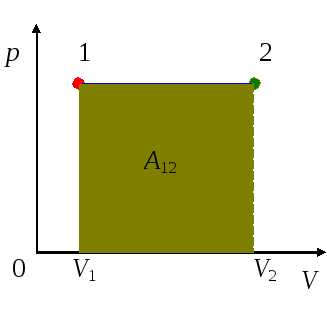 ычислим
работу идеального газа при изопроцессах.
ычислим
работу идеального газа при изопроцессах.
I. Рассмотрим изобарический процесс (рис. 11.8).
П
Рис. 11.8
ри изобарическом процессе. Если в результате этого процесса объём газа изменился от до
до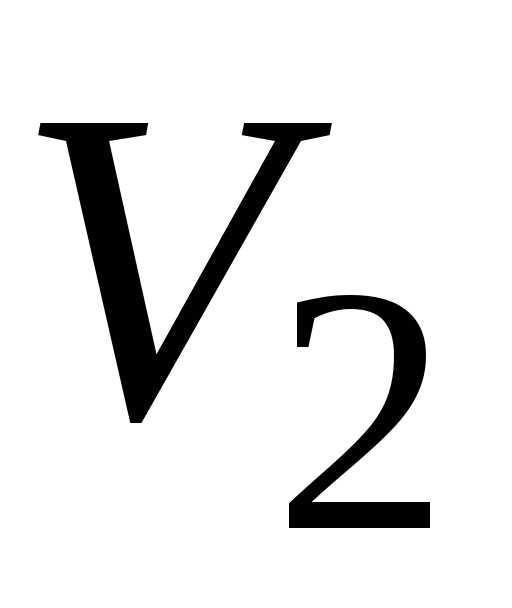 ,
то работа газа
,
то работа газа  ; (11.9)
; (11.9)
Построим график
процесса в координатах 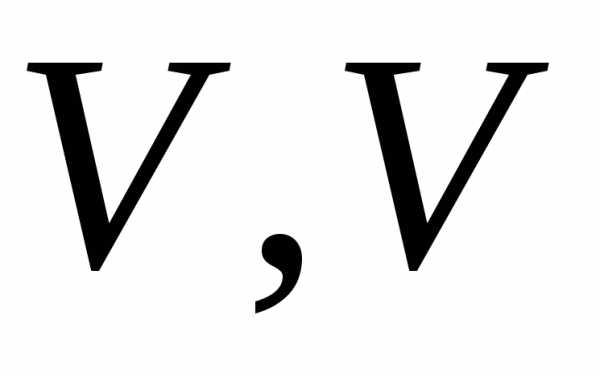 .
Работа
.
Работа графически выражается площадью
заштрихованного прямоугольника.
графически выражается площадью
заштрихованного прямоугольника.
II. Рассмотрим
изохорический процесс (рис. 11.9).
При изохорическом процессе
и изменение объёма газаdV = 0
равно нулю. Следовательно, согласно
формулам (11.6) и (11.9) работа  газа при изохорическом процессе равна
нулю.
газа при изохорическом процессе равна
нулю.
III. Рассмотрим изотермический процесс. При изотермическом процессе и внутренняя энергия газа
. (11.10)
Изменение внутренней
энергии
,
т.к. .
.
Если в результате
этого процесса объём газа изменился от  до
до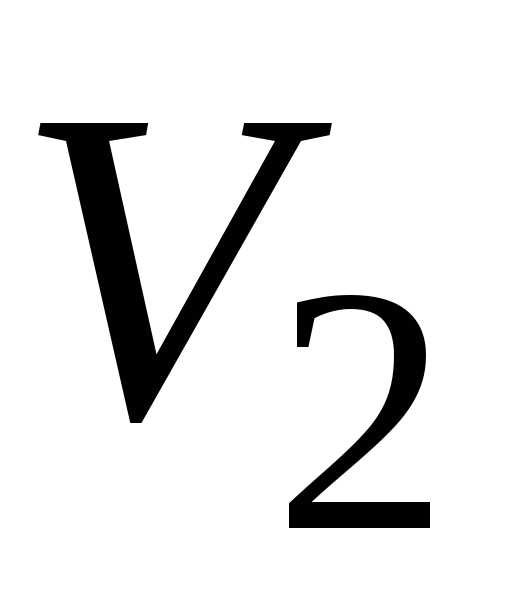 ,
то работа газа равна:
,
то работа газа равна: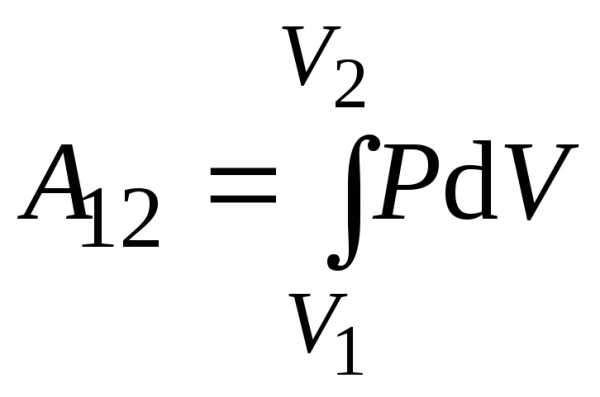 .
.
Но здесь
.
Найдём давление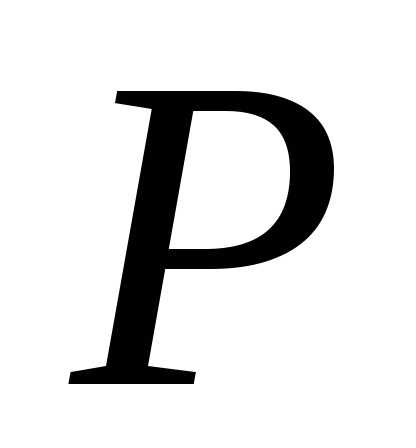 из уравнения Менделеева – Клапейрона:
из уравнения Менделеева – Клапейрона:
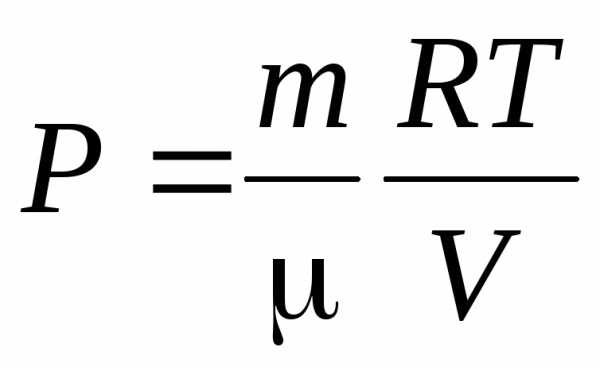 .
.
Тогда
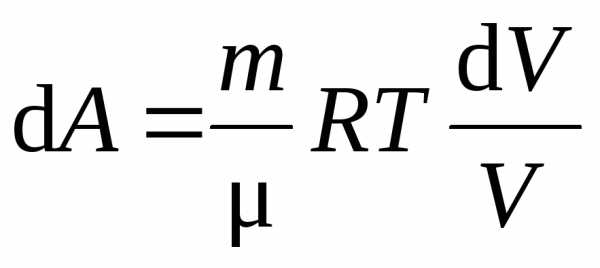 ,
и
,
и
.
Итак, при изотермическом процессе:
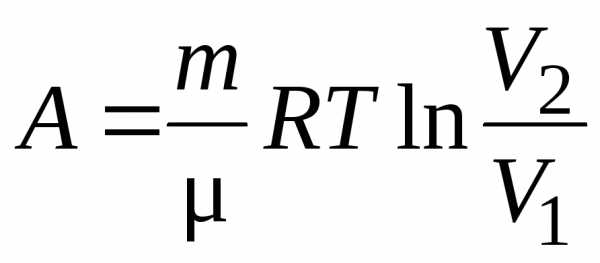 . (11.11)
. (11.11)
Строим график
процесса в координатах 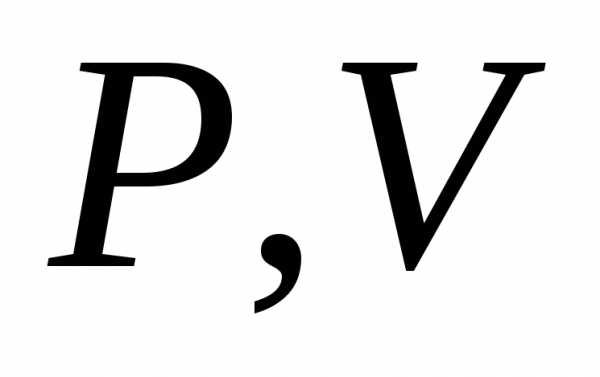 .
.
Работа  графически выражается заштрихованной
площадью под изотермой.
графически выражается заштрихованной
площадью под изотермой.
11.3. Первое начало термодинамики
Рассмотрим газ в теплоизолированном цилиндре (теплоизолированную термодинамическую систему), рис. 11.11. Цилиндр разделен жесткой теплопроводящей перегородкой на два отсека C и D. Объём отсека С поддерживается постоянным, над этой частью газа не может быть совершена работа. Объём отсека D может меняться при помощи подвижного поршня. За счет теплопроводящей перегородки отсеки могут обмениваться внутренней энергией.
Если в результате
совершения над системой C+D внешними силами работы  ,
система перешла из произвольного
состояния1 в произвольное состояние 2,
то при этом изменилась внутренняя
энергия системы. Тогда
.
,
система перешла из произвольного
состояния1 в произвольное состояние 2,
то при этом изменилась внутренняя
энергия системы. Тогда
.
Тогда,
изменение внутренней энергии газа в
отсекеС произошло за счет теплообмена без
совершения работы и равно количеству
теплоты Q,
полученному газом через жёсткую
перегородку. Обозначим
изменение внутренней энергии газа в
отсекеD.
Тогда получим:
.
Это равенство является математическим
выражениемпервого
начала термодинамики. Оно подразумевает, что полученное
термодинамической системой количество
теплоты Q равно приращению её внутренней энергии  за вычетом работы над системой внешних
сил
за вычетом работы над системой внешних
сил .
.
Если переход
системы из состояние 1 в состояние 2 является равновесным, то  =
–A,
где А – работа системы против внешних сил.
В таком случае
=
–A,
где А – работа системы против внешних сил.
В таком случае
. (11.12)
Это выражение представляет собой интегральную форму записи первого начала термодинамики.
Равенство
подразумевает, что полученное
термодинамической системой в равновесном
процессе количество теплоты Q идет на приращение его внутренней
энергии  и совершение работы над внешними телами.
и совершение работы над внешними телами.
Для бесконечно малого (элементарного) равновесного процесса уравнение принимает вид:
. (11.13)
Это выражение представляет собой дифференциальную форму записи первого начала термодинамики.
Первое начало термодинамики – это закон сохранения и превращения энергии. I начало термодинамики – частный случай всеобщего закона сохранения энергии: полная энергия замкнутой системы может изменяться только качественно, количественно оставаясь неизменной.
Таким образом, первое начало термодинамики является фундаментальным постулатом, утверждающим собой закон сохранения энергии. Оно устанавливает закон взаимопревращения теплоты, энергии и работы. За всю историю развития науки не обнаружено опытных фактов, которые противоречили бы этому постулату.
Дифференциальная форма записи закона подчеркивает важные свойства теплоты, энергии и работы. Обратим на это внимание.
Внутренняя энергия термодинамической системы (или тела) – это сумма всех видов энергии (энергии теплового движения атомов или молекул, потенциальная энергия их взаимодействия и т.п.), заключающихся в данной системе, за исключением энергии, которой система обладает в результате взаимодействия с другими телами. Внутреннюю энергию можно изменить двумя способами.
1. Газ находится под поршнем. Вдвигая поршень, совершаем работу. Газ сжимается и нагревается, его внутренняя энергия изменяется. Совершение работы – первый способ изменения внутренней энергии тела.
2. Но можно изменить внутреннюю энергию тела и другим способом, не совершая работы А, а только подводя к телу тепло. Газ находится под поршнем. Пусть поршень закреплён. При подведении тепла к газу, его внутренняя энергия меняется.
Подведение некоторого количества теплоты – второй способ изменения внутренней энергии тела. Но тогда теплота и работа должны быть эквивалентными формами передачи энергии.
Работа – способ передачи энергии. В процессе работы происходит переход энергии из одного вида энергии в другой.
Теплота – тоже способ передачи энергии.
Внутренняя энергия 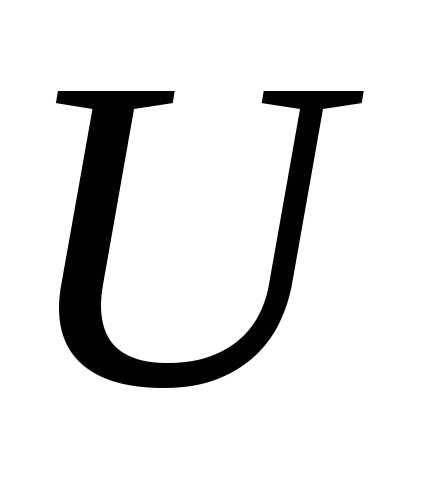 является функцией состояния системы
(или тела, если система состоит из одного
тела). Это означает, что
является функцией состояния системы
(или тела, если система состоит из одного
тела). Это означает, что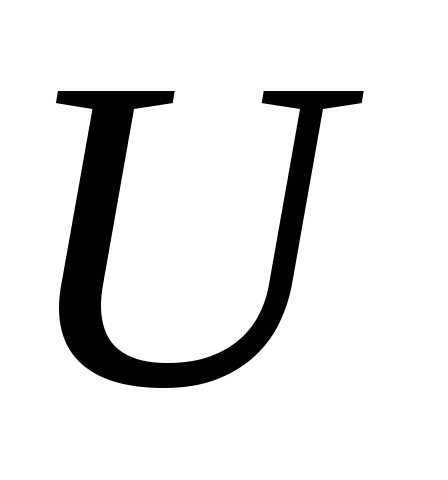 однозначно определяется термодинамическим
состоянием тела, т.е. каждому состоянию
тела соответствует одно значение
однозначно определяется термодинамическим
состоянием тела, т.е. каждому состоянию
тела соответствует одно значение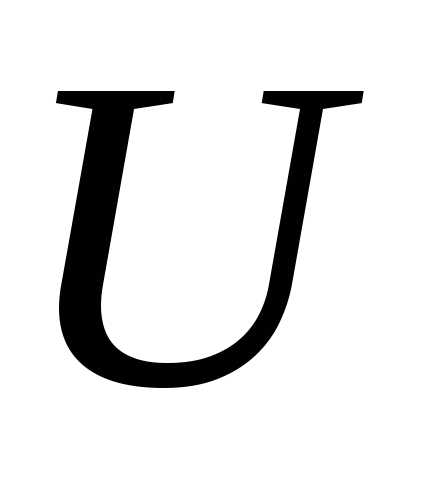 .
.
Если тело в состоянии 1 имеет энергию 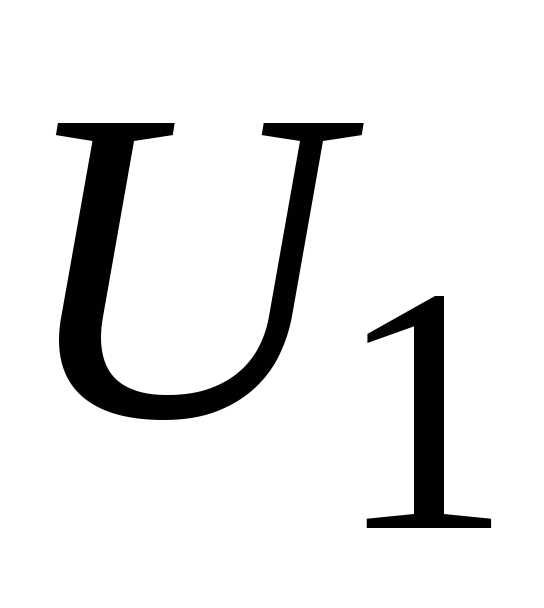 ,
а в состоянии2 – энергию
,
а в состоянии2 – энергию 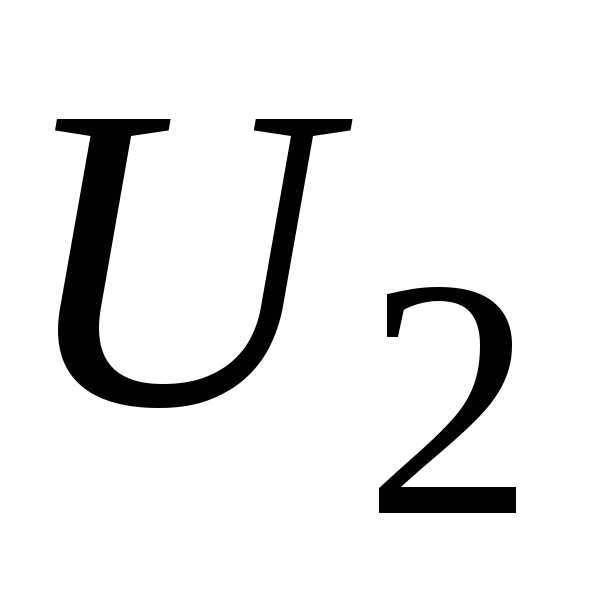 ,
то изменение энергиине зависит от того, каким путём совершается
переход из одного состояния в другое.
Следовательно, бесконечно малое изменение
,
то изменение энергиине зависит от того, каким путём совершается
переход из одного состояния в другое.
Следовательно, бесконечно малое изменение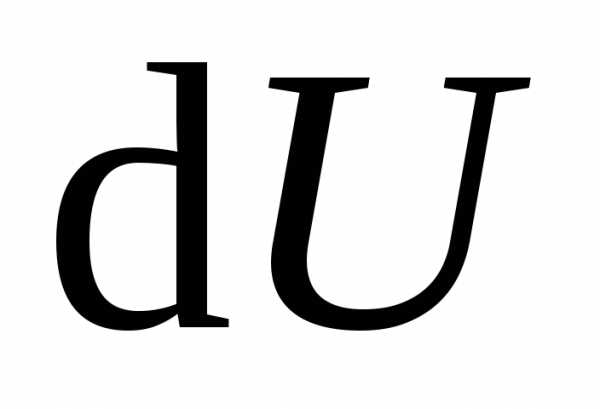 внутренней энергии является полным
дифференциалом (11.13).
внутренней энергии является полным
дифференциалом (11.13).
Количества теплоты
и работы зависят от пути перехода системы
из начального в конечное состояние, они
не являются функциями состояния системы,
их бесконечно малые изменения 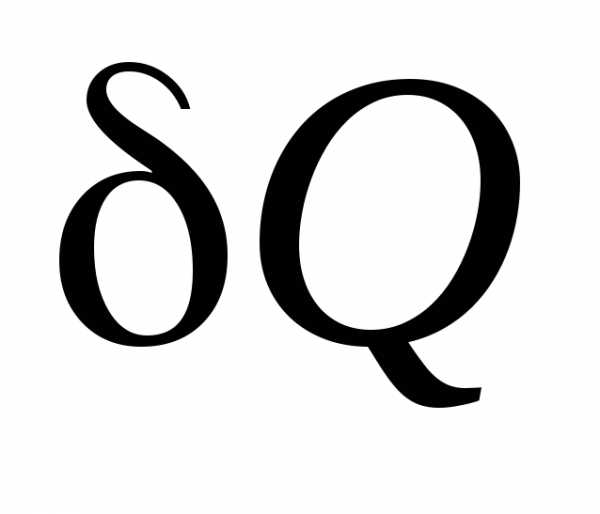 и
и не являются полными дифференциалами,
что подчёркивается в записи этих величин
в формуле (11.13).
не являются полными дифференциалами,
что подчёркивается в записи этих величин
в формуле (11.13).
В СИ количество теплоты, энергия и работа измеряются в джоулях (Дж).
studfiles.net
основные формулы и законы. Первый закон термодинамики, КПД
Основные формулы термодинамики и молекулярной физики, которые Вам пригодятся.
Вот он, еще один отличный день для практических занятий по физике. Сегодня, дорогие друзья, мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.
Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.
Идеальный газ
Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.
Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.
Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева
Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).
Универсальная газовая потоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)
Масс
zaochnik.ru
Работа при изопроцессах
Модель иллюстрирует учебную тему «Термодинамика. Работа газа».
Вводится понятие «работа газа», рассматриваются особенности работы газа при изохорном, изобарном, изотермическом и адиабатном процессах.
Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A’. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = –A’. Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение.
При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
В изохорном процессе (V = const) газ работы не совершает, A = 0.
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением:
| A = p (V2 – V1) = pΔV. |
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Первый закон термодинамики для изотермического процесса выражается соотношением Q = A.
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими.
Работа газа в адиабатическом процессе выражается через температуры T1 и T2 начального и конечного состояний:
Модель может быть использована в режиме ручного переключения кадров и в режиме автоматической демонстрации ().
files.school-collection.edu.ru
6.5. Работа изменения давления. Энтальпия
Кроме понятия «работа изменения объема», в термодинамических расчетах широко используют понятие «работа изменения давления».
Работой изменения давления называется работа перемещения жидкостей, газов и паров из области высокого давления () в область низкого давления (). Ее значение определяют либо по формулам:
, (6.7)
, (6.8)
либо графически, пользуясь -диаграммой.
Здесь W – работа изменения давления; V – средний объем; w – удельная работа изменения давления; v – средний удельный объем.
Графически удельная работа изменения давления определяется площадью 1234 на -диаграмме (рис. 6.3), ограниченной осью ординат и двумя абсциссами , проведенными из крайних точек линии процесса.
В результате замены этой площади (пл.) равновеликой ей площадью прямоугольника 3456 высотой, равной разности , и основанием, равным среднему удельному объему газа (v) в процессе, устанавливаем, что
пл. 1234 = пл. 3456 = .
Работа изменения давления положительная, если > , и отрицательная, если < .
Найдем связь между удельными работами изменения объема (l) и изменения давления (w).
Пусть на -диаграмме линия 1 – 2 изображает процесс произвольного состояния рабочего тела (рис. 6.4). В этом случае пл. 1234 (заштрихованная вертикальными линиями) графически изображает удельную работу изменения объема (l) ,а пл. 1256 (заштрихованная горизонтальными линиями) – удельную работу изменения давления (w).
Рис. 6.3. PV-диаграмма
Рис. 6.4. PV-диаграмма
Из рисунка 6.4 видно что
пл. 1234 + пл. 6140 – пл. 5032 = пл. 6125
или
,
откуда
. (6.9)
После подстановки удельной работы изменения объема, определенной по формуле (6.9), в уравнение первого начала термодинамики (6.2) имеем:
.
Сгруппируем слагаемые последнего выражения следующим образом:
. (6.10)
Введем обозначение:
.
Величина h называется удельной энтальпией, и поскольку ее определяют три параметра состояния, то и сама она является параметром состояния.
Подставив значения h в формулу (6.9) ,получим еще один вид уравнения первого начала термодинамики:
. (6.11)
Значения удельной энтальпии определяют по справочникам.
Физический смысл величины h можно выяснить путем исследования уравнения (6.11), записанного в дифференциальной форме:
.
При p = const имеем:
,
т.е. dh есть элементарное количество теплоты, подведенное к термодинамическому телу в процессе при постоянном давлении.
libraryno.ru
Работа газа: задачки второго уровня
В этой статье будут рассмотрены чуть более сложные задачи, которые иногда потребуют от нас изображения графика процесса (или хотя бы четкого представления о нем). Нужно помнить, что работа численно равна площади под кривой, если процесс изображается в осях .
Задача 1. Некоторый газ расширяется от объема л до объема л. Давление при этом изменяется по закону , где Па/м. Найти работу, совершаемую газом. Поглощается или выделяется энергия в этом процессе?
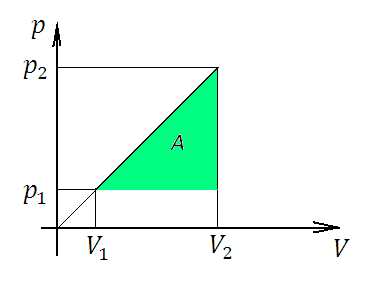
К задачам 1
График зависимости давления от объема для этого газа представляет собой прямую, проходящую через начало координат. Площадь фигуры под графиком численно равна работе. Нам остается только определить площадь треугольника, умножив его среднюю линию на высоту.
За высоту примем , тогда средняя линия равна . Отсюда работа газа:
Выясним, поглощается или выделяется энергия в этом процессе. Для этого можно определить внутреннюю энергию газа до и после расширения, или же ее изменение. Изменение внутренней энергии одноатомного газа определяется выражением:
Ответ: 0,24 мДж, энергия поглощается.
Задача 2. Один киломоль идеального газа первоначально находился при давлении и занимал объем . В процессе расширения до объема по закону газ совершает работу. Определить работу, совершенную газом, и найти изменение температуры газа в этом процессе.
Начальное состояние газа описывается уравнением:
Конечное – уравнением:
Тогда из первого уравнения начальная температура газа равна:
А конечная температура:
Изменение же температуры:
Из данного закона изменения объема получим: , тогда
Так как зависимость давления от объема линейная, то работа, как и в предыдущей задаче, найдется как площадь треугольника под графиком этой зависимости:
Ответ: ,
Задача 3. Газ расширяется от давления Па до давления Па по закону , где Па/м. Найти работу, совершаемую газом при таком расширении.
И снова линейная зависимость давления от объема. То бишь опять все тот же треугольник работы, площади которого она численно равна:
Из данного закона изменения давления определяем:
Тогда , .
Найдем работу:
Ответ: Дж
Задача 4. Температура некоторой массы идеального газа молярной массы меняется по закону , где . Найти работу, совершенную газом при увеличении объема от до . Поглощается или выделяется тепло в таком процессе?
Так как растет объем, то температура, очевидно, тоже растет:
Тогда увеличивается внутренняя энергия газа:
Из основного газового закона имеем:
Или
Сокращая, получим, что давление зависит от объема линейно:
Тогда работа численно равна площади под прямой (площади треугольника), и может быть вычислена как:
Тогда работа:
Ответ:
Задача 5. Объем газа увеличился в 2 раза: один раз изотермически, другой раз изобарически. В каком из этих случаев газ совершил большую работу?
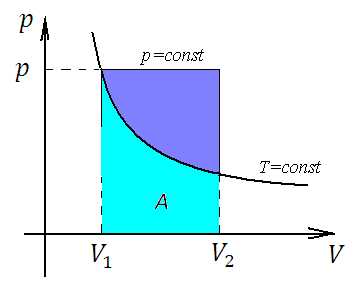
К задаче 5
Из рисунка хорошо видно, что при изобарическом процессе фигура под кривой (точнее, под прямой, потому что в координатах изобарный процесс – прямая, параллельная ос абсцисс) представляет собой прямоугольник, и его площади численно равна работа. При изотермическом процессе фигура обладает меньшей площадью (фигура голубого цвета).
easy-physic.ru
