Формула смещения в физике – Гармоническое колебание, уравнения, графики движения. Изменение координаты, скорости, ускорения со временем. Примеры, тесты

Механические колебания (Основные формулы)

Механические колебания

Основные формулы

Всякое колебательное движение, в том числе и гармоническое, характеризуется амплитудой \(A\), периодом колебаний \(T\), частотой \(\nu\), циклической (круговой) частотой \(\omega\) и фазой колебаний \(\varphi\).

Амплитудой \(A\) называют наибольшее значение колеблющейся величины.

Число полных колебаний в единицу времени называют частотой:

\(\nu=\frac{n}{t}\).

Циклическая (круговая) частота – это число полных колебаний в течении \(2\pi\) с:

\(\omega=\frac{2\pi{n}}{t}=2\pi{\nu}\).

Периодом называю время, в течении которого совершается одно полное колебание:

\(T=\frac{t}{n}=\frac{2\pi}{\omega}=\frac{1}{\nu}\).

Смещение, скорость и ускорение при гармоническом колебании определяются уравнениями

\(x=A\sin(\omega{t}+\varphi_0)\),

\(v=\dot x=A\omega\cos(\omega{t}+\varphi_0)\),

\(a=\ddot x=-A\omega^2\sin(\omega{t}+\varphi_0)=-\omega^2x\).

Здесь \((\omega{t}+\varphi_0)\) – фаза колебаний, а \(\varphi_0\) – начальная фаза.

Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила), всегда пропорциональна смещению и направлена в сторону, противоположную смещению:

\(F=ma=-m{\omega_0}^2x=-kx\)

где \(k=m{\omega_0}^2\) – коэффициент квазиупругой силы, измеряемый силой, вызывающей смещение \(x\), равное единице.

При отсутствии сопротивления среды циклическая частота \(\omega_0\) свободных гармонических колебаний, называемых собственной циклической частотой и период \(T\) равны:

\(\omega_0=\sqrt{\frac{k}{m}}\), \(T=2\pi\sqrt{\frac{m}{k}}\)

Период колебания математического маятника длиной \(l\) равен

\(T=2\pi\sqrt{\frac{l}{g}}\).

Период колебаний физического маятника

\(T=2\pi\sqrt{\frac{I}{mgd}}\),

где \(I\) – момент инерции маятника относительно оси качаний, \(d\) – расстояние от оси его до центра тяжести.

Полная энергия тела, совершающего гармонические колебания, постоянна и равна

\(W=\frac{m\omega^2A^2}{2}\).

Уравнение смещения в затухающих колебаниях при наличии силы сопротивления \(F_s\) пропорциональной скорости (\(F_s=-rv\), где \(r\) – коэффициент сопротивления) имеет вид:

\(x=A_0e^{-\beta{t}}\sin(\omega{t}+\varphi_0)\).

Здесь \(A_0e^{-\beta{t}}\) – убывающая по времени амплитуда смещения; \(\beta\) – коэффициент затухания; \(\omega\) – циклическая частота; \(A_0,\varphi_0\) – начальные амплитуда и фаза, определяются из начальных условий.

Величины \(\beta\) и \(\omega\) выражаются через параметры системы \(r,m,k\) формулами:

\(\beta=\frac{r}{2m}\),

\(\omega=\sqrt{{\omega_0}^2-\beta^2}=\sqrt{\frac{k}{m}-\frac{r^2}{4m^2}}\).

Логарифмический декремент затухания

\(\lambda=\ln(\frac{A_1}{A_2})=\beta{T}\),

где \(A_1,A_2\) – амплитуды двух последовательных колебаний.

Амплитуда вынужденных колебаний

\(A=\frac{h}{\sqrt{({\omega_0}^2-\omega^2)^2+4\beta^2\omega^2}}\),

где \(h\) – есть отношение амплитуды вынуждающей силы к массе тела; \(\omega_0\) – собственная циклическая частота; \(\omega\) – циклическая частота вынуждающей силы.

Резонансная циклическая частота равна

\(\omega_r=\sqrt{{\omega_0}^2-2\beta^2}\).

————-

Источник: sfiz.ru

sfiz.ru

Колебания

§ 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные формулы

• Уравнение гармонических колебаний

где х — смещение колеблющейся точки от положения равновесия; t — время; А, ω, φ— соответственно амплитуда, угловая частота, начальная фаза колебаний; — фаза колебаний в моментt.

• Угловая частота колебаний

, или ,

где ν и Т — частота и период колебаний.

• Скорость точки, совершающей гармонические колебания,

• Ускорение при гармоническом колебании

• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле

где a₁ и А₂— амплитуды составляющих колебаний; φ₁ и φ₂— их начальные фазы.

• Начальная фаза φ результирующего колебания может быть найдена из формулы

• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по зна­чению частотами ν₁ и ν₂,

• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A₁ и A₂ и начальны­ми фазами φ₁ и φ₂,

Если начальные фазы φ₁ и φ₂ составляющих колебаний одинако­вы, то уравнение траектории принимает вид

т. е. точка движется по прямой.

В том случае, если разность фаз , уравнение принимает вид

т. е. точка движется по эллипсу.

• Дифференциальное уравнение гармонических колебаний ма­териальной точки

, или ,где m — масса точки; k — коэффициент квазиупругой силы (k=тω²).

• Полная энергия материальной точки, совершающей гармони­ческие колебания,

• Период колебаний тела, подвешенного на пружине (пружин­ный маятник),

где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в ко­торых выполняется закон Гука (при малой массе пружины в срав­нении с массой тела).

Период колебаний математического маятника

где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника

где J — момент инерции колеблющегося тела относительно оси

колебаний; а — расстояние центра масс маятника от оси колебаний;

— приведенная длина физического маятника.

Приведенные формулы являются точными для случая бесконеч­но малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не болееошибка в значении периода не превышает 1 %.

Период крутильных колебаний тела, подвешенного на упругой нити,

где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.

• Дифференциальное уравнение затухающих колебаний , или ,

где r — коэффициент сопротивления; δ — коэффициент затухания: ;ω₀— собственная угловая частота колебаний *

• Уравнение затухающих колебаний

где A (t) —

амплитуда затухающих колебаний в момент t; ω — их угловая частота.

• Угловая частота затухающих колебаний

О Зависимость амплитуды затухающих колебаний от времени

I

где А₀ — амплитуда колебаний в момент t=0.

• Логарифмический декремент колебаний

где A (t) и A (t+T) — амплитуды двух последовательных колеба­ний, отстоящих по времени друг от друга на период.

• Дифференциальное уравнение вынужденных колебаний

, или

,

где — внешняя периодическая сила, действующая наколеблющуюся материальную точку и вызывающая вынужденные колебания; F₀ — ее амплитудное значение;

• Амплитуда вынужденных колебаний

• Резонансная частота и резонансная амплитуда и

Примеры решения задач

Пример 1. Точка совершает колебания по закону x(t)=,где А=2 см. Определить начальную фазу φ, если

x(0)=см их^,(0)<0. Построить векторную диаграмму для мо-­ мента t=0.

Решение. Воспользуемся уравнением движения и выразим смещение в момент t=0 через начальную фазу:

Отсюда найдем начальную фазу:

* В приведенных ранее формулах гармонических колебаний та же величина обозначалась просто ω (без индекса 0).

Подставим в это выражение заданные значения x(0) и А: φ= =. Значению аргументаудовлетворяютдва значения угла:

Для того чтобы решить, какое из этих значений угла φ удовлет-­ воряет еще и условию , найдем сначала:

Подставив в это выражение значение t=0 и поочередно значения начальных фаз и, найдем

Т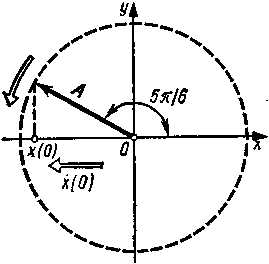ак как всегдаA>0 и ω>0, то условиюудовлетворяет толь­ко первое значение начальной фазы. Таким образом, искомая начальная фаза

По найденному значению φ постро-­ им векторную диаграмму (рис. 6.1). Пример 2. Материальная точка массой т=5 г совершает гармоничес-­ кие колебания с частотой ν =0,5 Гц. Амплитуда колебаний A=3 см. Оп-­ ределить: 1) скорость υ точки в мо-­ мент времени, когда смещение

х= = 1,5 см; 2) максимальную силу F_max, действующую на точку; 3) Рис. 6.1 полную энергию Е колеблющейся точ­ ки.

Решение. 1. Уравнение гармонического колебания имеет вид

(1)

а формулу скорости получим, взяв первую производную по времени от смещения:

(2)

Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квад­рат, разделим первое на А², второе на A² ω ² и сложим:

, или

Решив последнее уравнение относительно υ, найдем

Выполнив вычисления по этой формуле, получим

см/с.

Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус — ког­да направление скорости совпадает с отрицательным направлением оси х.

Смещение при гармоническом колебании кроме уравнения (1) может быть определено также уравнением

Повторив с этим уравнением такое же решение, получим тот же ответ.

2. Силу действующую на точку, найдем по второму закону Нью­тона:

(3)

где а — ускорение точки, которое получим, взяв производную по времени от скорости:

, или

Подставив выражение ускорения в формулу (3), получим

Отсюда максимальное значение силы

Подставив в это уравнение значения величин π, ν, т и A, найдем

3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента вре­мени.

Проще всего вычислить полную энергию в момент, когда кинети­ческая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия E колеблющейся точки равна максимальной кинетической энергии

T_max:

(4)

Максимальную скорость определим из формулы (2), положив : . Подставив выражение скорости в фор­-мулу (4), найдем

Подставив значения величин в эту формулу и произведя вычис­ления, получим

или мкДж.

Пример 3. На концах тонкого стержня длиной l = 1 м и массой m₃=400 г укреплены шарики малых размеров массами m₁=200 г и m₂=300г. Стержень колеблется около горизонтальной оси, перпен-

дикулярной стержню и проходящей через его середину (точка О на рис. 6.2). Определить период Т колебаний, совершаемых стержнем.

Решение. Период колебаний физического маятника, каким является стержень с шариками, определяется соотношением

(1)

гдеJ — момент инерции маятника относительно оси колебаний; т — его масса; l_С — расстояние от центра масс ма­ятника до оси.

Момент инерции данного маятника равен сумме моментов инерции шариков J₁ и J₂ и стержня J₃:

(2)

Принимая шарики за материальные точки, вы­разим моменты их инерции:

Так как ось проходит через середину стержня, то его момент инерции относительно этой оси J₃= =.Подставив полученные выражения J₁ , J₂ и J₃ в формулу (2), найдем общий момент инерции фи-­ зического маятника:

Произведя вычисления по этой формуле, найдем

Рис. 6.2 Масса маятника состоит из масс шариков и массы стержня:

Расстояние l_С центра масс маятника от оси колебаний найдем, исходя из следующих соображений. Если ось х направить вдоль стержня и начало координат совместить с точкой О, то искомое рас­стояние l равно координате центра масс маятника, т. е.

, или

Подставив значения величин m₁, m₂, m, l и произведя вычисле­ния, найдем

см.

Произведя расчеты по формуле (1), получим период колебаний физического маятника:

Пример 4. Физический маятник представляет собой стержень длиной l= 1 м и массой 3т₁ с прикрепленным к одному из его концов обручем диаметром и массойт₁. Горизонтальная ось Oz

маятника проходит через середину стержня перпендикулярно ему (рис. 6.3). Определить период Т колебаний такого маятника.

Решение. Период колебаний физического маятника опреде­ляется по формуле

(1)

где J — момент инерции маятника относительно оси колебаний; т — его масса; l_C — расстояние от центра масс маятника до оси колебаний.

Момент инерции маятника равен сумме мо­ментов инерции стержня J₁ и обруча J₂:

(2).

Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определяется по форму-­ ле . В данном случает=3т₁ и

Момент инерции обруча найдем, восполь-­ зовавшись теоремой Штейнера ,где J — момент инерции относительно про-­ извольной оси; J₀ — момент инерции отно-­ сительно оси, проходящей через центр масс параллельно заданной оси; а — расстояние между указанными осями. Применив эту фор-­ мулу к обручу, получим

Рис. 6.3

Подставив выражения J₁ и J₂ в форму­лу (2), найдем момент инерции маятника относительно оси вра­щения:

Расстояние l_С от оси маятника до его центра масс равно

Подставив в формулу (1) выражения J, l_с и массы маятника , найдем период его колебаний:

После вычисления по этой формуле получим T=2,17 с.

Пример 5. Складываются два колебания одинакового направле-­ ния, выражаемых уравнениями ;х₂= =, гдеА₁=1 см, A₂=2 см, с,с,ω = =. 1. Определить начальные фазыφ₁ и φ ₂ составляющих коле-

баний. 2. Найти амплитуду А и начальную фазу φ результирующего колебания. Написать уравнение результирующего колебания.

Решение. 1. Уравнение гармонического колебания имеет вид

(1)

Преобразуем уравнения, заданные в условии задачи, к такому же виду:

(2)

Из сравнения выражений (2) с равенством (1) находим начальные фазы первого и второго колебаний:

рад и рад.

2. Для определения амплитуды А результирую­щего колебания удобно воспользоваться векторной диаграммой, представленной на рис. 6.4. Согласно теореме косинусов, получим

(3)

где — разность фаз составляющих колебаний.Так как , то, подставляя найденныезначения φ₂ и φ₁ получим рад.

Рис. 6.4

Подставим значения А₁ , А₂ и в формулу(3) и произведем вычисления:

A=2,65 см.

Тангенс начальной фазы φ результирующего колебания опреде-­ лим непосредственно из рис. 6.4: ,отку-­ да начальная фаза

Подставим значения А₁, А₂, φ ₁, φ ₂ и произведем вычисления:

=рад.

Так как угловые частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту ω. Это позволяет написать уравнение результирующего колебания в виде , где A=2,65 см, ,рад.

Пример 6. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравне­ния которых

(1).

(2)

где a₁=1 см, A₂=2 см, . Найти уравнение траектории точ-­ки. Построить траекторию с соблюдением масштаба и указать направление движения точки.

Решение. Чтобы найти уравнение траектории точки, ис­ключим время t из заданных уравнений (1) и (2). Для этого восполь-

зуемся формулой . В данном случае, поэтому

Так как согласно формуле (1) , то уравнение траекто-­ рии

(3)

Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений (1) и (2) следует, что смещение точки по осям координат ограничено и заключено в пределах от —1 до +1 см по оси Ох и от —2 до +2 см по оси Оу.

Для построения траектории найдем по уравнению (3) значения у, соответствующие ряду значений х, удовлетворяющих условию см, и составим таблицу:

X , СМ	-1	—0,75	—0,5	0	+0,5	+ 1
у, см	0	±0,707	±1	±1,41	±1,73	±2

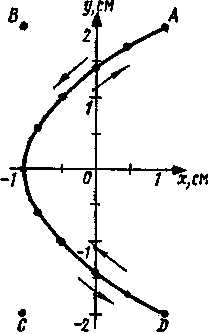
Начертив координатные оси и выбрав масштаб, нанесем на пло­скость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колеба­ния в соответствии с уравнениями движе­ния (1) и (2) (рис. 6.5).

Рис. 6.5

Для того чтобы указать направление движения точки, проследим за тем, как из­меняется ее положение с течением времени. В начальный момент t=0 координаты точ­ки равны x(0)=1 см и y(0)=2 см. В по­следующий момент времени, например при t₁=l с, координаты точек изменятся и ста­нут равными х (1)= —1 см, y(t)=0. Зная положения точек в начальный и последую­щий (близкий) моменты времени, можно указать направление движения точки по траектории. На рис. 6.5 это направление движения указано стрелкой (от точки А к началу координат). После того как в мо­мент t₂ = 2 с колеблющаяся точка достиг­нет точки D, она будет двигаться в обратном направлении.

Задачи

Кинематика гармонических колебаний

6.1. Уравнение колебаний точки имеет вид ,где ω=π с^-1, τ=0,2 с. Определить период Т и начальную фазу φ колебаний.

6.2. Определить период Т, частоту v и начальную фазу φ коле­баний, заданных уравнением , гдеω=2,5π с^-1, τ=0,4 с.

6.3. Точка совершает колебания по закону , гдеA=4 см. Определить начальную фазу φ, если: 1) х(0)=2 см и ; 2) х(0) =см и ; 3) х(0)=2см и ; 4) х(0)=и. Построить векторную диаграмму длямомента t=0.

6.4. Точка совершает колебания .по закону ,где A=4 см. Определить начальную фазу φ, если: 1) х(0)=2 см и ; 2)x(0)=см и; 3)х(0)=см и;4) x(0)=см и. Построить векторную диаграмму длямомента t=0.

studfiles.net

Гармонические колебания. | Объединение учителей Санкт-Петербурга

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают.
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0  смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.
Величина  – максимальная скорость колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при гармоническом колебании имеем: ,  а для случая нулевой начальной фазы  (см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени:  – вторая производная от координаты по времени. Тогда: . Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).
Величина  – максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы:  (см. график).
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
Сравним выражения для смещения и ускорения при гармонических колебаниях:    и    .
Можно записать:  – т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.
Часто бывает удобно записывать уравнения для колебаний в виде: , где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения.

www.eduspb.com

Гармоническое колебание, уравнения, графики движения. Изменение координаты, скорости, ускорения со временем. Примеры, тесты

Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

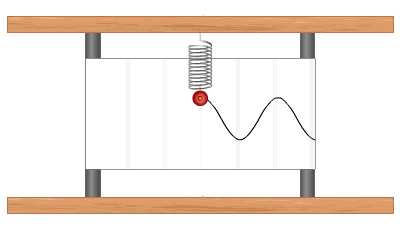
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия – достигает максимального значения.

Если колебание описывать по закону косинуса

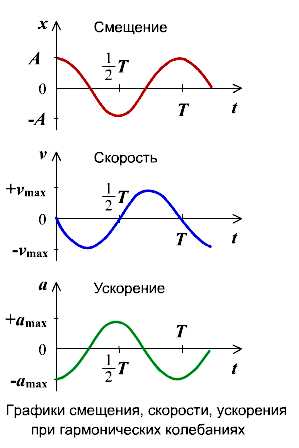
Если колебание описывать по закону синуса

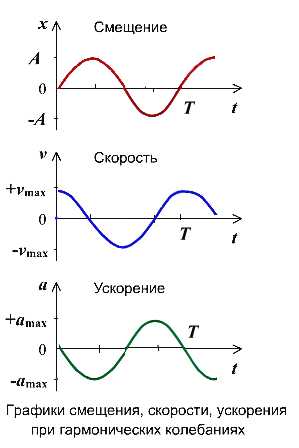
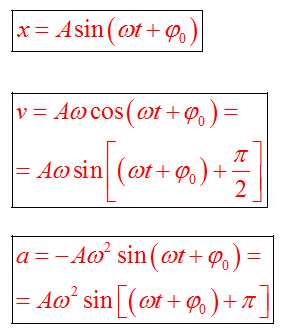
Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) – это первая производная x(t). А зависимость a(t) – это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Находим производную сложной функции.

fizmat.by

Основные формулы по физике – КВАНТОВАЯ ФИЗИКА

Физические законы, формулы, переменные	Формулы квантовой физики
Закон Стефана-Больцмана: где R – энергетическая светимость (излучательность) абсолютно черного тела, т.е. энергия, испускаемая в единицу времени с единицы площади: σ – постоянная Стефана-Больцмана:
Энергетическая светимость (излучательность) серого тела: где α – коэффициент черноты.
Закон смещения Вина: где λm – длина волны, на которую приходится максимум энергии излучения; b – постоянная Вина :
Импульс фотона: где λ – длина волны; h – постоянная Планка:
Энергия фотона: где ν – частота; с – скорость света в вакууме:
Формула Эйнштейна для фотоэффекта: где hν – энергия фотона, падающего на поверхность металла; А – работа выхода электрона из металла; – максимальная кинетическая энергия фотоэлектрона.
Красная граница фотоэффекта: где λк – максимальная длина волны, при которой возможен фотоэффект; νк – минимальная частота, при которой возможен фотоэффект.	или
Сериальные формулы спектра водородоподобного атома где R – постоянная Ридберга R=1,097·107 м-1, z – порядковый номер элемента; Серия Лаймана m=1, n=2,3,4… Серия Бальмера m=2, n=3,4,5… Серия Пашена m=3, n=4,5,6… Серия Брекета m=4, n=5,6,7… и т.д.
Длина волны де Бройля: где р – импульс частицы. В классическом приближении (при v m – масса частицы; v – скорость частицы; с – скорость света в вакууме. В релятивистском случае (при ):
Связь импульса с кинетической энергией Wк в релятивистском приближении: где E0 – энергия покоя частицы:
Плотность вероятности нахождения частицы в соответствующем месте пространства
Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме где l – ширина ямы, х – координата частицы в яме (0 ≤ x ≤ l), n – квантовое число (n=1,2,3…).
Энергия частицы в бесконечно глубокой одномерной потенциальной яме где m – масса частицы.
Электропроводность собственных полупроводников где е – заряд электрона, n – концентрация носителей заряда, uр – подвижность электронов, un – подвижность дырок.
Постоянная Холла для полупроводников типа алмаза, германия, кремния

traprat.ru

Формула Планка

Задание: Используя формулу Планка, получите закон Стефана — Больцмана для интегральной излучательной способности абсолютно черного тела.

Решение:

Энергетическую светимость абсолютно черного тела определим, как:

\[{\varepsilon }_T=\int\limits^{\infty }_0{{\varepsilon }_{\nu ,T}d\nu \ \left(1.1\right).}\]

Используем формулу Планка для излучательной способности абсолютно черного тела:

\[{\varepsilon }_{\nu ,T}=\frac{2\pi {\nu }^3}{c^2}\frac{h}{{exp \left(\frac{h\nu }{kT}\right)\ }-1}\ \left(1.2\right).\]

Подставим (1.2) в (1.1), получим интеграл:

\[{\varepsilon }_T=\int\limits^{\infty }_0{\frac{2\pi {\nu }^3}{c^2}\frac{h}{{exp \left(\frac{h\nu }{kT}\right)\ }-1}d\nu =\frac{2\pi h}{c^2}\ \int\limits^{\infty }_0{\frac{{\nu }^3d\nu }{{exp \left(\frac{h\nu }{kT}\right)\ }-1}}\left(1.3\right).}\]

Проведем замену переменных, подставим $x=\frac{h\nu }{kT}\to \nu =\frac{xkT}{h},\ \to d\nu =\frac{kTdx}{h}$, тогда интеграл в (1.3) преобразуется к виду:

\[{\varepsilon }_T=\frac{2\pi h}{c^2}\int\limits^{\infty }_0{\frac{{\left(\frac{xkT}{h}\right)}^3\frac{kTdx}{h}}{{exp \left(x\right)\ }-1}}=\frac{2\pi {\left(kT\right)}^4}{c^2h^3}\int\limits^{\infty }_0{\frac{x^3exp \sigma (-x)dx}{1-{exp \left(-x\right)\ }}}\left(1.4\right).\]

Разложим знаменатель интеграла из (1.4) в ряд:

\[1-e^{-x}=1+e^{-x}+e^{-2x}+\dots .\]

Найдем интеграл:

\[\int\limits^{\infty }_0{\frac{x^3e^{-x}dx}{1-e^{-x}}}=\int\limits^{\infty }_0{x^3e^{-x}(1+e^{-x}+e^{-2x}+\dots .)dx}=6\left(1+\frac{1}{2^4}+\frac{1}{3^4}+\dots \right)=\frac{{\pi }^4}{15}\]

Так, получаем интеграл в выражении (1.4) равен:

\[\int\limits^{\infty }_0{\frac{x^3dx}{{exp \left(x\right)\ }-1}}=\frac{{\pi }^4}{15}\approx 6,5\left(1.5\right).\]

В таком случае из (1.4) получим:

\[{\varepsilon }_T=\frac{2\pi {\left(kT\right)}^4}{c^2h^3}\frac{{\pi }^4}{15}= \sigma T^4\ \left(1.6\right),\]

где $\sigma=\frac{2\pi k^4}{c^2h^3}\frac{{\pi }^4}{15}$

Рассчитаем величину $\sigma$, которую мы получили, зная все составляющие ее формулу постоянные:

\[\pi =3,14;;\] \[k={1,38•10}^{-23}\frac{Дж}{К};\] \[c=3•{10}^8\frac{м}{с};;\] \[h=6,67\cdot {10}^{-34}Дж\cdot с.\] \[\sigma=\frac{2\cdot {\left(3,14\right)}^5\cdot {\left({1,38\cdot 10}^{-23}\right)}^4}{15\cdot {\left(3\cdot {10}^8\right)}^2\cdot {\left(6,67\cdot {10}^{-34}\right)}^3}=5,7\cdot {10}^{-8}\ \frac{Вт}{м^2К^4}.\]

Таким образом, мы получили закон Стефана Больцмана:

\[{\varepsilon }_T=\sigma T^4.\]

spravochnick.ru

Закон Стефана-Больцмана, формула смещения Вина

Закон Стефана – Больцмана

Довольно долго теоретический вид функции $f\left(\omega ,T\right)=\frac{c}{4}w_{\omega }\left(\omega ,T\right)$ получить не удавалось. Проводя анализ данных эксперимента, Стефан сделал вывод о том, что энергетическая светимость тела пропорциональна четвертой степени температуры (T). Стефан экспериментировал с нечерными телами. Больцман, используя термодинамические законы, получил теоретически формулу для энергетической светимости абсолютно черного тела:

где $\sigma =5,67\cdot {10}^{-8}\frac{Вт}{м^2К^4}$ — постоянная Стефана — Больцмана, $T$ — абсолютная температура. Выражение (1) называется законом Стефана — Больцмана.

Закон Стефана – Больцмана легко получить из формулы Планка.

где $k$ — постоянная Больцмана, $\hbar =1,05{\cdot 10}^{-34}Дж\cdot с$. Вычислим энергетическую светимость:

Для вычисления интеграла в правой части выражения (3) сделаем замену переменных: $\xi =\frac{\hbar \omega }{kT},\ \to \omega =\frac{\xi kT}{\hbar }\to {\omega }^3={\left(\frac{\xi kT}{\hbar }\right)}^3,\ d\omega =\frac{kT}{\hbar }d\xi \ \left(4\right).$ Значит имеем:

где $\int\limits^{\infty }_0{\frac{{\xi }^3d\xi }{{exp \left(\xi \right)\ }-1}=\frac{{\pi }^4}{15},}$ подставим в выражение (4), получим:

вычислим коэффициент, который находится перед $T^4$:

Формула смещения Вина

В. Вин доказал, что равновесное излучение, которое заключено в оболочке с идеально отражающими стенками, остается равновесным при квазистатическом сжатии или расширении оболочки. Значение теоремы Вина методическое. Адиабатически и квазистатический изменяя объем равновесного излучения в оболочке, можно получить равновесное излучение любой плотности, значит и температуры. Энергию или температуру данного излучения находят, вычисляя работу, совершенную над исследуемым объемом в данном процессе. Спектральный состав излучение будет найден, если вычислить доплеровское изменение частоты излучения при его отражении от движущейся оболочки. Так устанавливается соотношение параметров равновесного излучения в любой стадии процесса. В 1893 г. В. Вин используя законы термодинамики и электромагнетизма показал, что функция спектрального распределения имеет вид:

где $F$ — некоторая функция отношения частоты к температуре. Если переписать выражение (6), используя функция для длины волны ($\varphi (\lambda ,T)$), то получим:

где $\Psi \left(\lambda ,T\right)$ — некоторая функция от произведения $\lambda T.$ Из выражения (7) можно вычислить длину волны, на которую приходится максимум функции $\varphi \left(\lambda ,T\right)$. Найдем производную $\frac{d\varphi }{d\lambda }$, имеем:

В максимуме выражение (8) равно нулю (${\left.\frac{d\varphi }{d\lambda }\right|}_{\lambda ={\lambda }_{max}}=0$). Выражение в квадратных скобках формулы (8) — некоторая функция $\theta (\lambda T)$, то есть:

Известно, что длина волны конечна, то есть ${\lambda }_{max}\ne \infty .$ Следовательно, выполняется условие:

Решение уравнения (10) по отношению к ${\lambda }_{max}T$ дает некоторое число, которое чаще всего в данном случае обозначают буквой b:

Выражение (11) называют законом (формулой) смещения Вина в его специальной форме. Формула (11) показывает результат смещения максимума излучения при изменении температуры (T). Эмпирическим путем, получена постоянная $b=2,9\cdot {10}^{-3}м\cdot К$.

Закон Вина можно записать в другой форме:

где ${\omega }_m=\frac{2\pi с}{{\lambda }_{max}}$.

Пример 1

Какова мощность, требуемая для поддержания температуры расплавленного вещества $T=1500K$ постоянной, если площадь его поверхности равна $S=1м^2?$ Считать, что мы имеем дела с абсолютно черным телом. Потери энергии малы. Решение:

Мощность излучения можно рассчитать по формуле:

\[N=R_eS\ \left(1.1\right).\]

Используем закон Стефана — Больцмана для нахождения энергетической светимости черного тела:

\[R_e=\sigma T^4\left(1.2\right).\]

В таком случае искомая величина может быть вычислена с использованием выражения:

\[N=\sigma T^4S.\]

Проведем вычисления:

\[N=5,7\cdot {10}^{-8}\cdot {\left(1500\right)}^4\cdot 1=2,9\cdot 10^5\left(Вт\right).\]

Ответ: $N=2,9\cdot 10^5Вт.$

Пример 2

Считая, что Солнце является черным телом, используя то, что его максимальная спектральная плотность энергетической светимости соответствует длине волны $500$нм, определить какова температура поверхности данной звезды.

Решение:

Для решения задачи используем закон смещения Вина:

\[{\lambda }_{max}T=b\left(2.1\right).\]

Выразим из него искомую температуру, получим:

\[T=\frac{b}{{\lambda }_{max}}\left(2.2\right).\]

Переведем длину волны света, соответствующую максимальной спектральной плотности энергетической светимости в систему СИ ${\lambda }_{max}=500\ нм=5\cdot {10}^{-7}м.$ Проведем вычисления:

\[T=\frac{2,9\cdot {10}^{-3}}{5\cdot {10}^{-7}}=5,8\cdot {10}^3\left(К\right).\]

Ответ: $T=5,8\cdot {10}^3K.$

spravochnick.ru