Формула идеального газа в химии
Определение и формулы идеального газа
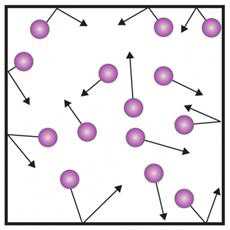
Допущения модели идеального газа:
- объём частиц газа пренебрежимо мал, молекулы – материальные точки;
- молекулы не взаимодействуют между собой, все столкновения абсолютно упругие;
- время взаимодействия между частицами газа пренебрежимо мало по сравнению со средним временем между столкновениями молекул.
К большинству реальных в довольно широком интервале температур и давлений применима модель идеального газа.
Формулы для идеального газа
Формула, связывающая макроскопические параметры идеального газа, называется уравнением состояния идеального газа или уравнением Менделеева Клапейрона :
где р – давление, Па; V – объем, м; m – масса (кг), T – абсолютная температура (К), R – универсальная газовая постоянная, R = 8,314 Дж/(моль • К), М – молярная масса газа (кг/моль).
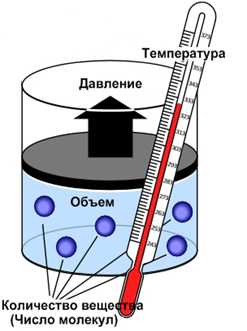
Если масса газа постоянна, то уравнение состояния можно записать в форме объединенного газового закона:
При постоянной температуре объединенный газовый закон переходит в уравнение Бойля Мариотта:
При постоянном давлении объединенный газовый закон переходит в уравнение Гей-Люссака:
При постоянном объеме объединенный газовый закон переходит в уравнение Шарля:
Основное уравнение молекулярно-кинетической теории идеального газа связывает давление газа и среднюю кинетическую энергию его частиц:
где n – число частиц газа в единице объема, m0 – масса одной частицы, υ – скорость частицы.
Средняя кинетическая энергия частиц и абсолютная температура газа связаны уравнением:
где k = 1,38 • 10−23 Дж/К – постоянная Больцмана.
Примеры решения задач
ru.solverbook.com
| Почему учителям и воспитателям следует проходить курсы повышения квалификации и профессиональной переподготовки в учебном центре «Инфоурок» ?• Огромный каталог: 677 курсов профессиональной переподготовки и повышения квалификации;• Очень низкая цена, при этом доступна оплата обучения в рассрочку – первый взнос всего 10%, оставшуюся часть необходимо оплатить до конца обучения; • Курсы проходят полностью в дистанционном режиме (форма обучения в документах не указывается); • Возможность оплаты курса за счёт Вашей организации. • Дипломы и Удостоверения от проекта «Инфоурок» соответствуют всем установленным законодательству РФ требованиям. (Согласно ФЗ «Об образовании в Российской Федерации» от 2012 года). |
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда: 24 слайд 
Описание слайда: 
infourok.ru
8. Среднее давление и средняя температура газа
Среднее давление и средняя температура газа Когда участок газопровода выводится в ремонт (то есть изолируется от действующей части газопровода), то в нем устанавливается одинаковое по всей длине давление газа и одинаковая температура. Если же газопровод открыт на проход, то есть имеет место транспорт газа, то давление и температура в начале участка газопровода всегда будут больше, чем в конце.
Запас газа на участке действующего газопровода рассчитывается по той же формуле, которая приведена в четвертой заметке, но в качестве давления и температуры газа указываются средние значения этих параметров.
В расчете среднего давления газа нет ничего занимательного:
А теперь начинается занимательное. Среднюю температуру газа на действующем участке магистрального газопровода можно рассчитать по упрощенной формуле:
Формула применима только в том случае, если температура газа в конце участка газопровода выше температуры грунта. Кроме того, в этом выражении не учитывается эффект дросселирования, то есть дополнительного снижения температуры газа в конце участка газопровода в результате снижения давления.
Более точно рассчитать температуру газа (с учетом эффекта дросселирования и в том числе для ситуаций, когда температура газа в конце трубы ниже, чем температура грунта) можно с помощью выражения:
В случае использования этой формулы расчет, как и при стравливании газа при критическом истечении, замыкается сам на себя, потому что:
Чтобы рассчитать среднюю температуру газа, необходимо знать среднюю теплоемкость газа. Для расчета средней теплоемкости газа необходимо знать среднюю температуру газа. Но не все так запущено, как кажется.
Этот нелинейный расчет можно выполнить по следующему алгоритму:
· По упрощенной формуле рассчитать предположительное значение средней температуры газа. Если температура газа в конце трубы ниже, чем температура грунта – средней температурой считать температуру газа в конце участка газопровода;
· Рассчитать теплоемкость газа и коэффициент теплопередачи;
· По точной формуле рассчитать среднюю температуру газа.
Для повышения точности расчета последние два пункта следует выполнить еще раз.
Я не реализовывал в онлайн-калькуляторе расчет средних значений давления и температуры газа на отдельной странице, но как составная часть более сложного расчета похожий алгоритм используется при определении пропускной способности участка магистрального газопровода и коэффициента гидравлической эффективности.
Кстати, расчет коэффициента гидравлической эффективности – тема следующей заметки.
gascount.livejournal.com
Зависимость функции распределения Максвелла от массы и температуры газа
Если у нас смесь газов, то в пределах каждого сорта газа будет своё распределение со своим m
f (υв )Tm , кроме тогоυв Tm .
Можно проследить за изменением f(υ) при
изменении m иT:m1>m2>m3 (T=const) илиT1>T2>T3 (m=const) (рис. 13.5). Площадь под кривойf(υ)=const=1
поэтому важно знать как будет изменяться положение максимальной кривой.
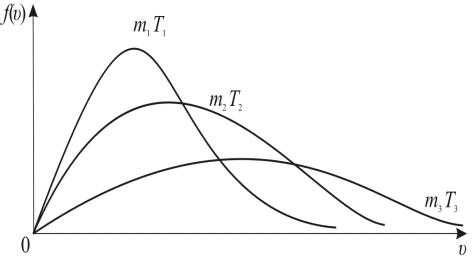
Рис. 13.5
Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. Закон статически и выполняется тем лучше, чем больше число молекул.
Формула Максвелла для относительных скоростей
Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена в относительных единицах. Относительную
U υ (13.23)
υв
|
|
|
| dn |
| 4 |
|
| |
где υв | 2kТ | . Тогда |
|
| e U 2U2 | ||||
| ndU |
|
|
| |||||
m |
| π | |||||||
|
|
|
|
| (13.24) | ||||
Это уравнение универсальное. В таком виде функция распределения не зависит ни от рода газа ни от температуры.
4. Барометрическая формула
Рассмотрим ещё один вероятный закон очень важно.
Атмосферное давление на какой-либовысотеh обусловлено весом выше лежащих слоёв газа. Пустьp
– давление на высоте h,p+Δp – на высотеh+Δh (рис. 13.6). Причёмdh>0,dр<0, так как на большой высоте давление меньше. Разность давленияp–(p+dp)равна весу газа, заключённого в объёме цилиндра с площадью основания равного единице и высотойdh,p=ρqh, медленно убывает с высотой.
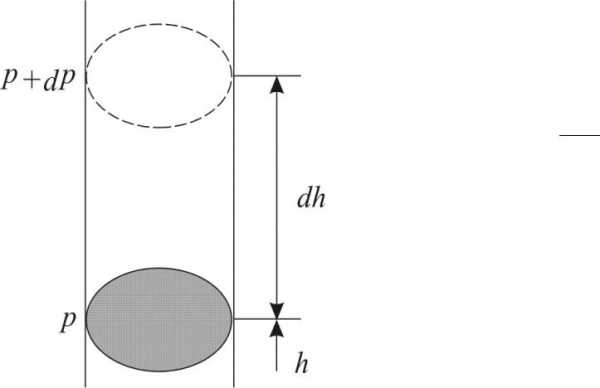
p–(p+dp)=ρqdh, (13.25) ρплотность газа на высоте h, тогда
μgh
p p0e RT , (13.26) гдер0 – давление на высоте
h=0.
Это барометрическая формула. Из формулы следует, что р убывает с высотой
тем быстрее, чем тяжелее газ Рис. 13.6 (чем большеμ) и чем ниже
температура.
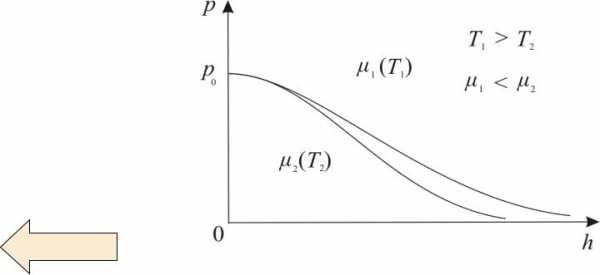
На больших высотах концентрация Не и Н2
гораздо больше чем у поверхности Земли. На (рис. 13.7) изображены две кривые, которые можно трактовать либо как соответствующие разным μ (при одинаковойТ) либо как отвечающие разнымТ (при одинаковыхμ), то есть чем тяжелее газ и чем ниже температура, тем быстрее убывает давление.
Cодержание | Рис. 13.7 |
|
5. Распределение Больцмана
Нам известна формула р=nkT – это основное уравнение МКТ (p0=nkT), заменимp иp0 в
барометрической формуле на n иn0. |
| |||||
Получим |
|
| μgh |
|
| |
n n e | RT , | (13.27) | ||||
|
| |||||
| 0 |
|
|
| ||
где n0 число молекул в единице объёма на высоте
h=0,n – число молекул в единице объёма на высотеh. | ||
Так как μ=mNА,R=NАk, то | mgh |
|
n n0e |
| |
kT . | (13.28) | |
Модель: Распределение Больцмана
С уменьшением температуры число молекул на высотах, отличных от нуля убывает. При Т=0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так какmgh – это потенциальная энергия, то на разных высотахWn=mgh – различно. Следовательно (13.28)
характеризует распределение частиц по значениям | ||
потенциальной энергии: | Wn |
|
n n e |
| |
kT | (13.29) | |
0 |
| |
– это функция распределения Больцмана.
Здесь n0 – число молекул в единице объёма в том месте, гдеWn=0. Пустьn/n0– доля молекул, обладающих именно таким значением потенциальной энергииWn при
данной температуре, тогда |
|
|
|
| |||||||
| n1 |
|
| Wп | Wп | 2 |
|
|
|
|
|
| e |
| 1 |
|
|
|
|
|
| ||
| kТ |
| – отношение концентраций молекул в | ||||||||
|
|
| |||||||||
| n |
| |||||||||
|
|
|
|
| точках с W | п1 | и W | п2 | . | ||
2 |
|
|
|
|
|
|
|
| |||
Больцман доказал, что соотношение (13.29) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.
Итак, Максвелл дал распределение частиц по значениям кинетической энергии, а Больцман – по значениям потенциальной энергии. Оба распределения можно объёдинить в один закон – распределение Максвелла–Больцмана.
studfiles.net