Закон всемирного тяготения формула Ньютона
Аристотель утверждал, что массивные предметы падают на землю быстрее лёгких.
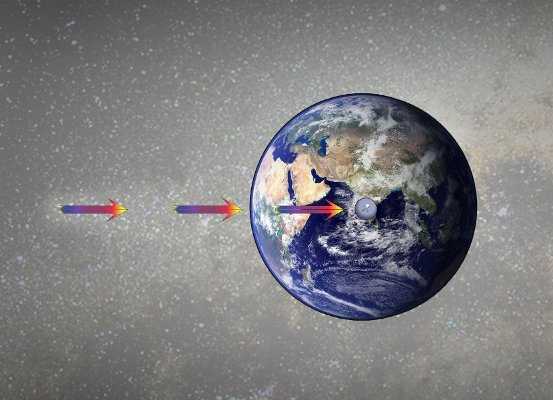
Ньютон предположил, что Луну следует рассматривать как снаряд, который движется по искривленной траектории, поскольку на него действует земное тяготение. Поверхность Земли тоже искривлена, так что при достаточно быстром движении снаряда его искривленная траектория будет следовать за кривизной Земли, и он станет «падать» вокруг планеты. Если увеличить скорость снаряда, его траектория вокруг Земли вытянется в эллипс.Галилей в начале XVII века показал, что все предметы падают «одинаково». И примерно в то же время Кеплер задумывался, что заставляет планеты двигаться по своим орбитам. Быть может, это магнетизм? Исаак Ньютон, работая над «Математическими началами», свел все эти движения к действию единой силы, называемой гравитацией, которая подчиняется простым универсальным законам.
Галилей экспериментально показал, что путь, пройденный телом, падающим под действием гравитации, пропорционален квадрату времени падения: шар, падающий в течение двух секунд, пройдет вчетверо больший путь, чем такой же предмет в течение одной секунды. Также Галилей показал, что скорость прямо пропорциональна времени падения, и вывел отсюда, что пушечное ядро летит по параболической траектории — одному из видов конических сечений, как и эллипсы, по которым, согласно Кеплеру, движутся планеты. Но откуда эта связь?
Когда в середине 1660-х годов Кембриджский университет закрылся на время Великой эпидемии чумы, Ньютон вернулся в семейную усадьбу и там сформулировал свой закон тяготения, хотя и держал его потом в тайне еще 20 лет. (Историю об упавшем яблоке никто не слыхал, пока восьмидесятилетний Ньютон не рассказал эту байку после большого званого ужина.)
Он предположил, что все предметы во Вселенной порождают гравитационную силу, притягивающую другие объекты (подобно тому, как яблоко притягивается к Земле), и эта самая сила гравитации определяет траектории, по которым движутся в космосе звезды, планеты и другие небесные тела.
Яблоко Ньютона

На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения, он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.
Закон обратных квадратов
Ньютон сумел рассчитать величину ускорения Луны под влиянием земной гравитации и нашел, что она в тысячи раз меньше, чем ускорение предметов (того же яблока) вблизи Земли. Как такое может быть, если они движутся под действием одной и той же силы?
Объяснение Ньютона состояло в том, что сила тяготения ослабевает с расстоянием. Объект на поверхности Земли в 60 раз ближе к центру планеты, чем Луна. Притяжение на орбите Луны составляет 1/3600, или 1/602, от того, что действует на яблоко. Таким образом, сила притяжения между двумя объектами — будь это Земля и яблоко, Земля и Луна или Солнце и комета — обратно пропорциональна квадрату разделяющего их расстояния. Удвойте расстояние, и сила уменьшится вчетверо, утройте его — сила станет меньше в девять раз и т. д. Сила также зависит от масс объектов — чем больше масса, тем сильнее гравитация.
Закон всемирного тяготения можно записать в виде формулы:
F = G(Mm/r2).
Где: сила гравитации равна произведению большей массы M и меньшей массы m, деленному на квадрат расстояния между ними r2
Эта постоянная определяет притяжение между любыми двумя массами в любой точке Вселенной. В 1789 году ее использовали для вычисления массы Земли (6·1024 кг). Законы Ньютона замечательно предсказывают силы и движения в системе из двух объектов. Но при добавлении третьего всё значительно усложняется и приводит (спустя 300 лет) к математике хаоса.
posmotrim.by
Какая сила тяжести в центре земли? Есть ли там невесомость?
Оглавление. X OВведение
Как мы знаем, массивные тела притягивают другие тела посредством гравитации. Сила тяжести зависит от массы притягивающего тела и расстояния от него. Чем больше масса — тем сильнее сила тяжести, чем больше расстояния до него — тем слабее. Поэтому яблоки падают на землю (большое массивное тело), а не на Луну (правда с Луной большую роль играет расстояние, а не масса). Луна тоже массивное тело, но она дальше от нас, чем Земля. Многие на этом останавливаются, и думают, что обычно так всегда — чем ближе к центру Земли, тем сила тяжести будет становиться больше
И так, чтобы понять что же на самом деле происходит с силой тяжести в центре земли нужно рассмотреть эти процессы поподробнее.
Простая школьная физика
Взглянем на то, как рассчитывают в школе силу тяжести — Землю считают за «материальную точку». И по формуле закона всемирного тяготения считают.
Сила между двумя точками , сила притяжения одной точки . Где F — сила в Ньютонах (можно считать, что это ускорение свободного падения), m – масса тел, r – расстояние, G=6,67428*10^-11 (гравитационная постоянная).
Подставив в эту формулу значение высот (для примера возьмём высоту до луны, до МКС, до поверхности Земли, и 1 км от центра Земли), мы получим следующее:
| км | м | F (м/с) | примечания |
| 390771 | 390771000 | 0,0026108 | до Луны |
| 6754,5 | 6754500 | 8,7382816 | МКС |
| 6371 | 6371000 | 9,8219392 | средний радиус Земли |
| 1 | 1000 | 398668984 | на таком расстоянии скорость свободного падения больше скорости света 299792458 м/с |
Как видно из этих данных, странные числа у центра земли — бесконечность, не иначе! Но это нам говорили в школе — при очень близких расстояниях эта формула неправильно работает. По этому, мы получили числа, похожие на гравитацию возле чёрной дыры.
Если построить график по большему числу точек, то получится так: 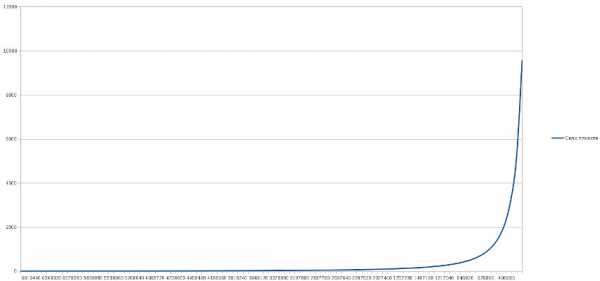
(на графике чем правее, тем ближе к центру Земли, синяя линия показывает силу тяжести)
Метод интерполяции
Тогда, как нам рассчитать силу тяжести в центре земли?
Простая формула для материальной точки не работает, потому что она не учитывает объёма физического тела, а работает лишь с точками. Однако, мы можем использовать эту формулу, если заменим одну материальную точку, представляющую Землю, «облаком» точек. Упрощённо, это всё равно, что поделить землю на несколько частей (как пиццу, или пирог). В этом случае мы не будем приближаться столь близко к одной точке, а вся масса Земли будет распределена равномерно.



Для лучшей точности нужно разбить Землю не на 8 частей, а на 100 и более, и не в плоскости, а в трёх измерениях (x, y, z). Конечно, в ручную я не собираюсь считать так много уравнений, заставим считать компьютер 🙂
Реальная сила тяжести
Теперь, когда компьютер посчитал силу тяжести по 1000000 материальным точкам, можно взглянуть на результаты в виде графика. 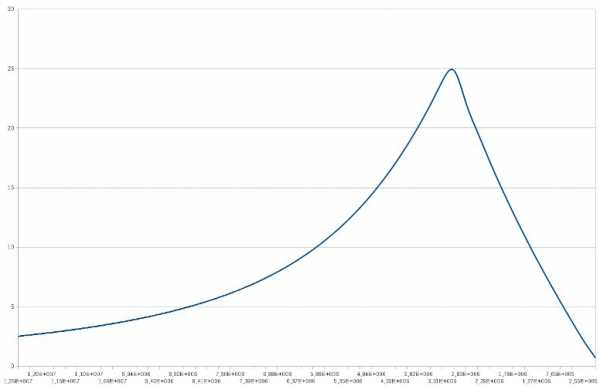
(на графике чем правее, тем ближе к центру Земли, синяя линия показывает силу тяжести)
Как мы видим, сила тяжести всё возрастает и возрастает, а ближе к центру земли, резко уменьшается. Из этих данных можно сделать вывод, что в центре земли — невесомость!
Другие методы решения
В нашем методе есть два недостатка: во-первых долго рассчитывать, и во-вторых он не очень уж точный. Гораздо лучше воспользоваться другими методами: воспользоваться чем-то вроде интегралов или дифференциалов. Но, для понимания, почему в центре земли — невесомость, вышеизложенного вполне достаточно, и такой метод наглядно показывает, почему так происходит.
В описанном методе погрешности можно уменьшить, взяв большее количество материальных точек. В данном расчёте на погрешности влияли:
- Количество точек и расстояние между ними — чем больше точек, тем меньше погрешность интерполяции. Например, с одной материальной точкой мы бы так и не смогли понять, какая сила тяжести в центре земли.
- Не учтена центробежная сила — вращение Земли вокруг своей оси (а так же солнца, силы взаимодействия луны и так далее, что могло бы уменьшить «силу тяжести» в плоскости экватора, точнее вес, так как он бы складывался из силы тяжести, притягивающей к земле и центробежной силы, «отталкивающей» от земли.
- Строение земли и плотности Земных пород — как минимум нужно учесть плотность разных геосфер. Даже в разных частях земли сила тяжести разная
- Прочие погрешности: точность вычислений, точность исходных данных и так далее (но их влияние настолько мало, что ими можно пренебречь).
Заключение
Не смотря на то, что в центре земли, как мы поняли, невесомость, но давление там очень большое.
Для чего это может пригодиться? Говорят про перемещение сквозь землю типа «лифтов» – здесь можно точнее рассчитать скорость и время для такого перемещения. Можно найти «киноляпы» в фильмах, в которых путешествуют к центру земли. А так же, просто показать, как, иногда, при помощи простой формулы, не работающей со сложными объектами можно применив разделение большого объекта на части и интерполяцию применять её к более сложным объектам.
Попробую сделать небольшое дополнение в скором времени, чтобы вы могли поиграться с графиками прямо на моём сайте.
alexeyk.com
Чему равна гравитационная постоянная? :: SYL.ru
После изучения курса физики в головах у учащихся остаются всевозможные постоянные и их значения. Тема гравитации и механики не становится исключением. Чаще всего ответить на вопрос о том, какое значение имеет гравитационная постоянная, они не могут. Но всегда однозначно ответят, что она присутствует в законе всемирного тяготения.
Из истории гравитационной постоянной
Интересно, что в работах Ньютона нет такой величины. Она появилась в физике существенно позже. Если быть конкретнее, то только в начале девятнадцатого века. Но это не значит, что ее не было. Просто ученые ее не определили и не узнали ее точное значение. Кстати, о значении. Гравитационная постоянная постоянно уточняется, поскольку является десятичной дробью с большим количеством цифр после запятой, перед которой стоит ноль.
Именно тем, что эта величина принимает такое маленькое значение, объясняется то, что действие сил гравитации незаметно на небольших телах. Просто из-за этого множителя сила притяжения оказывается ничтожно маленькой.
Впервые опытным путем установил значение, которое принимает гравитационная постоянная, физик Г. Кавендиш. И случилось это в 1788 году.

В его опытах использовался тонкий стержень. Он был подвешен на тоненькой проволоке из меди и имел длину около 2 метров. К концам этого стержня были прикреплены два одинаковых свинцовых шара диаметром 5 см. Рядом с ними были установлены большие свинцовые шары. Их диаметр был уже 20 см.
При сближении больших и маленьких шаров наблюдался поворот стержня. Это говорило об их притяжении. По известным массам и расстоянию, а также измеренной силе закручивания удалось достаточно точно узнать, чему равно гравитационное постоянное.
А началось все со свободного падения тел
Если поместить в пустоту тела разной массы, то они упадут одновременно. При условии их падения с одинаковой высоты и его начала в один и тот же момент времени. Удалось рассчитать ускорение, с которым все тела падают на Землю. Оно оказалось приблизительно равно 9,8 м/с2.
Ученые установили, что сила, с которой все притягивается к Земле, присутствует всегда. Причем это не зависит от высоты, на которую перемещается тело. Один метр, километр или сотни километров. Как бы далеко ни находилось тело, оно будет притягиваться к Земле. Другой вопрос в том, как ее значение будет зависеть от расстояния?
Именно на этот вопрос нашел ответ английский физик И. Ньютон.
Уменьшение силы притяжения тел с их отдалением
Для начала он выдвинул предположение о том, что сила тяжести убывает. И ее значение находится в обратной зависимости от расстояния, возведенного в квадрат. Причем это расстояние нужно отсчитывать от центра планеты. И провел теоретические расчеты.
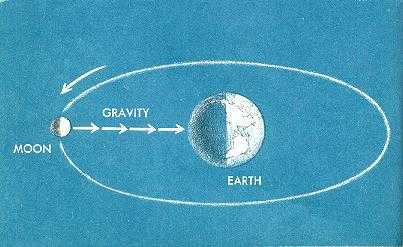
Потом этот ученый воспользовался данными астрономов о движении естественного спутника Земли — Луны. Ньютон рассчитал, с каким ускорением она вращается вокруг планеты, и получил те же результаты. Это свидетельствовало о правдивости его рассуждений и позволило сформулировать закон всемирного тяготения. Гравитационная постоянная в его формуле пока отсутствовала. На этом этапе было важно определить зависимость. Что и было сделано. Сила тяжести уменьшается обратно пропорционально расстоянию от центра планеты, возведенному в квадрат.
К закону о всемирном тяготении
Ньютон продолжил размышления. Поскольку Земля притягивает Луну, то и она сама должна притягиваться к Солнцу. Причем сила такого притяжения тоже должна подчиняться описанному им закону. А потом Ньютон распространил его на все тела вселенной. Поэтому и название закона включает слово «всемирное».
Силы всемирного тяготения тел определяются как пропорционально зависящие от произведения масс и обратные квадрату расстояния. Позже, когда был определен коэффициент, формула закона приобрела такой вид:
- Fт = G (m1 *х m2) : r2.
В ней введены такие обозначения:
| Сила тяготения | Fт |
| Гравитационная постоянная | G |
| Массы тел | m1, m2 |
| Расстояние между телами | r |
Формула гравитационной постоянной вытекает из этого закона:
- G = (Fт Х r2) : (m1 х m2).
Значение гравитационной постоянной
Теперь настал черед конкретных чисел. Поскольку ученые постоянно уточняют это значение, то в разные годы были официально приняты разные числа. К примеру, по данным за 2008 год гравитационная постоянная равна 6,6742 х 10-11 Нˑм2/кг2. Прошло три года – и константу пересчитали. Теперь гравитационная постоянная равна 6,6738 х 10-11 Нˑм2/кг2. Но для школьников в решении задач допустимо ее округление до такой величины: 6,67 х 10-11 Нˑм2/кг2.
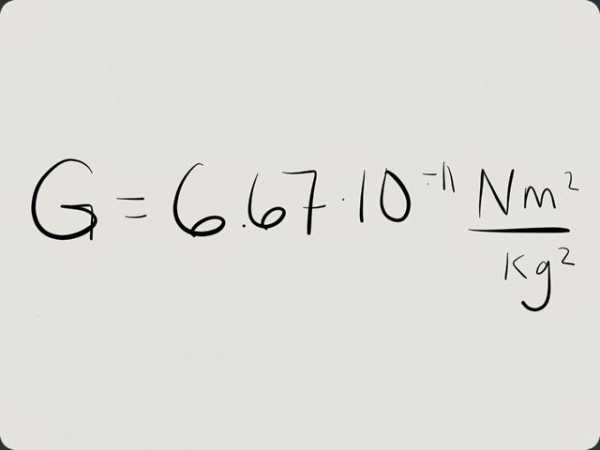
В чем физический смысл этого числа?
Если в формулу, которая дана для закона всемирного тяготения, подставить конкретные числа, то получится интересный результат. В частном случае, когда массы тел равны 1 килограмму, а расположены они на расстоянии 1 метра, сила тяготения оказывается равной самому числу, которое известно для гравитационной постоянной.
То есть смысл гравитационной постоянной заключается в том, что она показывает, с какой силой будут притягиваться такие тела на расстоянии одного метра. По числу видно, насколько мала эта сила. Ведь она в десять миллиардов меньше единицы. Ее даже невозможно заметить. Даже при увеличении тел в сотню раз результат существенно не изменится. Он по-прежнему останется гораздо меньше единицы. Поэтому становится понятно, отчего сила притяжения заметна только в тех ситуациях, если хотя бы одно тело имеет огромную массу. Например, планета или звезда.

Как связана гравитационная постоянная с ускорением свободного падения?
Если сравнить две формулы, одна из которых будет для силы тяжести, а другая для закона тяготения Земли, то можно увидеть простую закономерность. Гравитационная постоянная, масса Земли и квадрат расстояния от центра планеты составляют коэффициент, который равен ускорению свободного падения. Если записать это формулой, то получится следующее:
Причем в ней используются такие обозначения:
| Масса Земли | M |
| Радиус Земли | r |
Кстати, гравитационную постоянную можно найти и из этой формулы:
Если требуется узнать ускорение свободного падения на некоторой высоте над поверхностью планеты, то пригодится такая формула:
- g = (G х M) : (r + н)2, где н — высота над поверхностью Земли.
Задачи, в которых требуется знание гравитационной постоянной
Задача первая
Условие. Чему равно ускорение свободного падения на одной из планет Солнечной системы, например, на Марсе? Известно, что его масса 6,23·1023 кг, а радиус планеты 3,38·106 м.
Решение. Нужно воспользоваться той формулой, которая была записана для Земли. Только подставить в нее значения, данные в задаче. Получится, что ускорение свободного падения будет равно произведению 6,67 х 10-11 и 6,23 х 1023, которое потом нужно разделить на квадрат 3,38·106. В числителе получается значение 41,55 х 1012. А в знаменателе будет 11,42 х 1012. Степени сократятся, поэтому для ответа достаточно только узнать частное двух чисел.
Ответ: 3,64 м/с2.

Задача вторая
Условие. Что нужно сделать с телами, чтобы уменьшить их силу притяжения в 100 раз?
Решение. Поскольку массу тел изменять нельзя, то сила будет уменьшаться за счет удаления их друг от друга. Сотня получается от возведения в квадрат 10. Значит, расстояние между ними должно стать в 10 раз больше.
Ответ: отдалить их на расстояние, превышающее изначальное в 10 раз.
www.syl.ru
