Определение и формула: Что называется механическое движение

В школе, наверное, все помнят то, что называется механическим движением тела. Если нет, то эта статья будет стараться не только запомнить этот термин, но, чтобы освежить базовые знания из физики, а из раздела “Классическая механика”. Также будут показаны примеры, в которых это понятие используется не только в конкретной дисциплине, но и в других науках.
Механика
Для начала давайте рассмотрим, что обозначает это понятие. Механика-это отрасль физики, которая изучает движение различных тел, взаимодействие между ними, а также влияние третьих сил тела и явления. Движение автомобиля по трассе, положил мои ноги в ворота футбольный мяч, идущий на посадку самолет, он был изучен по этой дисциплине. Обычно, используя термин “механика”, вы имеете в виду “классическую механику”. Что это такое, мы рассмотрим с вами ниже.

Классическая механика состоит из трех основных разделов.

Очень часто в классической механике называется Ньютоновской, потому что она базируется на трех законах Ньютона.
Три закона Ньютона
Впервые их описал Исаак Ньютон в 1687 году.

Все три закона являются аксиомами. Другими словами, это постулаты, не требующие доказательств.
Что называется механическим движением
Это изменение положения тела в пространстве относительно других тел с течением времени. Материальной точки, таким образом, взаимодействуют по законам механики.
Подразделяется на несколько видов:
- Движение материальной точки измеряется путем поиска его координат и отслеживания координат меняется со временем. Чтобы найти эти цифры, то вычисления значений по осям абсцисс и ординат. Настоящее исследование посвящено кинематике точки, которая оперирует такими понятиями, как траектория, перемещение, ускорение, скорость. Движение объекта может быть прямолинейной и криволинейной.
- Движение твердого тела состоит из движущейся точки, хотя, и вращательное движение вокруг нее. Изучается кинематикой твердого тела. движение может быть поступательным, то есть, вращение вокруг заданной точки не происходит, и все тело движется равномерно, и плоским, если все тело движется параллельно плоскости.
- Существует также движение сплошной среды. Это движение большое количество точек, связанных только в любой сфере. Из-за многих движущихся тел (или материальных точек) в одной системе координат не хватает. Так как много тел, так много систем координат. Примером могут служить волны на море. Он является непрерывным, а состоит из большого числа отдельных точек на различных системах координат. Получается, что волновое движение движение сплошной среды.
Относительность движения
Есть такое понятие в механике, как относительность движения. Это влияние какой-либо системы отсчета механического движения. Как это понимать? Системой отсчета является система координат плюс часы, чтобы определить время. Проще говоря, это ось абсцисс и ординат в сочетании с минут. С помощью такой системы определяется, за какой период времени материальная точка совершил указанное расстояние. Другими словами, перемещается относительно осей или других органов.

Справочные системы может быть связано, инерциальные и неинерциальные. Объясняю:
- Инерциальная со-это система, где тело, производя то, что называется механическое движение материальной точки, делать это равномерно или даже в покое.
- Соответственно, с неинерциальной системе, движущейся с ускорением или поворотом по отношению к первой.
- И связанные с это система, которая, вместе с материальной точкой, совершает то, что называется механическим движением тела. Иными словами, где и как быстро объект движется, перемещается вместе с ним и этот.
Материальная точка
Почему иногда используют понятие “тело”, а иногда “материальная точка”? Во втором случае указывается, когда Размер объекта можно пренебречь. То есть такие параметры, как масса, объем и т. д. не имеют значения для решения задачи. Например, если цель состоит в том, чтобы выяснить, с какой скоростью пешеход движется относительно земли, то вес и рост пешехода можно пренебречь. Это материальная точка. Механическое движение этого объекта не зависит от его параметров.
Понятия и значения механического движения
Механики используют различные значения, которые определяют параметры, письменные задания и решения. Перечислите их.
- Изменение положение тела (или материальной точки) относительно пространства (или системы координат) с течением времени, называется перемещением. Механическое движение тела (материальной точки), по сути, синоним “движения”. Просто второй концепции, используемые в кинематике, и первый – в динамике. Разница между этими разделах было описано выше.
- Траектория-это линия, вдоль которой тело (материальная точка) делает то, что называется механическим движением. Его длина называется путь.
- Скорость-это скорость перемещения любой материальной точки (тела) относительно заданной системы отсчета. Доклад определение системы, приведенное выше.

Неизвестные используется для определения механического движения, в задачи находятся с помощью формулы: s=ц*т, где s-расстояние, U-это скорость, а T-время.
Из истории
Понятие “классическая механика” появилась в древние времена, привели к тому, что развивается быстрыми темпами строительства. Архимед сформулировал и описал правило рычага, теорема о сложении параллельных сил, введено понятие “центр тяжести”. Так я представляю себе статики.

Благодаря Галилею, в 17 веке начали развиваться “Динамика”. Закон инерции и принцип относительности-это его заслуга.
Исаак Ньютон, как уже упоминалось выше, ввел три закона, которые легли в основу механики Ньютона. Он также открыл закон всемирного тяготения. Так были заложены основы классической механики.
Неклассическая механика
С развитием физики как науки, а с появлением больших возможностей в области астрономии, химии, математики, и других классической механики постепенно становится не главным, но одним из многих востребованных наук. Когда активно начали вводить и оперировать такими понятиями как скорость света, квантовая теория поля и так далее, законы, лежащие в основе “механики”, не было достаточно.
Квантовая механика-это раздел физики, который занимается изучением ультра-низких тел (материальных точек) в виде атомов, молекул, электронов и фотонов. Эта дисциплина описывает очень хорошо свойства ультра-мелких частиц. Кроме того, он прогнозирует их поведение в той или иной ситуации, а также в зависимости от последствий. Предсказания квантовой механики могут быть очень разными из допущений классической механики, со второй не способна описать все явления и процессы, происходящие на уровне молекул, атомов и прочих очень мелкие и невидимые невооруженным глазом.
Релятивистская механика-раздел физики, занимающийся изучением процессов, явлений и законов, на скорости, сравнимой со скоростью света. Все события, которые изучают эту дисциплину происходят в четырехмерном пространстве, в отличие от классической трехмерной. То есть высота, ширина и длина, мы добавляем еще одно измерение – время.
Какое определение механического движения
Мы рассмотрели лишь основные понятия, связанные с физикой. Но термин используется не только в механике, будь то классическая или неклассическая.
В науке под названием “Социально-экономическая статистика” определение механического движения населения как миграция. Иными словами, это движение людей на большие расстояния, например, в соседних странах или на других континентах с целью смены места жительства. Причин для этого может быть невозможность продолжать жить на своей территории из-за природных катаклизмов, например, постоянные наводнения или засухи, экономических и социальных проблем в государстве, равно как и вмешательство внешних сил, таких как война.

В данной статье описывается то, что называется механическим движением. Приводятся примеры не только из физики, но и из других наук. Это означает, что этот термин многозначен.
Источник картинок – http://fb.ru/
образования за рубежом сам прочти и все поймешь
urok.pw
Механические колебания: определения, формулы и решения
Механические колебания – это периодически повторяющиеся механические движения. Например: звук, вибрация или колебания математического маятника.
Колебаниям присущи определенные характеристики:
- Амплитуда. Размах, максимальное отклонение от точки равновесия.
- Частота. Периодичность, повторяемость за единицу времени.
- Период. Время, которое требуется для одного колебания.
Если обозначить частоту буквой v, то связь между ним и периодом, будет выражаться следующей формулой:
Частота измеряется в герцах, в честь немецкого ученого Генриха Герца. Один герц означает выполнение одного колебания или процесса за секунду.
Гармонические колебания
Одним из важных видов колебаний являются так называемые гармонические колебания. Это те колебания, которые изменяются по гармонические закону, то есть их можно представить в виде функции, где значение определяется как синус (или косинус) от аргумента.
Координаты тела, совершающего колебания в такой системе, в общем виде будут выражены следующим образом:
Где:
Х(t) – значение колеблющейся величины x, в момент времени t.
A – максимальное смещение от точки равновесия, амплитуда колебаний.
w – циклическая частота, число колебаний за П2 сек.
ε0 – начальная фаза колебания.
Любые другие колебания, можно представить как сумму гармонических колебаний.
Примером таких колебаний, может служить математический маятник:
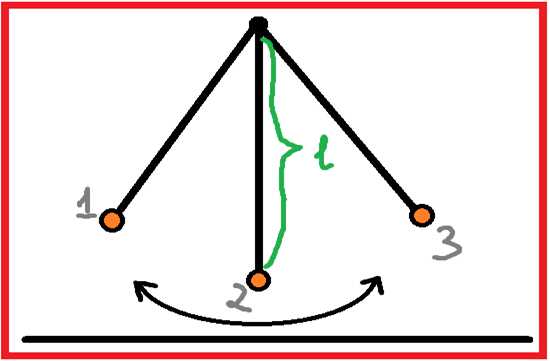
Это грузик, закрепленный на нити. Если чуть отведя в сторону из положения 1, отпустить грузик, то он начнёт совершать движение туда и обратно. Период колебаний маятника T, можно определить исходя из формулы:
Где:
L ¬– длина нити.
g – ускорение свободного падения.
П – число Пи.
Следует обратить внимание, что период зависит только от длины маятника.
Превращение энергии в колебательных сиcтемах
При колебаниях, кинетическая энергия переходит в потенциальную энергию.
Когда тело отклоняется на наибольшую величину от точки равновесия, потенциальная энергия максимальна, а кинетическая равна нулю.
По мере движения тела в положение равновесия, будет увеличиваться кинетическая энергия, так как увеличивается скорость.
В положении равновесия тело будет иметь минимальную потенциальную , чаще всего равное нулю, а кинетическая будет максимальной.
Рассмотрим это на примере механического маятника.

В точке 1, потенциальная энергия будет иметь наибольшее значение. По мере движения грузика до положения 2, она будет уменьшаться до наименьшего значения. Далее, при переходе тела от положения 2 к 3, будет уменьшаться кинетическая энергия, а потенциальная увеличиваться.
Суммарная энергия системы, будет оставаться неизменной, в какой бы точке не находилось тело, так как потерь энергии нет. Если увеличивается кинетическая энергия, то потенциальная уменьшается и наоборот.
fizikatyt.ru
Что называется механическим движением: определение и формула
Со школьной скамьи, наверное, все помнят, что называется механическим движением тела. Если нет, то в этой статье постараемся не только вспомнить этот термин, но и обновить базовые знания из курса физики, а точнее из раздела “Классической механики”. Также будут показаны примеры того, что это понятие употребляется не только в определенной дисциплине, но и в иных науках.
Механика
Для начала разберем, что обозначает это понятие. Механика – это раздел в физике, изучающий движение различных тел, взаимодействие между ними, а так же влияние на эти тела третьих сил и явлений. Движение автомобиля по шоссе, пущенный ударом ноги в ворота футбольный мяч, идущий на посадку самолет – все это изучается именно этой дисциплиной. Обычно, употребляя термин “Механика”, имеют в виду “Классическую механику”. Что это такое, мы разберем с вами ниже.

Классическую механику делят на три больших раздела.
- Кинематика – она изучает движение тел, не рассматривая вопроса, почему они движутся? Здесь интересуют такие величины, как путь, траектория, перемещение, скорость.
- Второй раздел – это динамика. Она изучает причины возникновения движения, оперируя такими понятиями, как работа, сила, масса, давление, импульс, энергия.
- И третий раздел, самый небольшой – это статика, изучающая такое состояние, как равновесие. Она делится на две части. Одна освещает равновесие твердых тел, а вторая – жидкостей и газов.

Очень часто классическую механику называют ньютоновой, ибо основывается она на трех законах Ньютона.
Три закона Ньютона
Впервые они были изложены Исааком Ньютоном в 1687 году.
- Первый закон гласит об инерции тела. Это свойство, при котором сохраняется направление и скорость движения материальной точки, если на него не действует никаких внешних сил.
- Второй закон утверждает, что тело, приобретая ускорение, совпадает с этим ускорением по направлению, но становится зависимым от своей массы.
- Третий закон утверждает, что сила действия всегда равна силе противодействия.

Все три закона являются аксиомами. Иными словами, это постулаты, которые не требуют доказательств.
Что называется механическим движением
Это изменение положения какого-либо тела в пространстве, относительно других тел с течением времени. Материальные точки при этом взаимодействуют по законам механики.
Подразделяется на несколько видов:
- Движение материальной точки измеряется с помощью нахождения ее координат и отслеживания изменений координат со временем. Найти эти показатели, значит вычислить значения по осям абсцисс и ординат. Изучением этого занимается кинематика точки, которая оперирует такими понятиями, как траектория, перемещение, ускорение, скорость. Движение объекта при этом может быть прямолинейное и криволинейное.
- Движение твердого тела складывается из перемещения какой-то точки, взятой за основу, и вращательного движения вокруг нее. Изучается кинематикой твердых тел. Перемещение может быть поступательным, то есть вращения вокруг заданной точки не происходит, и все тело движется равномерно, а также плоским – если все тело перемещается параллельно плоскости.
- Существует так же движение сплошной среды. Это перемещение большого количества точек, связанных только каким-либо полем или областью. Ввиду множества движущихся тел (или материальных точек) одной системы координат здесь недостаточно. Поэтому сколько тел, столько и систем координат. Примером тому может служить волна на море. Она – непрерывна, но состоит из большого количества отдельно взятых точек на множестве систем координат. Вот и получается, что движение волны – перемещение сплошной среды.
Относительность движения
Есть еще такое понятие в механике, как относительность движения. Это влияние какой-либо системы отсчета на механическое движение. Как это понимать? Система отсчета – это система координат плюс часы для определения времени. Проще говоря, это оси абсцисс и ординат в сочетании с минутами. Посредством такой системы определяется, за какой промежуток времени материальная точка проделала заданное расстояние. Иными словами, переместилось относительно оси координат или других тел.

Системы отсчета могут быть: сопутствующая, инерциальная и неинерциальная. Поясним:
- Инерциальная СО – это система, где тела, производя то, что называется механическим движением материальной точки, совершают это прямолинейно и равномерно либо вообще находятся в состоянии покоя.
- Соответственно, неинерциальная СО – система, движущаяся с ускорением или поворачивающаяся по отношению к первой СО.
- Сопутствующая же СО – это система, которая совместно с материальной точкой, совершает то, что называется механическим движением тела. Иными словами, куда и с какой скоростью перемещается объект, вместе с ним перемещается и данная СО.
Материальная точка
Почему иногда употребляется понятие “тело”, а иногда – “материальная точка”? Второй случай указывается, когда размерами самого объекта можно пренебречь. То есть такие параметры, как масса, объем и прочее, не имеют значения для решения возникшей задачи. Например, если цель состоит в том, чтобы узнать, с какой скоростью движется пешеход относительно планеты Земля, то ростом и весом пешехода можно пренебречь. Он является материальной точкой. Механическое движение этого объекта не зависит от его параметров.
Используемые понятия и величины механического движения
В механике оперируют различными величинами, с помощью которых задаются параметры, пишется условие задач и находится решение. Перечислим их.
- Изменение местоположения тела (или материальной точки) относительно пространства (или системы координат) с течением времени называется перемещение. Механическое движение тела (материальной точки), по сути дела, – это синоним к понятию “перемещение”. Просто второе понятие используют в кинематике, а первое – в динамике. Разница между этими подразделами была пояснена выше.
- Траектория – это линия, по которой тело (материальная точка) совершает то, что называется механическим движением. Ее длина называется путь.
- Скорость – это быстрота перемещения какой-либо материальной точки (тела), относительно заданной системы отчета. Определение системы отчета так же давалось выше.

Неизвестные величины, используемые для определения механического движения, в задачах находятся с помощью формулы: S=U*T, где “S” – расстояние, “U” – скорость, а “T” – время.
Из истории
Само понятие “классической механики” появилось еще в древности, и подтолкнуло к этому развивающееся быстрыми темпами строительство. Архимед сформулировал и описал правило рычага, теорему о сложении параллельных сил, ввел понятие “центр тяжести”. Так зачиналась статика.

Благодаря Галилею, в 17 веке стала развиваться “Динамика”. Закон инерции и принцип относительности – это его заслуга.
Исаак Ньютон, как уже говорилось выше, ввел три закона, которые легли в основу ньютоновой механики. Также он открыл закон всемирного тяготения. Так были заложены основы классической механики.
Неклассическая механика
С развитием физики, как науки, и с появлением больших возможностей в сферах астрономии, химии, математики и прочего классическая механика постепенно стала не основной, но одной из многих восстребованных наук. Когда активно стали вводить и оперировать такими понятиями, как скорость света, квантовая теория поля и так далее, законов, лежащих в основе “Механики”, стало не хватать.
Квантовая механика – это раздел физика, который занимается изучением сверхмалых тел (материальных точек) в виде атомов, молекул, электронов и фотонов. Эта дисциплина очень хорошо описывает свойства сверхмалых частиц. Помимо этого, она предсказывает их поведение в той или иной ситуации, а также в зависимости от воздействия. Предсказания, выполненные квантовой механикой, могут очень существенно отличаться от предположений классической механики, так как вторая не способна описать все явления и процессы, протекающие на уровне молекул, атомов и прочего – очень маленького и невидимого невооруженным глазом.
Релятивистская механика – это раздел физики, занимающийся изучением процессов, явлений, а так же законов при скоростях, сопоставимых со скоростью света. Все события, изучаемые этой дисциплиной, происходят в четырехмерном пространстве, в отличие от “классического” – трехмерного. То есть к высоте, ширине и длине мы прибавляем еще один показатель – время.
Какое еще бывает определение механического движения
Мы рассмотрели только базовые понятия, связанные с физикой. Но сам термин употребляется не только в механике, будь то классическая или неклассическая.
В науке под названием “Социально-экономическая статистика” определение механического движения населения дается, как миграция. Иными словами, это перемещение людей на большие расстояния, например, в соседние страны или на соседние континенты с целью смены места жительства. Причинами такого перемещения могут быть, как невозможность продолжать жить на своей территории из-за природных катаклизмов, например, постоянные наводнения или засуха, экономических и социальных проблем в своем государстве, так и вмешательство внешних сил, например, война.

В этой статье рассмотрено то, что называется механическим движением. Примеры приведены не только из физики, но и из других наук. Это указывает на то, что термин является многозначным.
fb.ru
Работа и мощность силы – основные понятия и определения.
Работа, мощность, энергия
Работа постоянной силы на прямолинейном участке
Рассмотрим материальную точку М, к которой приложена сила F. Пусть точка переместилась из положения М0 в положение М1, пройдя путь s (рис. 1).
Чтобы установить количественную меру воздействия силы F на пути s, разложим эту силу на составляющие N и R, направленные соответственно перпендикулярно направлению перемещения и вдоль него. Так как составляющая N (перпендикулярная перемещению) не может двигать точку или сопротивляться ее перемещению в направлении s, то действие силы F на пути s можно определить произведением Rs.
Эта величина называется работой и обозначается W.
Следовательно,
W = Rs = Fs cos α,
т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки.
Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении.
Работа является скалярной величиной.
Рассматривая работу силы, можно выделить три частных случая: сила направлена вдоль перемещения (α = 0˚), сила направлена в противоположном перемещению направлении (α = 180˚), и сила перпендикулярна перемещению (α = 90˚).
Исходя из величины косинуса угла α, можно сделать вывод, что в первом случае работа будет положительной, во втором – отрицательной, а в третьем случае (cos 90˚ = 0) работа силы равна нулю.
Так, например, при движении тела вниз работа силы тяжести будет положительной (вектор силы совпадает с перемещением), при подъеме тела вверх работа силы тяжести будет отрицательной, а при горизонтальном перемещении тела относительно поверхности Земли работа силы тяжести будет равна нулю.
Силы, совершающие положительную работу, называются движущимися силами, силы, а совершающие отрицательную работу – силами сопротивления.
Единицей работы принят джоуль (Дж):
1 Дж = сила×длина = ньютон×метр = 1 Нм.
Джоуль – это работа силы в один ньютон на пути в один метр.
***
Работа силы на криволинейном участке пути
На бесконечно малом участке ds криволинейный путь можно условно считать прямолинейным, а силу – постоянной.
Тогда элементарная работа dW силы на пути ds равна
dW = F ds cos (F,v).
Работа на конечном перемещении равна сумме элементарных работ:
W = ∫ F cos (F,v) ds.
На рисунке 2а изображен график зависимости между пройденным расстоянием и F cos (F,v). Площадь заштрихованной полоски, которую при бесконечно малом перемещении ds можно принять за прямоугольник, равна элементарной работе на пути ds:
dW = F cos (F,v) ds,
а работа силы F на конечном пути s графически выражается площадью фигуры ОАВС, ограниченной осью абсцисс, двумя ординатами и кривой АВ, которая называется кривой сил.
Если работа совпадает с направлением перемещения и возрастает от нуля пропорционально пути, то работа графически выражается площадью треугольника ОАВ (рис. 2 б), которая, как известно, может быть определена половиной произведения основания на высоту, т. е. половиной произведения силы на путь:
W = Fs/2.
***
Теорема о работе равнодействующей
Теорема: работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том же участке пути.
Пусть к материальной точке М приложена система сил (F1, F2, F3,…Fn), равнодействующая которых равна FΣ (рис. 3).
Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,
FΣ = F1 + F2 + F3 + …. + Fn.
Спроецируем это векторное равенство на касательную к траектории, по которой движется материальная точка, тогда:
FΣ cos γ = F1 cos α1 + F2 cos α2 + F3 cos α3 + …. + Fn cos αn.
Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем полученное равенство в пределах какого-то конечного перемещения s:
∫ FΣ cos γ ds = ∫ F1 cos α1 ds + ∫ F2 cos α2 ds + ∫ F3 cos α3 ds + …. + ∫ Fn cos αn ds,
что соответствует равенству:
WΣ = W1 + W2 + W3 + … + Wn
или сокращенно:
WΣ = ΣWFi
Теорема доказана.
***
Теорема о работе силы тяжести
Теорема: работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения.
Пусть материальная точка М движется под действием силы тяжести G и за какой-то промежуток времени перемещается из положения М1 в положение М2, пройдя путь s (рис. 4).
На траектории точки М выделим бесконечно малый участок ds, который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна.
Из заштрихованного треугольника получим, что
dy = ds cos α.
Элементарная работа силы G на пути ds равна:
dW = F ds cos α.
Полная работа силы тяжести G на пути s равна
W = ∫ Gds cos α = ∫ Gdy = G ∫ dy = Gh.
Итак, работа силы тяжести равна произведению силы на вертикальное перемещение точки ее приложения:
W = Gh;
Теорема доказана.
***
Пример решения задачи по определению работы силы тяжести
Задача: Однородный прямоугольный массив АВСD массой m = 4080 кг имеет размеры, указанные на рис. 5.
Определить работу, которую необходимо выполнить для опрокидывания массива вокруг ребра D.
Решение.
Очевидно, что искомая работа будет равна работе сопротивления, совершаемой силой тяжести массива, при этом вертикальное перемещение центра тяжести массива при опрокидывании через ребро D является путем, который определяет величину работы силы тяжести.
Для начала определим силу тяжести массива: G = mg = 4080×9,81 = 40 000 Н = 40 кН.
Для определения вертикального перемещения h центра тяжести прямоугольного однородного массива (он находится в точке пересечения диагоналей прямоугольника), используем теорему Пифагора, исходя из которой:
КО1 = ОD – КD = √(ОК2 + КD2) – КD = √(32 +42) – 4 = 1 м.
На основании теоремы о работе силы тяжести определим искомую работу, необходимую для опрокидывания массива:
W = G×КО1 = 40 000×1 = 40 000 Дж = 40 кДж.
Задача решена.
***
Работа постоянной силы, приложенной к вращающемуся телу
Представим себе диск, вращающийся вокруг неподвижной оси под действием постоянной силы F (рис. 6), точка приложения которой перемещается вместе с диском. Разложим силу F на три взаимно-перпендикулярные составляющие: F1 – окружная сила, F2 – осевая сила, F3 – радиальная сила.
При повороте диска на бесконечно малый угол dφ сила F совершит элементарную работу, которая на основании теоремы о работе равнодействующей будет равна сумме работ составляющих.
Очевидно, что работа составляющих F2 и F3 будет равна нулю, так как векторы этих сил перпендикулярны бесконечно малому перемещению ds точки приложения М, поэтому элементарная работа силы F равна работе ее составляющей F1:
dW = F1ds = F1Rdφ.
При повороте диска на конечный угол φ работа силы F равна
W = ∫ F1Rdφ = F1R ∫ dφ = F1Rφ,
где угол φ выражается в радианах.
Так как моменты составляющих F2 и F3 относительно оси z равны нулю, то на основании теоремы Вариньона момент силы F относительно оси z равен:
Мz(F) = F1R.
Момент силы, приложенной к диску, относительно оси вращения называется вращающим моментом, и, согласно стандарту ИСО, обозначается буквой Т:
Т = Мz(F), следовательно, W = Tφ.
Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловое перемещение.
***
Пример решения задачи
Задача: рабочий вращает рукоятку лебедки силой F = 200 Н, перпендикулярной радиусу вращения.
Найти работу, затраченную в течение времени t = 25 секунд, если длина рукоятки r = 0,4 м, а ее угловая скорость ω = π/3 рад/с.
Решение.
Прежде всего определим угловое перемещение φ рукоятки лебедки за 25 секунд:
φ = ωt = (π/3)×25 = 26,18 рад.
Далее воспользуемся формулой для определения работы силы при вращательном движении:
W = Tφ = Frφ = 200×0,4×26,18 ≈ 2100 Дж ≈ 2,1 кДж.
***
Мощность
Работа, совершаемая какой-либо силой, может быть за различные промежутки времени, т. е. с разной скоростью. Чтобы охарактеризовать, насколько быстро совершается работа, в механике существует понятие мощности, которую обычно обозначают буквой P.
Мощностью называется работа, совершаемая в единицу времени.
Если работа совершается равномерно, то мощность определяют по формуле
P = W/t.
Если направление силы и направление перемещения совпадают, что эту формулу можно записать в иной форме:
P = W/t = Fs/t или P = Fv.
Мощность силы равна произведению модуля силы на скорость точки ее приложения.
Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле:
P = W/t = Tφ/t или P = Tω.
Мощность силы, приложенной к равномерно вращающемуся телу, равна произведению вращающего момента на угловую скорость.
Единицей измерения мощности является ватт (Вт):
Ватт = работа/время = джоуль в секунду.
***
Понятие об энергии и КПД
Способность тела при переходе из одного состояния в другое совершать работу называется энергией. Энергия есть общая мера различных форм движения материи.
В механике для передачи и преобразования энергии применяются различные механизмы и машины, назначение которых – выполнение заданных человеком полезных функций. При этом энергия, передаваемая механизмами, называется механической энергией, которая принципиально отличается от тепловой, электрической, электромагнитной, ядерной и других известных видов энергии. Виды механической энергии тела мы рассмотрим на следующей странице, а здесь лишь определимся с основными понятиями и определениями.
При передаче или преобразовании энергии, а также при совершении работы, имеют место потери энергии, поскольку механизмы и машины, служащие для передачи или преобразования энергии преодолевают различные силы сопротивления (трения, сопротивления окружающей среды и т. п.). По этой причине часть энергии при передаче безвозвратно теряется и не может быть использована для выполнения полезной работы.
Коэффициент полезного действия
Часть энергии, потерянная при ее передаче на преодоление сил сопротивления, учитывается при помощи коэффициента полезного действия механизма (машины), передающего эту энергию.
Коэффициент полезного действия (КПД) обозначается буквой η и определяется, как отношение полезной работы (или мощности) к затраченной:
η = W2/W1 = P2/P1.
Если коэффициент полезного действия учитывает только механические потери, то его называют механическим КПД.
Очевидно, что КПД – всегда правильная дробь (иногда его выражают в процентах) и его значение не может быть больше единицы. Чем ближе значение КПД к единице (100 %), тем экономичнее работает машина.
Если энергия или мощность передаются рядом последовательных механизмов, то суммарный КПД может быть определен, как произведение КПД всех механизмов:
η = η1η2η3 ….ηn,
где: η1, η2, η3, …. ηn– КПД каждого механизма в отдельности.
***
Теоремы и законы динамики материальной точки
k-a-t.ru
