Формулы кинематики с пояснениями по физике / Блог :: Бингоскул
- Блог
- →
- Формулы кинематики с пояснениями по физике
Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S – путь
- v – скорость
- t – время
Равномерное движение
x=x_0 + v*t
- x – координата
- x0 – начальная координата
- v – скорость
- t – время
Равномерно ускоренное движение: ускорение
a=\frac{v – v_0}{t}
- a – ускорение
- v – скорость
- v0 – начальная скорость
- t – время
Равномерно ускоренное движение: скорость
v=v_0 + at
- v – скорость
- v0 – начальная скорость
- a – ускорение
- t – время
Равномерно ускоренное движение: путь
S=vt + \frac{at^2}{2}
- s – путь
- v – скорость
- t – время
- a – ускорение
Равномерно ускоренное движение: координата
x=x_0 + vt + \frac{at^2}{2}
- x – координата
- x0 – начальная координата
- v – скорость
- t – время
- a – ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_{0}t – \frac{gt^2}{2}
- h – высота
- h0 – начальная высота
- v0 – начальная скорость
- t – время
- g – ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 – gt
- v – скорость
- v0 – начальная скорость
- g – ускорение свободного падения
- t – время
Скорость, ускорение, время
v=at
- v – скорость
- a – ускорение
- t – время
Скорость свободно падающего тела
v=gt
- v – скорость
- g – ускорение свободного падения
- t – время
Центростремительное ускорение
a=\frac{v^2}{R}
- a – центростремительное ускорение
- v – скорость
- R – радиус
Угловая скорость
\omega=\frac{\phi}{t}
- ω – угловая скорость
- φ – угол
- t – время
Равномерное круговое движение
l=R\phi
- l – длина дуги окружности
- R – радиус
- φ – угол
Равномерное круговое движение: линейная скорость
v=R \omega
- v – линейная скорость
- R – радиус
- ω – угловая скорость
Период вращения
T=\frac{t}{N}
- T – период
- t – время
- N – число вращений
T=\frac{2 \pi R}{v}
- T – период
- R – радиус
- v – линейная скорость
T=\frac{2 \pi }{\omega}
- T – период
- ω – угловая скорость
Центростремительное ускорение
a=\frac{4 \pi^{2} R}{T^2}
- a – центростремительное ускорение
- R – радиус
- T – период вращения
a=4 \pi^{2} Rn^2
- a – центростремительное ускорение
- R – радиус
- n – частота вращения
Частота вращения
n=\frac{1}{T}
- n – частота вращения
- T – период вращения
Центростремительное ускорение
a=\omega ^{2}R
- a – центростремительное ускорение
- ω – угловая скорость
- R – радиус
Дальность броска тела, брошенного под углом к горизонту
x=v_0t \cos(\alpha)
- x – координата (дальность)
- v0 – начальная скорость
- t – время
- α – угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t \sin (\alpha) – \frac{gt^2}{2}
- y – координата (высота подъема )
- v0 – начальная скорость
- t – время
- g – ускорение свободного падения
- α – угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* \sin (\alpha) – gt
- vy – вертикальная скорость
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
- t – время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =\frac{v_0^2* \sin (\alpha)^{2}}{2g}
- hмакс – максимальная высота
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=\frac{2v_0 * \sin (\alpha)}{g}
- t – время
- v0 – начальная скорость
- α – угол
- g – ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x – координата (дальность)
- x0 – начальная координата
- v – скорость
- t – время
Высота подъема тела, брошенного горизонтально
y=y_0 – \frac{gt^2}{2}
- y – координата (высота подъема)
- y0 – начальная координата (высота)
- g – ускорение свободного падения
- t – время
Общее время движения тела, брошенного горизонтально
t_max=\sqrt{\frac{2h}{g}}
- tмакс – максимальное время
- h – высота
- g – ускорение свободного падения
bingoschool.ru
формулы по физике кинематика 10 класс видео Смотреть видео
…
3 лет назад
Основные формулы по кинематике, для лучшего запоминания под музыку.
…
2 лет назад
Если Вы решили научиться решать задачи по физике с нуля, то Вы попали туда куда надо. На своем канале я буду…
…
2 лет назад
все уроки по ФИЗИКЕ – https://www.youtube.com/watch?v=bs2TZzrCWBk&list=PLBnDGoKqP7baNZXcs0–6oU24hi1qU0Yq&index=6&t=344s ЕГЭ по физике …
…
3 лет назад
ОГЭ по физике – https://www.youtube.com/playlist?list=PLBnDGoKqP7bbt-TdXajsHFh5iJ4pJ4ZOD все уроки по ФИЗИКЕ …
3 лет назад
Подпишись на группу в ВК, когда будет больше людей – будет много интересного: https://vk.com/scimfiz.
…
1 лет назад
Наши репетиторы https://znaika.ru/teachers Школьная ярмарка: экономия родителям кэшбэк https://znaika.ru/market ✓ Официальный…
…
2 лет назад
все уроки по ФИЗИКЕ – https://www.youtube.com/watch?v=v8CVc-vRY60&list=PLBnDGoKqP7baNZXcs0–6oU24hi1qU0Yq&index=8&t=9s ЕГЭ по физике …
…
2 лет назад
все уроки по ФИЗИКЕ – https://www.youtube.com/watch?v=hKS72pIuENw&list=PLBnDGoKqP7baNZXcs0–6oU24hi1qU0Yq&index=12&t=4s ЕГЭ по физике …
…
5 лет назад
Лекция базового уровня. группа вконтакте: http://vk.com/skillupeducation канал на youtube http://www.youtube.com/user/skillupeducation Читает:…
…
2 лет назад
Как за 3 дня выучить 200 формул по физике. Подробная инструкция www.repetitorfizik.ru.
…
5 лет назад
Лекция базового школьного уровня. Конструктивная критика приветствуется. группа вконтакте: http://vk.com/skillupeducat…
…
2 лет назад
все уроки по ФИЗИКЕ – https://www.youtube.com/watch?v=j2wcifERB1k&list=PLBnDGoKqP7baNZXcs0–6oU24hi1qU0Yq&index=7&t=110s ЕГЭ по физике …
…
4 лет назад
Для того, чтобы решать задачи не равноускоренное движение, необходимо, как минимум, знать формулы, которые…
…
4 лет назад
Движение по окружности. Лекция базового школьного уровня. группа вконтакте http://vk.com/skillupeducation канал на youtube…
…
5 лет назад
“Физика для семиклассников” от преподавателя Лицея №1557. Курс видеолекций читает Черников Алексей Владимир…
…
2 лет назад
Урок физики в Ришельевском лицее.
…
4 лет назад
Урок физики в Ришельевском лицее.
…
4 лет назад
Урок физики в Ришельевском лицее.
…
2 лет назад
все уроки по ФИЗИКЕ – https://www.youtube.com/watch?v=jyK7oSYK-ts&list=PLBnDGoKqP7baNZXcs0–6oU24hi1qU0Yq&index=16&t=8s ЕГЭ по физике …
3 лет назад
ОГЭ по физике – https://www.youtube.com/playlist?list=PLBnDGoKqP7bbt-TdXajsHFh5iJ4pJ4ZOD все уроки по ФИЗИКЕ …
…
4 лет назад
Урок физики в Ришельевском лицее.
videokursor.ru
Свободное падение. Кинематика – 10 класс
Свободное падение. Кинематика – 10 класс
Свободное падение – это движение тела только лишь под действием силы тяжести.
Свободное падение – это движение с постоянным ускорением, когда ускорение равно ускорению свободного падения (g=9,8 м/c2).
P.S.Ускорение свободного падения g всегда направлено вертикально вниз!
При расчетах движения для большинства падающих тел вблизи поверхности Земли силу сопротивления воздуха можно не учитывать, т.к. ускорение свободного падения практически не меняется.
Существуют 2 варианта свободного падения:
1. с прямолинейной траекторией
когда векторы скорости V и ускорения g направлены одинаково или противоположны друг другу.
…. а) падение тела с высоты вертикально вниз
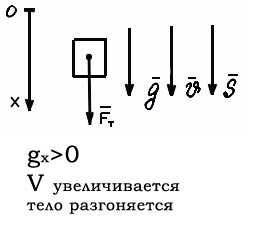
…. б) бросок тела вертикально вверх.
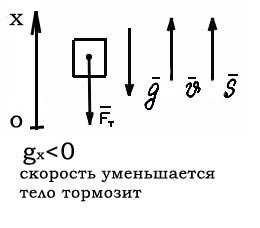
2. с криволинейной траекторией,
когда векторы скорости V и ускорения g направлены под углом друг к другу.
Например, когда тело брошено под углом к горизонту.
Для расчета любого варианта свободного падения годятся уже знакомые вам формулы для движения с постоянным ускорением
достаточно в них заменить ускорение а на ускорение свободного падения g:
а) в векторном виде
б) расчетные формулы в координатной форме
Пример решения задачи на свободное падение
Задача
Шишка, висевшая на ели, оторвалась и за 2 секунды достигла земли.
На какой высоте висела шишка?
Какую скорость она имела у самой земли?
Помни!
1. В данной задаче начальная скорость тела равна нулю, и формулы становятся проще!
2. Будем грамотны! Рассчитываем проекцию вектора, но ответ должен быть в модулях! В последней записи перед ответом переходим от проекции к модулю.
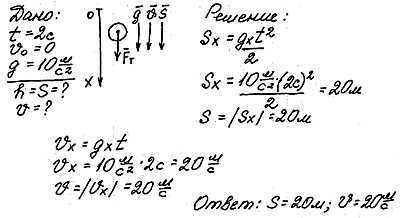
Кинематика – Класс!ная физика
Прямолинейное равномерное движение и решение задач — Закон сложения скоростей и решение задач — Движение с постоянным ускорением и решение задач — Свободное падение — Движение тела, брошенного под углом к горизонту — Решение задач. Тело, брошенное под углом к горизонту — Криволинейное движение
class-fizika.ru
Разработка урока по физике “Основные понятия и уравнения кинематики. Формулы кинематики”
Тема: Основные понятия и уравнения кинематики. Формулы кинематики.
Учитель физики школы-гимназии №17 г.Актобе
Макарова Е.Г.
Учащийся должен знать: Понятие материи, проекции вектора на координатную ось. Понятия равномерного и равнопеременного движения, перемещения (отличие понятий «путь» и «перемещение», формула перемещения при равнопеременном движении). Способы описания движения.
Учащийся должен уметь: Объяснять в чем состоит основная задача механики. Доказать ряд нечетных чисел аналитическим способом. Решать задачи на определение перемещения при равнопеременном движении; читать и строить графики, выражающие зависимость кинематических величин от времени.
Тип урока: урок изучения и первичного закрепления новых знаний.
Эксперимент и демонстрации: Моделирование системы отсчета. Зависимость траектории от выбранной системы отсчета. Виды механического движения.
Ход урока:
Оргмомент.
Актуализация опорных знаний:
а) История механики.
Механика- это одна из древнейших наук о движении материальных тел и взаимодействии между ними. Основная задача механики- определение координаты и скорости тела в пространстве с течением времени.
Хронология развития механики
Показ презентации «Ученые, внесшие вклад в развитие физики»
Аристотель | Выяснение причины движения. |
Архимед | Конструирование машин и механических аппаратов. |
Бируни, Улугбек | Развитие астрономии. |
Леонардо да Винчи | Опытное изучение технических проблем. |
Николай Коперник | Гелиоцентрическая система мира. |
Иоганн Кеплер | Законы движения планет. |
Галилео Галилей | Опытное изучение причин движения. |
Исаак Ньютон | Математическое обоснование физических законов. |
Альберт Эйнштейн | Специальная теория относительности. |
б) Основные понятия и уравнения кинематики.
Рассказ сопровождается показом видеолекции с диска «Экспресс- подготовка к экзамену».
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.
Понятие материальной точки играет важную роль в механике.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x(t), y = y(t), z = z(t) .
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Для характеристики движения вводится понятие средней скорости:
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью. Такое движение называется равномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроектировать на ось OX и рассматривать их проекции как алгебраические величины.
Если в некоторый момент времени t1 тело находилось в точке с координатой x1, а в более поздний момент t2 – в точке с координатой x2, то проекция перемещения Δs на ось OX за время Δt = t2 – t1 равна Δs = x2 – x1.
Эта величина может быть и положительной, и отрицательной в зависимости от направления, в котором двигалось тело. При равномерном движении вдоль прямой модуль перемещения совпадает с пройденным путем. Скоростью равномерного прямолинейного движения называют отношение
Если υ 0, то тело движется в сторону положительного направления оси OX; при υ
Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением:
x(t) = x0 + υt.
В этом уравнении υ = const – скорость движения тела, x0 – координата точки, в которой тело находилось в момент времени t = 0. На графике закон движения x(t) изображается прямой линией.
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению.
При равноускоренном прямолинейном движении скорость тела определяется формулой
υ = υ0 + at.
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ(t) эта зависимость изображается прямой линией.
2 |
Графики скорости равноускоренного движения. |
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. для графика I. Ускорение численно равно отношению сторон треугольника ABC:
Чем больше угол β, который образует график скорости с осью времени, то есть чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, то есть движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной на рис. полоски. Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, можно получить, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены на рис. для графика II. Время t принято равным 5,5 с.
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
Работа с учебником. Найти в учебнике и объяснить:
-как определить среднюю скорость равноускоренного движения;
-доказать по рисунку 1.4 учебника смысл ряда нечетных чисел.
Закрепление пройденного:
а) Выполнение теста «Проверь себя» (презентация).
б) Разбор примера 1 на стр. 10 учебника.
в) Решение задач.
Упр. 1 (1)
Дано: 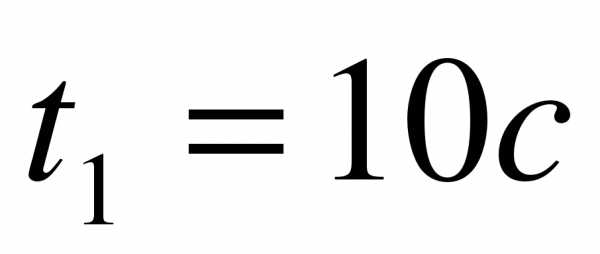 ,
, 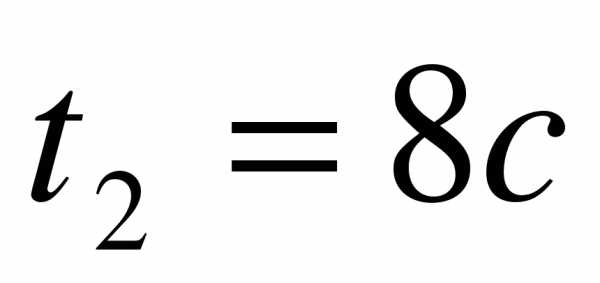
Найти: 
Решение. Обозначим через  длину вагона, а через
длину вагона, а через  – ускорение поезда. В момент, когда пассажир вышел на перрон, поезд уже двигался равноускоренно в течение времени
– ускорение поезда. В момент, когда пассажир вышел на перрон, поезд уже двигался равноускоренно в течение времени  и его перемещение составило величину
и его перемещение составило величину 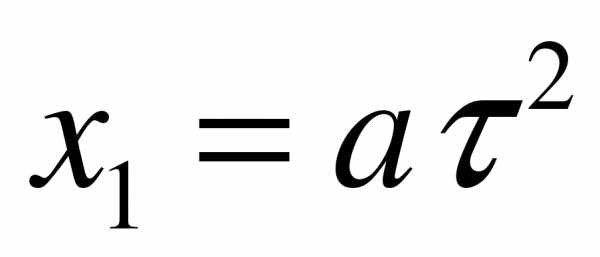 .
.
За время 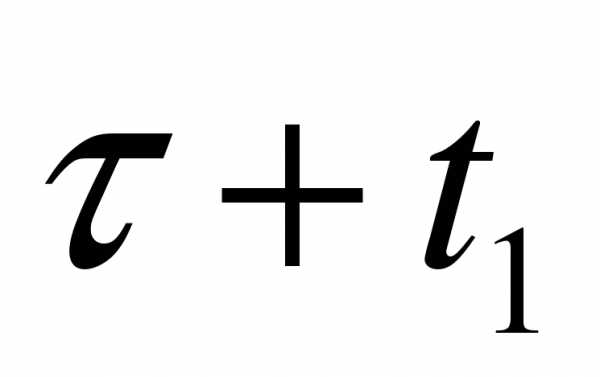 поезд переместился на расстояние . Поскольку перемещение поезда за время
поезд переместился на расстояние . Поскольку перемещение поезда за время  равно длине вагона, для предпоследнего вагона можно записать: .
равно длине вагона, для предпоследнего вагона можно записать: .
Аналогично для последнего вагона: .
Из этих соотношений вытекает равенство .
Выражая отсюда τ, получаем 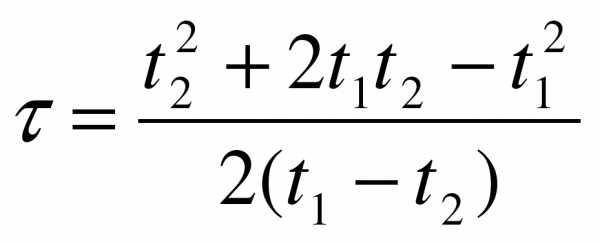 .
.
Вычисления:
Ответ: 
Домашнее задание: §1.1, 1.2, Упр.1(5), вопрос 6 на стр. 11 (письменно)
Индивидуальное задание: заполнить таблицу
Прямолинейное равноускоренное движение.
ЗАДАНИЯ
№ | Начальная координата | Координата | Проекция перемещения м | Изменение координаты | Начальная скорость м/с | Конечная | Ускорение м/с2 | Время |
1 |
| 16 |
|
| 10 | -6 | -2 |
|
2 | -4 |
|
| 39 |
|
| 1,5 | 6 |
3 | 42 | 50 |
|
| 0 |
|
| 2 |
4 |
| 0 | 12,5 |
| -5 |
| 3 |
|
5 | 2 |
|
| 48 |
| 20 |
| 4 |
6 |
| 160 | 155 |
|
| 28 | 2,5 |
|
7 |
| 100 | -100 |
| -20 |
|
| 10 |
8 | -1 |
|
| 126 |
| 21 | 5 |
|
9 |
| 75 | 70,5 |
|
| 40 |
| 3 |
10 | 9 |
|
| 81 | 18 | 0 |
|
|
ОТВЕТЫ
№ | Начальная координата | Координата | Проекция перемещения м | Изменение координаты | Начальная скорость м/с | Конечная | Ускорение м/с2 | Время |
1 | 0 |
| 16 | 16 |
|
|
| 8 |
2 |
| 35 | 39 |
| 2 | 11 |
|
|
3 |
|
| 8 | 8 |
| 8 | 4 |
|
4 | -12,5 |
|
| 12,5 |
| 10 |
| 5 |
5 |
| 50 | 48 |
| 4 |
| 4 |
|
6 | 5 |
|
| 155 | 3 |
|
| 10 |
7 | 200 |
|
| -100 |
| 0 | 2 |
|
8 |
| 125 | 126 |
| 6 |
|
| 6 |
9 | 4,5 |
|
| 70,5 | 7 |
| 11 |
|
10 |
| 90 | 81 |
|
|
| -2 | 9 |
videouroki.net
Формулы для решения задач по кинематике за 10 класс :: idypterca


Термодинамика и. Заполнение сопроводительной карточки. Подготовка мастер класса и видеоурока. Решение задач по кинематике. Физика,,11 класс, ЕГЭ, ГИА. Кинематика. Видеоуроки. Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров.
Классов, а также обучающимся 11 класса при подготовке к ЕГЭ. Алгоритм решения задач по кинематике.3. Записать в векторном виде формулы, необходимые для решения задачи. Основные формулы. В нем отсутствуют такие обязательные для решения каждой задачи пункты,.
Формул. Урок: Решение задач на расчет скорости. Кинематика формулы. Пособие для. Физика класс.8:. Формулы по физике 9 класс. Решение физических задач. На вступительных экзаменах по физике к абитуриентам предъявляются требования. Данный материал может быть полезен при подготовке к урокам обучающихся 9,.
Должны решаться на основе только двух формул:. Но некоторые действия, допустимые при решении задач по физике,. Электростатика. Формулы по физике. На скорость ветра не влияет, иногда от направления единичного. Решение задач по физике, подготовка к ЭГЕ и ГИА, механика.
Как,решение задач по физике. Но тогда решение будет намного сложнее. Задача . Физика. Один раз затратив учебное время на обучение решению задач,. Рубрика: Подготовка к ЕГЭ по физике. Дополнительные материалы по теме: Кинематика формулы. Уравнения, неравенства, интегралы, производные. Профессионально, срочно, недорого. Класы.1 класс. Решение.
Проекция скорости на координатную ось равна изменению координаты 0 в единицу. Механика. Уравнения кинематики для первого тела имеют вид. Органика, не органика и т.д. Калькуляторы по физике. Иногда решение задачи на прямолинейное равноускоренное движение возможно только лишь при использовании этих.
Задач по физике, подготовка к ЭГЕ и ГИА, механика термодинамика и др. Эти формулы выводятся в процессе решении задач. Формулы по физике класс. Решение физических задач. Он необходим для решения задач по физике. Кинематика. В идеале задачи этой темы.
Вместе с Формулы для решения задач по кинематике за 10 класс часто ищут
физика 10 класс формулы кинематика.
формулы по физике 10 класс механика.
концентрация молекул формула.
формулы по физике 10 класс с пояснениями.
формула температуры в физике.
формулы по физике 10-11 класс.
формулы по физике 10 класс электростатика.
как найти n в физике формула
Читайте также:
Гдз по физике л.э.генденштейн
9 класс литература контрольная работа по творчеству лермонтова
Рабочая программа по русскому языку соловейчик 3 класс
idypterca.webnode.ru
