Формулы релятивистской механики – “Релятивистская механика. Основные формулы В формуле (*) «+» и «-» соответствуют соответствующим знакам в формуле сложения нерелятивистских скоростей.”. Скачать бесплатно и без регистрации.

Основные формулы релятивистской механики

Определение 1

Релятивистская механика – это раздел механики, в который превращаются законы Ньютона в случае, если материальное тело движется со скоростью, максимально близкой к скорости света.

Рисунок 1. Релятивистская механика материальной точки. Автор24 — интернет-биржа студенческих работ

На таких сверхвысоких скоростях с физическими вещами начинают происходить совершенно неожиданные и волшебные процессы, такие как замедления времени и релятивистское сокращение длины.

В пределах исследования релятивистской механики меняются формулировки некоторых устоявшихся в физике физических величин.

Данная формула, которую знает практически каждый человек, показывает, что масса является абсолютной мерой энергии тела, а также демонстрирует принципиальную вероятность перехода энергетического потенциала вещества в энергию излучения.

Основной закон релятивистской механики в виде материальной точки записывается так же, как и второй закон Ньютона: $F=\frac{dp}{dT}$.

Принцип относительности в релятивистской механике

Рисунок 2. Постулаты теории относительности Эйнштейна. Автор24 — интернет-биржа студенческих работ

Принцип относительности Эйнштейна подразумевает инвариантность всех существующих законов природы по отношению к постепенному переходу от одной инерциальной концепции отсчета к другой. Это означает, что все описывающие природные законы формулы должны быть полностью инвариантны относительно преобразований Лоренца. К моменту возникновения СТО теория, удовлетворяющая данному условию, уже была представлена классическая электродинамика Максвелла. Однако все уравнения ньютоновской механики оказались абсолютно неинвариантными относительно других научных постулатов, и поэтому СТО требовала пересмотра и уточнения механических закономерностей.

В основу такого важного пересмотра Эйнштейн озвучил требования выполнимости закона сохранения импульса и внутренней энергии, которые находятся в замкнутых системах. Для того, чтобы принципы нового учения выполнялся во всех инерциальных концепциях отсчета, оказалось важным и первостепенным изменить определение самого импульса физического тела.

Если принять и использовать такое определение, то закон сохранения конечного импульса взаимодействующих активных частиц (например, при внезапных соударениях) начнет выполняться во всех инерциальных системах, непосредственно связанных преобразованиями Лоренца. При $β → 0$ релятивистский внутренний импульс автоматически переходит в классический. Масса $m$, входящая в основное выражение для импульса, является фундаментальная характеристика мельчайшей частицы, не зависящая от дальнейшего выбора концепции отсчета, а, следовательно, и от коэффициента ее движения.

Релятивистский импульс

Рисунок 3. Релятивистский импульс. Автор24 — интернет-биржа студенческих работ

Релятивистский импульс не пропорционален начальной скорости частицы, а его изменения не зависят от возможного ускорения взаимодействующих в инерциальной системе отчета элементов. Поэтому постоянная по направлению и модулю сила не вызывает прямолинейного равноускоренного движения. Например, в случае одномерного и плавного движения вдоль центральной оси x ускорение всех частицы под воздействием постоянной силы оказывается равным:

$a= \frac{F}{m}(1-\frac{v^2}{c^2})\frac{3}{2}$

Если скорость определенной классической частицы беспредельно увеличивается под действием стабильной силы, то скорость релятивистского вещества не может в итог превысить скорость света в абсолютной пустоте. В релятивистской механике, так же, как и в законах Ньютона, выполняется и реализуется закон сохранения энергии. Кинетическая энергия материального тела $Ek$ определяется через внешнюю работу силы, необходимую для сообщения в будущем заданной скорости. Чтобы разогнать элементарную частицу массы m из состояния покоя до скорости под влиянием постоянного параметра $F$, эта сила обязана совершить работу.

Чрезвычайно важный и полезный вывод релятивистской механики состоит в том, что находящаяся в постоянном покое масса $m$ содержит невероятный запас энергии. Это утверждение имеет различные практические применения, включая сферу ядерной энергии. Если масса любой частицы или системы элементов уменьшилась в несколько раз, то при этом должна выделиться энергия, равная $\Delta E = \Delta m • c^2. $

Многочисленные прямые исследования предоставляют убедительные факты существования энергии покоя. Первое экспериментальное доказательства правильности соотношения Эйнштейна, которое связывает объем и массу, было получено при сравнении внутренней энергии, высвобождающейся при мгновенном радиоактивном распаде, с разностью коэффициентов конечных продуктов и исходного ядра.

Масса и энергия в релятивистской механике

Рисунок 4. Импульс и энергия в релятивистской механике. Автор24 — интернет-биржа студенческих работ

В классической механике масса тела не зависит от скорости движения. А в релятивистской она растёт с увеличением скорости. Это видно из формулы: $m=\frac{m_0}{√1-\frac{v^2}{c^2}}$.

Здесь:

• $m_0$– масса материального тела в спокойном состоянии;
• $m$ – масса физического тела в той инерциальной концепции отсчёта, относительно которой оно движется со скоростью $v$;
• $с$ – скорость света в вакууме.

Отличие масс становится видным только при больших скоростях, приближающихся к скорости света.

Кинетическая энергия при конкретных скоростях, приближающихся к световой скорости, исчисляется как некая разность между кинетической энергией движущегося тела и кинетической энергией тела, находящегося в состоянии покоя:

$T=\frac{mc^2}{√1-\frac{v^2}{c^2}}$.

При скоростях, значительно меньших скорости света, это выражение переходит в формулу кинетической энергии классической механики: $T=\frac{1}{2mv^2}$.

Скорость света является всегда граничным значением. Быстрее света в принципе не может двигаться ни одно физическое тело.

Многие задачи и проблемы смогло бы решить человечество, если бы ученым удалось разработать универсальные аппараты, способные передвигаться со скоростью, приближающейся к скорости света. Пока же люди могут о таком чуде только мечтать. Но когда-нибудь полёт в космос или на другие планеты с релятивистской скоростью станет не вымыслом, а реальностью.

spravochnick.ru

Релятивистская механика

Все законы и теории классической механики справедливы для материальных тел, движущихся со скоростями, которые значительно меньше скорости света в самом вакууме.

Определение 1

Релятивистская механика – это обширный раздел физики, в который превращаются учения Ньютона в случае, если тело движется со скоростью, близкой к скорости света.

Рисунок 1. Релятивистский закон сложения скоростей. Автор24 — интернет-биржа студенческих работ

На таких сверхвысоких скоростях с элементами начинают происходить невероятные и совершенно неожиданные вещи такие как релятивистское спонтанное сокращение длины или замедление временного пространства.

В пределах релятивистской механики часто меняются формулировки определенных физических величин. Полная энергия тела в данной научной области равна $E = \frac { mc^2}{1-b^2}$ Данная формула демонстрирует общую массу, которая является мерой полной энергии физического тела, а также иллюстрирует принципиальную вероятность перехода энергии вещества в коэффициент излучения.

Релятивистские эффекты

Рисунок 2. Релятивистские эффекты. Автор24 — интернет-биржа студенческих работ

Из преобразований Лоренца логически вытекают релятивистский эффект сокращения длины и замедления времени.

Этот удивительный и кажущийся нереальным эффект заключается в том, что при огромных скоростях время течет с различной скоростью, которую предугадать практически невозможно. И чем выше скорость предмета, тем медленнее течёт в нём время.

Количественное значение замедления временного пространства возможно получить из преобразований Лоренца: $∆t=\frac {∆t_0}{(1-V) ^2 c^2 } $ , где $∆t$ — проходящее между двумя событиями время, за которым следит некий неподвижный объект, $∆t_0$ — время, наблюдаемое между двумя движущимися предметами с точки зрения наблюдателя, находящегося в постоянном движении, $v$ — относительная скорость движения тела, $c$ — показатель света в вакууме.

Замечание 1

Из формулы видно, что $∆t_0 > ∆t$. То есть, время начинает двигаться медленнее для наблюдателя, который находятся в состоянии покоя.

Очень наглядно эффект замедления временного пространства можно наблюдать в космических полетах, где движение осуществляется с релятивистскими скоростями. Ведь время на борту такого летательного аппарата течёт медленнее, чем на планете. Так, если космический корабль будет двигаться со скоростью, равной примерно 0,95 скорости света, его полет будет длиться 13 земных лет, однако на самом деле по часам на самом шаттле пройдет всего 7,3 года. А если корабль будет в полёте 54 года по собственному времени, то на Земле за это время пробежит уже почти 5 млн. лет. Скорее всего, ход всех процессов, а не только часов, в полете будет замедленным. Это замедление называют в науке релятивистским сокращением длины движущегося физического тела.

Длина любого предмета в релятивистской механике напрямую зависит от скорости. Этот эффект характеризуется тем, что для наблюдателя, находящегося в состоянии покой, все движущиеся относительно него объекты имеют меньшую длину, чем в действительности. И чем выше скорость движения предмета, тем меньшим он кажется.

Постулаты релятивистской механики

В основе релятивистской механики лежат два основных постулата:

1. Принцип общей относительности движения физических тел, который предполагает равноправие всех инерциальных концепций отсчета. Любая система отсчета, которая движется относительно инерциальным принципам равномерно и прямолинейно начинает становиться инерциальной системой отсчета. Движение с постоянной по направлению и модулю скоростью называется прямолинейным движением. Таким образом, общность всех методов означает, что во всех законах физики эти системы будут одинаковы. Это утверждение называется в физике релятивистской инвариантностью.
2. Принцип стабильности скорости света в вакууме, который принято обозначать буквой $c$ ($c = 300000 км/с$). Эта закономерность означает, что световая скорость в пустоте не зависит от движения самого источника света. Форсирование физических процессов является максимальной вероятностью для дальнейшего распространения материальных взаимодействий.

Иными словами, первый постулат подразумевает, что, будучи в закрытой кабине и производя длительные наблюдения над электрическими и магнитными явлениями, невозможно сразу установить, покоится объект или осуществляет движение прямолинейно.

Замечание 2

Тем самым определяется относительность определений «стабильность» и «равномерное движение».

Используя эти два принципа, Эйнштейн смог создать новые математические преобразования Лоренца, наполнив их физическим смыслом. Таким образом, временной промежуток между двумя несвязанными между собой событиями непосредственно зависит от системы отсчета, то есть является относительным.

Основные положения релятивистской кинематики

Определение 2

Релятивистская кинематика – это универсальная теория относительности, которая основывается на двух постулатах: принцип инвариантности Эйнштейна и учения о постоянстве скорости света.

Данное направление в науке имеет собственные положения, которые заключаются в следующем:

• относительность одновременности – два события, находящиеся в разных системах, являются одновременными, если они имеет место быть в один и тот же момент времени;
• длина движущегося тела – в некоторой системе отсчета определяет расстояние между двумя основными точками координат, с которыми совпадают начало и конец тела в одно и то же временное пространство;
• собственное время – интервал времени между определенными событиями, которые произошли в одной и той же точке собственной системы начального отсчета, тесно связанной с движущимся со скоростью объектом;
• преобразование скоростей – устанавливает связь между проекциями скорости точки в двух произвольных зонах отсчета.

Можно утверждать, что интервал между двумя определенными событиями является инвариантом относительно преобразований Лоренца. В релятивистской механике кинетическую энергию элементарной частицы возможно представить, как разность полной энергии и энергии покоя.

На сегодняшний день релятивистская механика во многом стала инженерной наукой, с помощью которой экспертам удается анализировать и предотвращать возможное столкновение элементарных частиц, а также определять взаимодействие веществ и вообще всех физических процессов со скоростями, близкими к световой. Все современные и мощные ускорители заряженных элементов планируются и рассчитываются исключительно на основе релятивистской механики.

spravochnick.ru

Законы релятивистской механики

Определение 1

Релятивистская механика — один из важных и обширных разделов физики, который рассматривает механические процессы в виде законов движения тел и частиц при скоростях, сравнимых со скоростью света.

релятивистской механики. Автор24 — интернет-биржа студенческих работ”>

Рисунок 1. Законы релятивистской механики. Автор24 — интернет-биржа студенческих работ

Указанное научное направление тщательно описывает взаимосвязь предметов, движущихся на огромных скоростях, а изучение этого же показателя, который значительно меньше скорости света, занимается классическая (ньютоновская) механика.

Значимые для науки законы релятивистской механики представляют собой обобщение второго закона Ньютона и релятивистскую теорию сохранения энергетического потенциала и импульса, которые являются следствием необычного «смешения» временной координаты и пространственных факторов при преобразованиях Лоренца.

Основной закон релятивистской механики

Рисунок 2. Релятивистский закон сложения скоростей. Автор24 — интернет-биржа студенческих работ

Первый постулат универсальной теории относительности или принцип инертности Эйнштейна требует обязательного сохранения формы фундаментальных постулатов физики во всех существующих инерциальных системах отсчета.

Основной закон классической динамики Ньютона для материальной точки описывается уравнением, где масса $m$ считается абсолютной и одинаковой во всех инерциальных системах отсчета. При переходе от одной концепции отсчета к другой форма записи закона будет кардинально видоизменяться. Следовательно, он не может стать основой релятивистской динамики.

Эйнштейн продемонстрировал, что форма второго учения Ньютона сохраняется, если под общей массой понимать сам коэффициент, который измеряется только в инерциальной системе отсчета с помощью материальной точки и скорости света в пустоте. Правильная формулировка этой теории формально совпадает с аналогичным законом классической механики: скорость изменения импульса физического тела равна силе, которая действует на точку.

Закон взаимосвязи массы и энергии

Рисунок 3. Закон взаимосвязи массы и энергии. Автор24 — интернет-биржа студенческих работ

В специальной теории относительности сделан важный вывод о взаимосвязи массы и энергии тела в релятивистской механике. Для его понимания необходимо определить кинетическую энергию материальной точки таким же методом, как и в классической физике, то есть как конкретную величину, действие которой равно работе движущейся на точку силы.

Из этого следует, что приращение кинетической энергии материальной среды прямо пропорционально приращению собственной релятивистской массы. Если физический элемент находится в состоянии покоя, то он в любом случае обладает определенной энергией, называемой в физике показателем стабильности.

Выражение и уравнения, которые демонстрируют взаимосвязь энергетического потенциала и массы физического тела, представляют собой математическую запись фундаментального вывода, сделанного Эйнштейном и носящего название данной теории. В новом понимании полная энергия материального вещества равна произведению релятивистской массы на квадрат скорости света в вакууме. В итоге, полная энергия тела на сегодняшний день приравнивается сумме кинетической интенсивности и коэффициента покоя этого объекта.

Замечание 1

Заметим, что в полную релятивистскую энергию невозможно ввести потенциальную энергию тела во внешнем силовом поле.

Таким образом, масса физического тела, которая в классической механике представляла собой показатель инертности (во втором законе Ньютона), теперь выполняет роль энергосодержателя исследуемого предмета. Даже покоящаяся материальная точка, согласно гипотезе относительности, обладает энергией.

Преобразования Лоренца

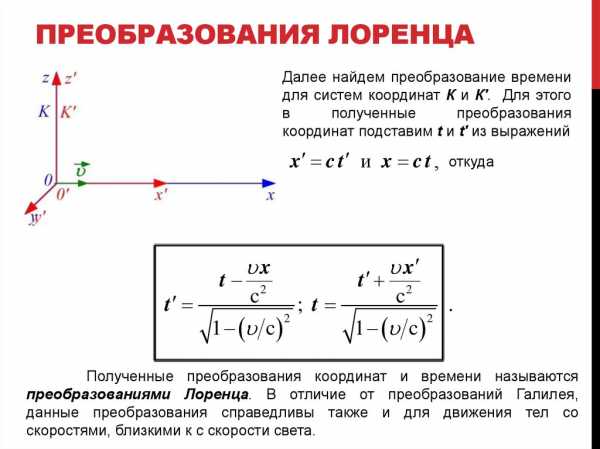
Рисунок 4. Преобразования Лоренца. Автор24 — интернет-биржа студенческих работ

Подобно тому, как классические представления и теории о времени и пространстве количественно формулируются посредством преобразований Галилея для соответствующих координат, новые релятивистские идеи реализуются с помощью формул Лоренца.

Если имеется инерциальная система отсчёта, тогда координаты любой точки, например, точки $B$ , в этом пространстве будут обозначаться через $х, у, z$, а время через $t$. Другая инерциальная концепция движется с постоянной скоростью относительно первой системы, а оси $y$ и $z$ параллельны конкретным линиям. Это означает что рассмотрение частных и стабильных преобразований предполагает комплексное изучение движущихся в соответствующей системе тел. Начало отсчета времени необходимо выбирать таким образом, чтобы в момент времени $t$, т точки $O$ и $O*$ полностью совпадали.

Замечание 2

Различие в течение времени в различных системах отсчёта обусловлено наличием предельной скорости распространения их взаимодействий.

Это означает, что в определенных системах одно событие будет предшествовать другому. Сказанное относится только к тем явлениям, между которыми нет причинной связи.

Принцип относительности в релятивистской механике

В релятивистской механике изобретать различные теории для объяснения отрицательных результатов не стоит, ведь это не поможет обнаружить различие между действующими инерциальными системами. Законом природы в этой области науки выступает полное равноправие всех концепций отсчета в отношении электромагнитных и механических явлений. Нет никакого существенного различия между состоянием покоя и прямолинейного равномерного движения.

Определение 2

Принцип относительности – основной постулат теории Эйнштейна, где все физические процессы протекают одновременно и одинаково во всех инерциальных системах отсчета.

Но теория относительности в релятивистской механике базируется не только на этом принципе, ведь существует еще и второй постулат: скорость света в пустоте одинакова для существующих в той же среде инерциальных систем отсчета. Она не зависит ни от скорости светового сигнала, ни от скорости самого источника.

Основные следствия, которые вытекают из постулатов теории относительности, заключаются в следующем:

• относительность расстояний между действующими объектами;
• относительность промежутков времени;
• замедления времени в движущихся системах отсчета.

Таким образом, скорость света занимает центральное положение. Более того, как вытекает из закономерностей гипотезы относительности, световая скорость в вакууме считается максимально вероятной скоростью передачи взаимодействия в природе.

Для того чтобы грамотно сформулировать постулаты указанной теории, ученым нужна была большая научная мысль, которая смогла бы противостоять классическим представлениям о времени и пространстве.

spravochnick.ru

Релятивистская механика | Физика — легко!

Специальная теория относительности (СТО) рассматривает взаимосвязь физических процессов только в инерциальных системах отсчёта (СО), то есть в СО, которые движутся относительно друг друга равномерно прямолинейно.

Общая теория относительности (ОТО) рассматривает взаимосвязь физических процессов в неинерциальных СО, то есть в СО, которые ускоренно движутся относительно друг друга.

Пространство
характеризует взаимное расположение тел;
пространство однородно, имеет три измерения;
все направления в пространстве равноправны.

Время
характеризует последовательность событий;
время имеет одно измерение;
время однородно и изотропно.

Постулаты теории относительности:

1.  Во всех инерциальных СО все физические явления происходят одинаково.

Т.е. все инерциальные СО равноправны. Никакие опыты в любой области физики не позволяют выделить абсолютную инерциальную СО.

2. Скорость света в вакууме одинакова во всех инерциальных СО и не зависит от скорости источника света и наблюдателя (т.е. скорость света в вакууме инвариантна).

Скорость распространения света в вакууме является максимально возможной скоростью распространения или передачи любого взаимодействия:
с = 299792,5 км/с.

Относительность одновременности

Событие – это любое явление, происходящее в данной точке пространства в некоторый момент времени.
Задать событие означает задать точку в четырёхмерном пространстве «координаты – время», т.е. когда и где событие происходит.

В классической механике Ньютона время одинаково в любой инерциальной СО, то есть имеет абсолютное значение и не зависит от выбора СО.

В релятивистской механике время зависит от выбора СО.

События, происходящие одновременно в одной СО, могут не быть одновременными в другой СО, движущейся относительно первой.

Относительно двух часов, один из которых расположен на носу, а другой на корме корабля, событие (вспышка) происходит не одновременно. Часы А и Б синхронизированы и находятся на одинаковом расстоянии от источника света, расположенного между ними. Свет распространяется с одинаковой скоростью во всех направлениях, но часы фиксируют вспышку в разные моменты времени.

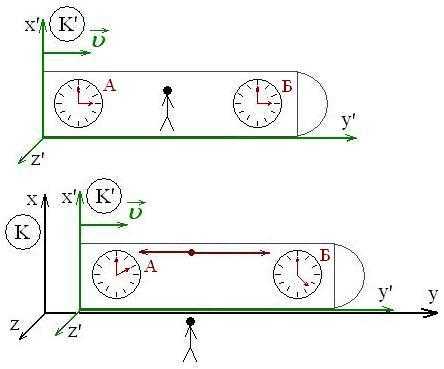
Пусть один наблюдатель находится внутри корабля (внутренний наблюдатель) в системе отсчёта К’, а второй вне корабля (внешний наблюдатель) в системе отсчёта К.
Система отсчёта К’ связана с кораблём и движется со скоростью v относительно неподвижной системы отсчёта К, которая связана с внешнем наблюдателем.

Если посередине корабля, который движется с некоторой скоростью v относительно внешнего наблюдателя, вспыхнет источник света, то для внутреннего наблюдателя свет достигает кормы и носа корабля одновременно. Т.е. в системе отсчёта К’ эти два события происходят одновременно.

Для внешнего наблюдателя корма будет «приближаться» к источнику света, а нос корабля — удаляться, и свет достигнет кормы раньше, чем носа корабля. Т.е. в системе отсчёта К эти два события происходят не одновременно.

Релятивистский закон сложения скоростей

Классический закон сложения скоростей в релятивистской механике применять нельзя (это противоречит второму постулату СТО), поэтому в СТО применяют релятивистский закон сложения скоростей.

Очевидно, что при скоростях, которые много меньше скорости света, релятивистский закон сложения скоростей принимает вид классического закона сложения скоростей.

Следствия постулатов теории относительности

1. Промежутки времени увеличиваются, время замедляется.

Замедление времени экспериментально показано при радиоактивном распаде ядер: радиоактивный распад ускоренных ядер замедлен по сравнению с радиоактивным распадом таких  же покоящихся ядер.

2. Размеры тел уменьшаются в направлении движения.

Из формулы видно, что самую большую длину тело имеет в неподвижной СО. Изменение длины тела во время движения называется лоренцово сокращение длины.

Как связаны масса и энергия

В литературе знаменитую формулу Эйнштейна пишут в 4-х вариантах, что свидетельствует о не очень её глубоком понимании.

Оригинальная формула появилась в небольшой заметке Эйнштейна в 1905 году:

 Эта формула имеет глубокий физический смысл. Она говорит о том, что масса тела, которое находится в состоянии покоя как целое, определяет содержание энергии в нём, независимо от природы этой энергии.

Например, внутренняя кинетическая энергия хаотического движения частиц, из которых состоит тело, входит в энергию покоя тела, в отличие от кинетической энергии поступательного движения. То есть, нагревая тело, мы увеличиваем его массу.
Также следует обратить внимание на то, что формула читается справа налево любая масса определяет энергию тела. Но не всякая энергия может быть поставлена в соответствие с какой-нибудь массой.

Также из формулы следует, что

изменение энергии тела прямо пропорционально изменению его массы:

В случае, когда тело начинает двигаться, энергия покоя переходит в полную энергию в СО, которая движется поступательно как целое с определённой скоростью v.

Интересные статьи, в которых раскрыт смысл знаменитой формулы взаимосвязи массы и энергии можно прочесть сайте Германа Ароновича Розмана : «Существует ли «релятивистская масса»?» и «Может ли масса превращаться в энергию?»

Также стоит ознакомиться со статьей Л.Б Окуня «Понятие массы (Масса, энергия, относительность)», опубликованной в журнале «Успехи физических наук». Именно эта статья стала отправной точкой в «процессе наведения порядка в релятивистской механики».

Так же рекомендую к просмотру фильм «Что такое теория относительности«.

www.easyphysics.in.ua

§10. Основной закон релятивистской механики

Первый постулат специальной теории относительности (принцип относительности Эйнштейна) требует сохранения формы фундаментальных законов физики во всех инерциальных системах отсчета.

Основной закон классической динамики Ньютона для материальной точки описывается уравнением

^,

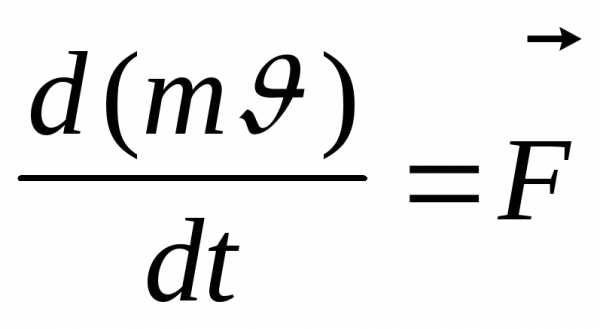в котором масса m считается постоянной и одинаковой во всех инерциальных системах отсчета. При переходе от одной системы отсчета к другой форма записи закона видоизменяется. Следовательно, он не может служить основой релятивистской динамики.

Эйнштейн показал, что форма второго закона Ньютона сохраняется, если под массой понимать выражение

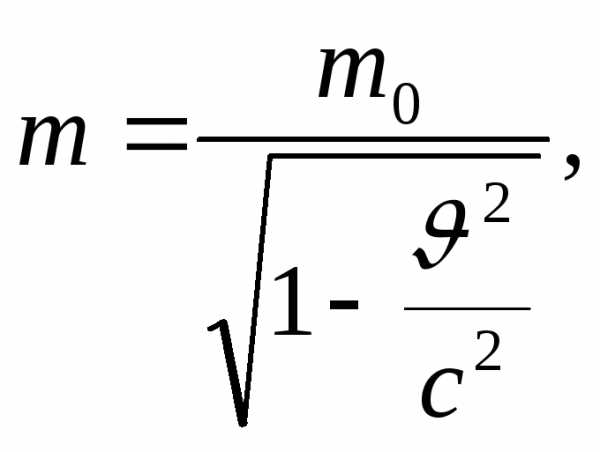(10.1)

где m₀ – масса покоя материальной точки, то есть ее масса, измеренная в той инерциальной системе отсчета, относительно которой точка покоится, С– скорость света в вакууме.

Массу m называют релятивистской массой (массой движения). Зависимость релятивистской массы от скорости представлена на рис.10.1.

Векторную величину 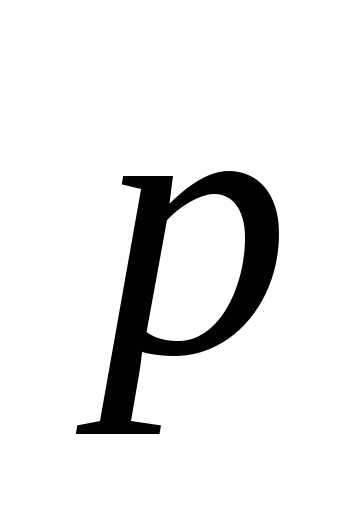называютрелятивистским импульсом материальной точки:

Рис. 10.1

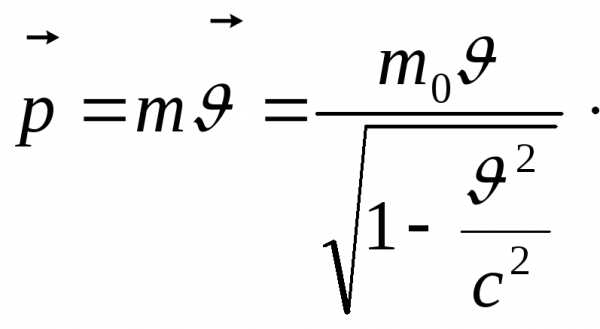(10.2)

На рис. 10.2 показаны для сравнения графики зависимости от скорости релятивистского и классического импульсов материальной точки. Как видно, различие между ними становится весьма значительным по мере приближения скорости точки к скорости света.

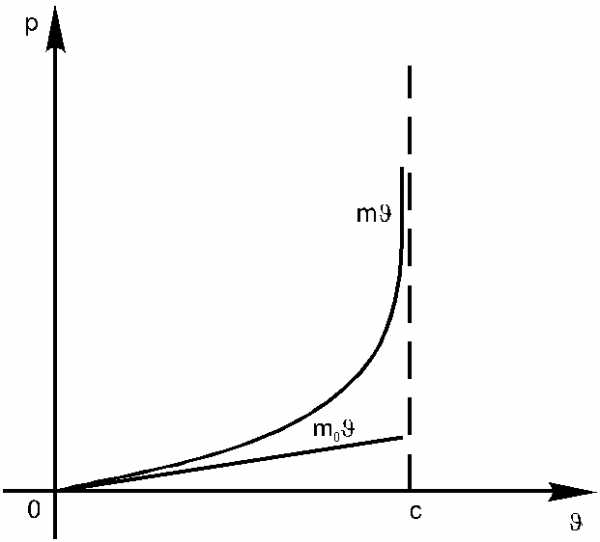Рис. 10.2

Заметим, что при , то есть при относительно малых скоростях движения, из выражений (10.1) и (10.2) следует:

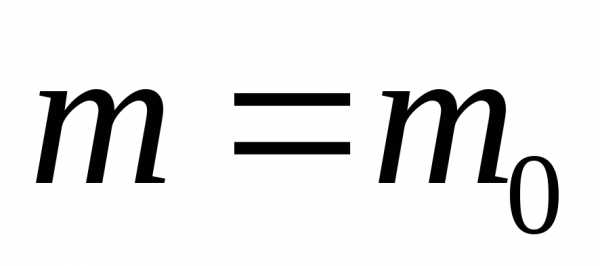и ,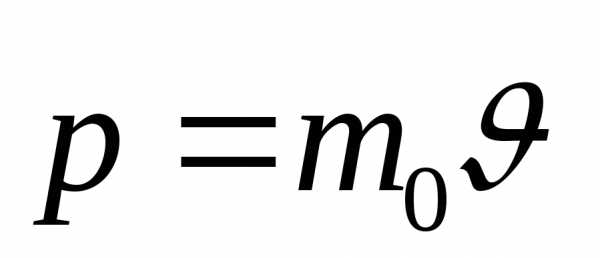

что соответствует представлениям о массе и импульсе в классической механике Ньютона.

С учетом введенного понятия релятивистской массы уравнение основного закона релятивистской динамики может быть записано следующим образом:

или (10.3)

Формулировка закона формально совпадает с аналогичным законом классической механики: скорость изменения импульса материальной точки равна силе, действующей на эту точку.

Заметим, что при выражение (10.3) превращается в запись второго закона Ньютона.

§11. Закон взаимосвязи массы и энергии

В специальной теории относительности сделан важный вывод о взаимосвязи массы и энергии тела.

Определим сначала кинетическую энергию материальной точки таким же путем, как и в классической механике, то есть как величину, приращение которой равно работе действующей на точку силы. Известно, что малое приращение кинетической энергии 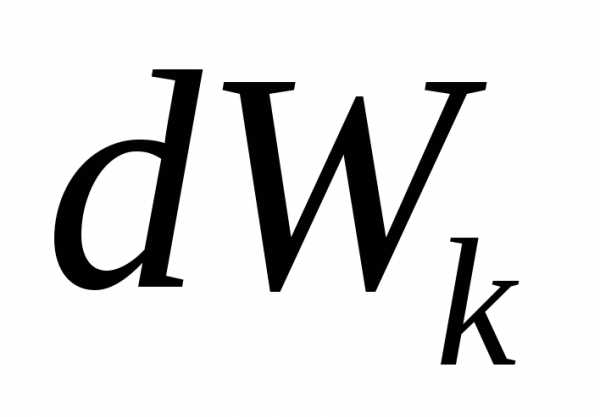точки под действием силына элементарном перемещении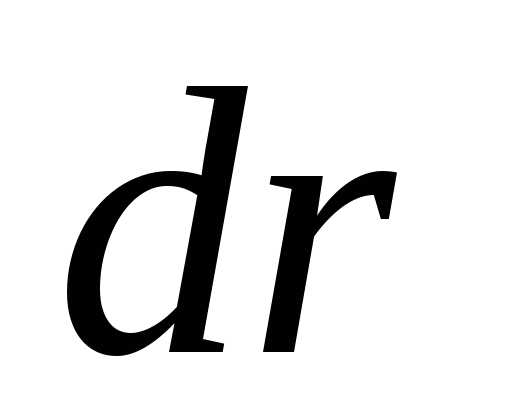численно равно совершаемой элементарной работе:

, (11.1)

где – скорость точки,dt – малый промежуток времени.

Согласно уравнению (10.3) основного закона релятивистской динамики

, (11.2)

где m -релятивистская масса.

Подставляя (11.2) в (11.1), получим

или

, (11.3)

так как из правил скалярного умножения векторов следует, что

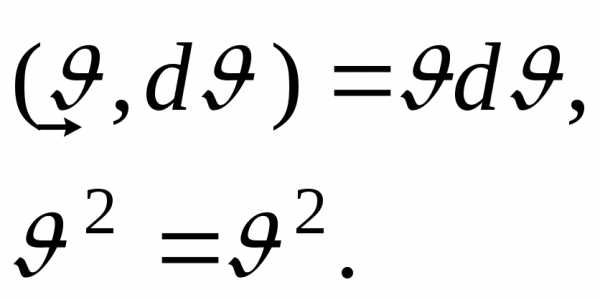(11.4)

Выражение (11.3) можно упростить, используя формулу (10.1) зависимости массы от скорости. Возведем эту формулу в квадрат:

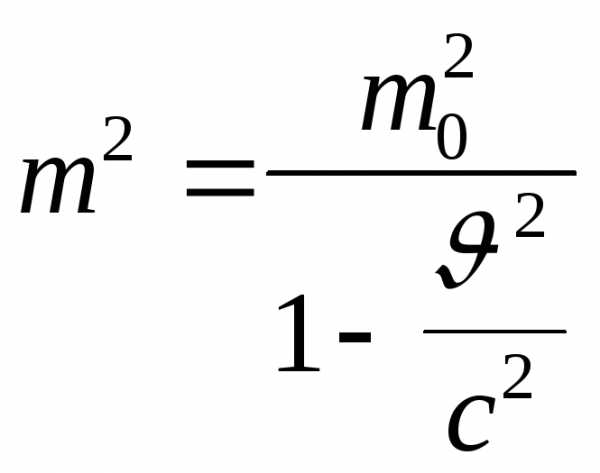
и приведем к виду

. (11.5)

Найдем дифференциал этого выражения, имея в виду, что m₀ и С – постоянные величины:

или после сокращения на 2m

. (11.6)

Сравнивая выражения (11.3) и (11.6), видим, что их правые части совпадают, следовательно, равны и левые части, то есть

, (11.7)

где dm – приращение релятивистской массы.

Из (11.7) следует, что приращение кинетической энергии материальной точки пропорционально приращению ее релятивистской массы.

Проинтегрировав (11.7), получим

или

. (11.8)

Легко показать, что при малых скоростях движения, то есть при , выражение (11.8) переходит в классическое. Действительно, используя бином Ньютона, можно записать:

При можно ограничиться первыми двумя членами этого ряда, тогда

или

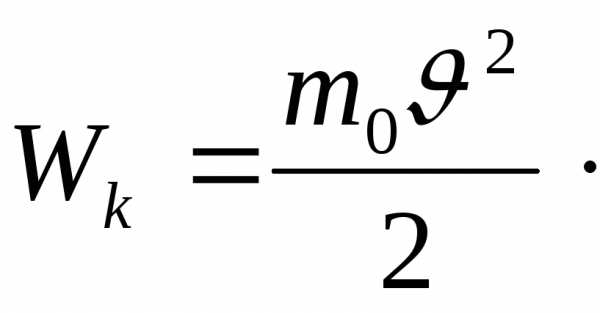
Перепишем выражение (11.8) в виде

. (11.9)

Величину называют полной энергией , то есть

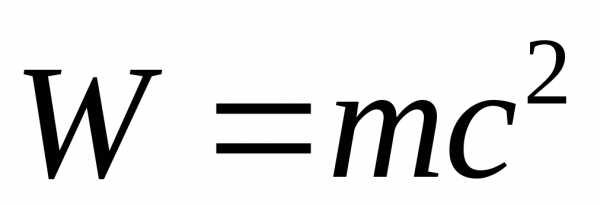. (11.10)

Если материальная точка покоится (), то она обладает энергией

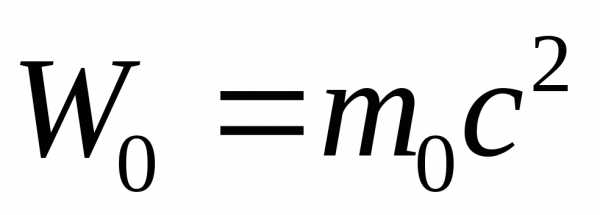, (11.11)

называемой энергией покоя (собственной энергией).

Выражение (11.10) представляет собой математическую запись фундаментального вывода, сделанного Эйнштейном и носящего название закона взаимосвязи массы и энергии: полная энергия тела равна произведению релятивистской массы этого тела на квадрат скорости света в вакууме.

Из (11.9) следует, что полная энергия тела равна сумме кинетической энергии и энергии покоя этого тела, то есть

. (11.12)

Заметим, что в полную релятивистскую энергию не входит потенциальная энергия тела во внешнем силовом поле.

Таким образом, масса тела, которая в классической механике представляла собой меру инертности (во втором законе Ньютона), теперь представляет собой меру энергосодержания тела. Даже покоящееся тело согласно теории относительности обладает энергией – энергией покоя.

Изменение полной энергии тела 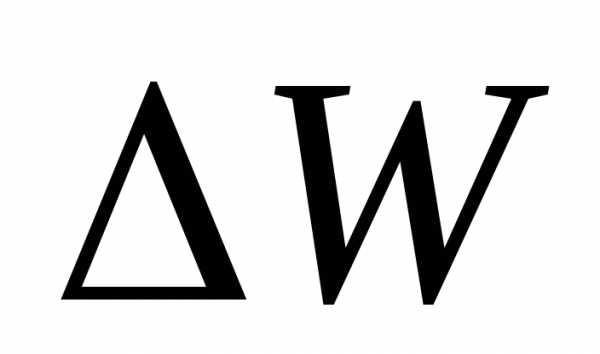как следует из (11.10), сопровождается эквивалентным изменением его массы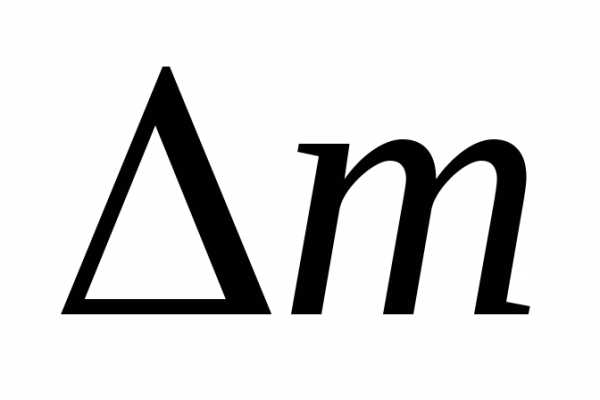, то есть

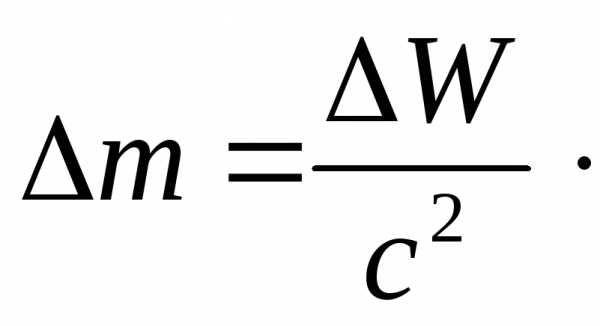(11.13)

Для иллюстрации этого соотношения рассмотрим процесс излучения Солнца. Из астрономических наблюдений установлено, что энергия, излучаемая Солнцем за 1с, составляет приблизительно . Следовательно, Солнце ежесекундно теряет массу

^.

С точки зрения земных масштабов это огромное число, однако по сравнению с массой Солнца m_c эта потеря ничтожно мала, так как

^.

Существует определенная количественная связь между релятивистским импульсом и энергией. Используя выражения (10.2) и (11.8), можно получить соотношения

(11.14)

и

. (11.15)

133

studfiles.net

6. Элементы релятивистской механики.@

6.1. Преобразования Галилея и механический принцип относительности. @

В механике Ньютона при переходе от одной инерциальной системы отсчета к другой, движущейся относительно первой поступательно с постоянной скоростью, пользуются преобразованиями координат и времени, которые называются преобра­зованиями Галилея. Они основаны на двух аксиомах:

Ход времени одинаков во всех системах отсчета;

Размеры тела не зависят от скорости его движения.

Рассмотрим две системы отсчета – инерци­альную систему К (с координатами x,y,z), которую будем считать неподвижной, и систему К’(с координатами x’,y’,z’), движущуюся относительно системы К прямолинейно и равномерно с постоянной скоростью , направленной вдоль оси х. Отсчет времени начнем с того момента, ко­гда начала координат обеих систем совпадают. В произвольный момент времени t системы распо­ложены, как показано на рисунке 6.1. Скорость направлена вдоль ОО’, радиус-вектор, проведенный из О в О’ . 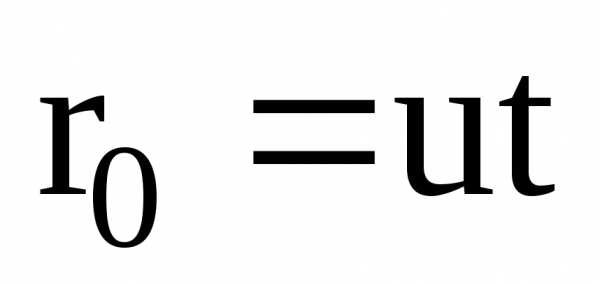Связь между координатами произ­вольной точки А в обеих системах будет иметь вид . В проекциях на оси координат это уравнение расписывается в следующем виде x = x’+ut; y = y’; z = z’. В классической механике предполагается, что ход времени не зависит от относи­тельного движения систем отсчета, откуда следует, чтоt =t’. Таким образом, мы получили совокупность четырех уравнений x = x’+ut; y = y’; z = z’; t =t’,

называемых преобразованиями Галилея.

Найдем правило сложения скоростей в классической механике. Для этого продиф­ференцируем выражение для r по времени и получим:

или .

Последнее выражение представляет собой правило сложения скоростей в классической механике: скорость материальной точки относительно системы К равна векторной сумме ее скорости относительно системы К’ и скорости системы К’ относительно К.

Найдем ускорение точки А в системе К, для этого продифференцируем формулу сложения скоростей по времени,

.

Мы получили, что, если система К’ движется относительно К прямолинейно и рав­номерно т.е. система К’ является инерциальной, то ускорения точки одинаковы в обеих системах. Следовательно, если на точку А не действуют другие тела (а=0), то и а’=0. Если ускорение какого-либо тела в двух произвольно выбранных инерциаль­ных системах отсчета одинаково, то согласно второму закону Ньютона силы, дейст­вующие на тело в системах К и К’ также будут одинаковыми. Следовательно, вто­рой закон Ньютона сохраняет вид в любой инерциальной системе отсчета.

Можно доказать, что и другие законы механики имеют одинаковый вид во всех инерциальных системах отсчета. Таким образом, можно сформулировать механический принцип относительности Галилея: при переходе от одной инерциальной системы отсчета к другой уравнения механики не изменяются, т.е. инвариантны по отношению к преобразованиям координат. Записанные соотношения справедливы лишь в случае u ‹‹ с, а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются наиболее об­щими преобразованиями Лоренца.

studfiles.net

Релятивистская механика — Юнциклопедия

Релятивистская механика — механика, учитывающая законы теории относительности, изучающая законы движения тел со скоростями, близкими к скорости света. Ничего еще не зная об этих законах, сразу можно утверждать: необходимое (но отнюдь недостаточное) требование к релятивистской механике таково — при «малых скоростях» v/с << 1 законы релятивистской механики должны переходить в законы механики Ньютона. Основание для такого утверждения состоит в том, что законы механики Ньютона проверены на многовековом опыте. (Слова «малые скорости» взяты в кавычки, чтобы подчеркнуть относительность этого понятия. Скажем, 100 км/с в данном случае ничтожно малая скорость: 10⁵м/с / 3•10⁸м/с.)

Приведем основные уравнения релятивистской механики.

Второй закон Ньютона формально имеет тот же вид, что и в классической механике:

dp^→/dt = F^→ (1)

где F^→ — сила.

Но в релятивистской механике формула, определяющая вектор импульса, выглядит так:

p^→ = mv^→/√(1-v²/c²). (1а)

Здесь m — масса покоя тела (масса в той системе, где тело покоится). Эта масса связана с энергией, «заключенной в теле», соотношением: Е = mc².

Второе основное соотношение — формула для кинетической энергии:

E_кин = [mc²/√(1-v²/c²) – mc²]. (2)

Прежде всего убедимся, что при v/c << 1 мы снова получим формулы ньютоновской механики. Для импульса это видно сразу. Пренебрегаем под корнем членом v²/c² и имеем: р^→ = mv^→.

Если точно так же поступить с формулой (2), получим нуль. Значит, такое приближение слишком грубо. В этом случае обратимся к математике и вспомним две следующие формулы.

Первая формула. Если α << 1, то √1—α ≈ 1-α/2 (с точностью до малых членов порядка а²). Доказывается прямым возведением в квадрат правой и левой частей.

Вторая формула. Если β << 1, то 1/(1-β) ≈ 1+β. Опять это верно с точностью до членов порядка β². Доказывается приведением к общему знаменателю. Тогда при v/с << 1

E_кин = mc²/√(1-v²/c²) – mc² ≈ mc²/(1-v²/2c²) – mc² ≈ mc²(1 + v²/2c²) – mc² = mv²/2.

В обоих случаях мы пренебрегали членами порядка v⁴/c⁴ и получали формулы ньютоновской механики.

Есть еще третья формула, связывающая полную энергию тела E_полн = E_кин = + mc² = mc²√(1-v²/c²) непосредственно с импульсом:

E_полн = c√(p² + mc²). (3)

Ее можно получить из первых двух формул с помощью простых арифметических расчетов. При p << mc мы снова придем к формулам механики Ньютона.

Но если v ~ с (хотя непременно v < с) законы релятивистской механики коренным образом отличаются от законов классической механики.

Например, как правило, вектор ускорения не параллелен силе. Это вытекает из формул (1) и (1а), но, чтобы получить этот результат, надо знать основы дифференцирования векторов. Ускорение ã = dṽ/d параллельно силе лишь в двух случаях — когда сила направлена параллельно скорости и когда она перпендикулярна скорости. Причем связь силы и ускорения различна. В первом случае:

F^→ = ma^→/(1-v²/c²)^3/2. (4)

Во втором:

F^→ = ma^→/(1-v²/c²)^1/2. (5)

В обоих случаях по мере приближения |v| к c требуется все большая рила для придания данного ускорения. И в первом и во втором случае сила стремится к бесконечности, когда |v| стремится к с. Однако, как видно из формул (4) и (5), разгонять частицу труднее, чем заставить ее «свернуть с пути».

Из теории относительности следует, что каждая частица в состоянии покоя имеет энергию Е = mс², причем эта энергия совершенно реальна. Ее можно использовать и необходимо учитывать.

Сегодня релятивистская механика во многом стала инженерной наукой. С ее помощью анализируют столкновения элементарных частиц, взаимодействие релятивистских частиц с ве^ ществом и вообще все процессы со скоростями, близкими к световой. Все современные ускорители заряженных частиц планируются и рассчитываются на основе релятивистской механики.

yunc.org