Формулы электромагнитной индукции
Если проводник замкнут, то есть является контуром, то в нем появляется ток индукции. Явление было открыто в 1831 г. М. Фарадеем.
Основной закон электромагнитной индукции
Основной формулой, при помощи которой определяют ЭДС индукции (), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает рассматриваемый контур:
где – скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.
При равномерном изменении магнитного потока основной закон электромагнитной индукции записывают как:
Формулы ЭДС индукции для частных случаев
ЭДС индукции для контура имеющего N витков, находящегося в переменном магнитном поле можно найти как:
где – потокосцепление.
Если прямолинейный проводник движется в однородном магнитном поле, то в нем появляется ЭДС индукции, равная:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
Разность потенциалов (U) на концах прямого проводника, движущегося в однородном магнитном поле с постоянной скоростью будет равна:
где – угол между направлениями векторов и .
При вращении плоского контура с постоянной скоростью в однородном магнитном поле вокруг оси, которая лежит в плоскости контура в нем появляется ЭДС индукции, которую можно вычислить как:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля .
Если вращающаяся рамка обладает N витками, при этом самоиндукцией рассматриваемой системы можно пренебречь, то:
Если проводник неподвижен в переменном магнитном поле, то ЭДС индукции можно найти как:
Примеры решения задач по теме «Электромагнитная индукция»
ru.solverbook.com
Формула индукции
В этом разделе мы рассмотрим только три вида индукции: электромагнитную индукцию, индукцию магнитного поля и электрическую индукцию и основные формулы, при помощи которых данные виды индукции вычисляют.
Формула индукции электрического поля
Электрическая индукция (или вектор электрического смещения ()) – это одна из основных векторных характеристик электрического поля. Формулой определяющей вектор электрической индукции является выражение:
где – вектор напряженности электрического поля; – вектор поляризации; – электрическая постоянная.
Для изотропного вещества индукция электрического поля связана с напряженность это поля как:
где – диэлектрическая проницаемость вещества.
Самой распространённой формулой, при помощи которой находят величину вектора индукции электростатического поля, является теорема Остроградского – Гаусса:
Поток () вектора электростатической индукции () в диэлектрике через произвольную замкнутую поверхность равен сумме свободных зарядов, которые находятся внутри рассматриваемой поверхности. В данной форме теорема Гаусса выполняется и для однородной и изотропной среды, так и для неоднородной анизотропной.
Формула вектора индукции магнитного поля
Модуль вектора равен частному от деления максимальной силы Ампера (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора :
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.
Основными законами, которыми пользуются чаще всего для расчета магнитных полей, являются: закон Био-Савара-Лапласа и теорема о циркуляции вектора магнитной индукции.
Формула электромагнитной индукции
Если проводник помещен в переменное магнитное поле, то в нем возникает электродвижущая сила – это сущность явления электромагнитной индукции.
Основной закон электромагнитной индукции состоит в следующем: ЭДС электромагнитной индукции () в контуре, помещенном в переменное магнитное поле, равна по величине скорости изменения магнитного потока (), который проходит через поверхность, которую ограничивает рассматриваемый контур. При этом знаки ЭДС и скорости изменения магнитного потока противоположны.
В системе международных единиц (СИ) закон электромагнитной индукции записывают так:
где – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур. (Часто индекс у магнитного потока опускают и обозначают его Ф). Когда вычисляют ЭДС индукции и магнитный поток, учитывают то, что направление нормали к плоскости контура () и направление его обода связаны. Вектор должен быть направлен так, чтобы из его конца обход контура проходил против часовой стрелки.
Примеры решения задач по теме «Индукция»
Формула закона электромагнитной индукции
Это основной закон, который используют при вычислениях, которые связаны с электромагнитной индукцией.
Формула данного закона выглядит следующим образом:
где – электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции. – магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность.
Магнитный поток, который пронизывает контур, может изменяться из-за разных причин, например, перемещения контура, его деформации, изменения самого магнитного поля. Полная производная в формуле закона электромагнитной индукции охватывает весь спектр действия этих причин.
Следует учесть, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки.
Знак минус в законе индукции отражает правило Ленца.
В виде (1), закон электромагнитной индукции записывается в международной системе единиц (СИ).
Если изменение магнитного потока происходит равномерно, то формулу закона электромагнитной индукции можно записать как:
Формулу закона для электромагнитной индукции, если контур состоит из N витков, соединенных последовательно, записывают в виде:
где – потокосцепление.
Результаты применения основного закона электромагнитной индукции
Формулы ЭДС индукции для частных случаев
ЭДС индукции в прямом проводнике, имеющем длину l, движущемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения () перпендикулярна вектору магнитной индукции (), равна:
Разность потенциалов (U), возникающая на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью v равна:
где – угол между направлением вектора скорости и направлением вектора магнитной индукции.
Если в однородном магнитном поле вращается плоский контур со скоростью , при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:
где S – площадь, которую ограничивает виток; – мгновенное значение угла между и вектором нормали к плоскости рамки; – поток самоиндукции витка.
Если в рамке, вращающейся со скоростью в однородном магнитном поле, имеется N витков, то
в формуле (6) самоиндукцией витков пренебрегли.
Пусть проводник находится в покое, при этом изменяется во времени само магнитное поле, тогда ЭДС индукции можно найти как:
Примеры решения задач по теме «Закон электромагнитной индукции»
ru.solverbook.com
Конспект “Электромагнитная индукция” – УчительPRO
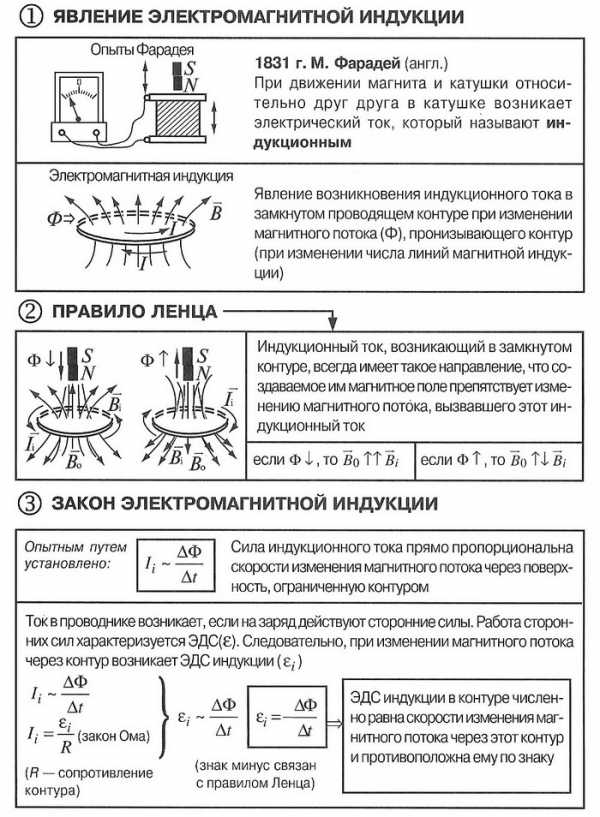
«Электромагнитная индукция»
Электромагнитная индукция — это явление, которое заключается в возникновении электрического тока в замкнутом проводнике в результате изменения магнитного поля, в котором он находится. Это явление открыл английский физик М. Фарадей в 1831 г. Суть его можно пояснить несколькими простыми опытами.
Описанный в опытах Фарадея принцип получения переменного тока используется в индукционных генераторах, вырабатывающих электрическую энергию на тепловых или гидроэлектростанциях. Сопротивление вращению ротора генератора, возникающее при взаимодействии индукционного тока с магнитным полем, преодолевается за счет работы паровой или гидротурбины, вращающей ротор. Такие генераторы
Вихревые токи, или токи Фуко
Если массивный проводник поместить в переменное магнитное поле, то в этом проводнике благодаря явлению электромагнитной индукции возникают вихревые индукционные токи, называемые токами Фуко.
Вихревые токи возникают также при движении массивного проводника в постоянном, но неоднородном в пространстве магнитном поле. Токи Фуко имеют такое направление, что действующая на них в магнитном поле сила тормозит движение проводника. Маятник в виде сплошной металлической пластинки из немагнитного материала, совершающий колебания между полюсами электромагнита, резко останавливается при включении магнитного поля.
Во многих случаях нагревание, вызываемое токами Фуко, оказывается вредным, и с ним приходится бороться. Сердечники трансформаторов, роторы электродвигателей набирают из отдельных железных пластин, разделенных слоями изолятора, препятствующего развитию больших индукционных токов, а сами пластины изготовляют из сплавов, имеющих высокое удельное сопротивление.
Электромагнитное поле
Электрическое поле, созданное неподвижными зарядами, является статическим и действует на заряды. Постоянный ток вызывает появление постоянного во времени магнитного поля, действующего на движущиеся заряды и токи. Электрическое и магнитное поля существуют в этом случае независимо друг от друга.
Явление электромагнитной индукции демонстрирует взаимодействие этих полей, наблюдаемое в веществах, в которых есть свободные заряды, т. е. в проводниках. Переменное магнитное поле создает переменное электрическое поле, которое, действуя на свободные заряды, создает электрический ток. Этот ток, будучи переменным, в свою очередь порождает переменное магнитное поле, создающее электрическое поле в том же проводнике, и т. д.
Совокупность переменного электрического и переменного магнитного полей, порождающих друг друга, называется электромагнитным полем. Оно может существовать и в среде, где нет свободных зарядов, и распространяется в пространстве в виде электромагнитной волны.
Классическая электродинамика — одно из высших достижений человеческого разума. Она оказала огромное влияние на последующее развитие человеческой цивилизации, предсказав существование электромагнитных волн. Это привело в дальнейшем к созданию радио, телевидения, телекоммуникационных систем, спутниковых средств навигации, а также компьютеров, промышленных и бытовых роботов и прочих атрибутов современной жизни.
Краеугольным камнем теории Максвелла явилось утверждение, что источником магнитного поля может служить одно только переменное электрическое поле, подобно тому, как источником электрического поля, создающим в проводнике индукционный ток, служит переменное магнитное поле. Наличие проводника при этом не обязательно — электрическое поле возникает и в пустом пространстве. Линии переменного электрического поля, аналогично линиям магнитного поля, замкнуты. Электрическое и магнитное поля электромагнитной волны равноправны.
Электромагнитная индукция в схемах и таблицах
(Явление электромагнитной индукции, опыты Фарадея, правило Ленца, закон электромагнитной индукции, вихревое электрическое поле, самоиндукция, индуктивность, энергия магнитного поля тока)

Дополнительные материалы по теме:
Конспект урока «Электромагнитная индукция».
Следующая тема: «».
Электромагнитная индукция
5 (100%) 2 votesuchitel.pro
формула явления, силы индукционного тока и скорости изменения магнитного потока
В нашем мире все виды существующих сил, за исключением сил тяготения, представлены электромагнитными взаимодействиями. Во Вселенной, несмотря на удивительное разнообразие воздействий тел друг на друга, в любых веществах, живых организмах всегда встречается проявление электромагнитных сил. Как произошло открытие электромагнитной индукции (ЭИ), расскажем ниже.
…
Вконтакте
Google+
Мой мир
Открытие ЭИ
 Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.
Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.
Так нельзя ли добиться его возникновения посредством магнитного поля — подобную задачу поставил Майкл Фарадей. В 1821 году он отметил это свойство в своем дневнике о превращении магнетизма в электричество.
Успех к ученому пришел не сразу. Лишь глубокая уверенность в единстве природных сил и упорный труд привели его через десять лет к новому великому открытию.
Решение задачи долго не давалось Фарадею и другим его коллегам, потому как они пытались получить электричество в неподвижной катушке, используя действие постоянного магнитного поля. Между тем, впоследствии выяснилось: изменяется количество силовых линий, пронизывающих провода, и возникает электроэнергия.
Явление ЭИ
Процесс появления в катушке электричества в результате изменения магнитного поля характерен для электромагнитной индукции и определяет это понятие. Вполне закономерно, что разновидность тока, возникающего в ходе данного процесса, называется индукционным. Эффект сохранится, если саму катушку оставить без движения, но перемещать при этом магнит. С использованием второй катушки можно и вовсе обойтись без магнита.
Если пропустить электричество через одну из катушек, то при их взаимном перемещении во второй возникнет индукционный ток. Можно надеть одну катушку на другую и менять величину напряжения одной из них, замыкая и размыкая ключ. При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй.
Закон
Во время опытов легко обнаружить, что увеличивается число пронизывающих катушку силовых линий — стрелка используемого прибора (гальванометр) смещается в одну сторону, уменьшается – в иную. Более тщательное исследование показывает, что сила индукционного тока прямо пропорциональна скорости изменения числа силовых линий. В этом заключен основной закон электромагнитной индукции.
Данный закон выражает формула:
Она применяется, если за период времени t магнитный поток изменяется на одну и ту же величину, когда скорость изменения магнитного потока Ф/t постоянна.
Важно! Для индукционных токов справедлив закон Ома: I=/R, где — это ЭДС индукции, которую находят по закону ЭИ.
Замечательные опыты, проведенные когда-то знаменитым английским физиком и ставшие основой открытого им закона, сегодня без особого труда способен проделать любой школьник. Для этих целей используются:
- магнит,
- две проволочные катушки,
- источник электроэнергии,
- гальванометр.
 Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.
Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.
Поворачивая, наклоняя и перемещая ее вверх и вниз, мы меняем число силовых линий магнитного поля, пронизывающих ее витки.
Гальванометр регистрирует возникновение электричества с постоянно меняющимися в ходе опыта величиной и направлением.
Находящиеся же относительно друг друга в покое катушка и магнит не создадут условий и для возникновения электричества.
Это интересно! Что такое закон всемирного тяготения: формула великого открытия
Другие законы Фарадея
На основе проведенных исследований были сформированы еще два одноименных закона:
- Суть первого состоит в такой закономерности: масса вещества m, выделяемая электрическим напряжением на электроде, пропорциональна количеству электричества Q, прошедшему через электролит.
- Определение второго закона Фарадея, или зависимости электрохимического эквивалента от атомного веса элемента и его валентности формулируется так: электрохимический эквивалент вещества пропорционален его атомному весу, а также обратно пропорционален валентности.
Из всех существующих видов индукции огромное значение имеет обособленный вид данного явления – самоиндукция. Если мы возьмем катушку, которая имеет большое количество витков, то при замыкании цепи, лампочка загорается не сразу.
На этот процесс может уйти несколько секунд. Очень удивительный на первый взгляд факт. Чтобы понять, в чем здесь дело, необходимо разобраться, что же происходит в момент замыкания цепи. Замкнутая цепь словно «пробуждает» электроток, начинающий свое движение по виткам провода. Одновременно в пространстве вокруг нее мгновенно создается усиливающееся магнитное поле.
Катушечные витки оказываются пронизанными изменяющимся электромагнитным полем, концентрирующимся сердечником. Возбуждаемый же в витках катушки индукционный ток при нарастании магнитного поля (в момент замыкания цепи) противодействует основному. Мгновенное достижение им своего максимального значения в момент замыкания цепи невозможно, оно «растет» постепенно. Вот и объяснение, почему лампочка не вспыхивает сразу. Когда цепь размыкается, основной ток усиливается индукционным в результате явления самоиндукции, и лампочка ярко вспыхивает.
Важно! Суть явления, названного самоиндукцией, характеризуется зависимостью изменения, возбуждающего индукционный ток электромагнитного поля от изменения силы текущего по цепи электротока.
Направление тока самоиндукции определяет правило Ленца. Самоиндукция легко сравнима с инерцией в области механики, поскольку оба явления обладают схожими характеристиками. И действительно, в результате инерции под влиянием силы тело приобретает определенную скорость постепенно, а не сиюминутно. Не сразу – под действием самоиндукции — при включении батареи в цепь появляется и электричество. Продолжая сравнение со скоростью, заметим, он так же не способен мгновенно исчезнуть.
Вихревые токи
 Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции.
Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции.
Специалисты знают, что металлические трансформаторные сердечники, якоря генераторов и электродвигателей никогда не бывают сплошными. При их изготовлении на отдельные тонкие листы, из которых они состоят, накладывается слой лака, изолирующий один лист от другого.
Нетрудно понять, какая сила заставляет человека создавать именно такое устройство. Под действием электромагнитной индукции в переменном магнитном поле сердечник пронизывают силовые линии вихревого электрополя.
Представим, что сердечник изготовлен из сплошного металла. Поскольку его электрическое сопротивление невелико, возникновение индукционного напряжения большой величины было бы вполне объяснимым. Сердечник бы в итоге разогревался, и немалая часть электрической энергии терялась бесполезно. Кроме того, возникла бы необходимость принятия специальных мер для охлаждения. А изолирующие слои не позволяют достигать больших величин.
Индукционные токи, присущие массивным проводникам, называются вихревыми не случайно – их линии замкнуты подобно силовым линиям электрополя, где они и возникают. Чаще всего вихревые токи применяются в работе индукционных металлургических печей для выплавки металлов. Взаимодействуя с породившим их магнитным полем, они иногда становятся причиной занимательных явлений.
Возьмем мощный электромагнит и поместим между вертикально расположенными его полюсами, к примеру, пятикопеечную монету. Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды.
 Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.
Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.
Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды. Передвижение монеты напоминает перемещение тела в вязкой среде. Почему такое происходит.
По правилу Ленца направления возникающих при передвижении монеты вихревых токов в неоднородном магнитном поле таковы, что поле магнита выталкивает монету вверх. Эту особенность используют для «успокоения» стрелки в измерительных приборах. Алюминиевая пластина, находящаяся между магнитными полюсами, прикрепляется к стрелке, и вихревые токи, возникающие в ней, способствуют быстрому затуханию колебаний.
Демонстрацию явления электромагнитной индукции поразительной красоты предложил профессор Московского университета В.К. Аркадьев. Возьмем свинцовую чашу, обладающую сверхпроводящей способностью, и попробуем уронить над ней магнит. Он не упадет, а будет словно «парить» над чашей. Объяснение здесь простое: равное нулю электрическое сопротивление сверхпроводника способствует возникновению в нем электричества большой величины, способных сохраняться продолжительное время и «удерживать» магнит над чашей. По правилу Ленца, направление магнитного поля их таково, что отталкивает магнит и не дает ему упасть.
Изучаем физику — закон электро-магнитной индукции
Правильна формулировка закона Фарадея
Вывод
Электромагнитные силы – это силы, которые позволяют людям видеть окружающий мир и чаще других встречаются в природе, например, свет — тоже пример электромагнитных явлений. Жизнь человечества невозможно представить без данного явления.
Это интересно! Специальная теория относительности Эйнштейна: кратко и простыми словами
uchim.guru
Явление электромагнитной индукции
Явление электромагнитной индукции было открыто М. Фарадеем в 1831 г. Это явление заключается в том, что если проводящий контур (проводник) поместить в переменное магнитное поле, то в контуре возникает электродвижущая сила индукции (ЭДС индукции). Если такой контур будет замкнут, то в нем потечет электрический ток, который называют током индукции.
Индукционный ток возникает в контуре, если он или его часть пересекает линии магнитной индукции, такой вывод сделал Фарадей. Магнитное поле – это вихревое поле, его линии всегда замкнуты. Линии индукции сцеплены с проводящим контуром. Изменение количества линий индукции, которые охвачены контуром, возникает, если они пересекают контур.
Значение явления электромагнитной индукции заключается в том, что оно показывает связь между электрическим и магнитными полями. Электрические токи порождают магнитные поля, а переменные магнитные поля вызывают токи.
Закон электромагнитной индукции
Закон электромагнитной индукции получен М. Фарадеем, современную формулировку данного закона мы знаем в интерпретации Максвелла.
ЭДС электромагнитной индукции () в контуре, помещенном в переменное магнитное поле, равна по величине скорости изменения магнитного потока (), который проходит через поверхность, которую ограничивает рассматриваемый контур. При этом знаки ЭДС и скорости изменения магнитного потока противоположны.
В системе международных единиц (СИ) закон электромагнитной индукции записывают так:
где – скорость изменения магнитного потока сквозь площадь, которую ограничивает контур. (Часто индекс у магнитного потока опускают и обозначают его Ф). Когда вычисляют ЭДС индукции и магнитный поток, учитывают то, что направление нормали к плоскости контура () и направление его обода связаны. Вектор должен быть направлен так, чтобы из его конца обход контура проходил против часовой стрелки.
Если контур составлен из N витков, соединенных последовательно (имеем соленоид), то закон электромагнитной индукции записывают как:
где величина называется потокосцеплением.
Знак минус в законе (1) отображает закон Ленца, который говорит о том, что ток индукции всегда направлен так, что созданный им магнитный поток, через поверхность, ограничиваемую контуром, старается уменьшить изменения магнитного потока, которые вызывают возникновение этого тока.
Магнитный поток, который охватывает контур, способен изменяться, если контур перемещается в поле или повергается деформации, магнитное поле может изменяться во времени. Величина , являясь полной производной, способна учесть все эти причины.
При движении контура в постоянном магнитном поле, ЭДС индукции возникает во всех частях контура, которые пересекают линии магнитной индукции поля. Результирующую ЭДС находят как алгебраическую сумму ЭСД участков.
Примеры решения задач
ru.solverbook.com
Явление электромагнитной индукции — Мегаобучалка
Энергия магнитного поля
Основные формулы
1. Закон Фарадея для электромагнитной индукции
2. Максвелловская формула явления электромагнитной индукции
где S – произвольная поверхность, опирающаяся на контур l.
3. ЭДС индукции в движущемся проводнике
4. ЭДС индукции во вращающемся проводнике
5. Переменная ЭДС
6. Самоиндукция
7. Взаимная индукция .
8. Коэффициент самоиндукции и взаимной индукции
9. Токи замыкания и размыкания цепей
10. Энергия магнитного поля в электрической цепи
11. Объёмная плотность энергии магнитного поля
12. Энергия неоднородного магнитного поля, заключённая в объёме V:
Примеры решения задач
Задача 1. Проволочное кольцо радиусом 10 см имеет сопротивление 2 Ом. Какой заряд течёт по кольцу с одинаковой скоростью, если однородное магнитное поле с индукцией 102 Тл быстро изменит своё направление на противоположное?
Дано: Решение
r = 10 см = 0,1 м При изменении направления индукции магнитного поля
R = 2 Ом в кольце появится кратковременный индукционный ток
B = 102 Тл за счёт изменения угла между силовыми линиями поля и
qi – ? нормалью, проведённой к плоскости кольца (рис.7.1).
α = 0 α2 = 1800.
а) б)
Рис.7.1
Магнитный поток сквозь площадь S, ограниченную кольцом:
Изменение магнитного потока
Поскольку α2 = 1800и α = 0, то
По закону Фарадея определим ЭДС индукции:
В замкнутой электрической цепи кольца ЭДС индукции вызывает появление индукционного тока, величина которого определяется законом Ома.
В свою очередь сила тока и величина индукционного заряда связаны соотношением
Объединяя формулы (1) – (3), для заряда окончательно получим
Подставим числовые значения:
Задача 2. В однородном магнитном поле с индукцией 0,05 Тл вращается стержень длиной 50 см с угловой скоростью 15 рад/с. Сопротивление стержня 0,5 Ом. Какой силы индукционный ток проходит по стержню, если индукция магнитного поля направлена перпендикулярно плоскости вращения стержня?
| Дано: В = 0,05 Тл ω = 15 рад/с l = 50 см = 0,5 м R = 0,5 Ом | Решение При вращении стержня в магнитном поле на его концах появляется разность потенциалов U, равная по модулю ЭДС индукции εi : U = εi . По закону Фарадея |
| I i – ? |
где dФ - мгновенное значение магнитного потока через поверхность dS, пересекаемую стержнем за время dt. dS определим как площадь треугольника (рис.7.2):
B = const
Рис.7.2
Тогда ЭДС индукции
и сила индукционного тока
Подставим числовые значения:
Задача 3. В длинном прямом соленоиде с радиусом сечения 5 см и густотой намотки 200 витков на метр изменяют ток с постоянной скоростью 5 А/с. Найти модуль вектора напряжённости вихревого электрического поля как функцию расстояния от оси соленоида и рассчитать её на расстоянии 3 см от центра.
| Дано: n = 200 витк /м r1 = 3 см = 3 . 10-2 м dI / dt = 5 А/с R = 5 см = 5 . 10-2 м | Решение Изменяющийся ток в соленоиде создаёт изменяющееся магнитное поле внутри соленоида, которое в свою очередь порождает вихревое электрическое поле (рис.7.3). |
| Eвихр (r) – ? E1 – ? |
Воспользуемся первым уравнением Максвелла
(1)
где – длина контура интегрирования, S – поверхность, натянутая на контур .
В качестве контура интегрирования выберем окружность радиусом r, тогда векторы Eвихр и dl будут направлены вдоль одной прямой, а величина вектора Eвихр будет одинаковой для всех точек окружности.
Рис.7.3 Рис. 7.4
С учётом того, что однородное магнитное поле сосредоточено только внутри соленоида, для всех точек, удовлетворяющих условию r < R, имеем
(2)
(3)
Подставим (2) и (3) в выражение (1):
откуда
(4)
Индукция поля в соленоиде
(5)
Подставляя (5) в (4), для напряжённости вихревого электрического поля окончательно получим
(6)
Величина Евихр линейно увеличивается при увеличении расстояния r до значения, определяемого из условия (6) при r = R (рис.7.4):
Подставим в числовые значения:
Задача 4. Соленоид с индуктивностью 0,1 Гн и сопротивлением 0,02 Ом включен в электрическую цепь (рис.7.5). Сопротивление резистора R = 0,03 Ом, ЭДС источника тока 2 В. Найти количество электричества (заряд), которое пройдет по соленоиду при размыкании ключа К ?
| Дано: L = 0,1 Гн R = 0,03 Ом ε0 = 2 В R0 = 0,02 Ом | Решение При разомкнутом ключе К по соленоиду протекает ток I0 = ε0 /R0. При размыкании ключа К ток в соленоиде и обусловленный им магнитный поток начнут уменьшаться. | |
| q – ? | ||
| Возникшая в соленоиде ЭДС индукции εi=-dФ/dtсоздаёт индукционный ток I, протекающий по соленоиду и сопротивлению R. Индукционный ток перенесёт количество электричества через соленоид: Рис. 7.5 (1) Сила электрического тока может быть определена по закону Ома для замкнутой цепи: | ||
(2)
Подставляя (2) в выражение для заряда (1), получаем
С учётом Ф0 = L . I0 (потокосцепление самоиндукции в начальный момент времени) окончательно находим
Подставим числовые значения:
Задача 5. Два концентрических тонких проводника в форме окружностей с радиусами a и b лежат в одной плоскости. Имея в виду, что a
| Дано: a b (a<<b) | Решение Для нахождения взаимной индуктивности воспользуемся выражением, определяющим потокосцепление взаимной индукции: |
| Lab – ? Фab – ? |
где Фаb – магнитный поток, сцепленный с контуром a и обусловленный током Ib, протекающим по контуру b (рис.7.6). С другой стороны, магнитный поток может быть вычислен по общему правилу:
.
| Так как a<<b, то значение Bb можно считать постоянным в пределах круга радиусом a, равным индукции в центре кругового тока радиусом b и направленным по нормали к поверхности контура. Учитывая это, получим Рис. 7.6 |
Отсюда
Для нахождения магнитного потока через поверхность контура b Фab при протекании тока Ia по контуру a воспользуемся тем, что Lab = Lba. Тогда
Подставляя значение Lba и Ia = I, находим
Задача 6. На железный тор намотано 500 витков. Найти энергию магнитного поля, если при токе 2 А магнитный поток через поперечное сечение тора 1 мВб.
По теореме о циркуляции вектора Н
По определению магнитного потока
Используя это, получим
Подставим числовые значения:
Задача 7. Ток 10 А течёт по длинному прямому проводнику круглого сечения с магнитной проницаемостью 103. Найти энергию магнитного поля внутри провода в расчёте на единицу его длины.
окружность радиусом r.
.
В нашем случае
где S = πr2 – площадь круга радиусом r.
Тогда ,
или . Рис. 7.8 (4)
Подставим формулы (2), (3) и (4) в интеграл (1):
Энергия магнитного поля, приходящаяся на единицу длины провода:
Подставим числовые значения:
megaobuchalka.ru
