Функция find в mathcad – Find(x) – Mathcad

8.3. Функции в MathCad

Вид одинаковый:

Имя(арг1,арг2)

8.4. выражения в MathCAD

Выражение – набор операторов(то действие которое выполняется) и операндов(над чем). Может содержать функции встроенные, пользователя.

Shift + : – присвоить

F(x):= x²

8.5. Дискретный аргумент.

Можно в одном имени, записать сразу же много значений.

W:=-5,-4.5:5

Нажимаем вертикальное, получаем горизонтальное

Нач, нач+шаг, конечное. Отображается не более 16 значений.

W= f(w) =

Если шаг равен единицы, то можно не указывать шаг.

8.6. действия с массивами.

8.6.1. понятие массива в MathCAD.

Массивы в MathCAD бывают 3 видов

С другими типами не работает

8.6.2. способы создания массивов

1. В ручную.

2. С помощью нижних индексов

3. С помощью дискретного аргумента, для перечисления индексов

4. Считывание вектора из внешнего файла. Записать в блокноте.t:=READRPN(“D:\asdf.txt”)

8.6.3. стандартные функции и операции для работы с векторами и матрицами

1. Сложение

2. Умножение

3. деление

4) Умножение векторов (скалярно – число , векторно – др)

5) вычисление длины вектора

6) умножение матриц

7) транспонирование

8) обратная матрица

9) сумма элементов вектора

10) выделение столбца из матрицы

11) RANK

12) max, min

13) sort

14) revers

15) rsort(M2,1) = (1 строку по возрастанию)

16) csort

8.6.4. Решение СЛУ

8.7. Работа с графиками в MathCAD

8.7.1. построение графика функции в одной переменной в декартовой системе координат.

1) задаем функцию

2) задаем дискретный аргумент, для которого будем строить график.

3) вызываем шаблон графика

8.7.2. построение несколько графиков на одном шаблоне в декартовых координатах

1 ситуация: когда строится график для одного значения аргумента

2 ситуация: для разных значений аргумента

3 ситуация: строится семейство кривых

• Задается несколько функций

• Задается значение аргумента

• Выбирается шаблон графика, имя аргумента

• На одном шаблоне можно построить до 16 графиков

  • Задаем функции

  • Задаем аргументы

  • Вызываем шаблон графиков

  • Можно построить 10 графиков, порядок совпадает.

    • Задаем функции одной переменной с параметром

    • F(a,x):=a*x^2

    • Задаем аргумент

    • Вызываем шаблон графиков, внизу = икс, нарисовать клеща с брюшком

8.7.3. Построение графика функции в полярных координатах.

• Задается функция d(r,ф)

• Задаем ф(от 0 до 2П.)

• Кардиоида( в полярных)

8.7.4. построение функций заданных параметрически в декартовых координатах.

Задача: построить окружность в декартовых координатах.

X=r*cos(a)

Y=r*sin(a)

8.7.5. построение вектора в декартовых координатах

• Задаем индексы элементов

• Задаем вектор

• Выбираем шаблон графика

• Изменить параметры графика (формат – nrace – points)

8.7.6. Построение одного вектора относительно другого

• Количество элементов должно быть одинаково

• Выбираем шаблон графика

• Россыпь бриллиантов из 300 элементов

(x²+y²-2ax)²-4a²(x²+y²)=0

X=a*cost(1+cost)

Y=a*sin t(1+cost)

8.7.7. Построение поверхностей.

Поверхность описывается функцией двух переменных.

1. Задаем функцию двух переменных. F(x,y):=x²-32y+x*y²

2. Задаем шаблон поверхности.

3. Внизу пишем только имя функции.

4. ПКМ на графике, формат – Квикплот дата – 1 – x, 2- y.

8.8. решение уравнений в MathCAD

1. привести уравнение к виду f(x)=0,

2. построить график этой функции.

3. подобрать график так чтобы корни уравнения было видно.

4. Задаем приближенное значение корня.w1:=1

5. находим настоящие значение. W2:=root(g(w1),w1), w2=

Замечания:

8.8.1. Решение полиномиальных уравнений.

1. 20x⁴-2.5x³+11x-23=0

2. задаем функцию. F(x):=

3. строим график.

4. полирутс. – много корней. Задаем вектор из коэффициентов уравнений . с конца. Polyroots(t)=

8.9. Решение оптимизационных задач в MathCAD

Оптимизационные задачи – на поиск оптимального значения.

Такие задачи решаются с помощью вычислительного блока Given – надо закрывать этот блок.

8.9.1. структура блока given.

• начальные значения

• Given

• уравнения

• ограничения

• окончание блока. Осуществляется одной из функций. Find(ищет конкретное решение) Minimize, Maximize, Minerr(ищет ближайшее значение к правильному).

8.9.2. определение экстремумом функций.

1. F(x)=50*sin(x)-e^x

2. Нужно найти max min на отрезке (-2;3,07) это x/

3. Шаблон графика

4. Ищем min:

X:=-1.5

Given

F(x)=50*sin(x)-e^x

x>-2

x<3

r:=Minimize(F,x)

r=

f(r)=

5. Для max создаем новый блок

X:=1.8

Given

F(x)=50*sin(x)-e^x

x>-2

x<3

r1:=Maximize(F,x)

r1=

f(r1)=

8.9.3. решение систем уравнений.

X²+Y²=25

Y=X+3

1. Строим графики функций.

2. Задаем диапозоны

3. Шаблон графика

4. Решение проводится для каждого корня отдельно.

5. См. 9.8.2.

8.9.4. решение оптимизационных задач.

Задача: индивидуальный предприниматель получил разрешение на постройку автостоянки возле стены завода. В разрешение оговорено длина трех сторон стоянки не больше 250 метров. Подобрать размеры сторон, так что бы площадь была максимальной.

Решение:

X:=6

Y:=6

S(x,y)=x*y

Given

x>6

y>6

2*x+y<=250

D:=Maximize(S,x,y)

д/з решить оптимизационную задачу из лабороторных в ексель

8.10. символьные вычисления в MathCAD

• Упростить выражение simplify

• Лучше использовать буквы, которые не встречались

• Solve – решение

• Неопределенные

8.11 обработка экспериментальных данных в MathCAD

8.11.1. общие понятия обработки экспериментальных данных

Суть: в том, что бы построить теоретическую зависимость, которая хорошо бы описывала существующие экспериментальные данные.

1 группа : аппроксимация – метод замена облака экспериментальных точек какой-либо простой функцией, обязательно проходящей через экспериментальные точки.

• Интерполяция – определение значение аппроксимирующей функции внутри облака экспериментальных точек

• Экстраполяция – предсказание значения аппроксимирующей функции вне облака экспериментальных точек.

2 группа: регрессия – замена облака экспериментальных точек какой-либо простой функцией, необязательно проходящей через экспериментальные точки.

В случае линейной регрессии замена экспериментальных точек производится прямой, такой, что сумма квадратов отклонений экспериментальных точек от теоретической прямой будет минимальным.

studfiles.net

Встроенная функция MathCAD polyroots (v).

Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v.

Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.

 

Решение систем уравнений

 

Системы уравнений в MathCAD решаются в следующем порядке:

1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически;

2. Записывается директива Given, и после нее записываются уравнения системы. Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как <Ctrl>+<=>.

3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.

 

 

Рисунок 3.1.4 – Нахождение корней полинома при помощи функции

polyroots

 

 

Пример 3.3 Найти решение системы уравнений

.

Процесс решения данной системы уравнений показан на рисунке 3.2.1

В результате функция Find вернула вектор-столбец и . Это значит, что решением системы уравнений являются значения и .

 

Символьное решение уравнений, неравенств и систем уравнений

 

Для символьного решения уравнений и неравенств надо выполнить следующее:

1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic.

2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить.

3. Щёлкнуть вне области решения, чтобы получить результат.

 

 

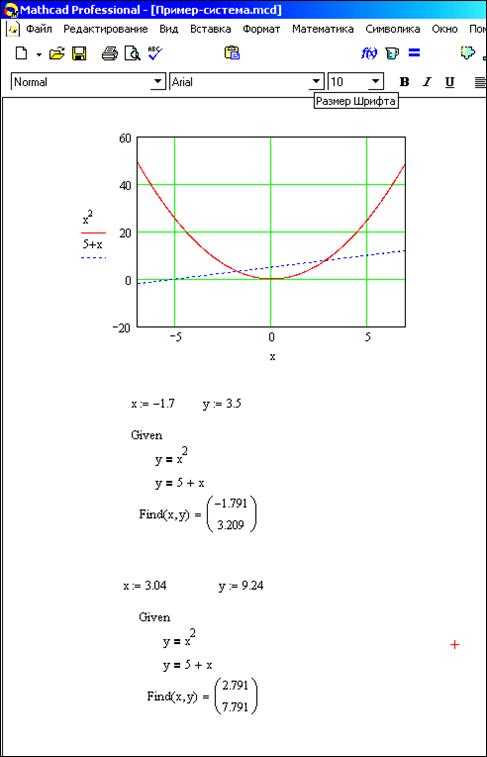
Рисунок 3.2.1 – Пример решения системы уравнений

 

 

При символьном решении уравнений и неравенств следует вводить знаки =, , находящиеся на панели инструментов Boolean.

При символьном решении системы уравнений после Find надо ввести с панели инструментов Simbolic.

Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3.3.1

 

 

 

 

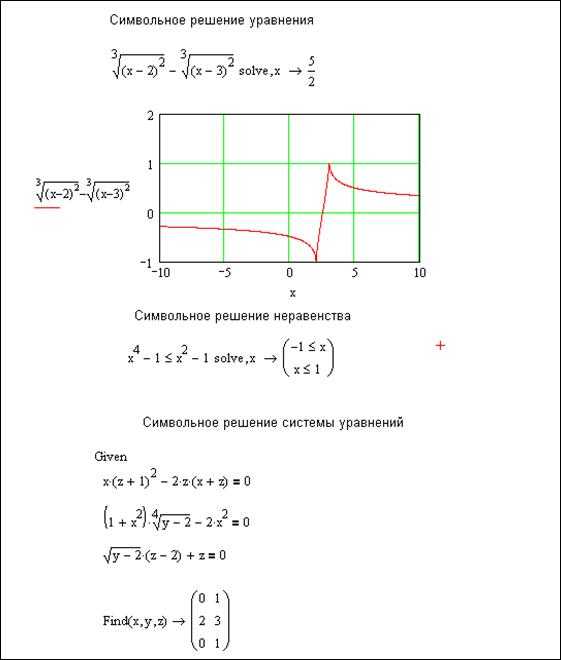
Рисунок 3.3.1 – пример символьного решения уравнения, неравенства

и системы уравнений

 

Некоторые возможности MathCAD

В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения.

Комплексные числа в MathCAD

MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j. Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.

MathCAD содержит следующие операторы и функции для работы с комплексными числами:

Re(z) – вещественная часть z.

Im(z) – мнимая часть z.

arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.

– модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».

– Комплексно сопряжённое к z= a+bi , то есть a-bi. Чтобы применить к выражению этот оператор, выделите его и нажмите клавишу двойные кавычки «”».

При использовании в комплексной области многие функции являются многозначными. Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.

Рисунок 3.4.1 – Комплексные числа в MathCAD

 

На рисунке 3.4.1 показан пример использования возможностей MathCADпри работе с комплексными числами.

 



infopedia.su

Оптимизация функций одной и нескольких переменных в PTC MathCAD

1. Поиск экстремума функции

Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.

Для решения задач поиска максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize. Все они используют те же градиентные численные методы, что и функция Find для решения уравнений.

2. Экстремум функции одной переменной

Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис.2 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).

В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.

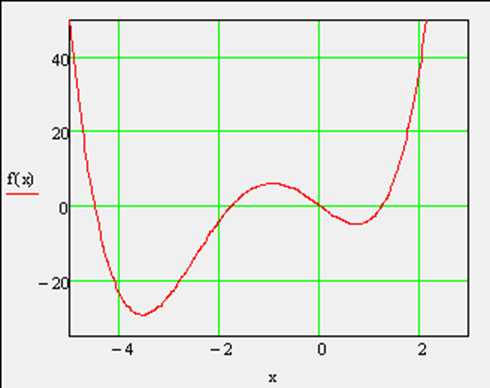Рис. 1. График функции f(х)=х⁴+5х³-10х

Построим график заданной функции (рис.1). По графику видны участки локальных экстремумов функции.

Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.

· Minimize (f, x1, … ,хм) — вектор значений аргументов, при которых функция f достигает минимума;

· Maximize (f, х1, … ,хм) — вектор значений аргументов, при которых функция f достигает максимума;

• f (x1, … , хм,…) — функция;

• x1, … , xм — аргументы, по которым производится минимизация (максимизация).

Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис.1) без дополнительных условий показаны в листинге на рис.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.

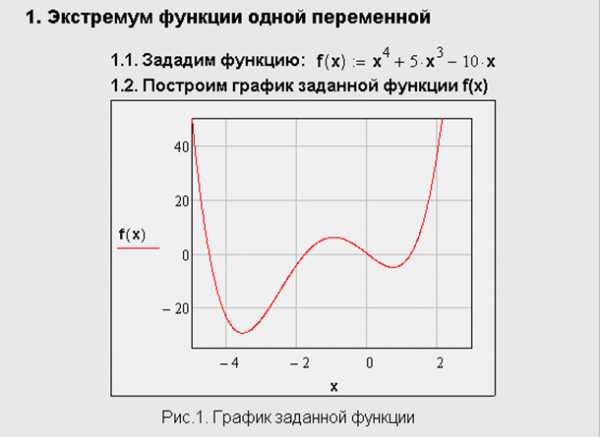
Рис.2. Поиск локальных экстремумов функции одной переменной

Как видно из листинга, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются локальные различные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).

3. Условный экстремум

В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. На рис.3 показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.

Рис. 3. Три примера поиска условного экстремума функции

Не забывайте о важности выбора правильного начального приближения и в случае задач на условный экстремум. Например, если вместо условия — 3<х<0 в последнем примере листинга задать -5<х<0, то при том же самом начальном х=-10 будет найден максимум Maximize(f,x) =-0.944, что неверно, поскольку максимальное значение достигается функцией f (х) на левой границе интервала при х=-5. Выбор начального приближения х=-4 решает задачу правильно, выдавая в качестве результата Maximize (f ,x) =-5.

4. Экстремум функции многих переменных

Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Поэтому ограничимся примером (рис.4) нахождения минимума функции, показанной в виде графика трехмерной поверхности (рис. 4).

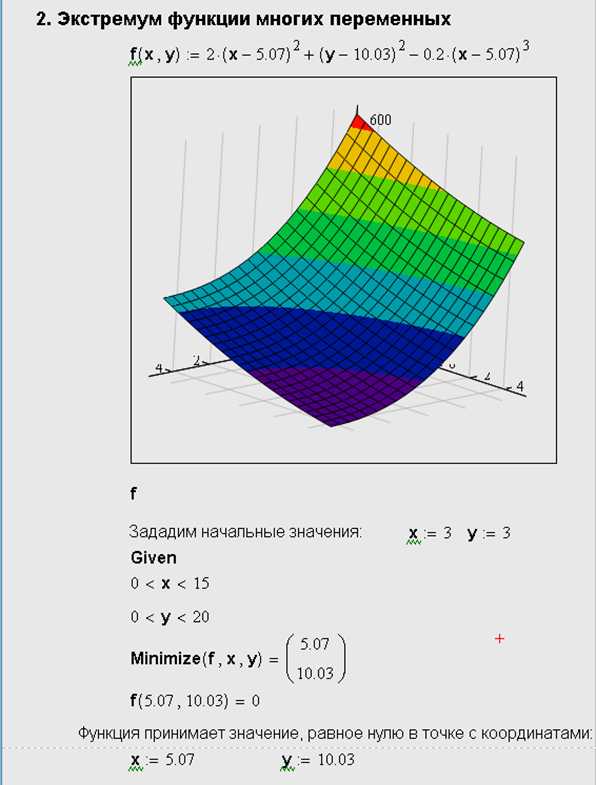
Рис. 4. Минимум функции двух переменных

Поиск минимума можно организовать и с помощью функции Minerr. Для этого в листинге (рис.4) надо поменять имя функции Minimize на Minerr, а после ключевого слова Given добавить выражение, приравнивающее функцию f (х,у) значение, заведомо меньшее минимального, например f (х,у) =0.

Скачать пример

cadregion.ru

Урок 5. Переменные и функции в Mathcad

Возможности Mathcad можно в полной мере оценить только при использовании переменных и функций.

Два знака равенства

В выражениях Вам необходимо использовать числа (константы), переменные, операторы и знаки равенства. В повседневной жизни мы используем знак равенства = для различных операций. Mathcad, однако, различает эти операции. Наиболее важные из них:

• определение (присвоить значение) – вводится через двоеточие [:]
• вычисление – вводится через знак равенства [=]

Оператор определения не менее важен, чем оператор вычисления. Значение выражения y можно отобразить только после присвоения ему какого-либо значения. x и y здесь являются переменными.

Введите следующие выражения:

Эти два знака равенства принципиально различны, поэтому их не следует путать.

Поместите курсор перед числом 4 в первом выражении:

Удалите число 4 с помощью клавиши [Delete] и введите 5. Щелкните по пустой области и убедитесь, что результат третьего выражения изменился на 25:

Попробуйте удалить число 25. Вы увидите, что при первом нажатии число станет красным, а при повторном нажатии удалится 25 и знак равенства:

Использование переменных

Введите следующие выражения:

Попробуйте изменить значение x на 100, 0.5, -4 и 0:

Первые два случая дадут в результате число. При -4 получится мнимое число. Да, Mathcadможет работать и с такими числами. При нуле программа выдаст ошибку, а результат будет обведен красным. Если Вы щелкните по неправильному выражению, то получите описание, что может быть не так:

Теперь о том, какие имена можно и нельзя использовать для переменных. Есть несколько правил: имя переменной не может начинаться с цифры и в имени переменной нельзя использовать пробелы и знаки операторов. Имена переменных могут начинаться:

• с любой строчной или прописной буквы
• другие символы, если они не являются операторами
• символы с вкладки Математика –> Операторы и символы –> Символы
• символы из Таблицы символов Windows

Вот несколько примеров:

Переменные можно использовать, только если они были определены ранее. «Ранее» означает, что объявление переменной должно располагать выше или левее выражения, где она используется. Если переменная не объявлена, появится сообщение об ошибке:

Подстрочные индексы

В Mathcad есть два различных вида подстрочных индекса для переменных:

1. Описательный подстрочный индекс.
2. Индекс массива (матрицы).

Чтобы набрать описательный подстрочный индекс, введите имя переменной, нажмите [Ctrl+-] и наберите подстрочный индекс:

Переменная с описательным подстрочным индексом – это обычная переменная, со своим именем. Индекс массива существенно отличается от него. Этот индекс можно ввести, нажав открывающую квадратную скобку [ после имени переменной. У переменной может быть один или два индекса массива:

Индекс массива должен быть числом. При этом не следует путать виды подстрочных индексов, т.к. они выглядят практически идентично:

Разница видна при щелчке мышью по выражению:

У переменной может быть сразу описательный индекс и индекс массива. Сначала всегда идет описательный индекс:

Функции

Переменные можно использовать, только если они были определены ранее. Однако есть одно важное исключение – определение функции. Можно определить собственную функцию, как на примере ниже:

Переменная a является локальной для функции. Она не определена за пределами функции:

Если Вы определили a до определения функции, значение a не будет изменено в процессе вычисления значения функции.

Внимание: если Вы дали переменной такое же имя, как и функции, Вы больше не сможете использовать эту функцию. У переменной и функции должны быть разные имена:

Этой проблемы можно избежать, задав для переменной и функции разные обозначения. Об этом мы поговорим в уроке 10 «Обозначения и единицы измерения».

Функции могут содержать две и более переменной:

Здесь значения переменных xи yтакже не изменяются при вычислении функции.

Встроенные функции

В Mathcad есть большое число встроенных функций. Зайдите на вкладку Функции:

Список всех функций можно увидеть, щелкнув по кнопке Все функции.

Заметьте, что тригонометрические функции принимаю в качестве аргумента угол в радианах, а не в градусах. Для использования градусов используйте символ с вкладки Математика –> Операторы и символы –> Символы:

 

Математика в тексте

В текст можно вставить математическую область. Таким образом, можно использовать над- и подстрочные символы в тексте. Для этого при редактировании текстовой области нажмите кнопку Математика с вкладки Математика –> Области:

Пример:

Резюме

1. В Mathcadесть два различных знака равенства: определить := и вычислить =.
2. Имя переменной обычно начинается с буквы; цифры нельзя использовать в начале переменной. Также можно использовать символы с клавиатуры, с панели Математика –> Операторы и символы –> Символы, с Таблицы символов Windows.
3. Чтобы определить переменную и задать ей значение:

• щелкните мышью на пустую область;
• введите имя переменной;
• нажмите [:] для ввода оператора определения;
• введите значение, которое Вы хотите присвоить.

4. Чтобы дать переменной описательный подстрочный индекс:

• щелкните мышью в конце имени переменной;
• нажмите [Ctrl+-];
• введите подстрочный индекс.

5. Чтобы дать переменной индекс массива:

• щелкните мышью в конце имени переменной;
• нажмите открывающую квадратную скобку [;
• введите число – подстрочный индекс.

6. Переменную можно использовать ниже или правее места, где она определена.
7. Имя функции следует набирать по тем же правилам, что и имя переменной, но ввод имени функции заканчивается вводом [(]. В скобках содержатся аргументы функции.
8. Переменные в функциях – локальные, т.е. они определены только при использовании функции.
9. Математическую область можно встроить в текст. Эту возможность следует использовать, если необходимо вставить над- и подстрочные символы в текст.

 

Другие интересные материалы

sapr-journal.ru