Given find mathcad как использовать – Иллюстрированный самоучитель по MathCAD 12 › Системы линейных уравнений › Хорошо обусловленные системы с квадратной матрицей. Вычислительный блок Given/ Find. [страница – 146] | Самоучители по математическим пакетам

Решение системы уравнений в Mathcad

Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.

Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b)

имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.

Пример решения СЛАУ:

Для решения системы нелинейных уравнений используются два блока: given…find() и given…minerr (). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено. На листинге представлены примеры использования блоков

given…find() и given…minerr () для решения систем нелинейных уравнений.

www.allmathcad.com

Урок 24. Решение уравнений в Mathcad – использование функций

Решение уравнений является важным для решения практических задач. Поэтому уделим уравнениям еще один урок.

Блок решения в функции

Если Вы хотите исследовать изобразить на графике поведение уравнения в зависимости от значения определенного параметра, Вам, возможно, придется решить систему уравнений много раз. Вы можете сделать это, используя блок решения в функции. Покажем на примере: предположим, мы хотим исследовать поведение решения следующего уравнения в зависимости от различных значения параметра A:

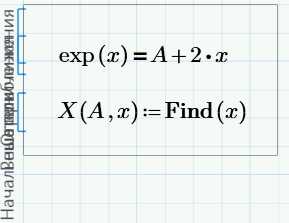
Блоку решения не нужно ни значение параметра, ни начальное приближение, поскольку решение есть функция этих двух значений. Эти значения мы будем задавать при вызове функции.

Функцию можно использовать сколько угодно раз:

Использовать функцию можно с диапазоном переменных:

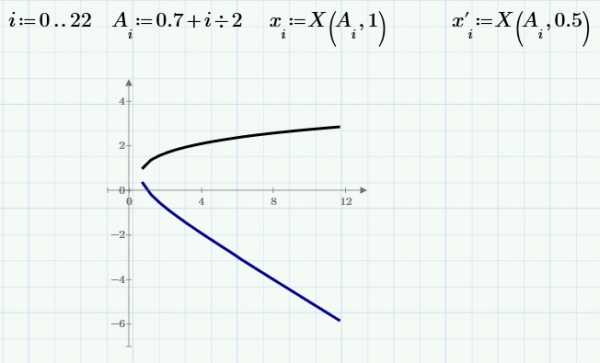
Такая техника решения не самая надежная. Если хотя бы одно решение не может быть найдено, Вы не получите и решений для других параметров (это произойдет, если задать A<0.7). Поэтому лучше заранее проверить свою функцию.

Сообщения об ошибке можно избежать, написав маленькую программу:

Если блок решения выдает сообщение об ошибке, на выходе получим значение NaN (Not a Number – «Не Число»), которое просто не отображается на графике:

Построим две ветки уравнения с использованием этого приема:

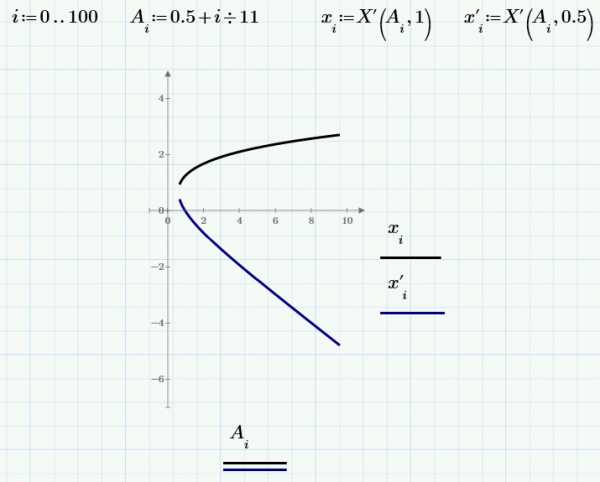
Когда переменных много

Расчеты часто содержат несколько переменных, но Вам, возможно, придется использовать лишь некоторые из них. В качестве примера рассмотрим систему восьми уравнений, где нам нужно получить только значения X и Y. Начальные приближения следует задать для всех переменных:

Решение представляет собой вектор из восьми элементов, но нам нужны лишь элементы с индексами 0 и 1.

Минимизация ошибки

Find() – не единственный решатель в Mathcad. Еще один полезным решателем является Minnerr(), находящий решения, которые минимизируют ошибку в системе уравнений. Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:

Мы хотим подобрать три константы в уравнении Бейтмена таким образом, чтобы ошибка приближения была минимальна. У нас есть семь уравнений (по одной для каждого эксперимента) и три константы, так что в системе избыток данных. Minerr() может обработать эту проблему:

Замечания:

1. Три константы являются переменными для этой системы.
2. Переменные не могут иметь счетных индексов.
3. У параметров (t и c) могут быть счетные индексы.

Возможно, Вам хотелось бы использовать цикл for для семи уравнений, но в блоке решений этого сделать нельзя.

Для полностью определенных систем (с одинаковым числом независимых уравнений и неизвестных) функция Minerr() дает тот же ответ, что и Find().

Резюме

В этом уроке мы определили способы расширенного использования блоков решения:

1. Вы можете определить вывод блока решения как функцию. Таким образом в блок решения можно передавать параметры и начальные приближения.
2. Если при вычислении точек для графика хотя бы одно решение не будет найдено, то график не будет построен. Этой ошибки можно избежать, написав небольшую программу с использованием “try/on error”, которая выводит NaN (Not a Number – Не Число), если результат отсутствует.
3. Для двух и более неизвестных (и уравнений) вывод блока решения является вектором. Если нужен один или два элемента этого вектора, их можно вывести, используя подстрочные индексы.
4. Вместо функции Find() можно использовать Minerr() – она минимизирует ошибку для заданного набора ограничений, в том числе, если данные избыточны. Minerr() часто может дать приближенный результат, когда Find() выдает ошибку.

Другие интересные материалы

sapr-journal.ru

8.1.1. Вычислительный блок Given/ Find MathCAD 12 руководство

Для того чтобы численным методом решить СЛАУ при помощи вычислительного блока (он был подробно описан в главе 5), следует после ключевого слова Given выписать ее, пользуясь логическими операторами. Рассмотрим в качестве примера систему трех уравнений, приведенную в листинге 8.1 (после ключевого слова Given). Неизвестными являются три компонента вектора х, поэтому именно эта векторная переменная является аргументом встроенной функции Find(x), решающей систему в последней строке листинга. Очень важно, что при использовании вычислительного блока Given/Find всем неизвестным требуется присвоить начальные значения, как это сделано в первой строке листинга 8.1.

ПРИМЕЧАНИЕ

Если матрица СЛАУ является невырожденной (точнее, если ее число обусловленности не слишком велико), то известно, что численное решение системы уравнений единственно. Поэтому начальные значения могут быть произвольными, т. к. результат работы численного метода все равно сойдется к точному решению.

Листинг 8.1. Решение СЛАУ с помощью вычислительного блока

Листинг 8.1 демонстрирует запись каждого уравнения системы (в промежутке между Given и Find), что очень неудобно, когда система содержит большое число уравнений. В последнем случае намного лучше применить матричную запись СЛАУ, как это показано в листинге 8.2. Первая строка листинга представляет собой определение матрицы СЛАУ А и вектора правых частей ь, а в остальном работа блока Given/Find полностью идентична предыдущему листингу.

Листинг 8.2. Решение СЛАУ, записанной в матричной форме

Проверка правильности решения СЛАУ прямой подстановкой, причем в матричной форме, приведена в листинге 8.3. Обратите внимание на матрицу в первой строке листинга, представляющую рассматриваемую систему уравнений. Во второй строке листинга 8.3 производится вычисление нормы невязки, характеризующей точность полученного решения СЛАУ.

ПРИМЕЧАНИЕ

Такая большая невязка может вызвать совершенно обоснованное удивление читателя. На самом деле точность решения гораздо выше (в данном примере ~10^-15, а полученное значение невязки -10^-3 объясняется соответствующим представлением вещественных чисел результата на экране (по умолчанию с точностью до 3-го знака).

Листинг 8.3. Проверка правильности решения СЛАУ

radiomaster.ru

Иллюстрированный самоучитель по MathCAD 12 › Нелинейные алгебраические уравнения › Символьное решение уравнений. Вычислительный блок Given/Find. [страница – 94] | Самоучители по математическим пакетам

Символьное решение уравнений. Вычислительный блок Given/Find.

Относительно небольшое количество задач отыскания корней алгебраических уравнений можно решить аналитически, а на практике почти всегда приходится искать решение при помощи численных методов. Тем не менее мы начнем знакомство с принципами решения алгебраических уравнений в Mathcad именно с описания использования символьного процессора, что позволит, с одной стороны, освоить соответствующий инструментарий Mathcad, а с другой – лучше понять специфику исследуемых задач.

---

Рассмотрим решение системы N нелинейных уравнений с м неизвестными:

Здесь f_i(x_i,…, х_M) =b₁,…, f_N (x_i,…, х_M) =b_N – некоторые скалярные выражения, зависящие от скалярных переменных x₁,x₂,…,х_M и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (5.1) можно формально переписать в – виде:

Где х – вектор, составленный из переменных x₁,x₂,…,х_N, b – вектор, составленный из правых частей уравнений, а f (х) – соответствующая векторная функция их левых частей.

Для решения систем в Mathcad применяется специальный вычислительный блок Given/Find (Дано/найти), состоящий из трех частей, идущих последовательно друг за другом:

• Given – ключевое слово;
• система, записанная логическими операторами в виде равенств и, возможно, неравенств;
• Find(xi,…,хм) – встроенная функция для решения системы уравнений относительно переменных x₁,…, х_M.

Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры, помните, что логический знак равенства вводится сочетанием клавиш CTRL + =. Значение функции Find представляет собой матрицу, составленную из всевозможных решений по каждой переменной, причем количество ее строк в точности равно числу аргументов Find. Структура матрицы решения станет сразу вам понятной, как только вы бросите взгляд на примеры, приведенные ниже в данном разделе.

Примечание
При решении уравнений в векторной форме в вычислительном б локе не рекомендуется, а, начиная с версии Mathcad 12, просто запрещено использование одних элементов вектора в качестве неизвестных, а других – в качестве параметров задачи.

samoychiteli.ru

Символьные вычисления

Уравнение и системы уравнений в математическом пакете Mathcad  в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:

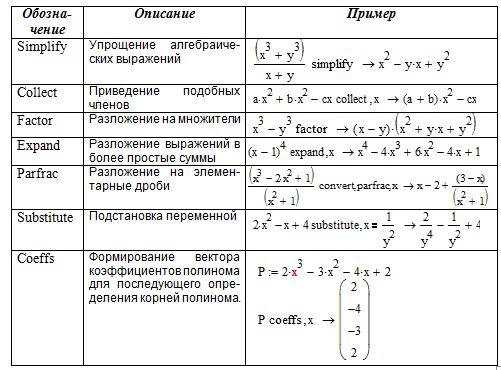
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню  Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:

Пример использования блока given…find для решения системы уравнений:

www.allmathcad.com

Решение нелинейных уравнений и систем уравнений в пакете MathCAD

Pers.narod.ru. Обучение. Лекции по MathCAD. Решение нелинейных уравнений и систем уравнений в пакете MathCAD

Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье

 

 

Вычисление корней численными методами включает два основных этапа:

·      отделение корней;

·      уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

 

Отделение корней нелинейного уравнения

 

Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.

Пример. Дано алгебраическое уравнение

.

Определить интервалы локализации корней этого уравнения.

 

 

Пример. Дано алгебраическое уравнение

.

Определить интервалы локализации корней этого уравнения.

На рисунке приведен график функции , построенный в MathCAD. Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨

 

Уточнение корней нелинейного уравнения

 

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root. В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root, которая может иметь два или четыре аргумента, т.е.  или , где  – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению,  – скалярная переменная, относительно которой решается уравнение,  – границы интервала локализации корня.

Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

 

 

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

 

Функция root с двумя аргументами требует задания (до обращения к функции) переменной  начального значения корня из интервала локализации.

 

Пример 8.1.5. Используя функцию root, вычислить изменения корня нелинейного уравнения   при изменении коэффициента а от 1 до 10 с шагом 1.

 

 

 

Функция polyroots. Для вычисления всех корней алгебраического уравнения порядка  (не выше 5) рекомендуется использовать функцию polyroots. Обращение к этой функции имеет вид polyroots(v), где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.

Пример. Используя функцию polyroots, найти все три корня уравнения , включая и два комплексных

 

 

Блок Given. При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given, имеющий следующую структуру:

 

 

Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логичес­кий.

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

 

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(x), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(x), которая возвращает приближенное значение корня.

 

Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find(x) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.

 

Аналогично можно задать алгоритм решения и для функции   Minerr(x).

 

Использование численных методов в функциях Find(x), Minerr(x) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

 

Пример. Используя блок Given, вычислите корень уравнения  в интервале отделения .

 

 

 

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

·      алгебраические системы уравнений;

·      трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

 

Системы линейных алгебраических уравнений

 

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

 

В матричном виде систему можно записать как

 

,

где  – матрица размерности ,  – вектор с  проекциями.

 

Для вычисления решения СЛАУ следует использовать функцию lsolve, обращение к которой имеет вид: lsolve(А,b), где А – матрица системы,  – вектор правой части.

Решение систем нелинейных уравнений

 

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD2001i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

 

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

 

 

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Вычисление решения системы уравнений с заданной точностью. Для этого используется уже известный вычислительный блок Given.

 

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find(x), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.

 

Следующие выражения недопустимы внутри блока решения:

·      ограничения со знаком ¹;

·      дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

·      блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr).

 

Пример. Используя блок Given, вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

 

 

Пример. Используя функцию , вычислите решение системы уравнений

 

 

 

 

 

pers.narod.ru