| 3. Сформулируйте вопросы по
графикам? (Запись вопросов на доске) |
1. Способы представления
функции(словесный, аналитический – формулой,
табличный, графический). 2. Что такое график? (graphikos – начертательный(греч), чертёж наглядно что-то изображающий, это линия, построенная определённым образом в определённой системе координат). 3. График и график функции – это равнозначные понятия? Какое является более общим? (График функции – это линия, дающая цельное представление о характере изменения функции по мере изменения аргумента, каждому значению х соответствует одно и только одно значение y.) 4. К чему относятся диаграммы? (Диаграммы – к графикам, например, диаграмма состояния, диаграмма растяжения материала.) 6. Какие требования мы предъявляем к графику? Что входит в понятие графика? (Оси координат, их обозначение, единицы измерения, масштаб, точки, название.) 7. Всегда ли вы встречаете числовые значения? (График без числовых значений называется эскизным.) 8. Какие графики встречаются в физике? (Графики движения, скорости, ускорения, изопроцессов, ВАХ….) 9. Может ли график иметь сразу несколько
названий? 10.Как графики используется в физике? (Результаты эксперимента, сравнение теории и практики, чтение, определение величин заданных явно и неявно, решение задач.) |
4. Очень часто графическое решение легче, чем аналитическое. Докажем на примере двух задач. | Решение задач: Задача 1. От движущегося поезда отцепляют последний вагон. Поезд продолжает двигаться с той же скоростью. Сравните пути, пройденные поездом и вагоном к моменту остановки вагона. Ускорение вагона можно считать постоянным. Аналитическое решение. t – время движения; Графическое решение Задача 2. Поезд прошел между станциями путь s=17 км со
средней скоростью v Решение: S = (t + (t – t1)) * v/2 = (2t – t1) * v/2 – площадь трапеции S = vсрt t = S/vср=17/60 V= |
1. На рисунке представлена зависимость
координаты центра шара, подвешенного на пружине,
от времени. Период колебаний равен:
2. Виток провода находится в магнитном поле, перпендикулярном плоскости витка, и своими концами замкнут на амперметр. Магнитная индукция поля меняется с течением времени согласно графику на рисунке. В какой промежуток времени амперметр покажет наличие электрического тока в витке:
3. На рисунке показан процесс изменения состояния идеального газа. Внешние силы совершили над газом работу, равную 5·104 Дж. Какое количество теплоты отдает газ в этом процессе? Ответ выразите в килоджоулях (кДж). Ответ: _______________. 4. 10 моль идеального одноатомного газа охладили, уменьшив давление в 3 раза. Затем газ нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты сообщено газу на участке 2 – 3? |
Использование графиков при изучении физики в средней школе
Разделы: Физика
Современная наука и техника очень широко использует графики, а потому, где бы ни учился, где бы ни работал человек после школы – ему обязательно придется иметь дело с графиками. График – международный язык техники. Использование в преподавании физики графиков, чертежей и рисунков не только способствует формированию связей учебного материала разных дисциплин школьного курса, но и помогает обучающимся понять основные факты и закономерности физики. Графическое представление физического процесса делает его более наглядным и тем самым облегчает понимание рассматриваемого явления, способствует развитию абстрактного мышления, интуиции, умения анализировать и сравнивать, находить более рациональный способ решения задач. Кроме того, применение графического метода способствует укреплению связей физики с математикой, наполняет абстрактные математические закономерности конкретным физическим содержанием. Вопрос об использовании графиков становится всё более актуальным ещё и потому, что КИМы итоговой аттестации за курс основной школы в новой форме и ЕГЭ содержат всегда графические задания. Следует указать здесь еще и на психологическую строну рассматриваемого вопроса. При широком использовании графического метода привлекаются и развиваются не только мышление и память учащихся, но также зрение и моторные действия,
В преподавании физики графический метод используется, начиная с 7-го класса и не только на уроках, но и при выполнении учащимися лабораторных и домашних заданий по физике. И необходимо отметить, графические задачи на уроках физики традиционно продолжают вызывать затруднения у большинства учащихся. Между тем, на уроках математики задачам на построение графиков различных функций отведено много времени и, как правило, с подобными задачами учащиеся справляются достаточно хорошо. Причин таких затруднений много.
Как известно, что решение любой физической задачи состоит из трёх основных частей:
- краткая запись условия задачи
- анализ и решение
- ответ
Графики могут использоваться и используются на всех этапах, при решении как расчетных, так и качественных задач.
Слайд №2 (Приложение 1) Наиболее часто встречаются графики линейных функций, в том числе и прямой пропорциональной зависимости, графики тригонометрических функций. Реже обратной пропорциональной зависимости, а также какой-то более сложной зависимости. Встречаются графики, содержащие несколько участков, которые соответствуют различным особенностям протекания физического процесса. Обратите внимание на разнообразие величин, отложенных по осям.
Наиболее часто графики встречаются при решении задач по механике (кинематика, динамика, законы сохранения, механические колебания и волны), тепловые явления (изменение агрегатных состояний вещества, молекулярная физика и термодинамика в 10 классе). Реже – в задачах по электричеству, электромагнетизму (в основном в 10–11 классах), в квантовой физике (фотоэффект в 11 классе).
Слайд №3 При работе с графиками можно выделить следующие приёмы:
- решение задач графическим способом, включающее построение графиков
- работа с предложенными графиками
- графическое отображение результатов измерений при выполнении лабораторных и практических работ
Слайд №4 Начну с решения задач графическим способом.
Все задачи, решаемые графически, можно условно разделить на несколько типов по методу решения:
- графическое решение уравнений (ответ даётся точками пересечения кривых)
- графическое интегрирование (ответ даётся величиной площади фигуры, ограниченной кривой, ординатами крайних точек и осью абсцисс. Это прием используется для нахождения перемещения в механике и в термодинамике для нахождения работы газа, в основном в классах углублённого изучения. В средней общеобразовательной школе для этого используются готовые графики)
- графическое усреднение (определение среднего значения некоторой физической величины, изменяющейся в определённых пределах, Наиболее часто встречается в лабораторных работах. В заданиях ЕГЭ используются уже готовые графики
- графическая оценка (определение условий, при которых наблюдается наибольшее или наименьшее физическое действие).
Слайд №5 Пример №1
Уравнения движения двух тел имеют следующий вид: Х1 = 10 +10t и Х2 = 50 – 15t. Найти место и время их встречи графическим и аналитическим способами.
И вот она первая трудность – буквенные обозначения. И теряются дети уже на первом шаге – составления таблицы. На уроках математики они очень хорошо усвоили и запомнили, что независимая переменная величина обозначается Х, а зависимая, функция, – Y. И с этого момента теряется так необходимая межпредметная связь. И не помогают им приобретенные навыки, так как дети не могут их применить. Другими словами, у обучающихся формируется мнение, что на уроках математики своя свадьба, а на уроках физики – своя. А если уравнение имеет вид S = 5t + 2t2 и надо построить график зависимости такой зависимости? В этом случае квадратичную зависимость дети трудом узнают.
Слайд №6 Работа с предложенными графиками.
Наиболее распространёнными заданиями являются задания, содержащие уже готовые графики. Готовые графики используются в разнообразных нестандартных ситуациях, как правило, детям незнакомых. И тут наряду с физическими знаниями навыки работы с графиками играют, не побоюсь этого слова, базовую роль. Одним из обязательных условий для успешного выполнения таких заданий является умение правильного математического прочтение графика, без которого невозможно правильное физическое чтение его. Анализ уже начерченных графиков открывает широкие методические возможности обучения.
1. С помощью графика можно наглядно представить функциональную зависимость физических величин, выяснить, в чем смысл прямой и обратной пропорциональности между ними, узнать, как быстро растет или падает численное значение одной физической величины в зависимости от изменения другой, когда он достигает наибольшего или наименьшего значения.
2. График дает возможность описать, как протекает тот или иной физический процесс, позволяет наглядно изобразить наиболее существенные стороны его, обратить внимание учащихся именно на то, что является наиболее важным в изучаемом явлении.
Задания, содержащие графики можно очень разнообразны. Но тем не менее их можно объединить по следующим типам, соответствующим разным видам мыслительной деятельности.
- Получение исходных данных, необходимых для решения задач и для ответа на поставленный вопрос
- Нахождение по значению известной величины значение неизвестной
- Нахождение значения величины, производной от отложенных по осям величин
- Идентифицирование объекта, для которого построен график
- Сравнение физических величин
- Установление соответствия между величинами
- Объяснение и установление особенностей протекания физического процесса, для которого построен график
- Выявление сходства и различия свойств изучаемых тел, веществ и процессов
- Составление задач
- Составление таблиц значений соответствующих физических величин по их графической зависимости
- Определение функциональной зависимости между предложенными физическими величинами
Рассмотрим некоторые виды на конкретных примерах, для то чтобы понятнее было какие трудности испытывают выпускники с целью их предупреждения.
1. Получение исходных данных, необходимых для решения задач.
Слайд №7 Пример №2.
На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 2 кг. Первоначально вещество находилось в твердом состоянии. Определите удельную теплоту плавления вещества.
Слайд №8 Пример №3. (Более сложный пример)
По графику зависимости координаты от времени для тела, брошенного с высоты 10 м вертикально вверх, определите путь и модуль перемещения тела за 6 с.
2. Нахождение по значению известной величины значение неизвестной
Слайд №9 Пример №4.
Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 5-ой секунды, считая, что характер движения тела не изменяется.
3. Нахождение значения величины, производной от отложенных по осям величин.
Слайд №10 Пример №5.
На рисунке представлен график волны вдоль упругого шнура. В некоторый момент времени. Определить длину волны.
Не ошибусь, если скажу, что в 9 классе графики тригонометрических функций не изучаются. А теперь посмотрите на такое задание. Графики похожи. Но требуется найти период колебаний.
4. Идентифицирование объекта, для которого построен график.
Слайд №11 Пример №6.
На рисунках приведены графики зависимости скорости и перемещения от времени. Какой график соответствует равноускоренному движению?
Слайд №12 Пример №7.
На рисунке приведён график зависимости температуры некоторого вещества от времени. Первоначально вещество находилось в жидком состоянии. Какая точка графика соответствует началу процесса отвердевания вещества?
5. Сравнение физических величин
Слайд №13 Пример №8.
На рисунке даны графики зависимости смещения от времени при колебаниях двух маятников. Сравните частоты колебаний маятников ν1 и ν2.
(Обращаю внимание – ответ надо дать в количественном соотношении)
Слайд №14 Пример №9.
По графикам зависимости давления жидкостей от высоты столба сравните их плотности.
6. Установление соответствия между величинами и процессами
Слайд №15 Пример №10.
На рисунке 1 приведен график зависимости скорости движения тела от времени. Укажите соответствующий ему график зависимости пути от времени (рис. 2).
7. Установление особенностей протекания физического процесса, для которого построен график
Слайд №16 Пример №11.
И последний пример. Определить во сколько раз изменилась скорость велосипедиста за 4 секунды.
Слайд №17 Пример №12.
На первый взгляд – простой график и простое задание. Чтобы правильно ответить на этот вопрос, необходимо не только знать формулу кинетической энергии и понимать квадратичную зависимость от скорости, но правильно определить по графику во сколько раз (а не на сколько) увеличилась скорость. А это, как показал опыт, тоже представляет трудность.
Подведём итог сказанному. Каковы же возможные причины затруднений при выполнении графических заданий? Их много, конечно же много. Я перечислю некоторые из них.
- Использование в графических заданиях непривычных буквенных обозначений.
- Использование графиков в непривычных, с точки зрения математики, ситуациях.
- Использование графиков, изучение которых не предусмотрено общеобразовательной программой по математике в основной школе, или нарушение преемственности между предметами.
- Нестандартные физические задания.
- Необходимость одновременного применения знаний по физике и математики.
- Использование нескольких графиков, построенных в одной координатной сетке.
- Использование графиков, содержащих несколько участков.
Пути выхода:
- Натаскивание – это то, что мы делаем сейчас при подготовке к итоговой аттестации
- Начиная с 7-го класса, использовать домашние практические задания, включая построение графиков (Например: Построить график изменения температуры воздуха за день, для чего измерять температуру воздуха с 8 до 20 часов через каждые 2 часа (8 класс))
- Включать построение графиков в привычных математических и физических обозначениях
- Постоянно использовать готовые графики, для демонстрации различных физических закономерностей
- Использовать разнообразные задания, содержащие графики
- Осуществление межпредметной связи (возможно через проведение элективного курса)
xn--i1abbnckbmcl9fb.xn--p1ai
Типовые задачи на уравнения и графики прямолинейного равномерного движения. Примеры решения задач по физике. 9-10 класс
Типовые задачи на уравнения и графики прямолинейного равномерного движения. Примеры решения задач по физике. 9-10 класс
Задачи по физике – это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Задача на составление описания движения и составление уравнения движения по заданному графику движения
Дано: график движения тела
Найти:
1.
составить описание движения
2. составить
уравнение движения тела.
Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c
Тогда:
Составляем уравнение движения тела:
Записываем формулу уравнения прямолинейного равномерного движения.
Подставляем в нее найденный коэффициент Vx (не забываем о минусе!).
Начальная координата тела (Xо) соответствует началу графика, тогда Xо=3
Составляем описание движения тела:
Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!
Тело движется прямолинейно и равномерно из начальной точки Xо=3м со скоростью 0,75 м/с противоположно направлению оси X.
Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)
Движение тел задано уравнениями движения для каждого тела.
Дано:
1.
уравнение движения первого тела
2. уравнение движения второго тела
Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел
По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.

Точка пересечения двух графиков движения определяет:
1.
на оси t – время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X – координату места встречи (относительно начала координат)
В результате:
Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.
Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:
Все было верно!
Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:
График движения – это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t1 и t2.
Для этих значений t подсчитываем соответствующие значения координат X1 и X2.
Откладываем 2 точки
с координатами (t1, X1) и (t2, X2) и соединяем их прямой – график готов!
Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения
Задача 1
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
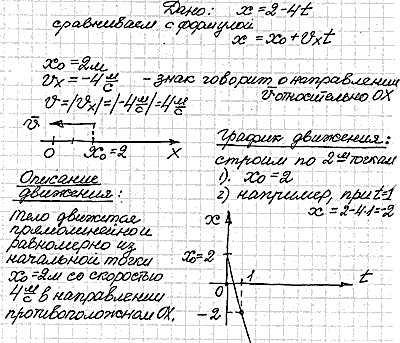
Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.
Задача 2
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения

Задача 3
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения

Задача 4
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения

Описание движения:
Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя – это частный случай движения, когда скорость тела равна нулю).
Задача 5
Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с
Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения

class-fizika.ru
Определение кинематических характеристик движения с помощью графиков
Определение кинематических характеристик движения с помощью графиков
«Физика – 10 класс»
Чем отличается равномерное движение от равноускоренного?
Чем отличается график пути при равноускоренном движении от графика пути при равномерном движении?
Что называется проекцией вектора на какую-либо ось?
В случае равномерного прямолинейного движения можно определить скорость по графику зависимости координаты от времени.
Проекция скорости численно равна тангенсу угла наклона прямой x(t) к оси абсцисс. При этом, чем больше скорость, тем больше угол наклона.
Прямолинейное равноускоренное движение.
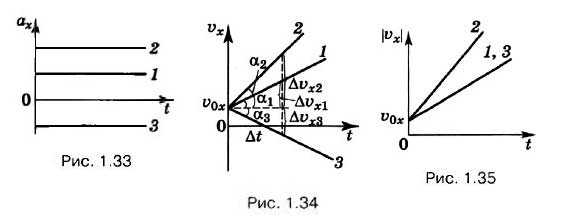
На рисунке 1.33 изображены графики зависимости проекции ускорения от времени для трёх разных значений ускорения при прямолинейном равноускоренном движении точки. Они представляют собой прямые линии, параллельные оси абсцисс: ах = const. Графики 1 и 2 соответствуют движению, когда вектор ускорения направлен вдоль оси ОХ, график 3 — когда вектор ускорения направлен в противоположную оси ОХ сторону.
При равноускоренном движении проекция скорости зависит от времени линейно: υx = υ0x + axt. На рисунке 1.34 представлены графики этой зависимости для указанных трёх случаев. При этом начальная скорость точки одинакова. Проанализируем этот график.
Проекция ускорения Из графика видно, что, чем больше ускорение точки, тем больше угол наклона прямой к оси t и соответственно больше тангенс угла наклона, который определяет значение ускорения.
За один и тот же промежуток времени при разных ускорениях скорость изменяется на разные значения.
При положительном значении проекции ускорения за один и тот же промежуток времени проекция скорости в случае 2 увеличивается в 2 раза быстрее, чем в случае 1. При отрицательном значении проекции ускорения на ось ОХ проекция скорости по модулю изменяется на то же значение, что и в случае 1, но скорость уменьшается.
Для случаев 1 и 3 графики зависимости модуля скорости от времени будут совпадать (рис. 1.35).
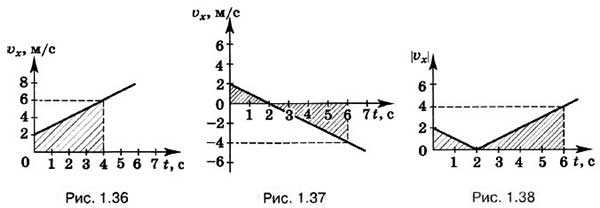
Используя график зависимости скорости от времени (рис. 1.36), найдём изменение координаты точки. Это изменение численно равно площади заштрихованной трапеции, в данном случае изменение координаты за 4 с Δx = 16 м.
Мы нашли изменение координаты. Если необходимо найти координату точки, то к найденному числу нужно прибавить её начальное значение. Пусть в начальный момент времени х0 = 2 м, тогда значение координаты точки в заданный момент времени, равный 4 с, равно 18 м. В данном случае модуль перемещения равен пути, пройденному точкой, или изменению её координаты, т. е. 16 м.
Если движение равнозамедленное, то точка в течение выбранного интервала времени может остановиться и начать двигаться в направлении, противоположном начальному. На рисунке 1.37 показана зависимость проекции скорости от времени для такого движения. Мы видим, что в момент времени, равный 2 с, направление скорости изменяется. Изменение координаты будет численно равно алгебраической сумме площадей заштрихованных треугольников.
Вычисляя эти площади, мы видим, что изменение координаты равно -6 м, это означает, что в направлении, противоположном оси ОХ, точка прошла большее расстояние, чем по направлению этой оси.
Площадь над осью t берём со знаком «плюс», а площадь под осью t, где проекция скорости отрицательна, — со знаком «минус».
Если в начальный момент времени скорость некоторой точки была равна 2 м/с, то координата её в момент времени, равный 6 с, равна -4 м. Модуль перемещения точки в данном случае также равен 6 м — модулю изменения координаты. Однако путь, пройденный этой точкой, равен 10 м — сумме площадей заштрихованных треугольников, показанных на рисунке 1.38.
Изобразим на графике зависимость координаты х точки от времени. Согласно одной из формул (1.14) кривая зависимости координаты от времени — x(t) — парабола.
Если движение точки происходит со скоростью, график зависимости которой от времени изображён на рисунке 1.36, то ветви параболы направлены вверх, так как ах > 0 (рис. 1.39). По этому графику мы можем определить координату точки, а также скорость в любой момент времени. Так, в момент времени, равный 4 с, координата точки равна 18 м.
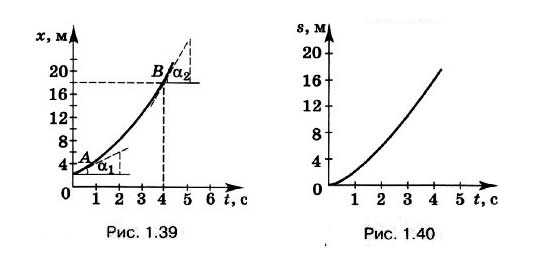
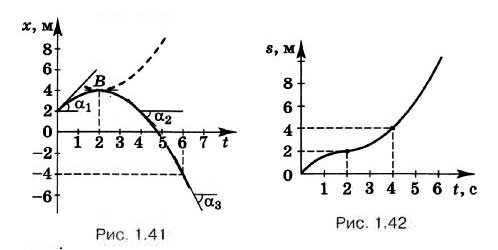
Для начального момента времени, проводя касательную к кривой в точке А, определяем тангенс угла наклона α1, который численно равен начальной скорости, т. е. 2 м/с.
Для определения скорости в точке В проведём касательную к параболе в этой точке и определим тангенс угла α2. Он равен 6, следовательно, скорость равна 6 м/с.
График зависимости пути от времени — такая же парабола, но проведённая из начала координат (рис. 1.40). Мы видим, что путь непрерывно увеличивается со временем, движение происходит в одну сторону.
Если движение точки происходит со скоростью, график зависимости проекции которой от времени изображён на рисунке 1.37, то ветви параболы направлены вниз, так как аx < 0 (рис. 1.41). При этом моменту времени, равному 2 с, соответствует вершина параболы. Касательная в точке В параллельна оси t, угол наклона касательной к этой оси равен нулю, и скорость также равна нулю. До этого момента времени тангенс угла наклона касательной уменьшался, но был положителен, движение точки происходило в направлении оси ОХ.
Начиная с момента времени t = 2 с, тангенс угла наклона становится отрицательным, а его модуль увеличивается, это означает, что движение точки происходит в направлении, противоположном начальному, при этом модуль скорости движения увеличивается.
Модуль перемещения равен модулю разности координат точки в конечный и начальный моменты времени и равен 6 м.
График зависимости пройденного точкой пути от времени, показанный на рисунке 1.42 отличается от графика зависимости перемещения от времени (см. рис. 1.41).
Как бы ни была направлена скорость, путь, пройденный точкой, непрерывно увеличивается.
Выведем зависимость координаты точки от проекции скорости. Скорость υx = υ0x + axt, отсюда
В случае x0 = 0, ах > 0 и υx > υ0x график зависимости координаты от скорости представляет собой параболу (рис. 1.43).
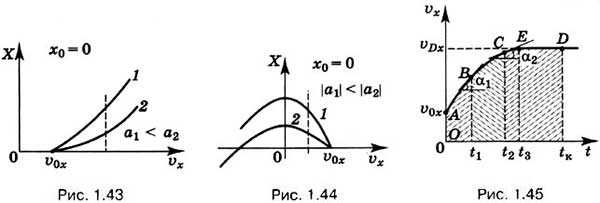
При этом, чем больше ускорение, тем ветвь параболы будет менее крутой. Это легко объяснить, так как, чем больше ускорение, тем меньше расстояние, которое должна пройти точка, чтобы скорость увеличилась на то же значение, что и при движении с меньшим ускорением.
В случае ах < 0 и υ0x > 0 проекция скорости будет уменьшаться. Перепишем уравнение (1.17) в виде где а = |аx|. График этой зависимостимости — парабола с ветвями, направленными вниз (рис. 1.44).
Ускоренное движение.
По графикам зависимости проекции скорости от времени можно определить координату и проекцию ускорения точки в любой момент времени при любом типе движения.
Пусть проекция скорости точки зависит от времени так, как показано на рисунке 1.45. Очевидно, что в промежутке времени от 0 до t3 движение точки вдоль оси X происходило с переменным ускорением. Начиная с момента времени, равного t3, движение равномерное с постоянной скоростью υDx. По графику мы видим, что ускорение, с которым двигалась точка, непрерывно уменьшалось (сравните угол наклона касательной в точках В и С).
Изменение координаты х точки за время t1 численно равно площади криволинейной трапеции OABt1, за время t2 — площади OACt2 и т. д. Как видим по графику зависимости проекции скорости от времени можно определить изменение координаты тела за любой промежуток времени.
По графику зависимости координаты от времени можно определить значение скорости в любой момент времени, вычисляя тангенс угла наклона касательной к кривой в точке, соответствующей данному моменту времени. Из рисунка 1.46 следует, что в момент времени t1 проекция скорости положительна. В промежутке времени от t2 до t3 скорость равна нулю, тело неподвижно. В момент времени t4 скорость также равна нулю (касательная к кривой в точке D параллельна оси абсцисс). Затем проекция скорости становится отрицательной, направление движения точки изменяется на противоположное.
Если известен график зависимости проекции скорости от времени, можно определить ускорение точки, а также, зная начальное положение, определить координату тела в любой момент времени, т. е. решить основную задачу кинематики. По графику зависимости координаты от времени можно определить одну из самых важных кинематических характеристик движения — скорость. Кроме этого, по указанным графикам можно определить тип движения вдоль выбранной оси: равномерное, с постоянным ускорением или движение с переменным ускорением.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика – Физика, учебник для 10 класса – Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
class-fizika.ru
Построение графиков в курсе физики на основе функциональной заивисимости
Разделы: Физика
Графический метод, основа которого - математика, используется в курсе физики на различных этапах ее изучения. Это естественно, так как график позволяет показать специфику происходящего, прогнозировать ожидаемый результат, наглядно пояснить ответ.
Он используется в физике для формирования и анализа изучаемых физических понятий путем раскрытия их связей с другими понятиями, для решения задач обобщения, систематизации знаний.
Графические задачи делятся на две большие группы:
- Задачи на построение графиков
- Задачи на получение информации из графиков
В свою очередь задачи на построение графиков делятся (по способу задания) на два вида:
- Табличный способ задания зависимости
- Функциональный способ задания зависимости
- Задачи на получение информации из графика делятся (по характеру информации) на три вида:
- Словесное описание процессов
- Аналитическое выражение функциональной зависимости, представленной графиком
- Определение по графику неизвестных величин
Чаще всего при построении графиков на зависимость одних величин от других учащиеся запоминают вид графика, не вдаваясь в подробности, почему он проходит именно так, а не иначе. Когда зависимостей накапливается достаточно много, начинаются ошибки в построении графиков. В своей работе при построении графиков на различные зависимости физических величин я использую функциональный подход. В школьном курсе физики для построения графиков используются всего семь функций. Почти все физические величины положительные, поэтому графики функций будем рассматривать только в первой четверти.
Графики этих функций учащиеся изучают в курсе математики. Они знают эти графики либо умеют их строить по точкам. Моя задача сводится к тому, чтобы научить учащихся в физической формуле увидеть зависимость, определить ее вид, а затем установить соответствующий график.
Покажу это на примере:
Пример № 1. Необходимо построить график зависимости силы тока от напряжения, которая выражена зависимостью I = . Учащиеся должны понимать, если необходимо построить зависимость силы тока от напряжения, то изменяться будет только напряжение и в зависимости от него сила тока, а остальные величины будут постоянными в частности сопротивление. Тогда нашу функцию (формулу) можно представить в виде . Если R -сопротивление постоянная величина, то и единица, деленная на сопротивление величина постоянная. Заменим эту величину на k, получим I = k U. Определяем вид функции, это прямая пропорциональность. Графиком будет прямая проходящая через начало координат.
Пример № 2. Необходимо построить график зависимости силы тока от сопротивления, которая выражена зависимостью I = . В донном примере изменяться будет сопротивление и в зависимости от него сила тока, а напряжение будет величиной постоянной. Сделаем следующие замены I = y; U = k; R = x; Получим функцию y = k\ x, графиком которой является ветвь гиперболы
Пример № 3. Постройте зависимость периода математического маятника от его длины. Запишем данную зависимость. . Изменяться будет только длина маятника и в зависимости от нее период. Все остальные величины постоянные, сделаем замену. 2 -число; = k; T = y; l = x; . Получим функцию y = 2 и строим ее график
План действий при построении графика физической зависимости:
Записываем аналитическое выражение данной зависимости (Формулу)
Устанавливаем, какие величины являются постоянными, и представляем их в виде коэффициента.
Если необходимо делаем замены: переменную величину обозначаем через x, зависящую через y.
- Определяем вид функции
- Определяем график
Приложение.
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Графическое представление информации бывает весьма полезным именно в силу своей наглядности. По графикам можно определять характер функциональной зависимости, определять значения величин. Графики позволяют сравнить результаты, полученные экспериментально, с теорией. На графиках легко находить максимумы и минимумы, легко выявлять промахи и т. д. 1. График строят на бумаге,
размеченной сеткой. Для ученических практических работ лучше всего брать
миллиметровую бумагу. 2. Особо следует сказать о размере графика: он определяется
не размером имеющегося у вас кусочка «миллиметровки», а масштабом. Масштаб
выбирают прежде всего с учетом интервалов измерения (по каждой оси он
выбирается отдельно). 3. Если планируете некую количественную обработку данных по графику, то экспериментальные точки надо наносить настолько «просторно», чтобы абсолютные погрешности величин можно было изобразить отрезками достаточно заметной длины. Погрешности в этом случае отображают на графиках отрезками, пересекающимися в экспериментальной точке, либо прямоугольниками с центром в экспериментальной точке. Их размеры по каждой из осей должны соответствовать выбранным масштабам. Если погрешность по одной из осей (или по обеим осям) оказывается слишком малой, то предполагается, что она отображается на графике размером самой точки. 4. По горизонтальной оси откладывают значения аргумента, по вертикальной – значения функции. Чтобы различать линии, можно одну проводить сплошной, другую – пунктирной, третью – штрихпунктирной и т.п. Допустимо выделять линии различным цветом. Вовсе не обязательно, чтобы в точке пересечения осей было начало координат 0:0). По каждой из осей можно отображать только интервалы измерения исследуемых величин. 5. Когда приходится откладывать по оси «длинные», многозначные числа, лучше множитель, указывающий порядок числа, учитывать при записи обозначения. 6. На тех участках графика, где имеются некие особенности, такие как резкое изменение кривизны, максимум , минимум, перегиб и др., следует брать большую густоту экспериментальных точек. Чтобы не пропустить такие особенности, есть смысл строить график сразу во время эксперимента. 7. В ряде случаев удобно пользоваться функциональными масштабами. В этих случаях на осях откладывают не сами измеряемые величины, а функции этих величин. 8. Проводить линию «на глаз» по экспериментальным точкам всегда довольно сложно, наиболее простым случаем, в этом смысле, является проведение прямой. Поэтому посредством удачного выбора функционального масштаба можно привести зависимость к линейной. 9. Графики обязательно нужно подписывать. Подпись должна отражать содержание графика. Следует объяснить в подписи либо основном тексте изображенные на графике линии. 10. Экспериментальные точки, как правило, не соединяются между собой ни отрезками прямой, ни произвольной кривой. Вместо этого строится теоретический график той функции (линейной, квадратичной, экспоненциальной, тригонометрической и т.д.), которая отражает проявляющуюся в данном опыте известную или предполагаемую физическую закономерность, выраженную в виде соответствующей формулы. 11. В лабораторном практикуме встречаются два случая: проведение теоретического графика преследует цель извлечения из эксперимента неизвестных параметров функции (тангенса угла наклона прямой, показателя экспоненты и т.д.), либо делается сравнение предсказаний теории с результатами эксперимента. 12. В первом случае график соответствующей функции проводится “на глаз” так, чтобы он проходил по всем областям погрешности возможно ближе к экспериментальным точкам. Существуют математические методы, позволяющие провести теоретическую кривую через экспериментальные точки в определенном смысле наилучшим образом. При проведении графика “на глаз” рекомендуется пользоваться зрительным ощущением равенства нулю суммы положительных и отрицательных отклонений точек от проводимой кривой. 13. Во втором случае график строится по результатам расчетов, причем расчетные значения находятся не только для тех точек, которые были получены в опыте, а с некоторым шагом по всей области измерений для получения плавной кривой. Нанесение на миллиметровку результатов расчетов в виде точек является рабочим моментом – после проведения теоретической кривой эти точки с графика убираются. Если в расчетную формулу входит уже определенный (или заранее известный) экспериментальный параметр, то расчеты проводятся как со средним значением параметра, так и с его максимальным и минимальным (в пределах погрешности) значениями. На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра. 1. http://iatephysics.narod.ru/knowhow/knowhow7.htm 2. Мацукович Н.А., Слободянюк А.И. Физика: рекомендации к лабораторному практикуму. Минск, БГУ, 2006 г. |
sites.fml31.ru
| Почему учителям и воспитателям следует проходить курсы повышения квалификации и профессиональной переподготовки в учебном центре «Инфоурок» ?• Огромный каталог: 677 курсов профессиональной переподготовки и повышения квалификации;• Очень низкая цена, при этом доступна оплата обучения в рассрочку – первый взнос всего 10%, оставшуюся часть необходимо оплатить до конца обучения; • Курсы проходят полностью в дистанционном режиме (форма обучения в документах не указывается); • Возможность оплаты курса за счёт Вашей организации. • Дипломы и Удостоверения от проекта «Инфоурок» соответствуют всем установленным законодательству РФ требованиям. (Согласно ФЗ «Об образовании в Российской Федерации» от 2012 года). |
infourok.ru

 Описание слайда: 2 слайд
Описание слайда: 2 слайд  Описание слайда: 3 слайд
Описание слайда: 3 слайд  Описание слайда: 4 слайд
Описание слайда: 4 слайд  Описание слайда: 5 слайд
Описание слайда: 5 слайд  Описание слайда: 6 слайд
Описание слайда: 6 слайд  Описание слайда:
Описание слайда: Описание слайда: 8 слайд
Описание слайда: 8 слайд  Описание слайда: 9 слайд
Описание слайда: 9 слайд  Описание слайда: 10 слайд
Описание слайда: 10 слайд 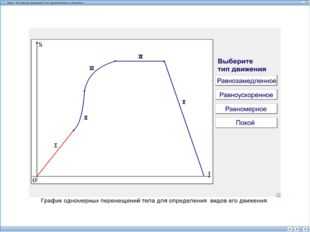 Описание слайда: 11 слайд
Описание слайда: 11 слайд  Описание слайда: 12 слайд
Описание слайда: 12 слайд  Описание слайда: 13 слайд
Описание слайда: 13 слайд  Описание слайда: 14 слайд
Описание слайда: 14 слайд  Описание слайда: 15 слайд
Описание слайда: 15 слайд  Описание слайда: 16 слайд
Описание слайда: 16 слайд  Описание слайда: 17 слайд
Описание слайда: 17 слайд  Описание слайда:
Описание слайда: 


