Момент силы и момент инерции
В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические величины — момент сил и момент инерции, физический смысл которых раскроем ниже.
Пусть некоторое тело под действием силы , приложенной в точке А, приходит во вращение вокруг оси ОО’ (рисунок 5.1).
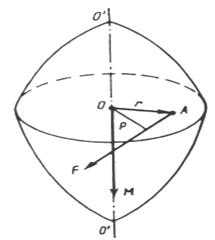
Рисунок 5.1 – К выводу понятия момента силы
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
(5.1)
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы
(5.2)
Единица момента силы — ньютон-метр (Н.м). Направление вектора момента силы находиться с помощью правила правого винта.
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Момент инерции материальной точки относительно оси вращения — произведение массы этой точки на квадрат расстояния от оси
(5.3)
Момент инерции тела относительно оси вращения — сумма моментов инерции материальных точек, из которых состоит это тело:
(5.4)
В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm, момент инерции определяется интегрированием:
, (5.5)
где r — расстояние от оси вращения до элемента массой dm.
Если тело однородно и его плотность ρ = m/V, то момент инерции тела
(5.6)
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.
Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню,
(5.7)
Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,
(5.8)
(5.9)
Момент инерции шара относительно диаметра
(5.10)
Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоскости вращения. Пусть масса диска – m, а его радиус – R.
Площадь кольца (рисунок 5.2), заключенного между r и , равна .
Рисунок 5.2 – К выводу момента инерции диска
Площадь диска . При постоянной толщине кольца,
откуда или .
Тогда момент инерции диска,
(5.11)
Для наглядности на рисунке 5.3 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
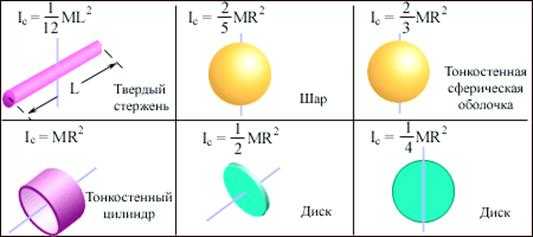
Рисунок 5.3 – Моменты инерции IC некоторых однородных твердых тел.
Теорема Штейнера
Приведенные выше формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться
(5.12)
где m — масса тела, d — расстояние от центра масс до выбранной оси вращения. Единица момента инерции — килограмм-метр в квадрате (кг . м2).
Так, момент инерции однородного стержня длиной
(5.13)
Похожие статьи:
poznayka.org
Момент инерции диска. Явление инерции
Многие люди замечали: когда они едут в автобусе, и он увеличивает свою скорость, их тела прижимаются к креслу. И наоборот, при остановке транспортного средства пассажиров будто выбрасывает из посадочных мест. Все это происходит из-за инерции. Рассмотрим это явление, а также объясним, что такое момент инерции диска.
Что представляет собой инерция?

Под инерцией в физике понимают способность всех тел, обладающий массой, сохранять покоящееся состояние либо двигаться с одинаковой скоростью в одном и том же направлении. Если необходимо изменить механическое состояние тела, то приходится прикладывать некоторую внешнюю силу к нему.
В данном определении следует обратить внимание на два момента:
- Во-первых, это вопрос состояния покоя. В общем случае такого состояния не существует в природе. Все в ней находится в постоянном движении. Тем не менее, когда мы едем в автобусе, то нам кажется, что водитель не двигается со своего места. В таком случае идет речь об относительности движения, то есть относительно пассажиров водитель находится в покое. Отличие между состояниями покоя и равномерного движения заключается лишь в системе отсчета. В примере выше пассажир в состоянии покоя относительно автобуса, в котором едет, но движется относительно остановки, которую проезжает.
- Во-вторых, инерция тела пропорциональна его массе. Наблюдаемые нами объекты в жизни все имеют ту или иную массу, поэтому все они характеризуются некоторой инертностью.

Таким образом, инерция характеризует степень трудности изменения состояния движения (покоя) тела.
Инерция. Галилей и Ньютон

Когда изучают вопрос инерции в физике, то как правило, связывают ее с первым ньютоновским законом. Этот закон гласит:
Любое тело, на которое не действуют внешние силы, сохраняет свое состояние покоя либо равномерного и прямолинейного движения.
Считается, что этот закон сформулировал Исаак Ньютон, и произошло это в середине XVII века. Отмеченный закон справедлив всегда и во всех процессах, описываемых классической механикой. Но когда ему приписывают фамилию английского ученого, следует сделать некоторую оговорку…
В 1632 году, то есть за несколько десятков лет до постулирования закона инерции Ньютоном, итальянский ученый Галилео Галилей в одной из своих работ, в которой он сравнивал системы мира Птолемея и Коперника, по сути сформулировал 1-й закон “Ньютона”!
Галилей говорит, что если тело движется по гладкой горизонтальной поверхности, и силами трения и сопротивления воздуха можно пренебречь, то это движение будет сохраняться вечно.
Вращательное движение

Приведенные выше примеры рассматривают явление инерции с точки зрения прямолинейного перемещения тела в пространстве. Однако существует еще один тип движения, который распространен в природе и Вселенной – это вращение вокруг точки или оси.
Масса тела характеризует его инерционные свойства поступательного движения. Для описания же аналогичного свойства, которое проявляет себя при вращении, вводят понятие момента инерции. Но перед тем как рассматривать эту характеристику, следует познакомиться с самим вращением.
Круговое перемещение тела вокруг оси или точки описывается двумя важными формулами. Ниже они приводятся:
1) L = I*ω;
2) dL/dt = I*α = M.
В первой формуле L – это момент импульса, I – момент инерции, ω – угловая скорость. Во втором выражении α – это ускорение угловое, которое равно производной по времени от угловой скорости ω, M – момент силы системы. Он рассчитывается как произведение результирующей внешней силы на плечо, к которому она приложена.
Первая формула описывает вращательное движение, вторая – его изменение во времени. Как видно, в обеих этих формулах присутствует момент инерции I.
Момент инерции
Сначала приведем его математическую формулировку, а затем объясним физический смысл.
Итак, момент инерции I рассчитывается следующим образом:
I = ∑i(mi*ri2).
Если перевести это выражение с математического на русский язык, то оно означает следующее: все тело, которое имеет некоторую ось вращения O, разбивается на мелкие “объемчики” массой mi, находящиеся на расстоянии ri от оси O. Момент инерции рассчитывается путем возведения в квадрат этого расстояния, его умножения на соответствующую массу mi и сложения всех полученных слагаемых.
Если разбить все тело на бесконечно малые “объемчики”, тогда сумма выше будет стремиться к следующему интегралу по объему тела:
I = ∫V(ρ *r2dV), где ρ – плотность вещества тела.
Из приведенного математического определения следует, что момент инерции I зависит от трех важных параметров:
- от значения массы тела;
- от распределения массы в теле;
- от положения оси вращения.
Физический смысл момента инерции заключается в том, что он характеризует, насколько “тяжело” привести в движение вращения данную систему или изменить ее скорость вращения.
Момент инерции диска однородного

Полученные в предыдущем пункте знания применимы для расчета момента инерции однородного цилиндра, который в случае h<r принято называть диском (h – высота цилиндра).
Для решения поставленной задачи достаточно рассчитать интеграл по объему этого тела. Выпишем исходную формулу:
I = ∫V(ρ *r2dV).
Если ось вращения проходит перпендикулярно плоскости диска через его центр, тогда можно представить этот диск в виде нарезанных мелких колечек, толщина каждого из них является очень малой величиной dr. В этом случае объем такого колечка можно рассчитать так:
dV = 2*pi*r*h*dr.
Это равенство позволяет интеграл по объему заменить на интегрирование по радиусу диска. Имеем:
I = ∫r(ρ *r2*2*pi*r*h*dr) = 2*pi*h*ρ*∫r(r3*dr).
Вычисляя первообразную подынтегрального выражения, а также учитывая, что интегрирование проводится по радиусу, который изменяется от 0 до r, получаем:
I = 2*pi*h*ρ*r4/4 = pi*h*ρ*r4/2.
Поскольку масса рассматриваемого диска (цилиндра) равна:
m = ρ*V и V = pi*r2*h,
то получаем конечное равенство:
I = m*r2/2.
Эта формула момента инерции диска справедлива для абсолютно любого цилиндрического однородного тела произвольной толщины (высоты), ось вращения которого проходит через его центр.
Разные виды цилиндров и положения осей вращения
Аналогичное интегрирование можно провести для разных тел цилиндрической формы и совершенно любого положения осей их вращения и получить момент инерции для каждого случая. Ниже приводится список часто встречающихся ситуаций:
Из всех этих формул следует, что при одинаковой массе m наибольшим моментом инерции I обладает кольцо.
Где используют инерционные свойства вращающегося диска: маховик

Наиболее ярким примером применения момента инерции диска является маховик в автомобиле, который жестко соединен с коленвалом. Благодаря наличию такого массивного атрибута обеспечивается плавность движения автомобиля, то есть маховик сглаживает любые моменты сил импульсивного характера, которые действуют на коленвал. Более того, этот тяжелый металлический диск способен запасать огромную энергию, обеспечивая тем самым инерционное движение транспортного средства даже при заглушенном двигателе.
В настоящее время инженеры некоторых автомобильных компаний работают над проектом использования маховика в качестве накопителя энергии торможения транспортного средства с целью ее последующего использования при ускорении авто.
Другие понятия об инерции
Хотелось бы завершить статью несколькими словами о других “инерциях”, отличных от рассмотренного явления.
В той же физике существует понятие о температурной инерции, которая характеризует, насколько “трудно” нагреть или охладить данное тело. Температурная инерция прямо пропорциональна теплоемкости.
В более широком философском смысле инерция описывает сложность изменения какого-либо состояния. Так, инертным людям сложно начинать делать что-то новое из-за лени, привычки к рутинному образу жизни и удобству. Кажется, лучше оставить вещи такими, какие они есть, поскольку так жить гораздо проще…
fb.ru
17. Момент инерции тела и его физический смысл. Примеры вычисления момента инерции твердых тел. Теорема Штейнера .
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
2. Физический смысл момента инерции. Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил, приложенных к телу. Сравните. Вращательное движение. Поступательное движение. Момент инерции представляет собой меру инерции тела во вращательном движении
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:
Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями :
18. Момент импульса твердого тела. Вектор угловой скорости и вектор момента импульса. Гироскопический эффект. Угловая скорость прецессии
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим .
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): . Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:.
угловую скорость как вектор, величина которого численно равна угловой скорости, и направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось2, что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен. Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») − если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.
Вращающееся тело ( колесо мотоцикла ) стремиться сохранять положение оси вращения в пространстве неизменным .( гироскопический эффект ) Поэтому возможно движение на 2-х колёсах, но не возможно стояние на двух колёсах Этот эфект используется в корабельных и танковых системах наведения орудий. ( корабль качается на волнах, а орудие смотрит в одну точку ) В навигации и др.
Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитация Земли — действует постоянно.
19. Идеальная и вязкая жидкость. Гидростатика несжимаемой жидкости. Стационарное движение идеальной жидкости. Уравнение Бирнулли.
Идеальной жидкостью назвается воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутреннее трение и теплопроводность. Так как в ней отсуствует внутреннее трение, то нет касательных напряжений
вязкая жидкость характеризуется наличием сил трения, которые возникают при ее движении. вязкой наз. жидкость, в которой при движении кроме нормальных напряжений наблюдаются и касательные напряжения
Рассматриваемые в Г. ур-ния относит. равновесия несжимаемой жидкости в поле сил тяжести (относительно стенок сосуда, совершающего движение по нек-рому известному закону, напр. поступательное или вращательное) дают возможность решать задачи о форме свободной поверхности и о плескании жидкости в движущихся сосудах – в цистернах для перевозки жидкостей, топливных баках самолётов и ракет и т. п., а также в условиях частичной или полной невесомости на космич. летат. аппаратах. При определении формы свободной поверхности жидкости, заключённой в сосуде, кроме сил гидростатич. давления, сил инерции и силы тяжести необходимо учитывать поверхностное натяжение жидкости. В случае вращения сосуда вокруг вертик. оси с пост. угл. скоростью свободная поверхность принимает форму параболоида вращения, а в сосуде, движущемся параллельно горизонтальной плоскости поступательно и прямолинейно с пост. ускорением а, свободной поверхностью жидкости является плоскость, наклонённая к горизонтальной плоскости под углом
studfiles.net
Формула момента инерции, J
Момент инерции тела
Момент инерции является скалярной (в общем случае тензорной) физической величиной, которую находят как сумму произведений масс материальных точек () (на которые следует провести разбиение рассматриваемого тела) на квадраты расстояний () от них до оси вращения:
Если тело считают непрерывным, то суммирование в выражении (1) заменяется интегрированием, массы элементов тела обозначают как :
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела. Если тело является однородным:
Момент инерции материальной точки
Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:
где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной.
Момент инерции является аддитивной величиной. Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции () отдельных точек:
Примеры моментов инерции некоторых тел
Момент инерции тонкого стержня вращающегося около оси, проходящей через его один конец и перпендикулярно стержню, равен:
Момент инерции прямого круглого конуса, массы высоты h и радиуса r вращающегося около своей оси:
Момент инерции однородного твердого параллелепипеда, c геометрическими параметрами и массой m вращающегося относительно своей самой длинной диагонали, вычисляют по формуле:
Момент инерции тонкой прямоугольной пластины массы m, ширины w и длины d, вращающейся относительно оси, которая проходит через точку пересечения диагоналей этого прямоугольника перпендикулярно плоскости пластины:
где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.
Примеры формул для вычисления моментов инерции других тел можно посмотреть в разделе «Момент инерции». В этом же разделе можно ознакомиться с теоремой Штейнера.
Примеры решения задач по теме «Момент инерции»
ru.solverbook.com
Момент инерции — WiKi
Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции
Осевые моменты инерции некоторых телМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
- Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
- dm = ρ dV — масса малого элемента объёма тела dV,
- ρ — плотность,
- r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
- Ja=ρ∫(V)r2dV.{\displaystyle J_{a}=\rho \int \limits _{(V)}r^{2}dV.}
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
- J=Jc+md2,{\displaystyle J=J_{c}+md^{2},}
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
- J=Jc+md2=112ml2+m(l2)2=13ml2.{\displaystyle J=J_{c}+md^{2}={\frac {1}{12}}ml^{2}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{3}}ml^{2}.}
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
- J=∑dJi=∑Ri2dm.(1).{\displaystyle J=\sum dJ_{i}=\sum R_{i}^{2}dm.\qquad (1).}
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
- J=∑R2dm=R2∑dm=mR2.{\displaystyle J=\sum R^{2}dm=R^{2}\sum dm=mR^{2}.}
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
- J=12mR2.{\displaystyle J={\frac {1}{2}}mR^{2}.}
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
- r=RhH,{\displaystyle r={\frac {Rh}{H}},}
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(RhH)4dh;{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {Rh}{H}}\right)^{4}dh;}
Интегрируя, получим
- J=∫0HdJ=12πρ(RH)4∫0Hh5dh=12πρ(RH)4h55|0H==110πρR4H=(ρ⋅13πR2H)310R2=310mR2.{\displaystyle {\begin{aligned}J=\int _{0}^{H}dJ={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\int _{0}^{H}h^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\left.{\frac {h^{5}}{5}}\right|_{0}^{H}=={\frac {1}{10}}\pi \rho R^{4}H=\left(\rho \cdot {\frac {1}{3}}\pi R^{2}H\right){\frac {3}{10}}R^{2}={\frac {3}{10}}mR^{2}.\end{aligned}}}
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
- r=R2−h3.{\displaystyle r={\sqrt {R^{2}-h^{2}}}.}
Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(R2−h3)2dh=12πρ(R4−2R2h3+h5)dh.{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left(R^{2}-h^{2}\right)^{2}dh={\frac {1}{2}}\pi \rho \left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh.}
Момент инерции шара найдём интегрированием:
- J=∫−RRdJ=2∫0RdJ=πρ∫0R(R4−2R2h3+h5)dh==πρ(R4h−23R2h4+15h5)|0R=πρ(R5−23R5+15R5)=815πρR5==(43πR3ρ)⋅25R2=25mR2.{\displaystyle {\begin{aligned}J&=\int _{-R}^{R}dJ=2\int _{0}^{R}dJ=\pi \rho \int _{0}^{R}\left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh=\\&=\pi \rho \left.\left(R^{4}h-{\frac {2}{3}}R^{2}h^{3}+{\frac {1}{5}}h^{5}\right)\right|_{0}^{R}=\pi \rho \left(R^{5}-{\frac {2}{3}}R^{5}+{\frac {1}{5}}R^{5}\right)={\frac {8}{15}}\pi \rho R^{5}=\\&=\left({\frac {4}{3}}\pi R^{3}\rho \right)\cdot {\frac {2}{5}}R^{2}={\frac {2}{5}}mR^{2}.\end{aligned}}}
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
- J0=25MR2=815πρR5.{\displaystyle J_{0}={\frac {2}{5}}MR^{2}={\frac {8}{15}}\pi \rho R^{5}.}
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
- J=dJ0dRdR=ddR(815πρR5)dR==83πρR4dR=(ρ⋅4πR2dR)23R2=23mR2.{\displaystyle {\begin{aligned}J&={\frac {dJ_{0}}{dR}}dR={\frac {d}{dR}}\left({\frac {8}{15}}\pi \rho R^{5}\right)dR=\\&={\frac {8}{3}}\pi \rho R^{4}dR=\left(\rho \cdot 4\pi R^{2}dR\right){\frac {2}{3}}R^{2}={\frac {2}{3}}mR^{2}.\end{aligned}}}
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
- dm=mdrl;dJ=r2dm=mr2drl.{\displaystyle dm={\frac {mdr}{l}};\qquad dJ=r^{2}dm={\frac {mr^{2}dr}{l}}.}
Интегрируя, получим
- J=∫−l/2l/2dJ=2∫0l/2dJ=2ml∫0l/2r2dr=2mlr33|0l/2=2mll324=112ml2.{\displaystyle J=\int _{-l/2}^{l/2}dJ=2\int _{0}^{l/2}dJ={\frac {2m}{l}}\int _{0}^{l/2}r^{2}dr={\frac {2m}{l}}\left.{\frac {r^{3}}{3}}\right|_{0}^{l/2}={\frac {2m}{l}}{\frac {l^{3}}{24}}={\frac {1}{12}}ml^{2}.}
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
- J=J0+mr2=J0+m(l2)2=112ml2+14ml2=13ml2.{\displaystyle J=J_{0}+mr^{2}=J_{0}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{12}}ml^{2}+{\frac {1}{4}}ml^{2}={\frac {1}{3}}ml^{2}.}

Безразмерные моменты инерции планет и спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
- Jxy=∫(m)xydm=∫(V)xyρdV,{\displaystyle J_{xy}=\int \limits _{(m)}xydm=\int \limits _{(V)}xy\rho dV,}
- Jxz=∫(m)xzdm=∫(V)xzρdV,{\displaystyle J_{xz}=\int \limits _{(m)}xzdm=\int \limits _{(V)}xz\rho dV,}
- Jyz=∫(m)yzdm=∫(V)yzρdV,{\displaystyle J_{yz}=\int \limits _{(m)}yzdm=\int \limits _{(V)}yz\rho dV,}
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].
Геометрические моменты инерции
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
- JVa=∫(V)r2dV,{\displaystyle J_{Va}=\int \limits _{(V)}r^{2}dV,}
где, как и ранее r — расстояние от элемента dV до оси a.
Размерность JVa — длина в пятой степени (dimJVa=L5{\displaystyle \mathrm {dim} J_{Va}=\mathrm {L^{5}} } ), соответственно единица измерения СИ — м5.
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
- JSa=∫(S)r2dS,{\displaystyle J_{Sa}=\int \limits _{(S)}r^{2}dS,}
где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.
Размерность JSa — длина в четвёртой степени (dimJSa=L4{\displaystyle \mathrm {dim} J_{Sa}=\mathrm {L^{4}} } ), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.
Через геометрический момент инерции площади выражается момент сопротивления сечения:
- W=JSarmax.{\displaystyle W={\frac {J_{Sa}}{r_{max}}}.}
Здесь rmax — максимальное расстояние от поверхности до оси.
Момент инерции относительно плоскости
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].
Если через произвольную точку O{\displaystyle O} провести координатные оси x,y,z{\displaystyle x,y,z} , то моменты инерции относительно координатных плоскостей xOy{\displaystyle xOy} , yOz{\displaystyle yOz} и zOx{\displaystyle zOx} будут выражаться формулами:
- JxOy=∑i=1nmizi2 ,{\displaystyle J_{xOy}=\sum _{i=1}^{n}m_{i}z_{i}^{2}\ ,}
- JyOz=∑i=1nmixi2 ,{\displaystyle J_{yOz}=\sum _{i=1}^{n}m_{i}x_{i}^{2}\ ,}
- JzOx=∑i=1nmiyi2 .{\displaystyle J_{zOx}=\sum _{i=1}^{n}m_{i}y_{i}^{2}\ .}
В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) JO{\displaystyle J_{O}} — это величина, определяемая выражением[9]:
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:
- JO=12(Jx+Jy+Jz),{\displaystyle J_{O}={\frac {1}{2}}\left(J_{x}+J_{y}+J_{z}\right),}
- JO=JxOy+JyOz+JxOz.{\displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором s→=‖sx,sy,sz‖T,|s→|=1{\displaystyle {\vec {s}}=\left\Vert s_{x},s_{y},s_{z}\right\Vert ^{T},\left\vert {\vec {s}}\right\vert =1} , можно представить в виде квадратичной (билинейной) формы:
- Is=s→T⋅J^⋅s→,{\displaystyle I_{s}={\vec {s}}^{T}\cdot {\hat {J}}\cdot {\vec {s}},\qquad } (1)
где J^{\displaystyle {\hat {J}}} — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 3×3{\displaystyle 3\times 3} и состоит из компонент центробежных моментов:
- J^=‖Jxx−Jxy−Jxz−JyxJyy−Jyz−Jzx−JzyJzz‖,{\displaystyle {\hat {J}}=\left\Vert {\begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\\-J_{yx}&J_{yy}&-J_{yz}\\-J_{zx}&-J_{zy}&J_{zz}\end{array}}\right\Vert ,}
- Jxy=Jyx,Jxz=Jzx,Jzy=Jyz,{\displaystyle J_{xy}=J_{yx},\quad J_{xz}=J_{zx},\quad J_{zy}=J_{yz},\quad } Jxx=∫(m)(y2+z2)dm,Jyy=∫(m)(x2+z2)dm,Jzz=∫(m)(x2+y2)dm.{\displaystyle J_{xx}=\int \limits _{(m)}(y^{2}+z^{2})dm,\quad J_{yy}=\int \limits _{(m)}(x^{2}+z^{2})dm,\quad J_{zz}=\int \limits _{(m)}(x^{2}+y^{2})dm.}
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора J^{\displaystyle {\hat {J}}} :
- J^d=Q^T⋅J^⋅Q^,{\displaystyle {\hat {J}}_{d}={\hat {Q}}^{T}\cdot {\hat {J}}\cdot {\hat {Q}},}
- J^d=‖JX000JY000JZ‖,{\displaystyle {\hat {J}}_{d}=\left\Vert {\begin{array}{ccc}J_{X}&0&0\\0&J_{Y}&0\\0&0&J_{Z}\end{array}}\right\Vert ,}
где Q^{\displaystyle {\hat {Q}}} — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины JX,JY,JZ{\displaystyle J_{X},J_{Y},J_{Z}} — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- Is=JX⋅sx2+JY⋅sy2+JZ⋅sz2,{\displaystyle I_{s}=J_{X}\cdot s_{x}^{2}+J_{Y}\cdot s_{y}^{2}+J_{Z}\cdot s_{z}^{2},}
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на Is{\displaystyle I_{s}}
- (sxIs)2⋅JX+(syIs)2⋅JY+(szIs)2⋅JZ=1{\displaystyle \left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{X}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Y}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Z}=1}
и произведя замены:
- ξ=sxIs,η=syIs,ζ=szIs,{\displaystyle \xi ={s_{x} \over {\sqrt {I_{s}}}},\eta ={s_{y} \over {\sqrt {I_{s}}}},\zeta ={s_{z} \over {\sqrt {I_{s}}}},}
получаем канонический вид уравнения эллипсоида в координатах ξηζ{\displaystyle \xi \eta \zeta } :
- ξ2⋅JX+η2⋅JY+ζ2⋅JZ=1.{\displaystyle \xi ^{2}\cdot J_{X}+\eta ^{2}\cdot J_{Y}+\zeta ^{2}\cdot J_{Z}=1.}
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
- r2=ξ2+η2+ζ2=(sxIs)2+(syIs)2+(szIs)2=1Is.{\displaystyle r^{2}=\xi ^{2}+\eta ^{2}+\zeta ^{2}=\left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}={1 \over I_{s}}.}
См. также
ru-wiki.org
Момент инерции. Теорема Штейнера
Момент инерции. Теорема Штейнера.
| Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат расстояния от оси. | |
| Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси. | |
В случае непрерывного распределения масс эта сумма сводится к интегралу , где интегрирование производится по объему тела.
^ – момент инерции относительно главной оси вращения, проходящей через центр масс.
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Моменты инерции однородных тел массой т, имеющих правильную геометрическую форму и равномерное распределение массы по объёму:
| Тело | Положение оси вращения | ^ |
| Полый тонкостенный цилиндр радиуса R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиуса R | Ось симметрии | |
| Прямой тонкий стержень длиной I | Ось перпендикулярна стержню и проходит через его середину | |
| Шар радиусом R | Ось проходит через центр шара | |
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера.
| Момент инерции тела ^ относительно произвольной оси z равен сумме момента его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, и произведения массы m тела на квадрат расстояния а между осями. | |
Момент инерции, по определению:
Радиус-вектор можно расписать как разность двух векторов:
,
где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
Вынося за сумму , получим:
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
,
где — известный момент инерции относительно оси, проходящей через центр масс тела.
Пример
Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью ) равен
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен
где — расстояние между искомой осью и осью . В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле :
^
Абсолютно твердое тело вращается около неподвижной оси r, проходящей через него. Все точки движутся с одинаковой угловой скоростью = const. Кинетическая энергия тела
где ^ z – момент инерции тела относительно оси z.
Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна сумме кинетических энергий.
Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела.
Моментом силы относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора , проведенного из точки О в точку А приложения силы, на силу :
Модуль момента силы М = F·r·sin a = Fl, где l = r·sina – плечо силы – кратчайшее расстояние между линией действия силы и точкой О , a – угол между r и F.
Моментом силы относительно неподвижной оси z – называется скалярная величина М, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на оси z.
^
При повороте тела под действием силы на бесконечно малый угол точка приложения силы А проходит путь и работа равна
Работа вращения тела идет на увеличение его кинетической энергии
Тогда
или
откуда следует уравнение динамики вращательного движения твердого тела:
Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство , где J – главный момент инерции тела (момент инерции относительно главной оси).
^
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением
Моментом импульса относительно неподвижной оси z называется скалярная величина L, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса L не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси каждая точка тела движется по окружности постоянного радиуса со скоростью перпендикулярной радиусу. Момент импульса отдельной частицы равен и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скорости ).
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
Продифференцируем по времени:
В векторной форме:
– ещё одна форма уравнения динамики вращательного движения твердого тела.
В замкнутой системе момент внешних сил = 0, следовательно, и = 0.
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени:
Это – фундаментальный закон природы. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.
При равномерном вращении твердого тела относительно некоторой оси z закон сохранения момента импульса равносилен: .
Сравнительная таблица основных величин и соотношений для поступа-тельного движения тела и для его вращения вокруг неподвижной оси:
zavantag.com
Момент инерции Википедия
Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции
Осевые моменты инерции некоторых телМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
- Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
- dm = ρ dV — масса малого элемента объёма тела dV,
- ρ — плотность,
- r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
- Ja=ρ∫(V)r2dV.{\displaystyle J_{a}=\rho \int \limits _{(V)}r^{2}dV.}
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
- J=Jc+md2,{\displaystyle J=J_{c}+md^{2},}
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
- J=Jc+md2=112ml2+m(l2)2=13ml2.{\displaystyle J=J_{c}+md^{2}={\frac {1}{12}}ml^{2}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{3}}ml^{2}.}
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
- J=∑dJi=∑Ri2dm.(1).{\displaystyle J=\sum dJ_{i}=\sum R_{i}^{2}dm.\qquad (1).}
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
- J=∑R2dm=R2∑dm=mR2.{\displaystyle J=\sum R^{2}dm=R^{2}\sum dm=mR^{2}.}
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
- J=12mR2.{\displaystyle J={\frac {1}{2}}mR^{2}.}
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
- r=RhH,{\displaystyle r={\frac {Rh}{H}},}
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(RhH)4dh;{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {Rh}{H}}\right)^{4}dh;}
Интегрируя, получим
- J=∫0HdJ=12πρ(RH)4∫0Hh5dh=12πρ(RH)4h55|0H==110πρR4H=(ρ⋅13πR2H)310R2=310mR2.{\displaystyle {\begin{aligned}J=\int _{0}^{H}dJ={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\int _{0}^{H}h^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\left.{\frac {h^{5}}{5}}\right|_{0}^{H}=={\frac {1}{10}}\pi \rho R^{4}H=\left(\rho \cdot {\frac {1}{3}}\pi R^{2}H\right){\frac {3}{10}}R^{2}={\frac {3}{10}}mR^{2}.\end{aligned}}}
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
- r=R2−h3.{\displaystyle r={\sqrt {R^{2}-h^{2}}}.}
Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(R2−h3)2dh=12πρ(R4−2R2h3+h5)dh.{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left(R^{2}-h^{2}\right)^{2}dh={\frac {1}{2}}\pi \rho \left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh.}
Момент инерции шара найдём интегрированием:
- J=∫−RRdJ=2∫0RdJ=πρ∫0R(R4−2R2h3+h5)dh==πρ(R4h−23R2h4+15h5)|0R=πρ(R5−23R5+15R5)=815πρR5==(43πR3ρ)⋅25R2=25mR2.{\displaystyle {\begin{aligned}J&=\int _{-R}^{R}dJ=2\int _{0}^{R}dJ=\pi \rho \int _{0}^{R}\left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh=\\&=\pi \rho \left.\left(R^{4}h-{\frac {2}{3}}R^{2}h^{3}+{\frac {1}{5}}h^{5}\right)\right|_{0}^{R}=\pi \rho \left(R^{5}-{\frac {2}{3}}R^{5}+{\frac {1}{5}}R^{5}\right)={\frac {8}{15}}\pi \rho R^{5}=\\&=\left({\frac {4}{3}}\pi R^{3}\rho \right)\cdot {\frac {2}{5}}R^{2}={\frac {2}{5}}mR^{2}.\end{aligned}}}
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
- J0=25MR2=815πρR5.{\displaystyle J_{0}={\frac {2}{5}}MR^{2}={\frac {8}{15}}\pi \rho R^{5}.}
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
- J=dJ0dRdR=ddR(815πρR5)dR==83πρR4dR=(ρ⋅4πR2dR)23R2=23mR2.{\displaystyle {\begin{aligned}J&={\frac {dJ_{0}}{dR}}dR={\frac {d}{dR}}\left({\frac {8}{15}}\pi \rho R^{5}\right)dR=\\&={\frac {8}{3}}\pi \rho R^{4}dR=\left(\rho \cdot 4\pi R^{2}dR\right){\frac {2}{3}}R^{2}={\frac {2}{3}}mR^{2}.\end{aligned}}}
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
- dm=mdrl;dJ=r2dm=mr2drl.{\displaystyle dm={\frac {mdr}{l}};\qquad dJ=r^{2}dm={\frac {mr^{2}dr}{l}}.}
Интегрируя, получим
- J=∫−l/2l/2dJ=2∫0l/2dJ=2ml∫0l/2r2dr=2mlr33|0l/2=2mll324=112ml2.{\displaystyle J=\int _{-l/2}^{l/2}dJ=2\int _{0}^{l/2}dJ={\frac {2m}{l}}\int _{0}^{l/2}r^{2}dr={\frac {2m}{l}}\left.{\frac {r^{3}}{3}}\right|_{0}^{l/2}={\frac {2m}{l}}{\frac {l^{3}}{24}}={\frac {1}{12}}ml^{2}.}
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
- J=J0+mr2=J0+m(l2)2=112ml2+14ml2=13ml2.{\displaystyle J=J_{0}+mr^{2}=J_{0}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{12}}ml^{2}+{\frac {1}{4}}ml^{2}={\frac {1}{3}}ml^{2}.}

Безразмерные моменты инерции планет и спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
- Jxy=∫(m)xydm=∫(V)xyρdV,{\displaystyle J_{xy}=\int \limits _{(m)}xydm=\int \limits _{(V)}xy\rho dV,}
- Jxz=∫(m)xzdm=∫(V)xzρdV,{\displaystyle J_{xz}=\int \limits _{(m)}xzdm=\int \limits _{(V)}xz\rho dV,}
- Jyz=∫(m)yzdm=∫(V)yzρdV,{\displaystyle J_{yz}=\int \limits _{(m)}yzdm=\int \limits _{(V)}yz\rho dV,}
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].
Геометрические моменты инерции
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
- JVa=∫(V)r2dV,{\displaystyle J_{Va}=\int \limits _{(V)}r^{2}dV,}
где, как и ранее r — расстояние от элемента dV до оси a.
Размерность JVa — длина в пятой степени (dimJVa=L5{\displaystyle \mathrm {dim} J_{Va}=\mathrm {L^{5}} }), соответственно единица измерения СИ — м5.
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
- JSa=∫(S)r2dS,{\displaystyle J_{Sa}=\int \limits _{(S)}r^{2}dS,}
где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.
Размерность JSa — длина в четвёртой степени (dimJSa=L4{\displaystyle \mathrm {dim} J_{Sa}=\mathrm {L^{4}} }), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.
Через геометрический момент инерции площади выражается момент сопротивления сечения:
- W=JSarmax.{\displaystyle W={\frac {J_{Sa}}{r_{max}}}.}
Здесь rmax — максимальное расстояние от поверхности до оси.
Момент инерции относительно плоскости
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].
Если через произвольную точку O{\displaystyle O} провести координатные оси x,y,z{\displaystyle x,y,z}, то моменты инерции относительно координатных плоскостей xOy{\displaystyle xOy}, yOz{\displaystyle yOz} и zOx{\displaystyle zOx} будут выражаться формулами:
- JxOy=∑i=1nmizi2 ,{\displaystyle J_{xOy}=\sum _{i=1}^{n}m_{i}z_{i}^{2}\ ,}
- JyOz=∑i=1nmixi2 ,{\displaystyle J_{yOz}=\sum _{i=1}^{n}m_{i}x_{i}^{2}\ ,}
- JzOx=∑i=1nmiyi2 .{\displaystyle J_{zOx}=\sum _{i=1}^{n}m_{i}y_{i}^{2}\ .}
В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) JO{\displaystyle J_{O}} — это величина, определяемая выражением[9]:
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:
- JO=12(Jx+Jy+Jz),{\displaystyle J_{O}={\frac {1}{2}}\left(J_{x}+J_{y}+J_{z}\right),}
- JO=JxOy+JyOz+JxOz.{\displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором s→=‖sx,sy,sz‖T,|s→|=1{\displaystyle {\vec {s}}=\left\Vert s_{x},s_{y},s_{z}\right\Vert ^{T},\left\vert {\vec {s}}\right\vert =1}, можно представить в виде квадратичной (билинейной) формы:
- Is=s→T⋅J^⋅s→,{\displaystyle I_{s}={\vec {s}}^{T}\cdot {\hat {J}}\cdot {\vec {s}},\qquad } (1)
где J^{\displaystyle {\hat {J}}} — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 3×3{\displaystyle 3\times 3} и состоит из компонент центробежных моментов:
- J^=‖Jxx−Jxy−Jxz−JyxJyy−Jyz−Jzx−JzyJzz‖,{\displaystyle {\hat {J}}=\left\Vert {\begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\\-J_{yx}&J_{yy}&-J_{yz}\\-J_{zx}&-J_{zy}&J_{zz}\end{array}}\right\Vert ,}
- Jxy=Jyx,Jxz=Jzx,Jzy=Jyz,{\displaystyle J_{xy}=J_{yx},\quad J_{xz}=J_{zx},\quad J_{zy}=J_{yz},\quad }Jxx=∫(m)(y2+z2)dm,Jyy=∫(m)(x2+z2)dm,Jzz=∫(m)(x2+y2)dm.{\displaystyle J_{xx}=\int \limits _{(m)}(y^{2}+z^{2})dm,\quad J_{yy}=\int \limits _{(m)}(x^{2}+z^{2})dm,\quad J_{zz}=\int \limits _{(m)}(x^{2}+y^{2})dm.}
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора J^{\displaystyle {\hat {J}}}:
- J^d=Q^T⋅J^⋅Q^,{\displaystyle {\hat {J}}_{d}={\hat {Q}}^{T}\cdot {\hat {J}}\cdot {\hat {Q}},}
- J^d=‖JX000JY000JZ‖,{\displaystyle {\hat {J}}_{d}=\left\Vert {\begin{array}{ccc}J_{X}&0&0\\0&J_{Y}&0\\0&0&J_{Z}\end{array}}\right\Vert ,}
где Q^{\displaystyle {\hat {Q}}} — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины JX,JY,JZ{\displaystyle J_{X},J_{Y},J_{Z}} — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- Is=JX⋅sx2+JY⋅sy2+JZ⋅sz2,{\displaystyle I_{s}=J_{X}\cdot s_{x}^{2}+J_{Y}\cdot s_{y}^{2}+J_{Z}\cdot s_{z}^{2},}
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на Is{\displaystyle I_{s}}
- (sxIs)2⋅JX+(syIs)2⋅JY+(szIs)2⋅JZ=1{\displaystyle \left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{X}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Y}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Z}=1}
и произведя замены:
- ξ=sxIs,η=syIs,ζ=szIs,{\displaystyle \xi ={s_{x} \over {\sqrt {I_{s}}}},\eta ={s_{y} \over {\sqrt {I_{s}}}},\zeta ={s_{z} \over {\sqrt {I_{s}}}},}
получаем канонический вид уравнения эллипсоида в координатах ξηζ{\displaystyle \xi \eta \zeta }:
- ξ2⋅JX+η2⋅JY+ζ2⋅JZ=1.{\displaystyle \xi ^{2}\cdot J_{X}+\eta ^{2}\cdot J_{Y}+\zeta ^{2}\cdot J_{Z}=1.}
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
- r2=ξ2+η2+ζ2=(sxIs)2+(syIs)2+(szIs)2=1Is.{\displaystyle r^{2}=\xi ^{2}+\eta ^{2}+\zeta ^{2}=\left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}={1 \over I_{s}}.}
См. также
Комментарии
- ↑ В правильности использования знака «+» в этой формуле можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r1 к r2 формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
- Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
wikiredia.ru
