Таблица интегралов (неопределенных и т.д.)
Интегрирование — это одна из основных операций в матанализе. Таблицы известных первообразных могут быть полезны, но сейчас они, после появления систем компьютерной алгебры, теряют свою значимость. Ниже находится список больше всего встречающихся первообразных.
Таблица основных интегралов
Другой, компактный вариант

Таблица интегралов от тригонометрических функций
От рациональных функций

От иррациональных функций

https://uchim.org/matematika/tablica-integralov – uchim.org
Интегралы от трансцендентных функций

“C” – произвольная константа интегрирования, которая определяется, если известно значение интеграла в какой-либо точке. Каждая функция имеет бесконечное число первообразных.
У большинства школьников и студентов бывают проблемы с вычислением интегралов. На этой странице собраны таблицы интегралов от тригонометрических, рациональных, иррациональных и трансцендентных функций, которые помогут в решении. Еще вам поможет таблица производных.
Видео – как находить интегралы
Если вам не совсем понятна данная тема, посмотрите видео, в котором всё подробно объясняется.Всё для учебы » Математика в школе » Таблица интегралов (неопределенных и т.д.)
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-integralov
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
uchim.org
| 1. |
| ||||
| 2. |
| ||||
| 3. |
| ||||
| 4. |
| ||||
| 5. |
| ||||
| 6. |
| ||||
| 7. |
| ||||
| 8. |
| ||||
| 9. |
| ||||
| 10. |
| ||||
| 11. |
| ||||
| 12. |
| ||||
| 13. |
| ||||
| 14. |
| ||||
| 15. |
| ||||
| 16. |
| ||||
| 17. |
| ||||
| 18. |
| ||||
| |||||
| 20. |
| ||||
| 21. |
| ||||
| 22. |
| ||||
| 23. |
| ||||
| 24. |
| ||||
| 25. |
| ||||
| 26. |
| ||||
| 27. |
| ||||
| 28. |
| ||||
| 29. |
| ||||
| 30. |
| ||||
| 31. |
|
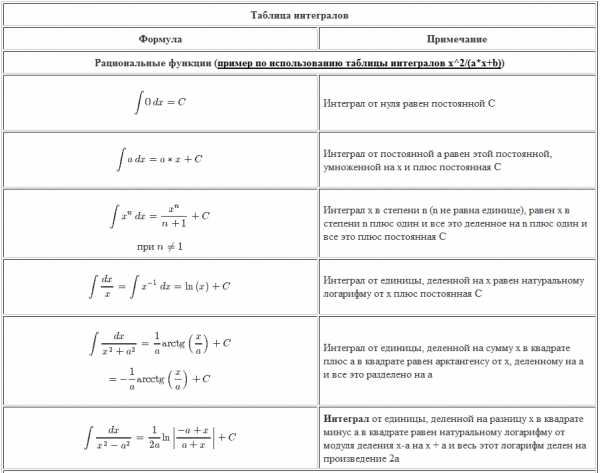
| Рациональные функции (пример по использованию таблицы интегралов x^2/(a*x+b)) | |
|---|---|
| $$\int 0\, dx = C$$ | Интеграл от нуля равен постоянной C |
| $$\int a\, dx = a*x + C$$ | Интеграл от постоянной a равен этой постоянной, умноженной на x и плюс постоянная C |
| $$\int x^{n}\, dx = \frac{x^{n}}{n + 1} + C$$ при $n \ne 1$ | Интеграл x в степени n (n не равна единице), равен x в степени n плюс один и все это деленное на n плюс один и все это плюс постоянная C |
| $$\int \frac{dx}{x} = \int x^{-1}\, dx = \ln{\left (x \right )} + C$$ | Интеграл от единицы, деленной на x равен натуральному логарифму от x плюс постоянная C |
| $$\int \frac{dx}{x^{2} + a^{2}} = \frac{1}{a}\operatorname{arctg}{\left (\frac{x}{a} \right )} + C$$ $$ = -\frac{1}{a}\operatorname{arcctg}{\left (\frac{x}{a} \right )} + C$$ | Интеграл от единицы, деленной на сумму x в квадрате плюс a в квадрате равен арктангенсу от x, деленному на a и все это разделено на a |
| $$\int \frac{dx}{x^{2} – a^{2}} = \frac{1}{2 a} \operatorname{ln}\left|{\frac{- a + x}{a + x}}\right| + C$$ | Интеграл от единицы, деленной на разницу x в квадрате минус a в квадрате равен натуральному логарифму от модуля деления x-a на x + a и весь этот логарифм делен на произведение 2a |
| Логарифмические функции (пример использования таблицы интегралов ln2(x)) | |
| $$\int \operatorname{ln}\left(x\right)\,dx = x \operatorname{ln}\left(x\right) – x + C$$ | Интеграл от натуральной логарифической функции равен произведению x на натуральный логарифм и минус переменная x |
| $$\int \frac{dx}{x \operatorname{ln}\left(x\right)} = \operatorname{ln}\left(\operatorname{ln}\left(x\right)\right) + C$$ | Integral от единицы, деленной на произведение x на натуральный логарифм равняется логарифму от логарифма от x – по сути получается такая сложная функция |
| $$\int \operatorname{log}_{b}\left(x\right)\,dx = x \operatorname{log}_{b}\left(x\right) – \operatorname{log}_{b}\left(e\right) + C$$ | Интеграл от логарифма от x по основанию b равен произведению x на логарифм от x по основанию b минус логарифм от экспоненты по основанию b |
| Экспоненциальные функции (например, как использовать таблицу интегралов ecxsin(bx)) | |
| $$\int e^{x}\,dx = e^{x} + C$$ | Значение интеграла от экспоненты в степени x равно самой экспоненте от x плюс константа C |
| $$\int a^{x}\,dx = \frac{a^{x}}{\operatorname{ln}\left(a\right)} + C$$ | Интеграл от числа a в степени x равняется a в степени x, деленное на натуральный логарифм от a |
| Иррациональные функции (к примеру, таблица интегралов действии: x3(x2 + 1)3/2) | |
| $$\int \frac{dx}{\sqrt{a^{2} – x^{2}}} = \operatorname{arcsin}\left(\frac{x}{a}\right) + C$$ | Интегральное выражение от 1 деленного на корень квадратный из разницы a в квадрате минус x в квадрате равняется арксинусу от деления x на a |
| $$\int \frac{- dx}{\sqrt{a^{2} – x^{2}}} = \operatorname{arccos}\left(\frac{x}{a}\right) + C$$ | Этот же интеграл, но со знаком минус равен арккосинусу от деления x на a |
| $$\int \frac{dx}{x \sqrt{x^{2} – a^{2}}} = \frac{1}{a} \operatorname{arcsec} \frac{\left|x\right|}{a} + C$$ | |
| $$\int \frac{dx}{\sqrt{x^{2} \pm a^{2}}} = \operatorname{ln}\left| x + \sqrt{x^{2} \pm a^{2}}\right| + C$$ | |
| Тригонометрические функции (пример для таблицы интегралчиков sin(c1*x)*sin(c2*x)) | |
| $$\int \operatorname{sin}\left(x\right)\,dx = – \operatorname{cos}\left(x\right) + C$$ | Интеграл от функции синус от x равен минус косинусу от того же x |
| $$\int \operatorname{cos}\left(x\right)\,dx = \operatorname{sin}\left(x\right) + C$$ | Интеграл от функции косинус от x равен синусу от x |
| $$\int \operatorname{tg}\left(x\right)\,dx = \frac{1}{2} \operatorname{ln}\left(\operatorname{tg}^{2}\left(x\right) + 1\right) + C$$ | Интегральное от тангенса от x равно одной второй от логарифма от суммы тангенса в квадрате от x плюс один |
| $$\int \frac{dx}{\operatorname{tg}\left(x\right)} = – \frac{1}{2} \operatorname{ln}\left(\operatorname{tg}^{2}\left(x\right) + 1\right) + \operatorname{ln}\left(\operatorname{tg}\left(x\right)\right) + C$$ | |
| $$\int \frac{dx}{\operatorname{cos}\left(x\right)} = – \frac{1}{2} \operatorname{ln}\left(\operatorname{sin}\left(x\right) -1\right) + \frac{1}{2} \operatorname{ln}\left(\operatorname{sin}\left(x\right) + 1\right) + C$$ | |
| $$\int \frac{dx}{\operatorname{sin}\left(x\right)} = \frac{1}{2} \operatorname{ln}\left(\operatorname{cos}\left(x\right) -1\right) – \frac{1}{2} \operatorname{ln}\left(\operatorname{cos}\left(x\right) + 1\right) + C$$ | |
| $$\int \frac{dx}{\operatorname{cos}^{2}\left(x\right)} = \frac{\operatorname{sin}\left(x\right)}{\operatorname{cos}\left(x\right)} + C$$ | интегралиус от 1 деленной на косинус в квадрате от x равен синусу от x, деленному на косинус от x |
| $$\int \frac{dx}{\operatorname{sin}^{2}\left(x\right)} = – \frac{\operatorname{cos}\left(x\right)}{\operatorname{sin}\left(x\right)} + C$$ | интегрализэ от единицы, деленной на синус в квадрате от x равен минус косинусу от x, деленному на синус от x |
| $$\int \frac{\operatorname{tg}\left(x\right)}{\operatorname{cos}\left(x\right)}\,dx = \frac{1}{\operatorname{cos}\left(x\right)} + C$$ | |
| $$\int \frac{dx}{\operatorname{sin}\left(x\right) \operatorname{tg}\left(x\right)} = \frac{1}{\operatorname{sin}\left(x\right)} + C$$ | |
| $$\int \operatorname{sin}^{2}\left(x\right)\,dx = \frac{1}{2} x – \frac{1}{2} \operatorname{sin}\left(x\right) \operatorname{cos}\left(x\right) + C$$ | |
| $$\int \operatorname{cos}^{2}\left(x\right)\,dx = \frac{1}{2} x + \frac{1}{2} \operatorname{sin}\left(x\right) \operatorname{cos}\left(x\right) + C$$ | |
| $$\int \operatorname{arctg}\left(x\right)\,dx = x \operatorname{arctg}\left(x\right) – \frac{1}{2} \operatorname{ln}\left(x^{2} + 1\right) + C$$ | |
| $$\int \operatorname{sin}^{n} \left(x\right)\,dx = – \frac{\operatorname{sin}^{n-1}\left(x\right)*x*\operatorname{cos}\left(x\right)}{n} + \frac{n-1}{n} \int \operatorname{sin}^{n-2}\left(x\right)\,dx$$ при $n \geq 2, n \in \mathbb{N}$ | |
| $$\int \operatorname{cos}^{n} \left(x\right)\,dx = \frac{\operatorname{cos}^{n-1}\left(x\right)*x*\operatorname{sin}\left(x\right)}{n} + \frac{n-1}{n} \int \operatorname{cos}^{n-2}\left(x\right)\,dx$$ при $n \geq 2, n \in \mathbb{N}$ | |
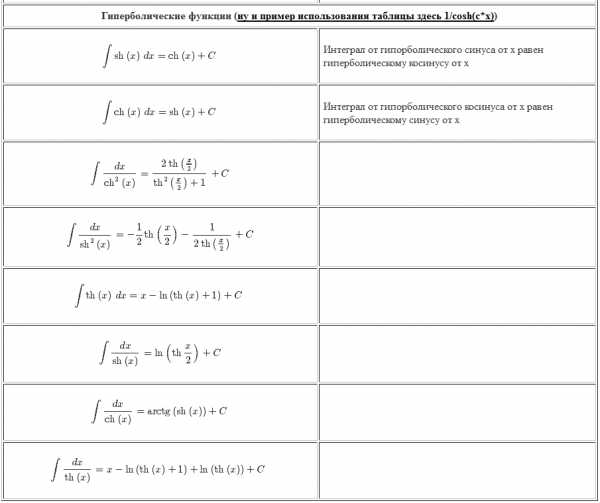
| Гиперболические функции (ну и пример использования таблицы здесь 1/сosh(c*x)) | |
| $$\int \operatorname{sh}\left(x\right)\,dx = \operatorname{ch}\left(x\right) + C$$ | Интеграл от гипорболического синуса от x равен гиперболическому косинусу от x |
| $$\int \operatorname{ch}\left(x\right)\,dx = \operatorname{sh}\left(x\right) + C$$ | Интеграл от гипорболического косинуса от x равен гиперболическому синусу от x |
| $$\int \frac{dx}{\operatorname{ch}^{2}\left(x\right)} = \frac{2 \operatorname{th}\left(\frac{x}{2}\right)}{\operatorname{th}^{2}\left(\frac{x}{2}\right) + 1} + C$$ | |
| $$\int \frac{dx}{\operatorname{sh}^{2}\left(x\right)} = – \frac{1}{2} \operatorname{th}\left(\frac{x}{2}\right) – \frac{1}{2 \operatorname{th}\left(\frac{x}{2}\right)} + C$$ | |
| $$\int \operatorname{th}\left(x\right)\,dx = x – \operatorname{ln}\left(\operatorname{th}\left(x\right) + 1\right) + C$$ | |
| $$\int \frac{dx}{\operatorname{sh}\left(x\right)} = \operatorname{ln}\left(\operatorname{th} \frac{x}{2}\right) + C$$ | |
| $$\int \frac{dx}{\operatorname{ch}\left(x\right)} = \operatorname{arctg}\left(\operatorname{sh}\left(x\right)\right) + C$$ | |
| $$\int \frac{dx}{\operatorname{th}\left(x\right)} = x – \operatorname{ln}\left(\operatorname{th}\left(x\right) + 1\right) + \operatorname{ln}\left(\operatorname{th}\left(x\right)\right) + C$$ | |
www.kontrolnaya-rabota.ru
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная диференциированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
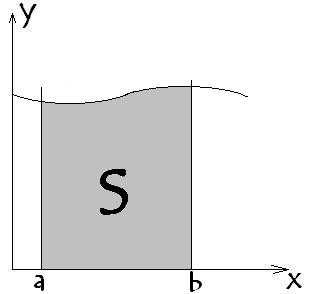
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
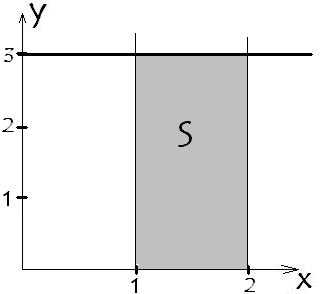
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов

Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов: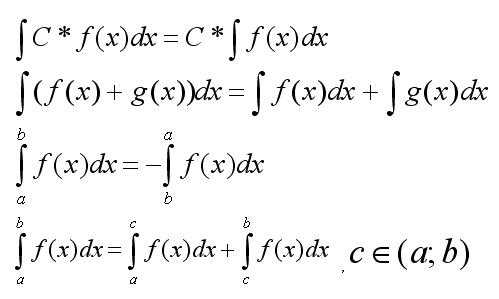
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.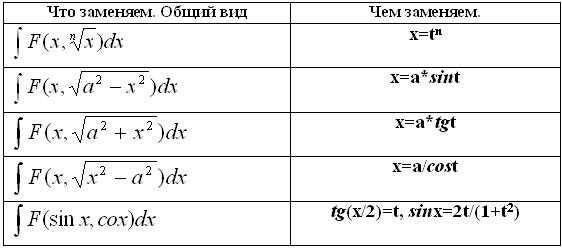
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
– разложить дробь на простейшие
– выделить полный квадрат.
– создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
– выделить под корнем полный квадрат
– создать в числителе дифференциал подкоренного выважения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1
m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2
Для выражений вида:
– Применяем свойство tg2x=1/cos2x – 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:
Примеры решения интегралов
Пример 1:
Решить интеграл:
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:
Проверим решение(найдем производную):
Пример 2. Решаем интеграл
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t5. t5 = x+5 . Получаем.
Но dx нужно тоже заменить на t. x= t5 – 5, dx = (t5 – 5)’ = 5t4. Подставляем:
Интеграл из таблицы. Считаем:
Подставляем в ответ вместо t ,
Решение интеграла:
Пример 3. Решение интеграла:
Для решения в этом случае необходимо выделить полный квадрат. Выделяем:
В данном случае коэфециент ? перед интегралом получился в результате замены dx на ?*d(2x+1). Если вы найдете производные x’ = 1 и ?*(2x+1)’= 1, то поймете почему так.
Находим первообразную.
В итоге получаем:
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Справочник репетитора по математике. Список табличных интегралов
Табличные интегралы для занятий по математическому анализу. В помощь студентам первых курсов технических, экономических и математических ВУЗов, преподавателям и репетиторам по математике.
Неопределенных интегралы от основных функций.
2. Интеграл от константы
3. Интеграл от синуса
4. Интеграл от косинуса
5. Интеграл от экспоненты
6. Интеграл от показательной функции
7. Интеграл от обратной пропорциональности
8.Интеграл, равный тангенсу
9. Интеграл, равный котангенсу
10. Интеграл от тангенса
11. Интеграл от котангенса
12. Интеграл, равный арксинусу
13. Интеграл, равный минус арккосинусу
14. Интеграл от секонса
15. Интеграл от косеконса
16. Интеграл, от обратной величины к разности квадратов
17. Полезный интеграл, сводящийся к арксинусу
18. Полезный интеграл, сводящийся к арктангенсу
19. Интеграл, сводящийся к натуральному логарифму
Комментарий репетитора по математике: к табличным обычно относят простейшие интегралы, в записи которых участвуют элементарные (основные) функции математического анализа. Табличные интегралы можно использовать для вычисления любых других интегралов (типовых или сложных) на любом этапе реализации алгоритма их нахождения. Техника интегрирования допускает следующий план: как только вам встетился табличный интеграл — применяйте его без каких-либо доказательств или вывода.
Интегралы расположены в порядке роста уровня сложности их вывода и частоте использования в решении задач. Удачи в совершенствовании умения вычислять интегралы.
Колпаков А.Н., профессиональный репетитор по математике в Москве.Строгино, м. Щукинская.
ankolpakov.ru
Таблица интегралов
В школе у многих не получается решить интегралы или возникают какие-либо трудности с ними. Данная статья поможет вам в этом разобраться, так как в ней вы найдете все таблицы интегралов.
Интеграл является одним из главных вычислений и понятием в математическом анализе. Его появление получилось от двух целей:
Первая цель – восстановить функцию с помощью ее производной.
Вторая цель – вычисление площади, находящейся на расстоянии от графика к функции f(x) на прямой где, а больше или равна х больше или равен b и ось абсцисс.
Данные цели подводят нас к определенным и неопределенным интегралам. Связь между данными интегралами лежит в поиске свойств и вычислении. Но все течет и все меняется со временем, находились новые пути решения, выявлялись дополнения тем самым приводя определенные и неопределенные интегралы к иным формам интегрирования.
Что такое неопределенный интеграл спросите Вы. Это первообразная функция F(x) одной переменной x в интервале а больше х больше b. называется любой функцией F(x), в данном интервале для любого обозначения х, производная равняется F(x). Понятно что F(x) первообразная для f(x) в промежутке а больше х больше b. Значит F1(x) = F(x) + C. С -является любым постоянным и первообразным для f(x) в данном интервале. Данное утверждение обратимо, для функции f(x) – 2 первообразные отличаются только постоянной. Опираясь на теорему интегрального исчисления получается, что каждая непрерывная в интервале a
Определенный интеграл понимается как предел в интегральных суммах, или в ситуации заданной функции f(x) определенной на некоторой прямой (а,b) имея на нем первообразную F, означающую разность ее выражений в концах данной прямой F(b) – F(a).
Для наглядности изучения данной темы, предлагаю посмотреть видео. В нем подробно рассказывается и показывается как находить интегралы.
Каждая таблица интегралов сама по себе очень полезна, так как помогает в решении конкретного вида интегралов.




Все возможные виды канцтоваров и не только. Вы можете приобрести через интернет-магазин v-kant.ru. Либо просто перейдите по ссылке Канцтовары Самара (http://v-kant.ru) качество и цены Вас приятно удивят.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Табличные интегралы
Интегралы, которые применяются для интегрирования элементарных функций и их комбинаций, называются табличными интегралами. Ниже приводятся основные табличные интегралы.
1. , n Î R, n ¹ –1
2.
3.
3а.
4.
5.
6.
7.
8.
9.
10.
11.
§4.3 Непосредственное интегрирование, интегрирование подстановкой, интегрирование по частям
Непосредственное интегрирование
Интегрирование называется непосредственным, если при интегрировании применяются только свойства интегралов и табличные интегралы.
@ Задача 1. Интегрировать функцию
.
Решение: Интеграл вычисляется непосредственно с помощью свойств неопределенных интегралов и табличных интегралов:
.
Замечание: Нет нужды выписывать при промежуточных вычислениях для каждого интеграла свое постоянное слагаемое; достаточно приписать его по выполнения всех интегрирований.
Способ подстановки
Этот способ применяется, как правило, если подинтегральная функция сложная и нет возможности сразу брать интеграл с помощью табличных интегралов.
В подинтегральное выражение вместо x вводится вспомогательная переменная z, связанная с x некоторой зависимостью (как правило, аргумент подинтегральной сложной функции), после чего интеграл сводится к табличному интегралу.
@ Задача 2. Вычислить .
Решение: Производится замена переменных 2x – 1 = z, после чего 2x – 1 = z и dx = dz/2 подставляются в подинтегральное выражение, и интеграл сводится к табличному интегралу:
.
@ Задача 3. Вычислить .
Решение: Производится замена переменных 1 + x2 = z, после чего находим 2xdx = dz. После подстановки получим:
.
@ Задача 4. Вычислить .
Решение: Под квадратным корнем, выделив полный квадрат, интеграл можно свести к табличному интегралу:
.
Похожие статьи:
poznayka.org
