определенный интеграл | математика-повторение
Пора познакомиться с мощнейшим средством исследования в математике, физике, механике и других точных дисциплинах. Это средство — определенный интеграл. В средней школе определенный интеграл применяют при вычислениях площадей криволинейных трапеций, объемов тел вращения, нахождении моментов инерции и т.д.
Что такое определенный интеграл? Чем он отличается от неопределенного, с которым мы уже достаточно знакомы.
Сравните:
a и b — это границы, в которых изменяется переменная интегрирования х.
Сравниваем далее:
Неопределенный интеграл графически представляет собой семейство кривых, совмещаемых параллельным переносом (11.1.9).
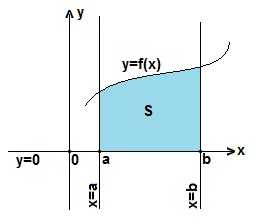 Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми
Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми
Значение определенного интеграла есть площадь S этой криволинейной трапеции:
Рассмотрим примеры на вычисление определенного интеграла.
Пример 1.
Найдем первообразную F (x) для подынтегральной функции f (x)=3x²-2x+1, а затем применим формулу Ньютона-Лейбница (ф. Н-Л).
Пример 2.
Возникает вопрос: раз определенный интеграл выражает собой площадь криволинейной трапеции, то нельзя ли увидеть эту криволинейную трапецию? А можно! Проиллюстрируем пример 2.
Полученный результат
выражает площадь криволинейной трапеции, ограниченной графиком функции y=(x+1)
График функции y=(x+1)4 – парабола, ветви которой направлены вверх,
а вершина находится в точке О′(-1; 0).
Площадь этой криволинейной трапеции:
www.mathematics-repetition.com
Неопределенный интеграл | Высшая математика
Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если F(x) дифференцируема на (a, b) и F'(x)=f(x).
Совокупность всех первообразных для функции f(x) на интервале (
- Свойства неопределенного интеграла
- где C – постоянная;
- .
| Таблица неопределенных интегралов | |
|---|---|
| , α ≠ −1 | |
| , α > 0, a ≠ 1 | |
Замена переменной в неопределенном интеграле (подстановка, подведение под знак дифференциала)
Если то
Формула интегрирования по частям:
- Основные типы интегралов, вычисляемые с помощью интегрирования по частям
- Интегрирование рациональных дробей
- Разложение рациональной дроби на простейшие:
- Тип дроби 1.
Простейшая дробь: - Тип дроби 2.
Простейшая дробь: - Тип дроби 3.
Простейшая дробь: < 0. - Тип дроби 4.
Простейшая дробь: < 0, k ∈ N.
matematika.electrichelp.ru
ИНТЕГРАЛ – это… Что такое ИНТЕГРАЛ?
ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ … Научно-технический энциклопедический словарь
интеграл — а, м. intégrale f. <лат. integer целый. Математическое понятие о целой величине как сумме своих бесконечно малых частей. Нахождение интеграла. БАС 1. Найти интеграл уравнения. 1766. Котельников Геодет 175. // Сл. 18. Алферинька недурно… … Исторический словарь галлицизмов русского языка
ИНТЕГРАЛ — муж., мат., лат. конечная, измеримая величина, в отношении к бесконечно малой части ее, к дифференциалу. Интегральное вычисление, искусство отыскивать интеграл по дифференциалу. Интегрировать, вычислять, находить интеграл; интеграция жен.… … Толковый словарь Даля
ИНТЕГРАЛ — (вово лат., от лат. integer ценный). В математике количество, дифференциал которого равен данной величине. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. интеграл (лат. integer целый) лет. 1) неопределенный и. от… … Словарь иностранных слов русского языка
интеграл — первообразная, термин Словарь русских синонимов. интеграл сущ., кол во синонимов: 2 • первообразная (1) • … Словарь синонимов
интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет … Справочник технического переводчика
ИНТЕГРАЛ
ИНТЕГРАЛ — (от лат. integer целый) см. Интегральное исчисление … Большой Энциклопедический словарь
ИНТЕГРАЛ — ИНТЕГРАЛ, интеграла, муж. (от лат. integer целый) (мат.). Конечная измеримая величина в отношении к бесконечно малой части ее к диференциалу. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ИНТЕГРАЛ — [тэ ], а, муж. В математике: величина, получающаяся в результате действия, обратного дифференцированию. | прил. интегральный, ая, ое. Интегральное исчисление. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
dic.academic.ru
ИНТЕГРАЛ – Интегралы – Математика – Каталог статей
ИНТЕГРАЛ
(от лат. integer-целый), одно из важнейших понятий математики, возникшее
в связи с потребностью, с одной стороны, отыскивать функции по их производным
(напр., находить функцию, выражающую путь, пройденный движущейся точкой,
по скорости этой точки), а с другой – измерять площади, объёмы, длины дуг,
работу сил за определённый промежуток времени и т. п. Соответственно с
этим различают неопределённые и определённые И., вычисление к-рых является
задачей интегрального исчисления.
Неопределённый интеграл. Первообразная функции f(x) одного действительного переменного
– функция F(x)<, производная к-рой при каждом значении х равна f(x).
Прибавляя постоянную к первообразной к.-л. функции, вновь получают первообразную
той же функции. Следовательно, имея одну первообразную F(X) функции f(x),
получают общее выражение всех первообразных этой функции в виде F(X) + С. Это общее выражение первообразных называют неопределённым интегралом:
∫f(x)sx
функции f(x).
Одна из основных теорем интегрального исчисления устанавливает, что каждая
непрерывная функция f(x) действительного переменного имеет неопределённый И.
Определённый интеграл. Определённый И. функции fix) с нижним пределом а и верхним
пределом Ь можно определить как разность
где F(X) есть первообразная функции f(x); определение не зависит от того, какая из первообразных
выбрана для вычисления определённого И. Если функция f(x) непрерывна, то
приведённое определение в случае а<b равносильно следующему определению,
данному О. Каши (1823): рассматривают произвольное разбиение отрезка [a,b] точками
α = x0<x1<…<xn = b; (2)
в каждом отрезке
ℇ1(x1-1≤ℇ1≤x1)
[xи образуют сумму
Сумма S зависит от выбора точек x.
Однако в случае непрерывной функции f(x) суммы Sпри различном выборе точек x,
стремятся к вполне определённому пределу, если максимальная из разностей x . Этот предел и является определённым интегралом
По определению,
Определённый
И., как указано выше,< выражается через любую первообразную F(X).
Обратно, первообразная F(x) может быть записана в виде
где а – произвольная постоянная. В соответствии с этим неопределённый И. записывается в виде
О возникновении понятия И., а также о свойствах неопределённых и определённых И. см. Интегральное
исчисление.
Обобщение понятия интеграла Интеграл Римана. О. Коши применял своё определение
И. только к непрерывным функциям. Назвать, по определению, интегралом
(6)предел сумм S во всех тех случаях, когда этот предел однозначно определён, предложил Б.
Римом. (1853). Он же исследовал условия применимости такого определения.
Более совершенную форму этим условиям придал А. Лебег (1902), пользуясь
введённым им понятием меры множества (см. Меры теория). Для интегрируемости в смысле Римана функции
f(x) на [а,b] является необходимой и достаточной совокупность двух условий:
f(x) ограничена на [а,b]; множество помещающихся на [а,b] точек разрыва
функции f(x) имеет меру, равную нулю. T. о., непрерывность в каждой точке
отрезка [а,b] совсем не обязательна для интегрируемости по Риману.
Неопределённый
И. и первообразную можно теперь определять формулами (5) и (4). Следует
только заметить, что при этом первообразная F(X) не обязана иметь подинтегральную
функцию f(x) своей производной в каждой точке. Но в каждой точке непрерывности
f(x), т. е., в силу результата Лебега, всюду, кроме, может быть, множества
меры, равной нулю, будет
d/dxF(x)= f(x) (7)
Г. Дарбу (1879) дал определение интеграла Римана, к-рое делает особенно наглядными условиями
существования такого И. Вместо сумм (3) Дарбу вводит суммы (наз. суммами Дарбу)где Mверхняя грань функции f(x) нa отрезке [xa m нижняя грань сумм S, I , а – верхняя грань сумм S то для
существования интеграла Римана необходимо и достаточно условие I=I
Общее значение I = I = I величин _ I и I и является I и I
интегралом Римана (6). Сами величины называются
верхним и, соответственно, нижним интегралами Дарбу.
Интеграл Лебега. Введённое Лебегом понятие меры множества позволило дать значительно
более широкое определение И. Чтобы определить И. (6), Лебег делит точками
…<y-2<y-1<y0<Y1<…<y1…
область возможных значений переменного у = f(x) и обозначает Mточек x из отрезка [a,b], для к-рых
t1-1≤f(x)<y1 Сумма S определяется равенством где берётся из отрезка а Ii(Mt)обозначает меру множества Mt. Функция f(x) называется интегрируемой в смысле
Лебега на отрезке [а,b], если ряды, определяющие суммы S, абсолютно сходятся
при max . Предел этих сумм и называется интегралом Лебега (6). .Можно определить первообразную в смыслеЛебега как функцию F(X), удовлетворяющую равенству (4), где И. в правой
части понимается по Лебегу. Как и в случае интеграла Римана, равенство
(7) 45удет при этом выполняться во всех точках, кроме, может быть, множества,
имеющего меру, равную нулю.
Для интегрируемости по Лебегу ограниченной функции f(x) необходимо и достаточно, чтобы она
принадлежала к числу измеримых функций в смысле Лебега. Все функции, встречающиеся
в матем. анализе, измеримы в этом смысле. Более того, до настоящего времени
(1972) не построено ни одного индивидуального примера неизмеримой функции.
T. о., для случая ограниченных функций Лебег решил задачу определения интеграла
(6) с общностью, исчерпывающей потребности матем. анализа. Среди функций,
интегрируемых по Лебегу, имеется сколько угодно функций, всюду разрывных
и, следовательно, неинтегрируемых по Риману. Наоборот, каждая интегрируемая
по Риману функция интегрируема и по Лебегу.
Определение Лебега обобщается на случай интегрирования по полупрямой и по полной прямой,
т. е. на случай И. вида
После этого обобщения теория Лебега охватывает все случаи абсолютно сходящихся несобственных
интегралов.
Общность, достигнутая в определении Лебега, весьма существенна во многих вопросах математич.
анализа; напр., только с введением интеграла Лебега могла быть установлена
теорема Фишера – Риса в теории тригонометрия, рядов, в силу к-рой любой ряд
для к-рого
представляет функциюf(x), порождающую коэффициенты aформулам
где И. понимаются в смысле Лебега.
Интеграл Стилтьеса. В кон. 19 в. определение интеграла Римана подверглось совершенно
иному обобщению, чем то, к к-рому привело введение понятия меры множества.
Это обобщение было дано T. Стилтьесом (1894). Пусть f(x)– непрерывная функция
действительного переменного х, определённая на отрезке [а,Ь], и U(x)– определённая
на том же отрезке ограниченная монотонная (неубывающая или невозрастающая)
функция. Для определения интеграла Стилтьеса берут произвольное разбиение
(2) отрезка [а,b] и составляют сумму
где ℇ1,ℇ2,…ℇn – произвольные точки, выбранные соответственно на отрезках [x[x-
наибольшее расстояние между двумя последовательными точками деления в разбиении
(2). Если взять любую последовательность разбиений, для к-рой S стремится
к нулю, то сумма (8) будет иметь определённый, всегда один и тот же предел,
как бы ни выбирались точкисоответствующих отрезках. Этот предел называют, следуя Стилтьесу, интегралом функции f(x) относительно функции U(x) и обозначают символом
Интеграл (9) (его называют также и н-тегралом Стилтьеса) существует и в том случае,
когда ограниченная функция U(x), не будучи сама монотонной, может быть
представлена в виде суммы или разности двух ограниченных монотонных функций U
U(x) = U1(x)-U2(x).
т. е. является функцией с ограниченным изменением (см. Изменение функции). Если интегрирующая
функция U(x) имеет ограниченную и интегрируемую по Риману производную U'(x),
то интеграл Стилтьеса сводится к интегралу Римана по формуле
В частности, когда U(x) = х + С, интеграл Стилтьеса (9) превращается в обыкновенный
интеграл Римана (6).
Дальнейшие обобщения. Концепции И., созданные Стилтьесом и Лебегом, удалось впоследствии
объединить и обобщить на интегрирование по любому (измеримому) множеству
в пространстве любого числа измерений. Классич. кратные интегралы вполне
охватываются этим подходом. Потребности таких дисциплин, как теория вероятностей
и общая теория динамич. систем, привели к ещё более широкому понятию абстрактного
интеграла Лебега, основанному на общих понятиях меры множества и измеримости
функций. Пусть X – пространство, в к-ром выделена определённая система
В его подмножеств, называемых “измеримыми”, причём эта система обладает
свойствами замкнутости по отношению к обычным теоретико-множественным операциям,
выполняемым в конечном или счётном числе. Пусть ц – конечная мера, заданная
на В. Для В-измеримой функции y = f(x),xXЄX, принимающей конечное или счётное число
значений y…, уAf(x) по мере μ , обозначаемый .
∫xf(x)μ(dx)
определяется как сумма ряда в предположении, что этот ряд абсолютно сходится. Для других f интегрируемость и И. определяются путём нек-рого естественного предельного перехода от указанных кусочнопостоянных функций. Пусть А – измеримое множество и φA(x) = 1 для х, принадлежащих А, и
для х, не принадлежащих А иφA(x)=0. Тогда интеграл от f(x) по множеству А определяют, полагая
При фиксированных мю. и А И. в зависимости от f может рассматриваться как линейный функционал;
при фиксированном f И., как функция множества А, есть счётно аддитивная функция.
Следует отметить, что, несмотря на кажущуюся отвлечённость, это общее понятие И. в наибольшей
степени подхо-дит для определения
такого понятия, как матем. ожидание (в теории вероятностей), и даже для
общей формулировки задачи проверки статистая, гипотез. И. по отношению
к т. н. мере Вивера и различным её аналогам используют в статистич. физике
(здесь в качестве X фигурирует пространство непрерывных на к.-л. отрезке
функций). Упоминавшиеся до сих пор обобщения понятия И. были такими, что
f и |f| оказывались интегрируемыми или неинтегрируемыми одновременно.
Обобщения первоначального понятия И. в другом направлении относятся к функциям одного
переменного, но зато дают много больше в исследовании интегрирования неогранич. функций.
Ещё Коши ” случае функции f(x), неограниченной в точке х = с, определил
интегралкогда а<с<b, как предел выражения
при . Аналогично И. с бесконечными пределами
определяется как предел И.
при
. Если при этом не требуется интегрируемости |f(x)|, т. е. f(x) интегрируема
“не абсолютно”, то это определение Коши не поглощается лебе-говским.
alexlat.ucoz.ru
Интегралы в математике, основные понятия и определения
Функция будет первообразной для функции , если будем иметь место равенство . Проверим его выполнение:
То есть действительно является первообразной функции .
Аналогично проверим выполнение равенства :
Итак, равенство выполняется, а тогда функция – первообразная для функции . Неопределенные интегралы от некоторых функций не берутся в элементарных функциях.
Что и требовалось доказать.
ru.solverbook.com
Интеграл – это… Что такое Интеграл?
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
Процесс нахождения интеграла называется интегрированием.
Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения.
Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана.
Типы интегралов
По области интегрирования
Интегралы, зависящие от параметров
Дифференцирование по параметру
Пусть задан интеграл вида
В таком случае, производная по параметру t будет равна[1]
История
Интеграл в древности
Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 г. до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н. э. Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод впоследствии использовали Цзу Чунчжи и Цзу Гэн для нахождения объёма шара.
Следующий крупный шаг в исчисление интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсамом (известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвёртой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определённого интеграла, чтобы найти объём параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов, но он не касается любых многочленов выше четвёртой степени.
Следующий значительный прогресс в исчислении интегралов появится лишь в XVI веке. В работах Кавальери с его методом неделимых, а также в работах Ферма, были заложены основы современного интегрального исчисления. Дальнейшие шаги были сделаны в начале XVII века Барроу и Торричелли, которые представили первые намеки на связь между интегрированием и дифференцированием.
Обозначение
Ньютон использовал (не везде) в качестве символа интегрирования значок квадрата (перед обозначением функции или вокруг него), но эти обозначения не получили широкого распространения. Современное обозначение неопределённого интеграла было введено Лейбницем в 1675 году. Он образовал интегральный символ из буквы ſ («длинная s») — сокращения слова лат. summa (тогда ſumma, сумма).[2] Современное обозначение определённого интеграла, с указанием пределов интегрирования, были впервые предложены Жаном Батистом Жозефом Фурье в 1819-20 годах.
См. также
Примечания
- ↑ Будылин А. М. Вариационное исчисление (рус.). Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета. — Цифровое издание. Часть 3.3.1. Дифференцирование интеграла по параметру.. Архивировано из первоисточника 18 февраля 2012. Проверено 10 июля 2011.
- ↑ Florian Cajori A history of mathematical notations. — Courier Dover Publications, 1993. — P. 203. — 818 p. — (Dover books on mathematics). — ISBN 9780486677668
Литература
- Никольский С. М. Глава 9. Определенный интеграл Римана // Курс математического анализа. — 1990. — Т. 1.
- Ильин В. А., Позняк, Э. Г. Глава 6. Неопределенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).
- Ильин В. А., Позняк, Э. Г. Глава 10. Определенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).
- Демидович Б.П. Отдел 3. Неопределенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
- Демидович Б.П. Отдел 4. Определенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
Ссылки
dic.academic.ru
Интеграл — Циклопедия
Интеграл — это математический термин, обозначающий непрерывную сумму произведений значений подынтегральной функции на дифференциал аргумента.
[править] Интеграл от функции
Нахождение интеграла от функции называется интегрированием. При интегрировании подынтегральной функции находят первообразную функцию, производная от которой равна подынтегральной функции. Интеграл от функции может быть неопределённым, а может быть определённым.
Суть неопределённого интеграла это класс функций (первообразная плюс константа), отличающихся только константой, производная которых равна подынтегральной функции.
Суть определённого интеграла это некое число, равное непрерывной алгебраической сумме произведений значений подынтегральной функции на дифференциал аргумента. Для положительных подынтегральных функций определённый интеграл равен величине площади криволинейной трапеции, ограниченной графиком функции, осью абсцисс и пределами интегрирования.
[править] Неопределённый интеграл от функции
Неопределённый интеграл от функции определяется по формуле:
f(x) – подынтегральная функция,
F(x) – первообразная функция.
C – константа.
[править] Свойства неопределённых интегралов
Для функций u=f(x) и v=g(x) верны правила:
При f(x) и g(x)=C1 получаем:
При f(x)=C1 и g(x) получаем:
[править] Интегрирование по частям
Для функций u=f(x) и v=g(x) верно правило:
[править] Примеры неопределённых интегралов
[править] Определённый интеграл от функции
Определённый интеграл от функции определяется по формуле Ньютона-Лейбница:
f(x) – подынтегральная функция,
F(x) – первообразная функция.
[править] Примеры определённых интегралов
[править] Другие понятия:
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Участник:Logic-samara
cyclowiki.org
