📝Что такое интеграл?
В переводе с латинского языка интеграл означает «целый». Это одно из наиболее важных и распространенных понятий в высшей математике, которое появилось из-за необходимости находить функции по их производным или измерять объёмы, площади, работу нескольких сил за конкретный промежуток времени, длины дуг и т.д. В соответствии с этими задачами принято выделять определённые и неопределенные интегралы.
Содержание статьи:
Обозначение
Первым символ для обозначения интегрирования придумал Ньютон. Он применял для этого небольшой квадрат. Однако данное обозначение не получило серьезного распространения. Сегодняшнее обозначение неопределенного интеграла было придумано в 1675 году Лейбницем:
Что касается обозначения определённого интеграла, где указаны пределы интегрирования, то его в 1819 году предложил Жан Батист Фурье.
Виды интегралов
Первообразная функции f(x) — функция F(x), производная которой при любом значении х равняется f(x). Добавляя постоянную к первообразной определенной функции, снова можно получить первообразную этой же функции. Соответственно, имея единственную первообразную F(x) функции f(x), можно получить единое выражение всех первообразных данной функции в виде F(x) + С. Подобное выражение первообразных принято называть неопределённым интегралом функции f(x):
Одно из главных правил интегрального исчисления определяет, что любая непрерывная функция f(x) имеет неопределённый интеграл.
Что касается определённого интеграл от функции f(x) с верхним пределом b и нижним пределом а, то он определяется в качестве разности:
где F(x) является первообразной функции f(x).
Определённый интеграл можно выразить посредством любой первообразной F(x). Верным является и обратное. Первообразную F(x) можно записать в следующем виде:
В этой формуле а – это произвольная константа. Таким образом, интеграл можно записать в виде:
История возникновения интеграла
Если углубиться в историю, то можно утверждать, что интегрирование зародилось в древнем Египте, приблизительно в 1800 году до нашей эры. Первой известной методикой вычисления интегралов считается способ исчерпывания Евдокса. Он предпринимал попытки найти объёмы и площади фигур, разрывая их на несколько частей, для которых уже известны площадь или объём. Через некоторое время данная методика была развита Архимедом. Он применял ее для вычислений площадей парабол и примерного расчёта площади круга. Подобные методы независимо разрабатывались в Китае в 3 столетии нашей эры Лю Хуэйем. Он использовал их с целью определения площади круга.
Следующий внушительный прогресс в исчислении интегралов произошел только в XVI веке. В работах с методом неделимых Кавальери, а также в научных трудах Ферма, были заложены основы сегодняшнего интегрального исчисления.
Последующие шаги были сделаны в середине XVII столетия Торричелли и Барроу, которые предоставили первые намеки на взаимосвязь между дифференцированием и интегрированием.
Зачем и кому нужны интегралы?
Ученые стремятся любые физические явления выражать в виде математических формул. Когда в руках есть определенная формула, то в дальнейшем уже можно с ее помощью посчитать все, что необходимо. А интеграл является одним из главных инструментов работы с любыми функциями.
К примеру, имея формулу круга, можно посредством интеграла вычислить его площадь. Если есть формула шара, то можно вычислить его объем. Посредством интегрирования можно найти работу, энергию, массу, давление, электрический заряд и прочие важные величины.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Определённый интеграл и методы его вычисления
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый
интеграл может быть как положительным, так и отрицательным числом (Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как
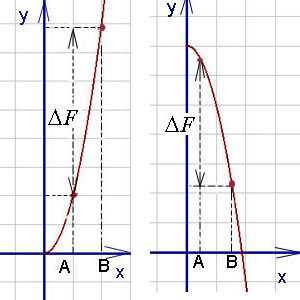
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее – значение нижнего предела a и вычисляется разность F(b) – F(a). Полученное число и будет определённым интегралом..
При a = b по определению принимается
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
получим
Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
(40)
Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F
На основании формулы (39) последнее равенство означает равенство интегралов
и
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
то
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать, т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл
(47)
где
,
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.
(48)
Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получим
так как F(x) – первообразная для f(x), а F(a) – постояная величина.
Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
получаем формулу интегрирования по частям для вычисления определенного интеграла:
(49)
Пример 6. Вычислить определённый интеграл
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (49) находим
Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение
Перейдём к вычислению определённого интеграла методом замены переменной. Пусть
где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения aи b, т.е.
Тогда
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть
поскольку F(x) – первообразная для f(x).
Итак,
(50)
Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
после замены переменной
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами и . Чтобы найти новые пределы, нужно в уравнение
поставить значения x = aи x = b, т.е. решить уравнения
и
относительно и . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9. Вычислить определённый интеграл
Решение. Произведём замену переменной, полагая
Тогда dt = 2x dx, откуда x dx = (1/2) dt, и подынтегральное выражение преобразуется так:
Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение
даёт
а
Используя теперь формулу (50), получим
После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Найти определённый интеграл заменой переменной самостоятельно, а затем посмотреть решение
Начало темы “Интеграл”
Продолжение темы “Интеграл”
Поделиться с друзьями
function-x.ru
Что значит Интеграл? Как понять слово Интеграл? Интеграл по простому…
 Во время учебного года у школьников возникает множество вопросов по непонятным словам, сегодня мы разберём такое слово, как Интеграл. Что значит Интеграл? Рекомендую к прочтению ещё несколько полезных публикаций, например, как понять слово Блокбастер, что значит Флейва, что такое Макнэ?
Во время учебного года у школьников возникает множество вопросов по непонятным словам, сегодня мы разберём такое слово, как Интеграл. Что значит Интеграл? Рекомендую к прочтению ещё несколько полезных публикаций, например, как понять слово Блокбастер, что значит Флейва, что такое Макнэ?Господа школьники, это весьма сложный вопрос, который не объяснить в двух словах, но я попытаюсь.
Вы наверное все знаете, что делить на ноль глупо, но если это число почти ноль? То есть представляет собой очень маленькую величину, то делить на ноль можно. А теперь представьте, сколько по вашему будет весить горсть таких величин? И чтобы это выяснить ввели в обиход интеграл.
Вообще понятие интеграл вещь довольно абстрактная, они бывают разных типов, да и приложений у них огромное количество. И спрашивать, что такое интеграл, это вроде, как спросить, “а ну-ка мил человек, расскажи мне прямо сейчас, как появилось государство российское, и как оно развивалось вплоть до наших дней“.
Интеграл – это результат непрерывного суммирования бесконечно большого числа бесконечно малых слагаемых
Вообще, зачем нужен интеграл? Дело в том, что учёные пытаются все физические явления выразить набором математических формул. Поэтому, когда они выводят формулу, какого-либо явления, то затем при помощи неё они могут подсчитать всё, что им необходимо. Интеграл, это один из главнейших элементов работы с функциями.
Например, если вам вдруг захотелось узнать объём шара, то при помощи интеграла это сделать вполне возможно, либо высчитать площадь круга тоже вполне по плечу. Вообще, интегрирование различных величин очень полезная в быту “штука”, она позволяет найти электрический заряд, давление, энергию, работу и т. п.
Ещё один жизненный пример, в любом смартфоне, ну почти в любом имеются акселерометры. Они нужны для точного измерения ускорения. Отсюда вопрос, как при помощи акселерометра измерить путь от дома до школы?
Ответ прост, нужно проинтегрировать его показания по времени, причём два раза. Поскольку пройденный путь – это интеграл от скорости, а скорость интеграл от ускорения.
И тогда у придирчивого школьника возникает вопрос, “слышь бро, а нафига оно мне нужно?”.
Да, я хз, зачем это тебе нужно, считай, что можешь понять интеграл из чистого любопытства, для саморазвития. Хотя интегралы входят в школьную программу, однако многие взрослые напрочь забыли что это такое.
xn—-7sb3abqfg0a4g2a.xn--p1ai
интеграл что это доступным и простым языком
Операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.:))
1977 год. В ЗИСТе (Заочном институте советской торговли) идет экзамен по высшей математике. Почти все студенты – труженики прилавка. Им известно, что молодой и симпатичный экзаменатор почти никогда не ставит двоек. Для него уже заготовили дефицитные харчи, сложили в пластиковый пакет два батона сервелата, икру, горилку с перцем и коньяк.
Вот он входит, улыбается, здоровается. Одна из заочниц искусно изображает испуг. Олицетворяя собой девственную невинность, она лепечет: “Ой, боюсь, ой, засыплюсь, ой, все забыла!.. ”
Преподаватель говорит: “Да не бойтесь вы, “неуд”, скорее всего, ставить не буду, гарантирую, что если студент ответит хотя бы на один вопрос, получит “уд”. Берите билеты, готовьтесь. И давайте постараемся, чтобы ни вы меня не огорчали, ни я вас”.
Действительно, через пару часов не сдала всего одна – томная розовощекая девица, зав. отделом крупного гастронома, та, которая шептала “Ой, боюсь”. У нее пустой лист, даже списать не смогла. По сути говорить с ней без толку. Была бы хоть какая-то зацепка.. .
– Я не успела подготовиться, – говорит она. – Вчера у нас был день рождения. Мамин. Уснула поздно.. . Ничего не помню. Может, вы мне дополнительный вопрос зададите?
– Ну ладно, – говорит препод. – Что такое интеграл? Расскажите своими словами.
Студентка долго молчит, потом говорит: “Я этот вопрос тоже не знаю. Может, вы мне еще один дополнительный вопрос зададите, последний, ну, пожалуйста? ”
Преподаватель говорит: “Деточка, а как пишется знак интеграла, вы хоть знаете? ”
Девица молчит. Препод подсказывает: “Вспоминайте, червячок такой, не спешите”. И студентка не спеша рисует на бумаге ~~.
– Вертикальный, – поправляет преподаватель. И студентка рисует.
– Ну вот, – подводит итог экзаменатор, – на один вопрос ответили, а говорите, что все забыли. Тройка!
otvet.mail.ru
Интеграл — WiKi
Интеграл — одно из важнейших понятий математического анализа, которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по её производной (неопределённый интеграл). Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть — двойной, тройной, криволинейный, поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана, Лебега, Стилтьеса и другие.
Интеграл функции одной переменной
Неопределённый интеграл
Пусть дана f(x){\displaystyle f(x)} — функция действительной переменной. Неопределённым интегралом функции f(x){\displaystyle f(x)} , или её первообразной, называется такая функция F(x){\displaystyle F(x)} , производная которой равна f(x){\displaystyle f(x)} , то есть F′(x)=f(x){\displaystyle F'(x)=f(x)} . Обозначается это так:
- F(x)=∫f(x)dx{\displaystyle F(x)=\int f(x)dx}
В этой записи ∫{\displaystyle \int } — знак интеграла, f(x){\displaystyle f(x)} называется подынтегральной функцией, а dx{\displaystyle dx} — элементом интегрирования.
Первообразная существует не для любой функции. Легко показать, что по крайней мере все непрерывные функции имеют первообразную. Поскольку производные двух функций, отличающихся на константу, совпадают, в выражение для неопределённого интеграла включают произвольную постоянную C{\displaystyle C} , например
- ∫x2dx=x33+C,∫cos(x)dx=sin(x)+C{\displaystyle \int x^{2}dx={\frac {x^{3}}{3}}+C,\qquad \int \cos(x)dx=\sin(x)+C}
Операция нахождения интеграла называется интегрированием. Операции интегрирования и дифференцирования обратны друг другу в следующем смысле:
- ddx∫f(x)dx=f(x),∫df(x)dxdx=f(x)+C{\displaystyle {\frac {d}{dx}}\int f(x)dx=f(x),\qquad \int {\frac {df(x)}{dx}}dx=f(x)+C}
Определённый интеграл
 Интеграл как площадь криволинейной трапеции
Интеграл как площадь криволинейной трапецииПонятие определённого интеграла возникает в связи с задачей о нахождении площади криволинейной трапеции, нахождении пути по известной скорости при неравномерном движении и т. п.
Что такое интеграл, анимация (нажмите для воспроизведения)Рассмотрим фигуру, ограниченную осью абсцисс, прямыми x=a{\displaystyle x=a} и x=b{\displaystyle x=b} и графиком функции y=f(x){\displaystyle y=f(x)} , называемую криволинейной трапецией (см. рисунок). Если по оси абсцисс отложено время, а по оси ординат — скорость тела, то площадь криволинейной трапеции есть пройденный телом путь.
Для вычисления площади этой фигуры естественно применить следующий приём. Разобьём отрезок [a;b]{\displaystyle [a;b]} на меньшие отрезки точками xi{\displaystyle x_{i}} , такими что a=x0<…<xi<xi+1<…<xn=b{\displaystyle a=x_{0}<…<x_{i}<x_{i+1}<…<x_{n}=b} , а саму трапецию — на ряд узких полосок, лежащих над отрезками [xi;xi+1]{\displaystyle [x_{i};x_{i+1}]} . Возьмём в каждом отрезке по произвольной точке ξi∈[xi;xi+1]{\displaystyle \xi _{i}\in [x_{i};x_{i+1}]} . Ввиду того, что длина i{\displaystyle i} -го отрезка Δxi=xi+1−xi{\displaystyle \Delta x_{i}=x_{i+1}-x_{i}} мала, будем считать значение функции f(x){\displaystyle f(x)} на нём примерно постоянным и равным yi=f(ξi){\displaystyle y_{i}=f(\xi _{i})} . Площадь криволинейной трапеции будет приблизительно равна площади ступенчатой фигуры, изображённой на рисунке:
- S≈∑i=0n−1yiΔxi(∗){\displaystyle S\approx \sum _{i=0}^{n-1}y_{i}\Delta x_{i}\qquad (*)}
Если же теперь увеличивать число точек разбиения, так, чтобы длины всех отрезков неограниченно убывали (maxΔxi→0{\displaystyle \max \Delta x_{i}\to 0} ), площадь ступенчатой фигуры будет всё ближе к площади криволинейной трапеции.
Поэтому мы приходим к такому определению:
Если существует, независимо от выбора точек разбиения отрезка и точек ξi{\displaystyle \xi _{i}} , предел суммы (*) при стремлении длин всех отрезков к нулю, то такой предел называется определённым интегралом (в смысле Римана) от функции f(x){\displaystyle f(x)} по отрезку [a;b]{\displaystyle [a;b]} и обозначается
- ∫abf(x)dx{\displaystyle \int \limits _{a}^{b}f(x)dx}
Сама функция при этом называется интегрируемой (в смысле Римана) на отрезке [a;b]{\displaystyle [a;b]} . Суммы вида (*) называются интегральными суммами.
Примеры интегрируемых функций:
Пример неинтегрируемой функции: функция Дирихле (1 при x{\displaystyle x} рациональном, 0 при иррациональном). Поскольку множество рациональных чисел всюду плотно в R{\displaystyle {\mathbb {R} }} , выбором точек ξi{\displaystyle \xi _{i}} можно получить любое значение интегральных сумм от 0 до b−a{\displaystyle b-a} .
Между определённым и неопределённым интегралом имеется простая связь. А именно, если
- F(x)=∫f(x)dx{\displaystyle F(x)=\int f(x)dx}
то
- ∫abf(x)dx=F(b)−F(a){\displaystyle \int \limits _{a}^{b}f(x)dx=F(b)-F(a)}
Это равенство называется формулой Ньютона-Лейбница.
Интеграл в пространствах большей размерности
Двойные и кратные интегралы
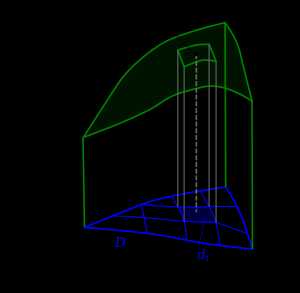 Двойной интеграл как объём цилиндрического бруса
Двойной интеграл как объём цилиндрического брусаПонятие двойного интеграла возникает при вычислении объёма цилиндрического бруса, подобно тому, как определённый интеграл связан с вычислением площади криволинейной трапеции. Рассмотрим некоторую двумерную фигуру D{\displaystyle D} на плоскости XY{\displaystyle XY} и заданную на ней функцию двух переменных f(x,y){\displaystyle f(x,y)} . Понимая эту функцию как высоту в данной точке, поставим вопрос о нахождении объёма получившегося тела (см. рисунок). По аналогии с одномерным случаем, разобьём фигуру D{\displaystyle D} на достаточно малые области di{\displaystyle d_{i}} , возьмём в каждой по точке ξi=(xi,yi){\displaystyle \xi _{i}=(x_{i},y_{i})} и составим интегральную сумму
- ∑if(xi,yi)S(di){\displaystyle \sum _{i}f(x_{i},y_{i})S(d_{i})}
где S(di){\displaystyle S(d_{i})} — площадь области di{\displaystyle d_{i}} . Если существует, независимо от выбора разбиения и точек ξi{\displaystyle \xi _{i}} , предел этой суммы при стремлении диаметров областей к нулю, то такой предел называется двойным интегралом (в смысле Римана) от функции f(x,y){\displaystyle f(x,y)} по области D{\displaystyle D} и обозначается
- ∫Df(x,y)dS{\displaystyle \int \limits _{D}f(x,y)dS} , ∫Df(x,y)dxdy{\displaystyle \int \limits _{D}f(x,y)dxdy} , или ∬Df(x,y)dxdy{\displaystyle \iint \limits _{D}f(x,y)dxdy}
Объём цилиндрического бруса равен этому интегралу.
Криволинейный интеграл
Поверхностный интеграл
Применение
К понятию интеграла естественным образом приводит также задача о массе неоднородного тела. Так, масса тонкого стержня с переменной плотностью ρ(x){\displaystyle \rho (x)} даётся интегралом
- M=∫ρ(x)dx{\displaystyle M=\int \rho (x)dx}
в аналогичном случае плоской фигуры
- M=∬ρ(x,y)dxdy{\displaystyle M=\iint \rho (x,y)dxdy}
и для трёхмерного тела
- M=∭ρ(x,y,z)dxdydz{\displaystyle M=\iiint \rho (x,y,z)dxdydz}
Обобщения
Интеграл Лебега
В основе определения интеграла Лебега лежит понятие σ{\displaystyle \sigma } -аддитивной меры. Мера является естественным обобщением понятий длины, площади и объёма.
Интеграл Лебега функции f{\displaystyle f} определённой на пространстве X{\displaystyle X} по мере μ{\displaystyle \mu } обозначают
- ∫Xfμ{\displaystyle \int \limits _{X}f\mu } , ∫x∈Xf(x)μ{\displaystyle \int \limits _{x\in X}f(x)\mu } или ∫Xf(x)μ(dx){\displaystyle \int \limits _{X}f(x)\mu (dx)}
последнее два обозначения употребляют если необходимо подчеркнуть что интегрирование ведётся по переменной x{\displaystyle x} . Однако часто пользуются следующим не вполне правильным обозначением
- ∫Xfdμ.{\displaystyle \int \limits _{X}fd\mu .}
Полагая меру отрезка (прямоугольника, параллелепипеда) равной его длине (площади, объёму), а меру конечного либо счётного объединения непересекающихся отрезков (прямоугольников, параллелепипедов), соответственно, сумме их мер, и продолжая эту меру на более широкий класс измеримых множеств, получим т. наз. Лебегову меру на прямой (в R2{\displaystyle {\mathbb {R} }^{2}} , в R3){\displaystyle {\mathbb {R} }^{3})} .
Естественно, в этих пространствах возможно ввести и другие меры, отличные от Лебеговой. Меру можно ввести также на любом абстрактном множестве. В отличие от интеграла Римана, определение интеграла Лебега остаётся одинаковым для всех случаев. Идея его состоит в том, что при построении интегральной суммы значения аргумента группируются не по близости к друг другу (как в определении по Риману), а по близости соответствующих им значений функции.
Пусть есть некоторое множество X{\displaystyle X} , на котором задана σ{\displaystyle \sigma } -аддитивная мера μ{\displaystyle \mu } , и функция f:X→R{\displaystyle f:X\to {\mathbb {R} }} . При построении интеграла Лебега рассматриваются только измеримые функции, то есть такие, для которых множества
- Ea={x∈X:f(x)<a}{\displaystyle E_{a}=\{x\in X:f(x)<a\}}
измеримы для любого a∈R{\displaystyle a\in {\mathbb {R} }} (это эквивалентно измеримости прообраза любого борелевского множества).
Сначала интеграл определяется для ступенчатых функций, то есть таких, которые принимают конечное или счётное число значений ai{\displaystyle a_{i}} :
- ∫Xfμ=∑iaiμ(f−1(ai)){\displaystyle \int \limits _{X}f\mu =\sum _{i}a_{i}\mu (f^{-1}(a_{i}))}
где f−1(ai){\displaystyle f^{-1}(a_{i})} — полный прообраз точки ai{\displaystyle a_{i}} ; эти множества измеримы в силу измеримости функции. Если этот ряд абсолютно сходится, ступенчатую функцию f{\displaystyle f} назовём интегрируемой в смысле Лебега. Далее, назовём произвольную функцию f{\displaystyle f} интегрируемой в смысле Лебега, если существует последовательность интегрируемых ступенчатых функций fn{\displaystyle f_{n}} , равномерно сходящаяся к f{\displaystyle f} . При этом последовательность их интегралов также сходится; её предел и будем называть интегралом Лебега от функции f{\displaystyle f} по мере μ{\displaystyle \mu } :
- ∫Xfμ=lim∫Xfnμ{\displaystyle \int \limits _{X}f\mu =\lim \int \limits _{X}f_{n}\mu }
Если рассматривать функции на Rn{\displaystyle {\mathbb {R} }^{n}} и интеграл по мере Лебега, то все функции, интегрируемые в смысле Римана, будут интегрируемы и в смысле Лебега. Обратное же неверно (например, функция Дирихле не интегрируема по Риману, но интегрируема по Лебегу, так как равна нулю почти всюду). Фактически, любая ограниченная измеримая функция интегрируема по Лебегу.
Историческая справка
Основные понятия интегрального исчисления введены в работах Ньютона и Лейбница в конце XVII века. Лейбницу принадлежит обозначение интеграла ∫ydx{\displaystyle \int ydx} , напоминающее об интегральной сумме, как и сам символ ∫{\displaystyle \int } , от буквы ſ («длинная s») — первой буквы в латинском слове summa (тогда ſumma, сумма)[1]. Сам термин «интеграл» предложен Иоганном Бернулли, учеником Лейбница. Обозначение пределов интегрирования в виде ∫ab{\displaystyle \int _{a}^{b}} введено Фурье в 1820 году.
Строгое определение интеграла для случая непрерывных функций сформулировано Коши в 1823 году, а для произвольных функций — Риманом в 1853 году. Определение интеграла в смысле Лебега впервые дано Лебегом в 1902 году (для случая функции одной переменной и меры Лебега).
См. также
Примечания
- ↑ Florian Cajori. A history of mathematical notations. — Courier Dover Publications, 1993. — P. 203. — 818 p. — (Dover books on mathematics). — ISBN 9780486677668.
Литература
- Виноградов И. М. (гл. ред.). Интеграл // Математическая энциклопедия. — М., 1977. — Т. 2.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, 1969.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1976.
Ссылки
ru-wiki.org
Что такое интеграл — это умножение
Интегралы чаще всего описываются как “площадь под кривой”. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это “нахождение площади прямоугольника”. Нахождение площади — это одно из полезных применений умножения, но не его суть. Интегралы помогают нам комбинировать числа тогда, когда умножение бессильно.
Так я размышлял про себя на парах математики в ВУЗе:
“Интегралы позволяют нам ‘умножать’ изменяющиеся числа. Мы привыкли к “3 × 4 = 12”, но что если одно из чисел изменяется? Мы не можем умножать меняющиеся числа, поэтому используем интегралы вместо умножения.
Вы услышите много разговоров насчет площади — но это всего лишь один из способов визуализировать умножение. Ключом является не площадь, а идея объединения множеств воедино. Конечно, мы можем интегрировать (“умножать”) длину и ширину, чтобы получить площадь на плоскости. Но мы также можем интегрировать скорость и время, чтобы получить расстояние, или длину, ширину и высоту для получения объема.
Когда мы хотим использовать обычное умножение, но не можем, мы достаем свое оружие и начинаем интегрировать. Площадь — это всего лишь прием визуализации, не зацикливайтесь на нем слишком сильно. А теперь давайте учить математику!”
И вот он, мой момент истины: интегрирование — это улучшенная версия умножения, которая работает с изменяющимися величинами. Давайте изучать интегралы в таком свете.
Понятие умножения
Вот как во все времена и эпохи понимали умножение:
- Если речь идет о натуральных числах (3 × 4), умножение — это повторяющееся сложение.
- С вещественными числами (3.12 × √2 ), умножение — это масштабирование.
- В случае с отрицательными числами (-2.3 × 4.3), умножение — это поворот и масштабирование.
- С комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.
Мы ходим вокруг да около “применения” одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.
Понятие площади
Площадь — очень тонкое понятие. На данный момент, давайте представим площадь как визуальную интерпретацию умножения:
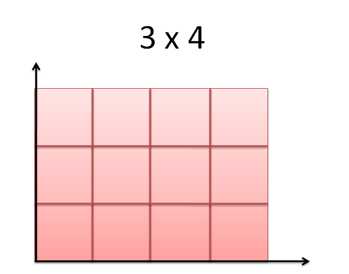
Мы можем “применять” числа на разных осях друг к другу (3 применяется к 4) и получить результат (12 единиц площади). Свойства каждого вводного значения (длина и длина) превратились в результат (единицы площади).
Легко, правда? Не так, как кажется на первый взгляд. Умножение может привести к “отрицательному результату” (3×(-4) = -12), которого не существует.
Мы понимаем график как представление умножения, и используем эту аналогию из-за удобства. Если бы все были слепыми, и в мире не существовало диаграмм, мы бы все равно хорошо справлялись с умножением. Площадь — это всего лишь интерпретация.
Умножение по частям
А теперь давайте умножим 3 × 4.5:

Что происходит? Ну, 4.5 — это не целочисленное число, но мы же можем воспользоваться “частичным” умножением. Если 3×4 = 3 + 3 + 3 + 3, то
3 × 4.5 = 3 + 3 + 3 + 3 + 3×0.5 = 3 + 3 + 3 + 3 + 1.5 = 13.5
Мы берем 3 (значение) 4.5 раза. Таким образом, мы объединили 3 с 4 полными сегментами (3 × 4 = 12), а также одним частичным сегментом (3 × 0.5 = 1.5).
Мы так привыкли к умножению, что даже забываем, как здорово оно работает. Мы можем разбить число на единицы (целые или частичные), умножать каждый кусочек и складывать результаты. Заметьте, как мы легко расправились с дробной частью? Это и есть начало интегрирования.
Проблема с числами
Числа не всегда ведут себя постоянно для наших расчетов. Сценарии типа “Вы ехали 3 часа со скоростью 30 км/ч” не имеют ничего общего с реальностью. Так условия описываются просто для удобства.
Формулы по типу “расстояние = скорость × время” только маскируют проблему; нам все еще нужно брать постоянные числа и умножать. А как узнать пройденное расстояние, если наша скорость постоянно изменялась во времени?
Описываем изменение
Первым испытанием для нас будет описание изменяющегося числа. Мы можем просто сказать: “Моя скорость менялась с 0 до 30 км/ч”. Это не совсем точно: как быстро она изменялась? Были ли изменения плавными?
Давайте будем точны: моя скорость в каждый момент времени равнялась удвоенному количеству секунд. В 1 секунду я двигался со скоростью 2 км/ч. Во 2 секунду скорость уже была 4 км/ч, в 3 секунду — уже 6 км/ч, и так далее:

Вот теперь у нас есть хорошее описание, достаточно подробное, чтобы знать свою скорость в каждый момент времени. Формальное описание звучит как “скорость — это функция времени”, и оно означает, что мы можем взять любой момент времени (t) и узнать нашу скорость в тот момент (“2t” км/ч).
(Это, конечно, не дает ответа на вопрос, почему скорость и время связаны. Я могу ускоряться за счет гравитации, или ослик может толкать меня сзади. Мы всего лишь установили, что с изменением времени изменяется и скорость).
Наше произведение “расстояние = скорость × время”, возможно, лучше написать так:
расстояние = скорость(t) × t
где скорость (t) — это скорость в любой момент времени. В нашем случае скорость (t) = 2t, так что мы пишем:
расстояние = 2t × t
Но это уравнение выглядит странно! “t” по-прежнему выглядит как единичный момент, который нужно выбирать (например, t=3 секунды), а значит и скорость (t) примет единичное значение (6 км/ч). А это нехорошо.
При обычном умножении, мы можем взять одну скорость и предположить, что она одинаковая во всем прямоугольнике. Но изменяющаяся скорость требует совмещения скорости и времени по частям (секунда за секундой). В каждый момент ситуация может быть разной.
Вот как это выглядит в большой перспективе:
- Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и “масштабируем ее”.
- Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные посекундно.
Мы видим, что обычное умножение — это частный случай интегрирования, когда количество пройденных метров не изменяется.
Насколько большая эта “часть”?
Насколько велика “часть”, при прохождении дистанции по частям? Секунда? Миллисекунда? Наносекунда?
Ответ навскидку: достаточно мала, чтобы значение было постоянным все время. Нам не нужна идеальная точность.
Более длинный ответ: такие понятия, как пределы, были придуманы, чтобы помочь в покусочном умножении. Принося пользу, они просто решают проблему и отвлекают от сути “объединения величин”. Мне очень не нравится, что пределы проходят в самом начале матанализа, еще перед тем, как студенты вникнут в проблему, которую они решают.
А что по поводу начала и конца?
Скажем, мы исследуем интервал от 3 до 4 секунд.
Скорость вначале (3×2 = 6 км/ч) отличается от скорости в конце (4×2 = 8 км/ч). Так какое же значение мне брать при вычислении “скорости × время”?
Решением будет разбить наши кусочки времени на достаточно мелкие отрезки (от 3.00000 до 3.00001 секунд), пока разность скоростей от начала до конца интервала будет для нас незначительной. Опять же, это более длинный разговор, но “поверьте мне”, что это временной отрезок, который делает разницу незначительной.
На графике представьте, что каждый интервал — это одна точка на прямой. Вы можете нарисовать ровную линию к каждой скорости, и ваша “площадь” будет представлять собой множество отрезков, которое и будет измерять умножение.
Где же “часть”, и каково ее значение?
Разделение части и ее значения далось мне нелегко.
“Часть” — это интервал, который мы рассматриваем (1 секунда, 1 миллисекунда, 1 наносекунда). “Позиция” — это то, где начинается секундный, миллисекундный или наносекундный интервал. Значение — это наша скорость в той позиции.
Например, рассмотрим интервал от 3.0 до 4.0 секунд:
- “Ширина” отрезка времени составляет 1.0 секунду
- Позиция (начальное время) равно 3.0
- Значение (скорость(t)) — это скорость(3.0) = 6.0 км/ч
Опять же, матанализ учит нас сокращать интервал до тех пор, пока разница между значениями в начале и конце интервала будет на столько мала, что ею можно пренебречь, считая этот интервал “точкой”. Не выпускайте из вида большую картинку: мы умножаем набор частей.
Понимание записи интеграла
У нас есть здравая идея “покусочного умножения”, но мы никак не можем ее выразить. “Расстояние = скорость(t) × t” все еще выглядит, как обычное уравнение, где t и скорость(t) принимают одно единственное значение.
В матанализе мы пишем это соотношение как
расстояние = ∫скорость(t)dt
- знак интеграла (s-образная кривая) означает, что мы умножаем покусочно и суммируем значения в одно.
- dt представляет временной “интервал”, который мы рассматриваем. Его называют “дельта t” а не “d раз по t”.
- t представляет положение dt (если dt — это промежуток от 3.0 до 4.0, то t равно 3.0)
- скорость(t) — это значение, на которое мы умножаем (скорость(3.0) = 6.0))
У меня есть парочка претензий к этой записи:
- То, как здесь используются буквы, немного смущает. “dt” выглядит как “d раз по t” в отличие от любого уравнения, которое вы ранее видели.
- Мы пишем скорость(t) × dt, вместо скорость(t_dt) × dt. Последний вариант четко указывает, что мы исследуем “t” на конкретном участке “dt”, а не какое-то глобальное “t”
- Вы часто встретите ∫скорость(t), без dt. Это вообще помогает легко забыть, что мы выполняем покусочное умножение двух элементов.
Похоже, уже поздно менять форму записи интегралов. Просто запомните эту идею насчет “умножения” чего-то, что изменяется.
Как это понимать
Когда я вижу вот это:
расстояние = ∫скорость(t)dt
Я думаю “Расстояние равно скорости t раз (читая левую часть первой) или “совместите скорость и время, чтобы получить расстояние” (читая правую часть первой).
В уме я перевожу “скорость(t)” как скорость и “dt”, и это превращается в умножение, при условии, что скорости позволено изменяться. Представление интегрирования подобным образом помогает мне сконцентрироваться на том, что на самом деле происходит (“Мы совмещаем скорость и время, чтобы получить расстояние!”) вместо зацикливания на деталях действия.
Бесплатный сюрприз: новые идеи
Интегралы — это очень глубокая идея, также, как и умножение. У вас могло появиться много вопросов, основанных на этой аналогии:
- Если интегралы умножают изменяющиеся величины, есть ли что-то, что делит их? (ДА — производные).
- Являются ли интегралы (умножение) и производные (деление) взаимообратными? (Да, с некоторыми тонкостями).
- Можем ли мы преобразовать уравнение “расстояние = скорость × время” в “скорость = расстояние / время”? (Да).
- Можем ли мы совмещать несколько величин одновременно? (Да — это называется многократное интегрирование).
- Влияет ли как-то порядок совмещения на результат? (Обычно нет).
Как только вы начнёте воспринимать интегралы как “улучшенное умножение”, вы сразу начнете задумываться о таких вещах, как “улучшенное деление”, “повторное интегрирование” и так далее. Застряв на “площади под кривой”, вы не уловите связи между этими темами. (Математических заучек видение “площади под кривой” и “угла наклона кривой” обратными понятиями ставит в тупик).
Как читать интегралы
У интегралов масса применений. Одним из них является объяснение того, что две величины были “умножены” для получения результата.
Вот как мы представляем площадь круга с помощью интегралов:
Площадь = ∫Длина окружности (r) · dr = ∫2πr · dr = π · r2
Нам бы очень хотелось взять площадь кривой умножением. Но мы не можем — высота изменяется в каждой ее точке. Если мы “развернем” круг, мы увидим, что частичка площади под каждой порцией радиуса будет равна “радиус × отрезок окружности”. Мы можем описать эту связь с помощью интеграла (как описано выше).
А вот как интеграл описывает идею, что “масса = плотность × объем”:
масса = ∫V ρ(r) ∙ dv
Что здесь сказано? Греческая буква “ро” (“ρ”) — это функция плотности, которая говорит нам, насколько плотен материал в определенном положении. Так, r∙dv — это частичка объема, который мы рассматриваем. Так что мы умножаем маленький кусочек объема (dv) на плотность в том интервале ρ(r), и потом складываем все эти части, чтобы получить массу.
Мы привыкли просто умножать плотность на объем, но если плотность изменяется, то нужно интегрировать. Индекс V просто означает “интеграл объема”, что по сути является тройным интегралом длины, ширины и высоты! Интеграл предполагает четыре “умножения”: 3 для поиска объема, и еще одно для умножения на плотность.
Что это нам дало?
Сегодняшней целью было не научное понимание интегральных исчислений. Наша цель — расширить модель мышления, и получить представление об интеграле как о надстройке над такими низкоуровневыми операциями как сложение, вычитание, умножение и деление.
Рассматривайте интегралы как улучшенный способ умножения: вычисления станут проще, и вам под силу станут понятия типа кратного интеграла и производной. Приятных вычислений!
Перевод статьи “A Calculus Analogy: Integrals as Multiplication”.
zero2hero.org
Лекция (Интегралы)
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Первообразная функция. Понятие неопределенного интеграла.
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу — нахождение самой функции по ее производной или дифференциалу.
Функция  называетсяпервообразной функцией для функции
называетсяпервообразной функцией для функции  на
промежутке
на
промежутке ,
если в каждой точке
,
если в каждой точке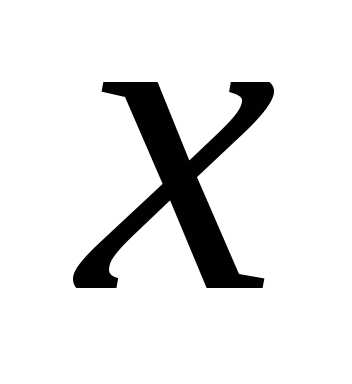 этого промежутка.
этого промежутка.
Например, 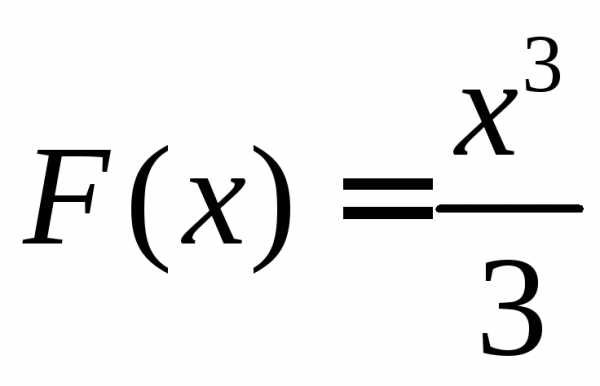 является первообразной для функции
является первообразной для функции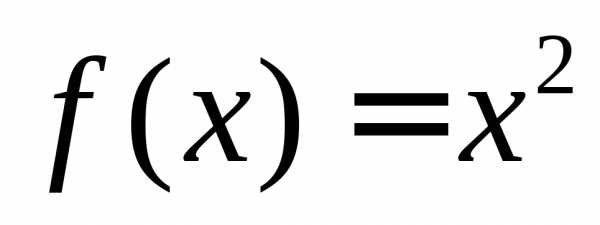 ,
так как
,
так как .
.
Следует
отметить, что для заданной функции 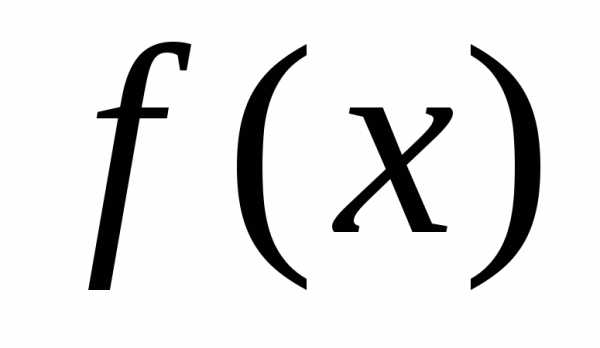 ее
первообразная определена неоднозначно.
Дифференцируя, нетрудно убедиться, что
все функции
ее
первообразная определена неоднозначно.
Дифференцируя, нетрудно убедиться, что
все функции ,
где
,
где — некоторое число, являются первообразными
для функции
— некоторое число, являются первообразными
для функции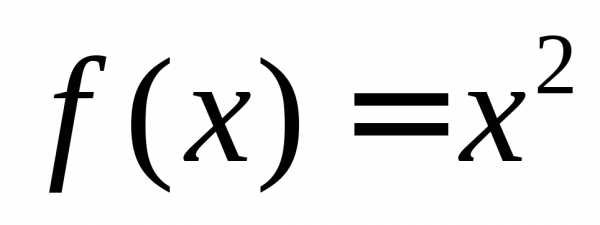 .
.
Аналогично
в общем случае, если 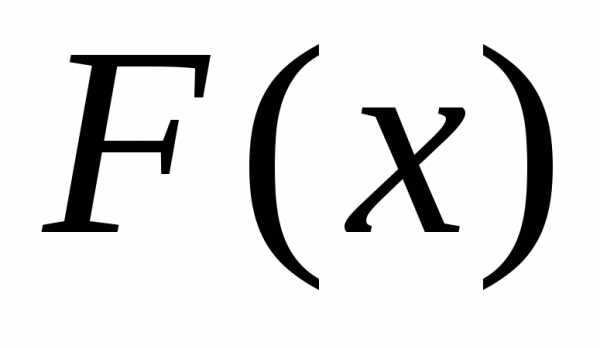 —
некоторая первообразная для
—
некоторая первообразная для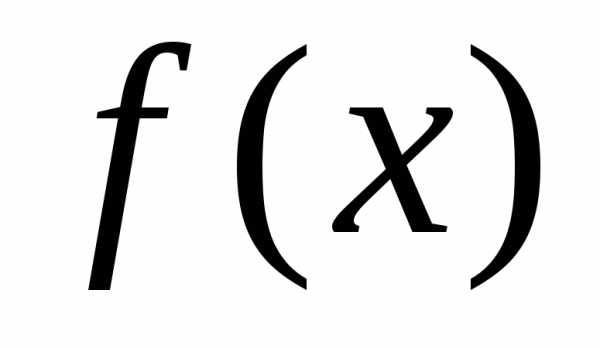 ,
то, поскольку,
функции вида,
где
,
то, поскольку,
функции вида,
где – произвольное число, также являются
первообразными для
– произвольное число, также являются
первообразными для .
.
Совокупность
всех первообразных для функции  на
промежутке
на
промежутке называетсянеопределенным
интегралом от функции
называетсянеопределенным
интегралом от функции 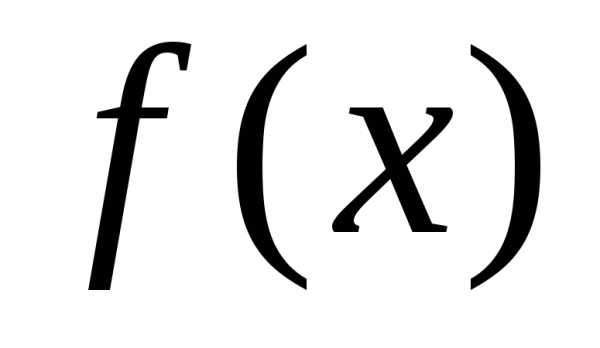 и
обозначается
и
обозначается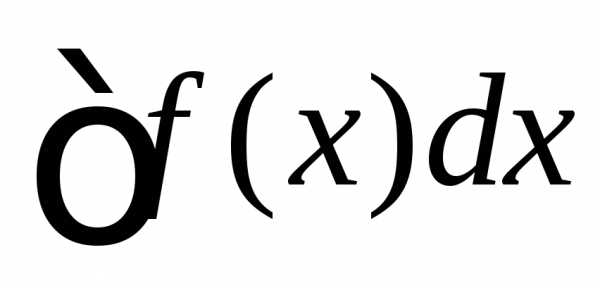 ,
где
,
где — знак интеграла,
— знак интеграла,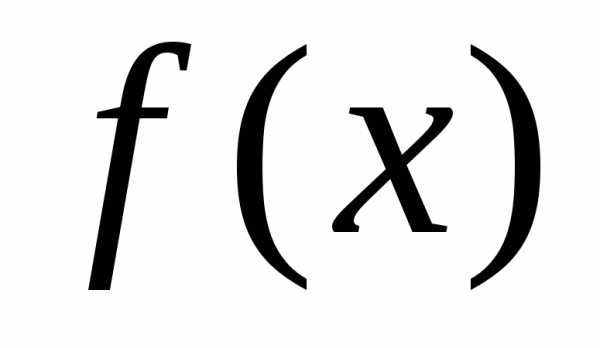 —подынтегральная
функция,
—подынтегральная
функция,  —подынтегральное
выражение.
Таким образом,
—подынтегральное
выражение.
Таким образом,
где 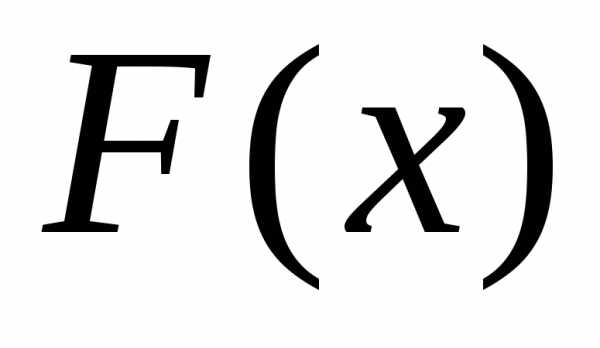 — некоторая первообразная для
— некоторая первообразная для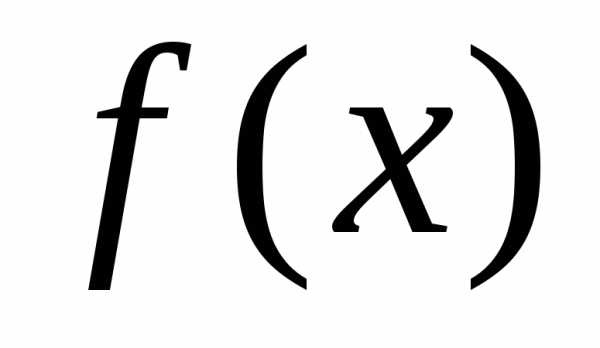 ,
, —
произвольная постоянная.
—
произвольная постоянная.
Например,  – первообразная для функции
– первообразная для функции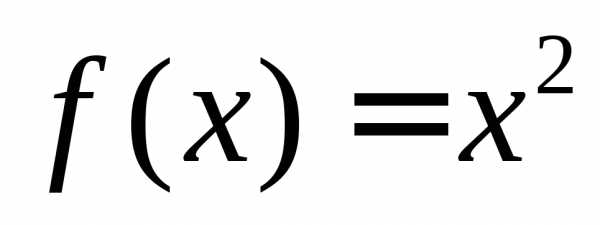 ,
то
,
то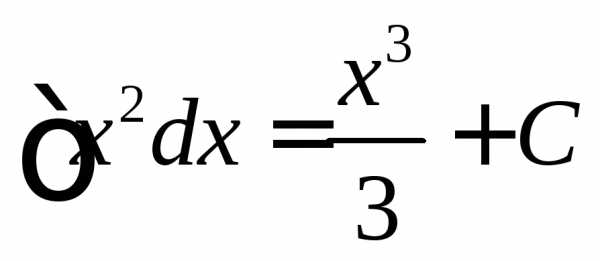 .
.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Основные свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е,
.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.
.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
где  — произвольное число.
— произвольное число.
4. Постоянный множитель можно выносить за знак интеграла, т.е.
где  — произвольное число.
— произвольное число.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
Перечислим интегралы от элементарных функций, которые в дальнейшем мы будем называть табличными:

.
Пример
. Найти  .
.
Решение.
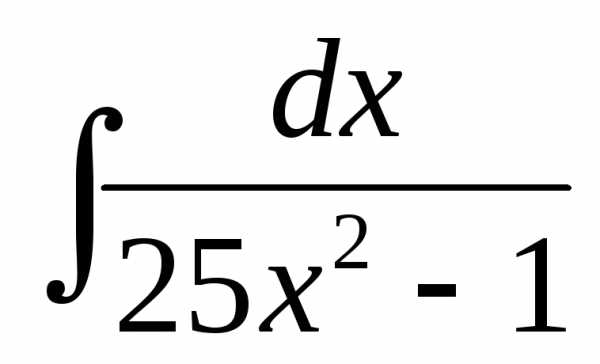 =.
=.
Интегрирование заменой переменных (подстановкой).
Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый следующей формулой:
где  — функция, дифференцируемая на
рассматриваемом промежутке.
— функция, дифференцируемая на
рассматриваемом промежутке.
Пример.
Найти 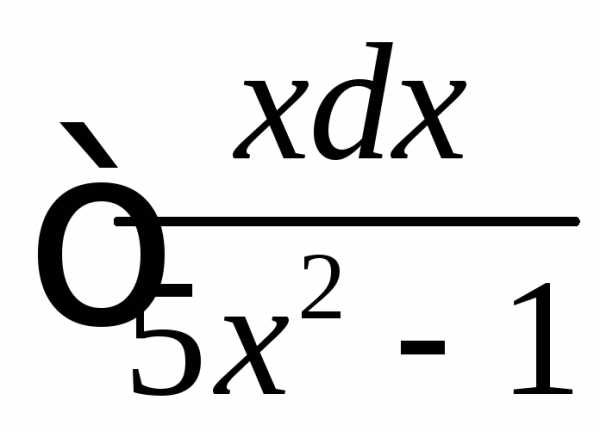 .
.
Решение.
.
Следует отметить, что новую переменную можно не выписывать явно (в таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала). Например,
Тогда
Пример
. Найти 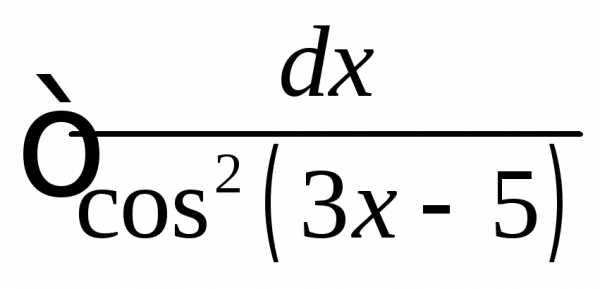 .
.
Решение.
.
Интегрирование по частям.
Пусть 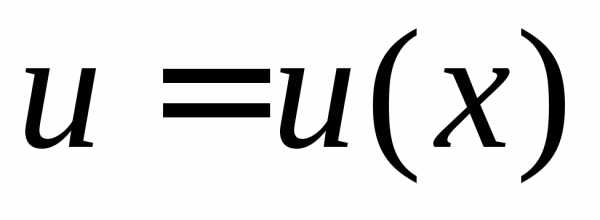 и
и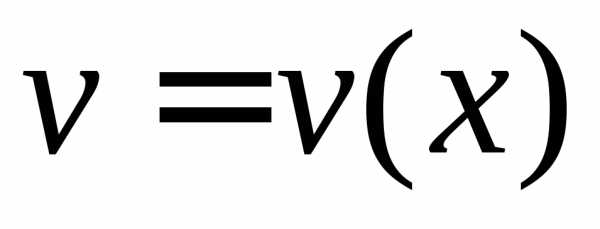 — дифференцируемые функции. По свойству
дифференциала
— дифференцируемые функции. По свойству
дифференциала
или
.
Интегрируя левую и правую части последнего равенства, получаем формулу интегрирования по частям для неопределенного интеграла
.
Пример
. Найти  .
.
Решение.
.
Пример . Найти .
Решение.
.
Пример. Найти 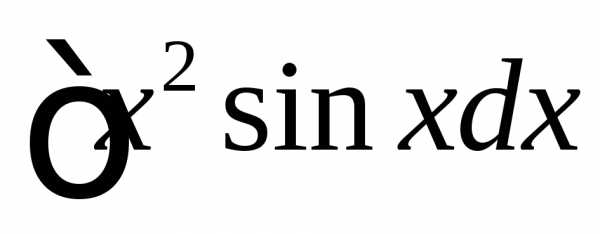 .
.
Положим ТогдаиПрименяя формулу интегрирования по частям, получаем
Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Действительно, положим теперь ТогдаСледовательно,
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Задача
о площади криволинейной трапеции.
Пусть на отрезке 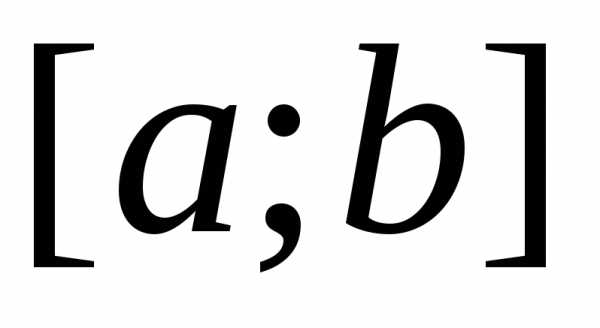 задан
неотрицательная функция
задан
неотрицательная функция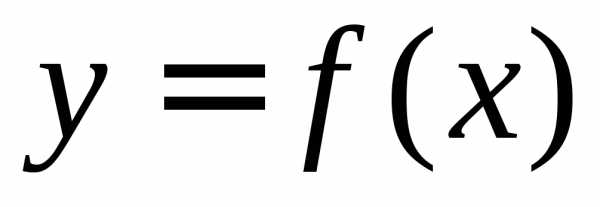 .
Требуется найти площадь
.
Требуется найти площадь криволинейной трапеции, ограниченной
кривой
криволинейной трапеции, ограниченной
кривой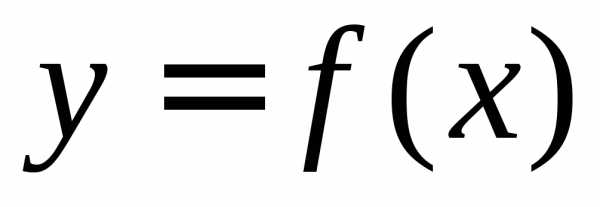 ,
прямыми
,
прямыми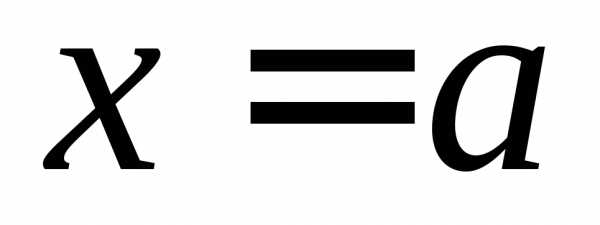 ,
,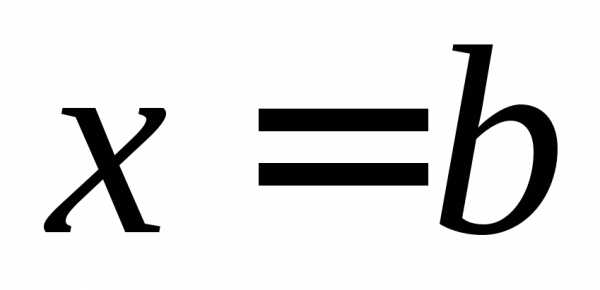 и осью абсцисс
и осью абсцисс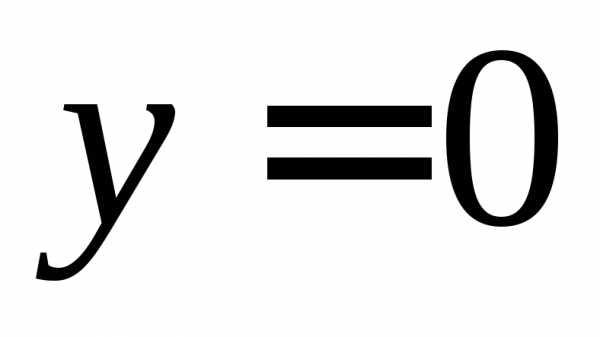 .
.
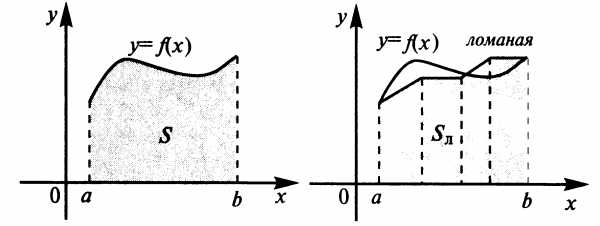
Наметим
общий подход к решению этой задачи.
Введем в рассмотрение некоторую ломаную,
которая расположена достаточно близко
к кривой  на
на .
Фигура под ломаной состоит из трапеций
(прямоугольников), и ее площадь
.
Фигура под ломаной состоит из трапеций
(прямоугольников), и ее площадь (равная сумме площадей этих трапеций)
может быть вычислена с использованием
известных формул планиметрии. Поскольку
ломаная выбрана достаточно близко к
кривой
(равная сумме площадей этих трапеций)
может быть вычислена с использованием
известных формул планиметрии. Поскольку
ломаная выбрана достаточно близко к
кривой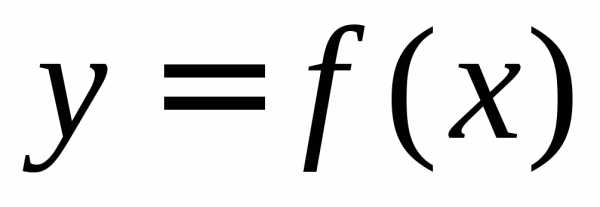 ,
то справедливо приближенное равенство
,
то справедливо приближенное равенство .
Это равенство оказывается тем более
точным, чем ближе расположена ломаная
к исходной кривой. Поэтому естественно
за искомую площадь
.
Это равенство оказывается тем более
точным, чем ближе расположена ломаная
к исходной кривой. Поэтому естественно
за искомую площадь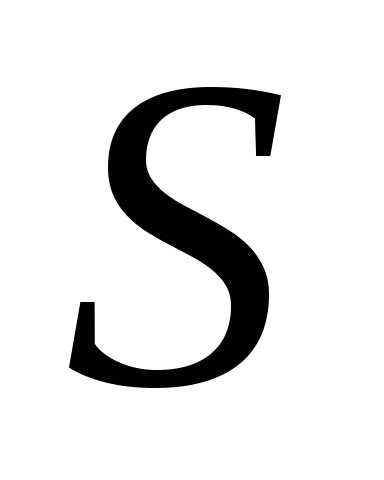 взять предел площади
взять предел площади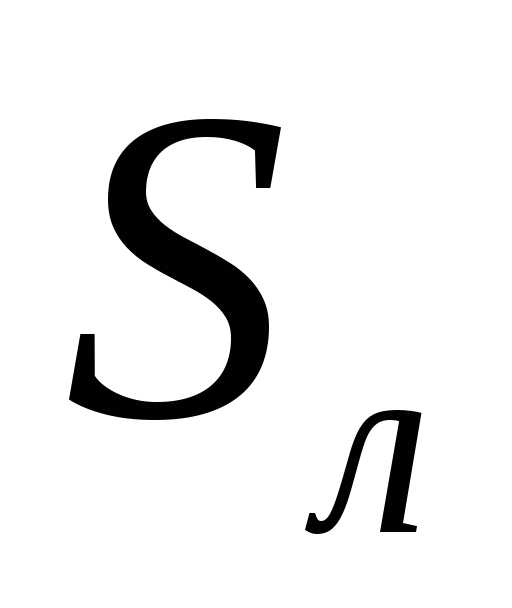 под
ломаной в предположении неограниченного
приближения ломаной к заданной кривой.
под
ломаной в предположении неограниченного
приближения ломаной к заданной кривой.
Понятие
интегральной суммы.
Пусть на 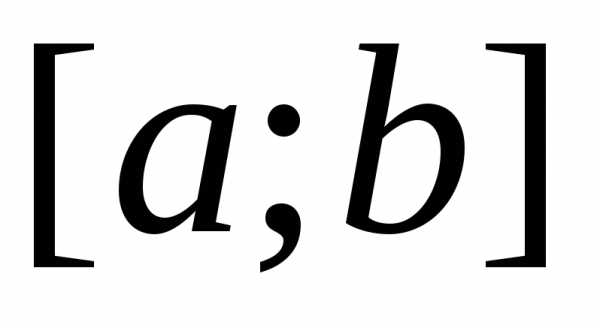 задана функция
задана функция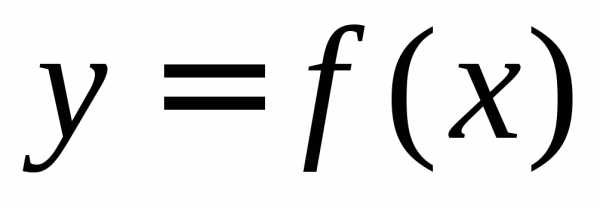 .
Разобьем отрезок
.
Разобьем отрезок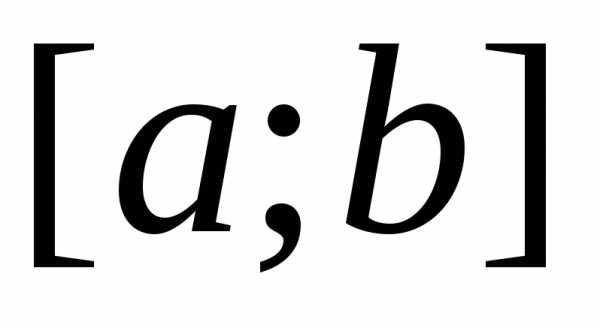 на
на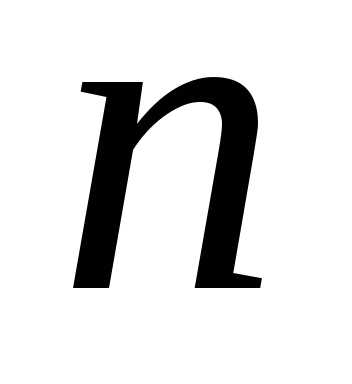 элементарных отрезков точками:.
элементарных отрезков точками:.
На
каждом отрезке 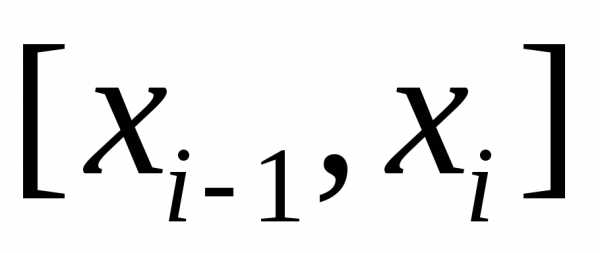 разбиения выберем некоторую точку
разбиения выберем некоторую точку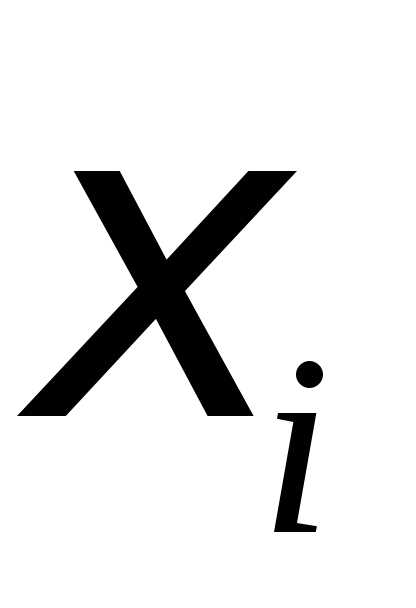 и положим,
где.
Сумму вида
и положим,
где.
Сумму вида

будем
называть интегральной
суммой для функции  на
на .
.
Очевидно,
что интегральная сумма зависит как от
способа разбиения отрезка 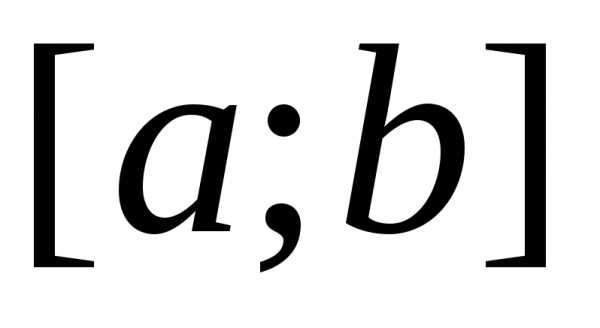 точками,
так и от выбора точекна каждом из отрезков разбиения
точками,
так и от выбора точекна каждом из отрезков разбиения ,.
,.
Геометрический
смысл интегральной суммы состоит в том,
что она равна площади под ломаной,
образованной на каждом из отрезков 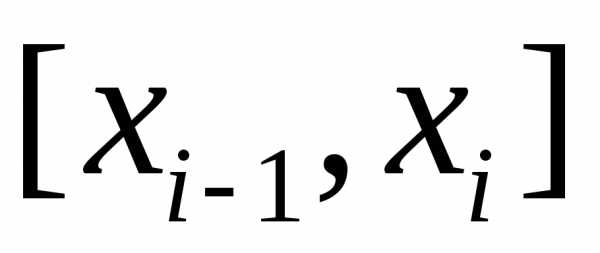 прямой
прямой ,
параллельной оси абсцисс.
,
параллельной оси абсцисс.
Для
избранного разбиения отрезка 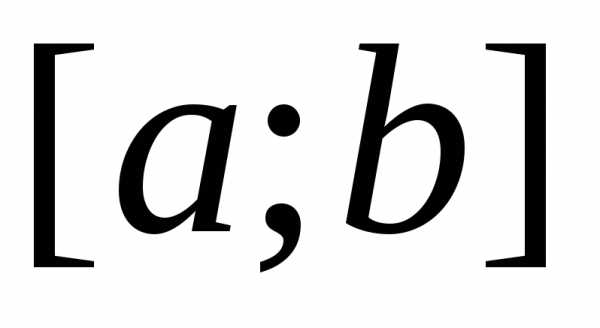 на части обозначим черезмаксимальную из длин отрезков
на части обозначим черезмаксимальную из длин отрезков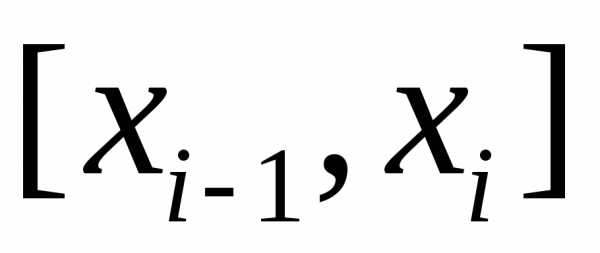 ,
где.
,
где.
Пусть
предел интегральной суммы  при стремлении
при стремлении к нулю существует, конечен и не зависит
от способа выбора точек,…
и точек.
Тогда этот предел называетсяопределенным
интегралом от
функции
к нулю существует, конечен и не зависит
от способа выбора точек,…
и точек.
Тогда этот предел называетсяопределенным
интегралом от
функции 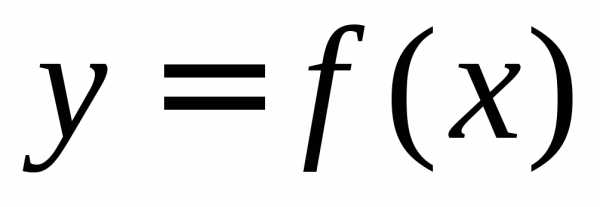 на
на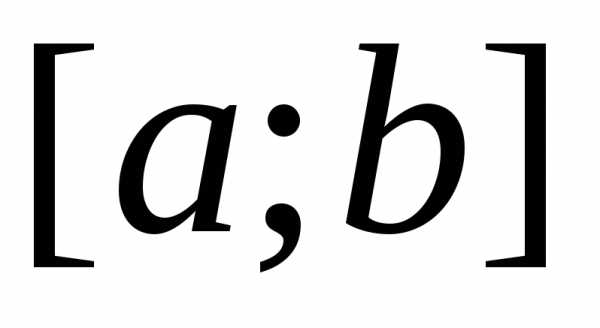 ,
обозначается
,
обозначается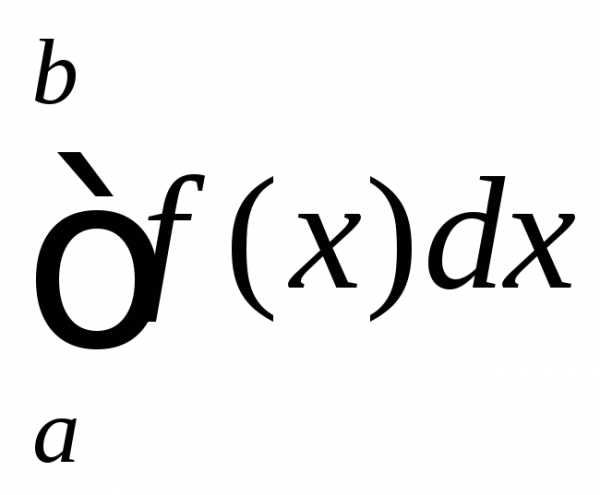 ,
а сама функция
,
а сама функция называется интегрируемой на отрезке
называется интегрируемой на отрезке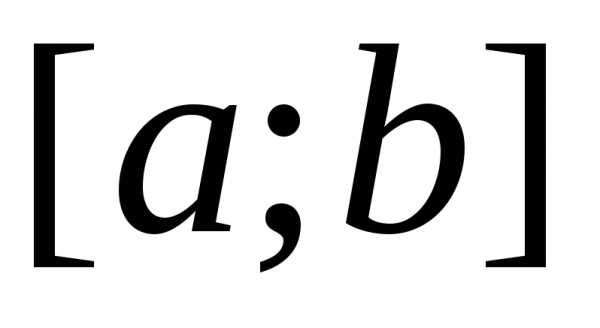 ,
т.е.
,
т.е.
.
При
этом число  называетсянижним
пределом,
число
называетсянижним
пределом,
число  — еговерхним
пределом;
функция
— еговерхним
пределом;
функция 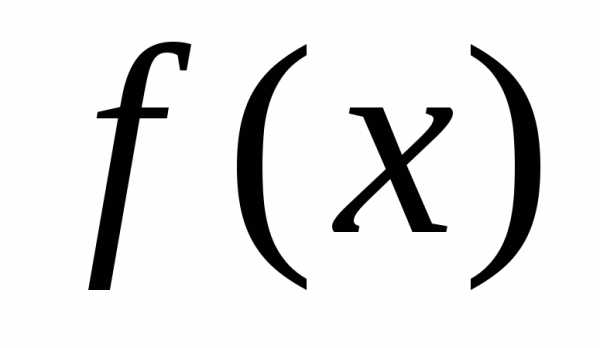 —подынтегральной
функцией,
выражение
—подынтегральной
функцией,
выражение 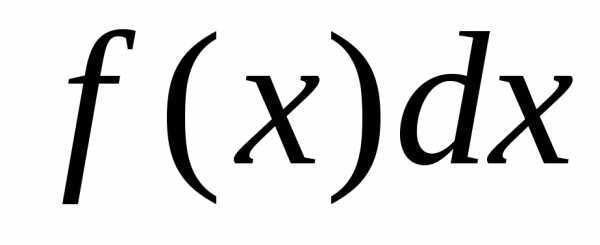 –подынтегральным
выражением,
а задача о нахождении
–подынтегральным
выражением,
а задача о нахождении  —интегрированием
функции
—интегрированием
функции 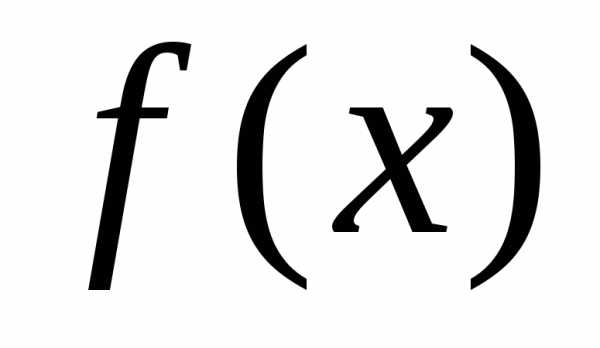 на отрезке
на отрезке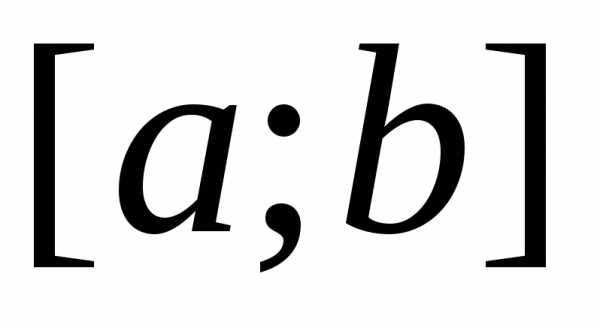 .
.
Несмотря
на сходство в обозначениях и терминологии, определенный
и неопределенный интегралы существенно
различные понятия:
в то время как 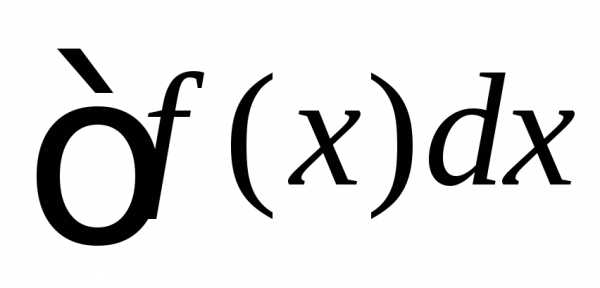 представляет семейство функций,
представляет семейство функций,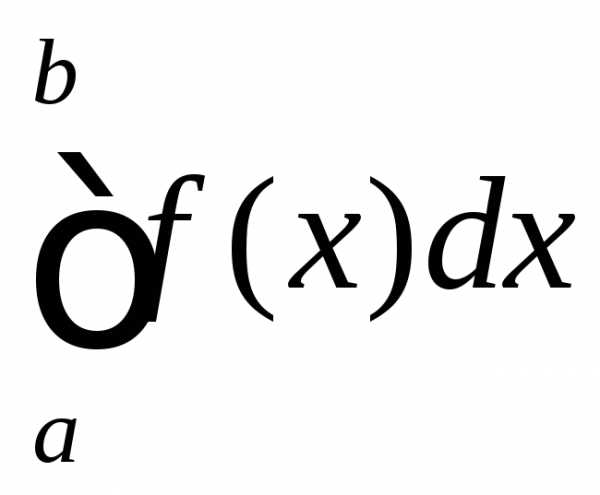 есть определенное число.
есть определенное число.
Во
введенном определении определенного
интеграла  предполагается, что
предполагается, что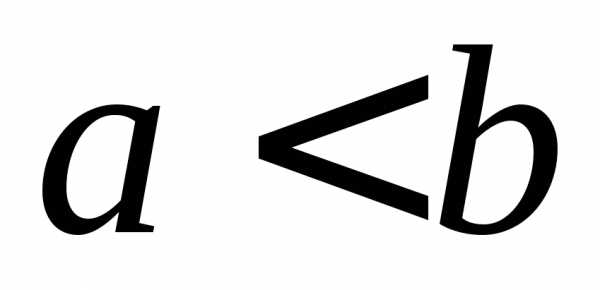 .
По определению положим
.
По определению положим
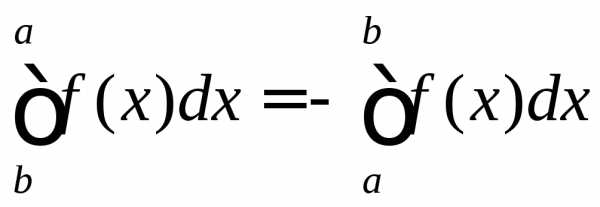 .
.
Геометрический
смысл определенного интеграла.
Понятие определенного интеграла введено
таким образом, что в случае, когда функция 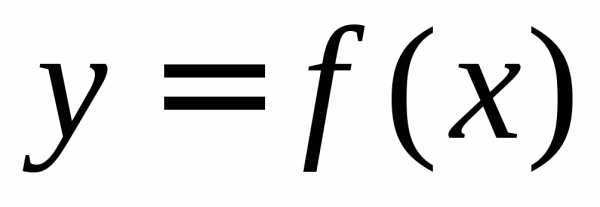 неотрицательна на отрезке
неотрицательна на отрезке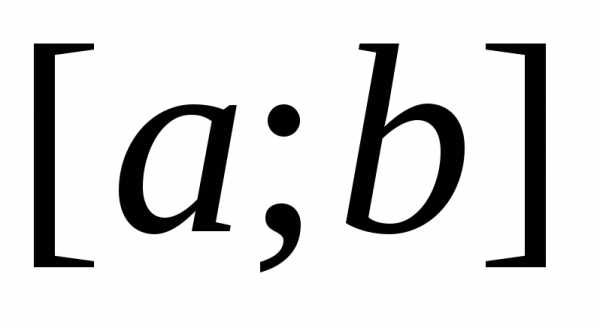 ,
где
,
где ,
,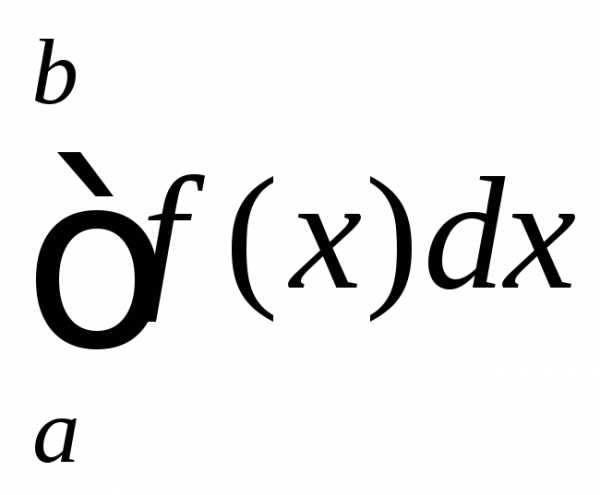 численно
равен площади под кривой
численно
равен площади под кривой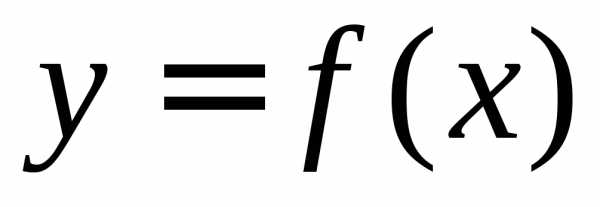 на
на .
.
Теорема. (Достаточное условие существования определенного интеграла)
Если
функция 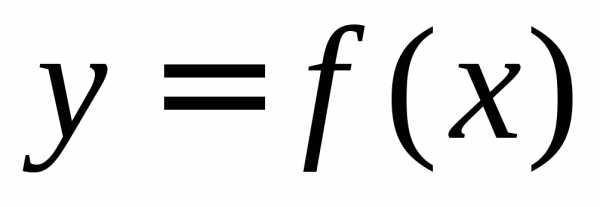 непрерывна на отрезке
непрерывна на отрезке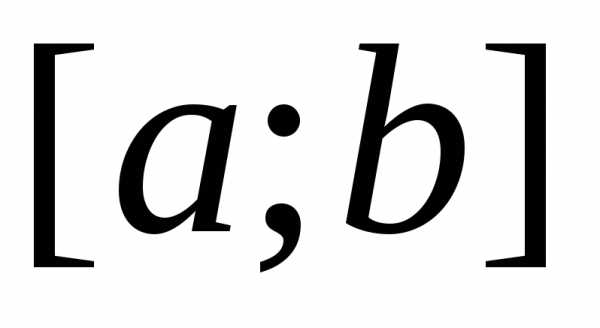 ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
Свойства определенного интеграла.
Постоянный множитель можно выносить за знак интеграла, т.е.
Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.
Если на отрезке
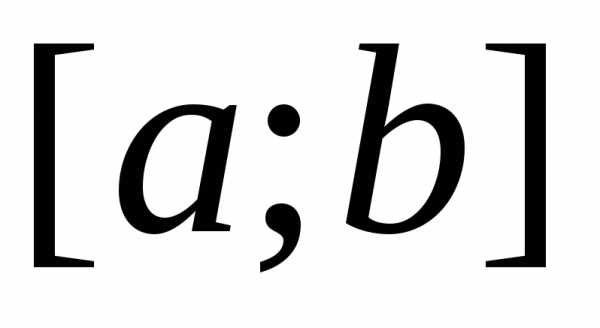 ,
то и
,
то и
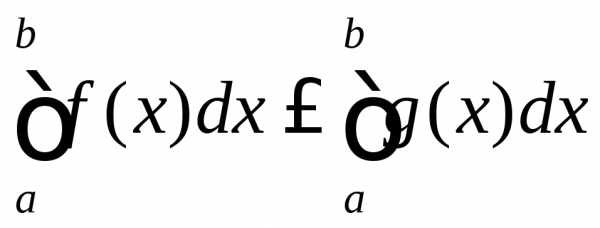 ,
,
т.е. обе части неравенства можно почленно интегрировать.
Основная теорема интегрального исчисления – формула Ньютона-Лейбница.
Теорема. Пусть функция  непрерывна на отрезке
непрерывна на отрезке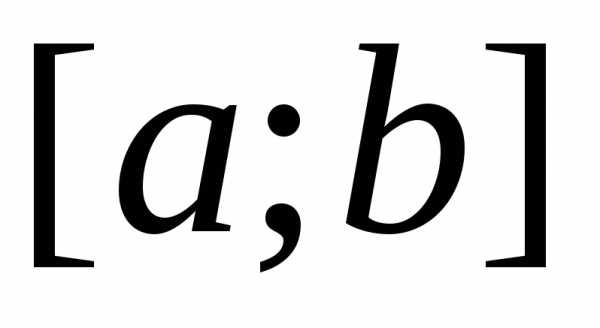 и
и — любая первообразная для
— любая первообразная для на
на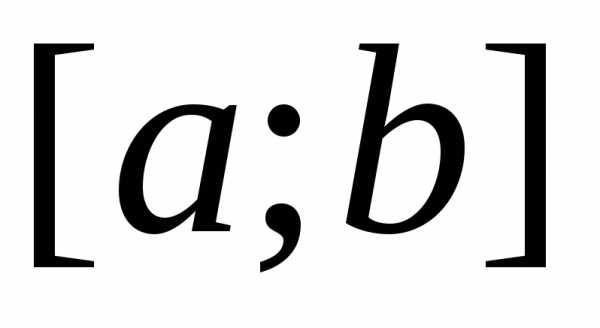 .
Тогда определенный интеграл от функции
.
Тогда определенный интеграл от функции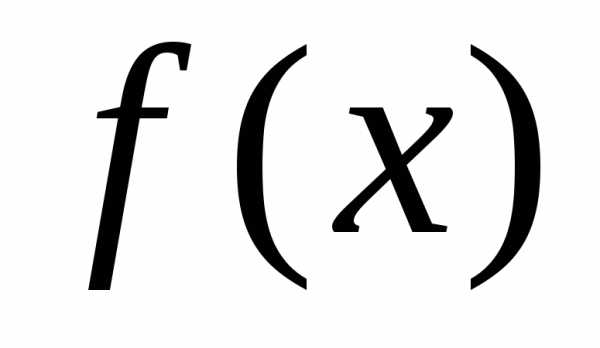 на
на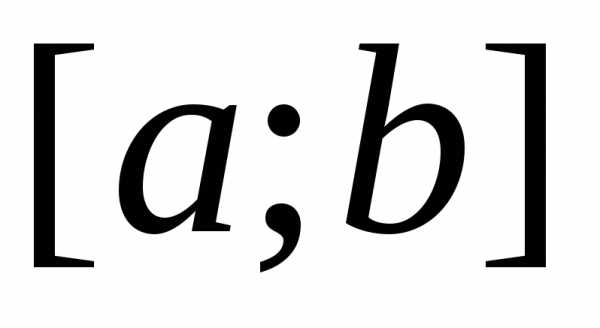 равен приращению первообразной
равен приращению первообразной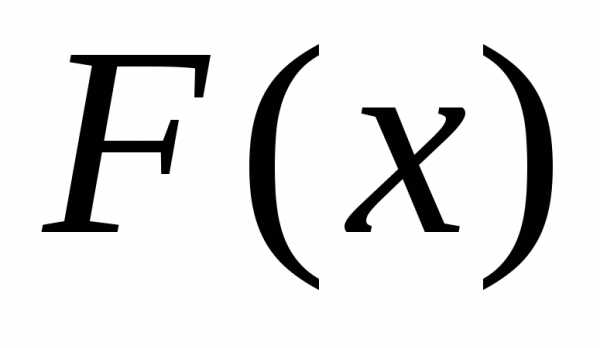 на этом отрезке, т.е.
на этом отрезке, т.е.
Нахождение
определенных интегралов с использованием
формулы Ньютона—Лейбница осуществляется
в два шага: на первом шаге, используя
технику нахождения неопределенного
интеграла, находят некоторую первообразную 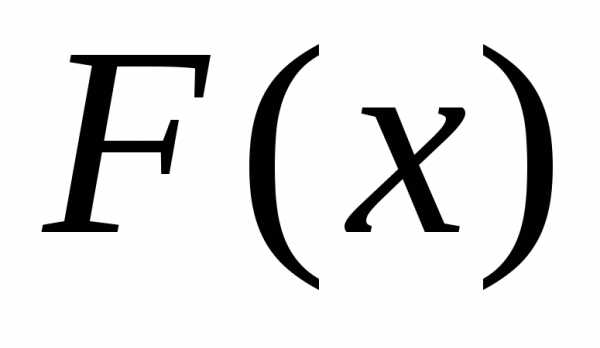 для подынтегральной функции
для подынтегральной функции ;
на втором применяется собственно формула
Ньютона—Лейбница — находится приращение
первообразной, равное искомому интегралу.
В связи с этим введем обозначение для
приращения первообразной, которое
удобно использовать при записи решений.
По определению положим
;
на втором применяется собственно формула
Ньютона—Лейбница — находится приращение
первообразной, равное искомому интегралу.
В связи с этим введем обозначение для
приращения первообразной, которое
удобно использовать при записи решений.
По определению положим
Вычисление определенного интеграла заменой переменных и по частям.
Теорема.
Пусть функция 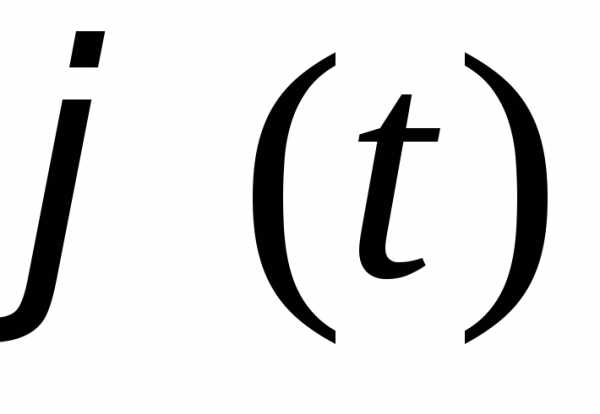 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке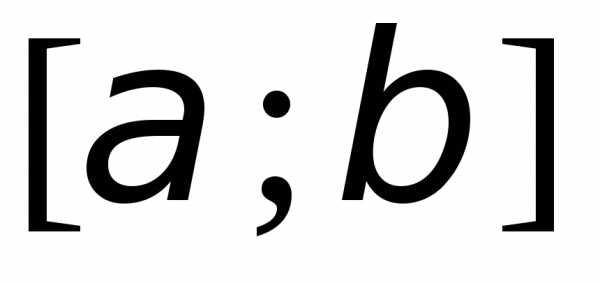 ,
,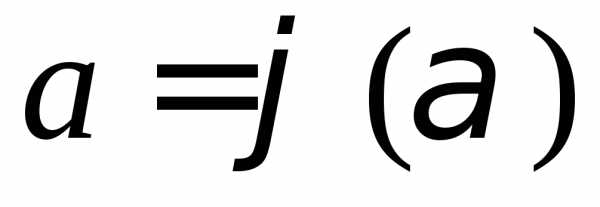 ,
,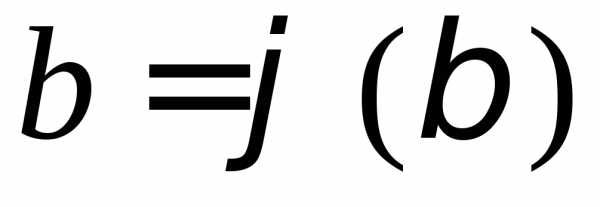 и
функция
и
функция непрерывна в каждой точке
непрерывна в каждой точке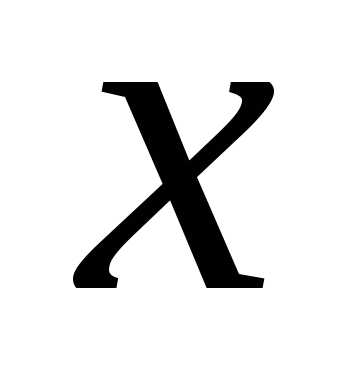 вида
вида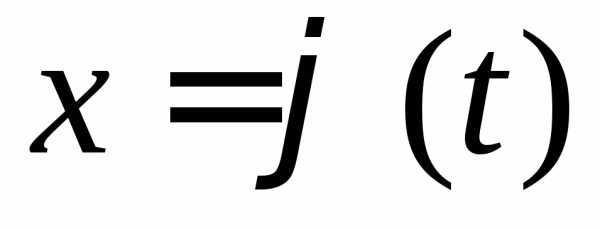 ,
где.
,
где.
Тогда справедливо следующее равенство
Эта формула носит название формулы замены переменной в определенном интеграле.
Теорема.
Пусть функции 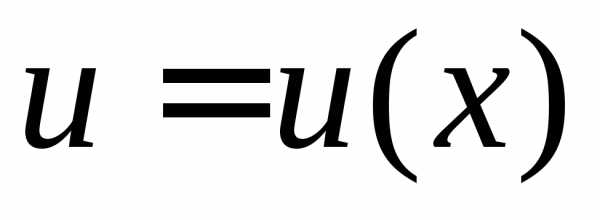 и
и имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке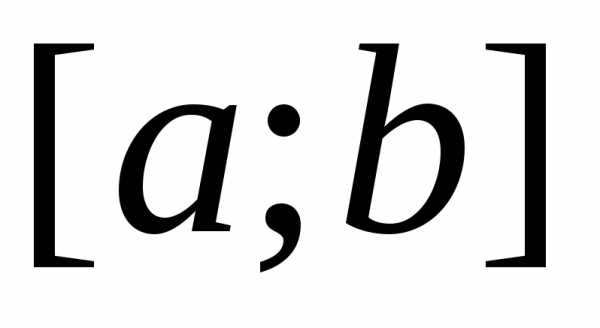 .
Тогда
.
Тогда
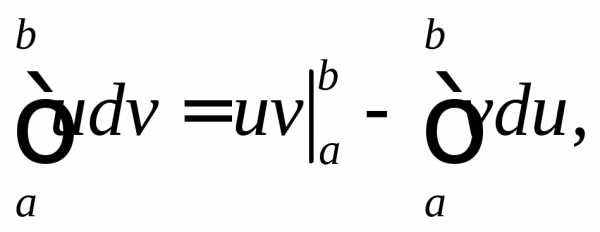 где .
где .
Эта формула называется формулой интегрирования по частям для определенного интеграла.
Вычисление площадей плоских фигур.
Пусть
функция  неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке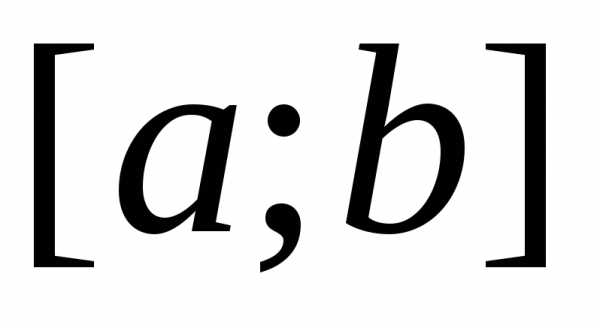 .
Тогда по геометрическому смыслу
определенного интеграла площадь
.
Тогда по геометрическому смыслу
определенного интеграла площадь под кривойна
под кривойна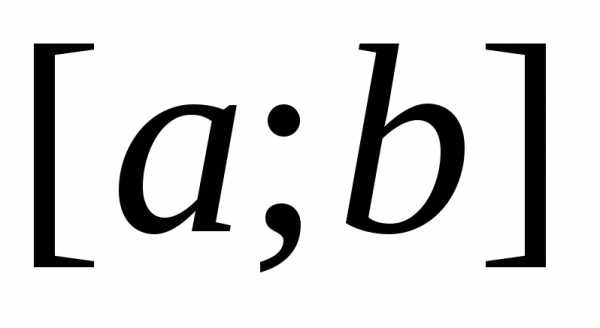 численно
равна определенному интегралу
численно
равна определенному интегралу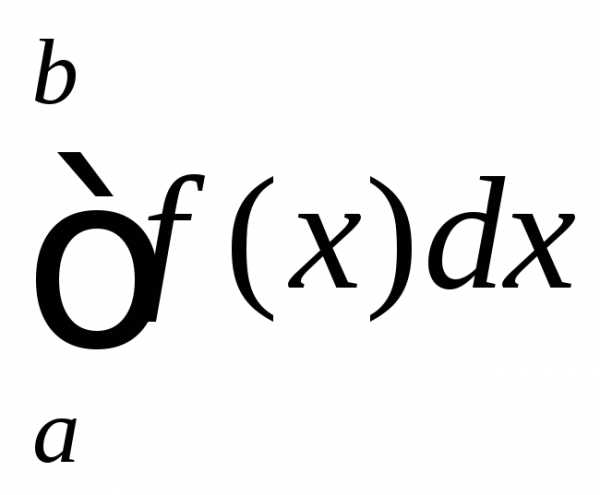 ,
т.е.
,
т.е. .
.
Теорема.
Пусть на отрезке  заданы непрерывные функции
заданы непрерывные функции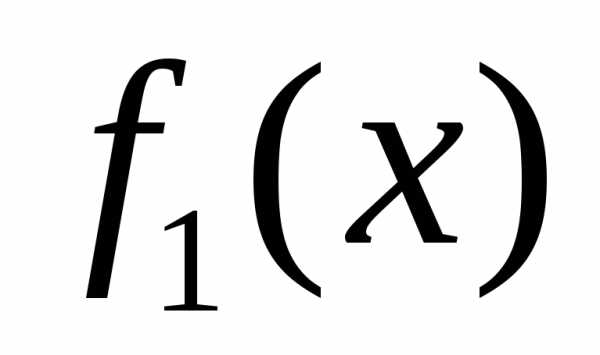 и
и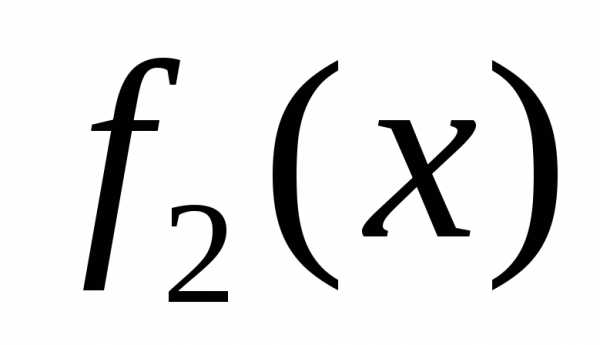 такие, что.
Тогда площадь
такие, что.
Тогда площадь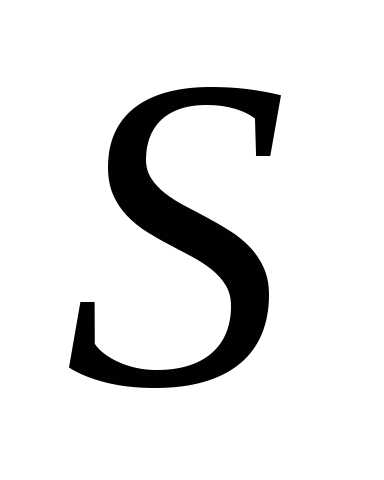 фигуры,
заключенной между кривыми
фигуры,
заключенной между кривыми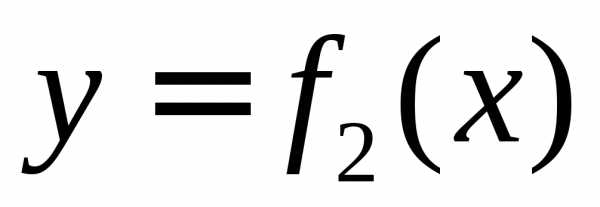 и
и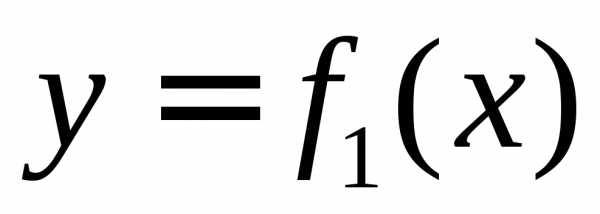 ,
на отрезке
,
на отрезке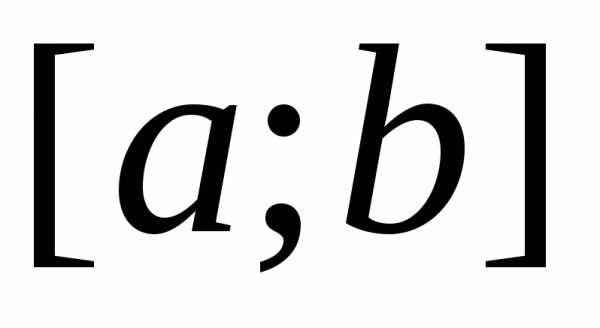 вычисляется по формуле
вычисляется по формуле
studfiles.net
