Конспект лекции_5 Неопределённый и определённый интегралы
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
НЕОПРЕДЕЛЁННЫЙ И ОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛЫ
Конспект лекции для студентов бухгалтерского факультета
заочной формы получения образования (НИСПО)
Горки, 2013
Неопределённый и определённый интегралы
Первообразная функция и неопределённый интеграл
В
дифференциальном исчислении решается
задача нахождения производной или
дифференциала данной функции. Пусть
дана функция 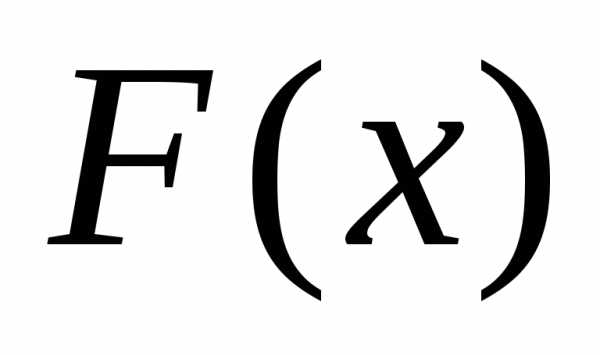 .
Тогда по определению производной
.
Тогда по определению производной 
В
интегральном исчислении решается
задача, обратная задаче нахождения
производной: отыскание функции  по заданной её производной
по заданной её производной  .
Таким образом, для заданной функции
.
Таким образом, для заданной функции нужно найти такую функцию
нужно найти такую функцию 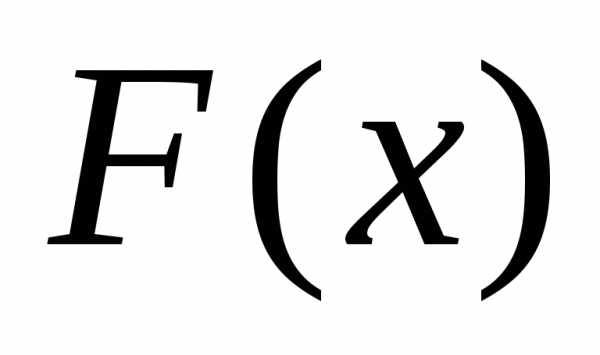 ,
чтобы
.
,
чтобы
.
Функция 
 на некотором множествеD,
если на этом множестве
.
на некотором множествеD,
если на этом множестве
. Если  есть первообразная функция для функции
есть первообразная функция для функции 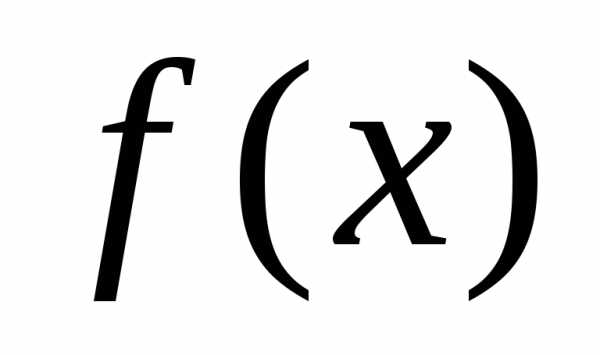 ,
то каждая из функций
,
то каждая из функций  ,
где C – произвольная постоянная, будет также
первообразной для функции
,
где C – произвольная постоянная, будет также
первообразной для функции 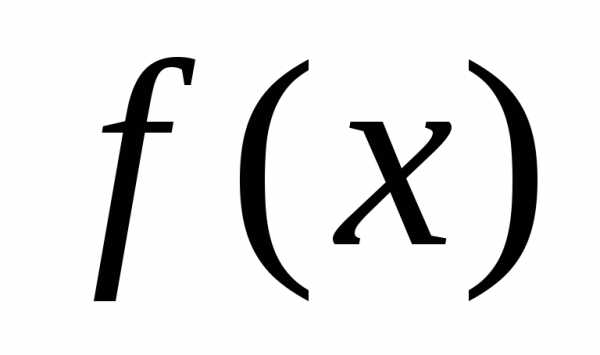
.
Таким
образом, если
функция 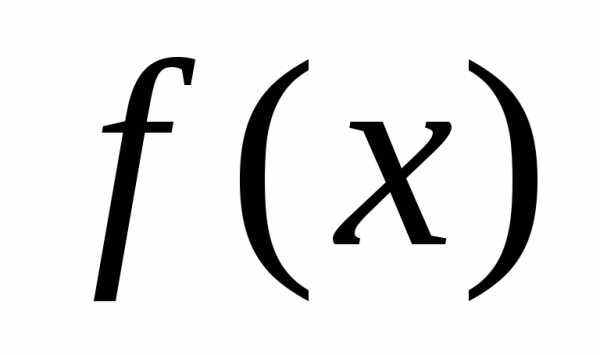 имеет
хотя бы одну первообразную функцию, то
она может иметь бесчисленное множество
первообразных функций и все они отличаются
одна от другой на постоянную величину.
имеет
хотя бы одну первообразную функцию, то
она может иметь бесчисленное множество
первообразных функций и все они отличаются
одна от другой на постоянную величину.
Совокупность всех первообразных функций F(x)+C для функции f(x) называется неопределённым интегралом от функции f(x) и обозначается . Процесс нахождения первообразной функции называетсяинтегрированием
Неопределённый интеграл обладает свойствами, использование которых в значительной степени может упростить интегрирование функций.
 Производная
от неопределённого интеграла равна
подынтегральной функции, т.е.
.
Производная
от неопределённого интеграла равна
подынтегральной функции, т.е.
.
 Дифференциал
неопределённого интеграла равен
подынтегральному выражению, т.е.
.
Дифференциал
неопределённого интеграла равен
подынтегральному выражению, т.е.
.
 Неопределённый
интеграл от дифференциала функции равен
этой функции плюс произвольная постоянная,
т.е.
.
Неопределённый
интеграл от дифференциала функции равен
этой функции плюс произвольная постоянная,
т.е.
.
 Постоянный
множитель можно выносить за знак
интеграла:
.
Постоянный
множитель можно выносить за знак
интеграла:
.
 Неопределённый
интеграл от алгебраической суммы функций
равен алгебраической сумме интегралов
от этих функций, т.е.
.
Неопределённый
интеграл от алгебраической суммы функций
равен алгебраической сумме интегралов
от этих функций, т.е.
.

Таблица основных интегралов
Интегралы данной таблицы называются табличными. Каждая из формул таблицы справедлива в области определения подынтегральной функции.
Основные методы интегрирования
При интегрировании функций не всегда можно сразу использовать таблицу интегралов. Как правило, вначале нужно данный интеграл преобразовать таким образом, чтобы свести его к одной или нескольким формулам таблицы. Для этого используются специальные методы интегрирования, основными из которых являются
Суть метода непосредственного интегрирования состоит в том, что данный интеграл с помощью алгебраических преобразований и свойств неопределённого интеграла сводится к табличным интегралам.
Примеры 1 –3. Найти неопределённые интегралы:
а)  ;
б);
в).
;
б);
в).
Решение. а) ;
б)
=
;
в) =

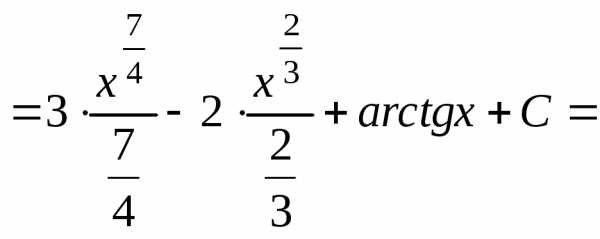 .
.
Если интеграл непосредственно не находится, то во многих случаях результат может быть достигнут с помощью метода замены переменной (подстановки). Данный метод помогает значительно упростить подынтегральное выражение и свести интеграл к одной из формул таблицы.
Если подынтегральная функция представляет собой дробь, у которой числитель есть производная знаменателя, то такой интеграл равен логарифму натуральному от абсолютной величины знаменателя, т.е. .
Примеры
4 –
7.
Найти интегралы: а)  ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.
Решение
 {заменимu=3x,
тогда du=3dx,
{заменимu=3x,
тогда du=3dx, 
=;
б) 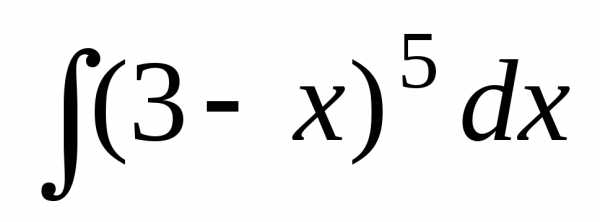 ={заменимu=3x, du=dx, dx=du}=
={заменимu=3x, du=dx, dx=du}= 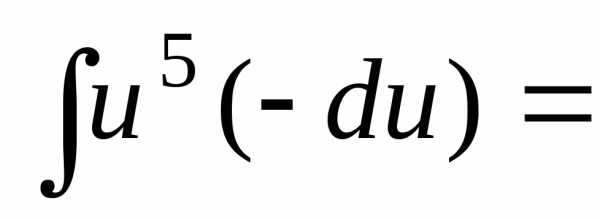
=;
в) 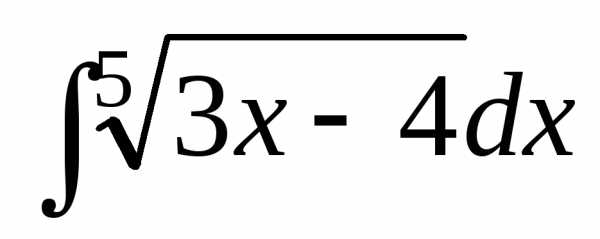 ={u=3x4, du=3dx,
={u=3x4, du=3dx, 
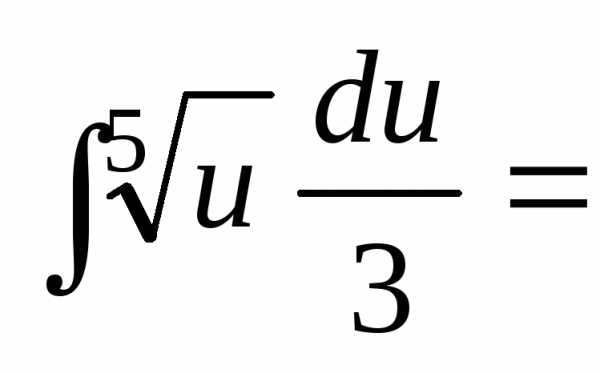
 =
= =
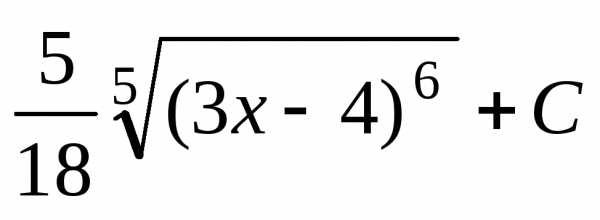 ;
;
г) 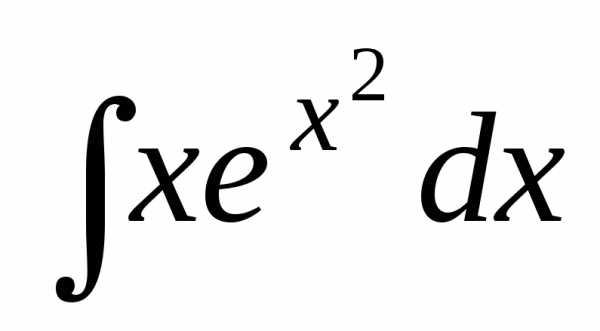 ={
={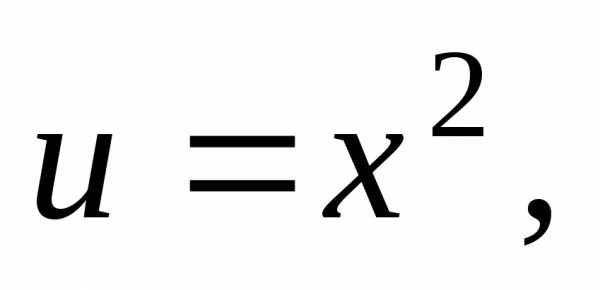 du=2xdx,
du=2xdx,  }=
}=
=.
Для
нахождения интеграла вида 
При использовании данного метода интегрирования удобно пользоваться следующими рекомендациями:

 ,,имеет смысл положитьu=P(x),
а в качестве dv взять оставшуюся часть подынтегрального
выражения;
,,имеет смысл положитьu=P(x),
а в качестве dv взять оставшуюся часть подынтегрального
выражения;  в
интегралах вида
,,,,
в
интегралах вида
,,,, следует положитьdv=P(x)dx,
а оставшуюся часть подынтегрального
выражения обозначить через u;
следует положитьdv=P(x)dx,
а оставшуюся часть подынтегрального
выражения обозначить через u;
 в
интегралах вида
,можно положить
в
интегралах вида
,можно положить ,
а оставшуюся часть подынтегрального
выражения принять заdv.
,
а оставшуюся часть подынтегрального
выражения принять заdv.
Примеры
8 – 9.
Найти интегралы: а)  ;
б)
;
б)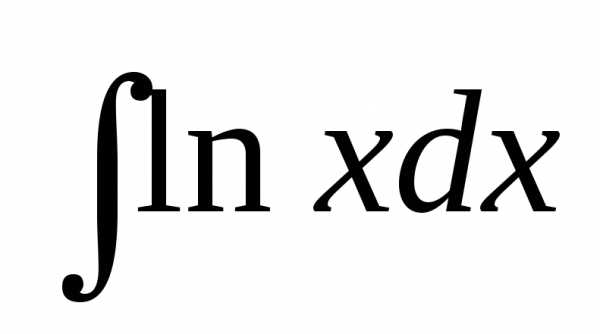 .
.
Решение.
а) 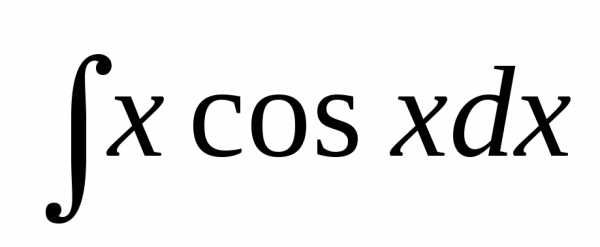 =
=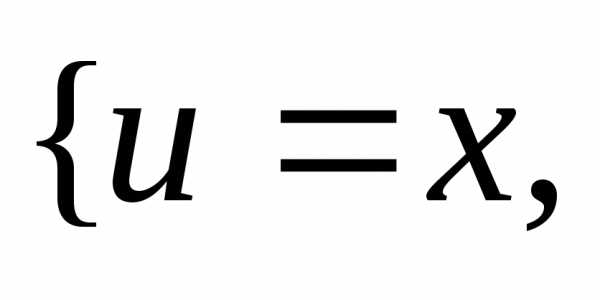

 =;
=;
б)  =
=


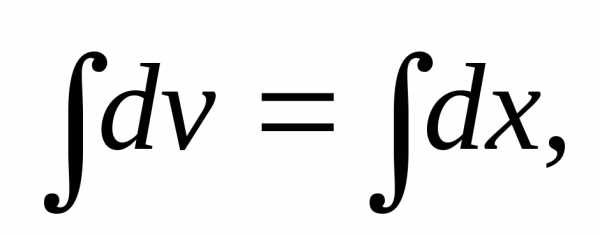
 =
=
= .
.
Определённый интеграл и его основные свойства
Пусть
функция 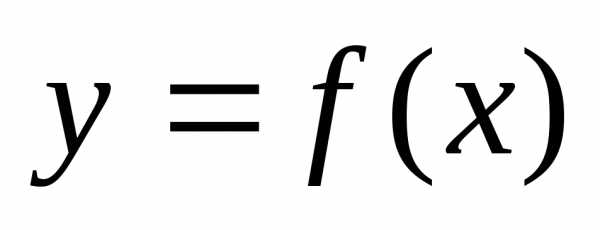 определена на отрезке
определена на отрезке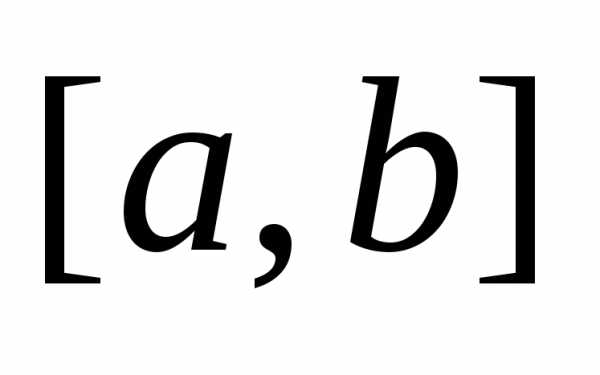 .
Выполним следующие действия.
.
Выполним следующие действия.
 Разобьём
отрезок
Разобьём
отрезок  точками
точками

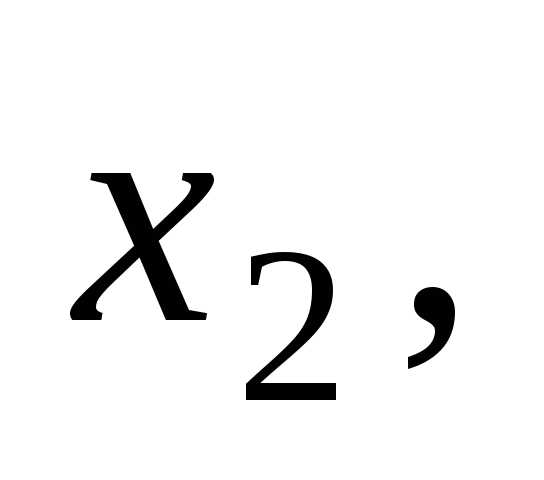 …
,
…
, наn отрезков
наn отрезков  ,
, ,
… ,
,
… ,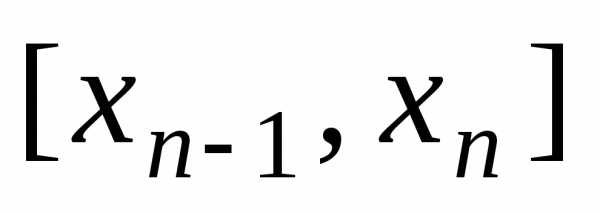 ,
которые называются частичными.
,
которые называются частичными.
 В
каждом частичном отрезке
В
каждом частичном отрезке  произвольно выберем точку,
вычислим значение функции в этой точке
произвольно выберем точку,
вычислим значение функции в этой точке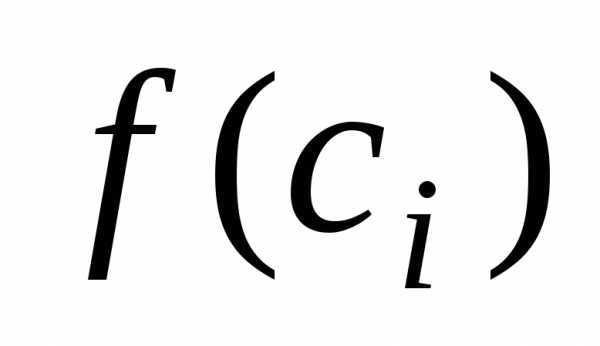 и произведение
и произведение ,
где.
,
где.
 Если
существует предел
Если
существует предел  ,
который не зависит ни от способа
разбиения отрезка
,
который не зависит ни от способа
разбиения отрезка ,
ни от выбора точек,
то он называетсяопределённым
интегралом от функции
,
ни от выбора точек,
то он называетсяопределённым
интегралом от функции  на отрезкеи обозначается
на отрезкеи обозначается

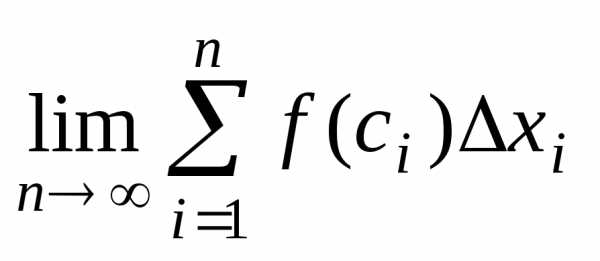 .
.
Числа a и b называются нижним
и верхним пределами интегрирования.
Функция  называетсяподынтегральной
функцией,
выражение
называетсяподынтегральной
функцией,
выражение  –подынтегральным
выражением, x – переменной
интегрирования,
–подынтегральным
выражением, x – переменной
интегрирования,  –отрезком
интегрирования.
–отрезком
интегрирования.
Пусть
на отрезке  задана непрерывная функция.
Фигура, ограниченная сверху графиком
функции
задана непрерывная функция.
Фигура, ограниченная сверху графиком
функции ,
снизу осьюOx,
сбоку – прямыми x=a и x=b,
называется криволинейной
трапецией.
,
снизу осьюOx,
сбоку – прямыми x=a и x=b,
называется криволинейной
трапецией.
Определённый интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определённого интеграла.
Основными свойствами определённого интеграла являются следующие:
 постоянный
множитель можно выносить за знак
определённого интеграла, т.е.
постоянный
множитель можно выносить за знак
определённого интеграла, т.е.  ;
;
 определённый
интеграл от алгебраической суммы
непрерывных на отрезке
определённый
интеграл от алгебраической суммы
непрерывных на отрезке  функций
функций и
и равен алгебраической сумме определённых
интегралов от этих функций, т.е.
равен алгебраической сумме определённых
интегралов от этих функций, т.е.
;
 если
верхний и нижний пределы интегрирования
поменять местами, то определённый
интеграл изменит знак на противоположный,
т.е.
если
верхний и нижний пределы интегрирования
поменять местами, то определённый
интеграл изменит знак на противоположный,
т.е. 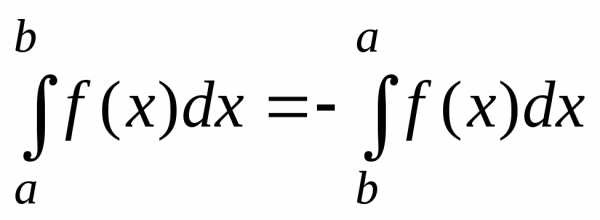 ;
;
 если
пределы интегрирования равны между
собой, то определённый интеграл равен
нулю, т.е.
если
пределы интегрирования равны между
собой, то определённый интеграл равен
нулю, т.е. 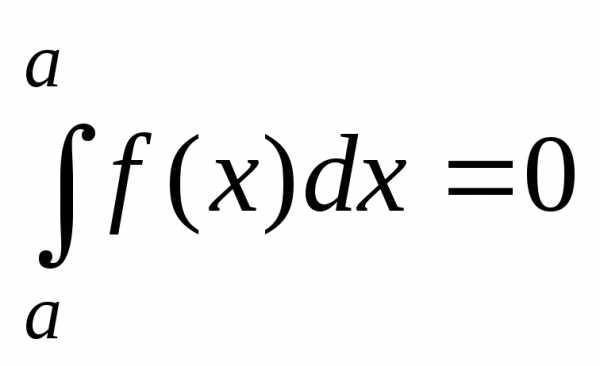 ;
;
 определённый
интеграл не зависит от обозначения
переменной интегрирования, т.е.
определённый
интеграл не зависит от обозначения
переменной интегрирования, т.е. 
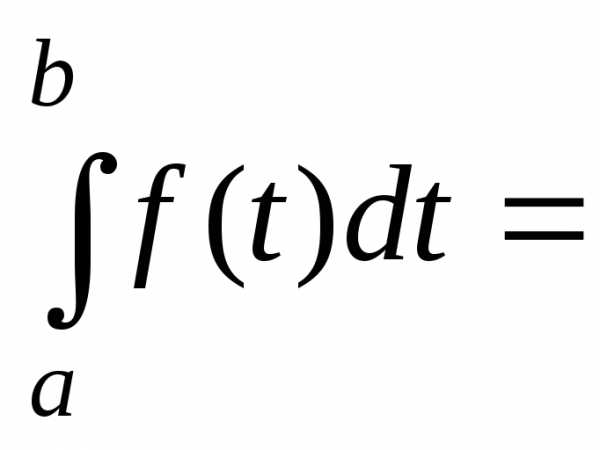
 …;
…;
 если
отрезок интегрирования
если
отрезок интегрирования  разбит на две части
разбит на две части и
и и если существуют интегралы
и если существуют интегралы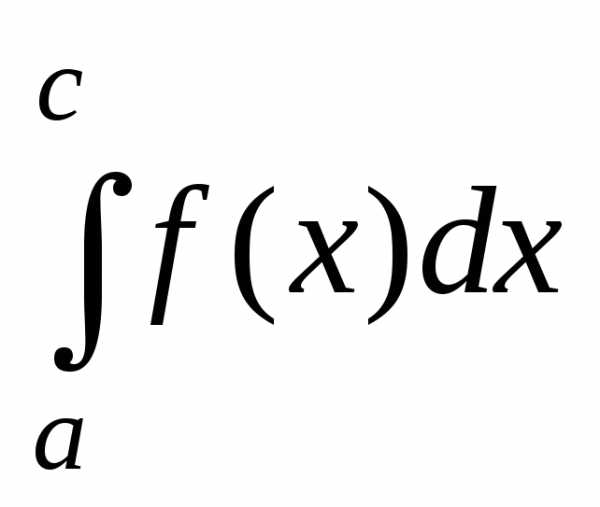 и
и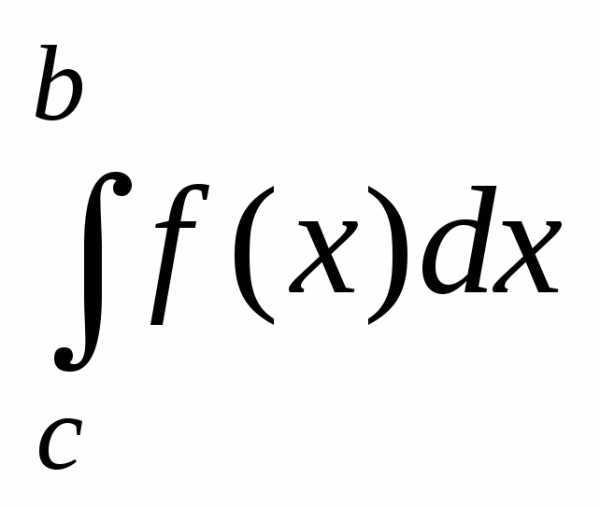 ,
то
,
то
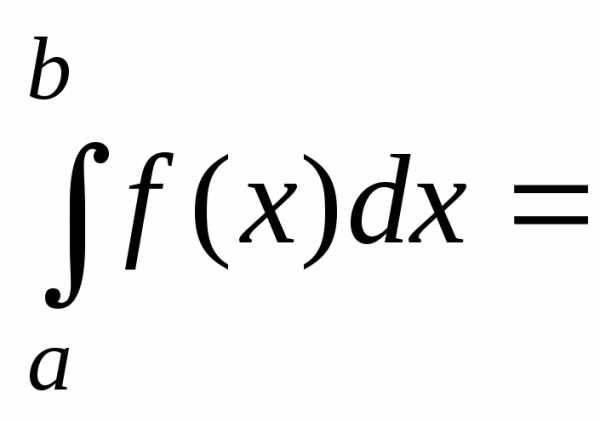

 .
.
Для вычисления определённых интегралов используется формула Ньютона-Лейбница
,
где
,
т.е. – любая первообразная функция для
– любая первообразная функция для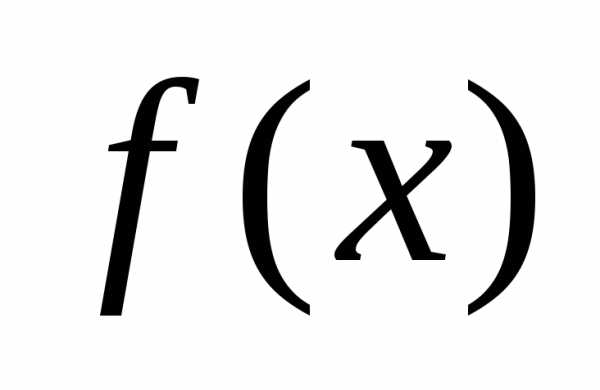 .
.
Методы вычисления определённых интегралов
При вычислении определённых интегралов используются методы непосредственного интегрирования, замены переменной (подста-
новки) и интегрирования по частям.
Непосредственное интегрирование предполагает сведение данного интеграла с помощью алгебраических и арифметических преобразований к формулам таблицы основных интегралов и использование формулы Ньютона-Лейбница.
Примеры
10-11.
Вычислить интегралы: а) 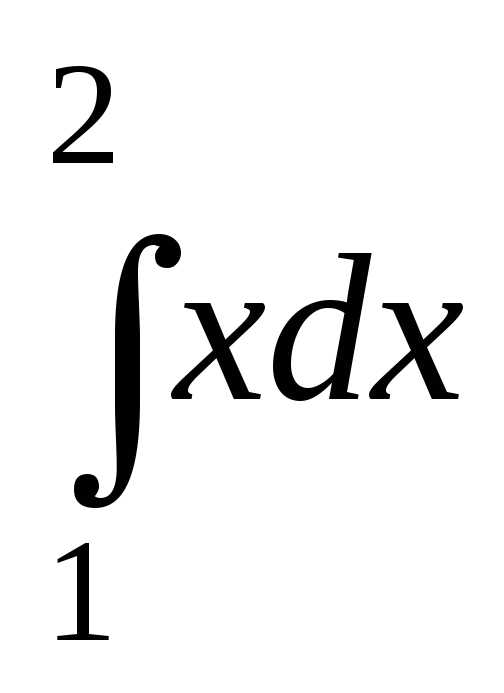 ;
б)
;
б) .
.
Решение.
а)  =;
=;
б)  =.
=.
Метод замены переменной в определённом интеграле предполагает следующее. Пусть выполнены условия:
 функция
функция  непрерывна на отрезке
непрерывна на отрезке ;
;
 функция
функция  определена
на отрезке
определена
на отрезке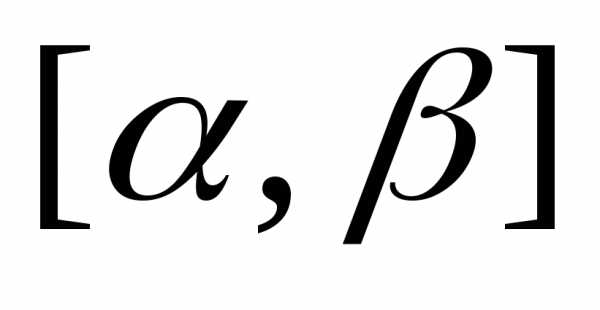 и имеет на нём непрерывную производную;
и имеет на нём непрерывную производную;

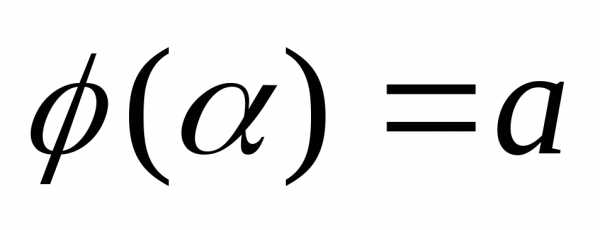 ,
,  .
.
Тогда
определённый интеграл  может быть вычислен с помощью введения
новой переменной и при этом справедлива
формула.
Часто вместо замены
может быть вычислен с помощью введения
новой переменной и при этом справедлива
формула.
Часто вместо замены применяют обратную замену
применяют обратную замену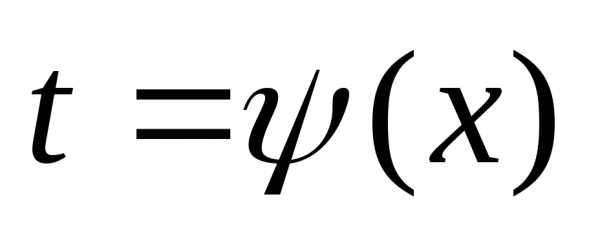 .
.
Примеры
12–13.
Вычислить интегралы: а)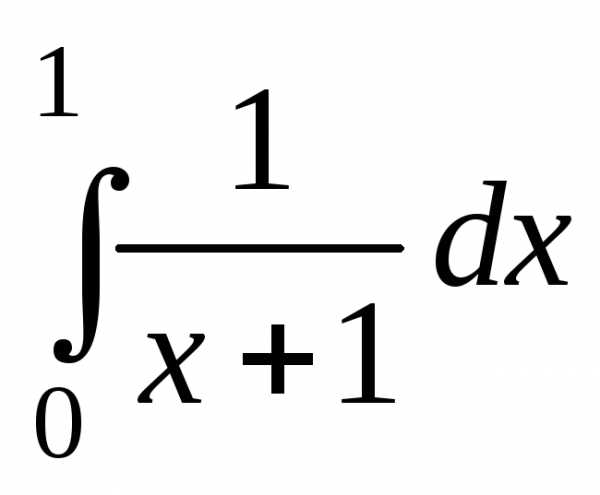 ;
б)
;
б) .
.
Решение.
а) Выполним замену 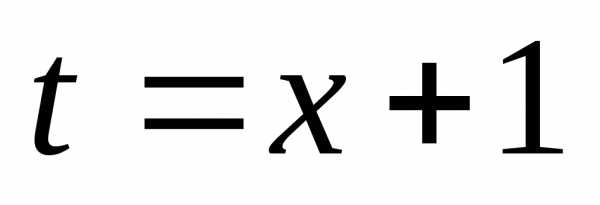 ,
, .
Вычислим пределы интегрирования для
переменнойt:
.
Вычислим пределы интегрирования для
переменнойt:
Тогда  =.
=.
б)
Выполним замену
и продифференцируем обе части равенства:, .
Изменим пределы интегрирования:
.
Изменим пределы интегрирования:
В
результате  =
=
 .
.
Пусть
функции  и
и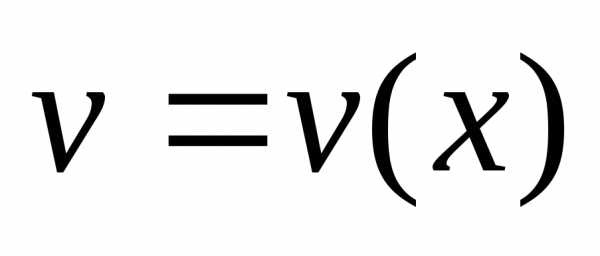 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке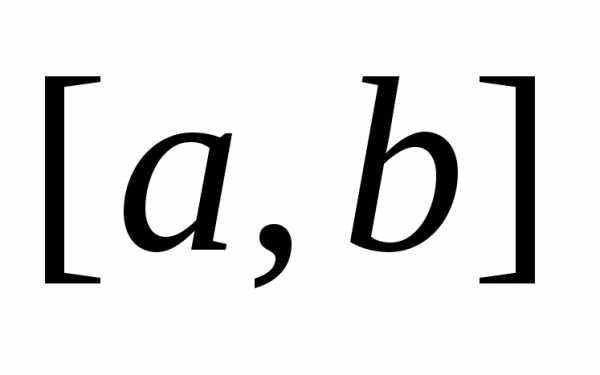 .
Тогда для определённого интеграла
справедливаформула
интегрирования по частям
.
Тогда для определённого интеграла
справедливаформула
интегрирования по частям 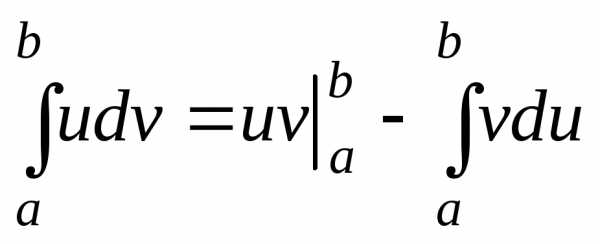 .
.
Пример
14.
Вычислить интеграл 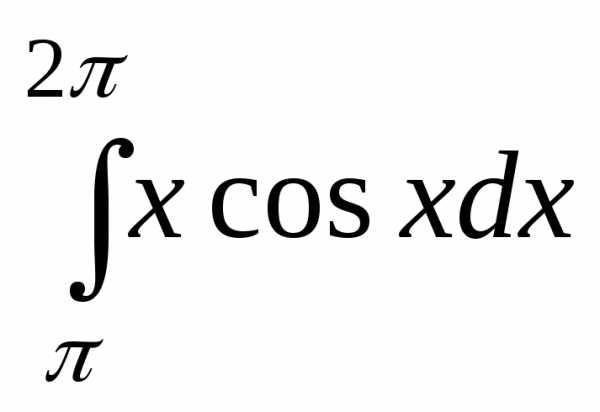 .
.
Решение.
Положим u=x,
тогда du=dx.
Оставшуюся часть подынтегрального
выражения примем за dv:
.
Проинтегрируем это выражение:, .
Тогда по формуле интегрирования по
частям получим
.
Тогда по формуле интегрирования по
частям получим =
= =
=
Вычисление площадей плоских фигур
Согласно
геометрическому смыслу определённого
интеграла площадь криволинейной
трапеции, расположенной выше оси абсцисс,
равна определённому интегралу от функции 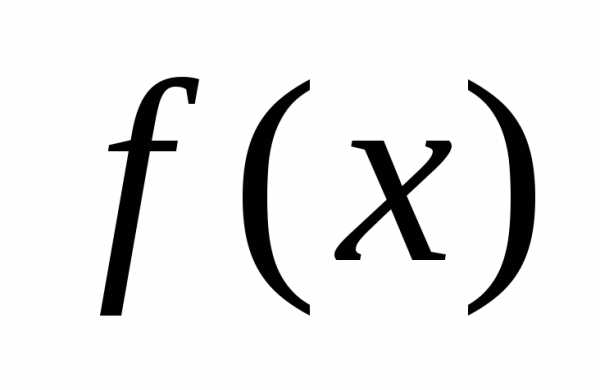 :
: .
Если криволинейная трапеция расположена
ниже оси абсцисс, то площадь такой
трапеции вычисляется по формуле:
.
Если криволинейная трапеция расположена
ниже оси абсцисс, то площадь такой
трапеции вычисляется по формуле: .
.
Пусть
фигура ограничена снизу графиком функции 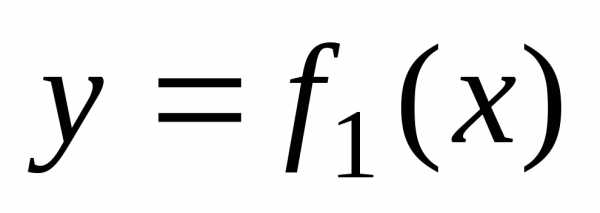 , сверху – графиком функции
, сверху – графиком функции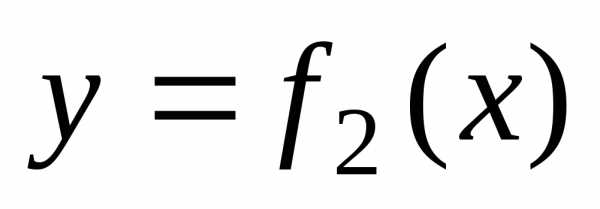 ,
слева – прямойx=a и справа – прямой x=b.
,
слева – прямойx=a и справа – прямой x=b.
Тогда
площадь фигуры, ограниченной этими
линиями, вычисляется по формуле: 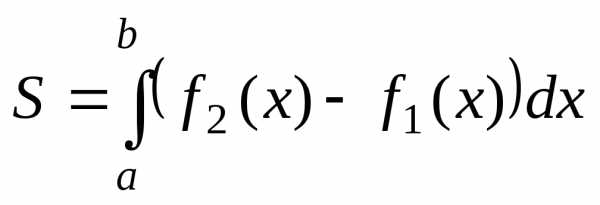 .
.
Пример 15. Вычислить площадь фигуры, ограниченной линиями ,.
studfiles.net
Неопределенный и определенный интегралы
Задача восстановления функции по ее производной
В дифференциальном исчислении рассматривались задачи, решение которых требовало отыскания производной данной функции. В ряде случаев приходится решать обратную задачу: по заданной производной отыскивать функцию, которую дифференцировали. Задачи такого рода решаются в разделе математического анализа, называемом интегральным исчислением. Методы интегрального исчисления позволяют решать задачи на вычисление площадей плоских фигур, длин дуг, объемов тел и другие геометрические и физические задачи.
Пример 1. Пусть скорость [cbm]{v}[/cbm] движения точки в момент времени [cbm]{t}[/cbm] равна [cbm]2t[/cbm] . Найдем выражение для координаты точки в момент времени [cbm]{t}[/cbm] (точка движется по прямой).
Решение. Известно, что [cbm]v=\frac{dx}{dt}[/cbm] . Так как в данном случае [cbm]\frac{dx}{dt}=2t[/cbm] , то ответом к задаче могут быть функции [cbm]x=t^2;[/cbm] [cbm]x=t^2+3[/cbm] и т.д.; в общем виде ответ на поставленный вопрос записывается в виде [cbm]x=t^2+C[/cbm] , где [cbm]C[/cbm] — произвольная постоянная.
Из приведенного примера видно, что обратная задача имеет бесконечное множество решений. Чтобы получить определенный закон движения, необходимо знать, например, положение точки в момент времени [cbm]t=0[/cbm] . Если при [cbm]t=0[/cbm] имеем [cbm]x=0[/cbm] , то [cbm]0=0+C[/cbm] , и потому [cbm]C=0[/cbm] .
Перемещение точки за промежуток времени [cbm][a;b][/cbm] равно [cbm](b^2+C)-(a^2+C)=b^2-a^2[/cbm] , и, следовательно, оно не зависит от [cbm]C[/cbm] .
Первообразная функция
Определение 1. Пусть на некотором промежутке [cbm]X[/cbm] задана функция [cbm]y=f(x)[/cbm] . Функция [cbm]y=F(x)[/cbm] называется первообразной для [cbm]f(x)[/cbm] на этом промежутке, если для всех [cbm]x\in X[/cbm]
[cbm]F'(x)=f(x).[/cbm]
Термин “первообразная” был введен французским математиком Ж. Л. Лагранжем (1736—1813).
Следующая теорема позволяет свести нахождение всех первообразных данной функции к отысканию одной из них.
Теорема 1. Если функция [cbm]y=f(x)[/cbm] имеет на промежутке [cbm]X[/cbm] первообразную [cbm]F(x)[/cbm] , то и все функции вида [cbm]F(x)+C[/cbm] будут для нее первообразными на том же промежутке. Обратно, любая первообразная [cbm]\Phi(x)[/cbm] для функции [cbm]y=f(x),\,x\in X[/cbm] , может быть представлена в виде [cbm]\Phi(x)+C[/cbm] , где [cbm]F(x)[/cbm] — одна из первообразных функций, а [cbm]C[/cbm] — произвольная постоянная.
Доказательство. По определению первообразной имеем [cbm]F'(x)=f(x)[/cbm] . Учитывая, что производная постоянной равна нулю, получаем:
[cbm](F(x)+C)’=F'(x)+C’=F'(x)=f(x).[/cbm]
Это и означает, что [cbm]F(x)+C[/cbm] является первообразной для [cbm]y=f(x)[/cbm] на промежутке [cbm]X[/cbm] .
Покажем теперь, что если функция [cbm]y=f(x)[/cbm] задана на промежутке [cbm]F[/cbm] и [cbm]F(x)[/cbm] — одна из первообразных для [cbm]f(x)[/cbm] , то любая первообразная [cbm]\Phi(x)[/cbm] может быть представлена в виде [cbm]\Phi(x)=F(x)+C[/cbm] .
В самом деле, по определению первообразной имеем: [cbm]\Phi'(x)=f(x)[/cbm] и [cbm]F'(x)=f(x)[/cbm] . Но две функции, имеющие на промежутке [cbm]X[/cbm] равные производные, отличаются лишь на постоянное слагаемое. Значит, [cbm]\Phi(x)=F(x)+C[/cbm] , что и требовалось доказать.
Определения неопределенного и определенного интегралов
Определение 2. Множество всех первообразных для функции [cbm]y=f(x)[/cbm] на промежутке [cbm]X[/cbm] называется неопределенным интегралом для [cbm]f(x)[/cbm] и обозначается [cbm]\textstyle{\int f(x)\,dx}[/cbm] .
Функцию [cbm]y=f(x)[/cbm] называют подынтегральной функцией для [cbm]\textstyle{\int f(x)\,dx}[/cbm] , а произведение [cbm]f(x)\,dx[/cbm] — подынтегральным выражением.
Таким образом, [cbm]\int f(x)\,dx=\{F(x)+C\mid C\in \mathbb{R}\}[/cbm] . На практике принята более короткая запись: [cbm]\int f(x)\,dx=F(x)+C[/cbm] .
Часто говорят: “взять неопределенный интеграл” или “вычислить неопределенный интеграл”, понимая под этим следующее: найти множество всех первообразных для подынтегральной функции.
Мы видели, что если функция имеет хоть одну первообразную, то она имеет бесконечно много первообразных. На практике часто приходится искать разность значений первообразной в точках [cbm]b[/cbm] и [cbm]a[/cbm] . Эта разность не зависит от выбора произвольной постоянной [cbm]C[/cbm] . В самом деле, если [cbm]\Phi(x)=F(x)+C[/cbm] , то
[cbm]\Phi(b)-\Phi(b)=(F(b)+C)-(F(a)+C)=F(b)-F(a).[/cbm]
Итак, [cbm]\Phi(b)-\Phi(b)=F(b)-F(a)[/cbm] , что и требовалось доказать.
Поскольку разность значений первообразной в точках [cbm]b[/cbm] и [cbm]a[/cbm] не зависит от того, какую именно первообразную функции [cbm]y=f(x)[/cbm] мы выбираем, эту разность называют определенным интегралом от функции по отрезку [cbm][a;b][/cbm] .
Определение 3. Пусть функция [cbm]y=f(x)[/cbm] задана на отрезке [cbm][a;b][/cbm] и имеет на нем первообразную [cbm]y=F(x)[/cbm] . Разность [cbm]F(b)-F(a)[/cbm] называют определенным интегралом функции [cbm]f(x)[/cbm] по отрезку [cbm][a;b][/cbm] и обозначают [cbm]\textstyle{\int\limits_{a}^{b}f(x)\,dx}[/cbm] . Итак,
[cbm]\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a).[/cbm]
Разность [cbm]F(b)-F(a)[/cbm] записывают в виде [cbm]\Bigl.{F(x)}\Bigr|_{a}^{b}[/cbm] , тогда [cbm]\textstyle{\int\limits_{a}^{b} f(x)\,dx= \Bigl.{F(x)}\Bigr|_{a}^{b}}[/cbm] . Числа [cbm]a[/cbm] и [cbm]b[/cbm] называют пределами интегрирования.
Например, [cbm]y=\frac{x^3}{3}[/cbm] одна из первообразных для функции [cbm]y=x^2[/cbm] . Поэтому
[cbm]\int\limits_{a}^{b}x^2\,dx=\left.{\frac{x^3}{3}}\right|_{a}^{b}=\frac{b^3}{3}-\frac{a^3}{3}=\frac{b^3-a^3}{3}\,.[/cbm]
Остановимся на геометрическом смысле введенных понятий. Пусть [cbm]F(x)[/cbm] является первообразной для [cbm]f(x)[/cbm] . Угловой коэффициент касательной в каждой точке графика функции [cbm]y=F(x)[/cbm] равен [cbm]F'(x)[/cbm] , т. е. [cbm]f(x)[/cbm] . Поэтому задача о нахождении первообразной геометрически означает следующее: зная угловой коэффициент касательной в каждой точке, найти кривую. Так как при параллельном переносе вдоль оси ординат угловой коэффициент касательной в точке с заданной абсциссой не изменяется, то, найдя одну такую кривую, все остальные искомые кривые получают из нее параллельным переносом в направлении оси ординат. Это семейство кривых (рис. 1) и представляет собой геометрическую иллюстрацию неопределенного интеграла.
Определенный интеграл [cbm]\textstyle{\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a)}[/cbm] показывает изменение ординаты каждой из кривых [cbm]y=F(x)+C[/cbm] при переходе от точки [cbm]a[/cbm] к точке [cbm]b[/cbm] . Так как все эти кривые получаются друг из друга параллельным переносом в направлении оси ординат, то указанное изменение ординаты для всех кривых одно и то же (рис. 2).

Рассмотрим задачи, решение которых сводится к вычислению определенных интегралов.
Задача 1. Пусть точка [cbm]M[/cbm] движется по прямой и пусть известна скорость [cbm]v=v(t)[/cbm] движения этой точки в любой момент [cbm]{x}[/cbm] времени [cbm]{t}[/cbm] промежутка [cbm][a;b][/cbm] . Найдем перемещение [cbm]{s}[/cbm] точки [cbm]M[/cbm] за этот промежуток времени.
Решение. Мы знаем, что если [cbm]x=x(t)[/cbm] — закон движения точки, то [cbm]v(t)=x'(t)[/cbm] . Поэтому [cbm]x(t)[/cbm] — одна из первообразных для функции [cbm]v=v(t)[/cbm] . Но перемещение [cbm]{s}[/cbm] точки [cbm]M[/cbm] за промежуток времени [cbm][a;b][/cbm] равно разности ее координат в моменты времени [cbm]b[/cbm] и [cbm]a[/cbm] , т.е. равно [cbm]x(b)-x(a)[/cbm] . Иными словами, это перемещение равно разности значений первообразной для функции [cbm]v=v(t)[/cbm] в моменты времени [cbm]b[/cbm] и [cbm]a[/cbm] . Таким образом, [cbm]s=\textstyle{\int\limits_{a}^{b}v(t)\,dt}[/cbm] .
Так, например, скорость тела при свободном падении выражают формулой [cbm]v=gt[/cbm] . В этом случае путь, пройденный падающим телом за [cbm]b[/cbm] секунд с начала падения, вычисляется так:
[cbm]s=\int\limits_{0}^{b}gt\,dt= \left.{\frac{gt^2}{2} }\right|_{0}^{b}= \frac{gb^2}{2}\,.[/cbm]
Задача 2. Найдем площадь криволинейной трапеции [cbm]aA\,Bb[/cbm] , ограниченной осью абсцисс, прямыми [cbm]x=a[/cbm] и [cbm]x=b[/cbm] и графиком непрерывной на [cbm][a;b][/cbm] функции [cbm]y=f(x)[/cbm] , принимающей на этом отрезке только неотрицательные значения (рис. 3).
Прежде чем переходить к решению задачи, заметим, что здесь мы используем наглядное представление о площади плоской фигуры (более детально вопрос об определении площади).
Решение. Обозначим через [cbm]S(x)[/cbm] площадь криволинейной трапеции [cbm]aA\,Nx\,(a<x<b)[/cbm] . Докажем, что [cbm]S'(x)=f(x)[/cbm] .
Дадим абсциссе [cbm]x[/cbm] приращение [cbm]\Delta x[/cbm] (положим для определенности [cbm]\Delta x>0[/cbm] ), тогда площадь получит приращение [cbm]\Delta S[/cbm] . Обозначим через [cbm]m[/cbm] наименьшее значение функции [cbm]y=f(x)[/cbm] на отрезке [cbm][a;b][/cbm] , а через [cbm]M[/cbm] — наибольшее значение той же функции на том же отрезке. Ясно, что тогда [cbm]m\cdot\Delta x\leqslant\Delta S\leqslant M\cdot\Delta x[/cbm] , а значит, [cbm]m\leqslant\frac{\Delta S}{\Delta x}\leqslant M[/cbm] .
Если [cbm]\Delta x\to 0[/cbm] , то в силу непрерывности функции [cbm]y=f(x)[/cbm] будем иметь:
[cbm]\lim_{\Delta x\to0}m=\lim_{\Delta x\to0}=f(x).[/cbm]
Значит, существует и [cbm]\lim\frac{\Delta S}{\Delta x}[/cbm] , причем этот предел равен [cbm]f(x)[/cbm] . Таким образом, [cbm]S'(x)=f(x)[/cbm] .
Полученное равенство означает, что [cbm]S(x)[/cbm] — одна из первообразных для функции [cbm]y=f(x)[/cbm] . Поскольку прямая [cbm]x=a[/cbm] “отсекает” от трапеции [cbm]aABb[/cbm] фигуру нулевой площади, то [cbm]S(a)=0[/cbm] . С другой стороны, [cbm]S(b)[/cbm] — площадь всей криволинейной трапеции [cbm]aABb[/cbm] . Значит, искомая площадь [cbm]S[/cbm] равна [cbm](S(b)-S(a))[/cbm] , т.е. равна разности значений одной из первообразных для функции [cbm]y=f(x)[/cbm] в точках [cbm]b[/cbm] и [cbm]a[/cbm] . Это означает, что
[cbm]\boldsymbol{S=\int\limits_{a}^{b}f(x)\,dx\,.}[/cbm]
Пример 2. Найдем площадь фигуры, ограниченной осью абсцисс и одной полуволной синусоиды [cbm]y=\sin{x}[/cbm] (рис. 4).
Решение. Искомая площадь [cbm]S[/cbm] выражается формулой [cbm]\textstyle{S= \int\limits_{0}^{\pi}\sin{x}\,dx}[/cbm] . Одной из первообразных для функции [cbm]y=\sin{x}[/cbm] является [cbm](-\cos{x})[/cbm] , так как [cbm](-\cos{x})’=\sin{x})[/cbm] . Значит,
[cbm]S= \int\limits_{0}^{\pi}\sin{x}\,dx=\Bigl.{-\cos{x}}\Bigr|_{0}^{\pi}= -(\cos\pi-\cos0)=-(-1-1)=2.[/cbm]
В заключение данного пункта остановимся на двух свойствах неопределенного интеграла, легко получающихся из определения.
1°. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
[cbm]d\!\left(\int f(x)\,dx\right)= f(x)\,dx,\quad \left(\int f(x)\,dx\right)’=f(x).[/cbm]
Доказательство. Так как [cbm]\textstyle{\int f(x)\,dx=F(x)+C}[/cbm] , где [cbm]F'(x)=f(x)[/cbm] , то [cbm]\textstyle{\left(\int f(x)\,dx\right)’= \bigl(F(x)+C\bigr)’=F'(x)+C’=f(x)}[/cbm] .
Но тогда [cbm]\textstyle{d\!\left(\int f(x)\,dx\right)= \left(\int f(x)\,dx\right)’dx=f(x)\,dx}[/cbm] .
Это утверждение часто используется для проверки результата интегрирования. Пусть, например, нужно показать, что
[cbm]\int5x\,dx=\frac{5}{2}\,x^2+C\quad (C=\text{const}).[/cbm]
Дифференцируя правую часть равенства, получим подынтегральную функцию:
[cbm]\left(\frac{5}{2}\,x^2+C\right)’=\frac{5}{2}\cdot 2x+0=5x[/cbm] . Значит, [cbm]\int5x\,dx=\frac{5}{2}\,x^2+C[/cbm] .
2°. Неопределенный интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной:
[cbm]\int F'(x)\,dx=F(x)+C.[/cbm]
Доказательство. Так как [cbm]\bigl(F(x)+C\bigr)’=F'(x)[/cbm] , то по определению неопределенного интеграла [cbm]\textstyle{\int F'(x)\,dx=F(x)+C}[/cbm] , что и требовалось доказать.
Учитывая, что [cbm]F'(x)\,dx=d\bigl(F(x)\bigr)[/cbm] , свойство 2° можно записать и так: [cbm]\textstyle{\int d\bigl(F(x)\bigr)=F(x)+C}[/cbm] .
Таблица основных интегралов
Пользуясь свойством 1° из предыдущего пункта, можно по таблице производных составить таблицу основных интегралов. Например, так как
[cbm](\sin{x})’=\cos{x}[/cbm] , то [cbm]\int\cos{x}\,dx=\sin{x}+C.[/cbm] .
Докажем, что [cbm]\int\dfrac{1}{x}\,dx=\ln|x|+C[/cbm] . В самом деле, если [cbm]x>0[/cbm] , то [cbm]|x|=x[/cbm] и, следовательно, [cbm]\bigl(\ln|x|\bigr)’=\bigl(\ln{x}\bigr)’=\frac{1}{x}\,[/cbm] .
Если [cbm]x<0[/cbm] , то [cbm]|x|=-x[/cbm] и, следовательно, [cbm]\bigl(\ln|x|\bigr)’=\bigl(\ln(-x)\bigr)’= \frac{1}{-x}\cdot(-1)=\frac{1}{x}[/cbm] .
Итак, [cbm]\bigl(\ln|x|\bigr)’=\frac{1}{x}[/cbm] , а значит, [cbm]\int\frac{1}{x}\,dx=\ln|x|+C[/cbm] .
Эту формулу можно применять или на открытом луче [cbm](0;+\infty)[/cbm] , или на открытом луче [cbm](-\infty;0)[/cbm] .
Таблица основных интегралов
[cbm]\begin{aligned}&\boldsymbol{1.}\quad \int 0\,dx=C; &\quad &\boldsymbol{2.}\quad \int 1\,dx=\int dx=x+C;\\ &\boldsymbol{3.}\quad \int x^{a}\,dx=\frac{x^{a+1}}{a+1}+C,~a\ne-1; &\quad &\boldsymbol{4.}\quad \int \frac{dx}{x}=\ln{x}+C;\\ &\boldsymbol{5.}\quad \int \frac{dx}{a^2+x^2}=\frac{1}{a}\operatorname{arctg}\frac{x}{a}+C; &\quad &\boldsymbol{6.}\quad \int \frac{dx}{\sqrt{a^2-x^2}}=\arcsin\frac{x}{a}+C;\\ &\boldsymbol{7.}\quad \int a^x\,dx=\frac{a^x}{\ln a}+C; &\quad &\boldsymbol{8.}\quad \int e^x\,dx=e^x+C;\\ &\boldsymbol{9.}\quad \int \sin{x}\,dx=-\cos{x}+C; &\quad &\boldsymbol{10.}\quad \int \cos{x}\,dx=\sin{x}+C;\\ &\boldsymbol{11.}\quad \int \frac{dx}{\sin^2x}=-\operatorname{ctg}x+C; &\quad &\boldsymbol{12.}\quad \int \frac{dx}{\cos^2x}=\operatorname{tg}x+C;\\ &\boldsymbol{13.}\quad \int \frac{dx}{x^2-a^2}=\frac{1}{2a}\ln\! \left|\frac{x-a}{x+a}\right|+C; &\quad &\boldsymbol{14.}\quad \int \frac{dx}{\sqrt{x^2\pm a^2}}=\ln \bigl|x+\sqrt{x^2\pm a^2}\bigr|+C.\\ \end{aligned}[/cbm]
Заметим, что переменную [cbm]x[/cbm] , входящую в эти формулы, можно заменить любой другой. Например, вместо формулы [cbm]\textstyle{\int\cos{x}\,dx= \sin{x}+C}[/cbm] можно написать [cbm]\textstyle{\int\cos{t}\,dt= \sin{t}+C}[/cbm] и т.д.
Пример 3. Вычислим неопределённые интегралы от различных дробей:
[cbm]\mathsf{1)}~\int\frac{dx}{\sqrt[3]{x}}\,;\quad \mathsf{2)}~\int\frac{dx}{x^2+16}\,;\quad \mathsf{3)}~\int\frac{dx}{x^2-16}\,;\quad \mathsf{4)}~\int\frac{dx}{\sqrt{3-x^2}}\,;\quad \mathsf{5)}~\int\frac{dx}{\sqrt{x^2-3}}\,.[/cbm]
Решение. 1) Воспользуемся формулой 3 из таблицы интегралов:
[cbm]\int\frac{dx}{\sqrt[3]{x}}= \int x^{-1/3}\,dx= \frac{x^{-1/3+1}}{-1/3+1}+C= \frac{3}{2}\,x^{2/3}+C;[/cbm]
2) Воспользуемся формулой 5: [cbm]\int\frac{dx}{x^2+16}= \int\frac{dx}{x^2+4^2}=\frac{1}{4} \operatorname{arctg}\frac{x}{2}+C;[/cbm] .
3) Воспользуемся формулой 12: [cbm]\int\frac{dx}{x^2-16}= \int\frac{dx}{x^2-4^2}= \frac{1}{8}\ln\!\left|\frac{x-4}{x+4}\right|+C;[/cbm] .
4) Воспользуемся формулой 6: [cbm]\int\frac{dx}{\sqrt{3-x^2}}= \int\frac{dx}{\sqrt{(\sqrt{3})^2-x^2}}= \arcsin\frac{x}{\sqrt{3}}+C;[/cbm] .
5) Воспользуемся формулой 13: [cbm]\int\frac{dx}{\sqrt{x^2-3}}= \ln\Bigl|x+\sqrt{x^2-3}\Bigr|+C.[/cbm] .
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
calcsbox.com
Первообразная. Неопределённый и определённый интегралы.(Беспалов Е.Г.)
Первообразная
Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого .
Операция нахождения первообразной функции f(x), называется интегрированием.
Неопределенный интеграл
Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:
,
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.
Дифференциал-произвольное, бесконечно малое приращение переменной величины.
Свойства неопределённого интеграла
Таблица основных неопределённых интегралов
В виде
,
где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.

Определённый интеграл
Определенный интеграл– Приращение одной из первообразных функции f(x) на отрезке [a;b].
Общий вид определённого интеграла:
где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал
Свойства определённого интеграла: см. св-ва определённого интеграла.
Определённый интеграл вычисляется по формуле Ньютона –Лейбница:
Применение определённого интеграла:
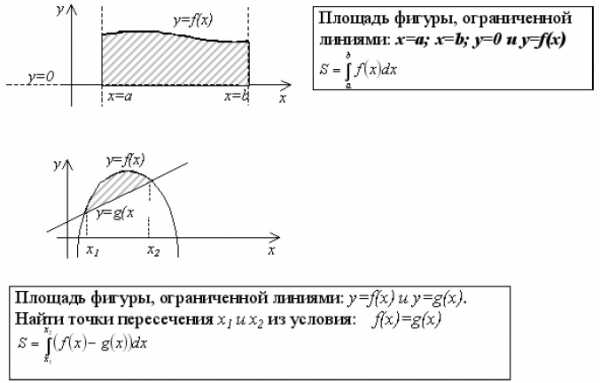
1. Нахождение площади криволинейной трапеции
2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е
Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.
Решение:
3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.
Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.
Решение:
Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.
ya-znau.ru
Неопределенный и определенный интеграл Понятие первообразной и неопределенный интеграл
Функция  называетсяпервообразной
функцией для функции
называетсяпервообразной
функцией для функции  на промежутке
на промежутке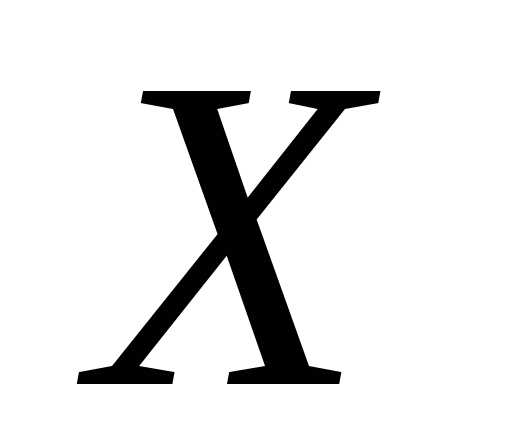 ,
если в каждой точке этого промежутка.
,
если в каждой точке этого промежутка.
Пример. А) 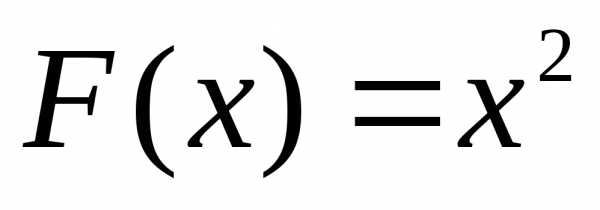 является первообразной для,
т.к..
Б)является первообразной для,
т.к..
является первообразной для,
т.к..
Б)является первообразной для,
т.к..
Если
для функции  существует первообразная
существует первообразная ,
то она не является единственной. Например,
функции
,
то она не является единственной. Например,
функции ,
, и вообще
и вообще (
(
некоторая произвольная постоянная)
являются первообразными для функции
.
Таким образом можно сформулировать
следующую теорему.
некоторая произвольная постоянная)
являются первообразными для функции
.
Таким образом можно сформулировать
следующую теорему.
Теорема. Если 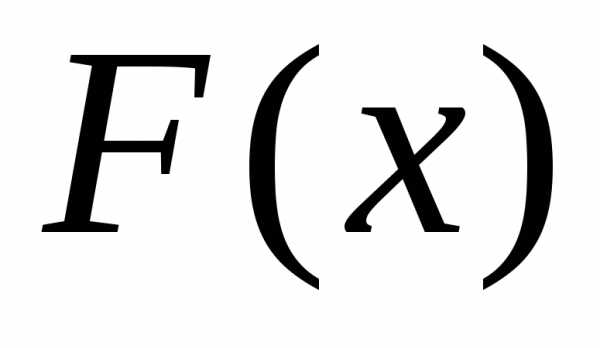 и
и
первообразные для функции
первообразные для функции 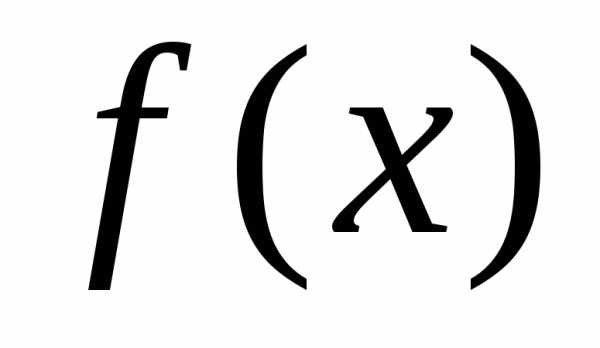 на некотором промежутке
на некотором промежутке ,
то найдется такое число
,
то найдется такое число ,
что будет справедливо равенство:.
,
что будет справедливо равенство:.
Из
данной теоремы следует, что, если 
первообразная для функции
первообразная для функции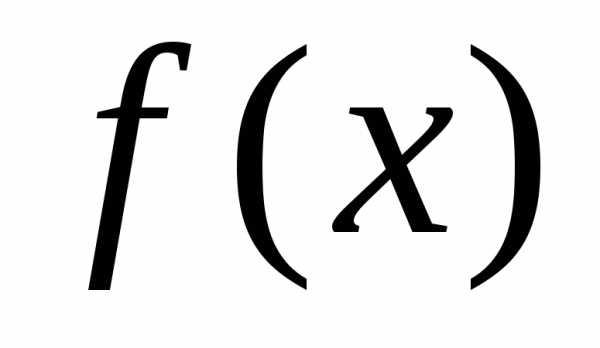 ,
то выражение вида,
где
,
то выражение вида,
где
произвольное число, задает все возможные
первообразные для
произвольное число, задает все возможные
первообразные для 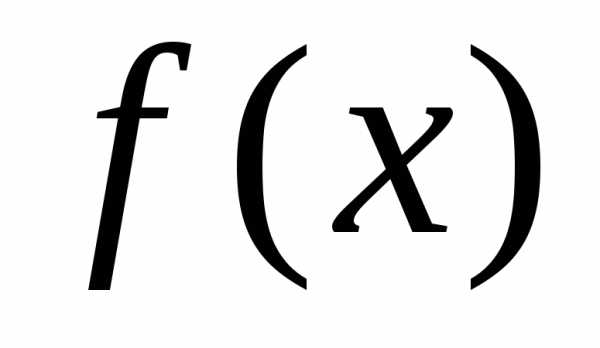 .
.
Совокупность
всех первообразных функции 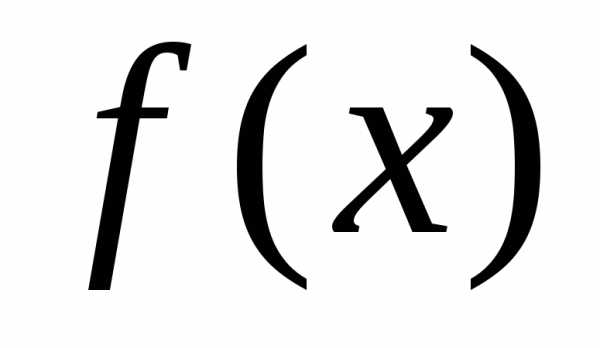 на промежутке
на промежутке называетсянеопределенным
интегралом от функции
называетсянеопределенным
интегралом от функции  и обозначается,
где
и обозначается,
где
знак интеграла,
знак интеграла, 
подынтегральная функция,
подынтегральная функция, 
подынтегральное выражение,
подынтегральное выражение, 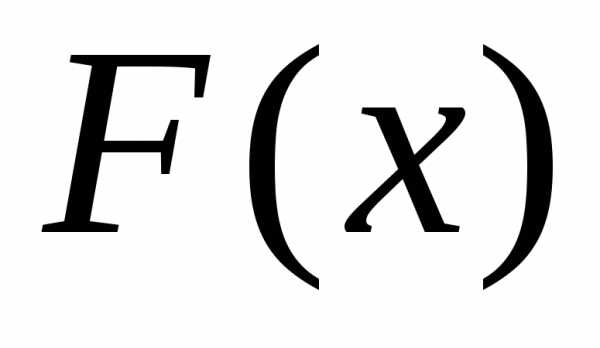
некоторая первообразная для
некоторая первообразная для  ,
,
произвольная постоянная.
произвольная постоянная.
Операция нахождения неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции. Данная операция является обратной для операции дифференцирования.
Правила интегрирования неопределенного интеграла:
Производная от неопределенного интеграла равна подынтегральной функции, т.е. .
Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. .
Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .
Постоянный множитель можно выносить за знак интеграла, т.е. , где

некоторое число.
некоторое число.Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .
Таблица простейших интегралов
Основные методы интегрирования неопределенного интеграла:
Непосредственное интегрирование. Вычисление интегралов с использованием основных правил и таблицы простейших интегралов.
Пример. Найти  .
.
Пример. Найти  .
.
Метод замены переменной (метод подстановки). Данный метод основан на следующей теореме: Пусть функция
 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке  ,
а
,
а 
множество значений этой функции, на
котором определена функция
множество значений этой функции, на
котором определена функция  .
Тогда если
,
то получаем или .
.
Тогда если
,
то получаем или .
Пусть
заданный интеграл 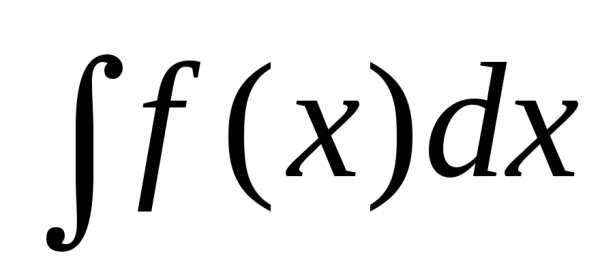 не может быть непосредственно преобразован
к табличному интегралу. Введем новую
переменную
не может быть непосредственно преобразован
к табличному интегралу. Введем новую
переменную :
:  .
Тогда , ,
т.е.
.
.
Тогда , ,
т.е.
.
Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, свести его к табличному.
Замечание. Новую переменную можно не выписывать явно, а производить преобразования функции под знаком дифференциала (путем введения постоянных и переменных под знак дифференциала).
Теорема. Пусть  некоторая первообразная для функции
некоторая первообразная для функции  .
Тогда если вместо аргумента
.
Тогда если вместо аргумента  подынтегральной функции
подынтегральной функции  и первообразной
и первообразной  подставить выражение
подставить выражение  ,
то это приведет к появлению дополнительного
множителя
,
то это приведет к появлению дополнительного
множителя  перед первообразной:
,
где
перед первообразной:
,
где  и
и 
некоторые числа,
некоторые числа, 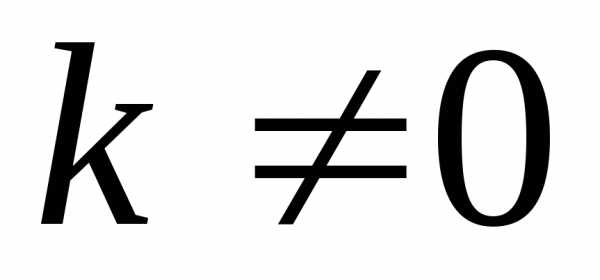 .
.
Алгоритм метода:
Делаем замену.
Дифференцируем замену .
Под знаком интеграла переходим к новой переменной.
Находим табличный интеграл.
Возвращаемся к старой переменной.
Пример. Найти 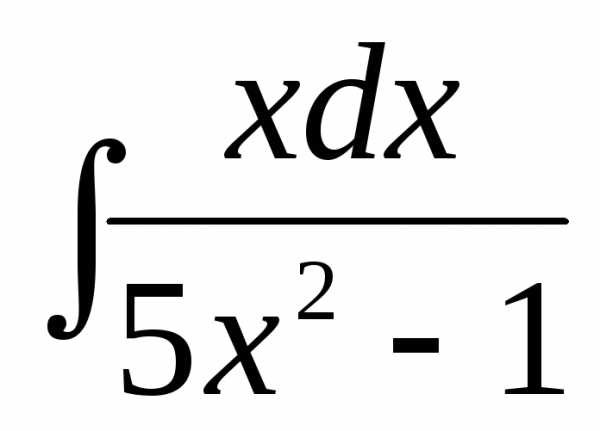 .
.
Метод интегрирования по частям. Метод основан на теореме: Пусть функции
 и
и  определены и дифференцируемы на
промежутке
определены и дифференцируемы на
промежутке  ,
и функция имеет первообразную на этом промежутке.
Тогда функция также имеет первообразную на промежутке
,
и функция имеет первообразную на этом промежутке.
Тогда функция также имеет первообразную на промежутке  ,
причем справедлива формула.
Учитывая, что,
получим.
,
причем справедлива формула.
Учитывая, что,
получим.
Интегрирование
по частям состоит в том, что подынтегральное
выражение  представляется каким-либо образом в
виде произведения двух множителей
представляется каким-либо образом в
виде произведения двух множителей  и
и  (последний обязательно содержит
(последний обязательно содержит  )
и согласно формуле данное интегрирование
заменяется двумя:
)
и согласно формуле данное интегрирование
заменяется двумя:
1)
при отыскании  из выражения для
из выражения для  ;
;
2)
при отыскании интеграла от  .
.
Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.
Замечание. За  нужно брать то, что после дифференцирования
упрощается.
нужно брать то, что после дифференцирования
упрощается.
Пример. Найти  .
.
Пример. Найти .
studfiles.net
Свойства интегралов (неопределённых и определённых)
Свойства неопределенного интеграла
Вычисление многих интегралов сводится к табличным, если использовать свойства неопределенных интегралов, вытекающие из соответствующих свойств дифференциалов. Рассмотрим некоторые из них:
а) Постоянный множитель можно вынести за знак неопределенного интеграла:
[cbm]\int\lambda\,f(x)\,dx= \lambda\int f(x)\,dx\,.[/cbm](1)
Доказательство. Продифференцировав правую часть равенства, получаем:
[cbm]d\!\left(\lambda\int f(x)\,dx\right)= \lambda\,d\!\left(\int f(x)\,dx\right)= \lambda\,f(x)\,dx\,.[/cbm]
Таким образом, дифференциал правой части доказываемой формулы равен подынтегральному выражению левой части, а это и означает справедливость формулы (1).
б) Если существуют интегралы [cbm]\textstyle{\int f_1(x)\,dx}[/cbm] и [cbm]\textstyle{\int f_2(x)\,dx}[/cbm] , то не определенный интеграл суммы [cbm]f_1(x)+f_2(x)[/cbm] равен сумме неопределенных интегралов от этих функций:
[cbm]\int\Bigl(f_1(x)+f_2(x)\Bigr)dx= \int f_1(x)\,dx+\int f_2(x)\,dx\,.[/cbm](2)
Доказательство. Продифференцируем правую часть равенства (2):
[cbm]\begin{aligned} d\!\left(\int f_1(x)\,dx+\int f_2(x)\,dx\right)&= d\!\left(\int f_1(x)\,dx\right)+ d\!\left(\int f_2(x)\,dx\right)=\\[2pt] &=f_1(x)\,dx+f_2(x)\,dx= \Bigl(f_1(x)+f_2(x)\Bigr)dx\,. \end{aligned}[/cbm]
Мы получили подынтегральное выражение неопределенного интеграла, стоящего в левой части равенства (2), откуда и следует справедливость утверждения.
Пример 4. Вычислим неопределенный интеграл [cbm]\int\frac{x\sqrt{x}+x^2-5}{x^2\sqrt{x}}\,dx[/cbm] .
Решение. Разделив почленно числитель на знаменатель и использовав свойство б), получаем табличные интегралы:
[cbm]\begin{aligned}\int\frac{x\sqrt{x}+x^2-5}{x^2\sqrt{x}}\,dx&= \int\!\left(\frac{1}{x}+ \frac{1}{\sqrt{x}}-\frac{5}{x^2\sqrt{x}}\right)\!dx= \int\frac{dx}{x}+\int x^{-1/2}\,dx-5\int x^{-5/2}\,dx=\\[2pt] &=\ln|x|+\frac{x^{-1/2+1}}{-1/2+1}-5\,\frac{x^{-5/2+1}}{-5/2+1}+C= \ln|x|+2\sqrt{x}+\frac{10}{3x\sqrt{x}}+C. \end{aligned}[/cbm]
Замечание. Каждый из трех неопределенных интегралов содержит свою произвольную постоянную. В окончательном ответе через [cbm]C[/cbm] обозначают их сумму, которая также является произвольной постоянной.
Пример 5. Вычислим интеграл от тригонометрической функции [cbm]\int\frac{dx}{\sin^2x\cos^2x}[/cbm] .
Решение. Записав единицу, стоящую в числителе [cbm](dx=1\cdot dx)[/cbm] , в тригонометрическом виде [cbm]\bigl(1=\sin^2x+\cos^2x\bigr)[/cbm] , разделим числитель почленно на знаменатель. Применив затем свойство б), получим:
[cbm]\int\frac{dx}{\sin^2x\cos^2x}= \int\!\left(\frac{1}{\cos^2x}+\frac{1}{\sin^2x}\right)\!dx= \int\frac{dx}{\cos^2x}+\int\frac{dx}{\sin^2x}= \operatorname{tg}x-\operatorname{ctg}x+C.[/cbm]
Пример 6. Вычислим интеграл от иррациональной функции [cbm]\int\Bigl(1+\sqrt[3]{x}\Bigr)^3dx[/cbm] .
Решение. Раскроем скобки по формуле куба суммы [cbm](a+b)^3=a^3+3a^2b+3ab^2+b^3[/cbm] , перейдем к дробным показателям, а затем применим правила интегрирования:
[cbm]\begin{aligned}\int\Bigl(1+\sqrt[3]{x}\Bigr)^3dx&= \int\Bigl(1+3\sqrt[3]{x}+3\sqrt[3]{x^2}+x\Bigr)dx= \int\Bigl(1+3x^{1/3}+3x^{2/3}+x\Bigr)dx=\\ &=\int dx+3\int x^{2/3}\,dx+\int x\,dx= x+3\,\frac{x^{1/3+1}}{1/3+1}+ 3\,\frac{x^{2/3+1}}{2/3+1}+ \frac{x^2}{2}+C=\\ & =x+\frac{9}{4}x\sqrt[3]{x}+\frac{9}{5}x\sqrt[3]{x^2}+ \frac{x^2}{2}+C. \end{aligned}[/cbm]
Свойства определенного интеграла
Так как определенный интеграл равен разности значений первообразной, та его свойства выводятся из свойств неопределенного интеграла.
а) Если существует [cbm]\int\limits_{a}^{b}f(x)\,dx[/cbm] и [cbm]\lambda[/cbm] — любое число, то [cbm]\int\limits_{a}^{b}\lambda f(x)\,dx= \lambda\int\limits_{a}^{b}f(x)\,dx[/cbm] .
Доказательство. Из соответствующего свойства неопределенных интегралов следует, что если [cbm]F(x)[/cbm] — первообразная для [cbm]f(x)[/cbm] , то [cbm]\lambda F(x)[/cbm] — первообразная для [cbm]\lambda f(x)[/cbm] . Значит,
[cbm]\int\limits_{a}^{b}\lambda f(x)\,dx=\Bigl.{\lambda F(x)}\Bigr|_{a}^{b}= \lambda F(b)-\lambda F(a)=\lambda \Bigl(F(b)-F(a)\Bigr)= \lambda \int\limits_{a}^{b}f(x)\,dx\,.[/cbm]
б) Если функции [cbm]y=f_1(x)[/cbm] и [cbm]y=f_2(x)[/cbm] имеют первообразные на отрезке [cbm][a;b][/cbm] , то
[cbm]\int\limits_{a}^{b}\Bigl(f_1(x)+f_2(x)\Bigr)dx= \int\limits_{a}^{b}f_1(x)\,dx+ \int\limits_{a}^{b}f_2(x)\,dx\,.[/cbm]
Доказательство. Из соответствующего свойства неопределенных интегралов следует, что если [cbm]F_1(x)[/cbm] — первообразная для [cbm]f_1(x)[/cbm] , a [cbm]F_2(x)[/cbm] — первообразная для [cbm]f_2(x)[/cbm] на отрезке [cbm][a;b][/cbm] , то [cbm]F_1(x)+F_2(x)[/cbm] — первообразная для [cbm]f_1(x)+f_2(x)[/cbm] . Значит,
[cbm]\begin{aligned}\int\limits_{a}^{b}\Bigl(f_1(x)+f_2(x)\Bigr)dx&= \left.{\Bigl(F_1(x)+ F_2(x)\Bigr)}\right|_{a}^{b}= \Bigl(F_1(b)+F_2(b)\Bigr)-\Bigl(F_1(a)+F_2(a)\Bigr)=\\[-8pt] &=\Bigl(F_1(b)-F_1(a)\Bigr)+\Bigl(F_2(b)-F_2(a)\Bigr) =\int\limits_{a}^{b}f_1(x)\,dx+ \int\limits_{a}^{b} f_2(x)\,dx\,.\end{aligned}[/cbm]
в) Если функция [cbm]f(x)[/cbm] имеет первообразную на отрезке [cbm][a;b][/cbm] и если [cbm]a<c<b[/cbm] , то (аддитивное свойство определенного интеграла)
[cbm]\int\limits_{a}^{b}f(x)\,dx= \int\limits_{a}^{c}f(x)\,dx+ \int\limits_{c}^{b} f(x)\,dx\,.[/cbm]
Доказательство. Пусть [cbm]F(x)[/cbm] — первообразная для [cbm]f(x)[/cbm] . Тогда
[cbm]\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a),~~ \int\limits_{a}^{c}f(x)\,dx=F(c)-F(a),~~ \int\limits_{c}^{b}f(x)\,dx=F(b)-F(c).[/cbm]
Но [cbm]F(b)-F(a)=\bigl(F(c)-F(a)\bigr)+\bigl(F(b)-F(c)\bigr)[/cbm] . Значит,
[cbm]\int\limits_{a}^{b}f(x)\,dx= \int\limits_{a}^{c}f(x)\,dx+ \int\limits_{c}^{b} f(x)\,dx\,,[/cbm]
что и требовалось доказать.Доказанное свойство имеет простой геометрический смысл: оно выражает аддитивность площади криволинейной трапеции. Так, на рисунке 5
[cbm]S_{aABb}= \int\limits_{a}^{b}f(x)\,dx;\quad S_1=\int\limits_{a}^{c}f(x)\,dx;\quad S_2=\int\limits_{c}^{b}f(x)\,dx[/cbm] . Тогда [cbm]s_{aABb}=S_1+S_2[/cbm] .
г) Если функция [cbm]y=f(x)[/cbm] имеет первообразную на отрезке [cbm][a;b][/cbm] , то справедливо равенство
[cbm]\int\limits_{a}^{b}f(x)\,dx= -\int\limits_{b}^{a}f(x)\,dx\,.[/cbm]
Доказательство. Пусть [cbm]F(x)[/cbm] — первообразная для [cbm]f(x)[/cbm] . Тогда
[cbm]\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a),\qquad \int\limits_{b}^{a}f(x)\,dx=F(a)-F(b).[/cbm]
Но [cbm]F(b)-F(a)=-\bigl(F(a)-F(b)\bigr)[/cbm] , откуда и следует доказываемое утверждение.
д) [cbm]\int\limits_{a}^{a}f(x)\,dx=0[/cbm] . Доказательство: [cbm]\int\limits_{a}^{a}f(x)\,dx=F(a)-F(a)=0[/cbm] .
Пример 7. Вычислить интеграл от рациональной дроби: [cbm]\int\limits_{0}^{3} \frac{x^4}{x^2+1}\,dx[/cbm] .
Решение. Сначала выделим целую часть неправильной дроби, содержащейся под знаком интеграла:
[cbm]\int\limits_{0}^{3} \frac{x^4}{x^2+1}\,dx= \int\limits_{0}^{3} \frac{(x^4-1)+1}{x^2+1}\,dx= \int\limits_{0}^{3} \frac{(x^2-1)(x^2+1)+1}{x^2+1}\,dx= \int\limits_{0}^{3} \!\left(x^2-1+\frac{1}{x^2+1}\right)\!dx\,.[/cbm]
Воспользовавшись теперь свойством б) определенного интеграла, получим:
[cbm]\begin{aligned}\int\limits_{0}^{3} \!\left(x^2-1+\frac{1}{x^2+1}\right)\!dx&= \int\limits_{0}^{3}x^2\,dx-\int\limits_{0}^{3}dx+\int\limits_{0}^{3}\frac{dx}{x^2+1}= \left.{\frac{x^3}{3}}\right|_{0}^{3}- \Bigl.{x}\Bigr|_{0}^{3}+ \Bigl.{\operatorname{arctg}x}\Bigr|_{0}^{3}=\\ &=(9-0)-(3-0)+ (\operatorname{arctg}3- \operatorname{arctg}0)= 6+\operatorname{arctg}3.\end{aligned}[/cbm]
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
calcsbox.com
Неопределенный интеграл. История интеграла. Неопределенный интеграл x 2.
Интеграл является важной частью дифференциального исчисления. Интегралы могут быть двойные, тройные и т.д. Для нахождения площади поверхности и объема геометрических тел используются различные типы интегралов.Неопределенный интеграл имеет вид: \(∫f (x)\, dx\) и определенный интеграла имеет вид: \(\int_a^b \! f (x)\, dx\)
Область плоскости, ограниченной графиком определенный интеграла:

Операции интегрирования обратны дифференцированию. По этой причине надо вспомнить первообразную, функцию, таблицу производных .
Функция \( F (x) = x^2\) является первообразной для функции \(f ( х ) = 2х\). Функции \(f ( х ) = x^2+2\) и \(f ( х ) = x^2+7\) также является первообразными для функции \(f ( х ) = 2х\). \(2\) и \(7-\) это константы, производные которых равны нулю, поэтому мы можем подставлять их сколько угодно, значение первообразной не изменится. Для записи неопределенного интеграла использует знак \( ∫\). Неопределенный интеграл – это совокупность всех первообразных функции \(f ( х ) = 2х\). Операции интегрирования обратны дифференцированию. \(∫2x = x^2+C\), где \(C\) это константа интегрирования, то есть если мы вычислим производную \(x^2\), то получим \(2x\), а это и есть \( ∫2x\). Легко, не правда ли? Если вы не поняли, то вам надо повторить производную функции. Теперь мы можем вывести формулу по которой мы будем вычислять интеграл: \(∫u^ndu=\frac{u^n+1} {n+1}, n ≠ -1\). мы вычитали 1, теперь мы прибавляем 1 , n не может быть равно 0. Также существуют другие правила интегрирования для других основных функций которые надо выучить:

Решение неопределенного интеграла это обратный процесс нахождения первообразных дифференциального уравнения. Мы находим функцию, производная которой является интегралом, и не забываем добавлять “+ C” в конце.
Принципы интегрального исчесления были сформулированы независимо друг от друга Исааком Ньютоном и Готфридом Лейбницем в конце 17-го века. Бернхард Риман дал строгое математическое определение интегралов. Первым документированным систематическим методом, способным определять интегралы, является метод исчесления древнегреческого астронома Евдокса , который пытался найти площади и объемы, разбив их на бесконечное число известных площадей и объемов. Этот метод был далее разработан и использован Архимедом в 3-м веке до н. э. и использовался для расчета площадей парабол и приближения к площади круга.
Аналогичный метод был независимо разработан в Китае около 3-го века нашей эры Лю Хуэем, который использовал его, чтобы найти площадь круга. Этот метод позже был использован в 5-м веке китайскими математиками-отцом и сыном ЗУ Чунчжи и ЗУ Генгом, чтобы найти объем сферы.
Следующие значимые достижения в интегральном исчислении не появлялись до 17-го века. В это время работы Кавальери и Ферма начали закладывать основы современного исчисления.
В частности, фундаментальная теорема исчисления интегралов позволяет решать гораздо более широкий класс задач. Равным по важности является комплексная математическая структура, которую разработали Ньютон и Лейбниц. Эта структура интегралов взята непосредственно из работы Лейбница и стала современным интегральным исчислением.Исчисление было изменено Риманом, используя пределы. Впоследствии были рассмотрены более общие функции, особенно в контексте анализа Фурье, к которым определение Римана не применяется. Лебег сформулировал другое определение интеграла, основанное в теории мер (подполе реального анализа).
Современное обозначение неопределенного интеграла было введено Готфридом Лейбницем в 1675 году.
Интегралы широко используются во многих областях математики. Например, в теории вероятностей интегралы используются для определения вероятности попадания некоторой случайной величины в определенный диапазон.
Интегралы могут быть использованы для вычисления площади двумерной области, имеющей криволинейную границу, а также для вычисления объема трехмерного объекта, имеющего криволинейную границу.
Интегралы используются в физике, в таких областях, как кинематика, чтобы найти перемещение, время и скорость.
myalfaschool.ru
Неопределенный и определенный интегралы
Неопределенный и определенный интегралыНеопределённый интеграл.
Определение. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной дляF(x), т.е. .
Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x ) требуется найти функцию F(x), производная которой равна f(x).
Первообразная определена неоднозначно: для функции первообразными будут и функция arctg x, и функция arctg x-10: . Для того, чтобы описать все множество первообразных функции f(x), рассмотрим
Свойства первообразной.
1. Если функция F(x) – первообразная для функции f(x) на интервале X, то функция f(x) + C, где C – произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во: ).
2. Если функция F(x) – некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F1(x) может быть представлена в виде F1(x) = F(x) + C, где C – постоянная на X функция.
Из этих свойств следует, что если F(x) – некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C – произвольная постоянная.
Неопределённый интеграл и его свойства.
Определение. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .
Как следует из изложенного выше, если F(x) – некоторая первообразная функции f(x), то , где C – произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx – подынтегральным выражением.
Свойства неопределённого интеграла, непосредственно следующие из определения:
1. .
2. (или ).
Таблица неопределённых интегралов.
В формулах 14, 15, 16, 19 предполагается, что a>0. Каждая из формул таблицы справедлива на любом интервале, на котором непрерывна подынтегральная функция. Все эти формулы можно доказать дифференцированием правой части. Докажем, например, формулу 4: если x > 0, то ; если x < 0, то .
Простейшие правила интегрирования.
1. ( )
2.
Определённый интеграл
Определение определённого интеграла. Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 ,xi], …, [xn-1 , xn]; длину i-го отрезка обозначим : ; максимальную из длин отрезков обозначим . На каждом из отрезков [xi-1 , xi] выберем произвольную точку и составим сумму .
Сумма называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм при , не зависящий ни от способа разбиения отрезка [a,b]на части [xi-1 , xi], ни от выбора точек , то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается .
Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b – соответственно, нижним и верхним пределами интегрирования.
Кратко определение иногда записывают так: .
В этом определении предполагается, что b> a. Для других случаев примем, тоже по определению:
Если b=a, то ; еслиb<a, то .
Свойства определённого интеграла.
1. Линейность. Если функции f(x), g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и
.
2. Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то .
При формулировании следующих свойств предполагаем, что b > a.
3. Интеграл от единичной функции ( f(x) = 1). Если f(x) = 1, то .
Вычисление определённого интеграла.
Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) – некоторая первообразная функции , то .
Пример применения формулы Ньютона-Лейбница:
.
Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) – непрерывно дифференцируемые функции, то
Пример: .
Дата добавления: 2015-08-20; просмотров: 66 | Нарушение авторских прав
Определение убывающей функции. | Точки экстремума, экстремумы функции. | Достаточные условия возрастания и убывания функции. | Первое достаточное условие экстремума. | Алгоритм нахождения точек экстремума по первому признаку экстремума функции. | Графическая иллюстрация. | Второй признак экстремума функции. | Третье достаточное условие экстремума функции. | Точки экстремума | Задачи на нахождения экстремума функции |
mybiblioteka.su – 2015-2019 год. (0.007 сек.)
mybiblioteka.su


некоторое число.
некоторое число. определена и дифференцируема на отрезке
определена и дифференцируема на отрезке  ,
а
,
а 
множество значений этой функции, на
котором определена функция
множество значений этой функции, на
котором определена функция  .
Тогда если
,
то получаем или .
.
Тогда если
,
то получаем или . и
и  определены и дифференцируемы на
промежутке
определены и дифференцируемы на
промежутке  ,
и функция имеет первообразную на этом промежутке.
Тогда функция также имеет первообразную на промежутке
,
и функция имеет первообразную на этом промежутке.
Тогда функция также имеет первообразную на промежутке  ,
причем справедлива формула.
Учитывая, что,
получим.
,
причем справедлива формула.
Учитывая, что,
получим.