Исследование теплоотдачи при вынужденном движении воздуха в трубе
В качестве определяющего размера при расчете теплоотдачи в трубах и каналах принимают внутренний диаметр трубы ( R0 d ).
Определяющую скорость находят из уравнения неразрывности:
где G – расход флюида, кг/c; – плотность, кг/м3; f – площадь попе-
речного сечения для прохода теплоносителя, м2.
Конкретный вид функциональной зависимости в уравнениях подобия принимает ученый – автор формулы. В принципе для аппроксимации экспериментальных данных можно использовать любую полиноминальную зависимость. В отечественной литературе, как правило, в качестве аппроксимирующих уравнений применяют степенные функции вида:
— ламинарный режим течения флюида
|
|
|
|
|
Nu C Gr k Ren Prm t ; | (12) | |||
— переходный и турбулентный режимы течения флюида
(13)
где С, n, m, k – эмпирические коэффициенты, которые находят путем статистической обработки экспериментальных данных по методу наименьших квадратов; t – поправка, учитывающая зависимость фи-
зических свойств флюида от температуры; f ( / d) – поправка,
учитывающая влияние начального участка гидродинамической и тепловой стабилизации потока.
Для расчета поправочного коэффициента t академик М.А. Михеев предложил формулу:
|
|
| Pr |
| 0,25 |
|
|
|
| f |
| , | (14) |
t |
| |||||
|
|
|
|
|
| |
|
|
| Prw |
|
| |
где Prf – критерий Прандтля, который находят по таблицам физических свойств флюида при определяющей температуре;Prw – критерий
Прандтля, который находят по таблицам физических свойств флюида при температуре стенки.
В зависимости от значения критерия Рейнольдса в трубах и каналах существует ламинарный ( Ref ,d 2300 ), турбулентный (Ref ,d 104 )
и переходный ( 2300 Ref ,d 104 ) от ламинарного к турбулентному режимы течения.
studfiles.net
Лабораторная работа №4 Исследование теплопередачи при вынужденном движении воздуха в трубе ммтп 005
Цель работы: экспериментально определить локальные и средние по длине трубы значения коэффициента теплоотдачи при вынужденном движении воздуха в трубе при разных скоростях движения и сопоставить результаты опытов с известными критериальными зависимостями.
Краткие теоретические сведения:
Рабочие процессы в различных теплообменных устройствах, как правило, основаны на конвективном теплообмене между твердой поверхностью тела и омывающей его жидкостью или газа, а его интенсивность зависит в первую очередь от разности температур газа и поверхности (температурного напора), а также определяется динамическими условиями обтекания поверхности и теплофизическими свойствами газа.
Для расчета теплового потока обычно используют формулу Ньютона, согласно которой плотность теплового потока qw пропорциональна температурному напору:
где, qw, Вт/M2 – плотность теплового потока, равная количеству теплоты, отдаваемой с единицы поверхности за единицу времени,
TW, K– температура поверхности,
Тf , К– температура среды вне пограничного слоя.
Для конвективного теплообмена в каналах основными критериями подобия являются:
Критерий Нуссельта:

характеризующий отношение между потоком теплоты от жидкости к поверхности тела (теплоотдачей) и потоком теплоты теплопроводностью в жидкости у стенки.
где, λ – коэффициент теплопроводности жидкости,
l – характерный размер.
Критерий Рейнольдса:

характеризующий отношение между инерционной силой и силой внутреннего трения в жидкости (вязкости).
где, w – среднемассовая продольная скорость газа (в нашем случае воздуха),
l – характерный размер (для круглых труб l = d),
ϑ – кинематическая вязкость воздуха.
Критерий Прандтля:
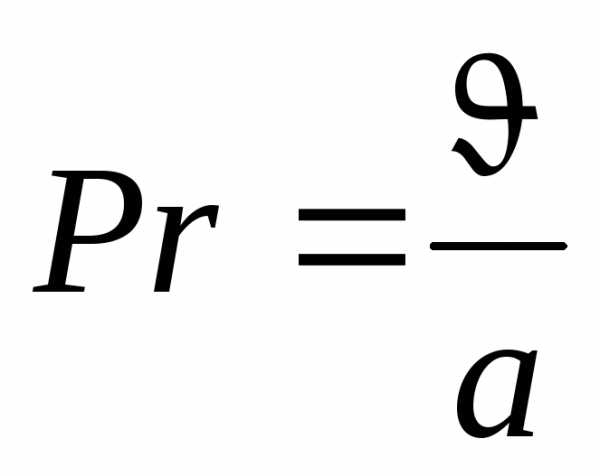
характеризующий совокупное отношение между силами инерции и вязкости и потоками теплоты – конвективным и вынужденным. Для газов критерий Рг определяется только атомностью и его значение близко к единице. Входящая в выражение величина а является температуропроводностью среды.
Критерий Пекле:
характеризующий отношение между потоком теплоты, переносимым движущимся газом (конвективным), и потоком теплоты теплопроводностью при одинаковом температурном напоре.
Критерий Грасгофа:
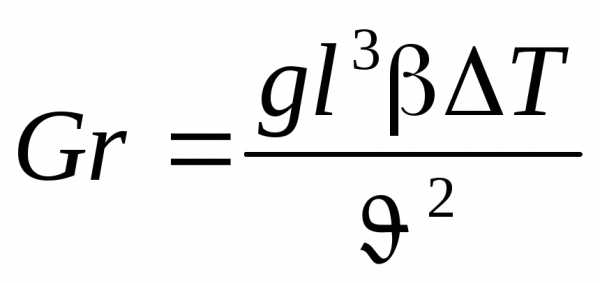
характеризующий отношение между подъемной силой в воздухе, возникающей вследствие разности плотностей, и силой вязкости.
где, β – коэффициент объемного расширения воздуха,
ΔT – разность температур воздуха и стенки.
В случае вынужденной конвекции при течении жидкости в трубах и каналах анализ методами теории подобия приводит в общем случае к функциональной связи:
где l/d – отношение длины трубы к ее диаметру, учитывающее изменение теплоотдачи по длине трубы на начальном участке.
Описание экспериментальной установки:
Лабораторная установка представляет собой цилиндрическую трубу длиной 1 м, наружный диаметр 8,5 мм, толщина стенки 1,5 мм. В трубу вмонтированы термопары (на различном расстоянии, см. табл. 1), датчики давления. Значения температур и давлений показывают цифровые вольтметры DP-6. Выбор термопар осуществляется переключателем S1. Труба нагревается при помощи электрического тока. Поток воздуха создается вентилятором.
Табл.1
Координаты термопар на трубке xi и длина участков li
№ участка | 0 | |||||||||
термопары | 0 | 1 | ||||||||
xi | 5 | 5 | 5 | 55 | 50 | 70 | 90 | 10 | 95 | 15 |
Li | 5 | 0 | 5 | 2,5 | 07,5 | 20 | 20 | 02,5 | 2,5 | 5 |
Порядок проведения эксперимента:
Установить напряжение на нагревателе, вращая ручку автотрансформатора «Регулятор напряжения». Через 10 минут после включения установки необходимо снять показания термопар, вращая ручку галетного переключателя S1 «Выбор термопар». Снять показания датчика перепада давления на трубе Δр, Па и датчика давления потока воздуха ΔH, Па.
Повторить опыт, изменяя напряжение на нагревателе.
Полученные данные внести в табл. 2.
Табл. 2.
№ режима | Напряжение нагрева, U,В | ΔH, Па | Δp, Па | Температура, ti ,°С | |||||||||||
t1 | t2 | t2 | t4 | t5 | t6 | t7 | t8 | t9 | t10 | t11 | t12 | ||||
Обработка результатов измерений:
Определяется тепловой поток Q:

где, U, В – напряжение, подаваемое на экспериментальный участок,
R = 0,0344 Ом – электрическое сопротивление рабочего участка.
Подсчитывается массовый расход воздуха G:
где, 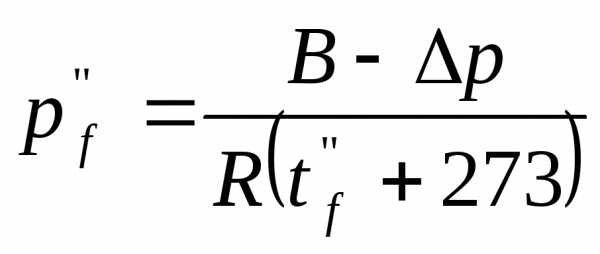 – плотность воздуха на выходе (tf“ = t12),
– плотность воздуха на выходе (tf“ = t12),
В = 133 Па – барометрическое давление,
R = 287 Дж/(кг·К) – газовая постоянная воздуха,
μ = 0,63 – коэффициент, полученный тарировкой,
d = 8,5 · 10-3 м – внутренний диаметр трубки.
Определяется средняя температура воздуха
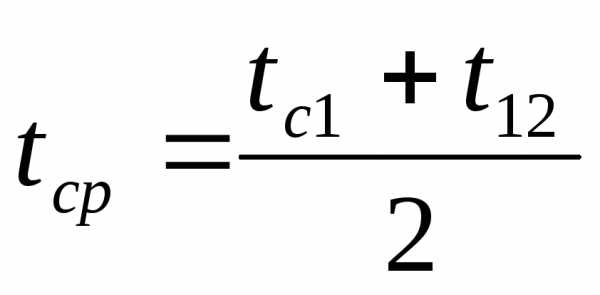
Рассчитывается средняя плотность воздуха
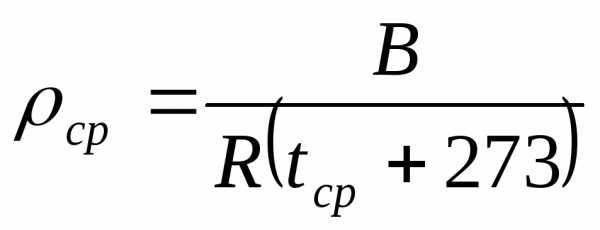
Определяется число Рейнольдса и средняя скорость на участке нагрева:

где, 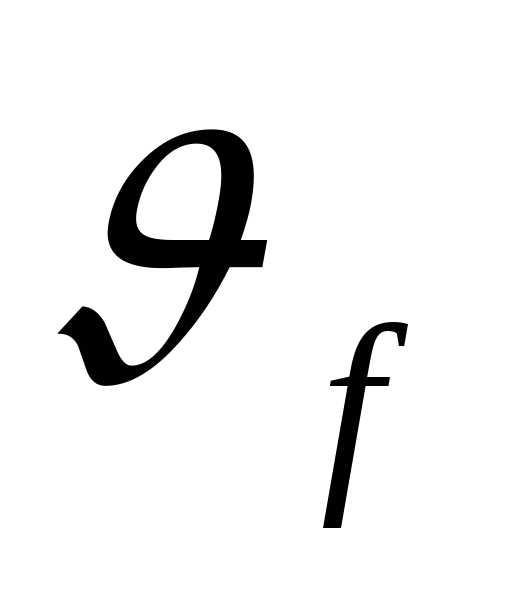 – кинематическая
вязкость при температуре tcp (см. прил. 1).
Вычисляются значения температурного
напора At£ в сечениях
трубки с координатами xi (см. табл.
1):
– кинематическая
вязкость при температуре tcp (см. прил. 1).
Вычисляются значения температурного
напора At£ в сечениях
трубки с координатами xi (см. табл.
1):
Определяются локальные значения коэффициента теплоотдачи αi.

где, QИ = 0,18(tw – t1) – потери тепла с наружной поверхности трубки,
tw – средняя температура стенки:

l = 720 мм – длина обогреваемой части трубки.
По полученным значениям αi строится график α = f(x) и определяется коэффициент теплоотдачи αосн на основном участке.
Определяются среднее значение а и критерий Нуссельта по опытным данным Nuf:

Значения Li даны в табл. 1. Крайние значения а2 и а12 исключаются ввиду влияния утечек тепла с торцов рабочего участка.

Теплопроводность воздуха λf приведена в приложении 1.
Определяются расчетные значения Nuf пo критериальной зависимости:
Nufpaсч = 0,021 · Rеf0,8 · Prf 0,43
По данным опыта рассчитывается коэффициент гидравлического сопротивления:
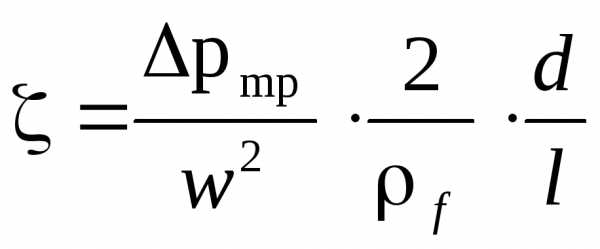
где, Δртр = Δр- Δру = Δ – w2pf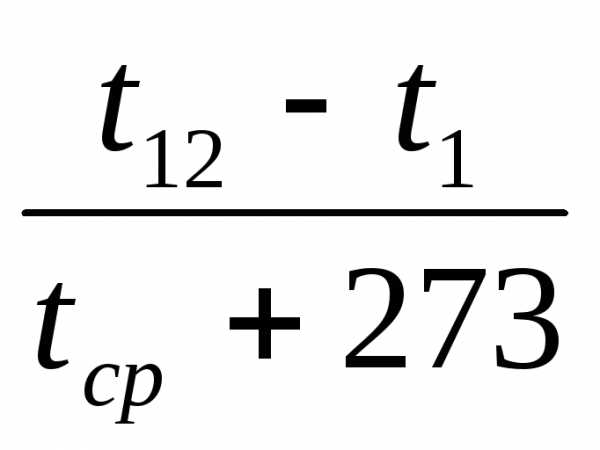
Δру – потеря давления на ускорение потока.
Полученное значение коэффициента гидравлического сопротивления сопоставляется с расчетным, по формуле Блазиуса:

Рассчитывается критерий Нуссельта по формуле, полученной на основе гидродинамической теории теплообмена:
Расчетные величины Nuf paсч и Nuf´ pacч сопоставляются с полученным в эксперименте Nuf.
Приложение 1
Физические параметры сухого воздуха при нормальном атмосферном давлении:
tl, | Ср. | ρ | λ·102 | μ·106 | ν·106 | Рr |
°С | кДж/(кг К) | кг/м3 | Вт/(м К) | Па · с | м2/с | |
10 | 1.005 | 1.247 | 2.51 | 20,06 | 14,16 | 0,705 |
20 | 1.005 | 1.205 | 2.59 | 21,42 | 15,06 | 0,703 |
30 | 1.005 | 1.165 | 2.67 | 22.54 | 16.00 | 0.701 |
40 | 1.005 | 1.128 | 2,75 | 24.26 | 16,96 | 0.699 |
50 | 1.005 | 1.093 | 2.82 | 25,72 | 17,95 | 0,698 |
60 | 1.005 | 1.060 | 2.89 | 27,26 | 18,97 | 0.696 |
70 | 1.009 | 1.029 | 2.96 | 28.85 | 20,02 | 0.694 |
80 | 1,009 | 1.000 | 3.04 | 30,48 | 21,09 | 0,692 |
90 | 1.009 | 0.972 | 3.12 | 32.03 | 22,10 | 0,690 |
100 | 1.009 | 0.946 | 3.20 | 33,62 | 23,13 | 0,6S8 |
120 | 1.009 | 0.898 | 3.33 | 37,10 | 25.45 | 0,686 |
140 | 1,013 | 0.854 | 3.48 | 40,64 | 27,80 | 0.684 |
160 | 1.017 | 0.815 | 3.63 | 44,12 | 30,09 | 0.682 |
180 | 1.022 | 0.779 | 3.77 | 47,71 | 32,49 | 0,681 |
200 | 1.026 | 0.746 | 4.55 | 51,25 | 34,88 | 0,680 |
Лабораторная работа №5
studfiles.net
Теплоотдача при вынужденном движении теплоносителей
в трубах и каналах
При вынужденном движении жидкости внутри трубы различают два основных режима течения: ламинарный и турбулентный. Ламинарный режим наблюдается при малых скоростях движения жидкости. При скоростях потока, больших некоторого значения Wкр, режим течения переходит в турбулентный. Для различных жидкостей и трубопроводов критическая скорость различна. Режим течения жидкости определяется по величине числа Рейнольдса Re. Если Reменьше критического Reкр, то режим течения ламинарный, т.е. при движении жидкости в трубах Reкр<2320. Развитый турбулентный режим течения устанавливается при значениях Re>104. Диапазон изменения Re от 2320 до 104 соответствует переходному режиму течения.
При турбулентном режиме движения перенос тепла внутри жидкости осуществляется в основном путем перемешивания. При этом процесс перемешивания протекает настолько интенсивно, что по сечению ядра потока температура жидкости практически постоянна. Резкое изменение температуры наблюдается лишь внутри тонкого слоя у поверхности.
На основе анализа и обобщения результатов экспериментальных исследований для расчета средней теплоотдачи установлена зависимость:
(9.6)
За определяющую температуру здесь принята средняя температура жидкости, а за определяющий размер – внутренний диаметр трубы. εе – поправочный коэффициент, учитывающий влияние на коэффициент теплоотдачи входного эффекта. Приближённо εе= 1+2/(l /d),при l/d>15имеем εе= 1.
При движении теплоносителя в изогнутых трубах (змеевиках)полученное значение коэффициента теплоотдачи умножают на поправку, учитывающую дополнительную турбулизацию потока в местах изгиба труб:
(9.7)
где d – внутренний диаметр трубки змеевика,
Dзм– диаметр витка змеевика (в нашем случае d=6 мм, Dзм=30 мм).
При ламинарном режиме движения перенос тепла одного слоя жидкости к другому в направлении нормали к стенке осуществляется путем теплопроводности. В то же время каждый слой имеет в общем случае различную скорость продольного движения. Поэтому наряду с поперечным переносом тепла путем теплопроводности происходит также конвективный перенос тепла в продольном направлении.
Обычно на практике ламинарный режим встречается при течении достаточно вязких теплоносителей, таких, как различные масла, для которых значения Pr обычно значительно превышают единицу.
Расчет средней теплоотдачи при ламинарном режиме течения жидкости может проводиться по формуле:
(9.8)
Для переходного режима (2320 ≤Re ≤ 104) уравнение теплоотдачи можно представить в виде следующей зависимости:
Pr 0,43 (9.9)
Похожие статьи:
poznayka.org
4.2 Теплоотдача при свободном движении около горизонтальной трубы.
Описанная картина свободного движения вдоль вертикальной трубы (стенки) типична для наклонной трубы, горизонтальной трубы, шара и других тел овальной формы.
Картина движения воздуха около горячих горизонтальных труб различных диаметров следующая:
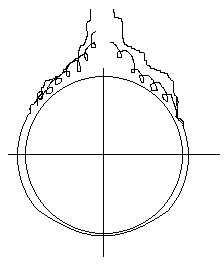
а) у труб малого диаметра восходящий поток сохраняет ламинарный режим даже вдали от трубы; б) при большом диаметре переход в турбулентный режим может происходить в пределах поверхности самой трубы.
Для
определения среднего значения  при свободном ламинарном движении
движения около горизонтальных труб,
можно рекомендовать формулу Михеева
И.М.:
при свободном ламинарном движении
движения около горизонтальных труб,
можно рекомендовать формулу Михеева
И.М.:
За
определяющий размер принят диаметр
трубы  ,
за определяющую температуру – температура
жидкости (
,
за определяющую температуру – температура
жидкости (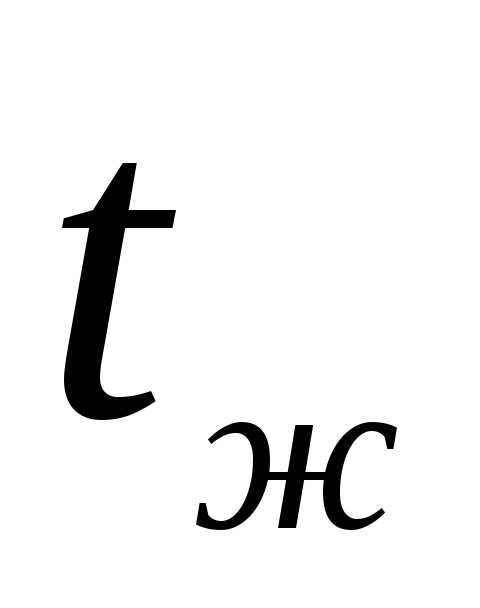 )
или температура газа вдали от трубы.
)
или температура газа вдали от трубы.
Приведенная выше формула применима в следующих пределах:
4.3 Движение жидкости около нагретых горизонтальных плоских стенок.
Характер движения около этих поверхностей зависит от положения и размеров поверхности.
a) Если поверхность нагрета, имеет небольшой размер и обращена вверх, то будет наблюдаться следующая картина:
б) Если стенка протяженная:
Чередуются потоки нагретого и холодного воздуха. Вентиляция происходит за счет притока холодной жидкости сверху.
в) Если нагретая поверхность обращена вниз, то свободное движение будет иметь следующий вид:
Для
приближенного определения коэффициента
теплоотдачи  для горизонтальных поверхностей
рекомендуется формула для горизонтальных
труб, причем, если нагретая горизонтальная
поверхность обращена кверху (а, б), то
полученное значение
для горизонтальных поверхностей
рекомендуется формула для горизонтальных
труб, причем, если нагретая горизонтальная
поверхность обращена кверху (а, б), то
полученное значение необходимо увеличить на 30%, а если
нагретая поверхность обращена книзу,
то
необходимо увеличить на 30%, а если
нагретая поверхность обращена книзу,
то необходимо уменьшить на 30%.
необходимо уменьшить на 30%.
За определяющий размер при расчетах берется меньшая сторона плиты.
4.4 Теплоотдача при свободном движении жидкости в ограниченном пространстве.
При свободном движении жидкости в неограниченном пространстве рассматривается одно явление – нагрев жидкости. Охлаждение жидкости происходит вдали от стенки и не влияет на теплоотдачу. При свободном движении в ограниченном пространстве нагревание и охлаждение жидкости протекают вблизи друг друга и разделить их невозможно, поэтому весь процесс и нагрев, и охлаждение рассматривается в целом. Вследствие ограниченности пространства и наличия восходящих и нисходящих потоков, условия движения сильно усложняются. Они зависят от формы тела и геометрических характеристик пространства, а также от рода жидкости и интенсивности процесса теплообмена (температуры и температурного напора).
Горизонтальные щели
Процесс определяется расположением нагретых и холодных поверхностей.
1. Нагретая поверхность расположена сверху:

 >
>
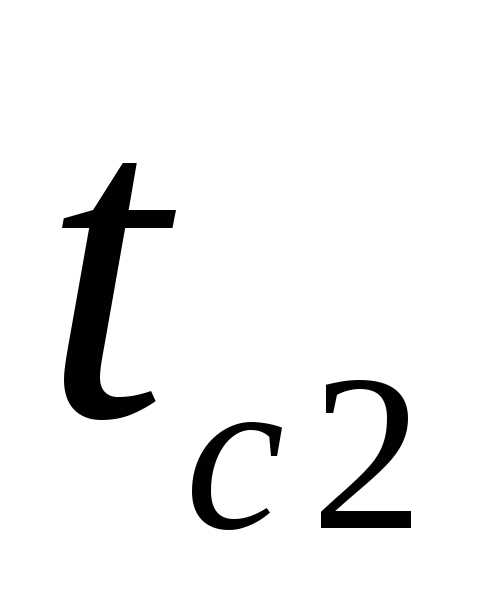
Свободное движение жидкости не наблюдается. Теплота передается теплопроводностью через жидкость и излучением.
2. Нагретая поверхность расположена снизу:
Возникают конвекционные токи.
При – наблюдаются чередующиеся между собой нисходящие и восходящие токи, поле потока имеет ячеистую структуру.
При – наступает развитое турбулентное движение.
Вертикальные щели
В
вертикальных щелях свободное движение
зависит от толщины щели ( ),
то есть от расстояния между стенками.
Если
),
то есть от расстояния между стенками.
Если между щелями велико, то характер
свободного движения такой же, как и у
неограниченной пластины.
между щелями велико, то характер
свободного движения такой же, как и у
неограниченной пластины.
1)
Если  >
>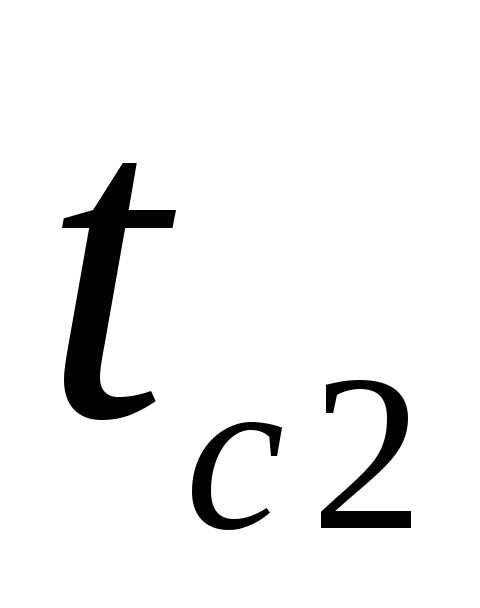 ,
то на левой стороне стенки возникает
восходящий ток, а на правой соответственно
нисходящий ток.
,
то на левой стороне стенки возникает
восходящий ток, а на правой соответственно
нисходящий ток.
studfiles.net
Министерство образования и науки рф
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Камская государственная инженерно-экономическая академия»
ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ГОРИЗОНТАЛЬНОЙ И ВЕРТИКАЛЬНОЙ ТРУБЫ ПРИ СВОБОДНОЙ КОНВЕКЦИИ ВОЗДУХА
Методические указания к лабораторным
работам
Набережные Челны
2012 г.
УДК
Исрафилов И.Х., Галиакбаров А.Т., Лобачева Е.Ф., Рахимов Р.Р. Исследование теплоотдачи горизонтальной и вертикальной трубы при свободной конвекции воздуха: Методические указания к лабораторным работам. – Набережные Челны: ИНЭКА, 2012. – 23 с.
Методические указания включают в себя два методических указания к лабораторным работам по исследованию теплоотдачи на горизонтальной и вертикальной трубах при свободной конвекции, и предназначены в помощь студентам при подготовке и выполнении лабораторных работ по курсу термодинамика и теплопередача.
Ил.5, библиогр. 3 назв., приложений 5
Рецензент доцент к.т.н. доцент И.Д. Галимянов
Печатается в соответствии с решением научно-методического совета ИНЭКА
Цель работы: Углубление знаний по теории теплоотдачи при свободном движении жидкости или газа, ознакомление с техникой экспериментального исследования процесса теплоотдачи на примере свободной конвекции, освоение методики обобщения опытных данных на основе методов теории подобия.
Задание.
Изучить основы теории конвекционного теплообмена и теории подобия.
Определить коэффициент теплоотдачи горизонтальной или вертикальной трубы при свободной конвекции воздуха и установить его зависимость от температурного напора.
Результаты опытов обработать методами теории подобия и сравнить их с соответствующими уравнениями подобия.
Основные теоретические положения
Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос теплоты осуществляется одновременно конвекцией и теплопроводностью. Под конвекцией теплоты понимают перенос теплоты при перемещении макрочастиц жидкости или газа в пространстве из области с одной температурой в область с другой. Конвекция возможна только в текучей среде, здесь перенос теплоты неразрывно связан с переносом самой среды. Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно происходит соприкосновение отдельных частиц, имеющих различные температуры.
Различают свободную (естественную) и вынужденную конвекцию. При свободной конвекции движение в рассматриваемом объеме жидкости возникает за счет неоднородности в нем массовых сил. Если жидкость с неоднородным распределением температуры, и, как следствие, с неоднородным распределением плотности, находится в поле земного тяготения, может возникнуть свободное гравитационное движение. Пример естественной конвекции — распространение теплоты в помещении от горячей батареи. Слои воздуха, находящиеся в соприкосновении с горячей батареей, нагреваются, плотность нагретого объема воздуха уменьшается и он вытесняется вверх более тяжелым холодным воздухом.
При вынужденной конвекции движение рассматриваемого объема жидкости происходит под действием внешних поверхностных сил, приложенных на его границах за счет предварительно сообщенной кинетической энергии (например, за счет работы насоса, вентилятора, ветра).
Вынужденное движение в общем случае может сопровождаться свободным движением. Относительное влияние последнего тем больше, чем больше разница температур отдельных частиц среды и чем меньше скорость вынужденного движения. При больших скоростях вынужденного движения влияние свободной конвекции становится пренебрежимо малым.
Рассмотрим случай. Холодная жидкость омывает нагретую поверхность или нагретая жидкость находится у поверхности холодной стенки. Теплообмен между твердым телом и жидкостью осуществляется конвекцией в массе жидкости, расположенной вдали от поверхности тела, и теплопроводностью с конвекцией вблизи поверхности, или внутри так называемого пограничного слоя. Теплообмен через такой слой к общей массе жидкости происходит как теплопроводностью, так и путем конвекции. Конвективный теплообмен между потоками жидкости или газа и поверхностью соприкасающегося с ним тела называется конвективной теплоотдачей или теплоотдачей.
В
расчетах конвективного теплообмена
большие затруднения вызывает определение коэффициента
теплоотдачи  ,находящегося
в зависимости от многочисленных факторов,
характеризующих процесс теплопередачи:
скорости движения газа или жидкости
(Wf),
их физических параметров — плотности
(
,находящегося
в зависимости от многочисленных факторов,
характеризующих процесс теплопередачи:
скорости движения газа или жидкости
(Wf),
их физических параметров — плотности
( ),
вязкости (v),
теплоемкости (Ср),
коэффициента теплопроводности
(),
температуры (Тw) и
(Tf,),
режима движения, формы (Ф), размеров
(I1, I2, …….,Iп)
и расположения поверхности по отношению
к движущемуся газу или жидкости и многих
других. Таким образом, коэффициент
теплоотдачи
),
вязкости (v),
теплоемкости (Ср),
коэффициента теплопроводности
(),
температуры (Тw) и
(Tf,),
режима движения, формы (Ф), размеров
(I1, I2, …….,Iп)
и расположения поверхности по отношению
к движущемуся газу или жидкости и многих
других. Таким образом, коэффициент
теплоотдачи  (в
системе СИ измеряется в Вт/м2К)
является сложной функцией различных
величин:
(в
системе СИ измеряется в Вт/м2К)
является сложной функцией различных
величин:
(1)
Интенсивность
теплоотдачи оценивается коэффициентом
теплоотдачи  .Согласно закону Ньютона-Рихмана,
конвективный тепловой поток Qk пропорционален разности температур
стенки
.Согласно закону Ньютона-Рихмана,
конвективный тепловой поток Qk пропорционален разности температур
стенки 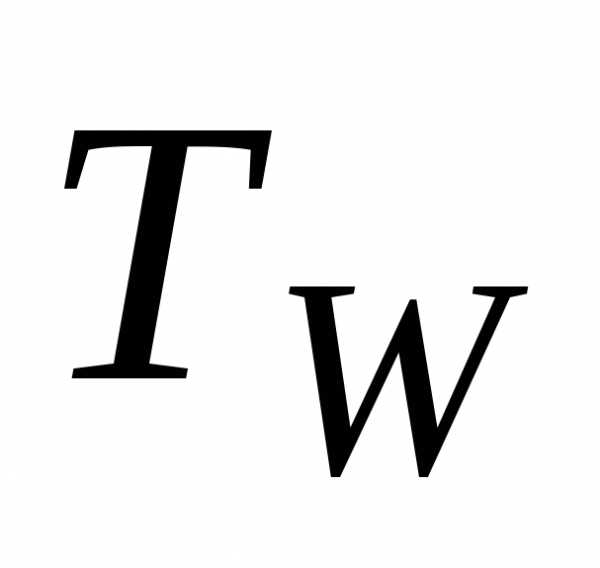 и жидкости
и жидкости и
поверхности теплообмена
и
поверхности теплообмена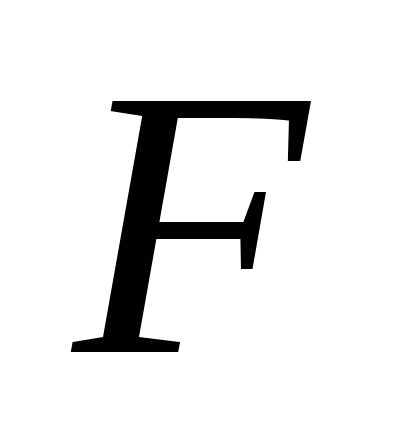 .
.
(2)
Общий
принцип экспериментального определения
коэффициента теплоотдачи  состоит
в измерении количества тепла Qк и температурного напора между стенкой
и жидкостью
в стационарном режиме. В действительных
условиях работы различных теплообменных
устройств теплота передается одновременнотеплопроводностью,
конвекцией и излучением.
Такое явление называется сложным
теплообменом.
(Напоминаем, что теплопроводность представляет
собой молекулярный перенос теплоты в
телах (или между ними), обусловленный
переменностью температуры в рассматриваемом
пространстве. Тепловое
излучение — процесс распространения теплоты с
помощью электромагнитных волн,
обусловленный только температурой
и оптическими свойствами излучающего
тела.)
состоит
в измерении количества тепла Qк и температурного напора между стенкой
и жидкостью
в стационарном режиме. В действительных
условиях работы различных теплообменных
устройств теплота передается одновременнотеплопроводностью,
конвекцией и излучением.
Такое явление называется сложным
теплообменом.
(Напоминаем, что теплопроводность представляет
собой молекулярный перенос теплоты в
телах (или между ними), обусловленный
переменностью температуры в рассматриваемом
пространстве. Тепловое
излучение — процесс распространения теплоты с
помощью электромагнитных волн,
обусловленный только температурой
и оптическими свойствами излучающего
тела.)
Вледствие
этого для определения коэффициента
теплоотдачи  применяют
зависимость:
применяют
зависимость:
(3)
Отсюда
определяем  :
:
(4)
здесь  –
степень черноты тела,
–
степень черноты тела,
 Вт/(м2К4)
– коэффициент
излучения абсолютно
черного тела,
Вт/(м2К4)
– коэффициент
излучения абсолютно
черного тела,
Q – полное количество теплоты (тепловой поток), отдаваемое телом (в опыте соответствует мощности нагревателя, вт) в стационарном режиме.
Теоретическое
значение коэффициента теплоотдачи  может
быть получено решением системы, состоящей
из дифференциальных уравнений
теплопроводности,
движения,
неразрывности, теплоотдачи и краевых
услловий. Совокупность этих уравнений
математически полностью описывает
процесс конвективного теплообмена.
Аналитические решения вышеуказанной
системы получены лишь для ограниченного
числа задач, поэтому процессы конвективного
теплообмена в основном изучаются
экспериментальными методами. Но здесь
необходимо отметить, что в последнее
время в связи с развитием численных
методов решения подобных систем
дифференциальных уравнений и внедрением
персональных компьютеров широкий класс
задач конвективного теплообмена решается
на ЭВМ.
может
быть получено решением системы, состоящей
из дифференциальных уравнений
теплопроводности,
движения,
неразрывности, теплоотдачи и краевых
услловий. Совокупность этих уравнений
математически полностью описывает
процесс конвективного теплообмена.
Аналитические решения вышеуказанной
системы получены лишь для ограниченного
числа задач, поэтому процессы конвективного
теплообмена в основном изучаются
экспериментальными методами. Но здесь
необходимо отметить, что в последнее
время в связи с развитием численных
методов решения подобных систем
дифференциальных уравнений и внедрением
персональных компьютеров широкий класс
задач конвективного теплообмена решается
на ЭВМ.
Задача
по определению коэффициента
теплоотдачи  ,значительно
упрощается, если ее решать экспериментальным
путем, пользуясь методом моделирования,
основанным на теории
подобия.
,значительно
упрощается, если ее решать экспериментальным
путем, пользуясь методом моделирования,
основанным на теории
подобия.
Теория подобия – это система понятий и законов, которые обосновывают возможность переноса результатов экспериментов с одного объекта (модели) на другой (реальный). Понятие подобия может быть распространено на любые физические явления. Можно, например, говорить о кинематическом подобии (подобие движения потоков жидкости), о тепловом подобии (подобии распределения температур и тепловых потоков) и т.д.
Объединение математических методов с экспериментом с помощью теории подобия позволяет распространить результаты единичного опыта на целую группу явлений.
Сформулированные ниже условия в виде трех правил, являются определением подобия физических процессов.
Подобные процессы должны быть качественно одинаковыми, т. е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями.
Условия однозначности подобных процессов должны быть одинаковыми во всем, кроме числовых значений размерных постоянных, содержащихся в этих условиях.
Одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение.
Первое условие говорит, что подобные процессы должны относиться к одному и тому же классу физических явлений. Помимо одинаковой физической природы подобные процессы должны характеризоваться одинаковыми по записи дифференциальными уравнениями.
Второе условие подобия требует, чтобы условия однозначности подобных процессов были одинаковыми во всем, кроме числовых значений постоянных, содержащихся в этих условиях.
Таким образом, запись размерных условий однозначности подобных процессов в общем виде (буквенном) должна быть идентична. При этом конкретные значения скорости набегающего потока, температуры стенки и т. д. могут иметь различные числовые значения.
Из первого и второго условий подобия следует, что подобные процессы должны описываться одинаковыми (тождественными) безразмерными дифференциальными уравнениями и безразмерными граничными условиями.
При соблюдении первых двух условий подобия исследуемые процессы будут зависеть от одних и тех же безразмерных переменных. Этот вывод неизбежно вытекает из того, что подобные процессы описываются тождественными безразмерными уравнениями и граничными условиями.
Первых двух условий недостаточно для установления физического подобия. Нужно добавить третье условие, что одноименные определяющие безразмерные переменные подобных процессов должны иметь одинаковое числовое значение.
Теория подобия позволяет, не решая дифференциальные уравнения, описывать физическое явление, получить числа подобия и, используя опытные данные, установить функциональную зависимость между ними, т.е. уравнения подобия, справедливые для всех подобных процессов.
Критериями подобия называются числа подобия, которые по существу являются определяющими безразмерными переменными, составленные из постоянных величин не являющихся функцией независимых переменных.
Конвективный
теплообмен характеризуется четырьмя основными числами (критериями) подобия – Nu, Pr, Re, Gr (см. приложение 1). Критерий
Нуссельта (Nu)
представляет собой безразмерный
коэффициент теплоотдачи. Критерий
Рейнольдса (Re)
отражает влияние вынужденного движения, критерий
Грасгофа (Gr) – влияние
свободного движения, критерий
Прандтля (Pr) – влияние физических свойств теплоносителя
на коэффициент теплоотдачи.
Числа подобия, составленные из независимых
переменных и постоянных величин,
определяющих характер процесса, но не
включающих искомые величины, называются определяющими. Числа,
включающие искомые зависимые
переменные,
называются определяемыми. Так, при расчёте конвективного теплообмена
критерий Nu является определяемым, так
как в него входит искомая величина  .
Критерии же Re, Pr, Gr
в этих же расчётах – определяющие.
.
Критерии же Re, Pr, Gr
в этих же расчётах – определяющие.
Уравнением подобия называют зависимость между каким-либо определяемым числом подобия и другими определяющими числами подобия.
При
расчете конвективного теплообмена в
различных теплообменных аппаратах
искомой величиной, как правило, является
коэффициент теплоотдачи  .
Поэтому уравнение подобия может быть
представленно в следующем виде:
.
Поэтому уравнение подобия может быть
представленно в следующем виде:
(5)
Это уравнение в некоторых случаях упрощается. Так, при свободном движении теплоносителя, из (5) можно получить:
(6)
где  – есть степенная функция. Тогда:
– есть степенная функция. Тогда:
(7)
Здесь с, п – постоянные числа, которые определяются количественно из экспериментальных данных.
безразмерные переменные можно разделить на два вида:
Для обработки экспериментальных данных и составления критериальных уравнений теплообмена необходимо выбрать определяющую температуру и определяющий размер. Определяющей температурой может быть средняя температура жидкости Тw, температура стенки Тf или средняя температура пограничного слоя
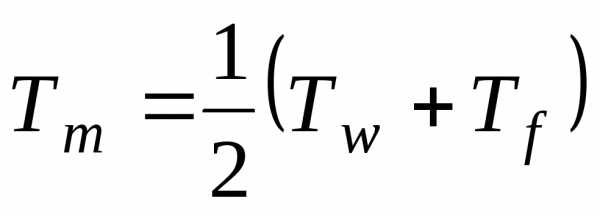 .
.
Как правило, определяющая температура отмечается в форме подстрочных индексов у символа каждого числа подобия. При этой температуре и должны быть взяты все значения физических констант. Используемые при вычислении чисел подобий (, , а, , с).
За определяющий размер L, как правило, принимают диаметр трубы. Определяющий размер тоже указывается подстрочным индексом числа подобия.
За определяющий размер в наших опытах на вертикальной трубе принимаем длину рабочего участка l, а на горизонтальной – внешний диаметр трубы D, за определяющую температуру – среднюю температуру пограничного слоя Tm. Тогда уравнение (7) для вертикальной трубы принимает вид:
(8)
а для горизонтальной:
(9)
Прологарифмируя, к примеру, (8), получим
(10)
Это
уравнение прямой в логарифмических
координатах.
Вычисленные
значения  отмечаются
на графике (рис.1) напротив соответствующего
значения
.
По этим точкам проводится наилучшая
прямая. Величина коэффициента
С находится
из соотношения:
отмечаются
на графике (рис.1) напротив соответствующего
значения
.
По этим точкам проводится наилучшая
прямая. Величина коэффициента
С находится
из соотношения:
п (11)
или из графика на рис. 1.
Показатель
степени n
определяют как тангенс угла между осью
абсцисс и прямой: 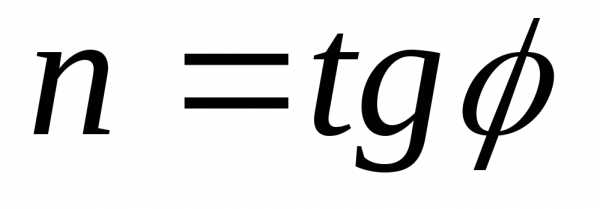 .
Некоторые значения С и n приведены в приложении 2.
.
Некоторые значения С и n приведены в приложении 2.

Рис. 1 График критериальной зависимости в логарифмических координатах
studfiles.net
Движение воздуха в трубах – Энциклопедия по машиностроению XXL
XII.6. Вода протекает по трубе диаметром 25 мм со скоростью 50 см/с. Определить скорость движения воздуха в трубе диаметром 100 мм из условия, что оба потока гидродинамически подобны. Температура воды 20° С, температура воздуха 50° С. [c.299]Решение. Определяем скорость движения воздуха в трубе [c.300]
Используя метод конечных разностей, решить обратною задачу теплопроводности с целью определения локальных коэффициентов теплоотдачи на начальном участке трубы, нагреваемой электрическим током. По данным экспериментального исследования теплоотдачи при вынужденном движении воздуха в трубе температура внутренней [c.206]
Пример 2.3. Рассчитать погрешность измерения коэффициента теплоотдачи в лабораторной работе № 32 Местная теплоотдача при турбулентном движении воздуха в трубе ( 4.5). [c.80]
ДВИЖЕНИИ ВОЗДУХА В ТРУБЕ [c.166]
Теплоотдача при вынужденном движении воздуха в трубе [c.147]
Содержание работы. Определение локальных и среднего значений коэффициента теплоотдачи при движении воздуха в трубе. Оценка по данным эксперимента длины участка тепловой стабилизации. Исследование влияния скорости воздуха на коэффициент теплоотдачи. Представление результатов эксперимента на стабилизированном участке в критериальной форме и сравнение с известными в литературе критериальными зависимостями. [c.147]
Движение воздуха в трубах [c.175]
В пневматических системах производственных машин наиболее часто применяются d = 5-г 25 мм, рекомендуемые скорости движения воздуха в трубах составляют 10—15 м/с. В пневматических системах производственных машин скорость движения воздуха определяется разностью давлений на концах воздухопровода, его сопротивлением, местными потерями и т. д. и обычно бывает значительно выше. Во многих случаях скорость движения воздуха определяется также технологическими требованиями, но как правило, даже при очень коротких воздухопроводах в производственных машинах она не превосходит скорости звука. Путем простых подсчетов, используя уравнение (Х.19), можно убедиться, что для воздухопроводов производственных машин характерным является турбулентный режим движения воздуха. [c.177]
При расчете пневматических механизмов в связи с определением законов их движения и времени срабатывания необходимо знать скорости движения воздуха в трубах и его расходы. Для установления этих зависимостей обратимся к схеме, приведенной на рис. Х.5. Предположим, происходит наполнение рабочего цилиндра 1 из ресивера 2 достаточно больших размеров, чтобы можно было пренебречь изменением давления и скоростью в нем. Пренебрегая влиянием инерционных сил и коэффициентами, учитывающими неравномерность распределения скоростей по сечению потока, можно записать уравнение Бернулли для сечения О—О и /—I следующим образом [c.178]
В конвективных печах атмосферой большей частью является воздух. На рис. 6—9 [9 ] даны зависимости коэффициента теплоотдачи конвекцией от скорости воздуха и характерного размера для тел простой конфигурации и некоторых видов насыпной загрузки. Если загрузка печи состоит из ряда одиночных деталей, относительно небольших по сравнению с размерами печной камеры, их можно свести к одиночным плите, цилиндру или шару и использовать соответствующие графики. При нагреве крупных деталей, занимающих значительную часть печного пространства, коэффициент теплоотдачи определяют отдельно для различных частей их поверхностей, используя графики для плиты, цилиндра и т. д. и выбирая среднее из полученных значений. Для труб, профилей, листов и т. п., когда воздух продувается вдоль пакета, следует, подсчитав эквивалентный диаметр, использовать данные для расчета а при движении воздуха в трубе [6]. Изделия, эквивалентный диаметр которых больше 12 мм (при использовании графика рис. 9), следует рассматривать как одиночные детали. В этом случае необходимо применять соответствующие графики, а на коэффициент теплоотдачи вводить поправку, равную 1,3, так как он увеличивается благодаря повышению турбулентности потока в слое [9]. [c.91]
Сопротивление движению воздуха в трубах в виде потери давления (энергии), обусловленное силами трения на стенках трубы, [c.72]
В ряде случаев может оказаться вполне достаточным выявление качественных или приближенных количественных зависимостей. Для этого достаточно проанализировать влияние интересующего нас фактора по формулам, относящимся к одному и другому теплоносителю. Покажем это на примере трубчатой конструкции воздухоподогревателя с движением воздуха в трубах, а газа — с поперечным движением в межтрубном пространстве [соответственные формулы — для воздуха (200)—(205), а для газа (206)—(211) ]. [c.160]
Фундаментальное значение для создания всей современной теории газового потока имеют работы Н. Е. Жуковского Истечение воздуха под большим напором , О трении газов , Движение воздуха в трубе с большими скоростями , а также исключительно важная по глубине идей работа С. А. Чаплыгина О газовых струях . Дальнейшее развитие работ Жуковского и Чаплыгина мы находим в трудах их многочисленных учеников, работающих в ряде научно-исследовательских институтов СССР. [c.115]
Определить средний коэффициент теплоотдачи и количество переданной теплоты при движении воздуха в трубе диаметром d = 56 мм и длиной 1 = 2 м со скоростью ш = 5 м/сек, если средняя температура воздуха //=120°, а средняя температура стенки трубы /то= 100° С. [c.184]
Для круглых труб гидравлический диаметр равен их геометрическому диаметру 0 —0). Движение воздуха в трубах характеризуется определенным профилем распределения скоростей по сечению потока. Скорости частиц непосредственно на стенках равны нулю (частицы прилипают к поверхности стенок), с приближением к центру потока они непрерывно возрастают и достигают максимальной величины на оси трубы. [c.27]
Движение воздуха в трубах сопровождается потерями давления, связанными с преодолением сил сопротивлений. Различают потери на трение (сопротивление трения) Ар р и местные потери (местное сопротивление) Ар . В соответствии с общепринятым принципом наложения потерь общие потери давления в трубопроводе определяют как арифметическую сумму потерь на трение и местных потерь [c.27]
Между нижней и верхней камерами воздухоочистителя на стержне свободно подвешен лёгкий зонтик, который предотвращает обратный унос скопившейся внизу жидкости при быстрых движениях воздуха в трубе, вызывающего разрежение над зонтиком. [c.847]
Распределение давления. Анализ уравнения (40) показывает, что наличие материала в трубе изменяет не только величину, но и направление градиента давления. Так при отсутствии направленного движения воздуха в трубе (например, когда материал перегружается в герметичную емкость) движение материала создает положительный градиент, равный [c.102]
Интеграл в первой части представляет собой перепад давления воздуха на участке трубы длиной X, обусловленный действием падающего материала. Величина этого перепада была нами названа эжекционным давлением [49, 70]. При отсутствии направленного движения воздуха в трубе величина эжекционного давления равна избыточному давлению в трубе. [c.105]
Пример XV.3. Найти потери давления на трение при движении воздуха в бетонной трубе диаметром d—1 м при давлении близком к атмосферному и температуре [c.282]
Движение воды в реках и в трубах, движение газа в трубопроводах и в проточной части машин, движение воздуха в атмосфере и многие другие виды движения жидкости и газа в природе и технике являются преимущественно турбулентными. [c.15]
Пример 6.2. Найти потери давления на трение при движении воздуха в бетонной трубе диаметром /=1 м при давлении, близком к атмосферному, и температуре /=20 С. Расход воздуха при заданных условиях [c.300]
Режим движения воздуха в воздухопроводах может быть ламинарным и турбулентным. Переход от ламинарного режима к турбулентному определяется критическим числом Рейнольдса. Для круглых гладких труб [c.177]
Значения поправки на неквадратичность ф, вычисленные по формуле (6.19) для движения воды в трубах при А, = 0,1 мм и 3=1 мм, приведены в табл. 6.2 (v=lX Х10- м /с), а для движения воздуха в трубах при кь= = 0,1 мм — в табл. 6.3 (v = 14,7 10 м / ). [c.276]
| Таблица 6.3. Значения поправок на неквадратичность ф при движении воздуха в трубах | 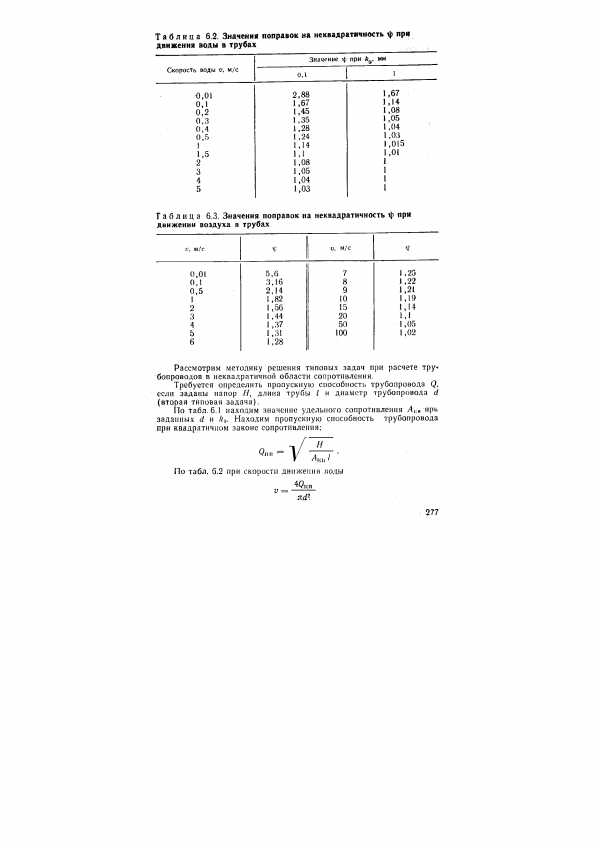 |
Как показывают расчеты, при одинаковых температурных условиях и одинаковой затрате мощности на преодоление сопротивления движению воздуха в трубе закрученный однофазный поток по сравнению с незакрученным дает выигрыш в теплообмене в 2—2,5 раза, а закрученный двухфазный поток по сравнению с закрученным однофазным дополнительно обеспечивает увеличение коэффициента теплообмена в зависимости от теплового потока и числа Re от 3 ([c.204]
Швец И. Т., Д ы б а н Е. П., С ел яви н Г. Ф., С т р а д о м с к и й М. В., Экспериментальное исследование влияния начальных возмущений на развитие турбулентного режима течения при движении воздуха в трубах, Изв. вузов, Энергетика , Ко 8, 19ею. [c.381]
Для турбулентного режима движения воздуха в трубе коэффициент сопротивления % зависит не только от числа Рейнольдса, но и от относительной шероховатости стенок трубы. Для гладких труб при турбулентном потоке коэффициент сопротивления определяется по известной формуле Блязиуса [c.72]
Если звук внезапно оборвать, колебания воздушной пробки спустя короткое время прекратятся. Отчего Теоретически они, казалось бы, должны продолжаться вечно , но, как и во всех вечных двигателях , движению препятствует трение, или уже знакомая нам сила вязкости. В трубе ближайший к стенкам слой воздуха прилипает к ним. Это явление связано с поверхностным натяжением етенок и воздуха. Если дуть вдоль трубы, воздух посередине трубы двинется вперед и при этом молекулы воздуха будут скользить по своим соседям, удерживаемым на стенках трубы. Сопротивление скольжению создает вязкое торможение и поглотит часть энергии, которая превратится в теплоту. Чем быстрее движение воздуха в трубе, тем больше вязкое торможение. [c.153]
Для образования электростатического поля иа коронирующий электрод подается высокое напряжение, создаваемое высоковольтным выпрямительным устройством В-140-5-2. Напряжение подается через ограничительное сопортнвление 10 для снятия остаточных зарядов с системы служит автоматический разрядник И, который смонтирован на изоляционной стойке 12. Управление высоковольтным устройством и пылевым вентилятором сосредоточено на щите 13. Для замера скорости движения воздуха в трубе служат пневмометрическая трубка Прандт.ля 4 (первичный прибор) и тягонаноромер ТНЖ-4 15 (вторичный прибор). [c.53]
Если скорость данной жидкости ири определенных размерах трубы превышает некоторую величину, критическое значение, тю течение становится неустойчивым, теряет ламинарньп) характер и переходит в турбулентное. При этом скорость в каждой точке по тока изменяется все время хаотически. Турбулентное течение — наиболее распрострапсиный в природе вид движения жидкостей и газов движение воды в трубах и каналах, в реках и в морях, течение около. твижущихся в жидкости или газе твердых тел, движение воздуха в земной атмосфере и газа в атмосферах Солнца II звезд, в межзвездных туманностях и т. и. [c.145]
Значения коэффициента ф, вычисленные при движении воды в трубах с разной, абсолютной шероховатостью, кэ, приведены в табл. XV.2 и при движении воздуха— в табл. XV.3. Приведенные в таблицах данные вычислены по фор 11уле (XV.12). [c.251]
Назначение работы. Работа посвящена изучению основных закономерностей теплоотдачи при турбулентном движении воздуха в равномерно обогреваемой круглой трубе onst). Требуется определить коэффициенты [c.166]
Исследование теплоотдачи при охлаждении воздуха в условиях сверхзвукового течения (М 3,5) при ламинарном движении в пограничном слое [Л. 5-17]. Объектом исследования является медная цилиндрическая труба 4 длиной около 30 диаметров (рис. 5-14). Сверхзвуковое течение воздуха в трубе создается с помощью сопл 2, которые выполняются из нержавеющей стали. Плавный переход на стыке сопла с опытной трубой достигается с помощью пе[)сходнон втулки (5. Вну- [c.242]
Определить расход воздуха, засасываемого двигателем вутреннего сгорания из атмосферы, при котором, вакуум в горловине ди( узора составляет Рвак 15 кПа, если диаметр трубы Z) = 40 мм, диаметр диффузора d = 20 мм, коэффициенты сопротивления воздухоочистителя t,i = б, колена = 0,3, воздушной заслонки 3 = 0,5 отнесены к скорости в трубе, а коэффициент сопротивления диффузора 4 = 0,04 отнесен к скорости движения воздуха в его горловине (рис. 4.6). Плотность воздуха р = 1,23 кг/м . Потерями напора на трение пренебречь. [c.45]
mash-xxl.info
Определение коэффициента теплоотдачи при вынужденном движении воздуха в прямом кольцевом канале
Определение коэффициента теплоотдачи при вынужденном движении воздуха в прямом кольцевом канале
скачать (42.9 kb.)
Доступные файлы (1):
8.doc
Реклама MarketGid:Калининградский государственный технический университет
Кафедра судовых энергетических установок и теплоэнергетики
Теоретические основы теплотехники
Лабораторная работа №8
Определение коэффициента теплоотдачи при вынужденном
движении воздуха в прямом кольцевом канале.
Выполнил:
Проверил:
Таблица 1
Наименование измеряемых величин | Обозна-чение | Размер- ность | Опыт I | Опыт II | ||
| текущ. зн. | среднее | текущ. зн. | среднее | |||
Температура воздуха на выходе из калориметра | | | 31,1 31,2 31,2 | 31,17 | 29,2 29,2 29,2 | 29,2 |
Перепад высот столбов воды на дифманометре I | | мм.в.ст | 105 106 104 | 105 | 195 195 195 | 195 |
Перепад высот столбов воды на дифманометре II | | мм.в.ст | 82 80 84 | 82 | 150 150 152 | 151 |
Барометрическое давление | мм.р.ст | 755 | 755 | 755 | 755 | |
Падение напряжения на электронагревателе | U | В | 43 | 43 | 43 | 43 |
Сила тока в цепи нагревателя | I | А | 0,8 | 0,8 | 0,8 | 0,8 |
Эл. сопротивление термометра сопротивления | R | Ом | 30,82 | 30,82 | 30,08 | 30,08 |
Температура воздуха на входе в кольцевой канал | | | 20,5 20,5 20,5 | 20,5 | 21,2 21,1 21,0 | 21,1 |
Расход воздуха через калориметр | m | кг/с | | | | |
Средняя температура стенки | | | 57,26 | 57,26 | 50,25 | 50,25 |
Обработка результатов опыта
Средняя температура стенки,
, Ом
Ом
,
Опыт I:
Опыт II:
Тепловой поток от поверхности нагревателя к воздуху, Q
Опыт I,II: Q = I∙U, Вт
Q= 0,8∙43=34,4 Вт
Средняя температура воздуха,
=,
Опыт I: =
Опыт II: =
Площадь поверхности нагревателя,
F=
Коэффициент теплоотдачи,
Опыт I:
Опыт II:
Эквивалентный диаметр канала,
= мм = 0,008
Площадь поперечного сечения кольцевого канала,
Среднее давление воздуха в канале,
, Па
1 Па = 0,0075 мм.р.ст.
мм.р.ст. = = 100667 Па
1 Па = 0,102 мм.в.ст
Опыт I: = 105 мм.в.ст. == 1029 Па
= 82 мм.в.ст = = 803 Па
Опыт II: = 195 мм.в.ст = Па
= 151 мм.в.ст. = Па
Опыт I: Па
Опыт II: Па
9. Средняя плотность воздуха в канале,
,
Опыт I:
Опыт II:
10. Среднемассовая скорость воздуха в канале, W
, м/с
Опыт I: м/с
Опыт II: 22 м/с
11. Физические параметры для сухого воздуха воздуха, ,
Средняя температура воздуха = 25= 298 K ,коэффициент теплопроводности
для сухого воздуха: =, коэффициент
кинематической вязкости для сухого воздуха =
12. Число Нуссельта, Nu
Nu =
Опыт I: Nu=
Опыт II: Nu=
13. Число Рейнольдса, Re
Re=
Опыт I: Re = 8242
Опыт II: Re = 11332
Так как число Рейнольдса Re > 2300, поэтому уравнение подобия будет иметь вид:
Nu =
ln(26)=3,25
ln(33)=3,49
ln(8242)=9,0
ln(11332)=9,3
0,8
Для опыта I: 0,019
Nu =
Для опыта II: 0,019
Nu =
Наименование измеряемых величин | Обозначение | Размерность | Опыт I | Опыт II |
| Средняя температура воздуха | | | 25,80 | 25,15 |
| Коэффициент теплоотдачи | | | 84,85 | 106,35 |
| Средняя плотность воздуха в канале | | | 1,16 | 1,14 |
| Среднемассовая скорость воздуха в канале | W | м/с | 16 | 22 |
| Число Нуссельта | Nu | 26 | 33 | |
| Число Рейнольдса | Re | 8242 | 11332 |
Вывод: в результате проведенного опыта я определил коэффициент теплоотдачи при
вынужденном движении воздуха в прямом кольцевом канале:
. И представил результат опыта в виде уравнения подобия:
Nu = , а по литературным данным : Nu = .
Цель работы: определить коэффициент теплопередачи при вынужденном движении
воздуха в прямом кольцевом канале для двух опытов, а также представить результат
опытов в виде уравнения подобия.
Используемое оборудование: опытная установка, вентилятор, дифференциальный
манометр с измерительной шайбой.
Скачать файл (42.9 kb.)
gendocs.ru
