Изменения магнитного потока формула – 24)Поток вектора магнитной индукции!! Теорема гаусса для магнитного поля!!!

24)Поток вектора магнитной индукции!! Теорема гаусса для магнитного поля!!!

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна   (1) где B_n=Вcosα – проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS=dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.  Поток вектора магнитной индукции Ф

B через произвольную заданную поверхность S равен (2)  Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В, B_n=B=const и  Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м², который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл•м²).  Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: (3)  Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.  Следовательно, для потоков векторов 

В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы.  В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна  Магнитный поток сквозь один виток соленоида площадью S равен  а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением, 

25)Явление электромагнитной индукции!! Закон Фарадея и правило Ленца!! эдс индукции в движущихся проводниках!!!

Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени 

магнитного потока, пронизывающего контур.

Магнитным потоком Φ через площадь S контура называют величину 

Φ = B · S · cos α,

где B – модуль вектора магнитной индукции, α – угол между вектором и нормальюк плоскости контура (рис. 1.20.1).

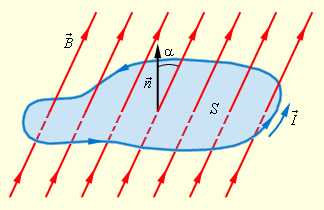
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером(Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м²: 

1 Вб = 1 Тл · 1 м2.

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции _инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус: 

Эта формула носит название закона Фарадея.

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.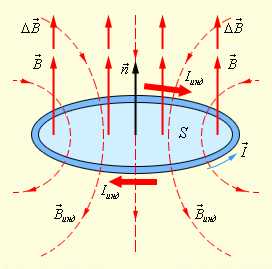

Правило Ленца отражает тот экспериментальный факт, что _индивсегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренцаиграет в этом случае роль сторонней силы.

Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длинойlскользит со скоростьюпо двум другим сторонам (рис. 1.20.3).

studfiles.net

Поток магнитной индукции, теория и примеры

Определение и общие понятия потока магнитной индукции

Исходя из формулы (1), магнитный поток через произвольную поверхность S вычисляется (в общем случае), как:

   

Магнитный поток однородного магнитного поля сквозь плоскую поверхность можно найти как:

   

Для однородного поля, плоской поверхности, расположенной перпендикулярно вектору магнитной индукции магнитный поток равен:

   

Поток вектора магнитной индукции может быть отрицательным и положительным. Это связано с выбором положительного направления . Очень часто поток вектора магнитной индукции связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру связано с направлением течения тока правилом правого буравчика. Тогда, магнитный поток, который создается контуром с током, сквозь поверхность, ограниченную этим контуром является всегда большим нуля.

Единица измерения потока магнитной индукции в международной системе единиц (СИ) – это вебер (Вб). Формулу (4) можно использовать для определения единицы измерения магнитного потока. Одним вебером называют магнитный поток, который проходит сквозь плоскую поверхность площадь, которой 1 квадратный метр, размещенную перпендикулярно к силовым линиям однородного магнитного поля:

   

Теорема Гаусса для магнитного поля

Теорема гаусса для потока магнитного поля отображает факт отсутствия магнитных зарядов, из-за чего линии магнитной индукции всегда замкнуты или уходят в бесконечность, у них нет начала и конца.

Формулируется теорема Гаусса для магнитного потока следующим образом: Магнитный поток сквозь любую замкнутую поверхность (S) равен нулю. В математическом виде данная теорема записывается так:

   

Получается, что теоремы Гаусса для потоков вектора магнитной индукции () и напряженности электростатического поля (), сквозь замкнутую поверхность, отличаются принципиальным образом.

Примеры решения задач

ru.solverbook.com

Глава 23. Закон электромагнитной индукции

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

(23.1)

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м² однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

(23.2)

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле. Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

(23.3)

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

(23.4)

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

(23.5)

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23.1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется. При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3).

Используя формулу (23.3) находим в задаче 32.2.3 Гн (ответ 4).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).

online.mephi.ru

определение, направление и количество + пример

 

Если мы поместим контур с током в магнитное поле, то линии индукции магнитного поля будут проходить через этот контур. Линия магнитной индукции это магнитная индукция в каждой точке этой линии. То есть, мы можем говорить о том, что линии магнитной индукции это поток вектора индукции по пространству, ограниченному и описываемому этими линиями. Можно сказать короче магнитный поток.

В общих чертах с понятием «магнитный поток» знакомятся в девятом классе. Более детальное рассмотрение с выводом формул и пр., относится к курсу физики старших классов. Итак, магнитный поток это определенное количество индукции магнитного поля в какой-либо области пространства.

Направление и количество магнитного потока

Магнитный поток имеет направление и количественное значение. В нашем случае контура с током, говорят, что этот контур пронизывает определенный магнитный поток. При этом понятно, что чем больше по размеру будет контур, тем больший магнитный поток пройдет сквозь него.

То есть, магнитный поток зависит от площади пространства, через которую он проходит. Если мы имеем неподвижную рамку определенного размера, пронизываемую постоянным магнитным полем, то магнитный поток, проходящий через эту рамку, будет постоянным.

Если же мы увеличим силу магнитного поля, то соответственно увеличится магнитная индукция. Величина магнитного потока также возрастет, причем пропорционально возросшей величине индукции. То есть, магнитный поток зависит от величины индукции магнитного поля и площади пронизываемой поверхности.

Магнитный поток и рамка – рассмотрим пример

Рассмотрим вариант, когда наша рамка расположена перпендикулярно магнитному потоку. Площадь, ограничиваемая этой рамкой, будет максимальна по отношению к проходящему через нее магнитному потоку. Следовательно, величина потока будет максимальной для данной величины индукции магнитного поля.

Если же мы начнем вращать рамку относительно направления магнитного потока, то площадь, через которую может проходить магнитный поток, будет уменьшаться, следовательно, будет уменьшаться величина магнитного потока через эту рамку. Причем, она будет уменьшаться вплоть до нуля, когда рамка станет расположена параллельно линиям магнитной индукции.

Магнитный поток будет как бы скользить мимо рамки, он не будет ее пронизывать. В таком случае и действие магнитного поля на рамку с током будет равно нулю. Таким образом, мы можем вывести следующую зависимость:

Магнитный поток, пронизывающий площадь контура, меняется при изменении модуля вектора магнитной индукции B, площади контура S и при вращении контура, то есть при изменении его ориентации к линиям индукции магнитного поля.

В случае вращения контура, при котором в любой момент его плоскость остается параллельна линиям магнитной индукции, магнитный поток через этот контур все время будет равен нулю.

Нужна помощь в учебе?

Предыдущая тема: Индукция магнитного поля: формула, от чего зависит, линии индукции
Следующая тема:&nbsp&nbsp&nbspЯвление электромагнитной индукции: опыт Фарадея, выводы

Все неприличные комментарии будут удаляться.

www.nado5.ru