Интегрирование по частям: объяснение, решение примеров
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u, а остальная часть относится ко второму множителю и обозначается через dv. Затем дифференцированием находится du и интегрированием – функция v. При этом за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv – такую часть подынтегрального выражения, которая легко интегрируется.
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:
1) – логарифмические
функции, а также обратные тригонометрические функции (с приставкой “arc”), тогда на основании продолжительного опыта
интегрирования по частям эти функции обозначаются через
2) , , – синус, косинус и экспоненту, умноженные на P(x) – произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен – через u;
3) , , , , в этом случае интегрирование по частям применяется дважды.
Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную в самом начале урока формулу интегрирования по частям
,
получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) – функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.
Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:
Так как
то её можно записать в виде
который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Есть у метода интегрирования по частям совершенно особенное применение: с его помощью можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например, функций, как синусы и косинусы в степени более второй и их произведения. Рекуррентная формула – это формула для нахождения очередного члена последовательности через предыдущий член. Для обозначенных случаев цель достигается последовательным понижением степени. Так, если подынтегральная функция – синус в четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей степени и так далее. Описанной задаче посвящен последний параграф этого урока.
Пример 1. Найти неопределённый интеграл методом интегрирования по частям
.
Решение. В подынтегральном выражении – логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что , .
Тогда , .
Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) – функцию, не содержащую логарифма):
И снова логарифм…
Пример 2. Найти неопределённый интеграл:
.
Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) – функцию, не содержащую логарифма).
Находим изначальный интеграл:
Пример 3. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть , .
Тогда
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл находим методом замены переменной.
Возвращаясь к переменной x, получаем
.
Находим изначальный интеграл:
.
Пример 4. Найти неопределённый интеграл методом интегрирования по частям
Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что
находим
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть , .
Тогда , .
По формуле интегрирования по частям находим:
.
Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем , .
Тогда , .
По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем , .
Тогда , .
Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие, которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из практики известно, что лучше обозначать через u, а что через dv. Поэтому в этих случаях нужно пользоваться соображением удобства, также приведённым в параграфе “Суть метода интегрирования по частям”: за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv – такую часть подынтегрального выражения, которая легко интегрируется. Последний пример этого урока – решение именно такого интеграла.
Пример 11. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Примем как руководство к действию общее соображение относительно обозначений. Обозначаем , .
Тогда , .
По формуле интегрирования по частям получаем:
Случаев, когда требуется понижения степени подынтегральной функции, мы уже коснулись во вводной части урока. Теперь – практика использования для этой цели метода интегрирования по частям.
Пример 12. Используя интегрирование по частям, вывести рекуррентную формулу для
,
найти I4.
Решение. Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали бы и синус, и косинус. Используя тригонометрические тождества, получаем
Ко второму слагаемому – интегралу – применяем метод интегрирования по частям. Для этого обозначим
Тогда
Находим это второе слагаемое – интеграл:
Теперь находим рекуррентную формулу для исходного интеграла:
С помощью полученной формулы найдём I4:

Начало темы “Интеграл”
Продолжение темы “Интеграл”
Поделиться с друзьями
function-x.ru
Как находить интеграл. Вычисление определенного интеграла
Если определения из учебника слишком сложны и непонятны, прочитайте нашу статью. Мы постараемся максимально просто, “на пальцах” объяснить основные моменты такого раздела математики, как определенные интегралы. Как вычисляется интеграл, читайте в данной инструкции.
1
С геометрической точки зрения интеграл функции – это площадь фигуры, образуемой графиком данной функции и осью в пределах интегрирования. Запишите интеграл, проанализируйте функцию под интегралом: если подынтегральное выражение возможно упростить (сократить, вынести множитель на знак интеграла, разбить на два простых интеграла), сделайте это.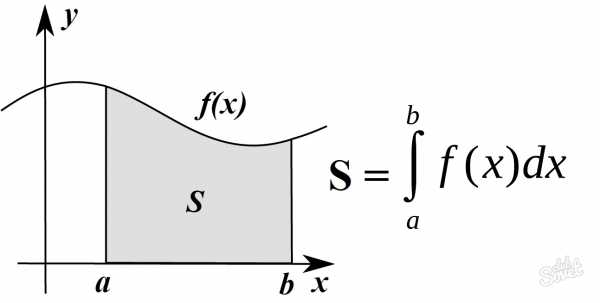
2
Откройте таблицу интегралов, чтобы определить, производная какой функции стоит под интегралом. Ответ найден? Выпишете множитель, вынесенный за интеграл (если это имело место), запишите найденную из таблицы функцию, подставьте границы интеграла.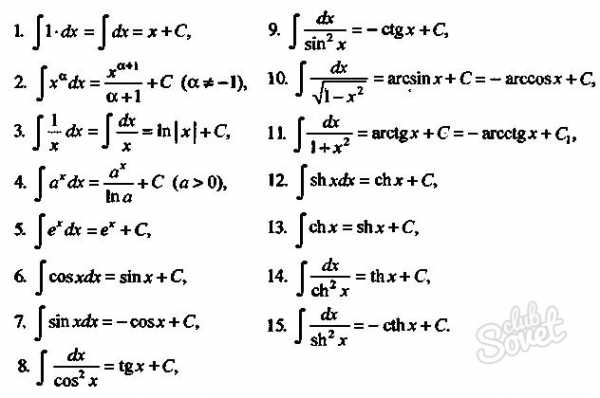
3
Для вычисления значения интеграла рассчитайте его значение в верхней границе и вычтите его значение в нижней границе. Разница – и есть искомая величина.
4
Чтобы проверить себя или хотя бы уяснить ход решения задачи на интегралы, удобно пользоваться онлайн-сервисом нахождения интегралов, однако прежде чем приступать к решению, ознакомьтесь с правилами ввода функций. Огромнейшее его преимущество в том, что здесь пошагово расписывается все решение задачи с интегралом.
Конечно, здесь рассмотрены лишь самые простые варианты интегралов – определенные, на самом деле разновидностей интегралов великое множество, изучаются они в курсе высшей математики, математического анализа и дифференциальных уравнений в ВУЗах для студентов технических специальностей.
sovetclub.ru
Как брать интеграл
Понятие «взятия интеграла» тесно сопряжено с нахождением первообразной функции. Функция F(x) называется первообразной к f(x), если ее производная F’(x) равняется f(x). Так как производная любой константы равна нулю, то и первообразных у f(x) будет бесконечно много. Все они совпадают между собой с точностью до константы. Традиционное обозначение неопределенного интеграла представлено на рис.1.Вам понадобится
- Таблица простейших интегралов.
Инструкция
В математике существует довольно большое количество способов «взять» интеграл. В данной статье коротко рассмотрены те из них, которые принято называть простейшими приемами интегрирования. Эти приемы используют свойства неопределенных интегралов и тождественные преобразования подынтегральной функции.
- 1. Непосредственное интегрирование.Непосредственное интегрирование заключается в вычислении интегралов с помощью их определенных свойств и специальных таблиц. Пример 1. Вычислить интеграл ∫(4/(cosx^2)- 3cosx +2/(x-1))dxРешение. ∫(4/(cosx^2)- 3cosx +2/(x-1))dx= 4∫dx/(cosx^2)- 3∫cosxdx +2∫dx/(x-1)=4tgx-3sinx+2ln|x-1| + C.
- Теперь можно рассмотреть правило, которое позволяет расширить возможности иcпользования таблицы основных интегралов. Если ∫f(x)dx=F(x)+C, то ∫f(kx+b)dx=(1/k)F(kx+b)+CПример 2. ∫sin(5x)dx=-(1/5)cos(5x)+ C.
- 2. Разложение подынтегральной функции. Данный прием заключается в преобразовании подынтегральной функции, используя формулы алгебры и тригонометрии. Подынтегральная функция представляется в виде суммы функций, интегралы от которых можно легко брать.Пример 3. ∫(1+(cosx)^2/(1+cos(2x))dx=[1+cos(2x)=2(cosx)^2 ]=∫(1+(cosx)^2/2(cosx)^2)dx==(1/2)∫1/(cosx)^2)dx+(1/2)∫dx=(1/2)(tgx+x)+C.Пример 4. ∫dx/((sinx)^2)(cosx)^2))= ∫((sinx)^2+(cosx)^2)/((sinx)^2)(cosx)^2))dx=∫(1/(cosx)^2+1/(sinx)^2)dx=tgx-ctgx+C.
- 3. Подведение под знак дифференциала. Этот прием основан на свойстве инвариантности формул интегрирования. Подынтегральная функция преобразуется к виду f(u(x))u’(x), а затем сомножитель u’(x) подводится под знак дифференциала (интегрируется) – u’(x)dx=d(u(x)), после чего применяется формула ∫(f(u(x))du(x))=u(x)+C.
- Пример 5. ∫(arctgx/(1+x^2))dx=|dx/(1+x^2)=d(arctgx)|=∫(arctgxd(arctgx))=(1/2)(arctgx)^2+C.Пример 6. ∫xsqrt(1-x^2)dx=|d(1-x^2)=-2xdx|=-(1/2) ∫((1-x^2)^(1/2+1))/(1/2+1) + C =-(1/3)sqrt((1-x^2)^3) + C.Пример 7. ∫((cosx)^3)sin(2x)dx=2∫(cosx)^3)cosxsinxdx=-2∫((cosx)^4)d(cosx)=-(2/5)(cosx)^5+C.
completerepair.ru
