Как научиться быстро считать в уме?
Знания, полученные на уроках алгебры и геометрии, в жизни люди применяют крайне редко. Наиболее ценное и необходимое умение, связанное с математикой – способность быстро считать в уме, поэтому стоит разобраться, как этому научиться. В обычной жизни это позволяет быстро подсчитывать сдачу, рассчитывать время и т.п.
Лучше всего развивать способности с самого детства, когда мозг намного быстрее усваивает информацию. Есть несколько эффективных методик, которыми пользуется много людей.
Как научиться очень быстро считать в уме?
Чтобы достичь хороших результатов, необходимо проводить тренировки регулярно. После достижения определенных целей стоит усложнять задание. Большое значение имеют способности человека, то есть умение удерживать в памяти сразу несколько вещей и концентрировать внимание. Наибольший успех могут достичь люди с математическим складом ума. Чтобы быстро научиться считать, необходимо хорошо знать таблицу умножения.
Наиболее популярные методики подсчета:
- Разберемся, как быстро считать двухзначные числа в уме, если нужно умножить на 11. Чтобы разобраться в методике, рассмотрим один пример: 13 умножить на 11. Задача заключается в том, что между цифрами 1 и 3 нужно вставить их сумму, то есть 4. В итоге получается, что 13х11=143. Когда сумма цифр дает двузначное число, к примеру, если на 11 умножать 69, то 6+9=15, тогда вставлять нужно только вторую цифру, то есть 5, а к первой цифре множителя следует добавить 1. В итоге получает 69х11=759. Есть еще один способ умножения числа на 11. Для начала следует произвести умножение на 10, а затем, прибавить к нему исходное число. Например, 14х11=14х10+14=154.
- Еще один способ, как быстро считать в уме большие числа, работает для умножения на 5. Это правило подходит для любого числа, которое для начала необходимо разделить на 2. Если в итоге получилось целое число, то нужно приписать в конце ноль. К примеру, чтобы узнать, сколько будет 504 умножить на 5. Для этого 504/2=252 и приписываем в конце 0. В итоге получается 504х5=2520. Если же при делении числа получается не целое число, то нужно просто убрать полученную запятую. К примеру, чтобы узнать, сколько будет 173 умножить на 5, нужно 173/2=86,5, а после просто убрать запятую, и получается, что 173х5=865.
- Узнаем, как быстро считать в уме двузначные числа, путем сложения. Сначала необходимо произвести сложение десятков, а затем, единиц. Для получения итогового результата, следует прибавить два первых результата. К примеру, разберемся, сколько будет 13+78. Первое действие: 10+70=80, а второе: 3+8=11. Итоговый результат будет таким: 80+11=91. Этим методом можно пользоваться, когда из одного числа нужно вычесть другое.
Еще одна актуальная тема – как быстро считать проценты в уме. Опять же для лучшего понимания рассмотрим пример, как найти 15% от какого-либо числа. Вначале следует определить 10%, то есть разделить на 10 и прибавить половину от результата –5%. Найдем 15% от 460: чтобы найти 10%, делить число на 10, получается 46. Следующий шаг – находим половину: 46/2=23. В итоге 46+23=69, что и является 15% от 460.
Есть еще один метод, как высчитывать проценты. Например, если нужно определить, сколько будет 6% от 400. Для начала стоит выяснить 6% от 100 и это будет 6. Чтобы узнать 6% от 400, то нужно 6х4=24.
Если нужно найти 6% от 50, то следует пользоваться таким алгоритмом: 6% от 100 это 6, а для 50, это половина, то есть 6/2=3. В итоге получается, что 6% от 50, это 3.
Если число, от которого стоит найти процент меньше 100, то следует просто перенести запятую влево. К примеру, чтобы найти 6% от 35. Для начала найдите 6% от 350 и это будет 21. Значение же 6% для 35, это 2,1.
womanadvice.ru
Как быстро складывать числа в уме, правила счета в математике
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения.
Как быстро считать в уме: приемы устного счета больших чисел
Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
умножить на 4 — это дважды умножить на 2;
умножить на 6 — это значит умножить на 2, а потом на 3;
умножить на 8 — это трижды умножить на 2;
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
разделить на 4 — это дважды разделить на 2;
разделить на 6 — это сначала разделить на 2, а потом на 3;
разделить на 8 — это трижды разделить на 2;
разделить на 9 — это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: реш
c-univermag21.ru
Как научиться считать в уме. Как научиться быстро считать в уме
Не смотря на то, что наша жизнь в последние годы стала значительно легче благодаря обилию доступных электронных счетных устройств, навык быстрого устного счета не потерял своей актуальности для человека. Благодаря умению производить в уме арифметические вычисления вы всегда сможете решить бытовые задачи без калькулятора, компьютера или какого-нибудь другого высокотехнологичного гаджета. Если вы сможете производить такие вычисления быстро, это сразу же улучшит ваш имидж в глазах окружающих, которым вы будете казаться настоящим интеллектуалом.
Каких-либо специальных умений или знаний не требуется. Если вас интересует вопрос о том, как научиться быстро считать в уме, то ответ прост – секрет этого умения заключен в постоянных тренировках. Если вы будете ежедневно выделять им по нескольку минут, то очень скоро для вас перестанут представлять хоть какую-нибудь сложность любые вычисления с двузначными и даже трехзначными числами.
Как научиться быстро считать в уме? В настоящее время широко распространены несколько методик, но проанализировав их, можно увидеть, что практически все они базируются на трех основных принципах.
Первый принцип – это способности. Если вы хотите научиться быстро выполнять арифметические операции, то для этого очень важно, чтобы вы умели концентрировать свое внимание, а также удерживать в своей краткосрочной памяти результаты промежуточных вычислений. Также, желательно, чтобы вы обладали предрасположенностью к логическому мышлению и математике.
Второй принцип – алгоритмы. Если вы сможете запомнить алгоритмы устных вычислений и научитесь быстро выбирать наиболее подходящие из них для решения каждой определенной задачи, то вы быстро сможете добиться выдающихся результатов.
Третий принцип – постоянные тренировки. Тренировки являются обязательным условием. Только благодаря им вы сможете придать своему уму необходимую остроту и сможете производить необходимые вычисления молниеносно.

Следует сказать о том, что наиболее важным принципом из трех представленных является именно последний. Если вы не будете заниматься постоянными тренировками своего ума, вряд ли вы сможете удивить хоть кого-нибудь вашими арифметическими способностями. При этом нельзя недооценивать и роли двух первых принципов. Ведь если будете знать, каким именно алгоритмом необходимо воспользоваться в данной ситуации, и при этом сможете приложить к этому алгоритму свои математические таланты, это поможет вам одолеть в скорости счета даже тех, кто занимается счетом на профессиональном уровне.
Перед тем, как научиться быстро считать в уме, предлагаем вам несколько самых простых алгоритмов, при помощи которых вы сможете улучшить свои навыки устного счета. Освоив их можно приступать к изучению других правил и алгоритмов, которые смогут существенно облегчить вашу жизнь.
Правило 1.
Складывая многозначные слагаемые, сначала сложите старший разряд меньшего из слагаемых, а потом – старший. Например, чтобы сложить пару двузначных чисел, начните со сложения десятков, потом сложите единицы, а после этого прибавьте единицы к результату сложения десятков.
Правило 2.
Производя операцию вычитании между многозначными числами, отнимите от уменьшаемого старшие разряды вычитаемого, а потом – младшие разряды. Если вычитаемое из вашего примера близко к какому-либо удобному для счета круглому числу, то отнимите это число, а потом сделайте коррекцию результата.
Правило 3.
Производя умножение на число, состоящее из единицы и нулей, просто припишите к вашему первому множителю столько же нулей, сколько их имеется у второго множителя. Деля на число, из единицы и нулей, отделите запятой от делимого столько же позиций, сколько нулей имеется в составе делителя.
Удачи в счетах!
kanks.ru
Как научиться быстро считать в уме?

В век кассовых аппаратов и калькуляторов люди все реже считают в уме. Они практически полностью перешли на вычислительную технику, но и она частенько дает сбои, или ее просто не будет рядом, когда она нужна. Незаметно мы утрачиваем навыки точного и быстрого счета и иногда с опозданием понимаем, что мы уже не так хороши в этом деле. Но, быстро считать в уме – это неоспоримое достоинство и преимущество. Человек, которые запросто оперирует цифрами, практически никогда не будет обманут при расчетах. Но важно то, что это будут развивать и поддерживать в форме умственные способности, что важно для детей и молодых людей.
Как научиться быстро считать в уме ребенку
Все навыки лучше всего развиваются и закрепляются в детстве. Учиться считать, также, как и читать, можно с 1.5-2 лет. Особенности этого возраста заключаются в том, что у ребенка сначала накопятся пассивные знания – он будет понимать, знать, но из-за малого словарного запаса, будет мало разговаривать. До пяти лет малыш может обучиться в уме производить простые действия – вычитания и сложения в пределах двадцати. Если в два – три с половиной годика вы будете использовать наглядные методы в обучении, то позже малыш сможет оперировать только цифрами, без подкрепления наглядным материалом.
Если вы хотите, чтобы у вашего ребенка было больше шансов, что процесс оперирования крупными значениями и математическими действиями будет даваться легче и пойдет быстрее, тогда нужно как можно раньше научить его считать.
Обучать детей до четырех лет лучше с наглядными материалами. Считать можно все, что хотите. Пожарные машины, которые спешат на пожар, мотоциклисты, которые с грохотом пролетают мимо вас, кошки, которые греются на солнышке, стайки птиц – все, что вокруг вас можно посчитать. С навыками счета одновременно будут развиваться наблюдательность и внимание. Постепенно увеличивайте нагрузку. Утром вы видели 2 кошек, а когда возвращались домой, еще 3. Спросите у ребенка: «Заметил ли он, что сегодня так много кошек! Сколько он заметил?». Похвалите его за точность и наблюдательность, ведь эти качества пригодятся ему в жизни.
В начальной школе малышу необходимо быстро и свободно производить любые вычисления в пределах, определенных школьной программой. Чтобы научиться считать быстро, необходимы постоянные тренировки. Поэтому задачей родителей является побуждение малыша к счету и делать так, чтобы это происходило интересно. Чем чаще ваш ребенок будет тренироваться, тем легче ему будет делать точные и быстрые вычисления в уме.
Как научиться быстро считать взрослому
Если ребенок с детства обучался быстрому счету, то со временем он без особых усилий будет оперировать с большими значениями. Но если человек более зрелого возраста или студент решил овладеть быстрым счетом, то необходимо применить незамысловатую методику, которая несомненно принесет положительные результат.
Любое обучения начинается с малого. Если вы знаете таблицу умножения, это отлично. Если же забыли, или никогда не знали, стоит воспользоваться таким методом счета. К примеру, необходимо узнать, сколько будет 8х6. Записываем пример таким образом:
2 4
—-=48
8х6
Ответ 48. Мы его получили, записав пример 8х6, провели над ним прямую линию и над каждой цифрой записали, сколько не хватает до 10. Над 8 пишем 2, на 6 пишем 4. Первая цифра ответа – это разница между числами в нижней и верхней строках по диагонали. 8-4=4, 6-2=4 – для вычисления можете взять любую пару – ответ будет всегда одинаковым. Итак мы поняли, что первая цифра это 4. Теперь найдем вторую. Для этого следует умножить цифры верхней строки 2х4=8. Наш пример решен: 8х6=48.
Немного по-другому считаются более крупные числа. Например, вам необходимо подсчитать 11х13.
1 3
——=140+3=143
11х13
В нижней строчке записываем пример 11х13. В верхней пишем, на сколько эти числа превышают 10. Получаем 1 и 3. Сложим числа по диагонали. Получаем 11+3=14, 13+1=14. Мы получили 14 десятков, поскольку исходные цифры превышают 10. Поэтому 14 умножим на 10. 14х10=140. Осталось лишь умножить верхние числа 1х3=3 и прибавить полученную цифру к ответу.
Такие способы вычисления сложно проводить только сначала. Поэтому начинайте с простых примеров и постепенно усложняйте. Но дабы научиться считать в уме, необходимо полностью избавиться от записей, а делать все в голове.
По таким способам можно учить и детей, однако только тогда, когда они полностью знают школьную программу. В ином случае вы не добьетесь положительных результатов, а лишь навредите усвоению школьных знаний.
Когда освоите манипулирование двузначными числами, можете переходить к вычислению многозначных – сотен и даже тысяч.
Видео уроки
hr-portal.ru
Как научиться быстро считать в уме
Многие спрашивают, как научиться быстро считать в уме, чтобы это выглядело незаметно и не глупо. Ведь современные технологии позволяют меньше пользоваться своей памятью и умственными способностями. Но иногда нет под рукой данных технологий и порой легче и быстрее посчитать что-то в уме. Многие люди начали считать на калькуляторе или телефоне даже элементарные вещи, что также не очень хорошо.
В статье вы узнаете, как научиться быстро считать в уме, что для этого нужно день и как быстро этому можно научиться. Ведь тот, кто научится быстро и просто считать в уме, будет жить проще. Каждому человеку нужно уметь считать в уме быстро, но при этом помнить, что сейчас не пещерный век и если сомневаетесь можно проверить себя, используя, калькулятор.
Учите таблицу умножения
Чтобы научиться считать в уме быстро, вам нужно полностью и на зубок знать таблицу умножения. Найдите напарника и тренируйтесь вместе. Вам нужно научиться моментально, отвечать на любые значения из таблицы умножения. Когда вы научитесь быстро умножать, то считать не составит труда. Узнайте: как вежливо отказать.
Выполняйте задания на подсчеты, найдите учителя
Чтобы научиться быстро считать в уме, вам нужно тренироваться, нет волшебных методик, чтобы с первого раза начать быстро считать в голове. Вам нужно найти наставника, учителя, который умнее вас и умеет быстро считать в уме. Попросите его, чтобы он научил и вас. Тогда он будет вас тренировать и давать задания и вскоре, вы также будете быстро считать в голове.
Читайте книги
Чтобы научиться считать быстро в уме, вам нужно постоянно тренировать свой мозг и заставлять его быстро работать и считать. Читайте полезные книжки, чтобы не только тренировать скорость мозга, но и память и воплощать в себя новые, полезные знания. Узнайте: как научиться контролировать себя.
Никогда не пользуйтесь калькулятором
Чтобы научиться быстро считать в уме, вам нужно отвыкнуть от постоянного подсчета на калькуляторе. Когда вы полностью от него откажитесь, то мозгу просто придется научиться считать быстро самому. Считайте всегда, в магазине, когда забираете сдачу и вечерами научитесь продумывать большие и сложные математические примеры. Решайте задания, в которых нужно считать. Но лучше просто найти умного учителя, который вас быстро всему научит.
СОВЕТЫ ПСИХОЛОГА
psyh–olog.ru
psyh-olog.ru
Как научиться быстро считать в уме

- Зачем в уме, когда можно на калькуляторе или в столбик?
Минимальные навыки счёта, чувство числа – такой же элемент общечеловеческой культуры, как грамотное письмо и речь, владение иностранным языком, базовое представление об искусстве и окружающем мире.
Кроме того, когда вы легко считаете без подручных средств, вы чувствуете совершенно другой уровень управления реальностью – вы заранее знаете, сколько сдачи вам дадут в магазине или стоит ли набиваться всемером в лифт грузоподъемностью 400 килограммов.
Подумайте и о том, что калькулятор и действия в столбик – это же такая разновидность магии. Скорее всего, вы не понимаете, как это работает, и вынуждены просто доверять им. А когда вы хорошо понимаете, как устроены математические операции и можете их воспроизвести «в уме», ваше чувство контроля и уверенности в себе получает серьёзный бонус.
И наконец, устный счёт развивает ваши ментальные способности: внимание, память, концентрацию, переключение между несколькими потоками мышления, а также может послужить средством для медитации или отвлечения от грустных мыслей.
- Где брать задания для тренировки? Самому себе примеры придумывать?
Конечно, нет. В сети полно мобильных приложений, которые предложат вам тренировку математических навыков на любой вкус.
При выборе учтите, что хорошее приложение, как минимум, должно обладать достаточно гибкими настройками сложности и вести статистику решённых вами заданий.
Попробуйте эти приложения под iOS и Android или поищите альтернативные варианты в App Store и Google Play.
- А как именно нужно тренироваться?
Основных математических действий всего четыре – сложение, вычитание, умножение и деление. У каждого действия есть свои особенности, но они не сложные. Надо один раз разобраться, а потом тренироваться минут по 5-10 в день, и очень скоро вы почувствуете, что считаете значительно лучше. Скорее всего, за два-три месяца вы выйдете на достаточно приличный уровень, который можно будет поддерживать эпизодическими тренировками.
- И с чего же начать?
Начните с самого простого уровня – сложения однозначных чисел, и доведите его до совершенства: 99% правильных ответов, на каждый ответ 1-2 секунды. Для решения примеров «с переходом через 10» попробуйте использовать следующую технику – «Опора на десяток».
Допустим, вам нужно сложить 8 и 7.
1) Спросите себя, сколько числу 8 не хватает до 10 (это 2).
2) Представьте 7 как сумму 2 и какого-то второго кусочка (это 5).
3) Прибавляйте к 8 сначала ту часть числа 7, которой недоставало до 10, а потом тот второй кусочек – получится 10 и 5, и это, конечно, 15.
5. Как складывать многозначные числа?
Здесь самый важный принцип – это сложение одинаковых разрядов друг с другом. Разбив оба числа на «разрядные части», начните складывать со старших разрядов – тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами. То, что получится, при необходимости укрупняйте и снова считайте всё вместе.
Например, как сложить 456 и 789?
1) 456 состоит из трех разрядных частей — 400, 50 и 6. 789 тоже разбивается на три разрядные части — это 700, 80 и 9.
2) Складываем сотни с сотнями: 400+700 = 1100, десятки с десятками: 50+80 = 130, единицы с единицами: 6+9 = 15.
3) Укрупняем, разбивая на удобные части, снова группируем и складываем одинаковые разряды: 1100+130+15 – это 1100+100+30+10+5, то есть, 1200+40+5 = 1245.
6. Что насчёт вычитания?
И здесь надо начинать с базового уровня – вычитания однозначного числа из чисел первого и второго десятка – и довести этот навык до совершенства. Как и в случае со сложением, проблемы обычно возникают с вычитанием «с переходом через 10». И здесь поможет аналогичный способ «опоры на десяток».
Допустим, нам нужно из 12 вычесть 8.
1) Спросим себя, сколько нужно отнять от 12, чтобы получилось 10 (это 2).
2) Будем из 12 вычитать 8 по частям – сначала вычтем эту 2, а потом все остальное. А остальное – это сколько? (это 6).
3) После вычитания 2 из 12 мы получили 10, и нужно вычесть еще 6, получится 4. Готово!
7. А что с многозначными числами? С ними всё сложно?
Не особенно. Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.
Итак, допустим, нам нужно вычесть 512−259.
1) Число 259, которое мы вычитаем, состоит из трёх разрядных частей – 200, 50 и 9. Их-то по очереди мы и вычтем.
2) 512−200 – вычитание сотен никак не затрагивает десятков и единиц числа 512, влияет только на сотни, так что результат будет такой – 312.
3) Из того, что получилось после вычитания сотен, теперь вычтем десятки, 312−50.
Это похоже на вычитание через десяток. Вычтем из 312 сначала 10 до целых сотен (единицы не будут затронуты), получим 302. А потом вычтем всё остальное (всего нужно было вычесть 50, 10 уже вычли, осталось вычесть 40), получается 262.
4) Осталось вычесть единицы: 262−9.
Чистый переход через десяток – вычитаем сначала 2, получим 260, а потом вычитаем остальную часть, 7, получаем 260−7 = 253. Вот и ответ.
8. Как устроено умножение?
Начнём с умножения однозначных чисел. Для начала нужно вспомнить, что умножение – это когда несколько раз складывают одно и то же. Например, умножить 4 на 7 означает сложить четыре семёрки. Пользуясь техникой сложения, мы можем легко посчитать – две семёрки, 7 и 7, будет 14, если еще добавить третью 7, получится 21, и, добавляя последнюю, четвёртую семёрку, в результате получим 28.
Постепенно в результате тренировок вы запомните удобные вам опорные значения умножения и с их помощью сможете быстрее вычислять соседние. Например, если нужно умножить 6 на 7 (то есть, сложить шесть семёрок), а вы помните, что 5 умножить на 7 (то есть, сложить пять семерок) будет 35, то чтобы получить итоговый результат, нужно просто добавить шестую семёрку – получится 42.
Самым сложным примером в таблице умножения считается 7∙8. Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
9. Как умножать многозначное число на однозначное?
Разберём на примере. Допустим, нам нужно умножить 468 на 6.
1) 468 состоит из 400, 60 и 8, и все это нужно умножить на 6. Что ж, по отдельности эти задачи не сложнее умножения однозначных чисел.
2) Идём от старшего разряда к младшему: 400∙6 = 2400 (поскольку 400 в 100 раз больше, чем 4, то и результат 400∙6 будет в 100 раз больше, чем результат 4∙6).
Соответственно, 60∙6 = 360, а 8∙6 = 48.
3) А теперь, как при сложении, складываем всё это вместе, группируя одинаковые разряды:
(2000+400)+(300+60)+(40+8) = [перегруппируем] =
= 2000+(400+300)+(60+40)+8 = [сложим одинаковые разряды] =
= 2000+700+100+8 = [сгруппируем и сложим одинаковые разряды] =
= 2000+800+8 = [дальше укрупнять нечего, получаем ответ] = 2808.
10. Как перемножать двузначные числа?
Для обычного человека это уже высший пилотаж! Если вы освоили умножение двузначных, считайте, что вы приняты в мир элиты устного счёта. Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем её).
Итак, например, умножим 78 на 56. Это означает, что нам нужно число 78 сложить («взять») 56 раз.
1) Эти 56 раз можно разбить на этапы – сначала 78 сложим 50 раз, потом 6 раз, а потом объединим результаты.
2) Число 78 сложить 50 раз несложно – это в 10 раз больше, чем сложить его 5 раз. 78∙5 = 70∙5+8∙5 = 350+40 = 390. А значит, 78∙50 = 3900, запомним это число.
3) Теперь посчитаем 78∙6 = 70∙6+8∙6 = 420+48 = 468.
4) Ну, а теперь сложим вместе оба результата: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Вуаля!
11. Ничего себе, осталось последнее только действие – деление?
Да, мы на финишной прямой. И снова начнём с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
Итак, что же такое деление? По сути, это «обратная» операция к умножению.
Например, разделить 56 на 7 – значит подобрать такое число, что если его умножить на 7, то получится 56. Поскольку вы к этому моменту уже хорошо ориентируетесь в таблице умножения, то наверняка вспомните, что именно 8, умноженное на 7, дает 56. Значит, искомое число – это 8, 56:7 = 8.
И так всегда – вспоминайте, какое число при умножении даёт нужный результат – это и есть то число, которое вам нужно.
12. Как делить многозначные числа на однозначное?
Давайте разделим 6144 на 8. Наш способ – «отрезать» от исходного числа максимальные «круглые» части, каждая из которых будет гарантированно делиться на 8 по таблице умножения.
1) Выделим из 6144 как можно большую часть, которая делится на 8 по таблице умножения. Это будет 5600, ведь 56 делится на 8, а следующее число, которое делится на 8 – это уже 64, что нам не подходит, так как 6400 больше, чем 6144. Прекрасно, 6144 – это 5600 и 544 (тут нам пригодился навык вычитания).
По ходу дела будем делить:
6144:8 = [выделяем максимальную удобную круглую часть] =
= (5600+544):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 700+544:8.
700 запомним как частичный результат, а сами займемся делением 544:8.
2) Аналогично, из числа 544 самая большая часть, которую можно удобно разделить на 8 по таблице умножения, это 480 (ведь 48 делится на 8, а следующее число – 56 – нам не подходит, т. к. 560 > 544). Итак, 544 = 480+64.
Продолжаем деление:
544:8 = [выделяем максимальную удобную круглую часть] =
= (480+64):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 60+64:8.
60 добавим к 700, 700+60 = 760 – запомним это как вторую часть результата и перейдём к последнему делению, 64:8.
3) Оставшийся кусочек, 64, тоже делится на 8 по таблице умножения, 64:8 = 8.
Соответственно, полный результат деления — это 760+8=768. Всё!
13. Как делить на двузначное число?
Техника деления на двузначное число – самая разнообразная, не похожая ни на что, изысканная. Познакомимся с ней на примере 5148:66.
1) Подгадаем, в каком десятке лежит наш результат. Напомним, что 5148:66 означает: мы ищем число, которое при умножении на 66 даст 5148. Будем использовать технику «пристрелки».
Просто наугад попробуем число 20 как возможного кандидата. 20∙66 = 1320, это раза в 4 меньше, чем 5148, которое нам нужно.
В 4 раза больше, чем 20 – это 80, попробуем его. 80∙66 = 5280, получилось больше, чем нужное 5148, но немного, скорее всего, это «верхний» десяток.
Проверим для надежности 70, предыдущий перед 80 десяток. 70∙66 = 4620, это как раз меньше 5148, отлично! Значит, число, которое мы ищем, лежит между 70 и 80.
2) Воспользуемся математическим законом о последней цифре результата умножения двух чисел.
Оказывается, она всегда совпадает с последней цифрой результата умножения последних цифр этих чисел (попробуйте подумать, почему это так). Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Поэтому, если мы ищем число, которое при умножении на 66 даст 5148, то, чтобы гарантировать эту 8 на последнем месте, искомое число может заканчиваться только либо на 3, либо на 8 (3∙6 = 18, 8∙6 = 48).
3) С такими окончаниями между 70 и 80 у нас два всего кандидата — 73 и 78.
5148 явно ближе к 5280, поэтому сперва проверим 78.
78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, ура!
(Ну, а если бы результат не сошёлся, то мы бы проверили второе число, и оно бы уже точно подошло).
14. Какие рекомендации напоследок?
Вот, в общем-то, и все способы, которые достаточно знать для тренировки уверенного счёта в пределах 10 000 (а умение работать в уме с большими числами, пожалуй, уже выходит за рамки необходимого общего развития).
Наверняка вы также столкнетесь с другими приемами, т. н. «хитростями» быстрого счёта, но не торопитесь увлекаться ими. Кроме того, помните, что регулярность важнее интенсивности – старайтесь заниматься на тренажере каждый день по 5-10 минут, больше не нужно, иначе велик риск «перегореть» и забросить.
В процессе занятия никуда не торопитесь – ловите свой ритм, делайте упор на правильность ответов, а не на скорость, скорость придет потом.
Обязательно пробуйте проговаривать свои действия вслух, особенно на первых порах – у вас будет шанс почувствовать, как все это похоже на стихи, да и решать так будет проще.
И не расстраивайтесь, если что-то не выходит – дорогу осилит идущий, и рано или поздно у вас точно всё получится.
Источник: https://meduza.io/
mediabrest.by
Как научить ребенка быстро складывать и вычитать в уме в 1-2 классе | RUTELO.RU

С поступлением в начальную школу выходит смена основной деятельности ребенка: все большее время у него сейчас занимают учебные действия. Большое внимание в этот период начинает уделяться обучению устному счету. И в этом проблеме действия педагога и родителя должны быть едины: если от ребенка на заданье требуется умение считать в уме, а дома этот процесс не контролируется, то навык будет формироваться весьма долго.
Как развить навык устного счета?
Многие педагоги не рекомендуют приучать детей находить на пальцах, так как при таком способе они не стремятся к запоминанию результата, ведь необходимый инструмент вечно находится рядом. А если во время подсчитывания не хватит пальцев, то дитя будет испытывать затруднение.
Нежелательно постоянно применять и палочки, чтобы отыскать результат. Работая с большими числами, ребенок может запутаться и пришагать к неверному решению. Конечно, полностью игнорировать эти методы не удастся, но лучше их использовать для объяснения материала, а не всегда. Постепенно уменьшая их использование, нужно прийти к навыку устного счета.
Он опирается на трех компонентах:- Способности: ребенок, чтобы научиться считать в уме, должен вначале развить в себе умение концентрировать внимание и запоминать несколько предметов одновременно.
- Знание алгоритмов быстрого счета и умение выбрать максимально эффективный в конкретной ситуации.
- Беспрерывные тренировки, которые позволят автоматизировать решение сложных задач и улучшить стремительность и качество счета.
Последняя составляющая является основной, но и значение первых двух не стоит недооценивать: ведая удобный алгоритм и имея необходимые математические способности, можно скоро решить необходимый пример.
Развитие навыка счета в уме у младших школьников опирается на двух видах деятельности:- Речевой – перед выполнением действия дитя сначала проговаривает его вслух, затем – шепотом, а после – про себя. Так, решая пример «2+1», проговаривает: «чтобы прибавить 1, необходимо назвать следующее число», а в уме определяет, что это – 3 и называет результат.
- Двигательный – вначале добавляет или убирает предметы (палочки, машинки) для подсчета результата, после делает это пальчиком, а на последнем этапе – глазами, совершая в уме необходимые поступки.
Можно предложить ребенку работать с числами с помощью пособий, предлагаемых различными методиками.
Методика Зайцева
Позволяет воспитать ребенка логически размышляющего, умеющего анализировать информацию и обобщать ее, выделять существенное. Ученикам 1-2 класса эти пособия помогут разобраться в арифметических поступках с числами.
Для изучения математических приемов понадобятся специальные карточки («Стосчет») с числами 0 – 99 и таблицы, наглядно демонстрирующие состав чисел (закрашено нужное число ячеек).
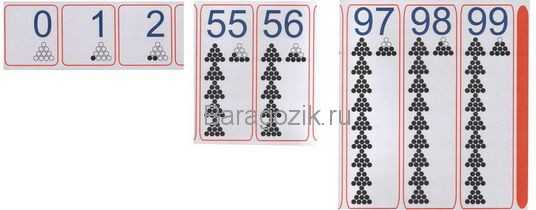
Сначала дитя знакомится с числами первого десятка, определяет состав его числа, а затем переходит к арифметическим поступкам с изученными цифрами.
Автор методики не рекомендует записывать сами образцы, изучая их наглядно и перемещаясь по числовой цепочке вверх или вниз в подневольности от того, складывают или вычитают числа.
Видеоурок с детьми по своей методике коротает Зайцев Н.А.
[embedded content]
Методика Полякова
Работа ведется с цветными кубиками и коробками с ячеями, где могут поместиться 10 кубиков. С помощью набора детям объясняют понятия «состав числа» и «десяток» и обучают навыку устного счета.

Даже смышленый ребенок порой может не понимать самых простых вещей. Это не сообщает о его непонятливости или несмышлености, скорее всего это свидетельствует об отсутствии интереса.
Ведь ребята могут воспринимать информацию и запоминать ее только тогда, когда она потребовала в них эмоциональный отклик. Яркие положительные эмоции дети испытывают во пора интересной игры, поэтому обучение навыку счета в уме лучше коротать в игровой деятельности.
Например, дети представляют, что кубики – это гномики, а коробка – их домик. В домике было 2 гномика, к ним в гости пришагало еще 3. Наглядно демонстрируется задача, закрывается крышка коробки и задается проблема: «Сколько гномиков стало в коробке?». Чтобы ответить на поставленный проблема, детям придется посчитать в уме, без опоры на кубики.
Постепенно задачи усложняются, ребята учатся складывать и вычитать с переходом через десяток, а потом и двузначные числа.
Видео сюжет расскажет об обучении детей по методике Сергея Полякова
[embedded content]
Алгоритмы
Скоро найти результат в уме поможет знание простых арифметических правил и закономерностей:
- Чтобы отнять 9, можно сначала вычесть 10, а затем прибавить 1. Аналогично вычитают числа 8 и 7, лишь потом прибавляют 2 и 3 соответственно.
- Числа 8 и 5 складывают так: сначала к 8 прибавляют 2 (чтобы вышло 10), а затем – 3 (5 – это 2 и 3). Аналогично решают все примеры на сложение с переходом сквозь десяток.
Для сложения двузначных чисел подойдут алгоритмы:
27+38=(27+40)-2=65
27+38=(20+30)+(7+8)=50+15=65
В первом случае второе слагаемое округляется до десятков, а затем вычитается добавленное число. Во втором — сначала складываются разрядные слагаемые, а затем – итоги.
При вычитании удобно округлять вычитаемое:
95-29=(95-30)+1=64
Или вычитать поразрядно: 75-24=75-20-4=51
Тренинги
Важный этап для развития навыка считать в уме.
Для тренировки можно использовать особые компьютерные программы или игры:- «Магазин». Ребенок может играть роль, как продавца, так и покупателя, все подсчеты должны проводиться в уме. Стоимости на товары устанавливаются в зависимости от способностей ученика.
- «Веселый счет». Взрослый кидает ребенку мяч и именует пример, на который нужно дать ответ. Таким образом, воспитывается счет на стволе.
- «Цепочки». Дается цепочка примеров, детям нужно найти последний результат, не записывая промежуточные результаты вычислений.
Если ребенок будет регулярно находить в уме, то этот навык будет развиваться. Такие занятия будут расцветай базой для изучения таблицы умножения и выполнения арифметических действий с трехзначными числами.
Видео сюжет расскажет, как научить школьника скоро считать в уме — не ментальная арифметика
[embedded content]
Поделитесь с друзьями:rutelo.ru
