КАК УМНОЖАТЬ В УМЕ: Эффективный счёт в уме или разминка для мозга | Не ври
 Если сумма цифр умножаемого на 111 двузначного числа Х меньше 10, то дважды «вставляем» сумму цифр между цифрами Х и, таким образом, получаем произведение. Нужно последовательно перемножить цифры в числах, чтобы получились сотни, единицы и десятки.
Если сумма цифр умножаемого на 111 двузначного числа Х меньше 10, то дважды «вставляем» сумму цифр между цифрами Х и, таким образом, получаем произведение. Нужно последовательно перемножить цифры в числах, чтобы получились сотни, единицы и десятки.
Примечание. Вообще, в начальной школе данная метода называется просто-напросто «умножение столбиком», но начальная школа — это было так давно, правда?.. 5 — цифра единиц произведения. Для наглядности выберем произвольное двузначное число. Пусть это будет 27. Именно его будем возводить в квадрат.
Количество десятков числа 27 – это 2. Умножаем: 27*2=54. Следующий шаг — возводим в квадрат количество единиц числа. Для числа 27 количество единиц равно 7. Следовательно 7*7=49. В заключение, к получившейся сумме 72 приписываем (не прибавляем!) единицы числа 49 (мы его получили перемножением единиц исходного числа). Прочитал инструкцию Violina про расчет процентов и захотелось написать как умножать двузначные числа в уме. С этим процессом постоянно всем приходиться сталкиваться.
И сложить эти три число тоже непросто. То есть у нас есть теперь два числа: 5940 и 297, которые надо сложить. Проще такие примеры решаются в 3 действия. Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат.

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные.
Как быстро считать? Хитрые приемчики счета в уме
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Подобные навыки позволяют не только обходиться без использования гаджетов для подсчета сдачи, но и позволяют человеку гораздо лучше организовать себя в различных жизненных ситуациях.
Облегчить подсчет в уме поможет использование специальных правил. Очень важным аспектом того, как правильно считать в уме, является знание таблицы умножения. В последнее время в анкетах для трудоустройства и непосредственно на собеседованиях работодатели требуют показать свои способности к математике.
Как умножать в уме
Кварцевание в домашних условиях: существует ли панацея? Дауншифтинг в России – блажь олигархов или серьезная национальная проблема? В Вашем браузере отключен JavaScript. Но самое главное, способности к вычислениям постоянно будут поддерживать в хорошей форме и развивать его умственные способности, что особенно важно для детей и молодежи в период обучения. Все навыки лучше всего развиваются и закрепляются в детстве.
Если в два – три с половиной годика вы будете использовать наглядные методы в обучении, то позже малыш сможет оперировать только цифрами, без подкрепления наглядным материалом.
В начальной школе малышу необходимо быстро и свободно производить любые вычисления в пределах, определенных школьной программой. В нижней строчке записываем пример 11х13. В верхней пишем, на сколько эти числа превышают 10. Получаем 1 и 3. Сложим числа по диагонали.
Быстрое умножение натуральных чисел
Но дабы научиться считать в уме, необходимо полностью избавиться от записей, а делать все в голове. В ином случае вы не добьетесь положительных результатов, а лишь навредите усвоению школьных знаний. Некоторые способы быстрого устного умножения мы уже с Вами разобрали, теперь давайте подробнее разберемся, как быстро умножать числа в уме, используя различные вспомогательные способы. Данный способ требует умения удерживать в памяти одновременно до четырех чисел, и делать с этими числами вычисления.
Этот один из самых универсальных способов устного умножения чисел, развивающий пространственное воображение и память. После этого Вы легко сможете умножать двухзначные числа в три действия. На самом деле, большая наглядность позволяет использовать этот способ гораздо эффективнее, чем умножение в столбик.
Не секрет, что есть некоторые люди, умеющие производить средне-сложные арифметические операции в уме с завидной скоростью. Но это не означает, что любой из нас, желающий узнать, как научиться считать в уме, обязан закончить математический ВУЗ. Итак, речь сегодня пойдет о том, как научиться считать.
Как научиться быстро считать взрослому
Без сомнений, ваш опыт и тренировка способностей сыграют важную роль в развитии подобных способностей. Но это ни в коем случае не означает того, что навык быстрого счета доступен только людям с опытом. Рассмотрим несколько общепринятых упрощений счета, с их помощью вам удастся научиться считать быстро.
Допустим, вам надо сложить 361 и 523. Сразу удержать в памяти будет не просто, согласитесь? Вот видите, было куда проще держать 3 числа в голове, чем единовременно складывать два трехзначных!
Как перемножать двузначные числа в уме?
Можно несколько схитрить, добавив в наш арсенал еще один навык – нарастить/отнять до круглого (удобного числа). Для начала отбросьте одинаковое кол-во нулей. В этом примере это просто — 39:4. Наш мозг гораздо охотнее оперирут с маленькими числами, чем с многоразрядными величинами.
Гораздо проще нашему мозгу воспринимать натуральные дроби, то есть представляем 0.25 как 1/4 (одна четвертая, четверть), и дальше будет совсем легко быстро посчитать в уме результат! Помните, не так сложно понять, как быстро научиться считать.
Возведение в квадрат чисел, оканчивающихся на 5
На самом деле делить большие числа на 5 очень просто. Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке.
Давайте умножим 99*20. В уме это просто 99*20=1980. Считать в уме – это путь рационализации, опирающийся на базовую арифметику. Со школьных времен многое забывается, и многие хотели бы еще раз узнать, как научиться считать в уме быстро. Для начала следует научиться умножать в столбик в уме двухзначные числа на однозначные.
Похожие материалы:
Как быстро умножить в уме двузначное число на 11? Занимательная математика | Мир вокруг нас
Это действительно очень просто! Занимает совсем мало времени и производит неизгладимое впечатление на собеседника, не знакомого с подобным математическим трюком.
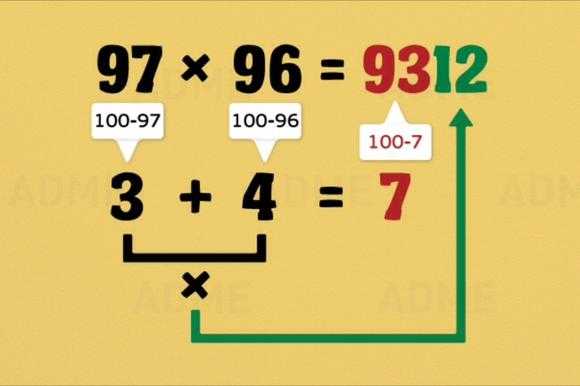
Итак, предложите собеседнику умножить любое двухзначное число на 11. И сделать это в уме. Пока он перемножает числа, вычислите ответ сами (метод ниже). Если ответ собеседника верный, похвалите гения математики и скажите, что вы это сделали быстрее. Если ответ неправильный и человек отказывается верить в то, что возможно перемножить эти числа в уме, переубедите его.
А все очень просто!
Чтобы любое двузначное число умножить на 11, нужно сложить его первую и последнюю цифру и цифру-результат вписать в середину двухзначного числа.
Примеры:
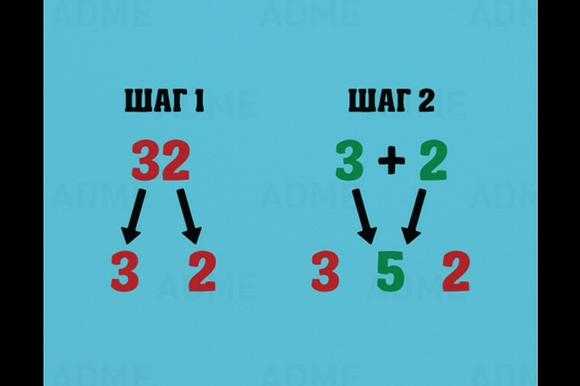
32×11
Пишем «32»
Складываем 3+2=5. А теперь вместо пробела впишите полученный результат.
Ответ: 352.
54×11
Пишем «54»
Складываем 5+4=9. А теперь вместо пробела впишите полученный результат.
Ответ: 594.
Всё еще не верите? Воспользуйтесь калькулятором!
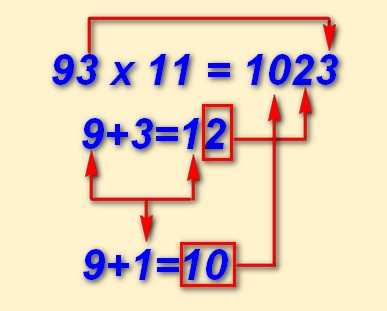
Если при сложении двух чисел получаем двухзначное число, поступаем немного по-другому.
Пример:
57×11
Пишем «57»
Складываем 5+7=12. Единицу прибавляем к пятерке, а двойку пишем в середину.
Ответ: 627.
Как видите, математика — это не только сухие цифры, статистика и скукота. Бывает еще и удивительная «занимательная математика».
Занимательная математика — это приятное развлечение на все времена, и в любом обществе. Свою историю она ведет с XX века до нашей эры! Да, именно в древних папирусах обнаружены занимательные задачи, которые включены и в современные сборники. Сочинением таких задач увлекались математики всех времен — Диофант Александрийский, Леонардо Пизанский (Фибоначчи), Никколо Тарталья…
Сборники математических развлечений, напоминающие современные, начали появляться с XVII в. Популярнейший сборник математических задач того времени «Приятные и занимательные задачи, рассматриваемые в числах» составил математик и поэт Клод Гаспар Баше де Мезирьяк. В то же время популярностью пользовались «Математические и физические развлечения» французского математика и писателя Жака Озанама.
Классическим стал четырехтомный труд по занимательной математике, созданный французским математиком Эдуардом Люка в XIX в.
На рубеже XIX и XX вв. большой вклад в занимательную математику внесли гениальные изобретатели игр и головоломок американский шахматист Сэмюэль Лойд и англичанин Генри Э. Дьюдени.
Занимательную математику второй половины XX в. представляет серия замечательных книг, принадлежащих перу знаменитого американского популяризатора математики Мартина Гарднера.
Сейчас в Интернете можно найти целые сайты, посвященные математическим головоломкам. А для нашего поколения настольными были «Математическая смекалка» Б. А. Кордемского, «В царстве смекалки» Е. И. Игнатьева и, конечно, замечательные книги Я. И. Перельмана «Живая математика», «Занимательная арифметика», «Занимательная алгебра» и «Занимательная геометрия».
Откройте их для себя и вы, и скучать не придется уже никогда!
shkolazhizni.ru
Как быстро умножать двузначные числа в уме
Правила_быстрого_устного_счета
Тест для начальных классов «как быстро умножить на 11 любое двузначное число» ab*11=a(a+b)b примеры 34*11=3(3+4)4=374 17*11=1(1+7)7=187 частные случаи если (a+b) двузначное число, то по-середине пишем (a+b-10) а к первой цифре прибавляем 1: ab*11=(a+1)(a+b-10)b примеры 47*11=(4+1)(4+7-10)(7)=517 95*11=(9+1)(9+5-10)5=1045
Как быстро умножать двузначные числа в уме?
А вот и не угадали, я не собираюсь научить вас пользоваться таблицей умножения и не буду учить вас считать в столбик. Я покажу вам способ как быстро считать в уме двузначные числа.
Инструкция
Уровень сложности: Легко
^
Полученное число умножаем на 10 – 24*10=240
3 шаг
Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
и всего-то,не верите проверьте на калькуляторе))))
^
Усвоив рекомендуемые приемы, можно выполнять быстрые расчеты в уме с безошибочностью письменных вычислений.
Умножение на однозначное число . Чтобы устно умножить число на однозначный множитель (например, 27 X 8) выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20×8 = 160), затем единицы (7*8 =56) и оба результата складывают.
Еще примеры:
34*7=30*7+4*7=210+28=238
47*6=40*6+7*6=240+42=282
^
Зная эту таблицу, можно умножение например, 147*8 выполнить в уме так: 147*8=140*8+7*8= 1120 + 56= 1176
Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350 Умножение на двузначное число
Умножение на двузначное число стараются облегчить для устного выполнения, приводя это действие к более привычному умножению на однозначное число.
Когда множимое однозначное, мысленно переставляют множители и выполняют действие.. Например:
6*28=28*6=120+48=168
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
29*12=29*10+29*2=290+58= 348
41*16=41*10+41*6 = 410+246 =656
(или 41*16=16*41 = 16*40+16*1=640+16=656
Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.
Если множимое или множитель легко разложить в уме на однозначные числа (напр., 14 = 2*7), то пользуются этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз . Например:
45*14 =90*7=630 Умножение на 4 и на 8
^
112*4 =224*2=448
335*4 = 670*2 =1340 .
Чтобы устно умножить число на 8, его трижды удваивают. Например:
217*8 = 434*4=868*2=1736
(Eще удобнее: 217*8=200*8 +17*8= 1600*13=1736. Деление на 4 и на 8 .
^ . Например:
76:4 =38:2=19
236:4=118:2=59 .
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
464:8=232:4=116:2=58
516:8=258:4=129:2= 64 1/2 Умножение на 5 и на 25 .
^ . Например:
74*5= 740:2= 370
243*5=2430:2=1215
При умножении на 5 числа четного удобнее сначала делить пополам и к полученному приписать ноль. Например:
74*5 = 74/2*10=370 .
^ . Например:
72*25=72/4*100= 1800
Если же число при делении на 4 дает остаток, то прибавляют
при остатке: к частному
1 25
2 50
3 75
Основание приема ясно из того, что
100:4=25;
200:4=50;
300:4=75 Умножение на 11/2, на 1 1/4, на 21/2, на 3/4 .
^ . Например:
34*11/2 = 34 + 17=51
23*11/2=23 + 111/2 = 341/2 (или 34,5)
Чтобы устно умножить число на 11/4 Прибавляют к множимому его четверть. Например:
48*11/4 =48 +12=60
58*11/4 = 58+14 1/2=721/2 или 72,5
Чтобы устно умножить число на 21/2. к удвоенному числу прибавляют половину множимого.
Например: 18*21/2.=36+9= 45;
39*21/2.= 78 + 191/2.= 971/2 (или 97,5)
Другой способ состоит в умножении на 5 и делении пополам:
18*21/2 = 90:2 = 45 .
Чтобы устно умножить число на 3/4 (т. е. чтобы найти 3/4 этого числа), умножают число на 11/2 и делит пополам. Например:
30 * 3/4 = (30+15)/2= 221/2 (или 22,5)
Видоизменение способа состоит в том, что от множимого отнимают его четверть или к половине множимого прибавляют половину этой половины. Умножение на 15, на 125, на 75
^ , (потому что 10*11/2 =15) Например:
18*15=18*11/2*10=270
45*15=450+225=675 .
Умножение на 125 заменяют умножением на 100 и на 11/4 (потому что 100*11/4=125). Например:
26*125 = 26*100*11/4 = 2600 + 650 = 3250
47*125 = 47*100*11/4 = 4700+4700/4= 4700+1175 = 5875 .
^ (потому что 100*3/4=75). Например:
18*75= 18*100*3/4 =1800* 3/4 =(1800 + 900)/2=1350
Примечание. Некоторые из приведенных примеров удобно выполняются также приемом
18*15 = 90*3 = 270
26*125 = 130*25 = 3250 Умножение на 9 и на 11 .
^ Например:
62*9=620-62=600—42=558
73*9=730-73=700—43=657
Чтобы устно умножить число на 11, приписывают к нему ноль и прибавляют множимое. Например:
87*11=870+87=957 Деление на 5, на 11/2,на 15
^ Например:
68:5=136:10=13,6
237:5 =474:10=47,4
Чтобы устно разделить число на 11/2 делят удвоенное число на 3. Например:
36:11/2=72:3=24
53:11/2=106:3=351/3
^ . Например
240:15=480:30=48:3=16
462:15=924:30=3024/30=304/5=30,8 (или 924:30 =308:10=30,8) Возвышение в квадрат .
^ (в нашем примере получается 7225). Еще примеры:
252; 2*3=6; 625
452; 4*5= 20; 2025
1452; 14*15 = 210; 21025
Прием этот вытекает из формулы (10х+5)2 = 100х2+100х+25=100х(х+1)+25 .
^
8,52 = 72,25
14,52=210,25
0,352 = 0,1225f и т. п. .
Так как 0,5= ½, а 0,25 = ¼, то приемом можно пользоваться также и для возвышения в квадрат чисел, оканчивающихся дробью ½:
(8½ )2 =72 ¼
(14½)2 = 210 ¼ и т п.
^
Например: 412=402 +1+2*40= 1601+80= 1681
692=702+1-2*70=4901-140=4761
362 =(35+1)2=1225+1+ 2*35=1296
^
(а+b) (а-b) = а2 — b2
Пусть требуется выполнить устно умножение 52*48
Мысленно представляем эти множители в виде (50 + 2)*(50—2)
и применяем приведенную в заголовке формулу:
(50+2)*(50—2)=502-22= 2496
^
69*71=(70—1)*(70+1)=4899
33*27=(30+3)*(30—3)=891
53*57=(55—2)*(55+2)=3021
84*86=(85-1)*(85+1)=7224 .
Указанным сейчас приемом удобно пользоваться и для вычислений следующего рода:
7 ½*6½=(7 + ½ )*(7 — ½)=48 ¾
11 3/4*12 1/4= (12 – 1/4)*(12 +1/4) =143 15/16 Полезно запомнить:
37*З =111
^
37*6=37*3*2=222
37*9=37*3*3=333
37*12=37*3*4=444
37*15=37*3*5 =555 и т. д,
7*11*13=1001
Запомнив это, легко выполнять устно умножения следующего рода:
77*13=1001
77*26=2002
77*39=3003 и т. д.
91*11=1001
91*22=2002
91*33=3003 и т. д.
143*7=1001
143*14=2002
143*21=3003 и т. д.
указаны только простейшие, наиболее удобоприменимые способы устного выполнения действий умножения, деления и возвышения в квадрат. Практикуясь в сознательном пользовании ими, вдумчивый выработайте для себя ряд еще и других приемов, облегчающих вычислительную работу.
www.velikol.ru
Как быстро умножать двузначные числа в уме
Правила_быстрого_устного_счета
Тест для начальных классов «как быстро умножить на 11 любое двузначное число» ab*11=a(a+b)b примеры 34*11=3(3+4)4=374 17*11=1(1+7)7=187 частные случаи если (a+b) двузначное число, то по-середине пишем (a+b-10) а к первой цифре прибавляем 1: ab*11=(a+1)(a+b-10)b примеры 47*11=(4+1)(4+7-10)(7)=517 95*11=(9+1)(9+5-10)5=1045
Как быстро умножать двузначные числа в уме?
А вот и не угадали, я не собираюсь научить вас пользоваться таблицей умножения и не буду учить вас считать в столбик. Я покажу вам способ как быстро считать в уме двузначные числа.
Инструкция
Уровень сложности: Легко
^
Полученное число умножаем на 10 – 24*10=240
3 шаг
Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
и всего-то,не верите проверьте на калькуляторе))))
^
Усвоив рекомендуемые приемы, можно выполнять быстрые расчеты в уме с безошибочностью письменных вычислений.
Умножение на однозначное число . Чтобы устно умножить число на однозначный множитель (например, 27 X 8) выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20×8 = 160), затем единицы (7*8 =56) и оба результата складывают.
Еще примеры:
34*7=30*7+4*7=210+28=238
47*6=40*6+7*6=240+42=282
^
Зная эту таблицу, можно умножение например, 147*8 выполнить в уме так: 147*8=140*8+7*8= 1120 + 56= 1176
Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350 Умножение на двузначное число
Умножение на двузначное число стараются облегчить для устного выполнения, приводя это действие к более привычному умножению на однозначное число.
Когда множимое однозначное, мысленно переставляют множители и выполняют действие.. Например:
6*28=28*6=120+48=168
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
29*12=29*10+29*2=290+58= 348
41*16=41*10+41*6 = 410+246 =656
(или 41*16=16*41 = 16*40+16*1=640+16=656
Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.
Если множимое или множитель легко разложить в уме на однозначные числа (напр., 14 = 2*7), то пользуются этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз . Например:
45*14 =90*7=630 Умножение на 4 и на 8
^
112*4 =224*2=448
335*4 = 670*2 =1340 .
Чтобы устно умножить число на 8, его трижды удваивают. Например:
217*8 = 434*4=868*2=1736
(Eще удобнее: 217*8=200*8 +17*8= 1600*13=1736. Деление на 4 и на 8 .
^ . Например:
76:4 =38:2=19
236:4=118:2=59 .
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
464:8=232:4=116:2=58
516:8=258:4=129:2= 64 1/2 Умножение на 5 и на 25 .
^ . Например:
74*5= 740:2= 370
243*5=2430:2=1215
При умножении на 5 числа четного удобнее сначала делить пополам и к полученному приписать ноль. Например:
74*5 = 74/2*10=370 .
^ . Например:
72*25=72/4*100= 1800
Если же число при делении на 4 дает остаток, то прибавляют
при остатке: к частному
1 25
2 50
3 75
Основание приема ясно из того, что
100:4=25;
200:4=50;
300:4=75 Умножение на 11/2, на 1 1/4, на 21/2, на 3/4 .
^ . Например:
34*11/2 = 34 + 17=51
23*11/2=23 + 111/2 = 341/2 (или 34,5)
Чтобы устно умножить число на 11/4 Прибавляют к множимому его четверть. Например:
48*11/4 =48 +12=60
58*11/4 = 58+14 1/2=721/2 или 72,5
Чтобы устно умножить число на 21/2. к удвоенному числу прибавляют половину множимого.
Например: 18*21/2.=36+9= 45;
39*21/2.= 78 + 191/2.= 971/2 (или 97,5)
Другой способ состоит в умножении на 5 и делении пополам:
18*21/2 = 90:2 = 45 .
Чтобы устно умножить число на 3/4 (т. е. чтобы найти 3/4 этого числа), умножают число на 11/2 и делит пополам. Например:
30 * 3/4 = (30+15)/2= 221/2 (или 22,5)
Видоизменение способа состоит в том, что от множимого отнимают его четверть или к половине множимого прибавляют половину этой половины. Умножение на 15, на 125, на 75
^ , (потому что 10*11/2 =15) Например:
18*15=18*11/2*10=270
45*15=450+225=675 .
Умножение на 125 заменяют умножением на 100 и на 11/4 (потому что 100*11/4=125). Например:
26*125 = 26*100*11/4 = 2600 + 650 = 3250
47*125 = 47*100*11/4 = 4700+4700/4= 4700+1175 = 5875 .
^ (потому что 100*3/4=75). Например:
18*75= 18*100*3/4 =1800* 3/4 =(1800 + 900)/2=1350
Примечание. Некоторые из приведенных примеров удобно выполняются также приемом
18*15 = 90*3 = 270
26*125 = 130*25 = 3250 Умножение на 9 и на 11 .
^ Например:
62*9=620-62=600—42=558
73*9=730-73=700—43=657
Чтобы устно умножить число на 11, приписывают к нему ноль и прибавляют множимое. Например:
87*11=870+87=957 Деление на 5, на 11/2,на 15
^ Например:
68:5=136:10=13,6
237:5 =474:10=47,4
Чтобы устно разделить число на 11/2 делят удвоенное число на 3. Например:
36:11/2=72:3=24
53:11/2=106:3=351/3
^ . Например
240:15=480:30=48:3=16
462:15=924:30=3024/30=304/5=30,8 (или 924:30 =308:10=30,8) Возвышение в квадрат .
^ (в нашем примере получается 7225). Еще примеры:
252; 2*3=6; 625
452; 4*5= 20; 2025
1452; 14*15 = 210; 21025
Прием этот вытекает из формулы (10х+5)2 = 100х2+100х+25=100х(х+1)+25 .
^
8,52 = 72,25
14,52=210,25
0,352 = 0,1225f и т. п. .
Так как 0,5= ½, а 0,25 = ¼, то приемом можно пользоваться также и для возвышения в квадрат чисел, оканчивающихся дробью ½:
(8½ )2 =72 ¼
(14½)2 = 210 ¼ и т п.
^
Например: 412=402 +1+2*40= 1601+80= 1681
692=702+1-2*70=4901-140=4761
362 =(35+1)2=1225+1+ 2*35=1296
^
(а+b) (а-b) = а2 — b2
Пусть требуется выполнить устно умножение 52*48
Мысленно представляем эти множители в виде (50 + 2)*(50—2)
и применяем приведенную в заголовке формулу:
(50+2)*(50—2)=502-22= 2496
^
69*71=(70—1)*(70+1)=4899
33*27=(30+3)*(30—3)=891
53*57=(55—2)*(55+2)=3021
84*86=(85-1)*(85+1)=7224 .
Указанным сейчас приемом удобно пользоваться и для вычислений следующего рода:
7 ½*6½=(7 + ½ )*(7 — ½)=48 ¾
11 3/4*12 1/4= (12 – 1/4)*(12 +1/4) =143 15/16 Полезно запомнить:
37*З =111
^
37*6=37*3*2=222
37*9=37*3*3=333
37*12=37*3*4=444
37*15=37*3*5 =555 и т. д,
7*11*13=1001
Запомнив это, легко выполнять устно умножения следующего рода:
77*13=1001
77*26=2002
77*39=3003 и т. д.
91*11=1001
91*22=2002
91*33=3003 и т. д.
143*7=1001
143*14=2002
143*21=3003 и т. д.
указаны только простейшие, наиболее удобоприменимые способы устного выполнения действий умножения, деления и возвышения в квадрат. Практикуясь в сознательном пользовании ими, вдумчивый выработайте для себя ряд еще и других приемов, облегчающих вычислительную работу.
velikol.ru
Перемножение двузначных чисел в уме – Быстрый ум. Как забывать лишнее и помнить нужное – Майк Байстер – rutlib5.com
Перемножение двузначных чисел в уме
На первый взгляд кажется, что какое бы то ни было перемножение — это чистая математика, но на самом деле это один из наиболее мощных способов комплексной тренировки мозга и применения на практике сложного искусства забывать. Это правда: осваивая быстрое перемножение двузначных чисел в уме при помощи моего остроумного алгоритма, вы волей- неволей должны будете забывать на пути к ответу определенную часть информации. Это упражнение, помимо всего прочего, демонстрирует еще один аспект забывания, о котором мы еще не говорили: иногда нам нужно быстро проработать какую-то информацию, а затем выбросить ее из головы, чтобы освободить пространство для новой информации. Перемножение двузначных чисел в уме чудесно иллюстрирует этот навык, и вы скоро сами это поймете, когда пройдете все шаги. Это умение применимо в самых разных ситуациях, не только в математике, потому что нам каждый день нужно стирать в мозгу устаревшие ненужные «файлы», чтобы записать на их место новые.
Изобретение этого метода когда-то стало поворотным пунктом в моей жизни. Я учился тогда в шестом классе, а в восьмом классе математику вел Арни Бенсон, славившийся необычайно быстрым умом и невероятной способностью работать с числами. Это был первый встреченный мной в жизни человек, который по-настоящему хорошо умел работать с числами (не считая, конечно, моего отца и его братьев). Я смотрел на Арни снизу вверх и мечтал когда-нибудь сравняться с ним и, может быть, даже превзойти его. Когда по школе прошел слух о том, что я мог бы потягаться с ним в умножении однозначного числа на двузначное, он вызвал меня на состязание. И я победил. После этого Арни сказал мне: «Майк, в следующий раз проделаем то же самое с двузначными числами». Он и не подозревал, что у меня нет коротких алгоритмов для умножения двузначного числа на двузначное. Умножать однозначные числа на двузначные я был готов хоть с утра до вечера, но перемножать двузначные? Я понятия не имел, как буду выходить из сложившейся ситуации. И тогда я сел и поклялся себе придумать такой алгоритм, который позволил бы мне вновь победить учителя.
Мне повезло, и вторая встреча между нами не состоялась. Но я все-таки придумал формулу для устных вычислений такого рода, и эта формула подтолкнула меня к придумыванию новых формул и алгоритмов. Как только до меня дошло, что задачи, как правило, можно решать не одним, а несколькими способами, я понял, что этот принцип приложим в жизни практически к любой задаче. Мне уже не нужно было полагаться целиком и полностью на правила и алгоритмы, которые приводились в учебнике или предлагались кем-то другим. Я мог как угодно прокладывать курс в море чисел, слов и других закономерностей, мог выбирать необычный путь, но достигать того же самого верного ответа.
Арни сейчас живет в Далласе (штат Техас) и умен по-прежнему. Мы до сих пор поддерживаем с ним отношения, ведь его влияние на меня и время, проведенное на его уроках, стали определяющими моментами моей жизни; именно тогда передо мной будто распахнулась дверь и я стал с неослабным интересом придумывать алгоритмы вычислений, чтобы быть впереди всех. Присутствие Арни давало мне дополнительный стимул; мне очень не хотелось опять столкнуться с кем-то, кто вызовет меня на поединок, который я не смогу выиграть! До сего дня одна мысль о том, что мне предстоит испытание или дуэль с сильнейшим противником, заставляет меня без конца выдумывать новые уловки и обходные пути.
Я призываю вас попробовать это упражнение, даже если вы всей душой ненавидите числа и математику. Обещаю, что, как только вы уловите суть этого приема, вам захочется проделывать его снова и снова и демонстрировать свое тайное умение приятелям.
Для начала позвольте показать вам пошагово, как выполняются эти выч
rutlib5.com
