Частные производные второго порядка, теория и примеры
Если задана функция и вычислены ее частные производные и то они в свою очередь также являются функциями независимых переменных и а поэтому от каждой из них можно найти производную по каждой из переменных.
ОПРЕДЕЛЕНИЕ Если найти частную производную по переменной от частной производной первого порядка то получаем частную производную второго порядка от функции которую взято два раза по переменной Это производная обознается как:
Итак,
Если взять частную производную по переменной от производной то получим частную производную второго порядка функции , которую взято вначале по переменной а потом – по переменной Такая производная называется смешанной производной и обозначается
Аналогично, частная производная по переменной от первой производной по переменной дает вторую смешанную частную производную функции вычисленную вначале по переменной а потом – по переменной Она обозначается символом
ТЕОРЕМА Смешанные производные, если они непрерывны, не зависят от порядка дифференцирования, то есть
Частная производная по переменной от производной первого порядка есть второй частной производной от функции по переменной Ее обозначают следующим образом:
Подобным образом задаются производные более высокого порядка, чем второй. Например, выражение определяет производную третьего порядка функции найденную три раза по переменной Аналогично – смешанная производная третьего порядка, взятая два раза по переменной и от полученной производной найдена один раз производная по переменной
| Задание | Найти все частные производные второго порядка функции |
| Решение | Чтобы найти производные второго порядка, вначале вычислим частные производные первого порядка:
Переходим к нахождению частных производных второго порядка. Для нахождения второй производной продифференцируем выражение по переменной
Аналогично
Смешанные производные:
Получили, что Таким же образом находим оставшиеся смешанные производные:
Проверка: Аналогично
и равенство выполняется. |
| Ответ |
ru.solverbook.com
Частные производные функции нескольких переменных
Рассмотрим функцию от двух переменных:
\[f=f\left( x,y \right)\]
Поскольку переменные $x$ и $y$ являются независимыми, для такой функции можно ввести понятие частной производной:
Частная производная функции $f$ в точке $M=\left( {{x}_{0}};{{y}_{0}} \right)$ по переменной $x$ — это предел
\[{{{f}’}_{x}}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{0}}+\Delta x;{{y}_{0}} \right)}{\Delta x}\]
Аналогично можно определить частную производную по переменной $y$ :
\[{{{f}’}_{y}}=\underset{\Delta y\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{0}};{{y}_{0}}+\Delta y \right)}{\Delta y}\]
Другими словами, чтобы найти частную производную функции нескольких переменных, нужно зафиксировать все остальные переменные, кроме искомой, а затем найти обычную производную по этой искомой переменной.
Отсюда вытекает основной приём для вычисления таких производных: просто считайте, что все переменные, кроме данной, являются константой, после чего дифференцируйте функцию так, как дифференцировали бы «обычную» — с одной переменной. Например:
$\begin{align}& {{\left( {{x}^{2}}+10xy \right)}_{x}}^{\prime }={{\left( {{x}^{2}} \right)}^{\prime }}_{x}+10y\cdot {{\left( x \right)}^{\prime }}_{x}=2x+10y, \\ & {{\left( {{x}^{2}}+10xy \right)}_{y}}^{\prime }={{\left( {{x}^{2}} \right)}^{\prime }}_{y}+10x\cdot {{\left( y \right)}^{\prime }}_{y}=0+10x=10x. \\\end{align}$
Очевидно, что частные производные по разным переменным дают разные ответы — это нормально. Куда важнее понимать, почему, скажем, в первом случае мы спокойно вынесли $10y$ из-под знака производной, а во втором — вовсе обнулили первое слагаемое. Всё это происходит из-за того, что все буквы, кроме переменной, по которой идёт дифференцирование, считаются константами: их можно выносить, «сжигать» и т.д.
Что такое «частная производная»?
Сегодня мы поговорим о функциях нескольких переменных и о частных производных от них. Во-первых, что такое функция нескольких переменных? До сих пор мы привыкли считать функцию как $y\left( x \right)$ или $t\left( x \right)$, или любую переменную и одну-единственную функцию от нее. Теперь же функция у нас будет одна, а переменных несколько. При изменении $y$ и $x$ значение функции будет меняться. Например, если $x$ увеличится в два раза, значение функции поменяется, при этом если $x$ поменяется, а $y$ не изменится, значение функции точно так же изменится.
Разумеется, функцию от нескольких переменных, точно так же как и от одной переменной, можно дифференцировать. Однако поскольку переменных несколько, то и дифференцировать можно по разным переменным. При этом возникают специфические правила, которых не было при дифференцировании одной переменной.
Прежде всего, когда мы считаем производную функции от какой-либо переменной, то обязаны указывать, по какой именно переменной мы считаем производную — это и называется частной производной. Например, у нас функция от двух переменных, и мы можем посчитать ее как по $x$, так и по $y$ — две частных производных у каждой из переменных.
Во-вторых, как только мы зафиксировали одну из переменных и начинаем считать частную производную именно по ней, то все остальные, входящие в эту функцию, считаются константами. Например, в $z\left( xy \right)$, если мы считаем частную производную по $x$, то везде, где мы встречаем $y$, мы считаем ее константой и обращаемся с ней именно как с константой. В частности при вычислении производной произведения мы можем выносить $y$ за скобку (у нас же константа), а при вычислении производной суммы, если у нас где-то получается производная от выражения, содержащего $y$ и не содержащего $x$, то производная этого выражения будет равна «нулю» как производная константы.
На первый взгляд может показаться, что я рассказываю о чем-то сложном, и многие ученики по началу путаются. Однако ничего сверхъестественного в частных производных нет, и сейчас мы убедимся в этом на примере конкретных задач.
Задачи с радикалами и многочленами
Задача № 1
Чтобы не терять время зря, с самого начала начнем с серьезных примеров.
\[z\left( x,y \right)=\sqrt{\frac{y}{x}}\]
Для начала напомню такую формулу:
\[{{\left( \sqrt{x} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{x}}\]
Это стандартное табличное значение, которое мы знаем из стандартного курса.
В этом случае производная $z$ считается следующим образом:
\[{{{z}’}_{x}}={{\left( \sqrt{\frac{y}{x}} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{\frac{y}{x}}}{{\left( \frac{y}{x} \right)}^{\prime }}_{x}\]
Давайте еще раз, поскольку под корнем стоит не $x$, а некое другое выражение, в данном случае $\frac{y}{x}$, то сначала мы воспользуемся стандартным табличным значением, а затем, поскольку под корнем стоит не $x$, а другое выражение, нам необходимо домножить нашу производную на еще одну из этого выражения по той же самой переменной. Давайте для начала посчитаем следующее:
\[{{\left( \frac{y}{x} \right)}^{\prime }}_{x}=\frac{{{{{y}’}}_{x}}\cdot x-y\cdot {{{{x}’}}_{x}}}{{{x}^{2}}}=\frac{0\cdot x-y\cdot 1}{{{x}^{2}}}=-\frac{y}{{{x}^{2}}}\]
Возвращаемся к нашему выражению и записываем:
\[{{{z}’}_{x}}={{\left( \sqrt{\frac{y}{x}} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{\frac{y}{x}}}{{\left( \frac{y}{x} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot \left( -\frac{y}{{{x}^{2}}} \right)\]
В принципе, это все. Однако оставлять ее в таком виде неправильно: такую конструкцию неудобно использовать для дальнейших вычислений, поэтому давайте ее немного преобразуем:
\[\frac{1}{2\sqrt{\frac{y}{x}}}\cdot \left( -\frac{y}{{{x}^{2}}} \right)=\frac{1}{2}\cdot \sqrt{\frac{x}{y}}\cdot \frac{y}{{{x}^{2}}}=\]
\[=-\frac{1}{2}\cdot \sqrt{\frac{x}{y}}\cdot \sqrt{\frac{{{y}^{2}}}{{{x}^{4}}}}=-\frac{1}{2}\sqrt{\frac{x\cdot {{y}^{2}}}{y\cdot {{x}^{4}}}}=-\frac{1}{2}\sqrt{\frac{y}{{{x}^{3}}}}\]
Ответ найден. Теперь займемся $y$:
\[{{{z}’}_{y}}={{\left( \sqrt{\frac{y}{x}} \right)}^{\prime }}_{y}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot {{\left( \frac{y}{x} \right)}^{\prime }}_{y}\]
Выпишем отдельно:
\[{{\left( \frac{y}{x} \right)}^{\prime }}_{y}=\frac{{{{{y}’}}_{y}}\cdot x-y\cdot {{{{x}’}}_{y}}}{{{x}^{2}}}=\frac{1\cdot x-y\cdot 0}{{{x}^{2}}}=\frac{1}{x}\]
Теперь записываем:
\[{{{z}’}_{y}}={{\left( \sqrt{\frac{y}{x}} \right)}^{\prime }}_{y}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot {{\left( \frac{y}{x} \right)}^{\prime }}_{y}=\frac{1}{2\sqrt{\frac{y}{x}}}\cdot \frac{1}{x}=\]
\[=\frac{1}{2}\cdot \sqrt{\frac{x}{y}}\cdot \sqrt{\frac{1}{{{x}^{2}}}}=\frac{1}{2}\sqrt{\frac{x}{y\cdot {{x}^{2}}}}=\frac{1}{2\sqrt{xy}}\]
Все сделано.
Задача № 2
\[z\left( x,y \right)=\frac{xy}{{{x}^{2}}+{{y}^{2}}+1}\]
Этот пример одновременно и проще, и сложней, чем предыдущий. Сложнее, потому что здесь больше действий, а проще, потому что здесь нет корня и, кроме того, функция симметрична относительно $x$ и $y$, т.е. если мы поменяем $x$ и $y$ местами, формула от этого не изменится. Это замечание в дальнейшем упростит нам вычисление частной производной, т.е. достаточно посчитать одну из них, а во второй просто поменять местами $x$ и $y$.
Приступаем к делу:
\[{{{z}’}_{x}}={{\left( \frac{xy}{{{x}^{2}}+{{y}^{2}}+1} \right)}^{\prime }}_{x}=\frac{{{\left( xy \right)}^{\prime }}_{x}\left( {{x}^{2}}+{{y}^{2}}+1 \right)-xy{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}}{{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}\]
Давайте посчитаем:
\[{{\left( xy \right)}^{\prime }}_{x}=y\cdot {{\left( x \right)}^{\prime }}=y\cdot 1=y\]
Однако многим ученикам такая запись непонятна, поэтому запишем вот так:
\[{{\left( xy \right)}^{\prime }}_{x}={{\left( x \right)}^{\prime }}_{x}\cdot y+x\cdot {{\left( y \right)}^{\prime }}_{x}=1\cdot y+x\cdot 0=y\]
Таким образом, мы еще раз убеждаемся в универсальности алгоритма частных производных: каким бы мы образом их не считали, если все правила применяются верно, ответ будет один и тот же.
Теперь давайте разберемся еще с одной частной производной из нашей большой формулы:
\[{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}={{\left( {{x}^{2}} \right)}^{\prime }}_{x}+{{\left( {{y}^{2}} \right)}^{\prime }}_{x}+{{{1}’}_{x}}=2x+0+0\]
Подставим полученные выражения в нашу формулу и получим:
\[\frac{{{\left( xy \right)}^{\prime }}_{x}\left( {{x}^{2}}+{{y}^{2}}+1 \right)-xy{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}}{{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}=\]
\[=\frac{y\cdot \left( {{x}^{2}}+{{y}^{2}}+1 \right)-xy\cdot 2x}{{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}=\]
\[=\frac{y\left( {{x}^{2}}+{{y}^{2}}+1-2{{x}^{2}} \right)}{{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}=\frac{y\left( {{y}^{2}}-{{x}^{2}}+1 \right)}{{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}\]
По $x$ посчитано. А чтобы посчитать $y$ от того же самого выражения, давайте не будем выполнять всю ту же последовательность действий, а воспользуемся симметрией нашего исходного выражения — мы просто заменим в нашем исходном выражении все $y$ на $x$ и наоборот:
\[{{{z}’}_{y}}=\frac{x\left( {{x}^{2}}-{{y}^{2}}+1 \right)}{{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{2}}}\]
За счет симметрии мы посчитали это выражение гораздо быстрее.
Нюансы решения
Для частных производных работают все стандартные формулы, которые мы используем для обычных, а именно, производная частного. При этом, однако, возникают свои специфические особенности: если мы считаем частную производную $x$, то когда мы получаем ее по $x$, то рассматриваем ее как константу, и поэтому ее производная будет равна «нулю».
Как и в случае с обычными производными, частную (одну и ту же) можно посчитать несколькими различными способами. Например, ту же конструкцию, которую мы только что посчитали, можно переписать следующим образом:
\[{{\left( \frac{y}{x} \right)}^{\prime }}_{x}=y\cdot {{\left( \frac{1}{x} \right)}^{\prime }}_{x}=-y\frac{1}{{{x}^{2}}}\]
Далее мы точно таким же образом считаем еще две конструкции, а именно:
\[{{\left( xy \right)}^{\prime }}_{x}=y\cdot {{{x}’}_{x}}=y\cdot 1=y\]
Вместе с тем, с другой стороны, можно использовать формулу от производной суммы. Как мы знаем, она равна сумме производных. Например, запишем следующее:
\[{{\left( {{x}^{2}}+{{y}^{2}}+1 \right)}^{\prime }}_{x}=2x+0+0=2x\]
Теперь, зная все это, давайте попробуем поработать с более серьезными выражениями, поскольку настоящие частные производные не ограничиваются одними лишь многочленами и корнями: там встречаются и тригонометрия, и логарифмы, и показательная функция. Сейчас этим и займемся.
Задачи с тригонометрическими функциями и логарифмами
Задача № 1
\[z\left( x,y \right)=\sqrt{x}\cos \frac{x}{y}\]
Запишем следующие стандартные формулы:
\[{{\left( \sqrt{x} \right)}^{\prime }}_{x}=\frac{1}{2\sqrt{x}}\]
\[{{\left( \cos x \right)}^{\prime }}_{x}=-\sin x\]
Вооружившись этими знаниями, попробуем решить:
\[{{{z}’}_{x}}={{\left( \sqrt{x}\cdot \cos \frac{x}{y} \right)}^{\prime }}_{x}={{\left( \sqrt{x} \right)}^{\prime }}_{x}\cdot \cos \frac{x}{y}+\sqrt{x}\cdot {{\left( \cos \frac{x}{y} \right)}^{\prime }}_{x}=\]
Отдельно выпишем одну переменную:
\[{{\left( \cos \frac{x}{y} \right)}^{\prime }}_{x}=-\sin \frac{x}{y}\cdot {{\left( \frac{x}{y} \right)}^{\prime }}_{x}=-\frac{1}{y}\cdot \sin \frac{x}{y}\]
Возвращаемся к нашей конструкции:
\[=\frac{1}{2\sqrt{x}}\cdot \cos \frac{x}{y}+\sqrt{x}\cdot \left( -\frac{1}{y}\cdot \sin \frac{x}{y} \right)=\frac{1}{2\sqrt{x}}\cdot \cos \frac{x}{y}-\frac{\sqrt{x}}{y}\cdot \sin \frac{x}{y}\]
Все, по $x$ мы нашли, теперь давайте займемся вычислениями по $y$:
\[{{{z}’}_{y}}={{\left( \sqrt{x}\cdot \cos \frac{x}{y} \right)}^{\prime }}_{y}={{\left( \sqrt{x} \right)}^{\prime }}_{y}\cdot \cos \frac{x}{y}+\sqrt{x}\cdot {{\left( \cos \frac{x}{y} \right)}^{\prime }}_{y}=\]
Опять же посчитаем одно выражение:
\[{{\left( \cos \frac{x}{y} \right)}^{\prime }}_{y}=-\sin \frac{x}{y}\cdot {{\left( \frac{x}{y} \right)}^{\prime }}_{y}=-\sin \frac{x}{y}\cdot x\cdot \left( -\frac{1}{{{y}^{2}}} \right)\]
Возвращаемся к исходному выражению и продолжаем решение:
\[=0\cdot \cos \frac{x}{y}+\sqrt{x}\cdot \frac{x}{{{y}^{2}}}\sin \frac{x}{y}=\frac{x\sqrt{x}}{{{y}^{2}}}\cdot \sin \frac{x}{y}\]
Все сделано.
Задача № 2
\[z\left( x,y \right)=\ln \left( x+\ln y \right)\]
Запишем необходимую нам формулу:
\[{{\left( \ln x \right)}^{\prime }}_{x}=\frac{1}{x}\]
Теперь посчитаем по $x$:
\[{{{z}’}_{x}}={{\left( \ln \left( x+\ln y \right) \right)}^{\prime }}_{x}=\frac{1}{x+\ln y}.{{\left( x+\ln y \right)}^{\prime }}_{x}=\]
\[=\frac{1}{x+\ln y}\cdot \left( 1+0 \right)=\frac{1}{x+\ln y}\]
По $x$ найдено. Считаем по $y$:
\[{{{z}’}_{y}}={{\left( \ln \left( x+\ln y \right) \right)}^{\prime }}_{y}=\frac{1}{x+\ln y}.{{\left( x+\ln y \right)}^{\prime }}_{y}=\]
\[=\frac{1}{x+\ln y}\left( 0+\frac{1}{y} \right)=\frac{1}{y\left( x+\ln y \right)}\]
Задача решена.
Нюансы решения
Итак, от какой бы функции мы не брали частную производную, правила остаются одними и теми же, независимо от того, работаем ли мы с тригонометрией, с корнями или с логарифмами.
Неизменными остаются классические правила работы со стандартными производными, а именно, производная суммы и разности, частного и сложной функции.
Последняя формула чаще всего и встречается при решении задач с частными производными. Мы встречаемся с ними практически везде. Ни одной задачи еще не было, чтобы там нам она не попадалась. Но какой бы мы формулой не воспользовались, нам все равно добавляется еще одно требование, а именно, особенность работы с частными производными. Как только мы фиксируем одну переменную, все остальные оказываются константами. В частности, если мы считаем частную производную выражения $\cos \frac{x}{y}$ по $y$, то именно $y$ и является переменной, а $x$ везде остается константой. То же самое работает и наоборот. Ее можно выносить за знак производной, а производная от самой константы будет равна «нулю».
Все это приводит к тому, что частные производные от одного и того же выражения, но по разным переменным могут выглядеть совершенно по-разному. Например, посмотрим такие выражения:
\[{{\left( x+\ln y \right)}^{\prime }}_{x}=1+0=1\]
\[{{\left( x+\ln y \right)}^{\prime }}_{y}=0+\frac{1}{y}=\frac{1}{y}\]
Задачи с показательными функциями и логарифмами
Задача № 1
\[z\left( x,y \right)={{e}^{x}}{{e}^{\frac{x}{y}}}\]
Для начала запишем такую формулу:
\[{{\left( {{e}^{x}} \right)}^{\prime }}_{x}={{e}^{x}}\]
Зная этот факт, а также производную сложной функции, давайте попробуем посчитать. Я сейчас решу двумя различными способами. Первый и самый очевидный — это производная произведения:
\[{{{z}’}_{x}}={{\left( {{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}={{\left( {{e}^{x}} \right)}^{\prime }}_{x}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{\left( {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}=\]
\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot {{\left( \frac{x}{y} \right)}^{\prime }}_{x}=\]
Давайте решим отдельно следующее выражение:
\[{{\left( \frac{x}{y} \right)}^{\prime }}_{x}=\frac{{{{{x}’}}_{x}}\cdot y-x.{{{{y}’}}_{x}}}{{{y}^{2}}}=\frac{1\cdot y-x\cdot 0}{{{y}^{2}}}=\frac{y}{{{y}^{2}}}=\frac{1}{y}\]
Возвращаемся к нашей исходной конструкции и продолжаем решение:
\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot \frac{1}{y}={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\left( 1+\frac{1}{y} \right)\]
Все, по $x$ посчитано.
Однако как я и обещал, сейчас постараемся посчитать эту же частную производную другим способом. Для этого заметим следующее:
\[{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}={{e}^{x+\frac{x}{y}}}\]
В этом запишем так:
\[{{\left( {{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}={{\left( {{e}^{x+\frac{x}{y}}} \right)}^{\prime }}_{x}={{e}^{x+\frac{x}{y}}}\cdot {{\left( x+\frac{x}{y} \right)}^{\prime }}_{x}={{e}^{x+\frac{x}{y}}}\cdot \left( 1+\frac{1}{y} \right)\]
В результате мы получили точно такой же ответ, однако объем вычислений оказался меньшим. Для этого достаточно было заметить, что при произведении показатели можно складывать.
Теперь посчитаем по $y$:
\[{{{z}’}_{y}}={{\left( {{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{y}={{\left( {{e}^{x}} \right)}^{\prime }}_{y}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{\left( {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{y}=\]
\[=0\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot {{\left( \frac{x}{y} \right)}^{\prime }}_{y}=\]
Давайте решим одно выражение отдельно:
\[{{\left( \frac{x}{y} \right)}^{\prime }}_{y}=\frac{{{{{x}’}}_{y}}\cdot y-x\cdot {{{{y}’}}_{y}}}{{{y}^{2}}}=\frac{0-x\cdot 1}{{{y}^{2}}}=-\frac{1}{{{y}^{2}}}=-\frac{x}{{{y}^{2}}}\]
Продолжим решение нашей исходной конструкции:
\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot \left( -\frac{x}{{{y}^{2}}} \right)=-\frac{x}{{{y}^{2}}}\cdot {{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\]
Разумеется, эту же производную можно было бы посчитать вторым способом, ответ получился бы таким же.
Задача № 2
\[z\left( x,y \right)=x\ln \left( {{x}^{2}}+y \right)\]
Посчитаем по $x$:
\[{{{z}’}_{x}}={{\left( x \right)}_{x}}\cdot \ln \left( {{x}^{2}}+y \right)+x\cdot {{\left( \ln \left( {{x}^{2}}+y \right) \right)}^{\prime }}_{x}=\]
Давайте посчитаем одно выражение отдельно:
\[{{\left( \ln \left( {{x}^{2}}+y \right) \right)}^{\prime }}_{x}=\frac{1}{{{x}^{2}}+y}\cdot {{\left( {{x}^{2}}+y \right)}^{\prime }}_{x}=\frac{2x}{{{x}^{2}}+y}\]
Продолжим решение исходной конструкции: $$
\[1\cdot \ln \left( {{x}^{2}}+y \right)+x\cdot \frac{2x}{{{x}^{2}}+y}=\ln \left( {{x}^{2}}+y \right)+\frac{2{{x}^{2}}}{{{x}^{2}}+y}\]
Вот такой ответ.
Осталось по аналогии найти по $y$:
\[{{{z}’}_{y}}={{\left( x \right)}^{\prime }}_{y}.\ln \left( {{x}^{2}}+y \right)+x\cdot {{\left( \ln \left( {{x}^{2}}+y \right) \right)}^{\prime }}_{y}=\]
Одно выражение посчитаем как всегда отдельно:
\[{{\left( {{x}^{2}}+y \right)}^{\prime }}_{y}={{\left( {{x}^{2}} \right)}^{\prime }}_{y}+{{{y}’}_{y}}=0+1=1\]
Продолжаем решение основной конструкции:
\[x\cdot \frac{1}{{{x}^{2}}+y}\cdot 1=\frac{x}{{{x}^{2}}+y}\]
Все посчитано. Как видите, в зависимости от того, какая переменная берется для дифференцирования, ответы получаются совершенно разные.
Нюансы решения
Вот яркий пример того, как производную одной и той же функции можно посчитать двумя различными способами. Вот смотрите:
\[{{{z}’}_{x}}=\left( {{e}^{x}}\cdot {{e}^{\frac{x}{y}}} \right)={{\left( {{e}^{x}} \right)}^{\prime }}_{x}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{\left( {{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}=\]
\[={{e}^{x}}\cdot {{e}^{\frac{x}{y}}}+{{e}^{x}}\cdot {{e}^{\frac{x}{y}}}\cdot \frac{1}{y}={{e}^{x}}\cdot {{e}^{^{\frac{x}{y}}}}\left( 1+\frac{1}{y} \right)\]
\[{{{z}’}_{x}}={{\left( {{e}^{x}}.{{e}^{\frac{x}{y}}} \right)}^{\prime }}_{x}={{\left( {{e}^{x+\frac{x}{y}}} \right)}^{\prime }}_{x}={{e}^{x+\frac{x}{y}}}.{{\left( x+\frac{x}{y} \right)}^{\prime }}_{x}=\]
\[={{e}^{x}}\cdot {{e}^{^{\frac{x}{y}}}}\left( 1+\frac{1}{y} \right)\]
При выборе разных путей, объем вычислений может быть разный, но ответ, если все выполнено верно, получится одним и тем же. Это касается как классических, так и частных производных. При этом еще раз напоминаю: в зависимости от того, по какой переменной идет взятие производной, т.е. дифференцирование, ответ может получиться совершенно разный. Посмотрите:
\[{{\left( \ln \left( {{x}^{2}}+y \right) \right)}^{\prime }}_{x}=\frac{1}{{{x}^{2}}+y}\cdot {{\left( {{x}^{2}}+y \right)}^{\prime }}_{x}=\frac{1}{{{x}^{2}}+y}\cdot 2x\]
\[{{\left( \ln \left( {{x}^{2}}+y \right) \right)}^{\prime }}_{y}=\frac{1}{{{x}^{2}}+y}\cdot {{\left( {{x}^{2}}+y \right)}^{\prime }}_{y}=\frac{1}{{{x}^{2}}+y}\cdot 1\]
В заключение для закрепления всего этого материала давайте попробуем посчитать еще два примера.
Задачи с тригонометрической функция и функцией с тремя переменными
Задача № 1
\[z\left( x,y \right)={{3}^{x\sin y}}\]
Давайте запишем такие формулы:
\[{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\cdot \ln a\]
\[{{\left( {{e}^{x}} \right)}^{\prime }}={{e}^{x}}\]
Давайте теперь решать наше выражение:
\[{{{z}’}_{x}}={{\left( {{3}^{x\sin y}} \right)}^{\prime }}_{x}={{3}^{x.\sin y}}\cdot \ln 3\cdot {{\left( x\cdot \sin y \right)}^{\prime }}_{x}=\]
Отдельно посчитаем такую конструкцию:
\[{{\left( x\cdot \sin y \right)}^{\prime }}_{x}={{{x}’}_{x}}\cdot \sin y+x{{\left( \sin y \right)}^{\prime }}_{x}=1\cdot \sin y+x\cdot 0=\sin y\]
Продолжаем решать исходное выражение:
\[={{3}^{x\sin y}}\cdot \ln 3\cdot \sin y\]
Это окончательный ответ частной переменной по $x$. Теперь посчитаем по $y$:
\[{{{z}’}_{y}}={{\left( {{3}^{x\sin y}} \right)}^{\prime }}_{y}={{3}^{x\sin y}}\cdot \ln 3\cdot {{\left( x\sin y \right)}^{\prime }}_{y}=\]
Решим одно выражение отдельно:
\[{{\left( x\cdot \sin y \right)}^{\prime }}_{y}={{{x}’}_{y}}\cdot \sin y+x{{\left( \sin y \right)}^{\prime }}_{y}=0\cdot \sin y+x\cdot \cos y=x\cdot \cos y\]
Решаем до конца нашу конструкцию:
\[={{3}^{x\cdot \sin y}}\cdot \ln 3\cdot x\cos y\]
Задача № 2
\[t\left( x,y,z \right)=x{{e}^{y}}+y{{e}^{z}}\]
На первый взгляд этот пример может показаться достаточно сложным, потому что здесь три переменных. На самом деле, это одна из самых простых задач в сегодняшнем видеоуроке.
Находим по $x$:
\[{{{t}’}_{x}}={{\left( x{{e}^{y}}+y{{e}^{z}} \right)}^{\prime }}_{x}={{\left( x\cdot {{e}^{y}} \right)}^{\prime }}_{x}+{{\left( y\cdot {{e}^{z}} \right)}^{\prime }}_{x}=\]
\[={{\left( x \right)}^{\prime }}_{x}\cdot {{e}^{y}}+x\cdot {{\left( {{e}^{y}} \right)}^{\prime }}_{x}=1\cdot {{e}^{y}}+x\cdot o={{e}^{y}}\]
Теперь разберемся с $y$:
\[{{{t}’}_{y}}={{\left( x\cdot {{e}^{y}}+y\cdot {{e}^{z}} \right)}^{\prime }}_{y}={{\left( x\cdot {{e}^{y}} \right)}^{\prime }}_{y}+{{\left( y\cdot {{e}^{z}} \right)}^{\prime }}_{y}=\]
\[=x\cdot {{\left( {{e}^{y}} \right)}^{\prime }}_{y}+{{e}^{z}}\cdot {{\left( y \right)}^{\prime }}_{y}=x\cdot {{e}^{y}}+{{e}^{z}}\]
Мы нашли ответ.
Теперь остается найти по $z$:
\[{{{t}’}_{z}}={{\left( x\cdot {{e}^{y}}+{{y}^{z}} \right)}^{\prime }}_{z}={{\left( x\cdot {{e}^{y}} \right)}^{\prime }}_{z}+{{\left( y\cdot {{e}^{z}} \right)}^{\prime }}_{z}=0+y\cdot {{\left( {{e}^{z}} \right)}^{\prime }}_{z}=y\cdot {{e}^{z}}\]
Мы посчитали третью производную, на чем решение второй задачи полностью завершено.
Нюансы решения
Как видите, ничего сложного в этих двух примерах нет. Единственное, в чем мы убедились, так это в том, что производная сложной функции применяется часто и в зависимости от того, какую частную производную мы считаем, мы получаем разные ответы.
В последней задаче нам было предложено разобраться с функцией сразу от трех переменных. Ничего страшного в этом нет, однако в самом конце мы убедились, что все они друг от друга существенно отличаются.
Ключевые моменты
Окончательные выводы из сегодняшнего видеоурока следующие:
- Частные производные считаются так же, как и обычные, при этом, чтобы считать частную производную по одной переменной, все остальные переменные, входящие в данную функцию, мы принимаем за константы.
- При работе с частными производными мы используем все те же стандартные формулы, что и с обычными производными: сумму, разность, производную произведения и частного и, разумеется, производную сложной функции.
Конечно, просмотра одного этого видеоурока недостаточно, чтобы полностью разобраться в этой теме, поэтому прямо сейчас на моем сайте именно к этому видео есть комплект задач, посвященных именно сегодняшней теме — заходите, скачивайте, решайте эти задачи и сверяйтесь с ответом. И после этого никаких проблем с частными производными ни на экзаменах, ни на самостоятельных работах у вас не будет. Конечно, это далеко не последний урок по высшей математике, поэтому заходите на наш сайт, добавляйтесь ВКонтакте, подписывайтесь на YouTube, ставьте лайки и оставайтесь с нами!
Смотрите также:
- Работа с формулами в задаче B12
- Как решать квадратные уравнения
- Пробный ЕГЭ 2012. Вариант 4 (без логарифмов)
- Пробный ЕГЭ 2012 от 7 декабря. Вариант 6 (без производной)
- Репетитор по математике — индивидуальные занятия
www.berdov.com
Частные производные. Примеры решений — Мегаобучалка
На данном уроке мы познакомимся с понятием функции двух переменных, а также подробно рассмотрим наиболее распространенное задание – нахождение частных производныхпервого и второго порядка, полного дифференциала функции.
Для эффективного изучения нижеизложенного материала Вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде.
Начнем с самого понятия функции двух переменных, постараемся ограничиться минимумом теории, так как сайт имеет практическую направленность. Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами.
Пример: – функция двух переменных.
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .
Полезно знать геометрический смысл функций. Функции одной переменной соответствует определенная линия на плоскости, например, – всем знакомая школьная парабола. Любая функция двух переменных с геометрической точки зрения представляет собой поверхность в трехмерном пространстве (плоскости, цилиндры, шары, параболоиды и т.д.). Но, собственно, это уже аналитическая геометрия, а у нас на повестке дня математический анализ.
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций.Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас.
Пример 1
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения:
или – частная производная по «икс»
или – частная производная по «игрек»
Начнем с .
Важно! Когда мы находим частную производную по «икс», то переменнаясчитается константой (постоянным числом).
Решаем. На данном уроке будем сразу приводить полное решение, а комментарии давать ниже.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всюфункцию в скобки под штрих с подстрочным индексом.
Внимание, важно!Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если Вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием (сразу откусить часть балла за невнимательность).
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования ; . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как считается константой, а любую константу можно вынести за знак производной, то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».
(3) Используем табличные производные и .
(4) Упрощаем ответ.
Теперь определим . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).
(1) Используем те же правила дифференцирования ; . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.
(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива для(и вообще для любой буквы).В данном случае, используемые нами формулы имеют вид: и .
Итак, частные производные первого порядка найдены
megaobuchalka.ru
Частные производные и дифференцируемость функций
Функции нескольких переменных
Многие явления, происходящие в природе, экономике, общественной жизни нельзя описать с помощью функции одной переменной. Например, рентабельность предприятия зависит от прибыли, основных и оборотных фондов. Для изучения такого рода зависимостей и вводится понятие функции нескольких переменных.
В данной теме рассматриваются функции двух переменных, так как все основные понятия и теоремы, сформулированные для функций двух переменных, легко обобщаются на случай большего числа переменных.
Пусть – множество упорядоченных пар действительных чисел .
Определение 1. Если каждой упорядоченной паре чисел по некоторому закону поставлено в соответствие единственное действительное число , то говорят, что задана функция двух переменных или . Числа называются при этом независимыми переменными или аргументами функции, а число – зависимой переменной.
Например, формула , выражающая объем цилиндра, является функцией двух переменных: – радиуса основания и – высоты.
Пару чисел иногда называют точкой , а функцию двух переменных – функцией точки .
Значение функции в точке обозначают или и называют частным значением функции двух переменных.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ
1. Частные производные первого порядка. Пусть функция определена в области и . Тогда при малых определено ее частное приращение по : .
Определение. Частной производной функции по переменной в точке называют предел
,
если он существует.
Частную производную по обозначают одним из следующих символов:
.
Аналогично определяется частная производная по и вводятся ее обозначения.
Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
Пример. Найти частные производные функции .
Имеем:
, . ^
2. Частные производные высших порядков. Рассматривая частные производные и как функции от , приходим к понятиям частных производных второго порядка. А именно, выражения
,
называют частными производными второго порядка функции по и по соответственно, а выражения
,
– смешанными частными производными второго порядка функции . Их обозначают также символами: , , и . Аналогично определяют частные производные 3-го порядка (их будет 8=23 ), 4-го порядка (их будет 16=24 ) и т. д.
Теорема 4. Если в некоторой окрестности точки функция имеет смешанные частные производные и , причем эти производные непрерывны в точке , то они равны в этой точке:
=.
Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции не зависят от порядка дифференцирования в точке .
Теорема 4 допускает обобщение: по индукции ее можно распространить на любые непрерывные смешанные частные производные.
3. Дифференцируемость функции. Пусть . Составим полное приращение функции в точке :
.
Определение. Функция называется дифференцируемой в точке , если ее полное приращение в этой точке можно представить в виде
, (1)
где и – некоторые числа, при , .
Другими словами, функция дифференцируема в точке , если ее приращение эквивалентно функции : при . Выражение в этом случае представляет собой главную часть приращения , линейно зависящую от и .
Определение. Если функция дифференцируема в точке , то главную линейную часть ее приращения называют полным дифференциалом в точке и обозначают в виде
.
Для независимых переменных и полагают и . Поэтому полный дифференциал записывают также в виде
.
Формула (1) показывает, что, как и в случае функции одной переменной, верна
Теорема 5. Если функция дифференцируема в точке , то она непрерывна в этой точке.
Обратное утверждение неверно, т. е. непрерывность является только необходимым, но не достаточным условием дифференцируемости функции. Покажем это.
Пример. Найдем частные производные функции :
.
Полученные формулы теряют смысл в точке .
Можно показать иначе, что функция не имеет частных производных в точке . В самом деле, . Эта функция одной переменной , как известно, не имеет производной в точке . Последнее и означает, что частная производная в точке не существует. Аналогично, не существует частная производная . При этом функция , очевидно, непрерывна в точке . ^
Итак, мы показали, что непрерывная функция может не иметь частных производных. Осталось установить связь между дифференцируемостью и существованием частных производных.
4. Связь между дифференцируемостью и существованием частных производных. Напомним, что для функции одной переменной существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.
Теорема 6 (необходимое условие дифференцируемости). Если функция дифференцируема в точке , то она имеет в точке частные производные по каждой переменной и .
При этом ,, где и – числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде
,
а полный дифференциал функции – в виде
.
Обратная теорема не верна, т. е. существование частных производных не является достаточным условием дифференцируемости функции.
Теорема 7 (достаточное условие дифференцируемости). Если функция имеет непрерывные частные производные и в точке , то она дифференцируема в точке (и ее полный дифференциал в этой точке выражается формулой ).
Обратная теорема не верна, т. е. непрерывность частных производных является только достаточным, но не необходимым условием дифференцируемости функции.
5. Геометрический смысл дифференцируемости функции. Напомним, что для функции одной переменной из дифференцируемости функции в точке следует существование касательной к графику функции в точке .
Рассмотрим непрерывную функцию двух переменных , . График этой функции, т. е. множество точек , представляет собой поверхность в пространстве . Пусть плоскость проходит через точку поверхности ; – произвольная (текущая) точка поверхности ; – ос
|
нование перпендикуляра, проведенного из точки к плоскости (рис. 6).
Рис. 6.
Определение. Плоскость , проходящая через точку поверхности , называется касательной плоскостью к поверхности в этой точке, если при () величина является бесконечно малой более высокого порядка, чем , т. е. .
Теорема 8. Если функция дифференцируема в точке , то в точке существует касательная плоскость к поверхности (графику этой функции), причем уравнение касательной плоскости имеет вид
.
Вектор нормали к касательной плоскости, т. е. , называется вектором нормали (или нормалью) к поверхности .
matematiku5.ru
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ.
Рассмотрим функцию двух переменных z = f(x, y).
Частной производной функции двух переменных z = f(x, y) по х в точке (х, у) называется предел , если он существует. Частная производная есть обычная производная от функции f(x,y), рассматриваемой как функция только от переменной х при фиксированному.
Аналогично определяется частная производная по ув точке (х,у):
.
Если у функции существует частная производная снова по переменной х, то ее называют частной производной второго порядка от функции f(x,y) по переменной х и обозначают . Таким образом, .
Аналогично для переменной у: .
Если существует частная производная от функции по переменной у, то эту производную называют смешанной частной производной второго порядка от функции z = f(x, y) и обозначают .
В курсе высшей математики доказывается теорема о том, что если функция двух переменных определена вместе со своими частными производными в окрестности некоторой точки, причем смешанные частные производные непрерывны в этой точке, то в этом случае результат дифференцирования не зависит от порядка дифференцирования, т. е. .
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Рассмотрим функцию двух переменных z = f(x, y). Если эта функция дифференцируема в точке (х,у), то для нее существует производная по направлению любого единичного вектора `n0 = (Cosa, Cosb), выражаемая формулой ,
где a и b – углы, которые вектор `n0составляет с осями хи у.
Если же необходимо найти производную по направлению произвольного вектора `n= a`i + в`j , то его необходимо сначала пронормировать и найти направляющие косинусы по формулам а потом воспользоваться приведенной выше формулой.
ГРАДИЕНТ ФУНКЦИИ
Градиентом функции z = f(x, y) в точке М(х0, у0) называется вектор grad z, координаты которого равны частным производным функции z = f(x, y), вычисленным в точке М(х0, у0)
.
ЗАДАЧА № 9
Найти частные производные функции z = f(x,y):
ЗАДАЧА № 10
Найти градиент и производную по направлению
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
При изучении дифференцированного исчисления решалась следующая задача: дана функция F(x), найти ее производную F¢(x) (в дальнейшем производную F¢(x) будем обозначать f(x)). Интегральное исчисление решает задачу обратную: для непрерывной функции f(x) найти такую функцию F(x), производная которой была бы тождественно равна функции f(x). Функция F(x) называется первообразной, f(x) – подынтегральной. Ясно, что если F¢(x) = f(x), то и [F¢(x) + C]¢ = f(x). Здесь С – произвольная постоянная величина.
Определение:
Неопределенным интегралом называется функция F(x) + C, производная которой равна подынтегральной функции f(x), т.е.
= F(x) + C, если [F(x) + C]¢ = f(x).
Подынтегральное выражение f(x)dx есть дифференциал для всех первообразных, т.е. d[F(x) + C] = f(x)dx.
Из определения следует, что процесс нахождения неопределенного интеграла сводится к нахождению первообразной данной функции.
Вообще, используя таблицу производных, можно составить таблицу основных интегралов:
ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. , т.е. знаки d и ò, стоящие перед некоторой функцией, друг друга уничтожают. Так .
2. , т.е. постоянный множитель можно выносить за знаки интеграла.
3. , т.е. неопределенный интеграл от суммы некоторых функций равен сумме интегралов от этих функций.
ЗАДАЧА № 11
Найти неопределенный интеграл .
=
МЕТОД ПОДСТАНОВКИ
Метод заключается в том, что вместо переменной x вводят новую переменную, например t. Так, если положить х = j(t), то
Получаемый интеграл должен быть значительно проще данного. В противном случае следует искать другую форму введения новой переменной. Часто переменную t вводят так: t = j(x), а dt = j¢(x)dx. Это удобно, если данное подынтегральное выражение содержит дифференциал j¢(x)dx.
ЗАДАЧА № 12
Найти неопределенный интеграл .
=
ЗАДАЧА № 13
Найти неопределенный интеграл .
.
ЗАДАЧА № 14
Найти неопределенный интеграл .
=
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Идея метода состоит в том, что подынтегральное выражение f(x)dx нужно представить в виде произведения U*dV , где U(x) и V(x) – дифференцируемые функции и воспользоваться формулой .
При этом вновь полученный интеграл должен быть проще данного.
ЗАДАЧА № 15
Найти неопределенный интеграл .
=
ЗАДАЧА № 16
Найти неопределенный интеграл .
=
infopedia.su
Как найти Частную Производную???
Решил добавить ещё немного информации по производным. В предыдущей статье мы говорили о производных высших порядков, а сегодня я расскажу вам немного о частных производных. Многим сложно разобраться, как правильно их находить, но я надеюсь, что те два примера, которые я рассмотрел в видео-уроке, вам должны помочь в этом.
Для начала немножко расскажу, что такое частная производная! Ну, вот если бы вам дали задание найти производную, от функции с трёмя переменными, то у вас возникает логический вопрос: «А по какой переменной брать эту производную?». Именно поэтому существуют частные производные, то есть это производные от функции с несколькими переменными по одной из этих переменных. Если, например, у вас функция от трёх переменных: $x, y, z$, то соответственно вы можете взять и частные производные по каждой из них.
Теперь вернёмся до видео-примера. Посмотрев его, вы узнаете ответы на такие вопросы:
- Что такое частная производная и как она обозначается?
- Как находить частные производные?
- Как вычислить полный дифференциал функции с несколькими переменными?
- Как найти частные производные высших порядков?
- Что такое смешанные частные производные?
Так, что качайте новый видео-урок, посмотрите его, подробно разберите примеры, что там данные и думаю, вы уже будете нормально решать подобные упражнения. Для лучшего закрепления материала рекомендую сделать несколько подобных упражнений, а если возникнут какие-то вопросы, то пишите в комментариях.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
1.3. Частные производные функции двух переменных
Дадим независимой
переменной х приращение 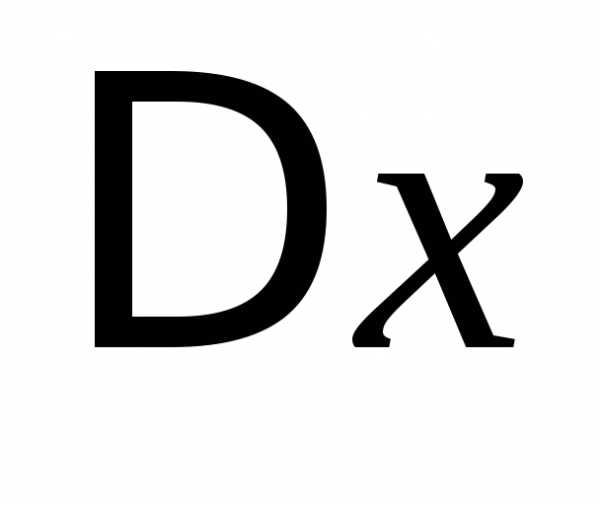
.
Аналогично определяется частное приращение z по у:
.
Если же приращение получают одновременно х и у, то приращение
называется полным.
Определение 8. Частной производной от функции пох называется предел
 ,
,
или другие обозначения
Аналогично,  ,
,
или .
Из этих определений
следует, что правила вычисления частных
производных совпадают с правилами для
функции одного переменного. При этом,
например, если мы вычисляем производную 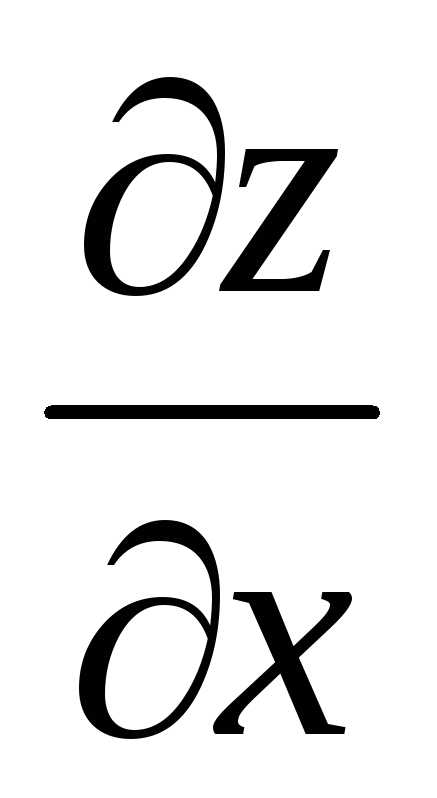 ,
то в процессе дифференцирования считаем,
что
,
то в процессе дифференцирования считаем,
что
Пример 5.
Найти 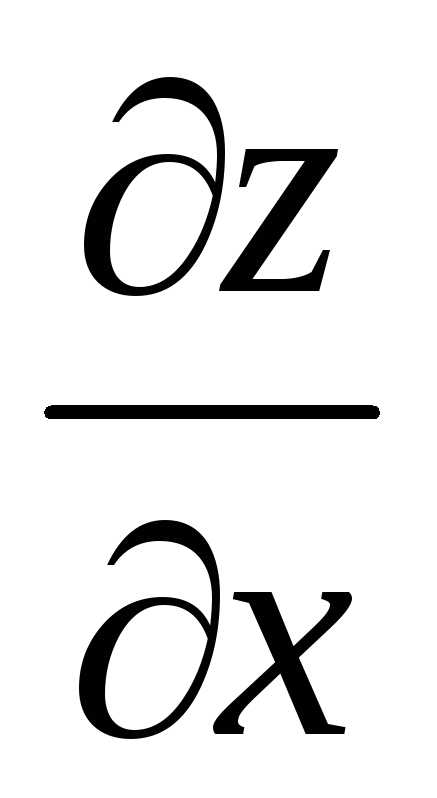 и
и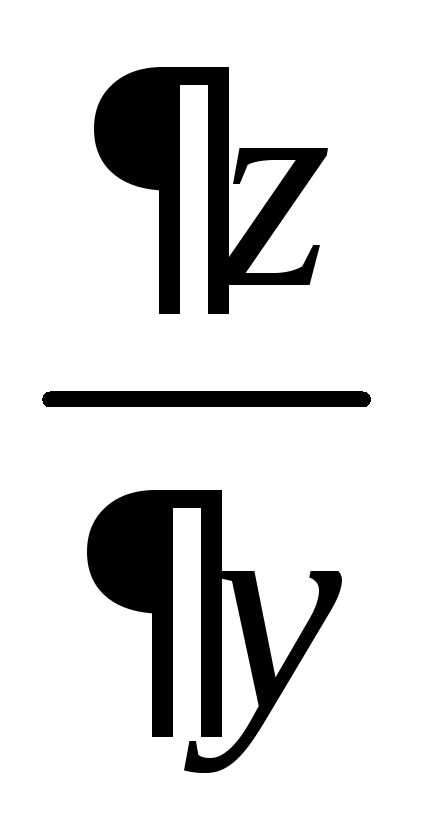 ,
если
,
если
1.4. Полный дифференциал функции двух переменных
Как известно, полное приращение функции определяется по формуле . Пустьимеет непрерывные частные производные, т.е. является дифференцируемой. Полное приращение представим в виде
.
К каждой разности применим теорему Лагранжа
,
где .
Так как в силу непрерывности существуют пределы:
; ,
то по теореме о пределе функции получим
где .
Это означает, что подчеркнутое слагаемое является б.м.в. при и тогда
,
где 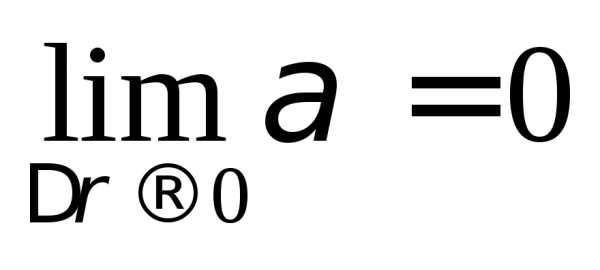 .
.
Таким образом, получаем еще одно эквивалентное определение дифференцируемой функции двух переменных.
Определение 8. Функция
называется дифференцируемой в точке,
если её приращение можно представить
в виде суммы двух слагаемых, линейных
относительно и
и и величины бесконечно малой. высшего
порядка относительно
и величины бесконечно малой. высшего
порядка относительно ,
т.е.
,
т.е.
При этом линейная
часть  называетсяполным
дифференциалом и обозначается
называетсяполным
дифференциалом и обозначается
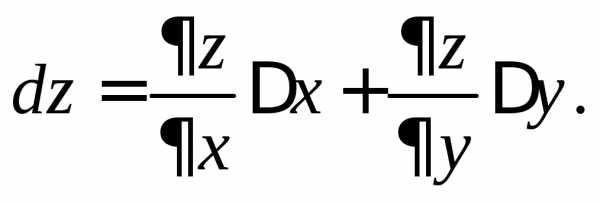
Так как приращения независимых переменных называются их дифференциалами, то окончательно

а 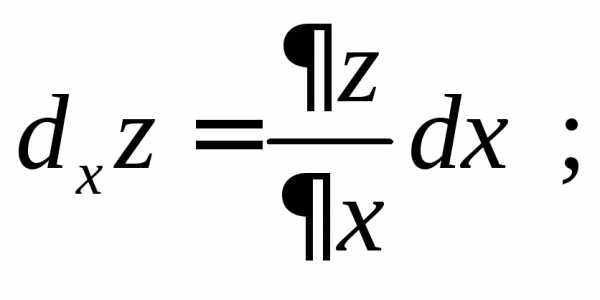
 частные
дифференциалы.
частные
дифференциалы.
1.5. Производная сложной функции
Пусть задана функция , где. В этом случаеz является сложной функцией аргументов х иу. Пусть все эти функции имеют непрерывные частные производные.
Дадим переменной х приращение  ,
тогда
,
тогда
где .
Разделим данное
равенство на  и перейдём к пределу при
и перейдём к пределу при
Отсюда следует .
Аналогично получим 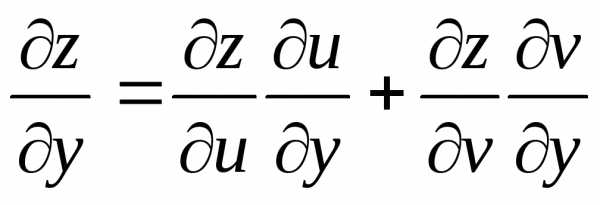 .
.
Пример 6.
Найти 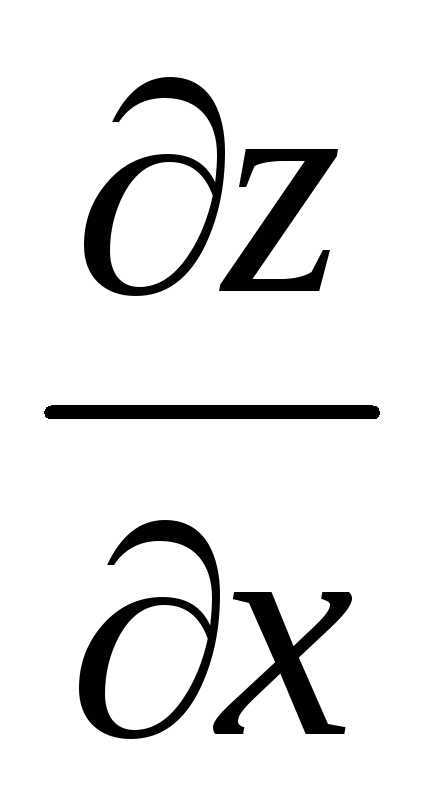 и
и ,
если
,
если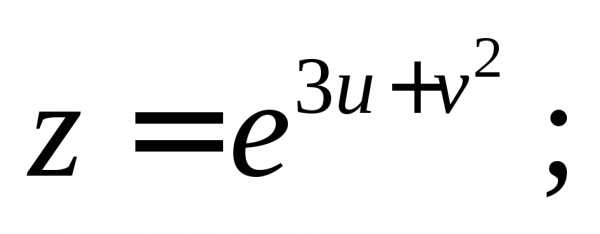
Лекция № 33. Тема 2 : Частные производные.
Производная по направлению. Градиент
2.1. Полная производная
Пусть дана функция , где. Тогда, обобщая формулу для случая производной функции двух переменных, получаем
. (1)
Формула (1) называется формулой полной производной.
Пример 1. Найти полную производную функции
,
если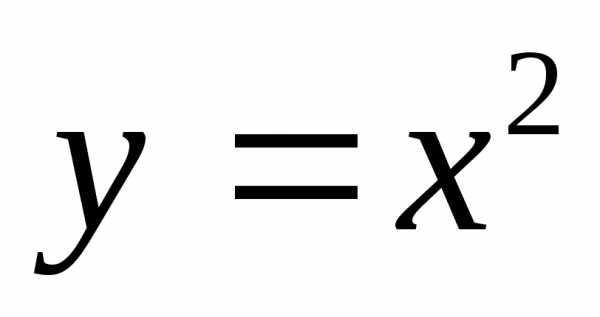 .
.
.
2 .2 . Частные производные функции, заданной неявно
Требуется найти
частные производные  и
и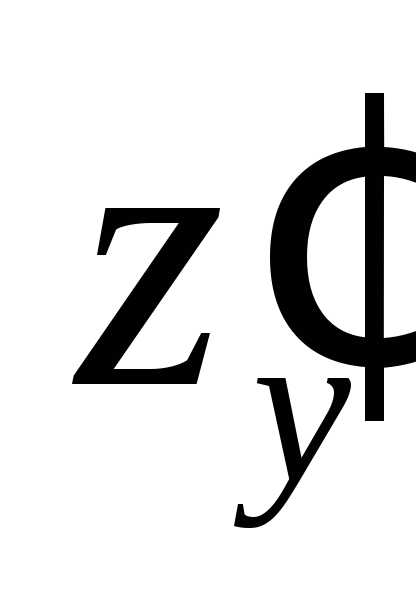 ,
если,
где.
Воспользуемся правилом дифференцирования
сложной функции для случая трёх
переменных
,
если,
где.
Воспользуемся правилом дифференцирования
сложной функции для случая трёх
переменных
.
Аналогично находим 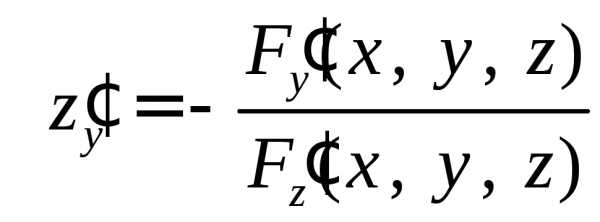 .
.
Замечание 1. Отсюда следует ранее рассмотренный случай для функции одной переменной: Если , где.
Пример 2. Найти частные производные функции, заданной неявно
.
2.3. Частные производные высших порядков
Рассмотрим функцию
.
Если частные производные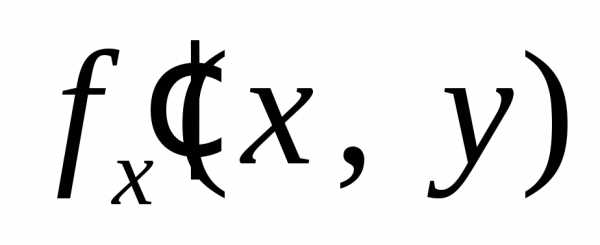 и
и являются дифференцируемыми функциями,
то от них можно снова находить частные
производные. Частные производные второго
порядка определяются следующим
образом
являются дифференцируемыми функциями,
то от них можно снова находить частные
производные. Частные производные второго
порядка определяются следующим
образом
Последние две производные называются смешанными производными второго порядка.
Аналогично определяются производные высших порядков. Например,
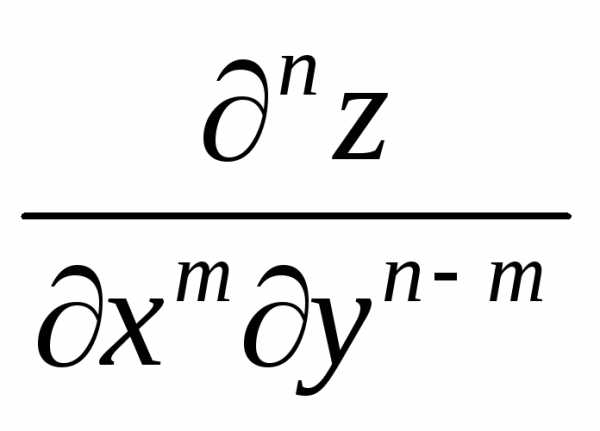 означает, что
функция
означает, что
функция 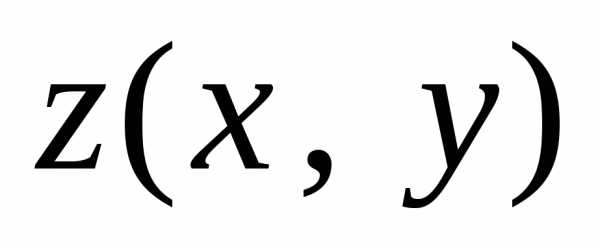 сначала дифференцируетсят раз по х,
а затем п т раз по у.
сначала дифференцируетсят раз по х,
а затем п т раз по у.
Пример 3. Найти смешанные производные второго порядка функции .
Получено равенство двух смешанных производных второго порядка. Зависит ли в общем случае результат дифференцирования от порядка дифференцирования?
Теорема. Если функция
и ее частные производные определены в некоторой окрестности
точкиМ и
определены в некоторой окрестности
точкиМ и 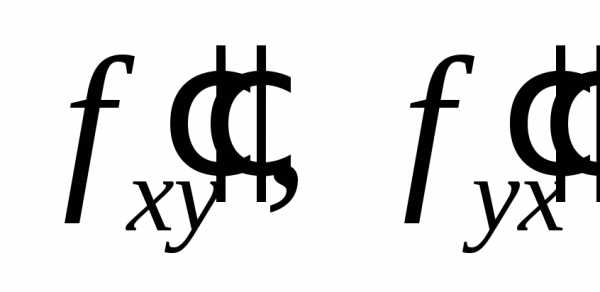 непрерывны, то в этой окрестности
смешанные производные равны
непрерывны, то в этой окрестности
смешанные производные равны
 .
.
studfiles.net

