Геометрический смысл производной
Геометрический смысл производной. Задачи на экзамене связанные данной темой у выпускников вызывают некоторые затруднения. Большинство же из них, на самом деле, очень просты. В этой статье разберём задания, в которых требуется найти производную при заданном графике функции и касательной к графику в определённой точке
*При чём в этих задачах на эскизе явно отмечены как минимум две точки, через которые эта касательная проходит. Что нужно знать для решения?
Геометрический смысл производной
Построим произвольный график некой функции y = f (x) на координатной плоскости, построим касательную в точке xо, обозначим угол между прямой о осью ox как α (альфа)

Из курса алгебры известно, что уравнение прямой имеет вид:
То есть производная функции y = f(x) в точке x0 равна угловому коэффициенту касательной:
А угловой коэффициент в свою очередь равен тангенсу угла α (альфа), то есть:
Угол α (альфа) может быть меньше, больше 90 градусов или равен нулю.
Проиллюстрируем, два случая:
1. Угол наклона касательной больше 90 градусов (тупой угол).
2. Угол наклона касательной равен нулю градусов (касательная параллельна оси ох).

То есть задачи, в которых дан график функции, касательная к этому графику в определённой точке, и требуется найти производную в точке касания, сводятся к нахождению углового коэффициента касательной (либо тангенса угла наклона касательной, что одно и тоже).
Ниже рассмотрим решение таких задач через нахождение тангенса угла между касательной и осью абсцисс (осью ох), ещё один способ решения (нахождение производной через угловой коэффициент) рассмотрим в недалёком будущем. Также будем рассматривать задачи, где требуется знание свойств производной для чтения графика функции. Не пропустите!
Обратите внимание, что на координатной плоскости обозначены две точки через которые проходит касательная – это очень важный момент (можно сказать ключевой в этих задачах).
Что ещё потребуется — это знание формулы приведения для тангенса тупого угла.
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
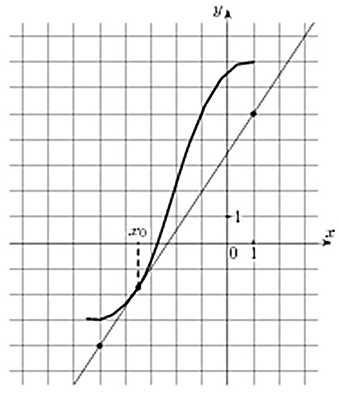
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Для того, чтобы найти тангенс этого угла, построим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой, а катеты параллельны осям. В данной задаче это точки (–5; –4), (1; 5).
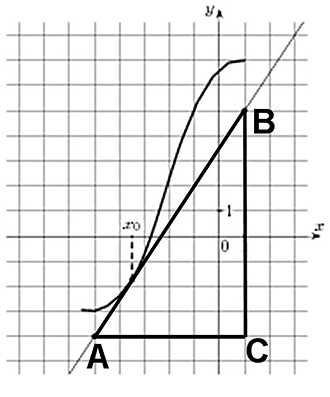
Напомню: тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Катеты определяем по числу клеток.
Угол наклона касательной к оси абсцисс равен углу BAC, так как катет АС параллелен оси ох. Значит
Ответ: 1,5
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
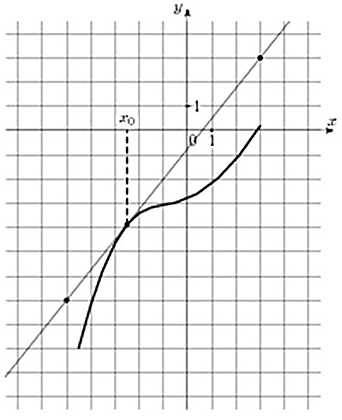
Задача аналогична предыдущей. Так же строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки (–5; –7), (3; 3).
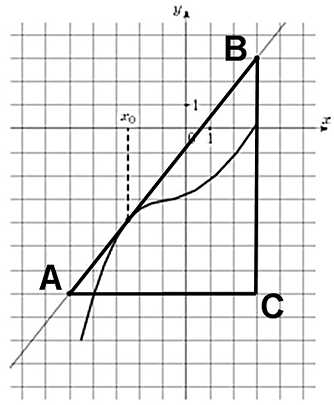
Катеты также определяем по числу клеток.
Угол наклона касательной к оси абсцисс равен углу ВАС, так как катет АС параллелен оси ох. Значит
Ответ: 1,25
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.

Строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки (–3; 3) и (5; 11). Из точки (5;11) построим продолжение катета так, чтобы получился внешний угол.
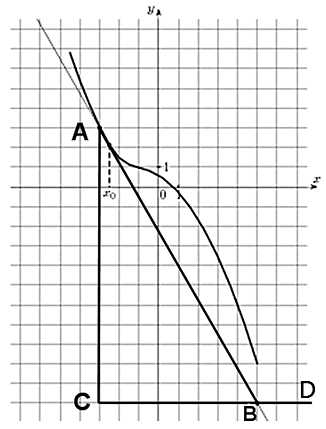
Так как CD параллельна оси ох, то угол ABD равен углу наклона касательной к оси ох. Таким образом, мы будем вычислять тангенс угла ABD. Отметим, что он больше 90 градусов, поэтому здесь необходимо воспользоваться формулой приведения для тангенса:
Значит
*Длины катетов считаем по количеству клеток.
Ответ: -1,75
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.

Решите задачу самостоятельно.
Ответ: -1,75
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке х0 = 10.
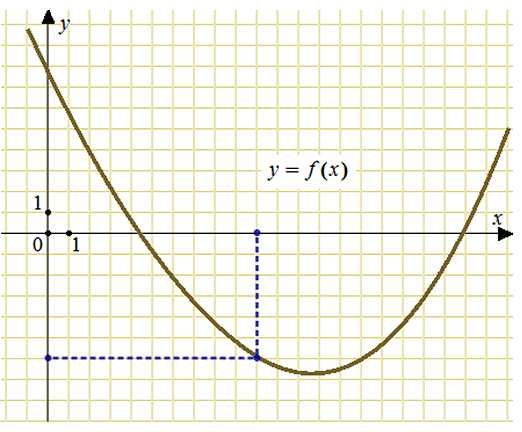
Построим касательную, проходящую через начало координат и точку графика с абсциссой равной 10. Обозначим угол наклона касательной как альфа, а смежный с ним угол как бета.
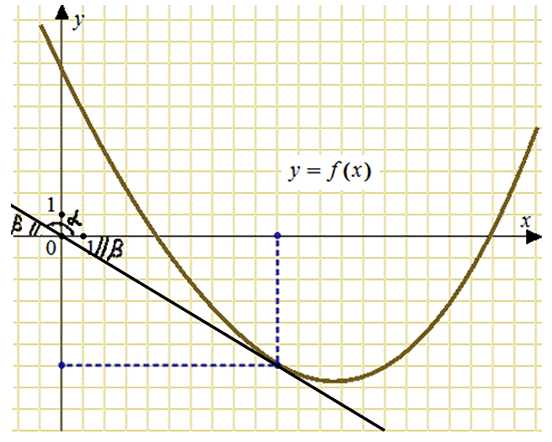
Значение производной в точке х0 = 10 равно тангенсу угла наклона касательной к оси абсцисс. То есть, для нахождения производной достаточно вычислить тангенс угла альфа. Воспользуемся формулой приведения:
Тангенс угла бета можем найти из прямоугольного треугольника, катеты которого равны 6 и 10:
Ответ: — 0,6
На первый взгляд задачи, связанные с использованием производной входящие в ЕГЭ по математике, довольно разнообразны. Но на самом деле для их решения нужно изучить совсем небольшой «кусочек» теории. На этом всё. Второй способ решения представленных задач обязательно разберем. Надеюсь, статья была полезна.
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Как найти значение производной функции в точке х0 по графику
Зная стороны или сторону и угол,в равнобедренном треугольнике, можно найти по формулам, его высоту, биссектрису, медиану.
Задача 7 — геометрический смысл производной
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
Значение производной в некоторой точке x0, Точки максимума или минимума (точки экстремума), Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу. Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
Точка x0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x). Точка x0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции. Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т. е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т. е. f’(x) ≥ 0. Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т. е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т. е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
- Бесплатная подготовка к ЕГЭ 7 простых, но очень полезных уроков + домашнее задание
Чтобы посмотреть видео, введите свой E-mail и нажмите кнопку «Начать обучение»
- © 2010—2018 ИП Бердов Павел Николаевич
ИНН 760708479500; ОГРНИП 309760424500020 При использовании материалов ссылка на сайт обязательна
Как найти значение производной функции в точке х0 по графику
08. В9. На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой Х0. Найдите значение производной функции f(x) в точке Х0.
На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой Х0. Найдите значение производной функции f(x) в точке Х0.
Мы должны знать, что производная функции f(x) в точке х0 равна коэффициенту K при х в уравнении прямой, касательной к f(x) в точке х0.
То есть, если нам надо найти f´(x0), то мы просто найдем K в уравнении прямой y = Kx + b.
Из графика видно, что наша касательная проходит через точки (-2; 0) и (0; -2). Подставим их в уравнение прямой: х1 = -2, у1 = 0 и х2 = 0, у2 = -2 и получим 2 уравнения:
Это система двух уравнений, найдем из нее K.
Как найти значение производной функции в точке х0 по графику
08. В9. На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой Х0. Найдите значение производной функции f(x) в точке Х0.
На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой Х0. Найдите значение производной функции f(x) в точке Х0.
Мы должны знать, что производная функции f(x) в точке х0 равна коэффициенту K при х в уравнении прямой, касательной к f(x) в точке х0.
То есть, если нам надо найти f´(x0), то мы просто найдем K в уравнении прямой y = Kx + b.
Из графика видно, что наша касательная проходит через точки (-2; 0) и (0; -2). Подставим их в уравнение прямой: х1 = -2, у1 = 0 и х2 = 0, у2 = -2 и получим 2 уравнения:
Это система двух уравнений, найдем из нее K.

poiskvstavropole.ru
Как по графику функции найти значение производной функции
а) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; — это решение к неравенстве в) б) 401, 402, 403….. — это решение к неравенству а) Решите подбором третье неравенство. Подберем числа, являющиеся решением неравенства 180: с
Задания №7. Применение производной к исследованию функции
Здесь смотрите части 1, 2, 4
Продолжаем разбор Задач №8 ЕГЭ по математике .
Сегодня нам понадобится при решении задач следующая таблица, показывающая связь знака производной с характером монотонности функции.
Как видим, таких точек – четыре.
Производная равна нулю в точках экстремума. У нас их 4:
Точки экстремума – это точки максимума (-3, -1, 1) и точки минимума (-2, 0, 3).
Сумма точек экстремума: -3-1+1-2+0+3=-2.
На рисунке выделены промежутки, на которых производная функции имеет знак плюс.
На рисунке выделены цветом все промежутки, на которых производная положительна, а значит сама функция возрастает на этих промежутках.
Длина наибольшего из них – 6.
При этом производная меняет знак с «+» на «-» в точке 8, помеченной красным цветом, и с «-» на «+» в двух точках (3 и 12), помеченных синим цветом.
Так вот при переходе через точку максимума функция меняет возрастание на убывание, а значит производная меняет знак с «+» на «-».
Итак, точка максимума одна (помечена красным цветом).
В точке -3 (точка минимума) производная равна нулю.
В точке 6 производная положительна, так как точки лежат на промежутке возрастания функции.
А вот в точках 1 и 8 производная отрицательна.
При этом в точке 8 угол наклона касательной явно меньше, чем в точке 1.
Поэтому в точке 8 тангенс угла наклона будет наименьшим, а значит и значение производной, будет наименьшее.
🙂 Самое время немного отдохнуть. Неправда ли? –> + показать
Вам было нелегко.
Этим ребятам, наверное, тоже не сладко… Не сдавайтесь!
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Подскажите пожалуйста, с чего начать подготовку к заданию В9? я в этой теме полный Ноль, а хотелось бы разобраться досконально во всех нюансах…
Сначала вам сюда, затем сюда. И начните с частей 1, 2.
Спасибо большущее! Очень досконально, но интересно!))
Скажите пожалуйста, в точке 1 угол наклона касательной “более” тупой, нежели в точке 8. Соответственно отрицательное значение там меньше. Неужели я неправильно рассуждаю?
«в точке 1 угол наклона касательной «более» тупой, нежели в точке 8»
АААА. Все ясно tg(-a)=-tg(a). Огромное Вам спасибо! На графике все наглядно-понятно:). Но такое увидеть надо же! Буду стараться. Спасибо Вам.
Добрый вечер! У меня вопрос, тоже по производной, но касаемый а спекта выпуклости/вогнутости функции. Почему в функции y=x^4/(X^3+1) критическая точка второго рода о входит в интервал вогнутости функции, это же критическая точка и в ней вторая производная равна 0, а нам нужно согласно теоремы брать только интервалы где вторая производная больше нуля. Заранее спасибо за ответ
Галина, я так понимаю, следует различать строгую и нестрогую выпуклость/вогнутость…
Елена Юрьевна, спасибо за ответ, по ошибке не ту функцию ввела. Собственно вопрос у меня в следующем, я преподаватель и меня интересует, как математически грамотно моим студентам первокурсникам объяснить выпуклость вогнутость для функции у=x^4, ведь здесь критическая точка второго рода 0, на основании чего им обьяснить что функция на всей области определения будет выпукла вниз, 0 камень преткновения. Спасибо.
В задаче 2 ответ не 3? Угловой коэффициент равен 0, значит у=0 пересекает функцию в трех точках.
Даша, если бы на рисунке был изображен график функции f'(x) (а не f(x)), то ваши рассуждения были бы верны.
Сравните задачи 2 и 3.
К заданию 7 – Почему не входит точка x=2? Ведь -“Если функция непрерывна на промежутке [a;b] и возрастает (убывает) на промежутке (a;b), то она возрастает (убывает) и на промежутке [a;b]”
Светлана, точно. Спасибо!
Добрый день! В №7 х=2 – разве не точка экстремума, почему у вас она относится к интервалу возрастания функции? И непонятно, почему 2+3+4+5=12, когда эта сумма =14. При этом ответ – 14.
Да, в точке 2 функция возрастает. Согласно определению.
К задаче 11: сравниваем отрицательные значения, поэтому ответ – в точке 1
Маргарита, сами себе противоречите. Ошибки нет.
А в первой задачке 3 точка разве не нулю равна?
Точнее…не она сама, а производная
В точке 3 не производная равна нулю, а функция. Посмотрите внимательно – на рисунке дан график не производной, а функции.
Добрый день. 7 номер. Почему точка 2 входит? разве она не экстрериум? разве в точке экстрериума функция имеет определенный знак? Поясните этот момент, пожалуйста
Функция возрастает на промежутках, где ее производная Неотрицательна!
Как по графику функции найти значение производной функции
Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7
Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7.
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Посмотрите ВИДЕОУРОК, в котором я подробно объясняю, в чем заключается геометрический смысл производной, и как выводится уравнение касательной. А затем мы рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике.
Геометрический смысл производной.
В этом уравнении:
Приведем несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике, в которых используется знание геометрического смысла производной.
Проведем через точку А прямую параллельно оси ОХ, а через точку В — параллельно оси OY. Получим прямоугольный треугольник ABC:
Угол А треугольника АВС равен углу между касательной и положительным направлением оси ОХ.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Длины катетов считаем по количеству клеточек.
Построим, как предыдущей задаче, прямоугольный треугольник АВС:
Запомните, если прямая наклонена влево, то коэффициент наклона прямой отрицателен.
Соединим отрезком точку начала координат с точкой касания:
Производная функции в точке касания равна тангенсу угла между касательной и положительным направлением оси ОХ:
Для вас другие записи этой рубрики:
Отзывов ( 25 )
Большое спасибо за объяснение!
Раньше боялся смотреть на В8, а сейчас, как орешки щелкаю.
Очень доступно и понятно!
А что если, дан график производной функции, а не сама функция?
«Запомните, если прямая наклонена влево, то коэффициент наклона прямой отрицателен.» Это написано под 2 примером. — наоборот мне кажется.. На 1 примере прямая наклонена влево, а на втором примере вправо.
Ты путаешь право и лево 🙂
Спасибо вам большое:)
Ваш сайт очень помогает подготовке к экзамену)
Откуда АВ=10 в примере 3 ?
Считаем по клеточкам.
Спасибо за ответ, уже нашла в банке заданий, там нарисованы клеточки, так что разобралась. И конечно, присоединяюсь к общим похвалам в адрес вашего прекрасного сайта.
Инна! Большое Вам спасибо за вашу работу! Благодаря Вам многие вопросы становятся более доступными. Когда у меня появляются какие-то проблемные вопросы-я захожу к Вам на сайт и часто нахожу ответы на вопросы. Дай Бог Вам здоровья и энергии!
Как по графику функции найти значение производной функции
Как по графику функции найти значение производной функции
Тип 5. Дан график функции и касательная к нему, найти значение производной.
Задача: На рисунке изображены график функции и касательная к нему в точке с абсциссой. Найдите значение производной функции в точке.
Помним, что производная равна тангенсу угла наклона касательной (т. е. угловому коэффициенту касательной)
Касательная есть, осталось найти тангенс её наклона к положительному направлению оси абсцисс.
Требуется изобразить какой-либо прямоугольный треугольник, в котором касательная была бы гипотенузой, а вершины лежали бы в узлах сетки.
Например, вот такой треугольник:
Угол для исследования : .
Известно, что тангенс угла в прямоугольном треугольнике равен отношению длины противолежащего катета к длине прилежащего.
Считаем клеточки, и получаем, что:
.
Итого:
Ответ: Производная в этой точке равна 4.
Задача: На рисунке изображены график функции и касательная к нему в точке с абсциссой. Найдите значение производной функции в точке.
Замечание: Задача аналогична предыдущей с тем отличием, что касательная «наклонена влево» и мы понимаем, что её угловой коэффициент отрицателен.
Замечание: Нужные точки касательной, точно расположенные в узлах координатной решетки, как бы невзначай обозначены жирненькими точками. Их то мы и возьмем за вершины треугольника.
Требуется найти. Из чертежа видно, что.
А из тригонометрии известно, что
Считаем клеточки, и получаем, что:
.
Итого:
Ответ: Производная в этой точке равна.

poiskvstavropole.ru
