Как находится мгновенная скорость – Неравномерное движение, мгновенная и средняя путевая скорость, перемещение. Графическое определение. Тест, упражнения - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Мгновенная скорость движения

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

Вектор мгновенной скорости всегда направлен по касательной к траектории тела в сторону движения тела.

Мгновенная скорость дает точную информацию о движении в определенный момент времени. Например, при езде в автомобиле в некоторый момент времени водитель смотрит на спидометр и видит, что прибор показывает 100 км/ч. Через некоторое время стрелка спидометра указывает на величину 90 км/ч, а еще спустя несколько минут – на величину 110 км/ч. Все перечисленные показания спидометра – это значения мгновенной скорости автомобиля в определенные моменты времени. Скорость в каждый момент времени и в каждой точке траектории необходимо знать при стыковке космических станций, при посадке самолетов и т.д.

Имеет ли понятие «мгновенной скорости» физический смысл? Скорость – это характеристика изменения перемещения тела в пространстве. Однако, для того, чтобы определить, как изменилось перемещение, необходимо наблюдать за движением в течение некоторого времени. Даже самые совершенные приборы для измерения скорости такие как радарные установки, измеряют скорость за промежуток времени – пусть достаточно малый , однако это все-таки конечный временной интервал, а не момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако, понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.

Примеры решения задач по теме «Мгновенная скорость»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

1. Мгновенная скорость.

Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории. Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:

Другими словами, мгновенная скорость – это первая производная радиус-вектора по времени.

2. Средняя скорость.

Средней скоростью на некотором участке называется величина равная отношению перемещения к промежутку времени, за который это перемещение произошло.

3. Угловая скорость. Формула. СИ.

Угловой скоростью называется векторная физическая величина равная первой производной угла поворота тела по времени. [рад/с]

4. Связь угловой скорости с периодом вращения.

Равномерное вращение характеризуется периодом вращения и частотой вращения.

5. Угловое ускорение. Формула. СИ.

Это физическая величина равная первой производной угловой скорости или второй производной угла поворота тела по времени. [рад/с²]

6. Как направлен вектор угловой скорости/углового ускорения.

Вектор угловой скорости направлен по оси вращения причем так чтобы вращение рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки(правило правой руки).

При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

7/8. Связь между нормальным ускорением и угловой скоростью/Связь между тангенциальным и угловым ускорением.

9. Что определяет и как направлена нормальная составляющая полного ускорения? Нормальное ускорение СИ.Нормальное ускорение определяет быстроту изменения скоро-сти по направлению и направлено к центру кривизны траектории.

В СИ нормальное ускорение [м/с²]

10. Что определяет и как направлена тангенциальная составляющая полного ускорения.

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

11. Тангенциальное ускорение в СИ.

м/с²

12. Полное ускорение тела. Модуль этого ускорения.

13.Масса. Сила. Законы Ньютона.

Масса − это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ [m] = кг.

Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ – Ньютон; кг*м/с²

Первый закон Ньютона (или закон инерции): если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.

Второй закон Ньютона: ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе. Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения.

Третий закон Ньютона: сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

studfiles.net

Мгновенная и средняя скорость | Физика

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.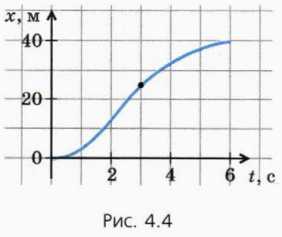

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).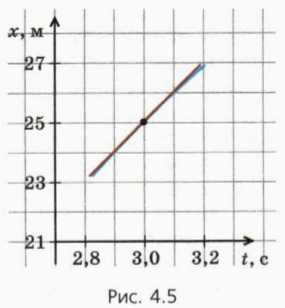

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

v_ср = l/t. (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v_ср = (l₁ + l₂)/(t₁ + t₂), (2)

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t².
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.

phscs.ru

понятие, формула расчета, рекомендации по нахождению

Скорость в физике означает быстроту перемещения какого-либо объекта (материальной точки) в пространстве. Эта величина бывает разной: линейной, угловой, средней, космической и даже сверхсветовой. В число всех существующих разновидностей входит также и мгновенная скорость. Что это за величина, какова ее формула и какие действия необходимы для ее расчета – об этом как раз и пойдет речь в нашей статье.

Мгновенная скорость: сущность и понятие

О том, как определить быстроту перемещения объекта по прямой, известно даже ученику начальных классов: достаточно пройденное расстояние разделить на время, которое было затрачено на такое перемещение. Однако стоит помнить, что результат, полученный таким способом, позволяет судить о среднем значении. Если объект движется неравномерно, то на определенных участках его пути быстрота перемещения может заметно варьироваться. Поэтому порой требуется такая величина как мгновенная скорость. Она позволяет судить о быстроте перемещения материальной точки в любой момент движения.

Мгновенная скорость: формула расчета

Данный параметр равен пределу (обозначается limit, сокращенно lim) отношения перемещения (разнице координат) к промежутку времени, за которое это изменение произошло, при условии, что этот промежуток времени стремится достичь нуля. Это определение можно записать в виде следующей формулы:

v = Δs/Δt при Δt → 0 либо так v = lim _Δt→0 (Δs/Δt)

Отметим, что мгновенная скорость есть величина векторная. Если движение происходит по прямой линии, то она меняется лишь по величине, а направление остается постоянным. В противном случае вектор скорости мгновенной направлен по касательной по отношению к траектории перемещения в каждой рассматриваемой точке. Какой смысл несет данный показатель? Мгновенная скорость позволяет выяснить, какое перемещение осуществит объект за единицу времени, если с рассматриваемого момента он движется равномерно и прямолинейно.

Советы

В случае равномерного движения никаких сложностей нет: нужно просто найти отношение расстояния к времени, за которое оно было объектом преодолено. В этом случае средняя и мгновенная скорость тела равны. Если же движение происходит непостоянно, то в этом случае следует узнать величину ускорения и определять мгновенную скорость в каждый определенный момент времени. При вертикальном перемещении следует учитывать влияние ускорения свободного падения. Мгновенную скорость автомобиля можно определить с помощью радара или спидометра. Следует иметь в виду, что перемещение в некоторых участках пути может принимать отрицательное значение. Для того чтобы найти ускорение, можно воспользоваться акселерометром либо составить функцию движения и воспользоваться формулой v=v0+a•t. Если перемещение начинается из состояния покоя, то v0 = 0. При расчетах нужно учитывать тот факт, что при торможении тела (уменьшении скорости) величина ускорения будет со знаком “минус”. Если объект совершает свободное падение, мгновенная быстрота его перемещения рассчитывается по формуле v= g•t. В этом случае начальная скорость также равна 0.

fb.ru

Как найти мгновенную скорость

Чтобы найти мгновенную скорость при равномерном движении, поделите расстояние, пройденное телом, на время, за которое оно преодолевалось. При неравномерном движении, узнайте значение ускорения и рассчитывайте скорость в каждый момент времени. При свободном падении мгновенная скорость зависит от ускорения свободного падения и времени. Мгновенную скорость можно измерить спидометром или радаром.

Вам понадобится

Для определения мгновенной скорости возьмите радар, спидометр, секундомер, рулетку или дальномер, акселерометр.

Спонсор размещения P&G Статьи по теме “Как найти мгновенную скорость” Как рассчитать среднюю скорость Как рассчитать скорость падения Как найти модуль скорости

Инструкция

Определение мгновенной скорости при равномерном движении

Если тело движется равномерно, измерьте с помощью рулетки или дальномера отрезок пути в метрах, после чего поделите полученное значение на промежуток времени в секундах, за которое этот отрезок был пройден. Время измерьте секундомером. После этого найдите среднюю скорость, поделив длину пути на время его прохождения (v=S/t). А поскольку движение равномерное, то средняя скорость будет равна мгновенной скорости.

Определение мгновенной скорости при неравномерном движении

Основным видом неравномерного движения является равноускоренное движение. С помощью акселерометра или любым другим способом измерьте значение ускорения. После этого, зная начальную скорость движения, прибавьте к ней произведение ускорения и времени, на протяжении которого тело находится в движении. Результатом будет значение мгновенной скорости в данный момент времени. (v=v0+a•t). При расчетах учтите, что если тело уменьшает свою скорость (тормозит), то значение ускорения будет отрицательным. В случае если движение начинается из состояния покоя, начальная скорость равна нулю.

Определение мгновенной скорости при свободном падении

Для определения мгновенной скорости свободно падающего тела нужно время падения умножить на ускорение свободного падения (9,81 м/с?), расчет произвести по формуле v= g•t. Учтите, что при свободном падении начальная скорость тела равна нулю. Если тело падает с известной высоты, то для определения мгновенной скорости в момент падения с этой высоты умножьте ее значение в метрах на число 19,62, а из полученного числа извлеките квадратный корень.

Определение мгновенной скорости спидометром или радаром

Если движущееся тело оборудовано спидометром (автомобиль), то на его шкале или электронном табло будет непрерывно отображаться мгновенная скорость в данный момент времени. При наблюдении за телом с неподвижной точки (земля), направьте на него сигнал радара, на его табло отобразится мгновенная скорость тела в данный момент времени.

Как просто

masterotvetov.com

Средняя и мгновенная скорость. Среднее и мгновенное ускорения. Полное ускорение

Быстроту перемещения материальной точки в пространстве характеризует скорость.

Средней скоростью называется векторная величина, равная по модулю отношению перемещения ко времени, за которое это перемещение произошло:

Направление вектора совпадает с вектором перемещения .

Движение с постоянной скоростью ( )называют равномерным.

При неравномерном (переменным) движении быстроту движения тела характеризует мгновенная скорость.

Мгновенная скорость – величина численно равная производной перемещения по времени:

Вектор мгновенной скорости направлен по касательной к траектории движения (рис.4).

Быстроту изменения скорости со временем характеризует ускорение.

Средним ускорением называется векторная величина, равная отношению изменения скорости ко времени, за кото-

Рис. 4 рое это изменение произошло: .

Вектор а_ср.направлен так же, как и вектор (рис.5).

Движение с постоянным ускорением называется равнопеременным.

При а > 0 – движение ускоренное, при а < 0 – замедленное.

Мгновенным ускорением называют предел:

т.е. ускорение – это производная скорости по времени.

В ряде случаев ускорение удобнее представить в виде двух взаимно перпендикулярных составляющих, одна из которых отражает изменение скорости по величине (тангенциальная) вторая – по направлению (нормальная или центростреми-

Рис. 5тельная) : ,

где и – единичные векторы, направленные первый – по касательной; второй – перпендикулярно ей в каждой точке траектории.

Таким образом: ,

или с учетом обозначений и запишем: .

В абсолютных значениях полное ускорение равно: .

В свою очередь каждое из них определяется следующим образом:

; ,

где R – радиус искривления траектории.

Мгновенная скорость | Физика

Рассмотрим автомобиль, движущийся прямолинейно и неравномерно (например, из Москвы в Санкт-Петербург, как на рис. 50). Понятно, что значения средней скорости этого автомобиля за различные промежутки времени при неравномерном движении могут меняться. Можно ли в этом случае ответить на вопрос: чему равна скорость автомобиля в какой-то конкретный момент времени? И существует ли вообще такая физическая величина? Ведь в определение средней скорости входит понятие определенного промежутка времени. А если этот промежуток времени будет равен нулю, то и перемещение тела, очевидно, будет равно нулю. Однако, наблюдая в движущимся автомобиле за спидометром, мы видим, что в каждый момент времени он показывает определенную величину, которая чаще всего изменяется со временем. Как же определить скорость тела в конкретный момент времени? Чтобы это сделать, рассмотрим очень маленький промежуток времени.

Под очень маленьким промежутком времени понимают такой промежуток, в течение которого движение тела практически неотличимо от равномерного прямолинейного движения. Это означает, что скорость тела в течение этого промежутка можно считать практически постоянной.

Из сказанного следует, что промежуток времени можно считать достаточно малым, если при его дальнейшем уменьшении полученные новые значения скорости практически не изменяются.

Понятно, что чем быстрее исследуемое тело изменяет свою скорость, тем меньше будет промежуток времени, в течение которого движение тела практически неотличимо от равномерного прямолинейного. И следовательно, тем меньший промежуток времени мы должны использовать для определения значения его скорости в конкретный момент времени.

Мгновенная скорость тела в данный момент времени t – это средняя скорость тела за достаточно малый промежуток времени Δt, начинающийся сразу после момента времени t.

Так же как и средняя скорость, мгновенная скорость является вектором. Чтобы подчеркнуть это, часто говорят «вектор скорости v», а при необходимости указать момент времени, для которого определена скорость, говорят «скорость в момент времени t».

При описании движения обычно говорят о скорости, имея при этом в виду мгновенную скорость в момент времени t. Поэтому мгновенную скорость обычно называют просто скорость. Если же речь идет, например, о средней скорости, то обязательно используют прилагательное «средняя», а для средней путевой скорости — прилагательные «средняя» и «путевая».

Итоги

Скорость (мгновенная скорость) тела в данный момент времени t – это средняя скорость тела за достаточно малый промежуток времени Δt, начинающийся сразу после момента времени t.

Вопросы

Какой промежуток времени при определении скорости можно считать достаточно малым?
Что такое мгновенная скорость?
Изменяется ли с течением времени мгновенная скорость тела, которое движется равномерно и прямолинейно?
Какие физические модели используют при введении понятия мгновенной скорости?

Упражнение

Представьте себе, что вы выехали на автомобиле со своего места на стоянке, находящейся рядом с вашим домом, в 8 часов утра, а в 17 часов вечера вернули автомобиль на то же место. За день вы проехали путь s = 360 км. При этом в течение промежутка времени от 10 до 12 часов дня вы ехали по прямолинейной трассе строго на север с постоянной скоростью 60 км/ч. Определите вашу скорость (модуль и направление) в моменты времени: а) t = 11 часов; б) t = 17 часов.