2.13. Вычисление пределов функций. Раскрытие неопределенностей
Правило. Для
вычисления предела функции  в точке
в точке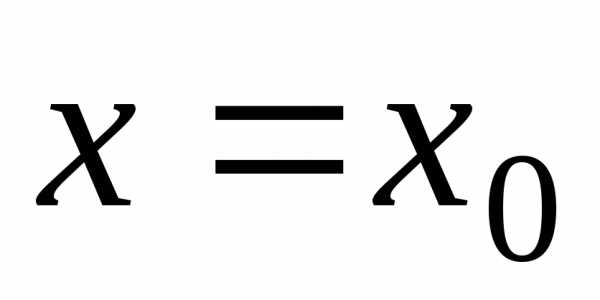 или принадо применить теоремы о пределах и
подставить предельное значение аргумента.
или принадо применить теоремы о пределах и
подставить предельное значение аргумента.
Для всех основных элементарных функций в любой точке их области определения имеет место равенство
.
Примеры
Найти пределы функций:
2. ;
3. ;
4. ;
5. 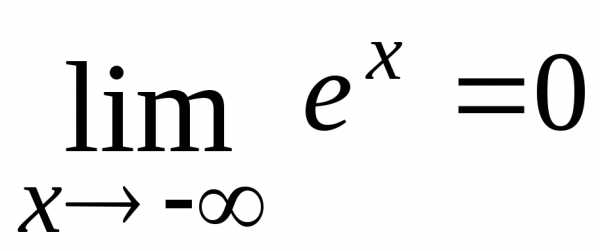 .
.
При вычислении
пределов функций формальная подстановка
вместо х предельного значения 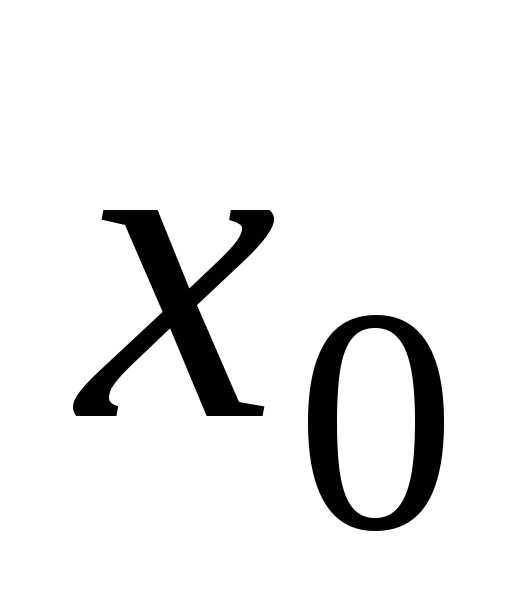
 ,
, ,
,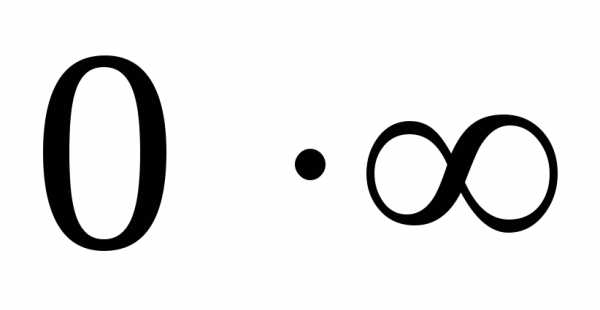 ,,
,,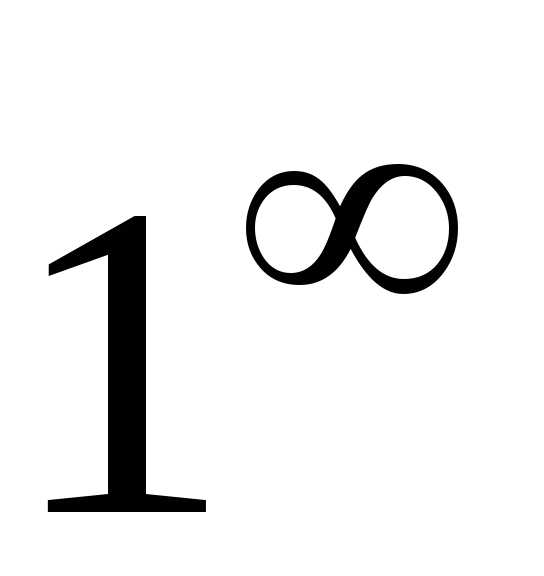 ,
, ,
,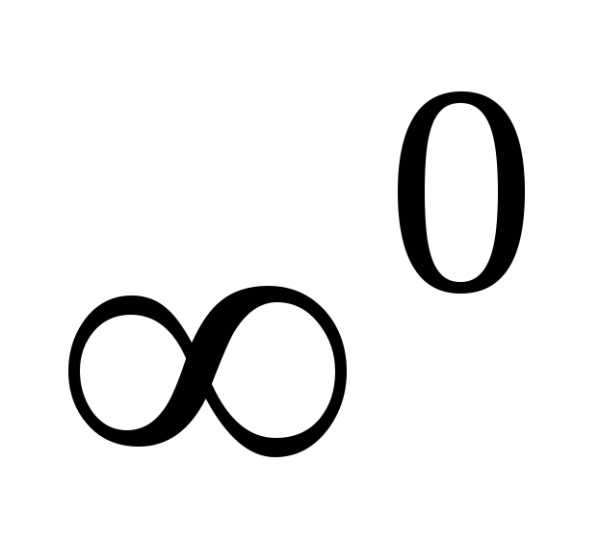 .
. Например,  или
или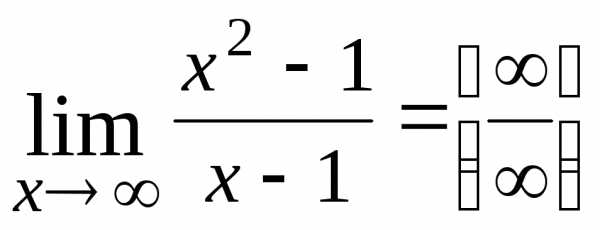
Выражения вида
, ,
,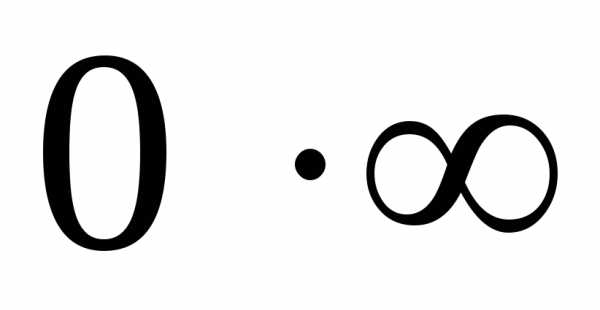 ,,
,,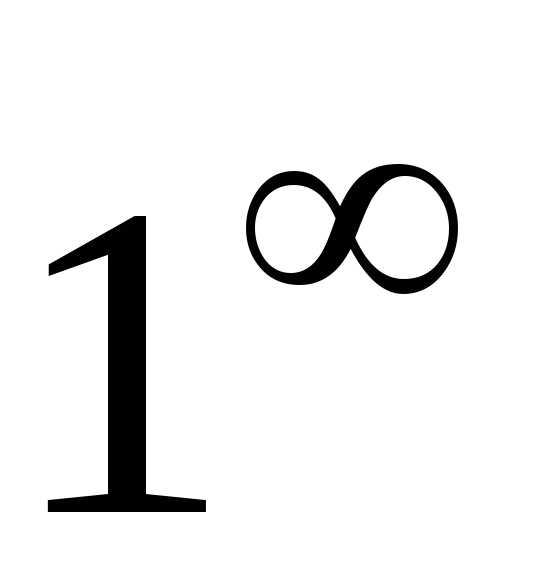 ,
,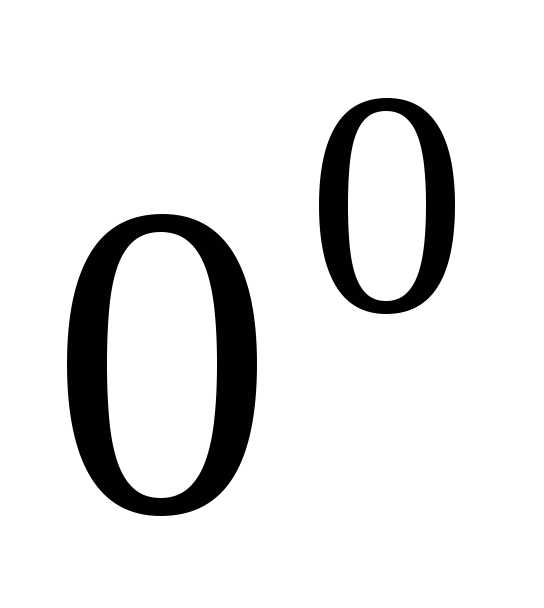 ,
,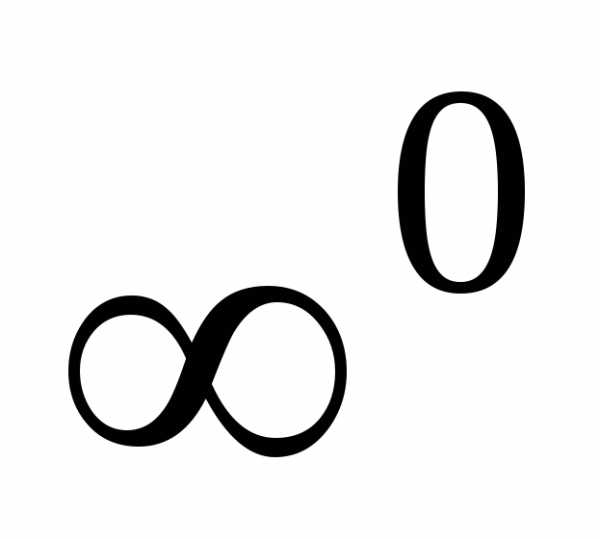 называютсянеопределенностями.
называютсянеопределенностями.
Вычисление предела функции в этих случаях называют раскрытием неопределенности.
Рассмотрим правила раскрытия таких неопределенностей.
Неопределенность вида
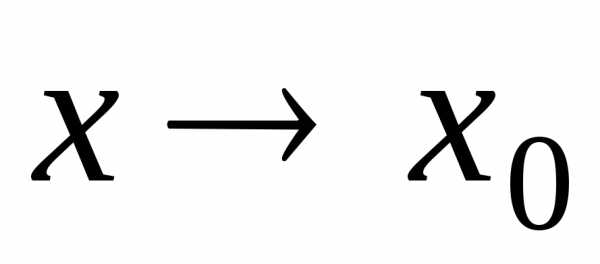 (),
то говорят, что их частное
(),
то говорят, что их частное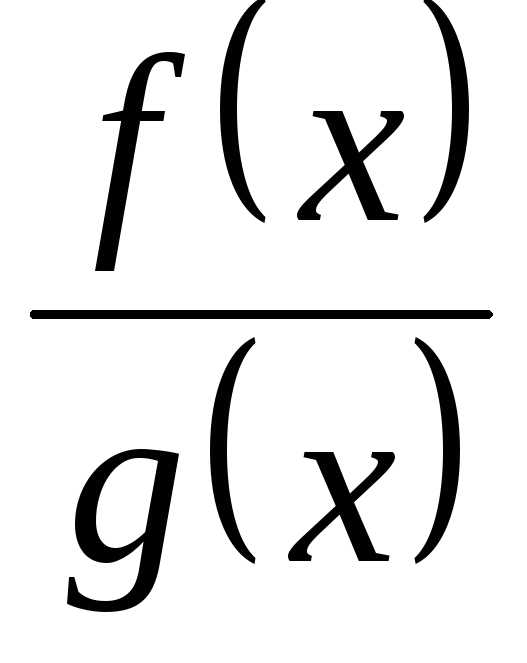 представляет собой неопределенность
вида
представляет собой неопределенность
вида .
. Правило. Чтобы
раскрыть неопределенность вида  ,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
Например,
.
(),
представляющую собой отношение двух многочленов относительно х степеней m и n соответственно, и исследуем поведение этой функции при .
При нахождении предела данной функции при могут иметь место три варианта ответа:
1. | |
2. | |
3. | |
Из этого следует, что предел отношения двух многочленов при во всех случаях равен пределу отношения их старших членов.
Примеры
Найти пределы функций:
1. ;
2. ;
3. .
Неопределенность
вида 
Если требуется
найти  ,
где
,
где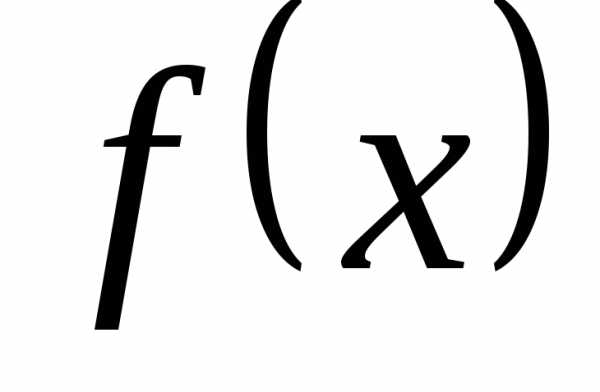 и
и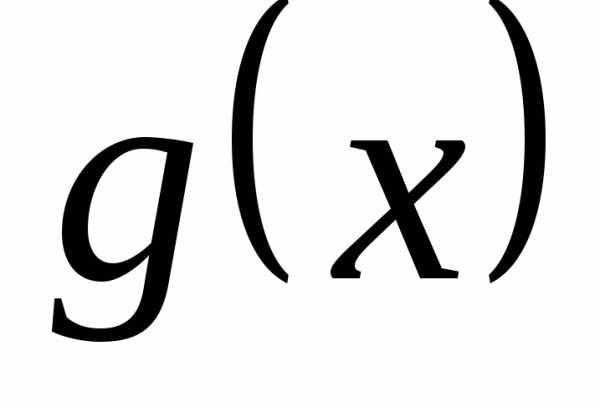 − бесконечно малые функции при
− бесконечно малые функции при (),
т.е.,
то в этом случае вычисление предела
называют раскрытием неопределенности
вида
(),
т.е.,
то в этом случае вычисление предела
называют раскрытием неопределенности
вида 
Рассмотрим возможные приемы раскрытия такой неопределенности.
Выделение критического множителя
Правило. Чтобы
раскрыть неопределенность вида  ,
заданную отношением двух многочленов,
надо и в числителе и в знаменателе
выделить критический множитель и
сократить на него дробь.
,
заданную отношением двух многочленов,
надо и в числителе и в знаменателе
выделить критический множитель и
сократить на него дробь.
Примеры
Найти пределы функций:
1. ;
2. ;
Преобразование иррациональных выражений
Правило. Чтобы
раскрыть неопределенность вида  ,
в которой числитель или знаменатель,
или тот и другой иррациональны, надо:
,
в которой числитель или знаменатель,
или тот и другой иррациональны, надо:
− перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель, домножив дробь на сопряженные выражения,
− либо сделать замену переменной.
Замечание.
Если под знаком предела делается замена переменной, то все величины, входящие под знак предела, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной.
Примеры
Найти пределы функций:
1.
;
2.
;
3.
 ;
;
4.
.
Применение первого замечательного предела
Правило. Для
раскрытия неопределенности вида  ,
содержащей тригонометрические выражения,
используют первый замечательный предел:
,
содержащей тригонометрические выражения,
используют первый замечательный предел:
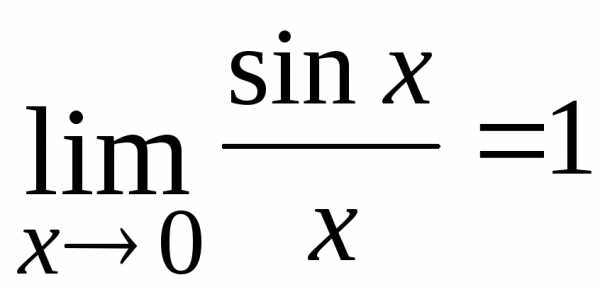 или
или 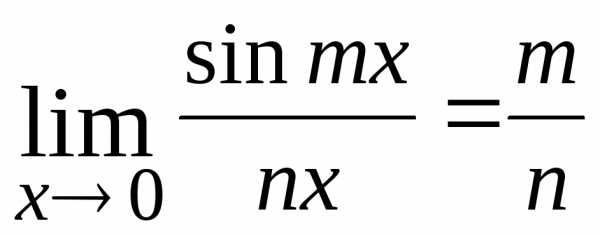 ,
,
где 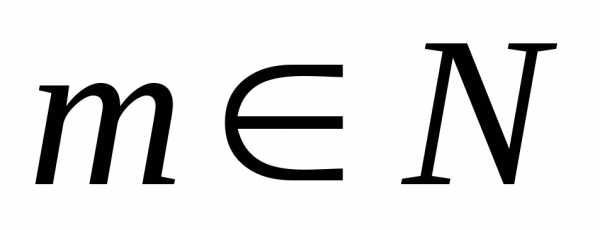 и
и .
.
Примеры
Найти пределы функций:
1. ;
2. ;
4. .
Применение эквивалентных бесконечно малых величин
 можно и числитель и знаменатель заменить
величинами им эквивалентными (п.2.12).
можно и числитель и знаменатель заменить
величинами им эквивалентными (п.2.12).Примеры
Найти пределы функций:
1. ;
2. ;
3. ;
4.
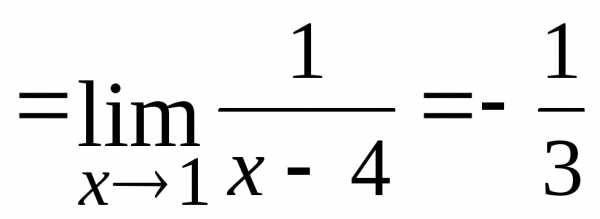 .
.
Неопределенности
вида
и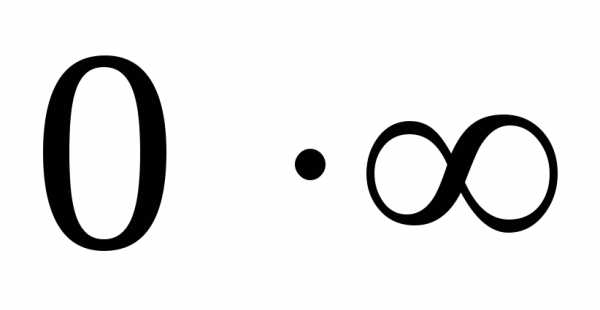
Если
ипри
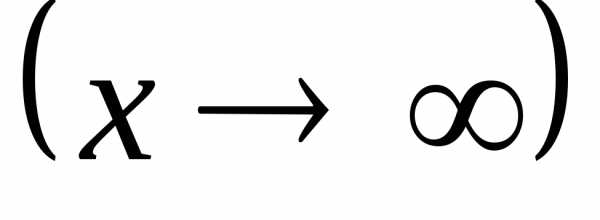 ,
то их разностьпредставляет собой неопределенность
вида .
,
то их разностьпредставляет собой неопределенность
вида . Если  ипри
ипри
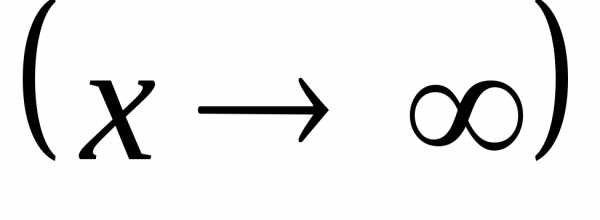 ,
то их произведение− это неопределенность вида
,
то их произведение− это неопределенность вида  .
.
Правило. Неопределенности
вида
и раскрываются путем их преобразования
и сведения к неопределенностям вида
раскрываются путем их преобразования
и сведения к неопределенностям вида
 .
.Примеры
Найти пределы функций:
.
Неопределенности
вида 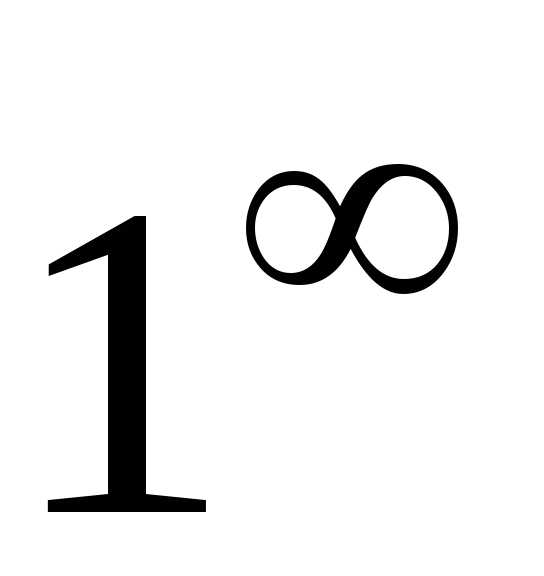 ,
, ,
,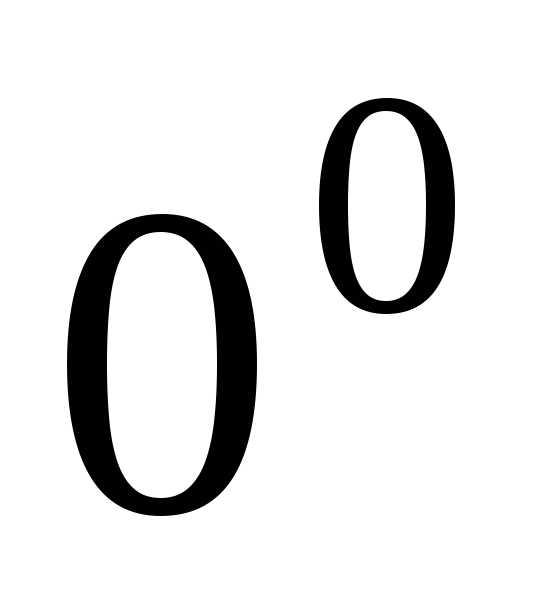
Пусть функция имеет вид:
.
Если при 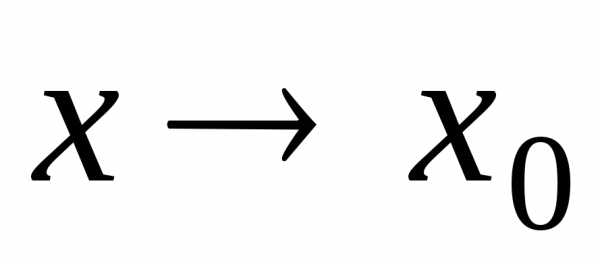
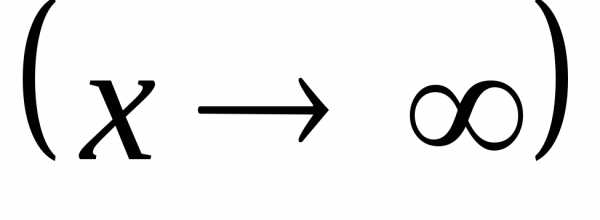 ,
,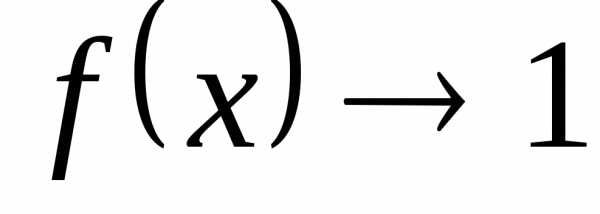 ,
а,
то имеем неопределенность вида
,
а,
то имеем неопределенность вида 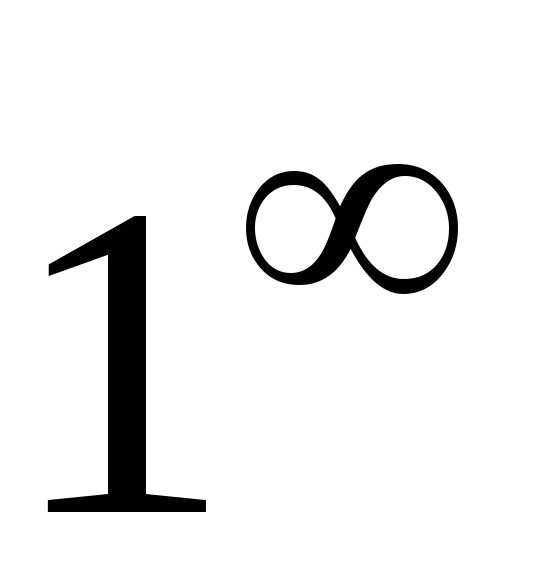 .
Для раскрытия этой неопределенности
применяют второй замечательный предел:
.
Для раскрытия этой неопределенности
применяют второй замечательный предел:
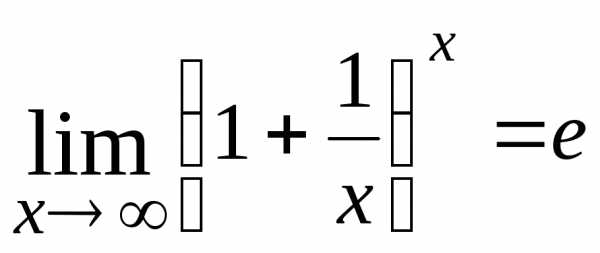 ;
; 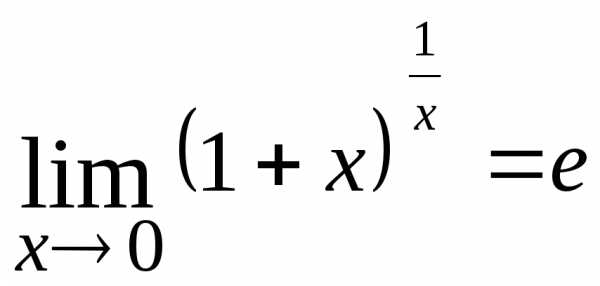 ;
;
или
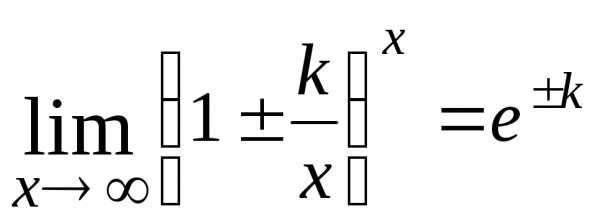 ;
; 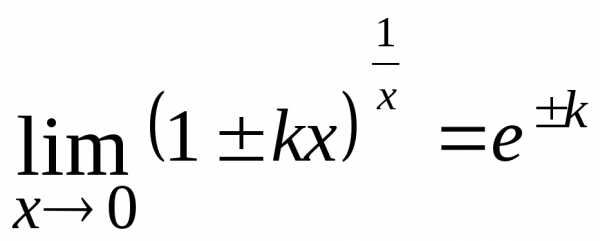 .
.
Примеры
Найти пределы функций:
1. ;
2. ;
3. ;
Если при 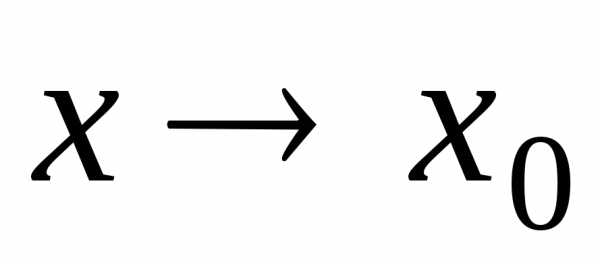
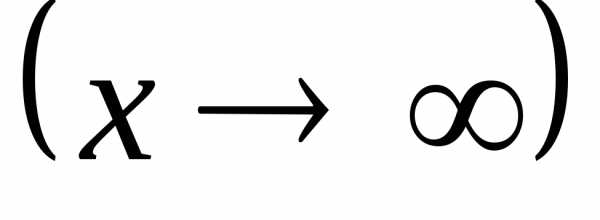 ,,
а
,,
а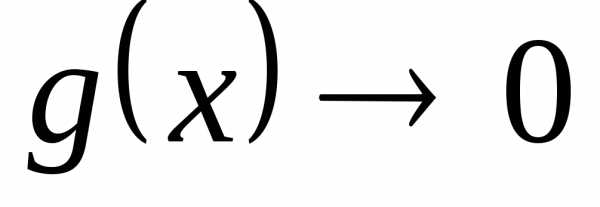 ,
то имеем неопределенность вида
,
то имеем неопределенность вида 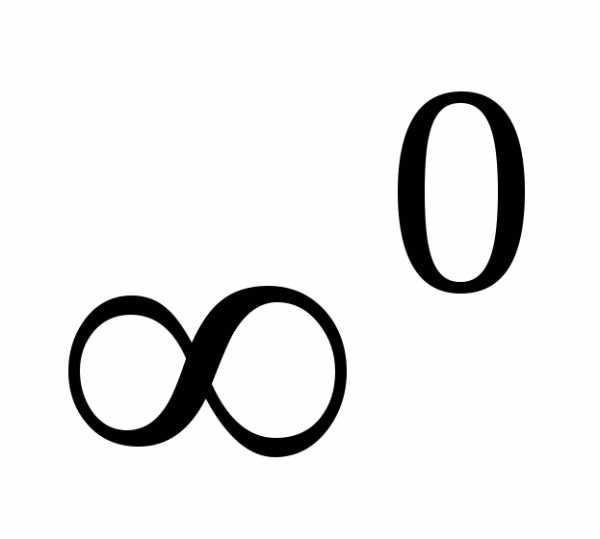 .
.
Если 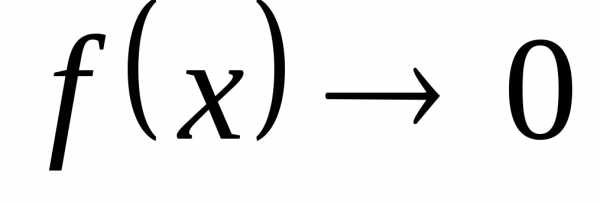 и
и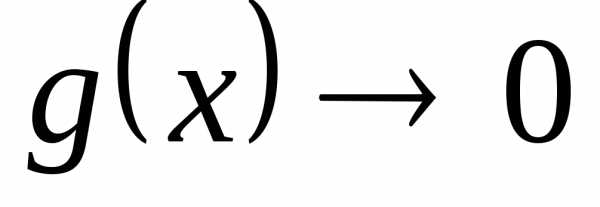 при
при ,
то имеет место неопределенность
,
то имеет место неопределенность  .
.
Для раскрытия
неопределенностей вида  и
и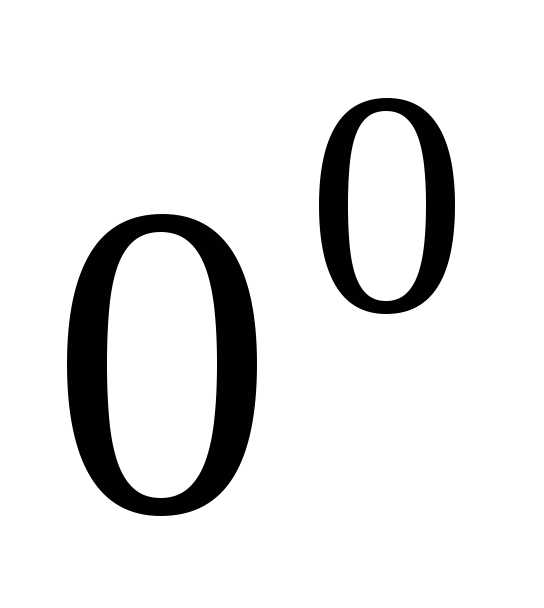 их преобразуют и сводят к неопределенности
вида
их преобразуют и сводят к неопределенности
вида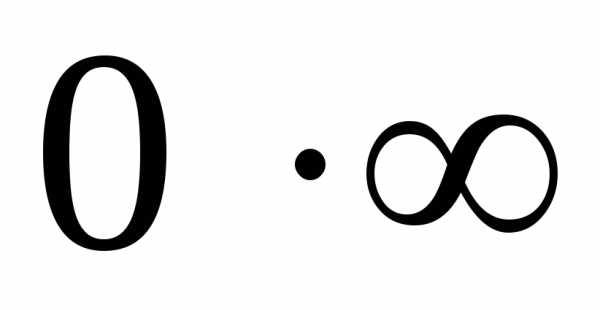 следующим образом:
следующим образом:
.
Примеры
Найти пределы функций:
1. ;
2. ;
В заключение отметим, что в дальнейшем будут рассмотрены более эффективные методы вычисления пределов функций, основанные на использовании понятия производной.
Упражнения
Односторонние пределы. Найти пределы:
1. 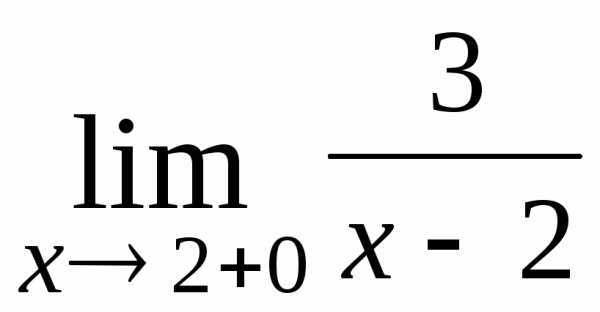 ; Ответ:
; Ответ: ;
;
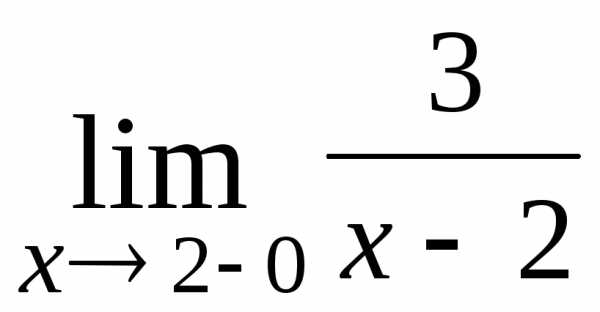 ; Ответ:
; Ответ:  ;
;
2. 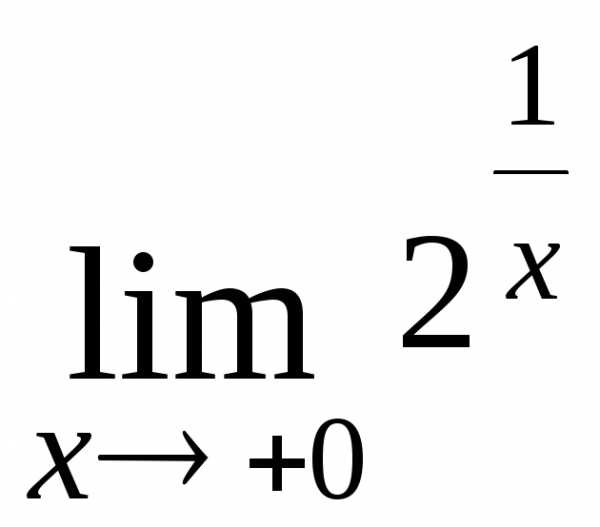 ; Ответь:
; Ответь: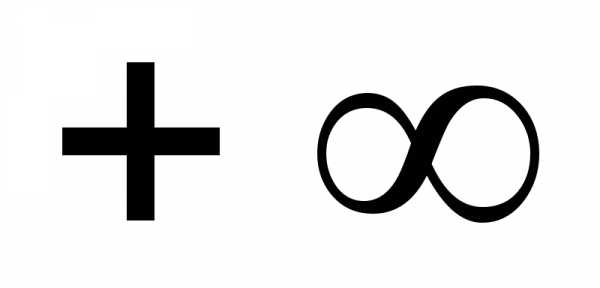 ;
;
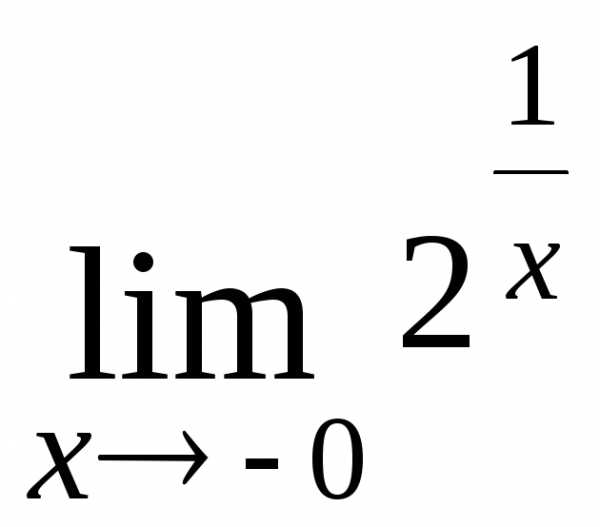 ; Ответ:
0.
; Ответ:
0.
Непосредственное вычисление пределов. Найти пределы:
3. ; Ответ: 15;
4.  ; Ответ:
; Ответ: .
.
5. 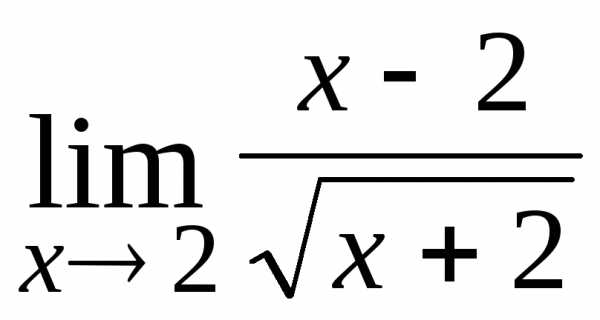 ; Ответ:
0.
; Ответ:
0.
Раскрытие
неопределенности  .
Найти пределы:
.
Найти пределы:
6. 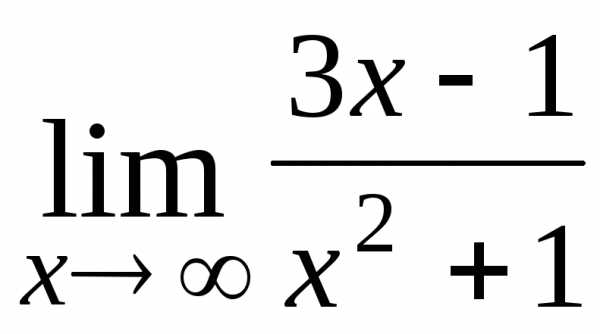 ; Ответ:
0;
; Ответ:
0;
7. 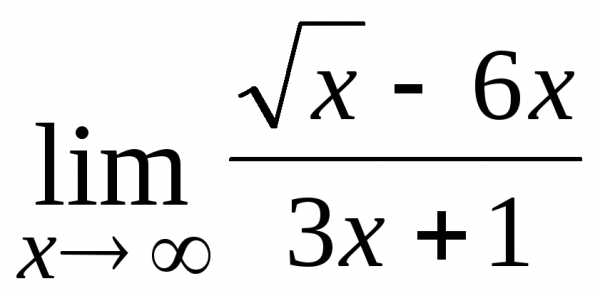 ; Ответ:
-2;
; Ответ:
-2;
8. 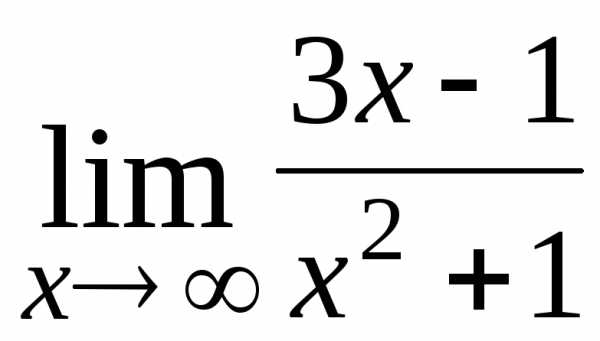 ; Ответ:
; Ответ: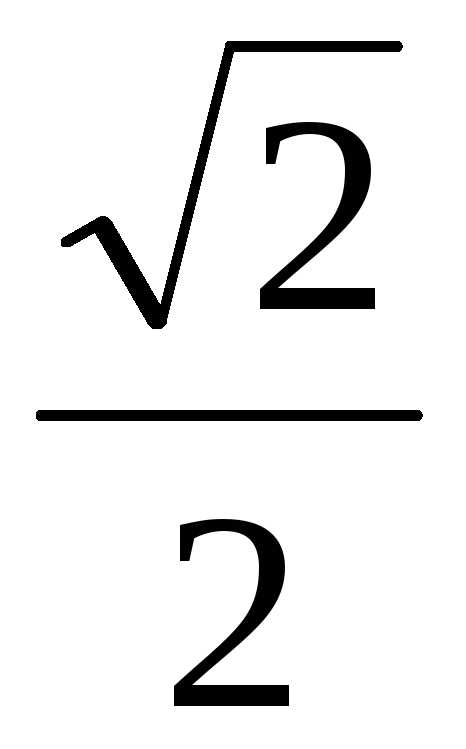 ;
;
9. 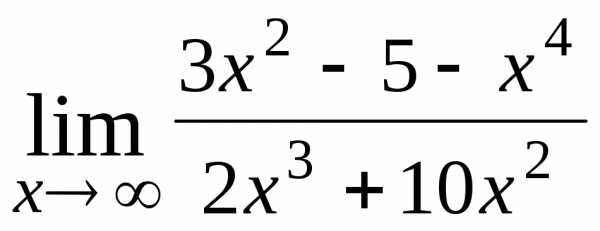 ; Ответ:
; Ответ: .
.
Раскрытие
неопределенности  .
Найти пределы:
.
Найти пределы:
10. 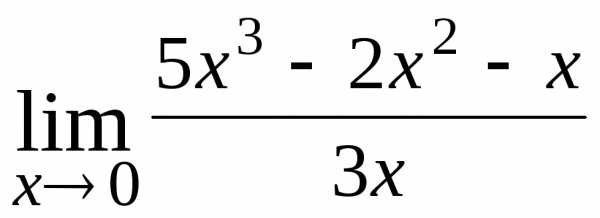 ; Ответ:
; Ответ: ;
;
11.  ; Ответ:
-2;
; Ответ:
-2;
12. 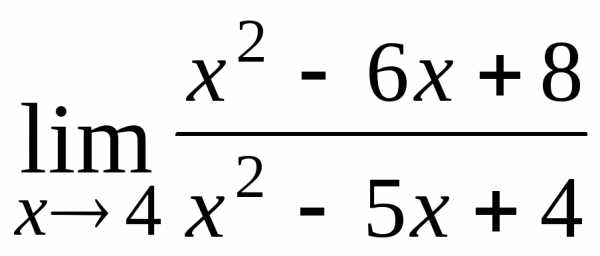 ; Ответ:
; Ответ: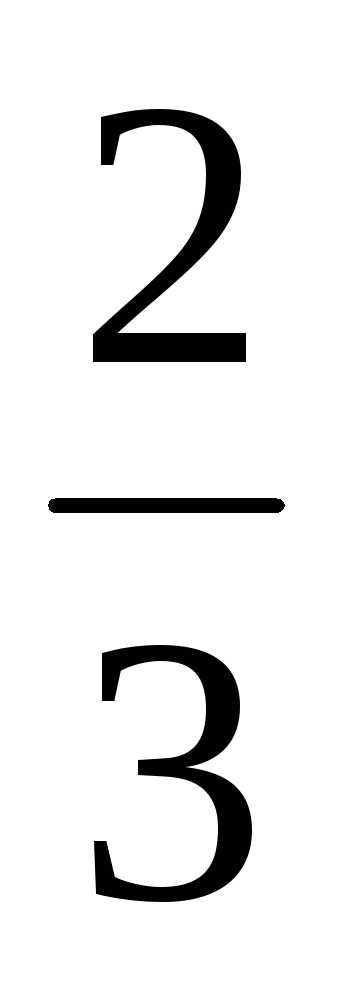 ;
;
13. 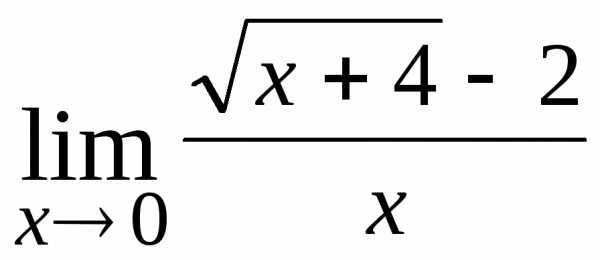 ; Ответ:
; Ответ: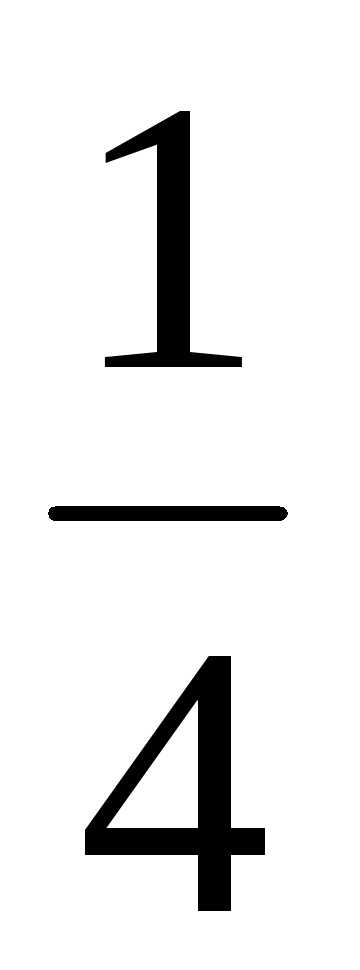 ;
;
14.  ; Ответ:
-12;
; Ответ:
-12;
15.  ; Ответ:
; Ответ: .
.
16. 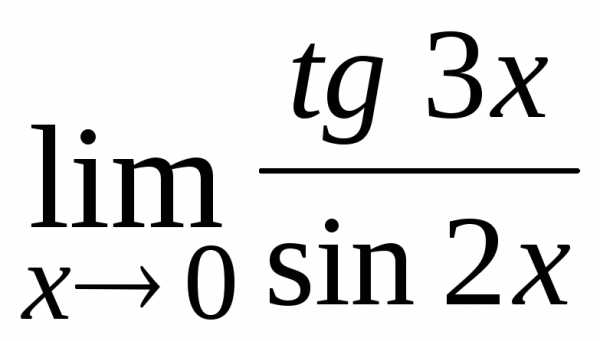 ; Ответ:
; Ответ: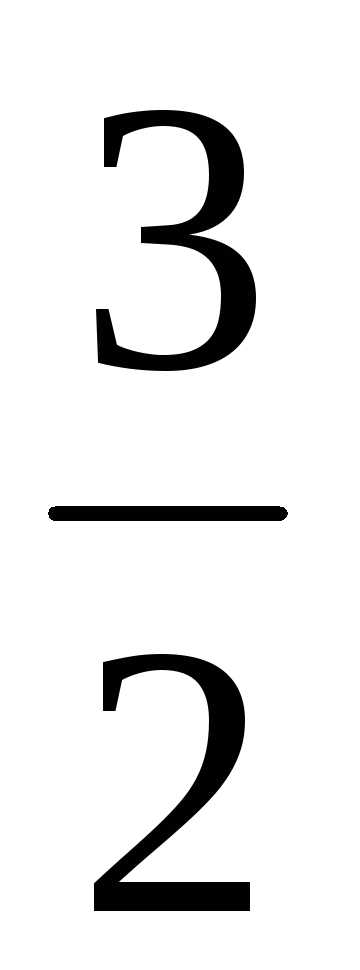 ;
;
17. 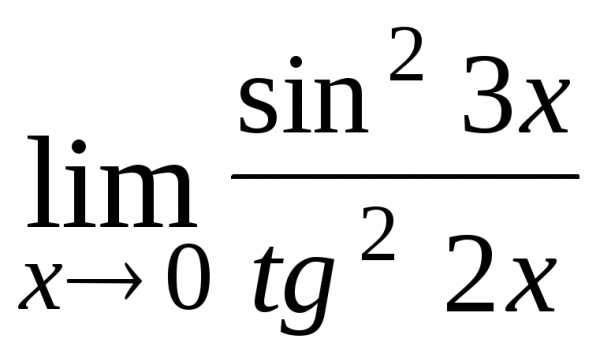 ; Ответ:
; Ответ: ;
;
18. 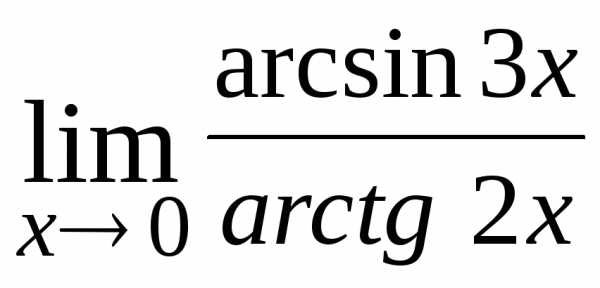 ; Ответ:
; Ответ: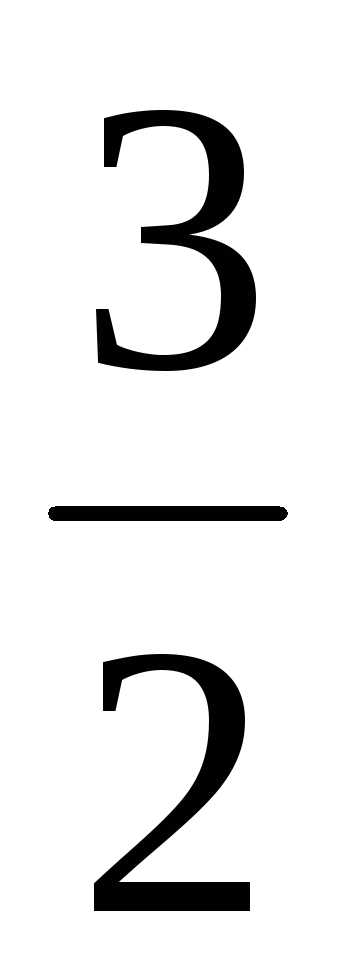 ;
;
19. 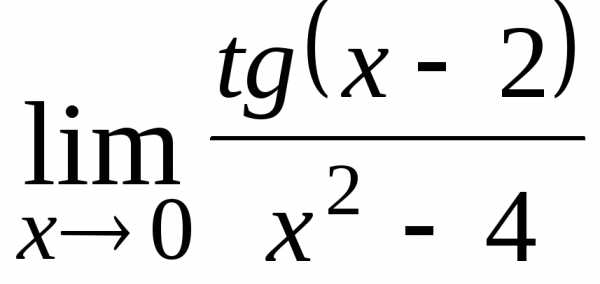 ; Ответ:
; Ответ: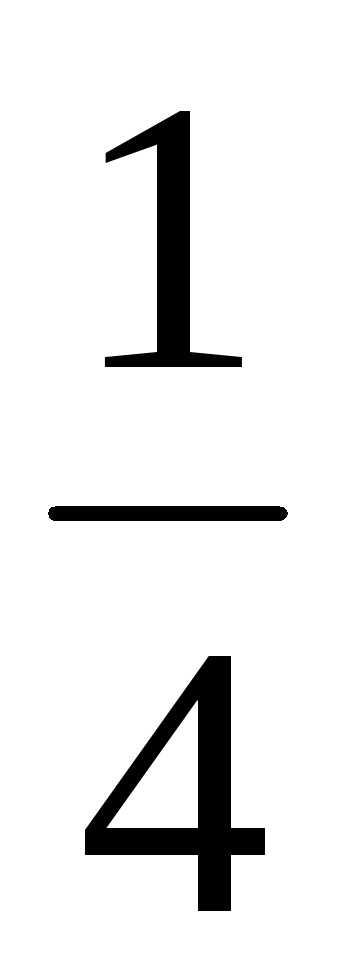 ;
;
20. 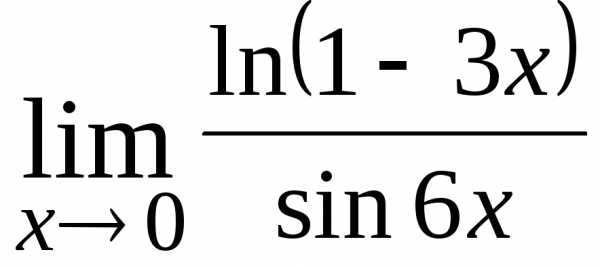 ; Ответ:
; Ответ: .
.
Раскрытие неопределенностей . Найти пределы:
21. 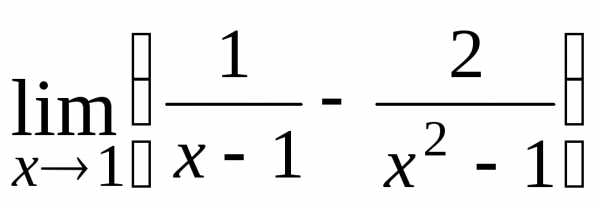 ; Ответ:
; Ответ: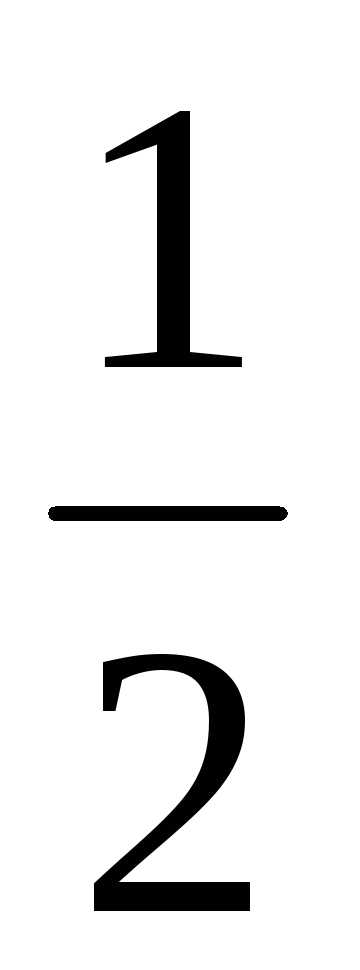 ;
;
22. 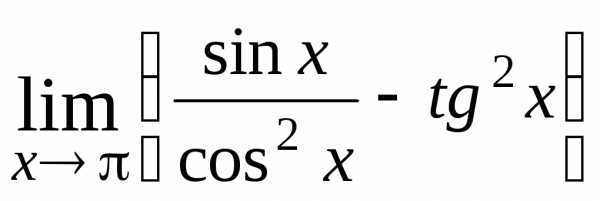 ; Ответ:
; Ответ: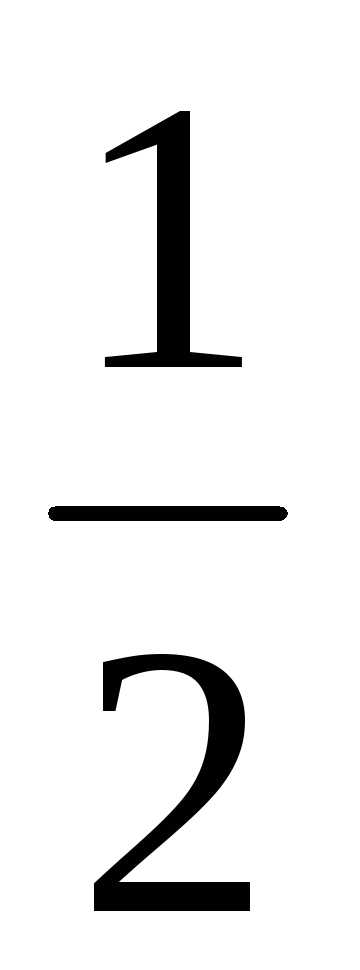 ;
;
23. ; Ответ: 0;
24. 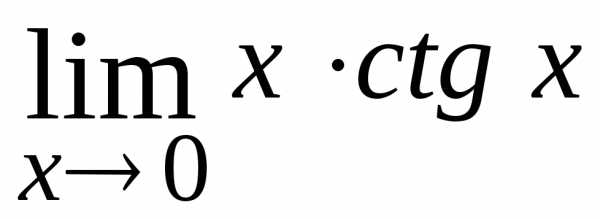 ; Ответ:
1.
; Ответ:
1.
Раскрытие
неопределенности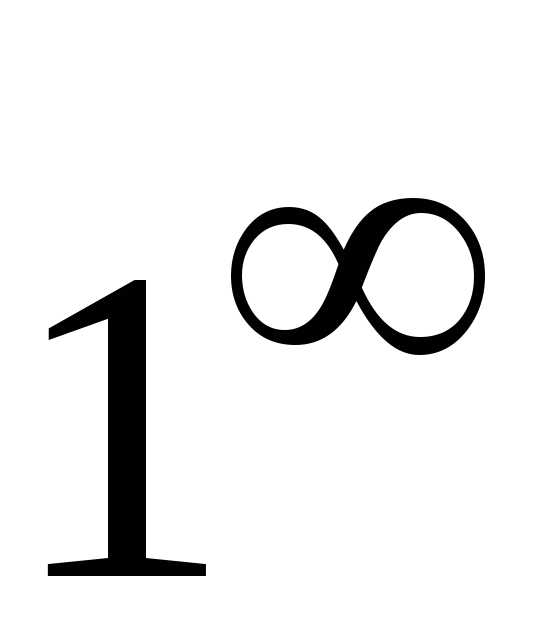 .
Найти пределы:
.
Найти пределы:
25.  ; Ответ:
; Ответ: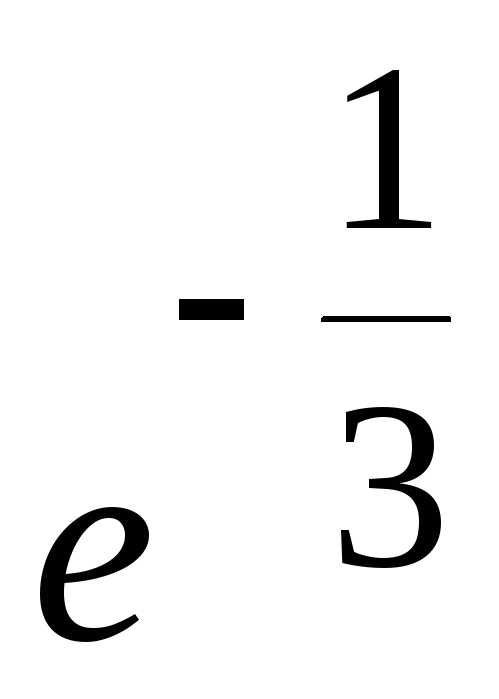 ;
;
26. 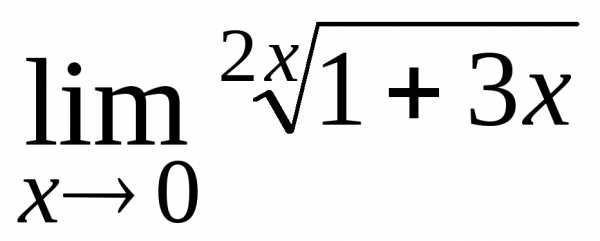 ; Ответ:
; Ответ: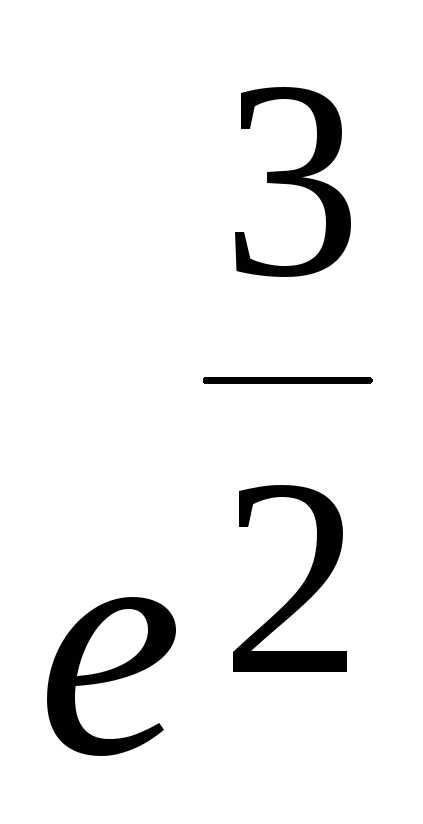 ;
;
27. 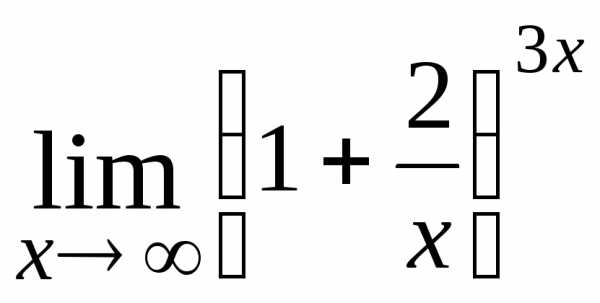 ; Ответ:
; Ответ: ;
;
28. 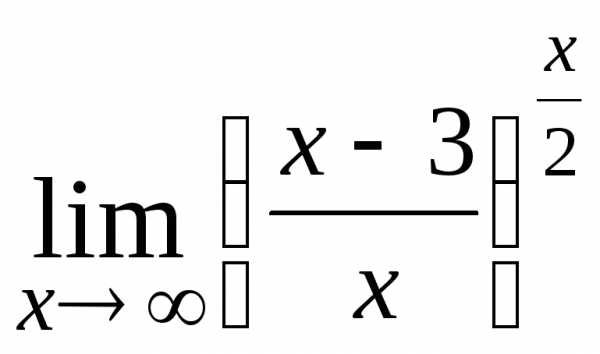 ; Ответ:
; Ответ: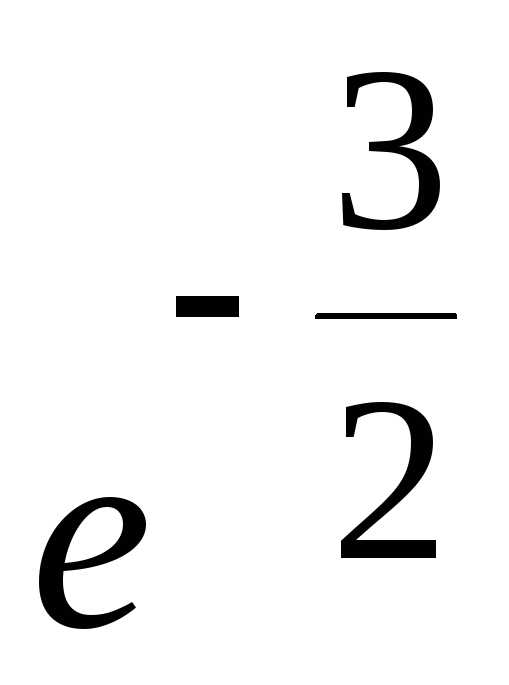 .
.
studfiles.net
Раскрытие неопределенностей — Мегаобучалка
При определении пределов часто возникают ситуации, называемые неопределенностями. Мы рассмотрим неопределенности следующих видов
1) – неопределенность “ноль делить на ноль”.
2) – неопределенность “бесконечность делить на бесконечность”.
3) –неопределенность “ноль умножить на бесконечность”.
Нахождение пределов в этих случаях называется раскрытием неопределенностей.
Рассмотрим некоторые приемы раскрытия каждой неопределенности в отдельности.
Неопределенность появляется при нахождении предела отношения двух бесконечно малых функций .
Пример 1.4
.
Здесь = 4 – 10 + 6 = 0 и = 0. Числитель и знаменатель дроби являются бесконечно малыми при , т.е. имеет место неопределенность . Для раскрытия неопределенности в рассматриваемом случае числитель и знаменатель дроби разложим на множители и сократим на величину , дающую 0 в числителе и знаменателе:
= = = = = – .
Пример 1.5
Найти предел: .
Решение
Здесь также имеем дело с неопределенностью . Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение , которое называется сопряженным выражению , тогда
= = = =
= = = .
Для раскрытия неопределенности в некоторых случаях могут быть полезны следующие определения и теоремы.
Определение 1.1. Пусть и две БМ при . Если
| , | (1.1) |
то БМ и называются эквивалентными. Эквивалентность БМ и обозначается .
Теорема 1.1. (Первый замечательный предел). Можно показать
[ ], что
| , | (1.2) |
Предел (1.2) называется первым замечательным пределом. Из теоремы 1.1 и определения 1.1 следует, что . Приведем еще некоторые примеры эквивалентных БМ при a® 0:
Таблица 1.1
Теорема 1.2.
Предел отношения двух бесконечно малых величин равен пределу отношения бесконечно малых, эквивалентных данным.
Поясним, что утверждает теорема. Пусть и две бесконечно малые функции. Известны еще две БМ и , причем и . Тогда .
Доказательство:
= , что и требовалось. доказать.
Каждый из пределов в рамках равен единице, т.к. это пределы отношений эквивалентных бесконечно малых.
Пример 1.6
Найти .
Решение
Здесь имеет место неопределенность , которая раскрывается
переходом к эквивалентным величинам: sin5x~5x, sin3x~3x, по теореме 1.2 получаем:
= = = .
Неопределенность появляется при нахождении предела отношения двух бесконечно больших .
Пример 1.7
Найти .
Решение
Здесь имеет место неопределенность . Отметим, что самая большая степень, в которой переменная входит в числитель и знаменатель дроби. Для раскрытия неопределенности вынесем за скобки и в числителе и в знаменателе и сократим. Получим
= =
= .
Отметим, что в данном примере высшая степень в числителе равна высшей степени в знаменателе. Предел равен отношению коэффициентов при высших степенях в числителе и знаменателе.
Пример 1.8
= = = = 0.
Отметим, что в данном примере высшая степень в числителе меньше высшей степени в знаменателе. Предел равен нулю.
Пример 1.9
= = =
= = .
В данном примере высшая степень в числителе больше высшей степени в знаменателе. Предел равен бесконечности. В результате рассмотрения примеров 1.7, 1.8 и 1.9 сформулируем общее правило нахождения предела вида
=
=
Пример 1.10
.
Решение
Здесь , , , поэтому предел равен :
.
megaobuchalka.ru
Раскрытие неопределённостей — WiKi
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
(Здесь 0{\displaystyle 0} — бесконечно малая величина, а ∞{\displaystyle \infty } — бесконечно большая величина)
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов ( 00){\displaystyle \left(~0^{0}\right)}, (1∞){\displaystyle \left(1^{\infty }\right)}, (∞0){\displaystyle \left(\infty ^{0}\right)} пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
- ( 00)=(e0⋅ln0)=(e0⋅(−∞)){\displaystyle \left(~0^{0}\right)=\left(e^{0\cdot ln{0}}\right)=\left(e^{0\cdot (-\infty )}\right)}
- ( 1∞)=(e∞⋅ln1)=(e∞⋅0){\displaystyle \left(~1^{\infty }\right)=\left(e^{\infty \cdot ln{1}}\right)=\left(e^{\infty \cdot 0}\right)}
- ( ∞0)=(e0⋅ln∞)=(e0⋅∞){\displaystyle \left(~\infty ^{0}\right)=\left(e^{0\cdot ln{\infty }}\right)=\left(e^{0\cdot \infty }\right)}
Для раскрытия неопределённостей типа ∞∞{\displaystyle {\frac {\infty }{\infty }}} используется следующий алгоритм:
- Выявление старшей степени переменной;
- Деление на эту переменную как числителя, так и знаменателя.
Для раскрытия неопределённостей типа (00){\displaystyle \left({\frac {0}{0}}\right)} существует следующий алгоритм:
- Разложение на множители числителя и знаменателя;
- Сокращение дроби.
Для раскрытия неопределённостей типа (∞−∞){\displaystyle (\infty -\infty )} иногда удобно применить следующее преобразование:
- Пусть f(x)→x→a∞{\displaystyle f(x){\xrightarrow {x\to a}}\infty } и g(x)→x→a∞{\displaystyle g(x){\xrightarrow {x\to a}}\infty };
- limx→a[f(x)−g(x)]=(∞−∞)=limx→a(11f(x)−11g(x))=limx→a1g(x)−1f(x)1g(x)⋅1f(x)=(00){\displaystyle \lim _{x\to a}[f(x)-g(x)]=(\infty -\infty )=\lim _{x\to a}\left({\frac {1}{\frac {1}{f(x)}}}-{\frac {1}{\frac {1}{g(x)}}}\right)=\lim _{x\to a}{\frac {{\frac {1}{g(x)}}-{\frac {1}{f(x)}}}{{\frac {1}{g(x)}}\cdot {\frac {1}{f(x)}}}}=\left({\frac {0}{0}}\right)}.
Данный вид неопределённостей может раскрываться с использованием асимптотических разложений уменьшаемого и вычитаемого, при этом бесконечно большие члены одного порядка должны уничтожаться.
При раскрытии неопределённостей также применяются замечательные пределы и их следствия.
ru-wiki.org
Вычисление пределов функций. Раскрытие неопределенностей — Мегаобучалка
Правило.Для вычисления предела функции в точке или при надо применить теоремы о пределах и подставить предельное значение аргумента.
Для всех основных элементарных функций в любой точке их области определения имеет место равенство
.
Примеры
Найти пределы функций:
2. ;
3. ;
4. ;
5. .
При вычислении пределов функций формальная подстановка вместо х предельного значения часто приводит к неопределенным выражениям вида: , , , , , , .
Например, или .
Выражения вида , , , , , , называются неопределенностями.
Вычисление предела функции в этих случаях называют раскрытием неопределенности.
Рассмотрим правила раскрытия таких неопределенностей.
Неопределенность вида
Если и при ( ), то говорят, что их частное представляет собой неопределенность вида .
Правило.Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
Например,
.
Рассмотрим дробно−рациональную функцию
( ),
представляющую собой отношение двух многочленов относительно х степеней m и n соответственно, и исследуем поведение этой функции при .
При нахождении предела данной функции при могут иметь место три варианта ответа:
Из этого следует, что предел отношения двух многочленов при во всех случаях равен пределу отношения их старших членов.
Примеры
Найти пределы функций:
1. ;
2. ;
3. .
Неопределенность вида
Если требуется найти , где и − бесконечно малые функции при ( ), т.е. , то в этом случае вычисление предела называют раскрытием неопределенности вида .
Рассмотрим возможные приемы раскрытия такой неопределенности.
Выделение критического множителя
Правило.Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо и в числителе и в знаменателе выделить критический множитель и сократить на него дробь.
Примеры
Найти пределы функций:
1. ;
2. ;
Преобразование иррациональных выражений
Правило.Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель, или тот и другой иррациональны, надо:
− перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель, домножив дробь на сопряженные выражения,
− либо сделать замену переменной.
Замечание.
Если под знаком предела делается замена переменной, то все величины, входящие под знак предела, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной.
Примеры
Найти пределы функций:
1.
;
2.
;
3.
;
4.
.
megaobuchalka.ru
Вычисление пределов. Пределы с неопределенностью
Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью “Пределы. Понятие пределов. Вычисление пределов”.
Теперь перейдем к рассмотрению пределов с неопределенностью.
Существует группа пределов, когда x , а функция представляет собой дробь, подставив в которую значение х = получим неопределенность вида .
Пример.
Необходимо вычислить предел
Воспользуемся нашим правилом №1 и подставим в функцию. Как видно мы получаем неопределенность .
В числителе находим х в старшей степени, которая в нашем случае = 2:
То же самое проделаем со знаменателем:
Здесь также старшая степень = 2.
Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.
Итак, для раскрытия неопределенности нам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x2:
Ответ: 2/3.
Существуют также пределы с другой неопределенностью – вида . Отличие от предыдущего случая лишь в том, что х стремится уже не к , а к конечному числу.
Пример.
Необходимо вычислить предел .
Снова воспользуемся правилом №1 и подставим в место х число -1:
Мы получили неопределенность , для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.
В нашем случае решаем уравнение:
Находим дискриминант:
.
Если корень не извлекается целый вероятней всего D вычислен неправильно.
Теперь находим корни уравнения:
Подставляем:
Числитель разложили.
В знаменателе у нас х + 1, что итак является простейшим множителем.
Тогда наш предел примет вид:
х + 1 красиво сокращается:
Теперь подставим вместо х значение -1 в функцию и получаем:
2*(-1) – 5 = -2 – 5 = -7
Ответ: -7.
Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:
На этом с вычислением пределов с неопределенностью всё. Еще в статье “Замечательные пределы: Первый и второй замечательный предел” мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Если у вас появились какие то вопросы по вычислению пределов с неопределенностью, то задавайте их в комментариях. Будем рады ответить.
Заметка: Если не хватает времени на учебу, вы можете заказать контрольную работу (http://forstuds.ru/kontrolnaya-rabota-na-zakaz), учтите правда наличие знаний по теме у вас после этого.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
неопределенность 0/0 | Математика
Если при подстановке предельного значения х получаем
то такое выражение называется неопределенностью вида ноль на ноль. Неопределенность 0 на 0 надо убрать.
Чтобы избавиться от непреденности вида ноль на ноль, заданной отношением двух многочленов, надо и в числителе, и в знаменателе выделить критический множитель и сократить на него. Чтобы выделить критический множитель — то есть множитель, равный нулю при предельном значении х — нужно многочлены разложить на множители.
Способы разложения многочлена на множители:
— вынесение общего множителя за скобки;
— по формулам сокращенного умножения;
— группировка;
— по теореме о разложении квадратного трехчлена на множители:
где
и
корни уравнения
.
Можно просто разделить многочлены в числителе и знаменателе уголком на
. Если кратность корня больше единицы, это придется сделать не раз.
adminПредел функцииwww.matematika.uznateshe.ru
Решение пределов через раскрытие неопределённостей — Мегаобучалка
Основные теоремы о пределах
Теорема 1.(о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.
Теорема 2.Если функции f(x) и g(x) имеют пределы в точке , то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
(5)
Замечание.Формулы (3) и (4) справедливы для любого конечного числа функций.
Следствие 1.Предел постоянной равен самой постоянной, т.е.
Следствие 2.Постоянный множитель можно выносить за знак предела, т.е.
Пример 3.Найти предел:
Решение.
Пример 4.Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
Теорема 3(о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке , то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5.Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
К началу страницы
Пройти тест по теме Предел
Решение пределов через раскрытие неопределённостей
При решении примера 5 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида – самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Освоим эти приёмы на примерах.
Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.
Неопределённость вида
Пример 6.Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или “супермалому числу”.
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Пример 7.Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем “икс” под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо “икса”.
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Неопределённость вида
Пример 8.Раскрыть неопределённость и найти предел .
Решение. В числителе – разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе – квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Пример 9. Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 10. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
megaobuchalka.ru

 ,
если
,
если  ;
;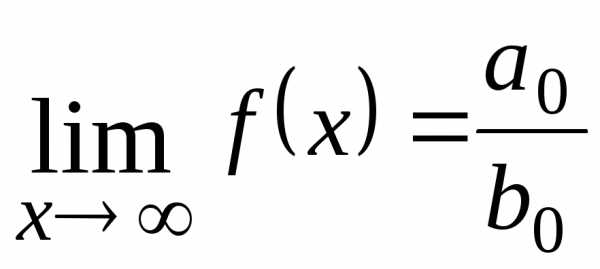 ,
если
,
если 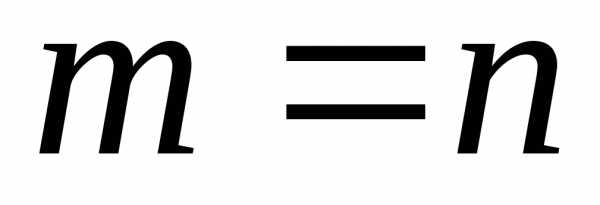 ;
;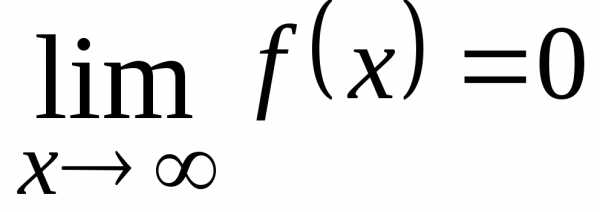 ,
если
,
если  .
.