Как найти производную функции, примеры решения
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
Как найти?
Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования:
- Вынос константы за знак производной:
- Производная суммы/разности функций:
- Производная произведения двух функций:
- Производная дроби:
- Производная сложной функции:
Примеры решения
| Пример 1 |
| Найти производную функции |
| Решение |
Производная суммы/разности функций равна сумме/разности производных: Используя правило производной степенной функции имеем: Так же было учтено, что производная от константы равна нулю. |
| Ответ |
| Пример 2 |
| Найти производную функции |
| Решение |
По правилу производной разности: По таблице интегрирования находим: С учетом того, что аргумент натурального логарифма отличен от , то нужно домножить ещё на производную самого аргумента: После упрощения получаем: |
| Ответ |
| Пример 3 |
| Найти производную функции |
| Решение |
В данном примере стоит произведение двух функций, а производная произведения находится по формуле номер 3: Производная первой функции вычисляется как разность фунций: Вторая функция является показательной, производная которой находится по формуле: : Продолжаем решение с учетом найденных производных: |
| Ответ |
| Пример 4 |
| Найти производную функции |
| Решение |
Производную дроби найдем по четвертой формуле. Положим и . Тогда их производные по таблице основных элементарных функций равны: Используя формулу №4 получаем: |
| Ответ |
| Пример 5 |
| Найти производную функции |
| Решение |
Данная функция является сложной, потому производную будем брать по цепочке. Сначала от внешней функции, затем от внутренней. При этом выполняя их перемножение. Заметим, что аргумент синуса отличен от , поэтому тоже является сложной функцией: Учитывая определение котангенса перепишем полученную производную в удобном компактном виде: |
| Ответ |
xn--24-6kcaa2awqnc8dd.xn--p1ai
Как найти производную. Таблица производных.
 Как мы знаем,
Как мы знаем,
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций
Тем, кто все же хочет понять, что такое предел числовой последовательности, я предлагаю посмотреть ВИДЕОУРОК:
Операция нахождения производной функции называется дифференцированием. В результате выполнения этой операции мы по определенным правилам получаем другую функцию:
В этом равенстве – функция, от которой мы берем производную,
– функция, которая получается в результате этой операции.
Для того, чтобы каждый раз не искать производные элементарных функций, используя определение производной, существует
1. Производная константы равна нулю:
2. Производная степенной функции:
Заметим, что может принимать любые действительные значения.
Примеры.
1.
2.
3.
3. Производная показательной функции:
Пример.
Частный случай этой формулы:
4. Производная логарифма:
Частный случай этой формулы:
5. Производные тригонометрических функций:
6. Производные обратных тригонометрических функций:
Правила дифференцирования:
1. Производная суммы двух функций:
2. Производная произведения двух функций:
3. Производная дроби:
4. Производная произведения функции на число равна произведению числа на производную функции (число “выносится” за знак производной):
Чтобы правильно найти производную функции , полезно придерживаться такого алгоритма:
1. Выделите, какие элементарные функции входят в состав уравнения функции.
2. Отделите в явном виде коэффициенты.
3. Если возможно, упростите выражение , используя свойства степени, свойства логарифмов или тригонометрические формулы в зависимости от того, какие элементарные функции входят в состав функции
4. Вспомните, чему равны производные этих функций или посмотрите в таблице производных.
5. Обратите внимание на то, какими арифметическими действиями связаны между собой элементарные функции, которые входят в состав функции и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций.
Пример 1. Найти производную функции:
Используя свойства логарифмов, упростим выражение в правой части уравнения функции:
Так как по условию , следовательно,
Таким образом:
Пример 2. Найти производную функции:
1. Упростим каждую дробь, используя свойства степени :
Мы видим, что наша функция представляет собой сумму степенных функций.
Следовательно:
Пример 3. Найти производную функции
Сначала запишем каждое слагаемое в виде степени и выделим в явном виде числовые коэффициенты:
Теперь легко найти производную:
Пример 4. Найти производную функции:
Мы видим, что наша функция представляет собой дробь, в числителе которой стоит степенная функция, а в знаменателе сумма косинуса и константы.
Найдем производную функции по формуле производной дроби:
В нашем случае:
Отсюда:
КАК ИСКАТЬ ПРОИЗВОДНУЮ СЛОЖНОЙ ФУНКЦИИ читайте здесь
Видеоурок “Производная сложной функции” смотрите здесь.
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Примеры решений производных
- Попробуйте найти производные от приведенных ниже функций.
- Нажмите на изображение или стрелку, чтобы попасть на страницу с подробным решением.
Примеры решений производных от явных функций
Найдите производные следующих функций, зависящих от переменной x:
Решение > > >
Решение > > >
Решение > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
> > > Здесь , , , – постоянные.
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры решений производных высших порядков от явных функций
Найти производные первого и второго порядка следующей функции:
.
Решение > > >
Найти производную третьего порядка:
.
Решение > > >
Найти производную шестого порядка следующей функции:
.
Решение > > >
Вычислить n-ю производную функции
.
Решение > > >
Найти n-ю производную следующей функции:
,
где и – постоянные.
Решение > > >
Примеры решения производных от функций, заданных параметрическим способом
Найдите производную от функции, заданной параметрическим способом:
Решение > > >
Найдите производную , где и выражены через параметр :
Решение > > >
Найдите производные второго и третьего порядка от функции, заданной параметрическим способом:
Решение > > >
Примеры решений производных от неявных функций
Найдите производную первого порядка от функции, заданной неявно уравнением:
.
Решение > > >
Найти производную второго порядка от неявно заданной функции:
.
Решение > > >
Найти производную третьего порядка при от функции, заданной уравнением:
.
Решение > > >
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Как найти производную?
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g’ означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- С’=0
- (sin x)’=cos x
- (cos x)’= –sin x
- (ex)’=ex
- (ln x)’=1/x
- (ax)’=axln a
- (logax)’=1/x ln a
- (tg x)’=1/cos2x
- (ctg x)’= – 1/sin2x
- (arcsin x)’= 1/√(1-x2)
- (arccos x)’= – 1/√(1-x2)
- (arctg x)’= 1/(1+x2)
- (arcctg x)’= – 1/(1+x2)
Пример 1. Найдите производную функции y=500.
Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
(500)’ = 0
Пример 2. Найдите производную функции y=x100.
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x100)’=100 x99
Пример 3. Найдите производную функции y=5x
Это показательная функция, вычислим ее производную по формуле 4.
(5x)’= 5xln5
Пример 4. Найдите производную функции y= log4x
Производную логарифма найдем по формуле 7.
(log4x)’=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также
elhow.ru
Вычисление производных | Высшая математика
Пример. Производная суммы функций.
Дано: сумма функций .
Найти:
Вычислить производную суммы функций
Решение:
Исходя из того, что производная алгебраической суммы (разности) функций, имеющих производную, равна такой же сумме (разности) производных этих функций: используя формулы производных (ссылка), вычислим производную, заданной в условии задачи суммы функций:
Ответ: производная суммы функций равна
Пример. Производная произведения функций.
Дано: произведение функций .
Найти:
Вычислить производную произведения функций
Решение:
Исходя из того, что производная двух функций, имеющих производную, вычисляется по формуле: найдем производную, заданного в условии задачи произведения функций:
Ответ: производная произведения функций равна
Пример. Производная отношения функций.
Дано: отношение функций .
Найти:
Вычислить производную отношения функций
Решение:
Исходя из того, что производная отношения двух функций, имеющих производную, вычисляется по формуле: определим производную, заданного в условии задачи отношения функций:
Ответ: производная отношения функций равна
Пример. Производная сложной функций.
Дано: сложная функция .
Найти:
Вычислить производную сложной функции
Решение:
Исходя из того, что функция имеет производную в точке а функция имеет производную в точке причем сложная функция будет иметь производную в точке и в нашем случае получаем следующее а Тогда а значит
Ответ: производная сложной функции равна
Пример. Производная функции заданной параметрически.
Дано: функция заданная параметрически .
Найти:
Вычислить производную функции заданной параметрически.
Решение:
Исходя из того, что производная функции, заданной параметрически, то есть в виде соотношения где изменяется в пределах некоторого множества, определяется по формуле вычислим производную, заданной в задаче функции:
Производная параметрически заданной функции будет тоже функция, заданная параметрически:
Ответ: производная параметрически заданной функции равна
matematika.electrichelp.ru
Производная функции одной переменной
В этой статье мы будем учиться находить производную от функции одной переменной. Дадим ее определение, вскользь затронем геометрический смысл. Разберемся с вопросом нахождения производной от сложной функции.
Итак, дадим определение производной: пусть в некоторой окрестности точки определена функция . Производной функции в точке называется предел, если он существует,
Из школы можно вспомнить формулу для нахождения касательной к функции в точке: . То есть если говорить о геометрическом смысле производной, то обозначим производную функции в точке как угловой коэффициент или тангенс угла наклона касательной прямой к графику функции в этой точке.
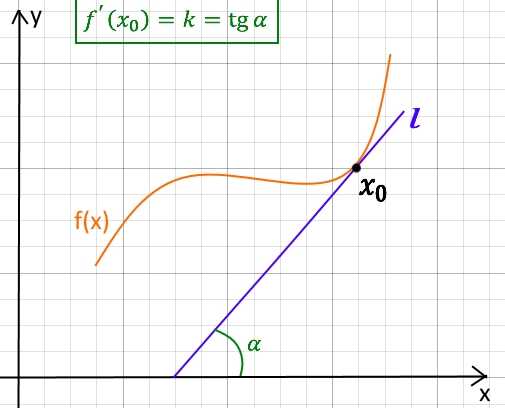
Правила дифференцирования:
- Производная суммы равна сумме производных, то есть:
- Производная произведения:
- Вынесение константы за знак производной:
- Производная частного:
Прежде чем перейти к задачам, необходимо обзавестись таблицей производных. В идеале вы должны ее знать наизусть, как таблицу умножения 🙂
Таблица производных
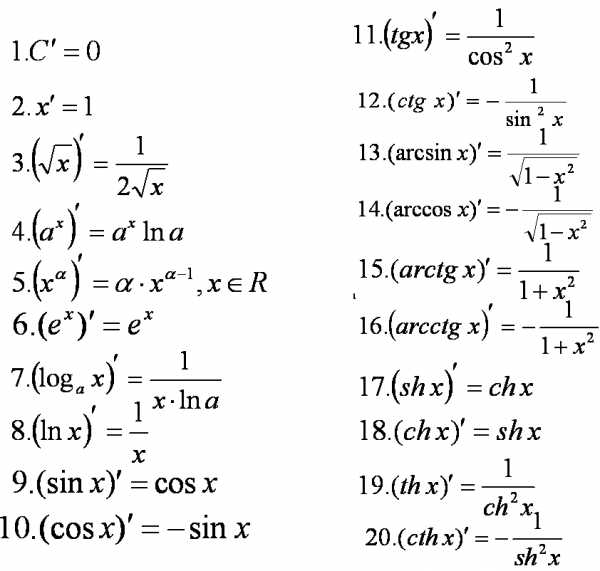
[свернуть]
Правилами дифференцирования и таблицей вооружились, двигаемся дальше.
Рассмотрим некоторую функцию . Как видим, функция зависит не просто от переменной , а от другой функции . Будем называть такую функцию сложной. Производная сложной функции вычисляется следующим образом:
Теперь всей необходимой теорией для решения стандартных задач на нахождение производной мы обладаем, а именно: правилами дифференцирования, таблицей производных и формулой производной от сложной функции. Давайте на примерах подробно разберемся с тем, как это работает.
Задачи на применение правила дифференцирования суммы
Пример 1. Найти производную функции
Решение: Применяем правило дифференцирования суммы функций:
Заглядываем в таблицу производных и ищем там производную от и от
Всё, производная найдена. В ответ запишем
Пример 2. Найти производную функции , где
Решение: Применяем правило дифференцирования суммы функций:
Открываем таблицу производных и находим производные от и
Производная найдена, в ответе записываем
Пример 3. Найти производную функции
Решение:
[свернуть]
Задачи на применение правила дифференцирования произведения
Пример 4. Найти производную функции
Решение: Применим правило дифференцирования произведения:
Обращаемся к таблице производных и ищем там производные тангенса и
или
Производная найдена.
Пример 5. Найти производную функции
Решение: Применим правило дифференцирования произведения:
Производная найдена.
Пример 6. Найти производную функции
Решение:
Производная найдена.
[свернуть]
Задачи с вынесением константы за знак производной
Это правило дифференцирования самое простое для понимания (редко у кого можно встретить здесь ошибки): мы просто выносим константу за знак производной и находим производную от оставшегося выражения.
Пример 7. Найти производную функции
Решение: Видим константу , поэтому поступаем в соответствии с нашим правилом:
Всё, задача решена 🙂 Давайте, на всякий случай, рассмотрим еще одну такую задачу.
Пример 8. Найти производную функции
Решение: Видим дробь. Производную от дроби находить пока не умеем, но может без проблем преобразовать выражение следующим образом:
Теперь константа очевидна, выносим и находим производную:
Производная найдена.
[свернуть]
Задачи на применения правила дифференцирования частного (дроби)
Ничего сложно в дифференцировании дробей нет, но на практике именно здесь чаще всего возникают ошибки, поэтому остановимся на этом моменте подробнее.
Пример 9. Найти производную функции
Решение: Видим дробь. Мысленно повторяем для себя: «Производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и всё это деленное на квадрат знаменателя«.
Числителем здесь является , а знаменателем — . Тогда, в соответствии с формулой, напишем:
Всё, производная успешно найдена.
Пример 10. Найти производную функции
Решение: Рассматриваем выражение. Числителем служит , знаменателем — . По формуле получим:
В принципе, на этом этапе можно остановиться, производная найдена. Но, взглянув на числитель, несложно заметить и применить основное тригонометрическое тождество :
.
Вспомнив, что отношение синуса к косинусу есть тангенс, легко проверить получившийся ответ по таблице производных.
Пример 11. Найти производную функции
Решение: Числитель здесь , знаменатель . По формуле производной для дроби запишем:
Производная найдена, но можно упростить полученное выражение, сделаем это:
Пример 12. Найти производную функции
Решение: Числитель и знаменатель . Получаем:
Заметим, что здесь необязательно было пользоваться именно формулой для дроби, так как знаменатель представляет собой константу. Эту константу можно было вынести по предыдущему правилу дифференцирования.
[свернуть]
С правилами дифференцирования ознакомились. Переходим к дифференцированию сложной функции. Пока еще нет достаточного опыта, рекомендую на каждом шаге повторять для себя: «Производная сложной функции равна производной внешней функции на производную внутренней функции«.
Пример 13
Найти производную функции .
Решение: Видим обыкновенный косинус, но воспользоваться таблицей производных сразу не можем, потому что зависит косинус не просто от , а от . Применяем формулу для сложной функции.
Необходимо очень чётко уяснить вопрос с тем, что является в некотором выражении внешней функцией, а что внутренней. Для этого нужно посмотреть на функцию как бы в целом (это может быть нечто очень громоздкое), понять, что это прежде всего: произведение, степень, дробь или что-то другое.
В данной задаче всё просто. Прежде всего наше выражение — это косинус. То есть косинус является внешней функцией. Внутренней функцией будет являться аргумент косинуса . Тогда по формуле запишем:
.
[свернуть]
В 13 и 14 примерах для нахождения производной достаточно было применить формулу для сложной функции всего один раз. Однако на практике чаще всего имеются выражения вида «функция от функции, зависящей от еще одной функции, которая зависит функции и т.д.». В этих случаях принцип нахождения производной не изменяется — мы просто используем формулу несколько раз.
Пример 15
Найти производную функции
Решение: Имеем натуральный логарифм, который зависит от синуса, который зависит от некоторого выражения. Внешняя функция здесь сам логарифм, то есть , внутренняя — выражение под логарифмом, т.е. .
Производную первого множителя уже можем написать из таблицы производных (сделаем это позже, чтобы не возникло путаницы). Для нахождения производной второго множителя вновь используем формулу, полагая, что внешней функцией является синус, а внутренней — выражение :
Давайте для наглядности покажем на картинке процесс работы с выражением:
Функция слева от стрелки внешняя, справа внутренняя. Количество стрелок равно количеству применений формулы для сложной функции.
[свернуть]
Пример 16
Найти производную функции
Решение: Нарисуем такую же картинку, как и в предыдущем примере:
Имеем три стрелки, то есть формулу для сложной функции будем последовательно применять именно три раза. На каждом шаге функция слева от стрелки — внешняя, справа — внутренняя.
Ответ получился некрасивым, но это нестрашно, потому что задания придумывал сам 🙂 Здесь все производные мы высчитываем на последнем шаге, чтобы не запутаться. На практике же чаще всего будет удобнее это делать после каждого применения формулы (для внешних функций).
[свернуть]
В первое время будет нелишним рисовать на черновике картинки из примеров 15 и 16 (понятно, применительно к своей задаче). Далее разберем пару примеров на комбинирование правил дифференцирования и формулы дифференцирования сложной функции.
Пример 17
Найти производную функции
Решение: Видим произведение, поэтому по формуле дифференцирования произведения функций запишем:
Обе полученные функции под знаком производной сложные, поэтому дифференцируем их по соответствующему правилу:
[свернуть]
Пример 18
Найти производную функции
Решение: Видим дробь, поэтому по формуле дифференцирования дробей запишем:
Обе полученные функции под знаком производной сложные, поэтому дифференцируем их по соответствующему правилу:
Опять получился не очень красивый ответ, но зато правильный 🙂
Здесь стоит заметить, что мы могли избавиться от дроби и перейти к произведению функций с помощью перенесения арксинуса в числитель (арксинус в этом случае получает степень ).
[свернуть]
На этом всё, спасибо за внимание!
higher-math.ru
Примеры вычисления производных
Для практического ознакомления с таблицей основных формул дифференцирования рассмотрим примеры.
Пример 1.
Вычислить производные
1)
2)
3)
4)
5)
6)
7)
Решение.
1) По формулам дифференцирования (1), (3), (9) получим
2) Вводим дробные и отрицательные степени и превращаем заданную функцию к виду
Используя формулы (3), (4), (9) находим
3) Данный пример вычисляем по правилу (6)
4) Производную функции ищем по правилу сложной функции (7)
5) Производные от функции
находим по правилу производной от произведения функций, и правилом производной от сложной функции
6) По правилу производной от сложной функции будем иметь
7) Много студентов которые еще толком не знают правил, сначала подносят к квадрату выражение в скобках
а затем проводят дифференцировки. Это неправильно, долго и трудно. Воспользовавшись правилом дифференцирования сложной функции получим
Если Вы будете подносить к квадрату, а затем дифференцировать то получите многочлен, который еще предстоит свести к компактному виду. Результат будет правильный, но зачем идти сложным путем, если за нас уже давно придумали правила дифференцирования, которые упрощают вычисления.
Изучайте их и пользуйтесь на практике.
yukhym.com
