Как решать задачи на растворы по химии – Учебно-методический материал по химии на тему: Технологическая «находка» по химии «Как научить решать задач на растворы, используя математический метод решения» | скачать бесплатно

Урок «Растворы. Решение задач на растворы» (11 класс)

Технологическая карта урока

Предмет: химия

Класс: 11

Тема: «Растворы. Решение задач на растворы».

Цель урока: воспитание убежденности в позитивной роли химии в жизни современного общества, необходимости грамотного отношения к своему здоровью и окружающей среде.

Задачи:

1. Подвести обучающихся к пониманию необходимости знаний о растворах.

2.Познакомить с новым способом решения задач. Способствовать развитию умения мыслить логически и владеть химическим языком,

3. Развивать навыки наблюдения, экспериментальные навыки, решения задач, умения выделять главное и делать выводы.

4. Воспитывать умение работать самостоятельно. Показать связь изученной темы с жизнью. Развивать смекалку учащихся.

5. Создать на уроке условия для сохранения здоровья.

Тип урока: комбинированный.

Необходимое оборудование: химические реактивы (растворы HCl, H₂SO₄, BaCl₂, Na₂CO₃, Mg), химическая посуда, презентация на тему «Растворы», компьютер, экран, проектор.

Формируемые универсальные учебные действия:

Личностные УУД: умение ориентироваться в социальных ролях и межличностных отношениях.

Познавательные УУД: умение анализировать и синтезировать причинно-следственные связи, доказывать свои суждения, сформулировать проблему и найти способы ее решения, умение исследовать, обобщать.

Регулятивные УУД: умение действовать по плану, контролировать, корректировать, оценивать процесс и результаты своей деятельности.

Коммуникативные УУД: умение сотрудничать, вступать в дискуссию, управлять поведением партнера, уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.

Структура и ход урока

№

Этапы урока

Деятельность учителя

Деятельность обучающихся

1

2

3

4

1

Ориентировочно-мотивационный этап

Учитель начитает урок словами Н. Заболоцкого.

Приложение 1.

Сообщает тему урока, затем в целях актуализации знаний проводит фронтальную беседу по вопросам

Слайды 3-11

Слушают учителя, фиксируют проблему, Высказывают предположение о важности растворов в повседневной жизни.

2.

Исполнительский этап

Учитель предлагает провести химический эксперимент. Проводит инструктаж по ТБ.

Приложение 2.

Учащиеся проводят эксперимент. Общаются в парах и делают вывод

Слайд 12

3.

Первичное усвоение новых знаний

Предлагает новый способ решения задач на смешение растворов. Приложение 3.

Приводит учащимся эвристические рекомендации к решению задач из книги известного американского математика Д. Пойа. (Автора книги «Как решить задачу»)

Слайд 14.

Приложение 4.

Слушают учителя, строят высказывания.

Анализируют услышанное, аргументируют свою точку зрения.

4.

Первичная проверка понимания

Предлагает решить задачи с использованием правила смещения

Приложение 5.

Решают задачи.

Осуществляют взаимоконтроль

Записывают решение на доске.

5.

Пауза для здоровья

Предлагает сделать профилактические упражнения для глаз.

Приложение 6.

Выполняют профилактические упражнения для глаз.

6.

Первичное закрепление

Учитель предлагает провести химический эксперимент. Проводит инструктаж по ТБ.

Приложение 7.

Учащиеся проводят эксперимент. Общаются в парах и делают вывод

Приложение 7.

7.

Контроль усвоения.

Предлагает решить задачи по выбору.

Решают задачи.

Осуществляют взаимоконтроль

Приложение 8

8.

Постановка и решение проблемной задачи

Предлагает поговорить о составе табачного дыма, и напоминает о Федеральном законе «Об охране здоровья граждан от воздействия окружающего табачного дыма и последствий потребления табака»

Предлагает решить задачу.

Приложение 9.

Изучая данные таблицы и решая задачу, учащиеся, отвечают на вопросы о вреде курения и влиянии сигаретного дыма на природу, а также делают вывод для себя, стоит ли курить или стоит отказаться от этого порока.

9.

Информация о домашнем задании, инструктаж по его выполнению

Приложение 10.

Получают карточки с домашним заданием

10.

Рефлексия

Учитель заканчивает урок словами великого химика XX столетия Л.К. Полинга: «Я думаю, что химики – это те, кто на самом деле понимает мир. Этот огромный мир – удел химиков»

И предлагает старшеклассникам выразить свое отношение к уроку.

Поднимают вверх смайлики.

Приложение 11.

Приложение 1.

Два мира есть у человека:

Один, который нас творит,

Другой, который мы от века

Творим по мере наших сил…

1) Что происходит с веществами при растворении их в воде?

2) Что такое растворы?

3) Какую роль играют растворы в жизни человека?

4) Какие способы выражения концентрации растворов вы знаете?

Приложение 2.

Опыт 1. К 1 мл 10 %-ного раствора хлорида натрия прилейте 1 мл. 5 %-ного раствора хлорида натрия. Что наблюдаете? Как меняется концентрация вещества в растворе при сливании двух этих растворов? Как изменится концентрация соли, если в раствор соли добавить 10 г хлорида натрия? А если добавить 50 мл воды?

При смешивании исходного раствора с более разбавленным раствором того же вещества, либо при разбавлении водой происходит понижение концентрации исходного раствора. Напротив, добавление к исходному раствору концентрированного раствора того же вещества или добавление дополнительного количества растворённого вещества концентрация исходного раствора увеличивается

Приложение 3.

Учитель предлагает новый способ решения таких задач.

Для решения подобных задач удобнее пользоваться правилом смещения (правило креста или квадрат Пирсона), согласно которому количества смешиваемых растворов обратно пропорциональны разностям концентраций смешиваемых растворов

; массовые концентрации исходных растворов помещают друг под другом в углу квадрата с левой стороны; задаваемая концентрация растворённого вещества помещается в центре квадрата, а разности между ней и концентрациями исходных растворов (из большего вычитается меньшее) размещаются на концах диагоналей по правым углам квадрата. Следует помнить, что концентрация воды равна 0%, концентрация твёрдого безводного вещества – 100%.

ω₁ ω ₃ – ω ₂ m₁

ω ₃

ω ₂ ω ₁ – ω ₃ m₂

Приложение 4.

Общие рекомендации к решению задач.

«Обдумай цель раньше, чем начать…» – люди начинают вносить предложения, обсуждать и даже бороться за дело, не поняв, какой цели они добиваются.

«С началом считается глупец, о конце думает мудрец» – если вы не уяснили конечной цели, не трудно при решении задачи сбиться с пути, а затем и вовсе забросить её.

«Мудрый меняет свои решения, а дурак никогда» – если мы терпим неудачу, приходится пробовать другие средства и другие пути.

«Подмечай главную возможность» – преимущество «знатока» в том, что он всегда начеку и лучше ориентируется в ситуации.

«Желаемое мы охотно принимаем за действительное» – наш план даёт лишь один общий контур решения. Надо убедиться, что детали соответствуют ему, поэтому мы должны внимательно рассмотреть каждую из них одну за другой.

Приложение 5.

Пример 1. Определить массы исходных растворов с массовыми долями серной кислоты 7,5 % и 60 %, если при их смешивании образовался раствор массой 350 г с массовой долей кислоты 15 %.

Решение

60 7,5 m₁

15

7,5 45 m₂ = 350 – m₁

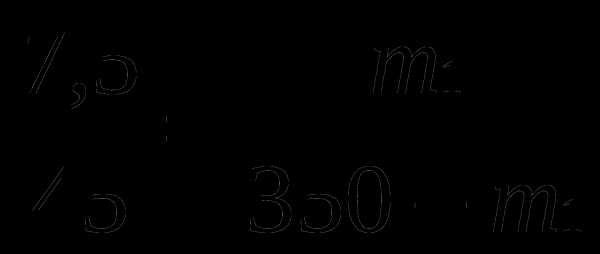m₁ = 50 г и m₂ = 300 г

Ответ: 50 г 60% раствора и 300 г 7,5% раствора.

Задачи для закрепления

1. В каких массовых соотношениях надо смешать 20% и 5% -ные растворы одного вещества, чтобы получить 10% раствор?

Решение.

20 (10 -5) = 5 вес.ч.(г.)

10

5 (20 -10) = 10 вес.ч.(г.)

Числа 5 и 10 показывают, в каком массовом отношении надо взять растворы. Следовательно, для приготовления 10% раствора нужно смешать 5 г 20% раствора с 10 г 5% раствора в соотношении 1:2. Это соотношение сохранится для данных растворов независимо от того, какое весовое количество 10 % – го раствора нужно приготовить.

2. Какой объём воды надо прибавить к раствору серной кислоты объёмом 100 мл с массовой долей 20 % и плотностью 1,14 г/мл, чтобы получить 5 % раствор?

Решение.

Найдём массу исходного раствора кислоты

m (раствора H₂SO₄) = ρV = 1,14 г/мл · 100 мл = 114 г

В соответствии с правилом смещения

20 5 114

5

0 15 m(H₂O) -?

Для приготовления 5 % -го раствора необходимо к 5 г 20 % -ной кислоты прибавить 15 г воды, т. е в соотношении 1:3.

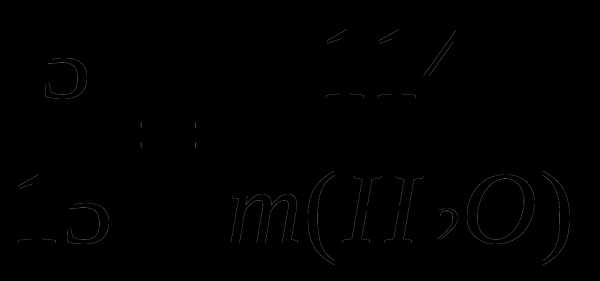m (H₂O) = г

V (H₂O) = m (H₂O) / ρ (H₂O) = 342 г/ 1 г/мл = 342 мл.

Ответ: 342 мл.

3. Определите массу раствора 9%-ого столового уксуса, который получают из 90 г 80 % уксусной кислоты?

Решение:

80 9 90 г

9

0 71 m(H₂O) -?

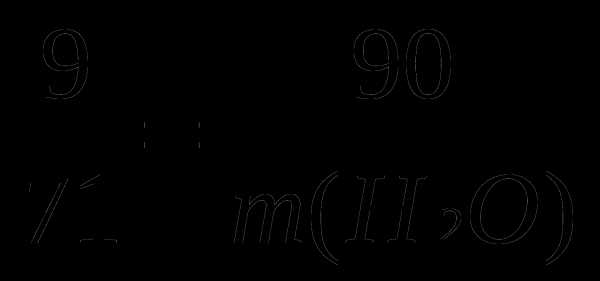m (Н₂О) = 710 г.

Масса образовавшегося столового уксуса: 710 + 90 = 800 г.

Приложение 6.

1. Посмотреть влево, затем вправо, вверх и вниз, не поворачивая головы (4 раза).

2. Посмотреть вправо вниз, влево вверх, влево вниз, вправо вверх (4 раза).

3. Сделать круговые движения глазным яблоком слева направо, и затем справа налево (каждое движение по 4 раза). Те же самые движения проделать при закрытых глазах.

4. Широко открыть глаза и посмотреть вверх, сосчитать до 10 и опустить их. При выполнении упражнения следует обратить внимание на то, чтобы не морщить лоб. Это можно контролировать, положив на лоб руку. Упражнение следует повторить 8 раз.

5. Открыть глаза и посмотреть вверх и влево, сосчитать до 10, затем опустить веки. То же самое проделать, смотря вверх и вправо. Упражнения повторить по 5 раз в каждую сторону

Приложение 7.

Опыт 1. Возьмите пробирку и поместите в неё магниевую стружку и прилейте 1 мл. соляной кислоты. Что наблюдаете? Напишите уравнение реакции.

Опыт 2. В две пробирки налейте 2 мл. раствора карбоната натрия. Затем в одну пробирку прилейте раствор соляной кислоты, а в другую – хлорида магния. Что наблюдаете? Напишите уравнение реакции.

Опыт 3. Возьмите пробирку и налейте в неё 1мл. «купоросной водки», затем добавьте 1-2 мл. раствора хлорида бария. Что наблюдаете? Напишите уравнение реакции.

«Купоросная водка» – серная кислота (М.В. Ломоносов)

Учитель: Как найти массу раствора в этих случаях после реакции?

Учащиеся делают вывод:

m_{р-ра полученного} = m_{реагента} + m_{р-ра 1}– m_{осадок (газ)}

m_{р-ра полученного} = m_р-ра1 + m_{р-ра 2}– m_{осадок (газ)}

Приложение 8.

Задачи для закрепления (карточки с заданиями)

1^**) Какую массу AgNO₃ необходимо добавить к 100 г 5,5 М раствора HCl (ρ = 1,1 г/мл), чтобы получить раствор, в котором массовая доля соляной кислоты равна 10 %? (Ответ: 34 г AgNO₃)

2^*) Рассчитайте массовые доли веществ в растворе, образовавшемся при действии 25 мл 20%-ной соляной кислоты (плотность 1,1 г/мл) на 4г сульфида железа (II). (Ответ: 19,3 % FeCl₂, 7,3 % HCl.)

Приложение 9.

Определить % содержание ядовитых веществ: табачного дегтя, синильной кислоты и оксида углерода, если никотин составляет 2% от всего табачного дыма, а синильная кислота 1\2 часть никотина, а табачного дегтя в 7, 5 раз больше чем никотина. Оксид углерода составляет 3\5 от табачного дегтя». Для решения задачи предлагаю воспользоваться таблицей, в которой указано содержание веществ в дыме 1 сигареты.

Состав дыма сигареты:

Табачный дым – аэрозоль из газов, жидкостей и твердых веществ.

Вещества

Количество

Никотин

3 * 10^-3 г

Фенол

120 * 10^-6 г

Цианистый водород

400 * 10^-6 г

Оксид углерода

10 * 10^-3 г

Формальдегид

100 * 10^-6 г

Бензол

40 * 10^-6 г

Приложение 10.

Задание на дом. 1) Какой объём воды надо добавить к 100 г 70 %-ного раствора уксусной кислоты, чтобы получить 9 %-ный раствор? (678 мл)

2) Какую массу хлорида натрия следует добавить к 200 г 10 %-ного раствора хлорида натрия, чтобы получить 25 %- ный раствор? (40 г)

Приложение 11.

1. На уроке было комфортно и все понятно

2. На уроке немного затруднялся не все понятно

3. На уроке было трудно, ничего не понял.

infourok.ru

Решение задач с использованием понятия “Массовая доля растворенного вещества”. Растворение и концентрирование растворов

Разделы: Математика, Химия

---

На уроках химии достаточно часто приходится решать задачи, в которых используются математические методы и приемы, вызывающие затруднения у учащихся, и учителю химии приходится брать на себя функции учителя математики и, в тоже время, задачи с химическим содержанием, с использованием специальных терминов сложно объяснить без специальной подготовки учителю математики. Так родилась идея подготовить и провести серию факультативных занятий совместно учителем химии и математики по решению задач на смеси с учащимися 9 классов.

ТЕМА: РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ ПОНЯТИЯ “МАССОВАЯ ДОЛЯ РАСТВОРЁННОГО ВЕЩЕСТВА. РАЗБАВЛЕНИЕ И КОНЦЕНТРИРОВАНИЕ РАСТВОРОВ” (ИНТЕГРАЦИЯ ХИМИИ И АЛГЕБРЫ)

ЦЕЛИ:

Существенно расширить круг алгебраических задач с химическим содержанием;

Показать возможность решения химической задачи алгебраическим способом;

Научить делать осознанный выбор способа и метода решения задач на уроке химии;

Показать наличие межпредметных связей в области химии и математики.

ОБОРУДОВАНИЕ: КОМПЬЮТЕР, МУЛЬТИМЕДИЙНАЯ ПРИСТАВКА, ЭКРАН, ПРЕЗЕНТАЦИЯ.

ХОД УРОКА.

Учитель химии: Количественный состав раствора выражается его концентрацией, которая имеет разные формы выражения. Чаще всего используют массовую концентрацию или массовую долю растворённого вещества. Вспомним математическую формулу для выражения массовой доли растворённого вещества.

Ученик:

1. Массовая доля растворённого вещества обозначается – W р.в.
2. Массовая доля растворённого вещества – это отношение массы растворённого вещества к массе раствора: W (р.в.) = m (р.в.)/m (р-ра) x 100%.
3. Масса раствора складывается из массы растворённого вещества и массы растворителя: m (р-ра) = m (р.в.) + m (р-ля)
4. Формула для массовой доли растворённого вещества будет выглядеть следующим образом: W (р.в.) = m (р.в.)/ m (р.в.) + m (р-ля) x 100%
5. Преобразуем данную формулу и выразим массу растворённого вещества и массу раствора: m (р.в.) = w (р.в.) x m (р-ра)/100%, m (р-ра) =m (р.в.)/w (р.в.) x 100%

Учитель химии: Предлагаю решить задачу, используя предложенные формулы.

Задача. Сколько грамм йода и спирта нужно взять для приготовления 500 грамм 5%-ной йодной настойки?

ДАНО:	РЕШЕНИЕ:
M (р-ра)=500 г.	W (р.в.)=m(р.в.)/m(р-ра)
W (р.в.)=5%=0,05	W (р.в.)=m(I2)/m(наст.)
НАЙТИ:	m (I2)=W(р.в.)x m(наст.)
m(I2)=?	m(I2)=0,05 x 500 г.=25 г.
m(спирта)=?	m(р-ра)=m(I2)+m(спирта)
	m(спирта)=m(р-ра)-m(I2)
	m(спирта)=500 г.-25г.=475 г.

ОТВЕТ: m (I2)=25 г., m (спирта)=475 г.

Учитель химии: Очень часто в работе химических лабораторий приходится готовить растворы с определённой массовой долей растворённого вещества смешиванием двух растворов или разбавлением крепкого раствора водой. Перед приготовлением раствора нужно провести определённые арифметические расчёты.

Задача. Смешаны 100 грамм раствора с массовой долей некоторого вещества 20% и 50 грамм раствора с массовой долей этого вещества 32%. Вычислите массовую долю растворённого вещества во вновь полученном растворе.

Учитель химии: Решим эту задачу, используя правило смешения.

Запишем условие задачи в таблицу:

	1 раствор	2 раствор	3 раствор
Масса раствора	m1=100 г.	m2=50 г.	m3=m1+m2
Массовая доля растворённого вещества %	W1=0,2	W2=0,32	W3
Масса растворённого в-ва в растворе	m1w1	m2w2	m3w3

Решим задачу, используя правило смешения:

• m₁w₁+m₂w₂=m₃w₃
• m₁w₁+m₂w₂=(m₁+m₂) w₃
• m₁w₁+m₂w₂=m₁w₃+m₂w₃
• m₁w₁-m₁w₃=m₂w₂-m₂w₂
• m₁(w₁-w₃)=m₂(w₃-w₂)
• m₁/m₂=(w₃-w₂)/(w₁-w₃)

ВЫВОД.

Отношение массы первого раствора к массе второго равно отношению разности массовых долей смеси и второго раствора к разности массовых долей первого раствора и смеси:

m

₁/m₂=(w₃-w₂)/(w₁-w₃)

100:50=(w₃-0,32):(0,2-w₃)

100(0,2-w₃)=50(w₃-0,32)

20-100w₃=50w₃-16

20+16=50w₃+100w₃

36=150w₃

W₃=0,24

ОТВЕТ: массовая доля растворённого вещества во вновь полученном растворе составляет 24%.

Учитель математики: Эту задачу можно решить, используя алгебраические преобразования:

РЕШЕНИЕ.

1.Найдём массу растворённого вещества в каждом из растворов:

20% от 100 г 32% от 50 г

0,2х100=20(г) 0,32х50=16(г)

2.Найдём массу растворённого вещества в смеси:

20+16=36(г)

3.Найдём массу раствора:

100+50=150(г)

4.Пусть концентрация полученного раствора составляет х%, тогда масса растворённого вещества в смеси:

Х% от 150 г

0,01Хх150=1,5Х

5.Составим уравнение и решим его:

1,5Х=36

Х=36:1,5

Х=24

ОТВЕТ: концентрация полученного раствора составляет 24%.

Учитель химии: В курсе химии встречаются задачи, решение которых можно осуществить только методом систем уравнений

Задача: Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором этой же кислоты и получили 600 грамм 15%-ного раствора. Сколько грамм каждого раствора было взято?

ДАНО:

• W₁=30%=0,3
• W₂=10%=0,1
• W₃=15%=0,15
• m₃(р-ра)=600 г.

НАЙТИ:

• m1(р-ра)=?
• m2(р-ра)=?

РЕШЕНИЕ:

Учитель математики: Введём обозначения:

пусть m₁(р-ра)-X г., а m₂(р-ра)-Y г., тогда:

m₃(р-ра)=m₁(р-ра)+m₁(р-ра)=X+Y.

Рассчитаем массы растворённых в-в:

• m₁=0,3X,
• m₂=0,1Y,
• m₃=600 г. x 0,15=90 г.

Составим систему уравнений:

Решим подчёркнутое уравнение:

180-0,3Y+0,1Y=90

180-0,2Y=90

180-90=0,2Y

90=0,2Y

Y=450

• если Y=450 г., то X=600 г.-450 г.=150 г.

ОТВЕТ:

• масса 1 р-ра=150 г.
• масса 2 р-ра=450г.

Учитель химии. Решим эту же задачу методом смешения. Какой ответ у вас получился? (Ответы сходятся).

ДОМАШНЕЕ ЗАДАНИЕ.

ЗАДАЧА.

• В каких массовых надо смешать 20%-ный и 5%-ный растворы одного вещества, чтобы получить 10%-ный раствор?

АЛГОРИТМ РЕШЕНИЯ:

• 1.Ввести буквенные обозначения для масс растворов.
• 2.Вычислить массы растворённых веществ в первом, втором растворе и смеси.
• 3.Составить систему уравнений и решить её.
• 4.Записать ответ.

Презентация

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

КАК РЕШАТЬ ПРОСТЕЙШИЕ ЗАДАЧИ ПО ХИМИИ

КАК РЕШАТЬ ПРОСТЕЙШИЕ ЗАДАЧИ ПО ХИМИИКАК РЕШАТЬ ПРОСТЕЙШИЕ ЗАДАЧИ ПО ХИМИИВ реакцию с соляной кислотой вступило 13 г цинкаНовая страница 1

 

Как вычислить молекулярную  и молярную массы вещества?

 

Для этого нужно сложить массы всех атомов в этой молекуле.  

Пример 1. В молекуле воды   Н₂О 2 атома водорода и 1 атом кислорода. Атомная масса водорода = 1, а кислорода – 16. Поэтому молекулярная масса воды равна 1 + 1 + 16 = 18 атомных единиц массы, а молярная масса воды = 18 г/моль. 

Пример 2. В молекуле серной кислоты Н₂SO₄ 2 атома водорода, 1 атом серы и 4 атома кислорода. Поэтому молекулярная масса этого вещества составит 1 2 + 32 + 4 16 = 98 а.е.м, а молярная масса – 98 г/моль. 

Пример 3. В молекуле сульфата алюминия А1₂(SO₄)₃ 2 атома алюминия, 3 атома серы и 12 атомов кислорода. Молекулярная масса этого вещества равна 27 ·  2 + 32 · 3 + 16 · 12 = 342 а.е.м., а молярная масса – 342 г/моль.

 

Как решить простейшую расчетную задачу

по химическому уравнению?

Сначала записываем числовые данные из условия задачи – массу вещества, или объем газа. Затем выясняем, что нужно определить в той задаче, и записываем вопрос под условием задачи. Далее действуем так: 

Определяем количества веществ, массы или объемы которых даны в условии задачи.

Записываем уравнение реакции, о которой сказано в условии задачи и расставляем в нем коэффициенты.

Вычисленное количество вещества записываем над формулой этого вещества в уравнении реакции.

Учитывая коэффициенты, определяем количества тех веществ, массы или объемы которых нужно определить в данной задаче.

По найденным количествам веществ рассчитываем массы или объемы этих веществ.

Проверяем, на все ли поставленные вопросы условия задачи найдены ответы.

Записываем ответы задачи. 

 

Как решать задачи с участием растворов веществ? 

Если в условии задачи указаны объем и плотность раствора, то по этим данным можно найти массу раствора (объем раствора в мл умножается на плотность раствора).

По массе раствора находится масса растворенного вещества (масса раствора умножается на массовую долю растворенного вещества и переводится в проценты).

По найденной массе растворенного вещества определяется его количество (масса растворенного вещества делится на его молярную массу)

Записывается уравнение реакции, о которой сказано в условии задачи, и в нем расставляются все коэффициенты.

Найденное в п.3 количество вещества записывается над формулой этого вещества в уравнении реакции.

Учитывая коэффициенты, определяется количество вещества, массу или объем которого нужно найти.

По найденному количеству вещества определяются его масса или объем. 

 

4.Как решать задачи, где одно из реагирующих веществ             дано в избытке? 

Если в условии задачи есть числовые данные (массы или объемы) по обоим веществам, участвующим в реакции, то, возможно, одно из них находится в избытке. Поэтому решение задачи начните  с расчета количеств этих веществ в моль.

Далее запишите уравнение нужной реакции со всеми коэффициентами.

По коэффициентам в уравнении и найденным количествам веществ определите, какое из веществ находится в избытке, а какое – в недостатке.

В уравнении реакции над формулой вещества, находящегося в недостатке, записываем его количество в моль и с учетом коэффициентов находим количества остальных веществ, участвующих в реакции.

Далее рассчитываются массы или объемы остальных веществ.

 

 

В реакцию с соляной кислотой вступило 13 г цинка. Определите массы  израсходованной кислоты и полученной соли, а также объем выделившегося газа.

 

Решение.

 

1.           Находим  количество вещества цинка, разделив его массу на молярную массу:

 

n(Zn)  =  m : M  =  13 г  :  65 г/моль  =  0,2 моль

2.           Вносим эту величину в уравнение реакции и с ее помощью определяем количества всех указанных в задаче веществ (с учетом коэффициентов):

 

          0,2 моль    0,4 моль           0,2 моль        0,2 моль

           Zn  +       2HCl  =>  ZnCl2  +       h3

 

 Далее расчеты по формулам:

 

    m(HCl) =  M · n = 36,5  г/моль · 0,4 моль  = 14,6 г

    m(ZnCl2)  =  M · n = 136 г/моль · 0,2 моль = 27,2 г

Объем водорода находим аналогично:

V(h3)  =  Vm  · n  =  22,4 л/моль  ·  0,2 моль  = 4,48 л 

 

ЗАДАЧИ НА ИЗБЫТОК РЕАГЕНТА

 

Главный отличительный признак таких расчетов – это наличие числовых данных (массы, объема, количества вещества или необходимых компонентов для их вычисления) по обоим веществам, реагирующим между собой. Чаще всего это говорит о том, что одно из этих веществ находится в избытке и вступит в реакцию не полностью. Определить же, что именно в избытке, удобнее всего, когда известны количества вещества реагентов. Если они не указаны в условии, их следует вычислить по исходным данным.

 

Задача 1.

 8 г серы нагрели с 28 г железа. Определите массу продукта реакции.

 

Решение.

 

1.                 Так как в условии указаны массы железа и серы одновременно, то одно из этих веществ  вполне может оказаться в избытке. Для выяснения этого находим количества вещества реагентов:

 n(

Fe)  =  m : M  =  28 г : 56 г/моль  =  0,5 моль

n(S)  =  m : M =  8 г : 32 г/моль  =  0,25 моль

 

2.                 Записываем уравнение реакции и по коэффициентам определяем мольные отношения реагентов:

 Fe  +  S   ®  FeS

3.                 Так как железа и серы должно реагировать равное количество молей, то ясно, что в этой реакции будет израсходовано по 0,25 моль их, избыток железа при этом составит 0,5 – 0,25 + 0,25 моль, и в реакцию не вступит.

4.                 Так как сера  взята в недостатке, то по ее количеству определяем количество продукта реакции, а затем его массу:

 

           0,25 моль          0,25 моль              0,25 моль

           Fe        +      S          ®       FeS

 

   m (FeS)   =   M · n   =  88  г/моль · 0,25 моль  =  22 г

 

Задача 2.

 

Для реакции взято 56 л хлора и 56 г железа. Определите массу полученного продукта.

 

Решение.

  2Fe  +  3Cl2    ®  2 FeCl3

 

 В этом случае расчет избытка более сложен, поэтому можно использовать такую хитрость:

 

Fe	Cl2
2	3
1
	2,5

 

В первой строке пишем формулы реагирующих веществ, во второй – их мольные отношения по уравнению реакции (по коэффициентам), а в двух следующих – количества  этих  веществ, имеющихся в наличии, причем на разных строках.  Далее по этим данным находим количества вещества реагента, необходимого для взаимодействия с этими количествами вещества железа  и хлора:

Fe	Cl2
2	3
1	1,5
1,67	2,5

  

  Далее анализируем полученные данные. Железа есть  1 моль, а для реакции с 2,5 моль хлора его нужно в полтора раза меньше, это составляет 1,67 моль, чего у нас нет. Следовательно, железо в недостатке, а число 1,67 можно зачеркнуть.  Хлора имеется 2,5 моль, а на реакцию с железом нужно лишь 1,5 моль, поэтому хлор взят в избытке. Избыток хлора составляет  2,5 – 1,5 = 1 моль.

 

   Таким образом, в недостатке железо, и дальнейшие расчеты ведем по его количеству:

 

1 моль         1,5 моль          1 моль

  2Fe     +  3Cl2    ®    2 FeCl3

   m (FeСl3)   =   M · n   =  162,5  г/моль · 1 моль  =  162,5  г

 

Задача 3.

 

 К раствору, содержащему 26,1 г нитрата бария, добавлен раствор, содержащий  35,5 г сульфата натрия, осадок отфильтрован. Что находится в фильтрате и в каком количестве?

 

Решение.

 n [

Ba(NO3)2]  =  26,1 г  :  261 г/моль   =  0,1  моль

n (Na2SO4)  =  35,5 г  :  142 г/моль  =  0,25 моль (избыток 0,15 моль)

0,1 моль                0,1 моль                 0,1 моль         0,2 моль

Ba(NO3)2  +  Na2SO4   ®    BaSO4    +    2HCl

 

В растворе после реакции окажется 0,2 моль нитрата натрия и остаток сульфата натрия  0,15 моль. При необходимости можно найти массы этих веществ.

 

  Иногда от количеств вещества реагентов может зависеть не только количество продуктов реакции, но и их состав.

 

Задача 4. 

К раствору, содержащему 49 г серной кислоты, добавлено 20 г гидроксида натрия. Определите состав и массу полученной соли.

 

Решение.

 

n (h3SO4) = 49 г  :  98 г/моль  = 0,5 моль

n (NaOH) = 20 г  :  40 г/моль  =  0,5 моль

 

  Так как серная кислота двухосновна, то она может образовать два ряда солей:

2 NaOH  +  h3SO4  ® Na2SO4  +  2h3O      средняя соль

 NaOH  +  h3SO4   ®  NaHSO4  +  h3O       кислая соль

 

  В нашей задаче оказалось равное мольное количество кислоты и щелочи, поэтому расчет следует вести по второму уравнению реакции:

0,5 моль         0,5 моль           0,5 моль

 

NaOH  +  h3SO4   ®  NaHSO4  +  h3O

 m (NaHSO4)  =  M

· n =  120 г/моль · 0,5 моль  =  60 г. 

 

Задача 5.

Через раствор, содержащий 60 г гидроксида натрия, пропущен углекислый газ, полученный при действии избытка соляной кислоты на 200 г карбоната  кальция. Определите состав и массу полученной соли.

 

Решение.

 

1.       Определяем количества вещества веществ, указанных в условии задачи:

 n (NaOH)  =  m : M  =  

60 г : 40 г/моль = 1,5 моль

n (CaCO3)  =  m : M  =  200 г : 100 г/моль  = 2 моль

 

2.       Записываем уравнение  реакции,  в которой был получен углекислый газ, и по количеству вещества СаСО₃ определяем, сколько моль газа выделилось:

2 моль                                                                       2 моль

CaCO3  +  2HCl   ®  CaCl2  +  h3O  +  CO2 ­

 

3.       Таким образом, для второй реакции у нас имеется 2 моль углекислого газа и 1,5 моль гидроксида натрия. Так как СО₂ – ангидрид двухосновной угольной кислоты Н₂СО₃, то при его взаимодействии с щелочами могут образоваться как средние, так и кислые соли:

 

NaOH  +  CO2  ®   NaHCO3

2NaOH  +  CO2  ®   Na2CO3  +  h3O

 

  Теперь нужно определиться, по какому из двух уравнений реакций нам вести расчет. Для образования средней соли щелочи должно быть вдвое больше, чем газа. У нас же наоборот, газа больше, чем щелочи. Следовательно, реакция пойдет по первому уравнению, с образованием кислой соли, причем СО₂ окажется в избытке (0,5 моль):

1,5 моль      1,5 моль      1,5 моль

 

NaOH  +  CO2  ®   NaHCO3

m (NaHCO3)   =  M · n = 84 г/моль · 1,5 моль  = 126 г.

 

 Решите самостоятельно.

 

1.       14 г оксида кальция обработали раствором, содержащим 36 г азотной кислоты. Какова масса полученной соли?   (41 г).

 

2.       К раствору, содержащему 40 г сульфата меди (II), добавили 12 г железных опилок. Останется ли в растворе сульфат меди после реакции?

 

3.       Хватит ли 15 л кислорода для сжигания 4 г серы?

 (да)

4.       В раствор, содержащий 16 г сульфата меди (II), пропустили сероводород объемом 5,6 л. Какова масса выпавшего осадка?  (9,6 г).

 

5.       К раствору, содержащему 10,4 г хлорида бария, добавили 9,8 г серной кислоты. Определите массу осадка и состав полученного раствора.  (11,65 г)

 

 

 

www.himiavmeste.narod.ru

Задачи на растворы по химии с решением 11 класс

Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала. Формула проста: чтобы найти площадь круга, нужно знать только его радиус.. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади.

Решение задач на растворы

Цели урока: Рассмотреть алгоритм решения задач на растворы: познакомиться с приемами решения задач в математике и химии, рассмотреть биологическое значение воды как универсального растворителя, развить практические умения решать задачи, расширить знания учащихся о значении этих веществ в природе и деятельности человека, сформировать целостную картину о взаимосвязи предметов в школе.

Организационный момент

Учитель математики: Здравствуйте! Сегодня мы проводим необычный урок – урок на перекрестке наук математики и химии.

Учитель химии: Здравствуйте, ребята! Мы с вами увидим, как математические методы решения задач помогают при решении задач по химии.

А чтобы сформулировать тему урока, давайте проделаем небольшой эксперимент.

(Наливаю в 2 хим. стакана воду, добавляю в оба одинаковое количество сульфата меди.) Что получилось? (Растворы). Из чего состоит раствор? (Из растворителя и растворённого вещества). А теперь добавим в один из стаканов ещё немного сульфата меди. Что стало с окраской раствора? (Он стал более насыщенным). Следовательно, чем отличаются эти растворы? (Массовой долей вещ-ва).

Учитель математики: А с математической точки зрения – разное процентное содержание вещества.

Итак, тема урока “Решение задач на растворы”.

Цель урока: Рассмотреть алгоритм решения задач на растворы, познакомить с приемами решения задач в математике и химии, расширить знания о значении этих растворов в быту, сформировать целостную картину о взаимосвязи предметов в школе.

Девиз: “Только из союза двух работающих вместе и при помощи друг друга рождаются великие вещи” Антуан де Сент-Экзюпери.

Учитель математики: Для урока необходимо повторить понятие процента.

– Что называют процентом? (1/100 часть числа).

– Выразите в виде десятичной дроби 17%, 40%, 6%.

– Выразите в виде обыкновенной дроби 25%, 30%, 7%.

Одним из основных действий с процентами – нахождение % от числа.

Как найти % от числа? (% записать в виде дроби, умножить число на эту дробь.)

– Найти 10% от 30 (10%=0,1 30·0,1=3).

– Что такое раствор? (Однородная система, состоящая из частиц растворенного вещества, растворителя и продуктов их взаимодействия.)

– Приведите примеры растворов, с которыми вы встречаетесь в повседневной жизни. (уксус, нашатырный спирт, раствор марганцовки, перекись водорода и др.)

– Какое вещество чаще всего используется в качестве растворителя? (Вода)

Часто понятие “раствор” мы связываем, прежде всего, с водой, с водными растворами. Есть и другие растворы: например спиртовые раствор йода, одеколона, лекарственные настойки.

Хотя именно вода является самым распространённым соединением и “растворителем” в природе.

3/4 поверхности Земли покрыто водой.

Человек на 70% состоит из воды.

В сутки человек выделяет 3 литра воды и столько же нужно ввести в организм.

Овощи – 90% воды содержат (рекордсмены — огурцы — 98%)

Рыба 80% (рекордсмен у животных – медуза 98%)

– Что такое массовая доля растворенного вещества? (Отношение массы растворенного вещества к общей массе раствора.)

– Вспомните формулу для вычисления массовой доли растворенного вещества и производные от нее (w = m (р. в.)/m (р-ра ) ; m (р. в.)= m (р-ра) · w ; m (р-ра) = m (р. в.)/ w )

– По какой формуле можно рассчитать массу раствора? (m(р-ра) = m (р. в.) + m (р-ля)).

Учитель химии предлагает решить учащимся задачу:

Задача №1. Перед посадкой семена томатов дезинфицируют 15%-ным раствором марганцовки. Сколько г марганцовки потребуется для приготовления 500 г такого раствора? (Ответ: 40 г.)

– Давайте посмотрим на эту задачу с точки зрения математики. Какое правило на проценты вы применили при решении этой задачи? (Правило нахождения процента от числа.)

500·0,15=75 (г) – марганцовки.

– Как видите, задачи, которые вы встречаете на химии, можно решать на уроках математики без применения химических формул.

Задачам на растворы в школьной программе уделяется очень мало времени, но эти задачи встречаются на экзаменах в 9 и 11 классах. В этом году на экзамене в 9 классе была задача на смешивание растворов, и она оценивалась в 6 баллов.

Задача №2. При смешивании 10%-го и 30%-го раствора марганцовки получают 200 г 16%-го раствора марганцовки. Сколько граммов каждого раствора взяли?

Можно ли решить эту задачу так быстро?

О чем говорится в этой задаче? (о растворах)

Что происходит с растворами? (Смешивают)

0,1х + 60 – 0,3х = 32

140 (г) – 10% раствора

200 – 140 = 60 (г) — 30% раствора.

Ответ: 140 г, 60 г.

Учитель математики. Рассмотрим еще один раствор – это уксусная кислота. Водный раствор уксусной кислоты, полученный из вина (5-8%) называют винным уксусом. Разбавленный (6-10%) раствор уксусной кислоты под названием “столовый уксус” используется для приготовления майонеза, маринадов и т. д. Уксусная эссенция 80% раствор. Ее нельзя применять без разбавления для приготовления пищевых продуктов. “Столовый уксус”, используют для приготовления маринадов, майонеза, салатов и других пищевых продуктов. Очень часто при приготовлении блюд под руками оказывается уксусная эссенция. Как из нее получить столовый уксус. Поможет следующая задача.

Задача №3. Какое количество воды и 80%-го раствора уксусной кислоты следует взять для того, чтобы приготовить 200 г столового уксуса (8%-ый раствор уксусной кислоты.)

Масса раствора (г)

Масса вещества (г)

20 (г) – уксусной кислоты

200 – 20 = 180 (г) – воды.

Ответ: 20 г, 180 г.

Учитель химии. А сейчас мы решим экспериментальную задачу.

Приготовить 20 г 5%-го раствора поваренной соли. (Расчётная часть). Затем выполняем практическую часть. (Напомнить правила Т-Б).

2. Экспериментальная часть (Соблюдать правила техники безопасности). Уравновесить весы. Взвесить необходимое количество соли. Отмерить мерным цилиндром воду. Смешать воду и соль в стакане.

Учитель математики. Проведем проверочную работу, в которую включили задачи из сборника для подготовке к экзаменам в 9-м классе.

Проверочная работа

0,15х + 5,6 — 0,08х = 7

20(г) – 15%-го раствора.

70 – 20 = 50 (г) — 8% раствора

Ответ: 20 гр., 50 г.

0,15х + 54 — 0,6х = 36

40 (г) -15% раствора.

90 — 40 = 50 (г) — 60% раствора.

Ответ: 40 гр., 50 г.

Подведение итогов урока

– Посмотрите на содержание всех решенных сегодня задач. Что их объединяет? (Задачи на растворы.)

– Действительно, во всех задачах фигурируют водные растворы; расчеты связаны с массовой долей растворенного вещества; и если вы обратили внимание, задачи касаются разных сторон нашего быта.

– Посмотрите на эти задачи с точки зрения математики. Что их объединяет? (Задачи на проценты.)

При решении всех этих задач мы используем правило нахождения процента от числа.

Оценки за урок.

Домашнее задание.

Важное место в рационе питания человека, а особенно детей занимает молоко и молочные продукты. Решим такую задачу:

Задача №1. Какую массу молока 10%-й жирности и пломбира 30%-й жирности необходимо взять для приготовления 100 г 20%-го новогоднего коктейля?

Масса раствора (г)

Масса вещества (г)

0,1х + 30 – 0,3х = 20

100 – 50 = 50(г) – пломбира.

Ответ:50 г молока, 50 г пломбира.

Задача №3. Для засола огурцов используют 7% водный раствор поваренной соли (хлорида натрия NaCl). Именно такой раствор в достаточной мере подавляет жизнедеятельность болезнетворных микроорганизмов и плесневого грибка, и в то же время не препятствует процессам молочнокислого брожения. Рассчитайте массу соли и массу воды для приготовления 1 кг такого раствора?

Растворять, смешивать, решать

Растворы широко встречаются в быту.

Наш урок подошел к концу. Сейчас каждый из вас оставит на парте тот смайлик, какое настроение вы приобрели на уроке.

Спасибо за урок!

Свидетельство о регистрации средства массовой информации ЭЛ №ФС77-69741 от 5 мая 2017 г.

Задачи на растворы по химии с решением 11 класс

Решение задач на растворы

Цели урока: Рассмотреть алгоритм решения задач на растворы: познакомиться с приемами решения задач в математике и химии, рассмотреть биологическое значение воды как универсального растворителя, развить практические умения решать задачи, расширить знания учащихся о значении этих веществ в природе и деятельности человека, сформировать целостную картину о взаимосвязи предметов в школе.

Организационный момент

Учитель математики: Здравствуйте! Сегодня мы проводим необычный урок – урок на перекрестке наук математики и химии.

Учитель химии: Здравствуйте, ребята! Мы с вами увидим, как математические методы решения задач помогают при решении задач по химии.

А чтобы сформулировать тему урока, давайте проделаем небольшой эксперимент.

(Наливаю в 2 хим. стакана воду, добавляю в оба одинаковое количество сульфата меди.) Что получилось? (Растворы). Из чего состоит раствор? (Из растворителя и растворённого вещества). А теперь добавим в один из стаканов ещё немного сульфата меди. Что стало с окраской раствора? (Он стал более насыщенным). Следовательно, чем отличаются эти растворы? (Массовой долей вещ-ва).

Учитель математики: А с математической точки зрения – разное процентное содержание вещества.

Итак, тема урока “Решение задач на растворы”.

Цель урока: Рассмотреть алгоритм решения задач на растворы, познакомить с приемами решения задач в математике и химии, расширить знания о значении этих растворов в быту, сформировать целостную картину о взаимосвязи предметов в школе.

Девиз: “Только из союза двух работающих вместе и при помощи друг друга рождаются великие вещи” Антуан де Сент-Экзюпери.

Учитель математики: Для урока необходимо повторить понятие процента.

– Что называют процентом? (1/100 часть числа).

– Выразите в виде десятичной дроби 17%, 40%, 6%.

– Выразите в виде обыкновенной дроби 25%, 30%, 7%.

Одним из основных действий с процентами – нахождение % от числа.

Как найти % от числа? (% записать в виде дроби, умножить число на эту дробь.)

– Найти 10% от 30 (10%=0,1 30·0,1=3).

– Что такое раствор? (Однородная система, состоящая из частиц растворенного вещества, растворителя и продуктов их взаимодействия.)

– Приведите примеры растворов, с которыми вы встречаетесь в повседневной жизни. (уксус, нашатырный спирт, раствор марганцовки, перекись водорода и др.)

– Какое вещество чаще всего используется в качестве растворителя? (Вода)

Часто понятие “раствор” мы связываем, прежде всего, с водой, с водными растворами. Есть и другие растворы: например спиртовые раствор йода, одеколона, лекарственные настойки.

Хотя именно вода является самым распространённым соединением и “растворителем” в природе.

3/4 поверхности Земли покрыто водой.

Человек на 70% состоит из воды.

В сутки человек выделяет 3 литра воды и столько же нужно ввести в организм.

Овощи – 90% воды содержат (рекордсмены — огурцы — 98%)

Рыба 80% (рекордсмен у животных – медуза 98%)

– Что такое массовая доля растворенного вещества? (Отношение массы растворенного вещества к общей массе раствора.)

– Вспомните формулу для вычисления массовой доли растворенного вещества и производные от нее (w = m (р. в.)/m (р-ра ) ; m (р. в.)= m (р-ра) · w ; m (р-ра) = m (р. в.)/ w )

– По какой формуле можно рассчитать массу раствора? (m(р-ра) = m (р. в.) + m (р-ля)).

Учитель химии предлагает решить учащимся задачу:

Задача №1. Перед посадкой семена томатов дезинфицируют 15%-ным раствором марганцовки. Сколько г марганцовки потребуется для приготовления 500 г такого раствора? (Ответ: 40 г.)

– Давайте посмотрим на эту задачу с точки зрения математики. Какое правило на проценты вы применили при решении этой задачи? (Правило нахождения процента от числа.)

500·0,15=75 (г) – марганцовки.

– Как видите, задачи, которые вы встречаете на химии, можно решать на уроках математики без применения химических формул.

Задачам на растворы в школьной программе уделяется очень мало времени, но эти задачи встречаются на экзаменах в 9 и 11 классах. В этом году на экзамене в 9 классе была задача на смешивание растворов, и она оценивалась в 6 баллов.

Задача №2. При смешивании 10%-го и 30%-го раствора марганцовки получают 200 г 16%-го раствора марганцовки. Сколько граммов каждого раствора взяли?

Можно ли решить эту задачу так быстро?

О чем говорится в этой задаче? (о растворах)

Что происходит с растворами? (Смешивают)

0,1х + 60 – 0,3х = 32

140 (г) – 10% раствора

200 – 140 = 60 (г) — 30% раствора.

Ответ: 140 г, 60 г.

Учитель математики. Рассмотрим еще один раствор – это уксусная кислота. Водный раствор уксусной кислоты, полученный из вина (5-8%) называют винным уксусом. Разбавленный (6-10%) раствор уксусной кислоты под названием “столовый уксус” используется для приготовления майонеза, маринадов и т. д. Уксусная эссенция 80% раствор. Ее нельзя применять без разбавления для приготовления пищевых продуктов. “Столовый уксус”, используют для приготовления маринадов, майонеза, салатов и других пищевых продуктов. Очень часто при приготовлении блюд под руками оказывается уксусная эссенция. Как из нее получить столовый уксус. Поможет следующая задача.

Задача №3. Какое количество воды и 80%-го раствора уксусной кислоты следует взять для того, чтобы приготовить 200 г столового уксуса (8%-ый раствор уксусной кислоты.)

Масса раствора (г)

Масса вещества (г)

20 (г) – уксусной кислоты

200 – 20 = 180 (г) – воды.

Ответ: 20 г, 180 г.

Учитель химии. А сейчас мы решим экспериментальную задачу.

Приготовить 20 г 5%-го раствора поваренной соли. (Расчётная часть). Затем выполняем практическую часть. (Напомнить правила Т-Б).

2. Экспериментальная часть (Соблюдать правила техники безопасности). Уравновесить весы. Взвесить необходимое количество соли. Отмерить мерным цилиндром воду. Смешать воду и соль в стакане.

Учитель математики. Проведем проверочную работу, в которую включили задачи из сборника для подготовке к экзаменам в 9-м классе.

Проверочная работа

0,15х + 5,6 — 0,08х = 7

20(г) – 15%-го раствора.

70 – 20 = 50 (г) — 8% раствора

Ответ: 20 гр., 50 г.

0,15х + 54 — 0,6х = 36

40 (г) -15% раствора.

90 — 40 = 50 (г) — 60% раствора.

Ответ: 40 гр., 50 г.

Подведение итогов урока

– Посмотрите на содержание всех решенных сегодня задач. Что их объединяет? (Задачи на растворы.)

– Действительно, во всех задачах фигурируют водные растворы; расчеты связаны с массовой долей растворенного вещества; и если вы обратили внимание, задачи касаются разных сторон нашего быта.

– Посмотрите на эти задачи с точки зрения математики. Что их объединяет? (Задачи на проценты.)

При решении всех этих задач мы используем правило нахождения процента от числа.

Оценки за урок.

Домашнее задание.

Важное место в рационе питания человека, а особенно детей занимает молоко и молочные продукты. Решим такую задачу:

Задача №1. Какую массу молока 10%-й жирности и пломбира 30%-й жирности необходимо взять для приготовления 100 г 20%-го новогоднего коктейля?

Масса раствора (г)

Масса вещества (г)

0,1х + 30 – 0,3х = 20

100 – 50 = 50(г) – пломбира.

Ответ:50 г молока, 50 г пломбира.

Задача №3. Для засола огурцов используют 7% водный раствор поваренной соли (хлорида натрия NaCl). Именно такой раствор в достаточной мере подавляет жизнедеятельность болезнетворных микроорганизмов и плесневого грибка, и в то же время не препятствует процессам молочнокислого брожения. Рассчитайте массу соли и массу воды для приготовления 1 кг такого раствора?

Растворять, смешивать, решать

Растворы широко встречаются в быту.

Наш урок подошел к концу. Сейчас каждый из вас оставит на парте тот смайлик, какое настроение вы приобрели на уроке.

Спасибо за урок!

Свидетельство о регистрации средства массовой информации ЭЛ №ФС77-69741 от 5 мая 2017 г.

Задачи на растворы по химии с решением 11 класс

Правильные решения пяти типовых задач «В9» по химии на тему «Растворы»

Массовая доля растворенных солей в некотором образце морской воды составляет 3,3%. Определите массу солей, содержащихся в 100,0 л такой воды (р = 1,12 г/мл). Ответ: . г (запишите число с точностью до целых).

Объем раствора морской воды: Vр-ра — 100,0 л;

Массовая доля солей : (НNO3) = 3,3%

Плотность раствора: pр-ра = 1,12 г/мл.

В первую очередь необходимо от объема раствора перейти к его массе, используя плотность. При этом следует учесть, что объем указан в литрах, а плотность в г/мл. Переведем значение

Объема в единицы измерения, соответствующие плотности.

Vр-ра = 100 л = 100000 мл

Далее используем соотношение для определения массовой доли.

Масса серной кислоты, содержащейся в 2 л ее водного 30%-ного раствора (р = 1,22 г/мл), равна. г (запишите число с точностью до целых).

Объем раствора: Vр-ра — 2 л;

Массовая доля раствора серной кислоты: (h3SO4) = 30%

Плотность раствора: pр-ра = 1,22 г/мл.

В первую очередь необходимо от объема раствора перейти к его массе, используя плотность. При этом следует учесть, что объем указан в литрах, а плотность в г/мл. Переведем значение объема в единицы измерения, соответствующие плотности.

Далее используем соотношение для определения массовой доли.

Масса сахарозы, содержащейся в 1 л ее водного 50%-ного раствора (р = 1,23 г/мл) равна….. г (запишите число с точностью до целых).

Объем раствора: Vр-ра — 1 л;

Массовая доля раствора сахарозы: (С12Н22О11) = 50%

Плотность раствора: pр-ра = 1,23 г/мл.

В первую очередь необходимо от объема раствора перейти к его массе, используя плотность. При этом следует честь, что объем указан в литрах, а плотность в г/мл. Переведем значение объема в единицы измерения, соответствующие плотности.

Далее используем соотношение для определения массовой доли.

Масса этанола, содержащегося в 2 л его 56%-ного водного раствора (р = 0,900 г/мл) равна. г (запишите число с точностью до целых).

Объем раствора: Vр-ра — 2 л;

Массовая доля раствора этанола: (С2Н6О) = 56%

Плотность раствора: pр-ра = 0,900 г/мл.

В первую очередь необходимо от объема раствора перейти к его массе, используя плотность. При этом следует учесть, что объем указан в литрах, а плотность в г/мл. Переведем значение

Объема в единицы измерения, соответствующие плотности.

Далее используем соотношение для определения массовой доли.

Массовая доля соляной кислоты, полученной растворением 33,6 л (н. у.) хлороводорода в 1,5 л воды, равна. % (запишите число с точностью до сотых).

Объем раствора: Vр-ра = 1,5 л;

Объем хлороводорода: V(HCl) = 33,6 л;

Найти: массовую долю раствора хлороводорода: (HCl) = ?

М(HCl) = 36,5 г/моль.

M(h3O) = 1500 мл. 1г/мл = 1500 г

В первую очередь необходимо найти массу газообразного хлороводорода, растворенного в 1,5 л воды.

M(HCl) = n(HCl) . M(HCl) = V(HCl)/Vm. M(HCl) = 33,6 л/22,4л/моль. 36,5 г/моль = 54,75 г.

2. Находим массу раствора:

Mр-ра = m(h3O) + m(HCl) = 1500 г + 54, 75 г = 1554,75 г.

3. Далее используем соотношение для определения массовой доли.

Ответ: (HCl) = 3,52%.

Вы здесь:   Определение индексов в формуле вещества | Задача 1. 1

Основное меню

Новые материалы

Похожие материалы

© 2018 Домашние задания, готовые решения задач по химии и биологии

poiskvstavropole.ru

Урок на тему: «Решение задач на растворы»

Урок на тему:

«Решение задач на растворы»

(Учебник: Кузнецова Н.Е., Титова И.М., Гара Н.Н.,

Жегин А.Ю., Химия-8. –М.; Вентана-Граф, 1997.)

Учитель химии:

Л.Г.Киракосян,

Лицей №49 г.Калининград;

2007

Тема урока : Решение задач по теме «Растворы»

Тип урока : Обобщение изученного материала

Вид урока : Беседа с использованием средств наглядности, решение расчётных задач.
Цели и задачи урока:
Обучающие: осмысление химической сущности явлений, применять усвоенные знания в конкретно заданной ситуации.

Развивающие: формирование научно-теоретического, логического, творческого мышления, самостоятельности в добывании знаний.

Воспитательные: развитие коммуникативных способностей и умения работать в группе.
Методы и методические приёмы: рассказ, беседа, применение и составление алгоритмов, решение расчётных задач.
Оборудование:

1. 
   Компьютер.
   
2. 
   Мультимедийный проектор.
   
3. 
   На столах учащихся конверты с заданиями.
   

Ход урока.

Эпиграф: Человек бывает счастлив, когда он определился в двух вещах: семейной жизни и работе.

Житейская мудрость.

1. 
   Вводное слово учителя.
   

У многих из вас, ребята, есть мечта. Это состояние свойственно вашему возрасту. Мечты бывают разные, но у многих они связаны с будущей профессией.

Учитель обращается к эпиграфу урока и говорит: «О первой проблеме вам думать пока рано, поговорим о второй».

В этом году вы начали изучать замечательный, волшебный предмет – химию. Многие из вас связывают свою будущую специальность с этой наукой, поэтому и решили изучать эту дисциплину дополнительно на элективных курсах.

Что изучает химия? Что представляет эта наука в вашем понимании?

Учащиеся (лидеры группы) дают свой ответ на поставленный учителем вопрос. Идёт обсуждение ответов, наиболее полное и научное определение учащиеся записывают в тетрадь.

Химия – одна из наук, которая относится к области естествознания. Как и любая другая наука, она возникла и развилась из практической потребности людей. С первых шагов своей жизни на Земле человек должен был использовать окружающие его природные материалы. Для этого необходимо знать и различать их свойства.

Учитель: Ещё в XVII в. Замечательный русский учёный-энциклопедист М.В.Ломоносов сказал: «Широко протянула свои руки химия в дела человеческие» (На мультимедийном проекторе высвечивается портрет М.В.Ломоносова).

В каких делах человеческих нужна химия?

Учащиеся высказывают свои ответы и записывают в тетради «лепестки» химии.

Подводятся итоги этой работы, учитель предлагает остановиться на наиболее значимых отраслях и представляет сформированные группы:

«Химия в быту»

«Химия на дачном участке»

«Химия в быту»

«Химия в строительстве».

Каждая группа сформирована заранее из 4-5 человек. В каждой группе есть свой лидер, это наиболее подготовленный ученик.

Учитель: Тема наших элективных курсов: «Решение расчетных задач». Общего рецепта для решения любой задачи нет, но целесообразно придерживаться определённой схемы её решения. Давайте уточним их.

Учащиеся коллективно сообщают.

1. 
   Внимательно прочитать условие задачи.
   
2. 
   Решение задачи всегда следует начать с анализа условия и составления плана её решения.
   
3. 
   Определить числовые данные задачи, которые при необходимости приводят в единую систему единиц (количественная сторона задачи).
   
4. 
   Определить перечень химических веществ и явлений в их взаимосвязи, основные теоретические положения, необходимые для решения задачи (качественная сторона задачи).
   
5. 
   Определить соотношения между качественными и количественными данными задачи в виде формул, уравнений, пропорций, законов.
   
6. 
   Определить алгоритм решения задачи, т.е. последовательность её решения, начиная с конечного вопроса задачи до данных по условию.
   
7. 
   Записываем краткое «дано».
   

Подводятся итоги этой коллективной работы.

Учитель: В вашей будущей специальности вам часто придётся готовить и использовать растворы, поэтому предлагаемые вам расчётные задачи будут на эту тему. Сегодня на уроке вы будете работниками «Справочного бюро», которое работает под девизом «Спрашивайте – отвечаем». Чтобы вы могли дать компетентный ответ на любой вопрос вам надо заполнить производственную анкету в виде следующих вопросов.

2. 
   Фронтальная беседа (актуализация знаний).
   

Учитель: Что такое растворы?

Ученик: Раствором называется однородная система, состоящая из двух или более компонентов.

Учитель: Что является компонентами раствора?

Ученик: Растворитель и растворённое вещество.

Учитель: Что такое растворитель?

Ученик: Растворителем является тот компонент, который в чистом виде существует в том же агрегатном состоянии, что и раствор, если оба компонента находятся в одном агрегатном состоянии, то растворитель тот, которого больше.

Учитель: Какие растворы называют концентрированными, а какие разбавленными?

Ученик: Концентрированным называют раствор с высоким содержанием растворённого вещества, разбавленным с низким содержанием растворённого вещества.

Учитель: Что показывает массовая доля растворенного вещества?

Ученик: Массовой долей растворённого вещества называют отношение массы растворённого вещества к общей массе раствора.

Учитель: Как обозначается массовая доля растворенного вещества?

Ученик: Массовая доля растворённого вещества обозначается греческой буквой ω (омега).

Учитель: Итак, вы отлично заполнили свою производственную анкету и можете дать квалифицированный ответ.

По команде учителя учащиеся открывают конверты с вопросами к каждой группе.
Химия на дачном участке
Бабушка звонит внучке и спрашивает какую массу воды надо добавить к 500г 20% раствора хлорида бария, чтобы раствор стал 4%? Этот раствор ей необходим для опрыскивания свеклы на дачном участке против долгоносика. Каков был ответ внучки?
Химия в промышленности
Для приготовления цементного раствора, применяемого в строительстве, смешивают цементный порошок, песок и воду в массовом отношении 1,5:6:2,5. Отец просит сына вычислить массы компонентов для приготовления 1кг раствора.
Химия в быту
Работник парикмахерской звонит своей подруге и спрашивает: какая масса пергидроля (30% раствора пероксида водорода) и воды потребуется для приготовления 100г 9% раствора пероксида водорода. Этот раствор ей необходим для осветления волос перед окраской. Какой был ответ?
Химия в медицине
5% раствор хлорида кальция используется в медицине для улучшения свёртываемости крови. Какие массы 3% и 10% растворов потребуются для приготовления 100г такого раствора? Раствор готовится для 5-летнего ребёнка. Не ошибись!

Учитель: Прежде чем приступить к выполнению поставленных задач воспользуйтесь мудрыми советами.

На мультимедийном проекторе высвечивают советы.

«Обдумай цель раньше, чем начать»
«С началом считается глупец, о конце думает мудрец»
«Мудрый меняет свои решения, а дурак никогда»
«Желаемое мы охотно принимаем за действительное»

Учащиеся приступают к решению задач, сдают на листке свои ответы учителю, учитель фиксирует правильность ответа.

Ученики в группе, успешно решившие задачу, оказывают помощь друг другу.

После окончания работы на мультимедийном проекторе высвечивается алгоритм решения каждой типовой задачи.

Учитель предлагает учащимся, не справившимся с заданием решить свою задачу по данному алгоритму. После определённого времени на экране появляются правильные ответы всех задач.
Химия на дачном участке:
Задача 1 2000г

Задача 2 600г

Задача 3 825г

Задача 4 3150г

Задача 5 200г
Химия в медицине:
Задача 1 71г и 29г

Задача 2 85,7г и 34,3г

Задача 3 114,2г и 45,8г

Задача 4 142,8г и 57,2г

Задача 5 178,6г и 71,4г
Химия в быту:
Задача 1 m(H₂O)=70г; m_р-ра=30г

Задача 2 m(H₂O)=84г; m_р-ра=36г

Задача 3 m(H₂O)=105г; m_р-ра=45г

Задача 4 m(H₂O)=140г; m_р-ра=60г

Задача 5 m(H₂O)=175г; m_р-ра=75г
Химия в строительстве:
Задача 1 m_цем.=150г; m(Si0₂)=600г; m(H₂O)=250г

Задача 2 m_цем.=300г; m(Si0₂)=1200г; m(H₂O)=500г

Задача 3 m_цем.=750г; m(Si0₂)=3000г; m(H₂O)=1250г

Задача 4 m_цем.=900г; m(Si0₂)=3600г; m(H₂O)=1500г

Задача 5 m_цем.=1200г; m(Si0₂)=4800г; m(H₂O)=2000г
Учитель предлагает каждому ученику самим оценить свою работу, затем обсудить эту оценку в группе, учитель выставляет итоговую оценку каждому ученику, учитывая его работу на каждом этапе урока.

Заключительное слово учителя: Если вы правильно научились делать расчёты на приготовление растворов, то это принесёт пользу больному ребёнку, окажут большую услугу любимой бабушке на её дачном участке, помогут подруге правильно окрасить волосы, сделать вас хорошими помощниками отцу в строительном деле. Все приобретённые вами знания пригодятся во всех человеческих делах.

Список используемой литературы:

1. 
   Боровских Т.А., Обучение химии в 8 классе. Методическое пособие. –М., АСТ. Апрель, 2002
   
2. 
   Кузнецова Н.Е., Титова И.М. и др. Химия – 8. –М.,; Вентана-Граф, 2005
   
3. 
   Кузнецова Н.Е., Левкин А.Н. Задачник по химии 8-класс, -М.; Вентана-Граф, 2002
   
4. 
   Штремплер Г.И., Хохлова А.И., Методика решения расчётных задач по химии 8-11 –М.; «Просвещение», 2001
   

edushk.ru

Технологическая «находка» по химии «Как научить решать задач на растворы, используя математический метод решения» Цели

Технологическая «находка» по химии «Как научить решать задач на растворы, используя математический метод решения»

Цели : Рассмотреть алгоритм решения задач на растворы: познакомиться с приемами решения задач в математике и химии, развить практические умения решать задач, сформировать целостную картину о взаимосвязи предметов в школе.

Здравствуйте! Сегодня мы проводим необычный урок – урок на перекрестке наук математики и химии.Мы с вами увидим, как математические методы решения задач помогают при решении задач по химии.Давайте проделаем небольшой эксперимент.

(Наливаю в 2 хим. стакана воду, добавляю в оба одинаковое количество сульфата меди.) Что получилось? (Растворы). Из чего состоит раствор? (Из растворителя и растворённого вещества). А теперь добавим в один из стаканов ещё немного сульфата меди. Что стало с окраской раствора? (Он стал более насыщенным). Следовательно, чем отличаются эти растворы? (Массовой долей вещ-ва).

А с математической точки зрения – разное процентное содержание вещества.

Необходимо повторить с детьми понятие процента.Вопросы:

– Что называют процентом? (1/100 часть числа).

– Выразите в виде десятичной дроби 17%, 40%, 6%.

– Выразите в виде обыкновенной дроби 25%, 30%, 7%.

– Установите соответствие:

40%	1/4
25%	0,04
80%	0,4
4%	4/5

Одним из основных действий с процентами – нахождение % от числа.

Как найти % от числа? (% записать в виде дроби, умножить число на эту дробь.)

– Найти 10% от 30 (10%=0,1 30·0,1=3).

– Вычислите:

1) 20% от 70;
2) 6% от 20;
3) х% от 7.

Вопросы по теме «Растворы»:Что такое раствор? (Однородная система, состоящая из частиц растворенного вещества, растворителя и продуктов их взаимодействия.)

Приведите примеры растворов, с которыми вы встречаетесь в повседневной жизни. (уксус, нашатырный спирт, раствор марганцовки, перекись водорода и др.)

Какое вещество чаще всего используется в качестве растворителя? (Вода)

Часто понятие “раствор” мы связываем, прежде всего, с водой, с водными растворами. Есть и другие растворы: например спиртовые раствор йода, одеколона, лекарственные настойки.

Хотя именно вода является самым распространённым соединением и “растворителем” в природе.

3/4 поверхности Земли покрыто водой.

Человек на 70% состоит из воды.

В сутки человек выделяет 3 литра воды и столько же нужно ввести в организм.

Овощи – 90% воды содержат (рекордсмены – огурцы – 98%)
Рыба 80% (рекордсмен у животных – медуза 98%)
Хлеб – 40%
Молоко – 75%

Что такое массовая доля растворенного вещества? (Отношение массы растворенного вещества к общей массе раствора.)

Вспомните формулу для вычисления массовой доли растворенного вещества и производные от нее (w = m (р.в.)/m (р-ра ) ; m (р.в.)= m (р-ра) · w ; m (р-ра) = m (р.в.)/ w )

По какой формуле можно рассчитать массу раствора? (m(р-ра) = m (р.в.) + m (р-ля)).

Далее  предлагаем решить учащимся задачу:

Задача №1. Перед посадкой семена томатов дезинфицируют 15%-ным раствором марганцовки. Сколько г марганцовки потребуется для приготовления 500 г такого раствора? (Ответ: 40 г.)

–Давайте посмотрим на эту задачу с точки зрения математики. Какое правило на проценты вы применили при решении этой задачи? (Правило нахождения процента от числа.)

15% от 500;

500·0,15=75 (г) – марганцовки.

Ответ: 75 г.

Как видите, задачи, которые вы встречаете на химии, можно решать на уроках математики без применения химических формул.

Задачам на растворы в школьной программе уделяется очень мало времени, но эти задачи встречаются на экзаменах в 9 и 11 классах. В этом году на экзамене в 9 классе была задача на смешивание растворов, и она оценивалась в 6 баллов.

Задача №2. При смешивании 10%-го и 30%-го раствора марганцовки получают 200 г 16%-го раствора марганцовки. Сколько граммов каждого раствора взяли?

Можно ли решить эту задачу так быстро?

О чем говорится в этой задаче? (о растворах)

Что происходит с растворами? (смешивают)

Решение:

Раствор	%-е содержание	Масса раствора (г)	Масса вещества (г)
1 раствор 2 раствор	10% = 0,1 30% = 0,3	х 200-х	0,1х 0,3(200-х)
Смесь	16% = 0,16	200	0,16 · 200

0,1х + 0,3(200-х) = 0,16 · 200
0,1х + 60 – 0,3х = 32
-0,2х = -28
х = 140
140 (г) – 10% раствора
200 – 140 = 60 (г) – 30% раствора.

Ответ: 140 г, 60 г.

 Рассмотрим еще один раствор – это уксусная кислота. Водный раствор уксусной кислоты, полученный из вина (5-8%) называют винным уксусом. Разбавленный (6-10%) раствор уксусной кислоты под названием “столовый уксус” используется для приготовления майонеза, маринадов и т.д. Уксусная эссенция 80% раствор. Ее нельзя применять без разбавления для приготовления пищевых продуктов. “Столовый уксус”, используют для приготовления маринадов, майонеза, салатов и других пищевых продуктов. Очень часто при приготовлении блюд под руками оказывается уксусная эссенция. Как из нее получить столовый уксус. Поможет следующая задача.

Задача №3. Какое количество воды и 80%-го раствора уксусной кислоты следует взять для того, чтобы приготовить 200 г столового уксуса (8%-ый раствор уксусной кислоты.)

Решение:

Раствор	%-е содержание	Масса раствора (г)	Масса вещества (г)
Уксусная кислота Вода	80%=0,8 0%=0	х 200-х	0,8х 0
Смесь	8%=0,08	200	0,08 · 200

0,8х = 0,08 · 200
0,8х = 16
х = 16 : 0,8
х = 20
20 (г) – уксусной кислоты
200 – 20 = 180 (г) – воды.

Ответ: 20 г, 180 г.

А сейчас мы решим экспериментальную задачу.

Приготовить 20 г 5%-го раствора поваренной соли. (Расчётная часть). Затем выполняем практическую часть. (Напомнить правила Т-Б).

Рефлексия. (Синквейн)

Раствор
Разбавленный, водный
Растворять, смешивать, решать
Растворы широко встречаются в быту.
Смеси

moyamatem.ru