Умножение на единичную матрицу
На основании правила умножения матриц получаем:
АЕ = | а11 | а12 . | 1 | 0 | = | а11 | а12 |
а21 | а22 | 0 | 1 | а21 | а22 | ||
EA= | 1 | 0 . | а11 | а12 | = | а11 | а12 |
0 | 1 | а21 | а22 | а21 | а22, | ||
т.е. АЕ = ЕА = А (11)
Произведение квадратной матрицы любого порядка на соответствующую единичную матрицу равняется первоначальной матрице. Таким образом, при умножении матриц единичная матрица играет роль единицы, поэтому и называется единичной.
Понятие обратной матрицы
Если А – квадратная матрица, то
А-1А = АА-1 = Е (12)
Если обратная матрица А-1 существует, то матрица А называется обратимой. Операция вычисления обратной матрицы называется обращением матрицы. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица
Нахождение матрицы, обратной данной
Пусть дана невырожденная матрица
а11 | а12 | а13 | ||
А= | а21 | а22 | а23 | |
а31 | а32 | а33 |
а11 | а12 | а13 | |||
DА = | а21 | а22 | а23 | ≠ 0 | |
а31 | а32 | а33 | |||
Обратной матрицей А-1 будет матрица
A | A21/DА | A31/DА | ||||
A-1 = | A12/DА | A22/DА | A32/DА | , | ||
A13/DА | A23/DА | A33/DА |
где Аij – алгебраическое дополнение элемента аij определителя DA.
Убедиться в этом
можно, умножая матрицу А на матрицу А-1.
Например, элементы с11
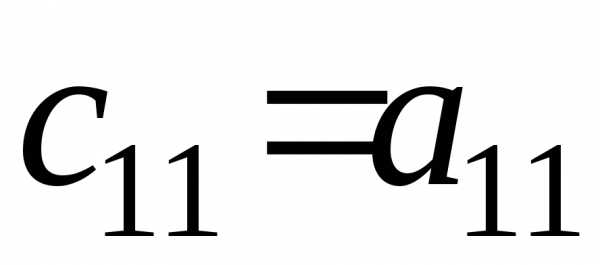 ·
·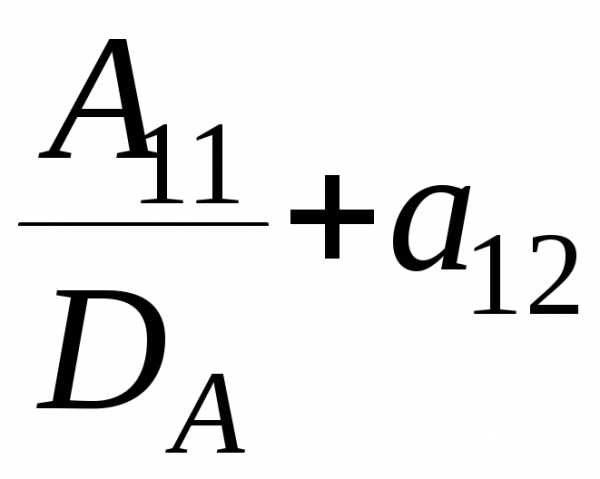 ·
· ·
·
c23=a21· ·
·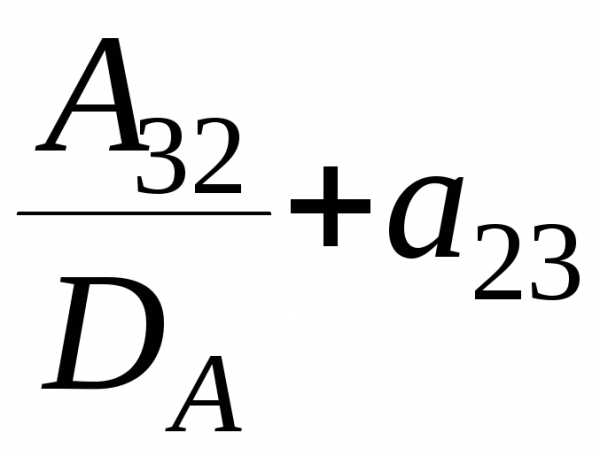 ·=
·=
= = 0
= 0
В итоге
а11 | а12 | а13 | A11/DА | A21/DА | A31/DА | 1 | 0 | 0 | |||
а21 | а22 | а23 | A12/DА | A22/DА | A32/DА | = | 0 | 1 | 0 | =E | |
а32 | а33 | A13/DА | A23/DА | A33/DА | 0 | 0 | 1 |
Матрица
A11 | A21 | A31 | ||||
| A12 | A22 | A32 | ( 14 ) | ||
A13 | A23 | A33 |
называется матрицей, присоединённой к А.
(Используется также обозначение  ).
Обратная матрица А-1 через присоединённую
).
Обратная матрица А-1 через присоединённую  выражается так:
выражается так:
| 1 |
| ( 15 ) |
DA |
Обратную матрицу будем находить по следующей схеме:
1. Находим определитель матрицы А.
2. Находим алгебраические дополнения всех элементов аij матрицы и записываем новую матрицу.
3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).
4. Умножаем полученную матрицу на 1/DA.
Пример 6. (Лена Иванова, КШ-061).
Дана матрица
Найти обратную матрицу.
1. Вычисляем определитель матрицы А:
2 | 5 | 7 | 2 | 5 | 7 | ||||
DA = | 6 | 3 | 4 | = | 0 | -12 | -17 | = | (492 – 493) = -1 |
5 | -2 | -3 | 0 | -29/2 | -41/2 |
Так как DA ≠ 0, то матрица А является невырожденной, и, значит, можно найти матрицу А-1.
2. Находим алгебраические дополнения элементов этого определителя:
A11 = | 3 | 4 | = -1, | A21= – | 5 | 7 | = 1, | A31= | 5 | 7 | = -1, |
-2 | -3 | -2 | -3 | 3 | 4 |
A12= – | 6 | 4 | = 38, | A22= | 2 | 7 | = -41, | A32= – | 2 | 7 | = 34, |
5 | -3 | 5 | -3 | 6 | 4 |
A13 = | 6 | 3 | = -27, | A23=- | 2 | 5 | = 29, | A33= | 2 | 5 | = -24. |
5 | -2 | 5 | -2 | 6 | 3 |
Следовательно,
-1 | 1 | -1 | 1 | -1 | 1 | ||
A-1 = (-1) | 38 | -41 | 34 | = | -38 | 41 | -34 |
-27 | 29 | -24 | 27 | -29 | 24 |
Лекция 4.
studfiles.net
Умножение матриц, обратная матрица — Мегаобучалка
Раздел 3. Матрицы.
1 Линейные операции над матрицами
2. Умножение матриц, обратная матрица
Линейные операции над матрицами.
Определение.Матрицей размера (формата ) называется прямоугольная таблица чисел, содержащая строк и столбцов.
Обозначаются матрицы заглавными латинскими буквами А, В, … . Числа, составляющие матрицу, называются элементами матрицы. В общем виде матрица размера выглядит следующим образом:
.
Если хотят компактно указать, что матрица А имеет размер , то записывают: или .
Если число строк равно числу столбцов, то матрица называется квадратной. Для всякой квадратной матрицы А естественным образом можно составить и вычислить определитель этой матрицы, который обозначается :
Замечание: нельзя «путать» скобки, – это не «мелочь»!!!
Если , то матрица А называется особой (или вырожденной), если , то неособой (невырожденной).
Матрица, сплошь состоящая из нулей, называется нулевой, обозначается .
У всякой квадратной матрицы, как и у определителя, можно выделить две диагонали: главную (соединяющую левый верхний и правый нижний углы таблицы) и побочную.
Матрица называется диагональной, если у нее все элементы, кроме элементов стоящих на главной диагонали, равны нулю. Диагональная матрица называется единичной, если все элементы главной диагонали равны единице, обозначается Е. Ясно, что
Рассмотрим далее операции (или действия), которые можно проводить с матрицами. Сначала рассмотрим линейные операции.
Во-первых, две матрицы называются равными, если они одинакового размера и все соответственные элементы (т.е. элементы, стоящие на одинаковых местах) равны.
Суммой двух матриц одинакового размера называется матрица , у которой
Проще говоря, матрицы складываются поэлементно. Например:
Произведениемчисла на матрицу называется матрица, у которой все элементы умножаются на это число: .
Например: .
На практике этой операцией удобно пользоваться «в обратном направлении» – если все элементы матрицы имеют общий множитель, его можно вынести за знак матрицы в качестве сомножителя.
Заметим отличие этой операции над матрицами и над определителями!!!
Операции сложения матриц и умножения на число называются линейными операциями. Эти операции являются простейшими – для них справедливы основные законы операций – переместительный (коммутативный): ; сочетательный (ассоциативный):
и распределительный (дистрибутивный): и
Следующая операция, умножение двух матриц, уже не столь проста.
Умножение матриц, обратная матрица.
Мы уже видели, что в матрице выделяют строки и столбцы. Матрица, состоящая из одной строки, называется матрицей – строкой. Матрица, состоящая из одного столбца, называется матрицей – столбцом. Поэтому ясно, что в матрице можно выделить строк. Все эти строки содержат элементов. Аналогично, такая матрица содержит столбцов, все они содержат элементов.
Определение.Произведением матрицы на матрицу называется такая матрица , для которой выполняется:
(1)
Поясним на первый взгляд громоздкую формулу (1). Заметим, что в матрице строка имеет вид , а в матрице столбец имеет вид
Теперь легко заметить, что формула (1) есть сумма произведений элементов строки первой матрицы на соответствующие элементы столбца второй матрицы, т.е. скалярное произведение вектора –строки первой матрицы на вектор –столбец второй. Поэтому говорят, что матрицы умножают по правилу «строка на столбец».
Например,
Надо немного «потренироваться» и умножение матриц не будет доставлять никаких трудностей.
Однако, из определения нетрудно заметить, что умножение матриц уже не обязательно удовлетворяет привычным для нас законам. Во – первых, из определения, т.е. из правила «строка на столбец», очевидно неравноправие сомножителей, поэтому ясно, что умножение матриц не обязательно перестановочно.
Пример 1. ;
;
Пример 2.
Пример 3.
Во – вторых, не всякие матрицы можно перемножить: ,
– надо, чтобы количество столбцов первой матрицы равнялось количеству строк второй.
Пример 4.
Квадратные матрицы одинакового порядка перемножить можно всегда. Для них вводим следующее понятие.
Определение.Квадратная матрица называется обратной для матрицы А, если , где – единичная матрица.
Отметим без доказательства, что для определителей матриц справедливо соотношение .
Пример 5.Проверим соотношение для матриц
.
.
Если это свойство применить к взаимно обратным матрицам, то получим, что т.к. определитель единичной матрицы равен единице. Из последней формулы следует, что а это означает, что обратная матрица существует лишь для неособых (невырожденных) матриц, а для вырожденных не существует.
Приведем без доказательства формулу для нахождения обратной матрицы:
(2)
Формула (2) вновь нам показывает, что стоит в знаменателе дроби и, следовательно, не может быть равным нулю. Кроме этого заметим, что элементами обратной матрицы являются алгебраические дополнения элементов матрицы , симметричных относительно главной диагонали (обратите внимание на индексы у элементов матрицы , стоящих на одинаковых местах).
Определение.Если в матрице все строки записать столбцами с теми же номерами, то такая операция называется транспонированием , а получившаяся матрица – транспонированной, она обозначается .
Теперь можно переходить к примерам. Во избежание путаницы рекомендуется нахождение обратной матрицы проводить в следующем порядке. Пусть, например, имеется матрица третьего пордка.
.
1. Находим пределитель матрицы
2. Находим алгебраические дополнения для каждого элемента матрицы
, причем для удобства (во избежание упомянутой путаницы) располагаем их в том же порядке что и сами элементы матрицы (не забудем таблицу знаков!).
3. Записываем так называемую присоединенную матрицу
4. Для получения обратной матрицы остается протранспонировать присоединенную и поделить на :
Разумеется, все выкладки («для первого раза») проведены излишне подробно. На практике этот пример оформляют значительно короче:
Начинаем в любом случае с вычисления , а далее:
Вычисление алгебраических дополнений, т.е. определителей второго порядка ( с учетом таблицы знаков!), легко проводить «в уме» (устно).
Как видим, даже для матриц третьего порядка приходится проводить много арифметических подсчетов. Поэтому всегда полезно сделать проверку: должно выполняться Проверим:
Пример 6. Даны матрицы .
Найти матрицу .
Решение. Сначала найдем матрицу
Ответ:Матрицы не существует.
Матрицы и определители находят непосредственное применение в теории и практике систем линейных алгебраических уравнений (СЛАУ), к изучению которых мы и приступаем.
megaobuchalka.ru
25. Матричная алгебра. Сложение матриц и умножение матрицы на число. Перемножение матриц. Диагональная и единичная матрицы. Обратная матрица.
Сложение матриц и умножение на число Сложение определено только для матриц одинаковых размеров. Определение 14.2 Суммой матриц иразмеровявляется матрицатаких же размеров, у которой,,.Определение 14.3 Произведением матрицы размеровна число называется матрицатаких же размеров, у которой,,.
Другими словами, при умножении матрицы на число все ее элементы умножаются на это число. Операцию вычитания матриц можно определить следующим способом: что соответствует вычитанию элементов, стоящих на одинаковых местах.
Используя операции сложения и умножения, мы можем находить линейные комбинации матриц, то есть выражения вида , где– числа,– матрицы одинаковых размеров. Операции сложения матриц и умножения матрицы на число, называемыелинейными операциями, обладают следующими свойствами:
— свойство коммутативности;
— свойство ассоциативности;
;
;
— свойство дистрибутивности;
;
;
.
Умножение матриц Определение 14.4 Произведением матрицы размеровна матрицуразмеровназывается матрицаразмеров, элементы которой вычисляются по формуле
(14.5) |
где ,. Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой — второй. Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено. В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя. Правило вычисления элементов произведения можно сформулировать следующим образом. Для того, чтобы вычислить элемент произведения, стоящий в-ой строке и-ом столбце, нужно взять-ую строку первого сомножителя и-ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить. (Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).) Предложение 14.4 Умножение матриц обладает следующими свойствами: — ассоциативность умножения;, где– число;,– дистрибутивность умножения;,, где– единичная матрица соответствующего порядка. Предполагается, что все указанные произведения имеют смысл. Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной. Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю. Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны 1. Для обозначения единичной матрицы обычно используется буква . Порядок матрицы при этом обычно ясен из контекста. Из определения единичной матрицы видно, что ее элементыравны нулю, если индексы различны, и равны 1, если индексы совпадают. В математике таким свойством обладает величина, называемаясимволом Кронекера: Поэтому.Обратная матрица Определение14.8 Матрица называетсяобратной матрицей для квадратной матрицы , если. Из определения следует, что обратная матрицабудет квадратной матрицей того же порядка, что и матрица(иначе одно из произведенийилибыло бы не определено). Обратная матрица для матрицыобозначается. Таким образом, еслисуществует, то. Из определения обратной матрицы следует, что матрицаявляется обратной для матрицы, то есть. Про матрицыиможно говорить, что они обратны друг другу или взаимно обратны. Предложение14.20 Если матрица имеет обратную, тои. Доказательство. Так как определитель произведения матриц равен произведению определителей, то ., поэтому, что невозможно при. Из предыдущего равенства следует также. Последнее предложение можно сформулировать в следующем виде. Если определитель матрицы равен нулю, то обратная к ней не существует. Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения. Определение14.9 Квадратную матрицу назовемвырожденной или особенной матрицей, если , иневырожденной или неособенной матрицей, если . Предложение14.21 Если обратная матрица существует, то она единственна. Доказательство. Пусть две матрицы иявляются обратными для матрицы. ТогдаиСледовательно,. Предложение14.22 Если квадратная матрица является невырожденной, то обратная для нее существует и
(14.14) |
где — алгебраические дополнения к элементам. Доказательство. Так как для невырожденной матрицыправая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, чтои что. Докажем первое из этих равенств, второе доказывается аналогично. Пусть. Найдем элементы матрицы, учитывая, что:
Если , то сумма справа равна нулю, то естьпри. Если, тоСумма справа представляет собой разложение определителя матрицыпо-ой строке. Таким образом,Итак, в матрицедиагональные элементы равны 1, а остальные равны нулю, то есть.Теорема 14.1 Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица– невырожденная, обратная матрица единственна, и справедлива формула (14.14)
studfiles.net
Умножение матриц » ProcMem.Ru Линейная Алгебра
Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:
.
Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.
Пример.
Определение. Произведением матрицы размера на матрицу размера называют матрицу размера , где элемент является результатом произведения – й строки матрицы А на – й столбец матрицы В для всех значений индексов , , т.е.
или
.
Обозначение: .
Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.
Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)
Пример.
.
Определение. Квадратную матрицу – го порядка называют единичной матрицей n-го порядка и обозначают буквой Е, если для любой квадратной матрицы А – го порядка справедливо равенство: .
Множество всех квадратных матриц n-го порядка будем обозначать через .
Теорема. Множество содержит единичную матрицу n-го порядка, которой является матрица
.
Доказательство этой теоремы предоставляется читателю.
Теорема. Единичная матрица Е является единственной в множестве .
Доказательство. Пусть еще одна единичная матрица. Тогда, по определению, . Положим , тогда . Далее, по определению, . Положим здесь . Получаем равенство, отсюда имеем , ч.т.д.
Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.
Теорема доказана.
Из теоремы следует, что никакая другая матрица, кроме матрицы не является единичной.
Теорема. (Свойства умножения матриц.)
Умножение матриц подчиняется следующим законам:
9) ассоциативность:
;
10) существование единичной матрицы:
: ;
дистрибутивность умножения относительно сложения матриц:
11) дистрибутивность умножения относительно сложения матриц:
и
12) умножение матриц связано с умножением матрицы на число естественным законом: и верно равенство:
.
Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.
Замечание. Умножение матриц не обладает свойством коммутативности. Для доказательства достаточно привести один контрпример.
Пусть , . Тогда , .
Аналогичный пример можно привести для квадратных матриц любого порядка.
Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.
Следствие. Множество всех квадратных матриц n-го порядка над полем K является некоммутативным кольцом с единицей и с делителями нуля.
Доказательство. На множестве всех квадратных матриц n-го порядка над полем K определены две операции: сложение матриц и их умножение, которые подчиняются законам 1) – 4) и 9) – 11), откуда и следует, по определению, что является кольцом с единицей (см. лекцию 1, п.14 и п.15). Пример, приведенный перед формулировкой данного следствия, показывает, что кольцо имеет делители нуля.
Следствие доказано.
Определение. Натуральной степенью квадратной матрицы А называется матрица .
Нулевую степень квадратной матрицы А – го порядка по определению полагают равной единичной матрице того же порядка: .
Еще записи по теме
procmem.ru
Умножение матриц.
Навигация по странице:
Определение.
Результатом умножения матриц Am×n и Bn×k будет матрица Cm×k такая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (cij), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:cij = ai1 · b1j + ai2 · b2j + … + ain · bnj
Замечание.
Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.Свойства умножения матриц
- (A · B) · C= A · (B · C) – произведение матриц ассоциативно;
- (z · A) · B= z · (A · B), где z – число;
- A · (B + C) = A · B + A · C – произведение матриц дистрибутивно;
- En · Anm = Anm · Em= Anm – умножение на единичную матрицу;
- A · B ≠ B · A – в общем случае произведение матриц не коммутативно.
- Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.
Примеры задач на умножение матриц
Пример 1.
| Найти матрицу C равную произведению матриц A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 |
Решение:
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 – 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9
Пример 2
| Найти матрицу C равную произведению матриц A = |
|
и B = |
|
. |
Решение:
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 2·5 + 1·(-3) = 10 – 3 = 7
c12 = a11·b12 + a12·b22 = 2·(-1) + 1·0 = -2 + 0 = -2
c13 = a11·b13 + a12·b23 = 2·6 + 1·7 = 12 + 7 = 19
c21 = a21·b11 + a22·b21 = (-3)·5 + 0·(-3) = -15 + 0 = -15
c22 = a21·b12 + a22·b22 = (-3)·(-1) + 0·0 = 3 + 0 = 3
c23 = a21·b13 + a22·b23 = (-3)·6 + 0·7 = -18 + 0 = -18
c31 = a31·b11 + a32·b21 = 4·5 + (-1)·(-3) = 20 + 3 = 23
c32 = a31·b12 + a22·b22 = (4)·(-1) + (-1)·0 = -4 + 0 = -4
c33 = a31·b13 + a32·b23 = 4·6 + (-1)·7 = 24 – 7 = 17
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
0oq.ru
умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
Сложение матриц:
Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В cij = aij + bij Аналогично определяется разность матриц.
Умножение матрицы на число:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что
bij = k × aij. В = k × A bij = k × aij. Матрица – А = (-1) × А называется противоположной матрице А.
Свойства сложения матриц и умножения матрицы на число:
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А – А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С – матрицы, α и β – числа.
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что сik = ai1 × b1k + ai2 × b2k + … + ain × bnk, т. е. находиться сумма произведений элементов i – ой строки матрицы А на соответствующие элементы j – ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е – единичная матрица того же размера.

Свойства умножения матриц:
Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А
Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ)Т = ВТАТ; 7. (АВС)Т = СТВТАТ; 8. (А + В)Т = АТ + ВТ;

2. Определители 2-го и 3-го порядков. Свойства определителей.
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6
Свойства определителей матриц
Свойства определителей матриц:
Свойство № 1:
Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т
Следствие:
Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.
Свойство № 2:
При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:
Свойство № 3:
Определитель матрицы, имеющий два одинаковых ряда, равен нулю.
Свойство № 4:
Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.
Следствия из свойств № 3 и № 4:
Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5:
Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.
Свойство № 6:
Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:
Свойство № 7:
Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.
Пример применения свойств для вычисления определителя матрицы:
studfiles.net
Умножение квадратной матрицы на матрицу-столбец — Мегаобучалка
Пример решения системы методом Гаусса
Пусть требуется решить систему трех уравнений с тремя неизвестными:
| (1.1) |
Будем последовательно “исключать” неизвестные. Для этого первое уравнение системы оставим без изменений, а второе и третье преобразуем:
1) ко второму уравнению прибавим первое, умноженное на –2, и приведем его к виду –3x2 –2x3 = –2;
2) к третьему уравнению прибавим первое, умноженное на – 4, и приведем его к виду –3x2 – 4x3 = 2.
В результате из второго и третьего уравнений будет исключено неизвестное x1 и система примет вид
Второе и третье уравнения системы умножим на –1, получим
Коэффициент 1 в первом уравнении при первом неизвестном х1называется ведущим элементом первого шага исключения.
На втором шаге первое и второе уравнения остаются без изменений, а к третьему уравнению применим тот же способ исключения переменной x2. Ведущим элементом второго шага является коэффициент 3. К третьему уравнению прибавим второе, умноженное на –1, тогда система преобразуется к виду
| (1.2) |
Процесс приведения системы (1.1) к виду (1.2) называются прямым ходом метода Гаусса.
Порядок действий решения системы (1.2) называется обратным ходом. Из последнего уравнения получим х3= –2. Подставляя это значение во второе уравнение, получим х2 = 2. После этого первое уравнение дает х1 = 1. Таким образом, – решение системы (1.1).
Понятие матрицы
Рассмотрим величины, входящие в систему (1.1). Набор из девяти числовых коэффициентов, стоящих в уравнениях перед неизвестными, образует таблицу чисел, которая называется матрицей:
| А = . | (1.3) |
Числа таблицы называются элементами матрицы. Элементы образуют строки и столбцы матрицы. Количество строк и количество столбцов образуют размерность матрицы. Матрица А имеет размерность 3´3 (“три на три”), причем первое число указывает количество строк, а второе – столбцов. Часто матрицу обозначают, указывая ее размерность А(3´3). Так как число строк и столбцов в матрице А одинаково, матрица называется квадратной. Количество строк (и столбцов) в квадратной матрице называется ее порядком, поэтому А – матрица третьего порядка.
Правые части уравнений, также образуют таблицу чисел, т.е. матрицу:
| B(3´1)= . | (1.4) |
Каждая строка этой матрицы образована единственным элементом, поэтому B(3´1)называется матрицей–столбцом, ее размерность 3´1. Набор неизвестных также можно представить как матрицу-столбец:
| Х(3´1)= . | (1.5) |
Умножение квадратной матрицы на матрицу-столбец
С матрицами можно производить различные операции, которые будут подробно рассмотрены в дальнейшем. Здесь же разберем только правило умножения квадратной матрицы на матрицу-столбец. По определению, результатом умножения матрицы А(3´3) на столбец В(3´1) является столбец D(3´1), элементы которого равны суммам произведений элементов строк матрицы А на элементы столбца В:
| (1.6) |
Таким образом, по определению:
1) первый элемент столбца D равен сумме произведений элементов первой строки матрицы А на элементы столбца В:
2)второй элемент столбца D равен сумме произведений элементов второй строки матрицы А на элементы столбца В:
3) третий элемент столбца D равен сумме произведений элементов третьей строки матрицы А на элементы столбца В:
Из приведенных формул видно, что умножить матрицу на столбец В можно только в случае, если число столбцов матрицы А равно числу элементов в столбце В.
Рассмотрим еще два числовых примера умножения матрицы (3´3) на столбец (3´1):
Пример 1.1
АВ = .
Пример 1.2
АВ = .
megaobuchalka.ru

 =
= 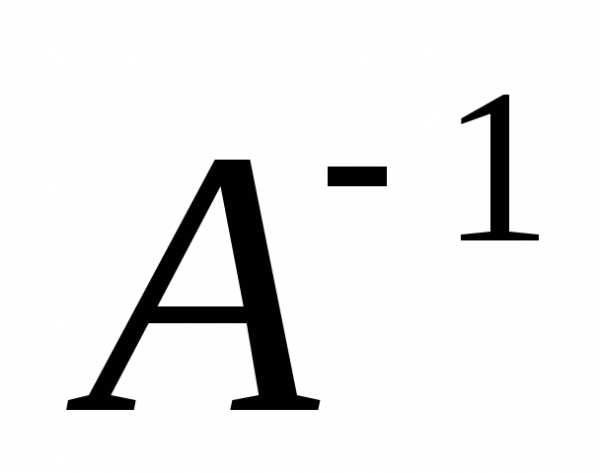 =
= 