Как перемножить матрицы в Excel

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
=МУМНОЖ(массив1;массив2)
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.

- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
- Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
- Будет выполнен запуск окна аргументов требуемой функции. В этом окне имеется два поля для ввода адресов матричных массивов. Ставим курсор в поле «Массив1» и, зажав левую кнопку мыши, выделяем на листе всю область первой матрицы. После этого её координаты отобразятся в поле. Ставим курсор в поле «Массив2» и аналогичным образом выделяем диапазон второй матрицы.
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки
- Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.



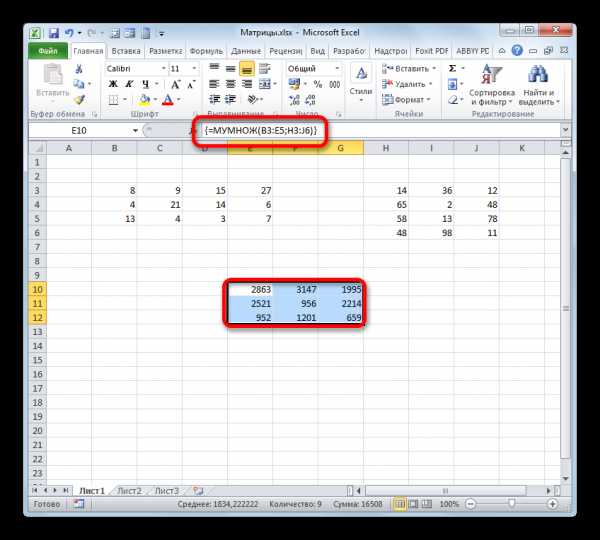
Урок: Функция МУМНОЖ в Экселе
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
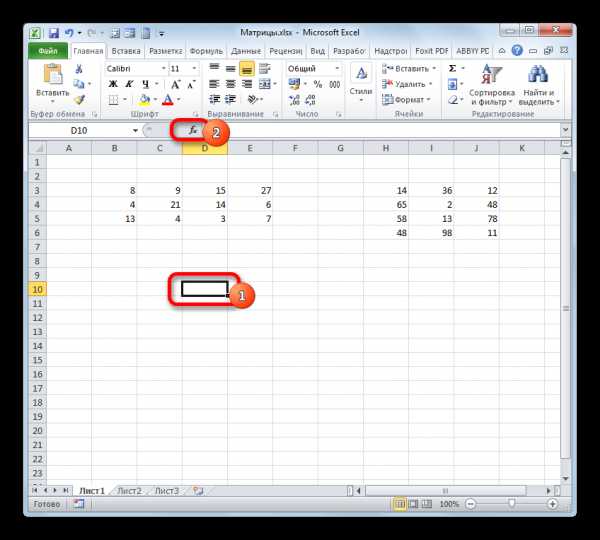
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
- Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
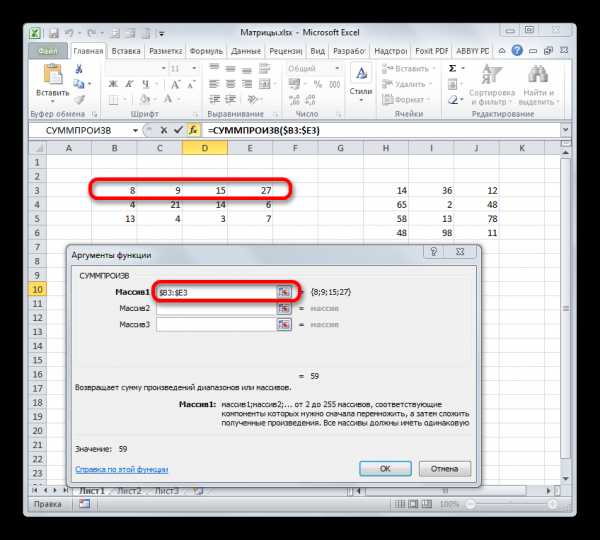
- Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
=СУММПРОИЗВ(массив1;массив2;…)В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу
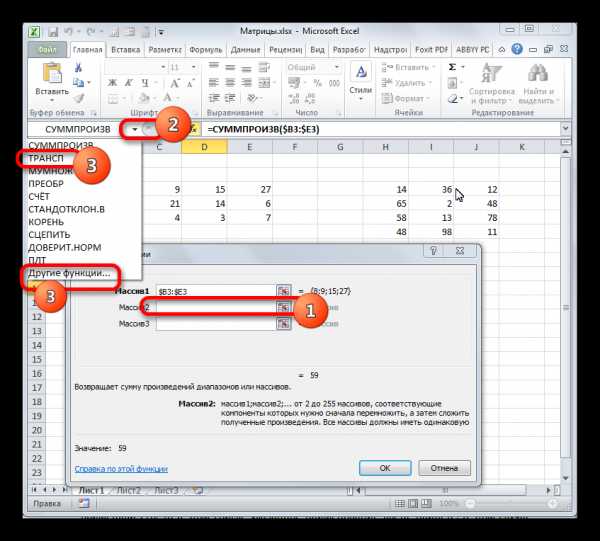
- После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту
- Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
- Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора
=ТРАНСП(массив)То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише
- Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
- Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
- Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора






Урок: Работа с массивами в Экселе
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Умножение матриц в MS EXCEL. Примеры и методы
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q – это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ(), которую нужно вводить как формулу массива.
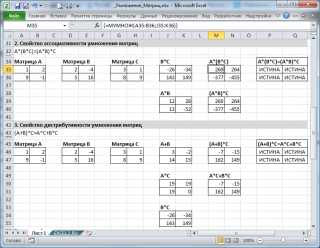
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9.
Для этого:
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2)
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо больший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся – только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2, исправьте формулу и нажмите CTRL+SHIFT+ENTER.
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)). Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER. Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
excel2.ru
Как на EXCEL вычислить произведение двух матриц
9 июня 2013 Автор: БакытжанУмножение матриц — операция не из легких. Часто бывает так, что эту операцию по книжке, чисто теоретически, без помощи преподавателя, изучить почти невозможно. И вот на помощь приходит EXCEL.
Допустим, надо умножить две матрицы A и B, где

Перед тем, как начинать выполнение операции умножения матриц, нужно обязательно учесть два важных правила:
- 1. Две матрицы можно умножить, если число столбцов первой матрицы равно числу строк второй матрицы.
- 2. В результате получится матрица, у которой строк сколько у первой матрицы и столбцов сколько у второй матрицы.
У нас первое правило выполняется (у матрицы А – три столбца, а у матрицы В — три строки ). В результате получится матрица с двумя строчками и двумя столбцами. Запомним это.
Открываем документ EXCEL. Запишем элементы матриц, разделяя их для определенности и отметим ячейку с которой начнем записывать ответ. С этой ячейки мы должны смочь отложить две строки и два столбца (не забыли еще, зачем это нам?).

Теперь нажимаем Формулы, затем Математические и в ниспадающем окне находим МУМНОЖ

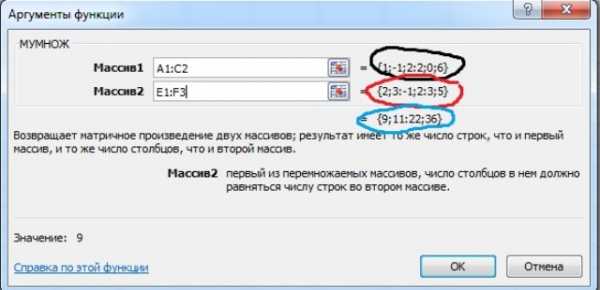
Появляется такое окно, в нем заносим адреса ячеек элементов первой матрицы в Массив1 (обведено красным), а в Массив2 — адреса ячеек элементов второй матрицы (обвел черным)
Если все сделали правильно, то автоматически появятся списком элементы матриц (обведено черным и красным) и покажется ответ (обвел синим)
Чтобы получить ответ в привычном матричном виде нужно нажать OK. Начиная с ячейки, которую мы изначально отметили, выделяем две строки и два столбца (помните?)
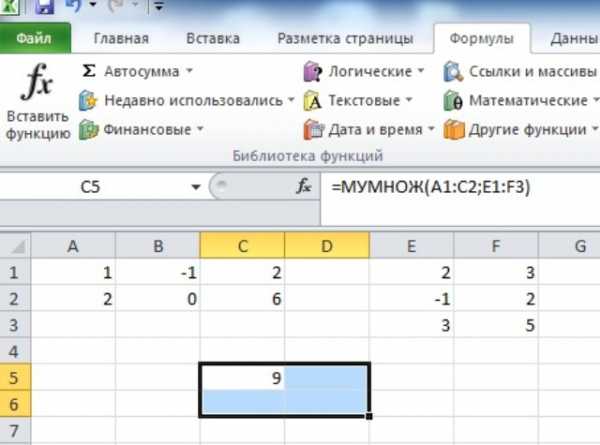
Теперь нажимаем клавишу F2, а затем три клавиши одновременно Ctrl+Shift+Enter (+ означает одновременное нажатие)

Все, матрицы перемножили. Окончательно это можно записать в виде
Теперь точно все. Отличных Вам результатов!
Рубрика: EXCEL в помощь, Статьи.Метки: EXCEL, ИКТ, матрицы
Навигация по записям
Предыдущий пост: ← Автора!Следующий пост: Прогрессияларды қолдану →
ourmath.ru
Умножение матриц
Определение произведения матриц. Пусть даны матрицы [cbm]A=(a_{ij})[/cbm] размеров [cbm]m\times p[/cbm] и [cbm]B=(b_{ij})[/cbm] размеров [cbm]p\times n[/cbm] . Матрицу [cbm]C[/cbm] размеров [cbm]m\times n[/cbm] , элементы [cbm]c_{ij}[/cbm] , которой вычисляются по формуле
[cbm]c_{ij}=a_{i1}\cdot b_{1j}+a_{i2}\cdot b_{2j}+\ldots+a_{ip}\cdot b_{pj},\quad i=1,\ldots,m;~j=1,\ldots,m;[/cbm]
называют произведением матриц [cbm]A[/cbm] и [cbm]B[/cbm] и обозначают [cbm]C=AB[/cbm] . Операция
умножения матрицы [cbm]A[/cbm] на матрицу [cbm]B[/cbm] определена только для согласованных матриц, у которых число столбцов матрицы [cbm]A[/cbm] равно числу строк матрицы [cbm]B:[/cbm]
[cbm]\underbrace{C}_{m\times n}= \underbrace{A}_{m\times p}\cdot \underbrace{B}_{p\times n}.[/cbm]
Рассмотрим подробнее процедуру нахождения произведения матриц. Чтобы получить элемент [cbm]c_{ij}[/cbm] , стоящий на пересечении i-й строки и j-го столбца матрицы [cbm]C[/cbm] , следует выделить i-ю строку матрицы [cbm]A[/cbm] и j-й столбец матрицы [cbm]B[/cbm] (рис. 1.3). Они содержат одинаковое число элементов, так как матрицы [cbm]A[/cbm] и [cbm]B[/cbm] согласованы. Затем найти сумму попарных произведений соответствующих элементов: первый элемент i-й строки умножается на первый элемент j-го столбца, второй элемент i-й строки умножается на второй элемент j-го столбца и т.д., а результаты перемножений складываются.

В произведения [cbm]A\cdot B[/cbm] матрицу [cbm]A[/cbm] называют левым множителем для [cbm]B[/cbm] и говорят об умножении матрицы [cbm]B[/cbm] на матрицу [cbm]A[/cbm] слева. Аналогично матрицу [cbm]B[/cbm] называют правым множителем для [cbm]A[/cbm] и говорят об умножении матрицы [cbm]A[/cbm] на матрицу [cbm]B[/cbm] справа.
Пример 1.6. Даны матрицы [cbm]A= \begin{pmatrix}1&2&1\\0&1&2\end{pmatrix}\!,~B= \begin{pmatrix}1&0\\0&1\\1&1\end{pmatrix}[/cbm] . Вычислить произведения [cbm]AB[/cbm] и [cbm]BA[/cbm]
.Решение. Используя правило умножения матриц, получаем
[cbm]\begin{aligned} \underbrace{A}_{2\times3}\cdot \underbrace{B}_{3\times2}&= \begin{pmatrix}1&2&1\\0&1&2\end{pmatrix}\!\cdot\! \begin{pmatrix}1&0\\0&1\\1&1\end{pmatrix}= \begin{pmatrix}1\cdot1+2\cdot0+1\cdot1&1\cdot0+2\cdot1+1\cdot1\\0\cdot1+1\cdot0+2\cdot1&0\cdot0+1\cdot1+2\cdot1\end{pmatrix}= \underbrace{\begin{pmatrix}2&3\\2&3\end{pmatrix}}_{2\cdot2}.\\[5pt] \underbrace{B}_{3\times2}\cdot \underbrace{A}_{2\times3}&= \begin{pmatrix}1&0\\0&1\\1&1\end{pmatrix}\!\cdot\! \begin{pmatrix} 1&2&1\\0&1&2\end{pmatrix}= \begin{pmatrix}1\cdot1+0\cdot0& 1\cdot2+0\cdot1& 1\cdot1+0\cdot2\\ 0\cdot1+1\cdot0& 0\cdot2+1\cdot1& 0\cdot1+1\cdot2\\ 1\cdot1+1\cdot0& 1\cdot2+1\cdot1& 1\cdot1+1\cdot2 \end{pmatrix}= \underbrace{\begin{pmatrix} 1&2&1\\ 0&1&2\\ 1&3&3 \end{pmatrix}}_{3\times3}. \end{aligned}[/cbm]
Оба произведения [cbm]A\cdot B[/cbm] и [cbm]B\cdot A[/cbm] определены, но являются матрицами разных размеров, т.е. [cbm]AB\ne BA[/cbm] .
Пример 1.7. Даны матрицы [cbm]A= \begin{pmatrix}1&2&1\\0&1&2\end{pmatrix}\!,~x= \begin{pmatrix} x_1\\x_2\\x_3\end{pmatrix}\!,~b= \begin{pmatrix}1&2&3\end{pmatrix}[/cbm] . Найти произведения [cbm]A\cdot x,~b\cdot x,~x\cdot b[/cbm] .
Решение. Используя правило умножения, получаем
[cbm]\begin{aligned} \underbrace{A}_{2\times3}\cdot\underbrace{x}_{3\times1}&= \begin{pmatrix}1&2&1\\0&1&2\end{pmatrix}\!\cdot\! \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}= \begin{pmatrix}1\cdot x_1+2\cdot x_2+1\cdot x_3\\0\cdot x_1+1\cdot x_2+2\cdot x_3\end{pmatrix}= \underbrace{\begin{pmatrix}x_1+2x_2+x_3\\x_2+2x_3\end{pmatrix}}_{2\times1}.\\[5pt] \underbrace{b}_{1\times3}\cdot\underbrace{x}_{3\times1}&= \begin{pmatrix}1&2&3\end{pmatrix}\!\cdot\! \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}= \underbrace{\begin{pmatrix}1\cdot x_1+2\cdot x_2+3\cdot x_3\end{pmatrix}}_{1\times1}= x_1+2x_2+3x_3;\\[5pt] \underbrace{x}_{3\times1}\cdot\underbrace{b}_{1\times3}&= \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}\!\cdot\! \begin{pmatrix}1&2&2\end{pmatrix}= \underbrace{\begin{pmatrix}x_1&2x_1&3x_1\\x_2&2x_2&3x_2\\x_3&2x_3&3x_3\end{pmatrix}}_{3\times3}. \end{aligned}[/cbm]
Пример 1.8. Даны матрицы [cbm]A=\begin{pmatrix}1&2\\3&4\end{pmatrix}\!,~ B=\begin{pmatrix}0&0\\1&1\end{pmatrix}\!,~ E=\begin{pmatrix}1&0\\0&1\end{pmatrix}\!,~ O=\begin{pmatrix}0&0\\0&0\end{pmatrix}\!.[/cbm]
Вычислить произведения [cbm]AB,~BA,~AE,~EA,~BO,~OB[/cbm] .
Решение. Все матрицы квадратные второго порядка. Следовательно, все произведения будут квадратными матрицами того же порядка. Используя правило умножения, получаем
[cbm]\begin{aligned} A\cdot B&= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}0&0\\1&1\end{pmatrix}=\begin{pmatrix}1\cdot0+2\cdot1&1\cdot0+2\cdot1\\3\cdot0+4\cdot1&3\cdot0+4\cdot1\end{pmatrix}= \begin{pmatrix}2&2\\4&4\end{pmatrix}\!;\\[3pt] B\cdot A&= \begin{pmatrix}0&0\\1&1\end{pmatrix}\!\cdot\! \begin{pmatrix}1&2\\3&4\end{pmatrix}=\begin{pmatrix}0\cdot1+0\cdot3&0\cdot2+0\cdot4\\1\cdot1+1\cdot3&1\cdot2+1\cdot4\end{pmatrix}= \begin{pmatrix}0&0\\4&6\end{pmatrix}\!;\\[3pt] A\cdot E&= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}1&0\\0&1\end{pmatrix}=\begin{pmatrix}1\cdot1+2\cdot0&1\cdot0+2\cdot1\\3\cdot1+4\cdot0&3\cdot0+4\cdot1\end{pmatrix}= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!;\\[3pt] E\cdot A&= \begin{pmatrix}1&0\\0&1\end{pmatrix}\!\cdot\! \begin{pmatrix}1&2\\3&4\end{pmatrix}= \begin{pmatrix}1\cdot1+0\cdot3&1\cdot2+0\cdot4\\0\cdot1+1\cdot3&0\cdot2+1\cdot4\end{pmatrix}= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!;\\[3pt] B\cdot O&= \begin{pmatrix}0&0\\1&1\end{pmatrix}\!\cdot\! \begin{pmatrix}0&0\\0&0\end{pmatrix}= \begin{pmatrix}0&0\\0&0\end{pmatrix}\!;\\[3pt] O\cdot B&= \begin{pmatrix}0&0\\0&0\end{pmatrix}\!\cdot\! \begin{pmatrix}0&0\\1&1\end{pmatrix}= \begin{pmatrix}0&0\\0&0\end{pmatrix}\!.\end{aligned}[/cbm]
Замечание 1.2. Непосредственным вычислением можно доказать основное свойство единичной матрицы:
[cbm]A\cdot E_n=E_m\cdot A[/cbm] для любой матрицы [cbm]A[/cbm] размеров [cbm]m\times n[/cbm] .
Пример 1.9. Найти произведения
[cbm]\begin{array}{ll}\mathsf{1)}~A=\begin{pmatrix}1&2&3\end{pmatrix}\!,~B=\begin{pmatrix}4\\5\\6\end{pmatrix}\!;&\qquad \mathsf{2)}~\begin{pmatrix}1&2\\3&1\end{pmatrix}\!,~ B=\begin{pmatrix}-1&3\\1&1\end{pmatrix}\!;\\\\[-7pt] \mathsf{3)}~A=\begin{pmatrix}6&1\\2&1\end{pmatrix}\!,~B=\begin{pmatrix}-4&-1\\-2&1\end{pmatrix}\!;&\qquad \mathsf{4)}~\begin{pmatrix}3&2&1\\0&1&2\end{pmatrix}\!,~ B=\begin{pmatrix}1&3\end{pmatrix}\!.\end{array}[/cbm]
Решение. 1) Произведением [cbm]A\cdot B[/cbm] является число:
[cbm]A\cdot B=\underbrace{\begin{pmatrix}1&2&3\end{pmatrix}}_{1\cdot3}\!\cdot\! \underbrace{\begin{pmatrix}4\\5\\6\end{pmatrix}}_{3\times1}= \begin{pmatrix}1\cdot4+2\cdot5+3\cdot6\end{pmatrix}= \underbrace{\begin{pmatrix}32\end{pmatrix}}_{1\times1}=32,[/cbm]
а произведением [cbm]B\cdot A[/cbm] — квадратная матрица третьего порядка:
[cbm]B\cdot A= \underbrace{\begin{pmatrix} 4\\5\\6\end{pmatrix}}_{3\cdot1}\!\cdot\! \underbrace{\begin{pmatrix}1&2&3\end{pmatrix}}_{1\times3}= \underbrace{\begin{pmatrix}4\cdot1&4\cdot2&4\cdot3\\ 5\cdot1&5\cdot2&5\cdot3\\6\cdot1&6\cdot2&6\cdot3\end{pmatrix}}_{3\times3}= \begin{pmatrix}4&8&12\\5&10&15\\6&12&18\end{pmatrix}\!.[/cbm]
Очевидно, что [cbm]A\cdot B\ne B\cdot A[/cbm] .
2)
[cbm]\begin{aligned}A\cdot B&= \underbrace{\begin{pmatrix}1&2\\3&1\end{pmatrix}}_{2\times2}\cdot\underbrace{\begin{pmatrix}-1&3\\1&1\end{pmatrix}}_{2\times2}= \underbrace{\begin{pmatrix}1\cdot(-1)+2\cdot1&1\cdot3+2\cdot1\\ 3\cdot(-1)+1\cdot1&3\cdot3+1\cdot1\end{pmatrix}}_{2\times2}= \begin{pmatrix}1&5\\-1&10\end{pmatrix}\!;\\[5pt] B\cdot A&= \underbrace{\begin{pmatrix}-1&3\\1&1\end{pmatrix}}_{2\times2}\cdot\underbrace{\begin{pmatrix}1&2\\3&1\end{pmatrix}}_{2\times2}= \underbrace{\begin{pmatrix}(-1)\cdot1+3\cdot3&(-1)\cdot2+3\cdot1\\ 1\cdot1+1\cdot3&1\cdot2+1\cdot1\end{pmatrix}}_{2\times2}= \begin{pmatrix}8&1\\4&3\end{pmatrix}\!. \end{aligned}[/cbm]
Оба произведения — это квадратные матрицы одного и того же порядка, но [cbm]A\cdot B\ne B\cdot A[/cbm] .
3)
[cbm]\begin{aligned}A\cdot B&= \underbrace{\begin{pmatrix} 6&1\\2&1\end{pmatrix}}_{2\times2}\cdot \underbrace{\begin{pmatrix}-4&-1\\-2&1\end{pmatrix}}_{2\times2}= \underbrace{\begin{pmatrix}6\cdot(-4)+1\cdot(-2)&6\cdot(-1)+1\cdot1\\ 2\cdot(-4)+1\cdot(-2)&2\cdot(-1)+1\cdot1 \end{pmatrix}}_{2\times2}= \begin{pmatrix}-26&-5\\-10&-1\end{pmatrix}\!;\\[5pt] B\cdot A&= \underbrace{\begin{pmatrix}-4&-1\\-2&1\end{pmatrix}}_{2\times2}\cdot \underbrace{\begin{pmatrix}6&1\\2&1\end{pmatrix}}_{2\times2}= \underbrace{\begin{pmatrix}(-4)\cdot6+(-1)\cdot2&(-4)\cdot1+(-1)\cdot1\\ (-2)\cdot6+1\cdot2&(-2)\cdot1+1\cdot1 \end{pmatrix}}_{2\times2}= \begin{pmatrix}-26&-5\\-10&-1\end{pmatrix}\!. \end{aligned}[/cbm]
Результаты умножения совпадают, т.е. [cbm]A\cdot B=B\cdot A[/cbm] .
4) произведение [cbm]A\cdot B[/cbm] не может быть найдено, так как число столбцов матрицы [cbm]A[/cbm] (три) не равно числу строк матрицы [cbm]B[/cbm] (одна). При этом говорят, что нельзя умножить матрицу [cbm]A[/cbm] на матрицу [cbm]B[/cbm] справа. В то же время можно умножить матрицу [cbm]A[/cbm] на матрицу [cbm]B[/cbm] слева:
[cbm]B\cdot A=\underbrace{\begin{pmatrix}1&3\end{pmatrix}}_{1\times3}\cdot \underbrace{\begin{pmatrix}3&2&1\\0&1&2\end{pmatrix}}_{2\times3}= \underbrace{\begin{pmatrix}1\cdot3+3\cdot0&1\cdot2+2\cdot1&1\cdot1+3\cdot2\end{pmatrix}}_{1\times3}= \begin{pmatrix}3&5&7\end{pmatrix}\!.[/cbm]
Свойства умножения матриц
Пусть [cbm]\lambda[/cbm] — любое число, [cbm]A,B,C[/cbm] — произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:
1. [cbm](AB)C=A(BC)[/cbm] ; (ассоциативность умножения матриц)
2. [cbm]A(B+C)=AB+AC[/cbm] ; (дистрибутивность умножения)
3. [cbm](A+B)C=AC+BC[/cbm] ; (дистрибутивность умножения)
4. [cbm]\lambda (AB)=(\lambda A)B[/cbm] .
Пример 1.10. Продемонстрировать справедливость свойств 1, 2, если
[cbm]A=\begin{pmatrix}1&2\\3&4\end{pmatrix}\!,\quad B=\begin{pmatrix}5&6\\7&8\end{pmatrix}\!,\quad C=\begin{pmatrix}1&0\\0&2\end{pmatrix}\!.[/cbm]
Решение. Проверим свойство 1: [cbm](AB)C=A(BC)[/cbm] .
[cbm]\begin{aligned}(A\cdot B)\cdot A&= \left[\begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}5&6\\7&8\end{pmatrix}\right]\!\cdot\! \begin{pmatrix}\1&0\\0&2\end{pmatrix}= \begin{pmatrix}19&22\\43&50\end{pmatrix}\!\cdot\! \begin{pmatrix}1&0\\0&2\end{pmatrix}= \begin{pmatrix}19&44\\43&100\end{pmatrix}\!,\\[3pt] A\cdot(B\cdot C)&= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \left[\begin{pmatrix}5&6\\7&8\end{pmatrix}\!\cdot\! \begin{pmatrix}1&0\\0&2\end{pmatrix}\right]= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}5&12\\7&16\end{pmatrix}= \begin{pmatrix}19&44\\43&100\end{pmatrix}\!.\end{aligned}[/cbm]
Проверим свойство 2: [cbm]A(B+C)=AB+AC[/cbm] .
[cbm]\begin{aligned}A\cdot(B+C)&= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \left[\begin{pmatrix}5&6\\7&8\end{pmatrix}+\begin{pmatrix}1&0\\0&2\end{pmatrix}\right]= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}6&6\\7&10\end{pmatrix}= \begin{pmatrix}20&26\\46&58\end{pmatrix}\!,\\[3pt] AB+AC&= \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}5&6\\7&8\end{pmatrix}+ \begin{pmatrix}1&2\\3&4\end{pmatrix}\!\cdot\! \begin{pmatrix}1&0\\0&2\end{pmatrix}= \begin{pmatrix}19&22\\43&50\end{pmatrix}+ \begin{pmatrix}1&4\\3&8\end{pmatrix}= \begin{pmatrix}20&26\\46&58\end{pmatrix}\!.\end{aligned}[/cbm]
Замечания 1.3
1. В общем случае умножение матриц не является коммутативным. Произведение зависит от перестановки множителей, т.е [cbm]A\cdot B\neB\cdot A[/cbm] . Во-первых, размеры матриц [cbm]A[/cbm] и [cbm]B[/cbm] могут быть такими, что произведение [cbm]AB[/cbm] определено, а произведение [cbm]BA[/cbm] — не существует и наоборот (в примере 1.7 найдено произведение [cbm]Ax[/cbm] , а произведение [cbm]xA[/cbm] не определено; в примере 1.9, г найдено произведение [cbm]BA[/cbm] , а произведение [cbm]AB[/cbm] не определено). Во-вторых, если оба произведения [cbm]AB[/cbm] и [cbm]BA[/cbm] определены, результаты могут оказаться матрицами разных размеров (см. пример 1.6 и 1.9, а). Если матрицы [cbm]A[/cbm] и [cbm]B[/cbm] квадратные одного порядка, то произведения [cbm]AB[/cbm] и [cbm]BA[/cbm] будут также квадратными матрицами того же порядка. Даже при этих условиях умножение матриц не коммутативно (см. пример 1.8 и 1.9,6, где [cbm]AB\ne BA[/cbm] ). С другой стороны, в примере 1.8 [cbm]AE=EA=A[/cbm] и [cbm]BO=OB=O[/cbm] , а в примере 1.9, в [cbm]AB=BA[/cbm] , т.е. существуют квадратные матрицы, произведение которых не зависит от перестановки множителей.
Матрицы [cbm]A[/cbm] и [cbm]B[/cbm] называются перестановочными, если [cbm]A\cdot B=B\cdot A[/cbm] . Перестановочными могут быть только квадратные матрицы одного и того же порядка. В частности, например, можно показать, что диагональные матрицы одного и того же порядка перестановочны.
2. Для любой квадратной матрицы [cbm]A[/cbm] порядка [cbm]n[/cbm] справедливы следующие равенства
[cbm]A\cdot E=E\cdot A=A[/cbm] , где [cbm]E[/cbm] — единичная матрица порядка [cbm]n[/cbm] .
Другими словами, единичная матрица перестановочна с любой квадратной матрицей того же порядка.
3. Для любой матрицы [cbm]A[/cbm] справедливы равенства
[cbm]A\cdot O=O[/cbm] и [cbm]O\cdot A=O[/cbm] , где [cbm]O[/cbm] — нулевые матрицы соответствующих порядков,
т.е. нулевая квадратная матрица перестановочна с любой квадратной матрицей того же порядка.
4. Множество квадратных матриц одного и того же порядка [cbm]n>1[/cbm] с операциями сложения матриц и умножения матриц на число представляет собой некоммутативное кольцо с единицей. Кольцо не является коммутативным, так как операция умножения квадратных матриц порядка [cbm]n>1[/cbm] не коммутативна. Единичным элементом кольца служит единичная матрица.
5. Заметим, что сумма и произведение диагональных (верхних треугольных, нижних треугольных) матриц одного и того же порядка являются диагональными (верхними треугольными, нижними треугольными) матрицами. Следовательно, операции сложения и умножения матриц определены на множествах диагональных (верхних треугольных, нижних треугольных) матриц одного и того же порядка. Поэтому каждое из указанных множеств является кольцом с единицей, причем кольцо диагональных матриц коммутативное.
Пример 1.11. Найти матрицы, перестановочные с матрицей [cbm]A=\begin{pmatrix}1&1\\0&1\end{pmatrix}[/cbm] .
Решение. Для выполнения равенства [cbm]AB=BA[/cbm] искомая матрица [cbm]B[/cbm] должна быть квадратной второго порядка. Пусть она имеет вид [cbm]B=\begin{pmatrix}x&y\\z&w\end{pmatrix}[/cbm] и удовлетворяет равенству
[cbm]\begin{pmatrix}1&1\\0&1\end{pmatrix}\!\cdot\! \begin{pmatrix}x&y\\z&w\end{pmatrix} =\begin{pmatrix}x&y\\z&w\end{pmatrix}\!\cdot\! \begin{pmatrix}1&1\\0&1\end{pmatrix}\!.[/cbm]
После умножения получаем в левой и правой частях равенства квадратные матрицы второго порядка:
[cbm]\begin{pmatrix}x+z&y+w\\z&w\end{pmatrix}= \begin{pmatrix}x&x+y\\z&z+w\end{pmatrix}\!.[/cbm]
Записывая равенство соответствующих элементов этих матриц, получаем систему уравнений
[cbm]\begin{cases}x+z=x,\\z=z,\\y+w=x+y,\\w=z+w.\end{cases}[/cbm]
Из первого уравнения следует, что [cbm]z=0[/cbm] , а из третьего: [cbm]x=w[/cbm] . Следовательно, искомые матрицы имеют вид [cbm]B=\begin{pmatrix}x&y\\0&x\end{pmatrix}[/cbm] , где [cbm]x,y[/cbm] — параметры, принимающие любые действительные значения.
Умножение матриц на столбцы и строки единичной матрицы
Рассмотрим два типа преобразований квадратной матрицы [cbm]A[/cbm] [cbm]n[/cbm] -го порядка при помощи умножения на строки и столбцы единичной матрицы.
Обозначим j-й столбец и i-ю строку единичной матрицы n-го порядка через [cbm]e_j[/cbm] и [cbm]e_i^T[/cbm] соответственно:
[cbm]e_j= \begin{pmatrix}0\\\vdots\\0\\1\\0\\\vdots\\0\end{pmatrix}\!_{j},\quad e_i^T= \mathop{\begin{pmatrix}0&\cdots&0&1&0&\cdots&0\end{pmatrix}}\limits_{i}= E_n=\mathop{\begin{pmatrix}1&0&\cdots&0\\0&1&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&1\end{pmatrix}}\limits_{\begin{matrix}e_1&e_2&\cdots&e_n\end{matrix}}.[/cbm]
1. Найдем произведения
[cbm]\begin{gathered}Ae_j= \begin{pmatrix}a_{11}&\cdots&a_{1j}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nj}&\cdots&a_{nn}\end{pmatrix}\!\! \begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix}=\begin{pmatrix}a_{1j}\\\vdots\\a_{ij}\\\vdots\\a_{nj}\end{pmatrix};\\ e_i^T\,A= \begin{pmatrix}0&\cdots&1&\cdots&0\end{pmatrix}\!\! \begin{pmatrix}a_{11}&\cdots&a_{1j}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nj}&\cdots&a_{nn}\end{pmatrix}=\begin{pmatrix}a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\end{pmatrix}\!. \end{gathered}[/cbm]
Как видим, в результате умножения матрицы [cbm]A[/cbm] справа на столбец [cbm]e_j[/cbm] выделяется j-й столбец матрицы [cbm]A[/cbm] , а при умножении слева на строку [cbm]e_i^T[/cbm] получаем i-ю строку матрицы [cbm]A[/cbm] . Элемент [cbm]a_{ij}[/cbm] матрицы [cbm]A[/cbm] может быть получен как произведение
[cbm]e_i^T\,A\,e_j= \begin{pmatrix}0&\cdots&1&\cdots&0\end{pmatrix}\!\! \begin{pmatrix}a_{11}&\cdots&a_{1j}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nj}&\cdots&a_{nn}\end{pmatrix}\!\! \begin{pmatrix}0\\\vdots\\1\\\vdots\\0\end{pmatrix}= a_{ij}.[/cbm]
Пример 1.12. Даны матрицы
[cbm]A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix},~ e_1^T=\begin{pmatrix}1&0&0\end{pmatrix}\!,~e_2=\begin{pmatrix}0\\1\\0\end{pmatrix}\!.[/cbm] Вычислить [cbm]Ae_2,~e_1^TA,~e_1^TAe_2[/cbm]
Решение. Перемножая матрицы, получаем:
[cbm]\begin{gathered}Ae_2= \begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\!\! \begin{pmatrix}0\\1\\0\end{pmatrix}= \begin{pmatrix}2\\5\\8\end{pmatrix}\!;\quad e_1^TA= \begin{pmatrix}1&0&0\end{pmatrix}\!\! \begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}= \begin{pmatrix}1&2&3\end{pmatrix}\!;\\[3pt] e_1^TAe_2= \begin{pmatrix}1&0&0\end{pmatrix}\!\! \begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\!\! \begin{pmatrix}0\\1\\0\end{pmatrix}= \begin{pmatrix}1&2&3\end{pmatrix}\!\! \begin{pmatrix}0&1&0\end{pmatrix}=2. \end{gathered}[/cbm]
В результате умножений из данной матрицы [cbm]A[/cbm] выделены 2-й столбец, первая строка, элемент [cbm]a_{12}=2[/cbm] .
2. Умножая справа матрицу [cbm]A[/cbm] сначала на столбец [cbm]a_j[/cbm] , а затем на строку [cbm]e_j^T[/cbm] получаем квадратную матрицу n-го порядка, в которой все элементы равны нулю, за исключением элементов j-го столбца, который совпадает с j-м столбцом матрицы [cbm]A:[/cbm]
[cbm]Ae_je_j^T= \begin{pmatrix}a_{1j}\\\vdots\\a_{ij}\\\vdots\\a_{nj}\end{pmatrix}\!\! \begin{pmatrix}0&\cdots&1&\cdots&0\end{pmatrix}= \begin{pmatrix}0&\cdots&a_{1j}&\cdots&0\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ 0&\cdots&a_{ij}&\cdots&0\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ 0&\cdots&a_{nj}&\cdots&0 \end{pmatrix}\!.[/cbm]
При помощи умножения на строки [cbm]e_j^T[/cbm] и столбцы [cbm]e_j[/cbm] можно, например, заменить j-й столбец матрицы [cbm]A[/cbm] i-м столбцом матрицы [cbm]B[/cbm] (квадратной n-го порядка):
[cbm]A-A\cdot e_j\cdot e_j^T+B\cdot e_i\cdot e_j^T.[/cbm]
Пример 1.13. Даны матрицы, вычислить [cbm]Ae_2e_2^T,~Be_1e_2^T,~A-Ae_2e_2^T+Be_1e_2^T[/cbm] .
[cbm]A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\!,\quad B=\begin{pmatrix}9&8&7\\6&5&4\\3&2&1\end{pmatrix}\!,\quad e_1=\begin{pmatrix}1\\0\\0\end{pmatrix}\!,\quad e_2=\begin{pmatrix}0\\1\\0\end{pmatrix}\!,\quad e_2^T=\begin{pmatrix}0&1&0\end{pmatrix}\!.[/cbm]
Решение. Выполняя действия, получаем:
[cbm]\begin{aligned}Ae_2e_2^T&= \begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\!\! \begin{pmatrix}0\\1\\0\end{pmatrix}\!\! \begin{pmatrix}0&1&0\end{pmatrix}= \begin{pmatrix}2\\5\\8\end{pmatrix}\!\! \begin{pmatrix}0&1&0\end{pmatrix}= \begin{pmatrix}0&2&0\\0&5&0\\0&8&0\end{pmatrix}\!;\\[5pt] Be_1e_2^T&= \begin{pmatrix}9&8&7\\6&5&4\\3&2&1\end{pmatrix}\!\! \begin{pmatrix}1\\0\\0\end{pmatrix}\!\! \begin{pmatrix}0&1&0\end{pmatrix}= \begin{pmatrix}9\\6\\3\end{pmatrix}\!\! \begin{pmatrix}0&1&0\end{pmatrix}= \begin{pmatrix}0&9&0\\0&6&0\\0&3&0\end{pmatrix}\!;\\[5pt] A-Ae_2e_2^T+Be_1e_2^T&= \begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}- \begin{pmatrix}0&2&0\\0&5&0\\0&8&0\end{pmatrix}+ \begin{pmatrix}0&9&0\\0&6&0\\0&3&0\end{pmatrix}= \begin{pmatrix}1&9&3\\4&6&6\\7&3&9\end{pmatrix}\!.\end{aligned}[/cbm]
В результате 2-й столбец матрицы [cbm]A[/cbm] заменен 1-м столбцом матрицы [cbm]B[/cbm] .
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
calcsbox.com
Содержание
Инструкция
|
completerepair.ru

