Как быстро умножать двузначные числа в уме?
Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.
Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7);
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Умножение на 11
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308
Умножение больших чисел
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
- Каждое число необходимо представить как разницу 100 и еще одного числа:
(100 — 13)*(100 — 9)
Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
87 – 9 = 78
91 – 13 = 78 - Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
- В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат:
interesno.cc
Правило умножения двузначных чисел на двузначные — Юридическое бюро
УМНОЖЕНИЕ СТОЛБИКОМ ДВУЗНАЧНЫХ ЧИСЕЛ
Тренажер по математике

Программа — тренажер по математике для закрепления навыков
Предлагается 20 примеров для решения. Два случайных двузначных числа нужно умножить столбиком.
Для перехода к началу решения примеров нажимаем кнопку «START»

В левой верхней части страницы тренажера по математике указывается число примеров, которые осталось решить.
В правой части страницы пример, который нужно решить. В левой части этот же пример записан столбиком.
Клавишами управления курсором передвигаемся вверх/вниз/вправо/влево по клеточками. Нажимаем на клавиатуре кнопки 0-9 и вводим промежуточные ответы и итоговый ответ.
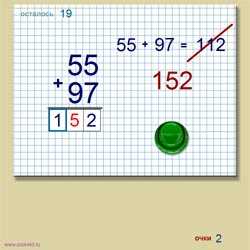
В случае, если пример решен верно, начисляется 5 очков. Если дать правильный ответ три раза подряд — начисляется бонус.

За неправильный ответ вычитается 3 очка.
Ошибки, допущенные в ходе вычисления, исправляются красным цветом. Сразу будет видно на каком этапе вычислений допущена ошибка.

В итоговой страничке тренажера по математике представлены результаты: количество очков, ошибок, бонусов.
Если при умножении столбиком были допущены ошибки, ниже будут перечислены примеры, в которых они были.
cool-kid.ru
Как быстро умножать двузначные числа в уме?
Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.
Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7);
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.
Умножение в столбик в уме
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.
Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.
Умножение на 11
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308
Умножение больших чисел
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
- Каждое число необходимо представить как разницу 100 и еще одного числа:
(100 — 13)*(100 — 9)
Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
91 – 13 = 78 - Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
- В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.
Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.
Поделитесь этим постом с друзьями
interesno.cc
Урок 3. Традиционное умножение в уме
Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
- Первое действие: 60*80 = 4800 — запоминаем
- Второе действие: 60*5+3*80 = 540 – запоминаем
- Третье действие: (4800+540)+3*5= 5355 – ответ
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
Третий способ — мысленная визуализация умножения в столбик
56*67 – посчитаем в столбик.
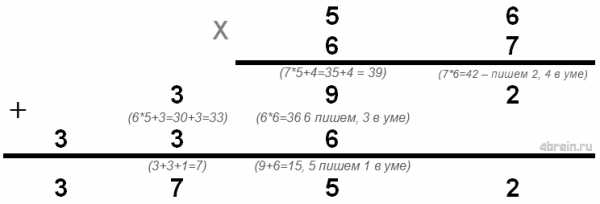
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
4brain.ru
Урок 6. Умножение в уме любых чисел до 100
Чтобы умножать любые числа до 100 в уме важно быстро подобрать нужный алгоритм. Для удобства этого подбора в данном уроке выделены наиболее удобные случаи для каждой методики умножения. Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).
Универсальные методики
Применимость универсальных методик умножения чисел до 100 такова:
Использование одного опорного числа (Урок 5):
- все числа в диапазонах до 30, 40-60, 85-100 – если оба множителя рядом с опорным числом.
Например: 13*17, 18*23, 29*22, 53*61, 88*97 и т.д. - если одно число очень близко к удобному опорному (+/- 3 от 10, 20, 50, 100), второе может быть любым.
Например: 21*67 (21 близко к 20), 48*33 (48 близко к 50), 98*32 (98 близко к 100)
Использование двух опорных чисел (Урок 5):
- Если одно опорное число является кратным другому и если одно из опорных чисел является удобным (10, 20, 50, 100)
Например: 98*24, 12*44, 43*103, 23*62
Иные числа удобно умножать традиционными методами из третьего урока, когда разряды десятков и единиц не очень большие (Урок 3). Кроме того, традиционный метод удобен, когда вы не знаете, какой другой метод вам применить.
Частные методики
Также полезно помнить о частных методиках, существенно упрощающих решение некоторых примеров:
Умножение на 10, 20, 25, 50 – должно осуществляться практически на автомате (Урок 2):
- Например: 88*25 = 2200 (деление на 4)
Умножение на 11 всегда по методике из урока 4
Числа, заканчивающиеся на 5 удобно возводить в квадрат по методу из четвёртого урока
Любые числа удобно возводить в квадрат используя формулы сокращенного умножения четверного урока
- Например: 69*69 = (70-1) 2 = 70 2 – 70*2*1 + 1 2 = 4 900-140+1 = 4 761
Теперь, вы имеете серьезный алгоритмический аппарат для решения примеров на умножение чисел до 100. Кроме того, вы уже можете умножать и некоторые примеры с множителями больше 100. Главным фактором, влияющим на вашу способность умножать в уме, в дальнейшем должен стать опыт и тренировка. Пройти тренировку можно ниже.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
4brain.ru
Правило умножения двузначных чисел на двузначные
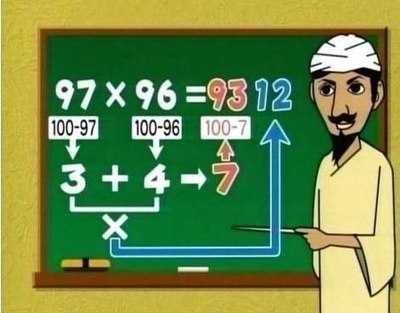
Интересно, сколько людей не воткнули, что это тот же столбик, которому их учили в 3-4 классе, только по-другому записанный.
а можно попродробнее? в каком именно месте это «тот же столбик»?
возьми и перемножь 64*38 обоими способами, в итоге делаешь одно и то же — умножаешь и складываешь цифры в несколько действий.
Ну а ничего, что такой способ годится только для вариантов, когда одно из чисел от 90 до 99. Иначе :
32 * 45 =
1. 32 — 55 = — 13
2. 68 * 55 = .
А ответ 1440
Запоминать способ для вариантов, где один из множителей в диапазоне 10 чисел.. ну несерьезно, передай Кондрашеву А.А.
Здравствуйте, а Вы не нашли название этой книги?
Приношу искренние извинения за своевременность.
Прошу прощения за столь поздний ответ — планировал поискать её на новогодних праздника.
К сожалению саму книгу найти не смог. Пытался узнать её по внешнему виду в интернете — тоже ничего не вышло.
Я и не рассчитывала на ответ. Спасибо, что уделили время на поиски книги! Ну, с кем не бывает, не всегда выходит найти искомое.

Почитай книгу эту, там все расписано подробно, комментарию 3 года, написано в спешке.
Я забыл в финальном этапе, что 18 надо умножить на 5 и прибавить к 1350. 18*5 = 90. 1350+90 = 1440, твое число.
у меня так же я перемножала 42*37
А я лет с 11-13 научилась умножать в уме числа 3х, 4х значные, 5тизначные на 2хзначные, например. Я просто в уме вижу перед собой листок и решаю на нем пример, элементарное умножение в столбик.
Конечно, эту процедуру можно и на листочке производить, но листочек память не тренирует)))
А двухзначные раскладываю на близкие круглые числа, потом прибавляю или отнимаю недостающие единицы
pikabu.ru
Популярное:
- Приказ о утверждении правил приема в доу Приказ об утверждении правил приема муниципальное автономное дошкольное образовательное учреждение детский сад комбинированного вида № 3 села Коноково муниципального образования Успенский район 352464 Краснодарский край, […]
- Центр экспертизы и координации информатизации Центр экспертизы и координации информатизации ЦИПР-2018: Цифровизация отраслей российской экономики Июн 09, 2018 6-8 июня в Иннополисе состоялась конференция «Цифровая индустрия промышленности». Директор ФГБУ «ЦЭКИ» Роман […]
- Приказы мчс по гдзс Газодымозащитная служба Газодымозащитная служба Деятельность ГДЗС выполняется в соответствии с требованиями приказов МЧС России от 09.01.2013 №3 «Об утверждении Правил проведения личным составом ФПС ГПС АСР при тушении с […]
- Пособие по беременности в 2014 Пособия в 2014 году В соответствии с Федеральным законом № 349-ФЗ от 02 декабря 2013 года «О федеральном бюджете на 2014 год и на плановый период 2015 и 2016 годов» размеры государственных пособий гражданам, имеющим детей, […]
- Договор поручения защита прав потребителя РЕШЕНИЯ СУДОВ Решение суда. Дело № 2-590 09 февраля 2011 года Именем Российской Федерации Выборгский районный суд Санкт-Петербурга в составе: судьи Симоновой И. Е. при секретаре Новоселовой О. П., рассмотрев в открытом судебном […]
- Акт об отказе в подписи в приказе Акт об отказе от подписи В случае отказа расписаться в официальном или ином документе не стоит нервничать – составьте акт об отказе от подписи. Как и акт об отказе от получения, такой документ фиксирует тот факт, что лицо […]
- Формы заявления о рождении Единовременное пособие при рождении ребенка Существующая система государственной социальной помощи в России предусматривает несколько видов компенсационных и стимулирующих выплат, предоставляемых семьям по случаю рождения детей. […]
- Кто прокурор в гшахты График приема в Прокуратуре Прокуратура города Шахты расположена по адресу: ул. Шевченко, 80 Прокурор города Шахты старший советник юстиции Петренко Евгений Александрович Зам. прокурора советник юстиции Яценко Д.А. Зам. […]
advokat343.ru
Быстрый счёт в уме: умножение
Числа окружают нас везде. Мы почти каждый день ходим в магазин, планируем расходы, переводим рубли в доллары, наконец.
Конечно же, сложение и вычитание небольших чисел большинство выполняет в уме, например, при покупке батона за 22 рубля мы сразу смекаем, что с отданных 50 должны получить 28 сдачи. Но иногда требуется более сложные операции — умножения (3 батона) или деления (500 граммов сыра).
Я, конечно, не в состоянии научить вас счёту в уме для любых чисел, тем более, что для этого есть калькулятор, но попытаюсь донести, что неплохо владея навыками сложения и вычитания, можно так же успешно, а главное быстро, умножать в уме. Конечно, речь не идёт о дробных или двузначных числах. Но с умножение на цифры в состоянии справится любой.

Если для вас является проблемой сложение и вычитание даже небольших чисел, не отчаивайтесь. Небольшая практика быстро заставит мозг «шуршать», а продолжив занятия, можно будет с каждым разом оперировать всё большими числами и за меньшее время. Именно эти простейшие арифметические опреции лежат в основе более сложных — умножения и деления, поэтому прежде, чем переходить к следующему шагу крайне желательно подтянуть азы.
Умножение
На 2
Для умножения на 2 достаточно сложить число само с собой: 123 × 2 = 123 + 123 = 246
На 3
Тоже довольно тривиальная задача. В простейшем случае можно трижды сложить число самим с собой: 123 × 3 = 123 + 123 + 123 = 369
Но иногда проще сделать поразрядное умножение: 123 × 3 = 100 × 3 + 20 × 3 + 3 × 3 = 300 + 60 + 9 = 369
На 4
Так как 4 это не что иное, как 2 × 2, достаточно умножаемое число сложить сперва самим с собой, а затем ещё раз сложить полученную сумму: 123 × 4 = (123 + 123) × 2 = 246 + 246 = 492
На 5
Данная цифра ровно в 2 раза меньше 10, сделовательно, можно сначала разделить на 2, а затем умножить на 10, либо поступить наоборот: умножить на 10 и разделить на 2 (смотря что проще): 123 × 5 = 123 × 10 / 2 = 1230 / 2 = 615
На 6
Цифру 6 можно представить с помощью произведения 2 × 3, а это мы уже разобрали: 123 × 6 = 123 × 3 × 2 = 369 × 2 = 738
На 7
Наиболее простой способ — поразрядное умножение: 123 × 7 = 100 × 7 + 20 × 7 + 3 × 7 = 700 + 140 + 21 = 861
На 8
Цифра 8 получается при тройном умножении двойки на себя: 123 × 8 = 123 × 2 × 2 × 2 = 246 × 2 × 2 = 492 × 2 = 984
Иногда проще бывает исходное число умножить на 10 и отнять удвоенное исходное числа: 123 × 8 = 123 × 10 — 123 × 2 = 1230 — 246 = 984
На 9
Несмотря на то, что цифру 9 можно получить, умножив тройку саму на себя, есть способ намного легче: нужно к умножаемому числу прибавить ноль (т. е. умножить на 10) и отнять от получившегося значения исходное число: 123 × 9 = 123 × 10 — 123 = 1230 — 123 = 1107
Вот мы и разобрались (я надеюсь) с цифрами. В качестве небольшого бонуса приведу ещё несколько вариантов умножения, на этот раз, с числами.
Умножение на 10, 100, 1000 и т. д.
Т. к. мы оперируем десятичной системой счисления, наиболее простое умножения как раз будет на числа, начинающие следующие разряды. Для умножения необходимо просто добавить 1 (2, 3, …) ноль в конец множителя: 123 × 100 = 12300
На 11
По аналогии с умножением на 9, только в данном случае необходимо прибавить исходное число: 123 × 11 = 123 × 10 + 123 = 1230 + 123 = 1353
На 20, 30, …
Здесь достаточно представить число в виде множителей, для которых нам известен порядок действий, например, 20 = 2 × 10, 300 = 3 × 100 и т. п.: 123 × 500 = 123 × 5 × 100 = ( 123 × 100 / 2 ) × 100 = 615 × 100 = 61500
Как видим, некоторые числа вполне можно представить в виде произведения и выполнить ряд более простых действий. А поупражнявшись некоторое время с удивлением обнаружите, что калькулятор будет нужен всё реже. В заключении, приведу ещё один интересный способ, который может быть полезен при перемножении двух чисел.
Умножение по формуле «разность квадратов»
Если кто-то не помнит эту формулу из школьного курса математики, вот она:
a2 — b2 = (a + b) × (a — b)
Допустим, нужно умножить 123 на 117. Данное произведение удобно разложить по этой формуле, т. к. 123 = 120 + 3, а 117 = 120 — 3. Составим простое выражение и убедимся, что можно легко «вертеть» в уме даже такими значениями, для которых, казалось бы, необходим калькулятор: 123 × 117 = (120 + 3) × (120 — 3) = 1202 — 32 = 14400 — 9 = 14391
Ещё пример, на этот раз попроще, для двузначных чисел: умножим 28 на 32. Снова раскладываем множители на составляющие: 28 = 30 — 2 и 32 = 30 + 2. Итоговая формула принимает вид: 28 × 32 = (30 + 2) × (30 — 2) = 302 — 22 = 900 — 4 = 896
Элементарно, не так ли? 😉
Автор публикации
1 892не в сети 1 неделя
x64 (aka andi)
Комментарии: 2772Публикации: 385Регистрация: 02-04-2009 Загрузка…a-panov.ru
Умножение двузначных чисел | Ментальная арифметика онлайн бесплатно
Упражнение считается выполенным после 7 правильных ответов
Для успешного выполнения упражнения ознакомьтесь с теорией и проработайте предыдущие уроки
Умножение двузначных чисел | Теория
В общем случае умножение в уме двузначных чисел удобно выполнять в следующем порядке:
- за базовое (первое или находящееся слева) число примите число с наибольшей второй цифрой;
- умножьте базовое (первое) двузначное число на десятки другого (второго) двузначного числа;
- умножьте базовое (первое) двузначное число на единицы другого (второго) двузначного числа;
- сложите два результата.
Задача: 42 x 36
Решение:
1) 36 x 42 (число 36 принято за базовое (первое) число, так как 6>1)
36 x 42(40+2)
2) 36 x 40 = (30+6) x 4 x 10
30 x 4 = 120; 6 x 4 = 24; 120 + 24 = 144[120+20=140;140+4=144]; 144 x 10 = 1440*
3) 36 x 2 = (30+6) x 2
30 x 2 = 60; 6 x 2 = 12; 60 + 12 = 72[60+10=70;70+2=72]
4) 1440 + 72 = 1752 [1440+70=1510;1510+2=1512]
Задача: 47 x 52
Решение:
1) 47 x 52 (число 47 принято за базовое (первое) число, так как 7>2)
2) 47 x 50 = 2350
3) 47 x 2 = 94
4) 2350 + 94 = 2444
Если одно из чисел заканчивается на 9, то задачу удобнее решать в следующем порядке:
- за второе (находящееся справа) число примите число, заканчивающееся на 9;
- округлите второе число в большую сторону до десятков, прибавив к нему 1;
- умножьте первое число на округлённое второе число;
- вычтите из результата пункта 3 первое число.
Задача: 39 x 56
Решение:
1) 56 x 39 (число 39 принято за второе (находящееся справа) число, так как оно заканчивается на 9)
2) 56 x 39(40-1)
3) 56 x 40 = (50+6) x 4 x 10
50 x 4 = 200; 6 x 4 = 24; 200 + 24 = 224; 224 x 10 = 2240
4) 2240 – 56 = 2184[2240-50=2190;2190-6=2184]
Если одно из двузначных чисел равно 11, то решить такую задачу будет намного проще, если вы воспользуетесь методикой, изложенной в Уроке 1.
Во многих случаях решение задачи умножения двузначных чисел в уме намного упрощается, если воспользоваться методом факторизации.
Факторизация – это преобразование числа в произведение более простых чисел. Например, число 24 можно преобразовать в произведение 8 и 3 (24 = 8 x 3) или 6 и 4 (24 = 6 x 4). Число 24 также можно представить в виде произведения 12 и 2 (24 = 12 x 2), но при выполнении арифметических операций в уме удобнее иметь дело с однозначными числами.
Отдельные двузначные числа также можно представить в виде произведения трёх однозначных чисел. Например, 84 = 7 x 6 x 2 = 7 x 4 x 3.
Решим задачу умножения с помощью факторизации.
Задача: 34 x 42
Решение:
Факторизация числа 24 даёт 8 и 3 или 6 и 4. Для решения задачи представим число 24 в виде произведения 6 и 4, но, если вам удобнее, вы можете выбрать произведение 8 и 3.
34 x 24(6×4)
Умножаем первое число на 6, после чего умножаем результат на 4:
34 x 6 = 204[30×6=180;4×6=24;180+24=204]
204 x 4 = 816[200×4=800;4×4=16;800+16=816]
Чтобы знать, какие из двузначных чисел поддаются факторизации, необходимо тщательно изучить таблицу умножения. Можно выписать все двузначные числа, поддающиеся факторизации, с указанием возможных способов их факторизации.
Если оба из перемножаемых двузначных чисел поддаются факторизации, то в большинстве случае удобнее факторизовать меньшее число.
Задача: 36 x 72
Решение:
Число 36 можно представить в виде произведения 6 и 6, а число 72 – в виде произведения 9 и 8.
Так как 36
72 x 36(6×6)
72 x 6 = 432[70×6=420;2×6=12;420+12=432]
432 x 6 = 2592[400×6=2400;30×6=180;2×6=12; 2400+180=2580;2580+12=2592]
Пример с факторизацией на три числа.
Задача: 57 x 75
Решение:
75 = 5 x 5 x 3
57 x 75(5x5x3)
57 x 5 = 285
285 x 5 = 1425
1425 x 3 = 4275
В случае, если одно из перемножаемых двузначных чисел состоит из одинаковых цифр (22, 33, 44 и т.д.), то его удобнее факторизовать на 11 и 2, 3, 4 и т.д.), так как умножение на 11 не представляет труда, как было показано в уроке 11.
Задача: 81 x 44
Решение:
81 x 44(11×4)
81 x 11 = 891;
891 x 4 = 3564
Если числа близки по значению с круглым числом, то при их перемножении в уме удобно пользоваться следующими формулами: (C+a)(C+b) = (C+a+b)C+ab; (C-a)(C-b) = (C-a-b)C+ab; (C+a)(C-b) = (C+a-b)C-ab**, где “C” – близкое к двум перемножаемым числам круглое число, а “а” и “b” – это разницы между перемножаемыми числами и круглым числом.
Задача: 67 x 64
Решение:
(60 + 7) x (60 + 4) = (60 + 7 + 4) x 60 + 7 x 4 = 71 x 60 + 28 = 4260 + 28 = 4288
Задача: 39 х 38
Решение:
(40 – 1) x (40 – 2) = (40 – 1 – 2) x 40 + 1 x 2 = 37 x 40 + 2 = 1480 + 2 = 1482
Задача: 41 x 38
Решение:
(40 + 1) x (40 – 2) = (40 + 1 – 2) x 40 + 1 x 2 = 39 x 40 – 2 = 1558
Умножение двузначных чисел, первые цифры (десятки) которых равны, а вторые цифры (единицы) дают в сумме 10, удобнее производить в следующем порядке:
- умножьте первую цифру двузначных чисел на эту же цифру, увеличенную на единицу;
- перемножить вторые цифры двузначных чисел;
- поместите один за другим результаты пункта 1 и пункта 2.
Задача: 76 x 74
Решение:
1) 7 x 8 = 56
2) 6 x 4 = 24
3) 5624
Не расстраивайтесь и не сдавайтесь, если на первых порах у вас возникнут трудности с умножением двузначных чисел. Для уверенного выполнения такой операции в уме необходима практика, а также творческий подход.
* Для запоминания в уме промежуточных результатов вычислений можете применять мнемотехники, основанные на ассоциации цифр с образами.
** Доказательства формул путём преобразования: (C+a)(C+b) = (C+a)C+(C+a)b = C2+Ca+Cb+ab = (C+a+b)C+ab; (C-a)(C-b) = (C-a)C-(C-a)b = C2-Ca-Cb+ab = (C-a-b)C+ab; (C+a)(C-b) = (C+a)C-(C+a)b = C2+Ca-Cb-ab = (C+a-b)C-ab.
*** Доказательство метода: согласно формуле, применяемой в предудущем методе (C+a)(C+b) = (C+a+b)C+ab; так как a+b=10, то (C+a)(C+b) = (C+10)C+ab; поскольку произведение двузначных круглых чисел С и С+10 даёт число с двумя нулями на конце, а произведение a и b даёт двузначное число, то для нахождения суммы этих двух выражений достаточно поставить произведение a и b вместо двух последних нулей первого выражения.
drdo.ru
Как умножать двузначные числа: в столбец и в уме
Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.

Как умножить двузначное число на однозначное?
Начнем с простой задачи – как умножать двузначные числа на однозначные.
Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.
Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.

Умножение двузначных чисел на десятки
Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:
- Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
- Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
- Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.

Как перемножить два двузначных числа?
После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.
- Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
- Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.
- После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
- Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.
Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.

Как умножать в уме
Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.
Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
- Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
- Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.
Некоторые хитрости при умножении двузначных чисел
Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?
Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.
- При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.
3 + 4 = 7
Ставим 7 в середину, 374. Это и есть ответ.
Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.
7 + 9 = 16
(7 + 1)69 = 869
- Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.
14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.
- Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
- Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.
Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.
Источник
1ku.ru
Как умножать двузначные числа: в столбец и в уме
Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.

Содержание страницы
Как умножить двузначное число на однозначное?
Начнем с простой задачи – как умножать двузначные числа на однозначные.
Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.
Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.

Умножение двузначных чисел на десятки
Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:
- Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
- Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
- Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.

Как перемножить два двузначных числа?
После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.
- Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
- Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.
- После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
- Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.
Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.

Как умножать в уме
Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.
Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
- Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
- Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.
Некоторые хитрости при умножении двузначных чисел
Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?
Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.
- При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.
3 + 4 = 7
Ставим 7 в середину, 374. Это и есть ответ.
Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.
7 + 9 = 16
(7 + 1)69 = 869
- Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.
14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.
- Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
- Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.
Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.
Источник
24simba.ru
Как быстро умножать двузначные числа в уме
Правила_быстрого_устного_счета
Тест для начальных классов «как быстро умножить на 11 любое двузначное число» ab*11=a(a+b)b примеры 34*11=3(3+4)4=374 17*11=1(1+7)7=187 частные случаи если (a+b) двузначное число, то по-середине пишем (a+b-10) а к первой цифре прибавляем 1: ab*11=(a+1)(a+b-10)b примеры 47*11=(4+1)(4+7-10)(7)=517 95*11=(9+1)(9+5-10)5=1045
Как быстро умножать двузначные числа в уме?
А вот и не угадали, я не собираюсь научить вас пользоваться таблицей умножения и не буду учить вас считать в столбик. Я покажу вам способ как быстро считать в уме двузначные числа.
Инструкция
Уровень сложности: Легко
1 шаг
Для примера возьмём два числа – 16 и 18.К оному из чисел прибавляем кол-во единиц втрого – 16+8=24
2 шаг
Полученное число умножаем на 10 – 24*10=240
3 шаг
Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
и всего-то,не верите проверьте на калькуляторе))))
БЫСТРЫЙ СЧЕТ Тридцать простых приемов устного счета
Усвоив рекомендуемые приемы, можно выполнять быстрые расчеты в уме с безошибочностью письменных вычислений.
Умножение на однозначное число . Чтобы устно умножить число на однозначный множитель (например, 27 X 8) выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20×8 = 160), затем единицы (7*8 =56) и оба результата складывают.
Еще примеры:
34*7=30*7+4*7=210+28=238
47*6=40*6+7*6=240+42=282
Полезно знать на память таблицу умножения до 19*9:
Зная эту таблицу, можно умножение например, 147*8 выполнить в уме так: 147*8=140*8+7*8= 1120 + 56= 1176
Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350 Умножение на двузначное число
Умножение на двузначное число стараются облегчить для устного выполнения, приводя это действие к более привычному умножению на однозначное число.
Когда множимое однозначное, мысленно переставляют множители и выполняют действие.. Например:
6*28=28*6=120+48=168
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
29*12=29*10+29*2=290+58= 348
41*16=41*10+41*6 = 410+246 =656
(или 41*16=16*41 = 16*40+16*1=640+16=656
Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.
Если множимое или множитель легко разложить в уме на однозначные числа (напр., 14 = 2*7), то пользуются этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз . Например:
45*14 =90*7=630 Умножение на 4 и на 8
Чтобы устно умножить число на 4, его дважды удваивают. Например:
112*4 =224*2=448
335*4 = 670*2 =1340 .
Чтобы устно умножить число на 8, его трижды удваивают. Например:
217*8 = 434*4=868*2=1736
(Eще удобнее: 217*8=200*8 +17*8= 1600*13=1736. Деление на 4 и на 8 .
Чтобы устно разделить число на 4, его дважды делят пополам. Например:
76:4 =38:2=19
236:4=118:2=59 .
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
464:8=232:4=116:2=58
516:8=258:4=129:2= 64 1/2 Умножение на 5 и на 25 .
Чтобы устно умножить число на 5 умножают его на 10/2, т. е. приписывают к числу ноль и делят пополам. Например:
74*5= 740:2= 370
243*5=2430:2=1215
При умножении на 5 числа четного удобнее сначала делить пополам и к полученному приписать ноль. Например:
74*5 = 74/2*10=370 .
Чтобы устно умножить число на 25, умножают его на 100/4 , т. е.—если число кратно 4-х —делят на 4 и к частному приписывают два ноля. Например:
72*25=72/4*100= 1800
Если же число при делении на 4 дает остаток, то прибавляют
при остатке: к частному
1 25
2 50
3 75
Основание приема ясно из того, что
100:4=25;
200:4=50;
300:4=75 Умножение на 11/2, на 1 1/4, на 21/2, на 3/4 .
Чтобы устно умножить число на 11/2 прибавляют к множимому его половину. Например:
34*11/2 = 34 + 17=51
23*11/2=23 + 111/2 = 341/2 (или 34,5)
Чтобы устно умножить число на 11/4 Прибавляют к множимому его четверть. Например:
48*11/4 =48 +12=60
58*11/4 = 58+14 1/2=721/2 или 72,5
Например: 18*21/2.=36+9= 45;
39*21/2.= 78 + 191/2.= 971/2 (или 97,5)
Другой способ состоит в умножении на 5 и делении пополам:
18*21/2 = 90:2 = 45 .
Чтобы устно умножить число на 3/4 (т. е. чтобы найти 3/4 этого числа), умножают число на 11/2 и делит пополам. Например:
30 * 3/4 = (30+15)/2= 221/2 (или 22,5)
Видоизменение способа состоит в том, что от множимого отнимают его четверть или к половине множимого прибавляют половину этой половины. Умножение на 15, на 125, на 75
Умножение на 15 заменяют умножением на 10 и на 11/2, (потому что 10*11/2 =15) Например:
18*15=18*11/2*10=270
45*15=450+225=675 .
Умножение на 125 заменяют умножением на 100 и на 11/4 (потому что 100*11/4=125). Например:
26*125 = 26*100*11/4 = 2600 + 650 = 3250
47*125 = 47*100*11/4 = 4700+4700/4= 4700+1175 = 5875 .
Умножение на 75 заменяют умножением на 100 и на 3/4 (потому что 100*3/4=75). Например:
18*75= 18*100*3/4 =1800* 3/4 =(1800 + 900)/2=1350
Примечание. Некоторые из приведенных примеров удобно выполняются также приемом
18*15 = 90*3 = 270
26*125 = 130*25 = 3250 Умножение на 9 и на 11 .
Чтобы устно умножить число на 9, приписывают к нему ноль и отнимают множимое. Например:
62*9=620-62=600—42=558
73*9=730-73=700—43=657
Чтобы устно умножить число на 11, приписывают к нему ноль и прибавляют множимое. Например:
87*11=870+87=957 Деление на 5, на 11/2,на 15
Чтобы устно разделить число на 5, отделяют запятой в удвоенном числ-последнюю цифру. Например:
68:5=136:10=13,6
237:5 =474:10=47,4
Чтобы устно разделить число на 11/2 делят удвоенное число на 3. Например:
36:11/2=72:3=24
53:11/2=106:3=351/3
Чтобы устно разделить число на 15, делят удвоенное число на 30. Например
240:15=480:30=48:3=16
462:15=924:30=3024/30=304/5=30,8 (или 924:30 =308:10=30,8) Возвышение в квадрат .
252; 2*3=6; 625
452; 4*5= 20; 2025
1452; 14*15 = 210; 21025
Прием этот вытекает из формулы (10х+5)2 = 100х2+100х+25=100х(х+1)+25 .
Сейчас указанный прием приложим и к десятичным дробям, оканчивающимся цифрой 5:
8,52 = 72,25
14,52=210,25
0,352 = 0,1225f и т. п. .
Так как 0,5= ½, а 0,25 = ¼, то приемом можно пользоваться также и для возвышения в квадрат чисел, оканчивающихся дробью ½:
(8½ )2 =72 ¼
(14½)2 = 210 ¼ и т п.
При устном возвышении в квадрат часто удобно бывает пользоваться формулой (a +-b)2 = a2 +b2+- 2ab.
Например: 412=402 +1+2*40= 1601+80= 1681
692=702+1-2*70=4901-140=4761
362 =(35+1)2=1225+1+ 2*35=1296
Прием удобен для чисел, оканчивающихся на 1, 4, 6 и 9. Вычисления по формуле
(а+b) (а-b) = а2 — b2
Пусть требуется выполнить устно умножение 52*48
Мысленно представляем эти множители в виде (50 + 2)*(50—2)
и применяем приведенную в заголовке формулу:
(50+2)*(50—2)=502-22= 2496
Подобным же образом поступают во всех вообще случаях, когда один множитель удобно представить в виде суммы двух чисел, другой — в виде разности тех же чисел:
69*71=(70—1)*(70+1)=4899
33*27=(30+3)*(30—3)=891
53*57=(55—2)*(55+2)=3021
84*86=(85-1)*(85+1)=7224 .
Указанным сейчас приемом удобно пользоваться и для вычислений следующего рода:
7 ½*6½=(7 + ½ )*(7 — ½)=48 ¾
11 3/4*12 1/4= (12 – 1/4)*(12 +1/4) =143 15/16 Полезно запомнить:
37*З =111
Запомнив это, легко выполнять устно умножение числа 37 на 6, 9, 12 и т. п.
37*6=37*3*2=222
37*9=37*3*3=333
37*12=37*3*4=444
37*15=37*3*5 =555 и т. д,
7*11*13=1001
Запомнив это, легко выполнять устно умножения следующего рода:
77*13=1001
77*26=2002
77*39=3003 и т. д.
91*11=1001
91*22=2002
91*33=3003 и т. д.
143*7=1001
143*14=2002
143*21=3003 и т. д.
указаны только простейшие, наиболее удобоприменимые способы устного выполнения действий умножения, деления и возвышения в квадрат. Практикуясь в сознательном пользовании ими, вдумчивый выработайте для себя ряд еще и других приемов, облегчающих вычислительную работу.
www.birmaga.ru
