кинематика
на главную
Официальный сайт АНО ДО Центра “Логос”, г.Глазов
http://logos-glz.ucoz.net/
ГОТОВИМСЯ К УРОКУ
Кинематика
Динамика
МКТ
Термодинамика
Электростатика
Электрический ток
Электрический ток в средах
Магнитное поле Электромагнитная индукция
Оптика
Методы познания
Кинематика немного о физике:
Кинематика – раздел механики, в котором изучается механическое движение, без учета масс тел и причин, которые обеспечивают это движение.
Основная задача кинематики – описать движение тела в пространстве в зависимости от времени, не выясняя причин движения.
Основные понятия.
Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.
Рассмотрение любого движения начинают с выбора
Материальная точка – модель тела, размерами которого в рассматриваемых условиях можно пренебречь.
Траектория – линия, вдоль которой движется тело.
Путь – длина траектории.
Перемещение – вектор, соединяющий начальное и конечное положения тела.
Положение тела в пространстве задается радиус – вектором
Следовательно закон движения – это зависимость радиус-вектора от времени или зависимость координат во времени.
где -радиус-вектор, x, y, z – координаты тела.
Скорость тела – векторная физическая величина, характеризующая изменение положения тела в пространстве с течением времени.
Средняя скорость перемещения равна отношению полного перемещения к промежутку времени, за которое это перемещение совершено.
гдеср -средняя скорость перемещения, – перемещение, ∆ t – интервал времени.
Средняя путевая скорость равна отношению полного пути к промежутку времени, за который этот путь пройден.
где υср – средняя путевая скорость , l – путь.
Мгновенная скорость – скорость в заданный момент времени.
Модуль мгновенной скорости определяется равенством:
где υx , υy , υz – проекции вектора скорости на оси,
Мгновенная скорость в каждой точке всегда направлена по касательной к траектории. Направление вектора скорости задается косинусами:
где α , β , γ –углы между вектором скорости и осями x, y, z соответственно.
Ускорение
где а– ускорение, 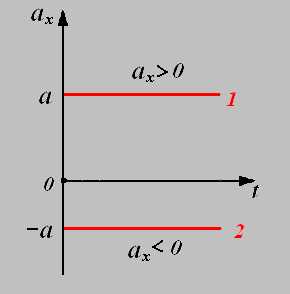 -изменение
скорости,
-изменение
скорости, 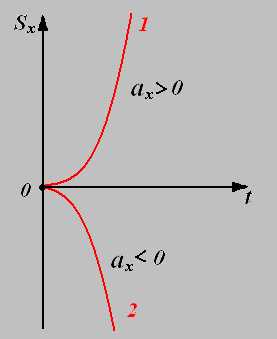 ,
, 0 – конечная и начальная скорости.
0 – конечная и начальная скорости.
Модуль ускорения определяется равенством:
где – x, y , z – проекции вектора ускорения на оси x, y, z соответственно.
Равномерное прямолинейное движение.
Равномерное движение – движение при котором материальная точка за любые равные промежутки времени совершает равные перемещения.
При равномерном прямолинейном движении скорость тела постоянна, ускорение равно нулю. Траектория равномерного прямолинейного движения – прямая линия.
Для физических величин характеризующих движение имеем:
 = 0
= 0
υ = const
Sx = υx· t
x = x0 + υx· t
Графики зависимости физических величин от времени
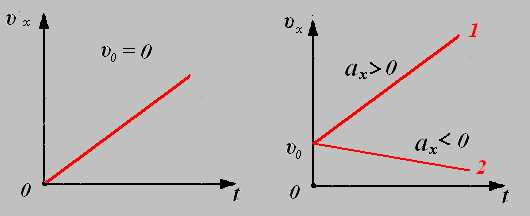
1. график зависимости проекции скорости от времени.

2. график зависимости проекции перемещения от времени
3. график зависимости координаты от времени.
Равноускоренное прямолинейное движение.
Равноускоренным движением называют движение с ускорением, постоянным по модулю и направлению. При равноускоренном движении скорость тела изменяется, ускорение остается постоянным. Траектория равноускоренного прямолинейного движения – прямая линия.
Для физических величин характеризующих движение имеем:
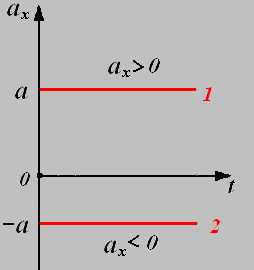
при равноускоренном прямолинейном движении.
1. график зависимости проекции ускорения от времени.
2. график зависимости проекции скорости от времени.
3. график зависимости проекции перемещения от времени.
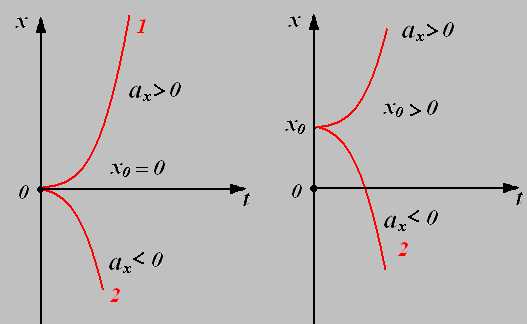
4. график зависимости координаты от времени.
Равномерное движение по окружности.
Скорость движения тела по окружности называют линейной скоростью. При равномерном движении по окружности модуль линейной скорости материальной точки со временем не изменяется, но изменяется ее направление.
Модуль линейной скорости равен отношению пройденного пути к промежутку времени. Учитывая. что при равномерном движении по окружности путь равен длине дуги, то для линейной скорости имеет место равенство:

где l – длина дуги, R – радиус описанной окружности, φ – угол поворота радиус-вектора, t- время движения.
Еще одной характеристикой движения по окружности является угловая скорость. Угловая скорость равна отношению угла поворота радиус-вектора к промежутку времени, за который этот угол пройден.
где ω – угловая скорость.
Связь между линейной и угловой скоростью определяется следующим равенством: υ = ω·R
При равномерном движении по окружности линейная скорость изменяется по направлению, поэтому движение по окружности – это движение с ускорением. При равномерном движении по окружности ускорение направлено к центру окружности и называется нормальным или центростремительным ускорением. Модуль ускорения не меняется:
где n -нормальное (центростремительное) ускорение.
Период вращения – промежуток времени, за который тело совершает один полный оборот.
где Т – период обращения.
Частота обращения – число оборотов, совершаемых телом в единицу времени. Частота обращения – величина , обратная периоду.
где ν – частота обращения.
Криволинейное движение.
Любое криволинейное движение можно представить как движение по дугам окружностей.
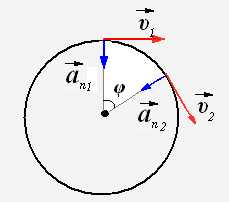
При произвольном криволинейном движении скорость может меняться как по модулю, так и по направлению. Ускорение так же является величиной переменной:
При криволинейном движении ускорение можно разложить на две составляющие:
где первое слагаемое – нормальная составляющая ускорения, второе слагаемое – тангенсальная составляющая ускорения.
Модуль полного ускорения равен:
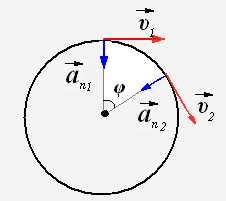
Модули нормального и тангенсального ускорений соответственно равны:
где – производная модуля скорости по времени.
nika-fizika.narod.ru
Кинематика материальной точки (основная школа)
Кинематика материальной точки
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения вдоль данной данной прямой линии. Скорость равномерного движения определяется по формуле:
|
Рис. 1. Перемещение, скорость и ускорение при равномерном прямолинейном движении |
|
Рис. 2. Равномерное движение |
Если при движении тела его скорость изменяется по модулю и (или) направлению, то можно ввести понятие ускорения. Ускорение есть векторная физическая величина, определяемая как отношение малого изменения скорости к малому промежутку времени за который произошло это изменение:
Равноускоренным прямолинейным движением называется прямолинейное движение, при котором скорость тела меняется линейно со временем:
|
Рис. 3. Перемещение, скорость и ускорение при равноускоренном прямолинейном движения |
В общем случае ускорение тела – векторная величина. При движении тела вдоль прямой линии ускорение можно определить по формуле:
Перемещение тела при равноускоренном прямолинейном движении выражается соотношением:
Выражение для перемещения s может быть представлено в виде:
|
Рис. 4. Равноускоренное движение |
Примером равноускоренного движения является свободное падение тела с высоты h в безвоздушном пространстве. Ускорение свободного падения тела не зависит от самого тела и всегда направлено вертикально вниз. Высота тела при этом определяется формулой (при условии, что начальная скорость равна нулю). Время падения с высоты h равно:
При равномерном движении со скоростью υ по окружности радиуса R ускорение (центростремительное ускорение) постоянно по величине:
|
Рис. 5. Равномерное движение по окружности |
Период обращения T – это промежуток времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Скорость движения тела при этом можно записать как:
Частота обращения ν – это число оборотов, совершаемых материальной точкой при равномерном движении по окружности за единицу времени:
В физике широко используют понятие круговой частоты:
В этом случае центростремительное ускорение записывается в виде:files.school-collection.edu.ru
Кинематика точки — WiKi
Основные кинематические понятия
Материальная точка — тело, размерами которого по сравнению с характерными расстояниями данной задачи можно пренебречь. Так Землю можно считать Материальной Точкой (М. Т.) при изучении её движения вокруг Солнца, пулю можно считать М. Т. при её движении в поле тяжести Земли, но нельзя считать таковой при учете её вращательного движения в стволе винтовки. При поступательном движении в ряде случаев при помощи понятия М. Т. можно описывать и изменение положения более крупных объектов. Так, например, тепловоз, проходящий расстояние 1 метр, может считаться М. Т., поскольку его ориентация относительно системы координат в процессе движения является фиксированной и не влияет на постановку и ход решения задачи.
Радиус-вектор — вектор, определяющий положение материальной точки в пространстве: r→={r1,r2,…,rn}{\displaystyle {\vec {r}}=\{r_{1},r_{2},…,r_{n}\}} . Здесь r1,r2,…,rn{\displaystyle r_{1},r_{2},…,r_{n}} — координаты радиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат ri=ri(t){\displaystyle r_{i}=r_{i}(t)} ) от времени r→=r→(t){\displaystyle {\vec {r}}={\vec {r}}(t)} называется законом движения.
Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется материальная точка. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путём и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:
- S=S0+vS0t+aSt22{\displaystyle S=S_{0}+v_{S_{0}}t+{\frac {a_{S}t^{2}}{2}}} ,
Где : vS0=|v→0|{\displaystyle v_{S_{0}}=|{\vec {v}}_{0}|} — модуль начальной скорости, а aS=aτ{\displaystyle a_{S}=a_{\tau }} — Тангенциальное ускорение.
Описание движения при помощи понятия траектории — один из ключевых моментов классической механики . В квантовой механике движения носит бестраекторный характер, а значит само понятие траектория теряет смысл.
Основные кинематические величины
Радиус-векторы и вектор перемещения (черные стрелки). Векторы средней и мгновенных скоростей (Зеленые стрелки). Траектория (красная линия)Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:
- Δr→(t2,t1)=r→(t2)−r→(t1){\displaystyle \Delta {\vec {r}}(t_{2},t_{1})={\vec {r}}(t_{2})-{\vec {r}}(t_{1})} .
Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.
Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:
- v→cp(t1,t2)=Δr→Δt=r→(t2)−r→(t1)t2−t1{\displaystyle {\vec {v}}_{cp}(t_{1},t_{2})={\frac {\Delta {\vec {r}}}{\Delta t}}={\frac {{\vec {r}}(t_{2})-{\vec {r}}(t_{1})}{t_{2}-t_{1}}}} .
Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:
- v→(t)=dr→(t)dt{\displaystyle {\vec {v}}(t)={\frac {d{\vec {r}}(t)}{dt}}} .
Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:
- v→(t1)=limt2→t1v→cp(t1,t2)=limΔt→0Δr→(t)Δt{\displaystyle {\vec {v}}(t_{1})=\lim _{t_{2}\rightarrow t_{1}}{\vec {v}}_{cp}(t_{1},t_{2})=\lim _{\Delta t\rightarrow 0}{\frac {\Delta {\vec {r}}(t)}{\Delta t}}} .
Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории.
Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:
- a→(t)=dv→(t)dt=d2r→(t)dt2{\displaystyle {\vec {a}}(t)={\frac {d{\vec {v}}(t)}{dt}}={\frac {d^{2}{\vec {r}}(t)}{dt^{2}}}} .
Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:
- a→(t)=an(t)n→+aτ(t)τ→{\displaystyle {\vec {a}}(t)=a_{n}(t){\vec {n}}+a_{\tau }(t){\vec {\tau }}} .
Здесь n→{\displaystyle {\vec {n}}} — единичный вектор нормали, τ→{\displaystyle {\vec {\tau }}} — единичный вектор касательной. Величина an{\displaystyle a_{n}} называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:
- an(t)=v(t)2R{\displaystyle a_{n}(t)={\frac {v(t)^{2}}{R}}} .
В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.
Величина aτ{\displaystyle a_{\tau }} называется тангенциальным ускорением и характеризует величину изменения модуля скорости:
- aτ=d|v|dt{\displaystyle a_{\tau }={\frac {d|v|}{dt}}} .
Преобразования Галилея
Если ИСО S’ движется относительно ИСО S с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:
x′=x−ut,{\displaystyle x’=x-ut,}
y′=y,{\displaystyle y’=y,}
z′=z,{\displaystyle z’=z,}
t′=t{\displaystyle t’=t}
или, используя векторные обозначения,
r′→=r→−u→t,{\displaystyle {\vec {r’}}={\vec {r}}-{\vec {u}}t,}
t′=t{\displaystyle t’=t}
(последняя формула остается верной для любого направления осей координат).
ru-wiki.org
Графики равномерного, равноускоренного движения, сравнение. Линейная, квадратная зависимость. Правила определения параметров
Тестирование онлайн
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают
Графики равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) – прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) – это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График s(t) – наклонная линия.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.
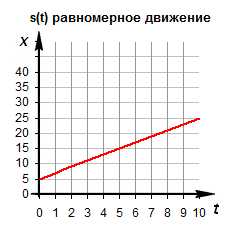
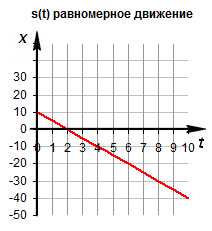
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
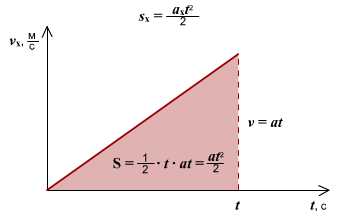
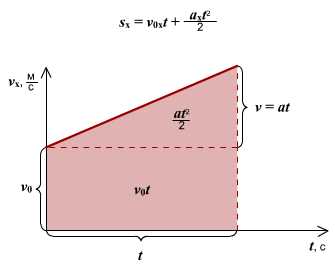
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
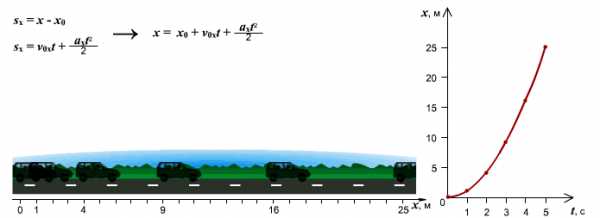
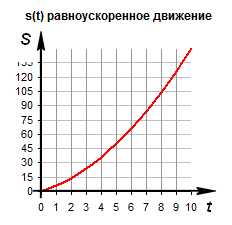
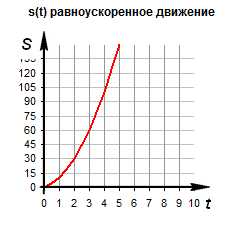
График движения при . График движения при
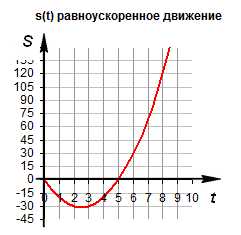
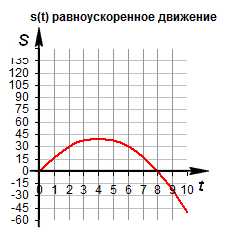
График движения при . График движения при
Сравнительная таблица графиков
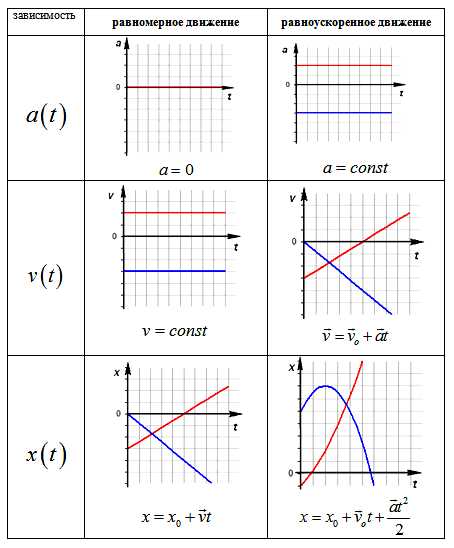
fizmat.by
