ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ | Социальная сеть работников образования
Образование — то, что остается после того, как забыто все, чему учили в школе.
Игорь Хмелинский, новосибирский учёный, ныне работающий в Португалии, доказывает, что без прямого запоминания текстов и формул развитие абстрактной памяти у детей затруднительно. Приведу выдержки из его статьи “Уроки образовательных реформ в Европе и странах бывшего СССР”
Заучивание наизусть и долговременная память
Незнание таблицы умножения имеет и более серьезные последствия, чем неспособность обнаружить ошибки в расчетах на калькуляторе. Наша долговременная память работает по принципу ассоциативной базы данных, то есть, одни элементы информации при запоминании оказываются связанными с другими на основе ассоциаций, установленных в момент знакомства с ними. Поэтому, чтобы в голове образовалась база знаний в какой-либо предметной области, например, в арифметике, нужно для начала выучить хоть что-то наизусть. Далее, вновь поступающая информация попадет из кратковременной памяти в долговременную, если в течение короткого промежутка времени (несколько дней) мы столкнемся с нею многократно, и, желательно, в разных обстоятельствах (что способствует созданию полезных ассоциаций). Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п. Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.
Формирование математического аппарата, при котором формулы не заучиваются, происходит медленнее, нежели в противном случае. Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий. Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.
Практика показывает, что интеллектуальное и математическое развитие ребенка, формирование его базы знаний и навыков, происходит значительно быстрее, если большая часть используемой информации (свойства и формулы) находиться в голове. И чем прочнее и дольше она там удерживается, тем лучше.
НАДО ЛИ ВАС ДАЛЬШЕ УБЕЖДАТЬ В ТОМ, ЧТО ФОРМУЛЫ НАДО ЗНАТЬ НАИЗУСТЬ?
nsportal.ru
Формулы EXCEL с примерами — Инструкция по применению
Для того чтобы понять как пользоваться этой программой, необходимо рассмотреть формулы EXCEL с примерами.
Программа Excel создана компанией Microsoft специально для того, чтобы пользователи могли производить любые расчеты с помощью формул.
Применение формул позволяет определить значение одной ячейки исходя из внесенных данных в другие.
Если в одной ячейке данные будут изменены, то происходит автоматический перерасчет итогового значения.
Что очень удобно для проведения различных расчетов, в том числе финансовых.
Содержание:
В программе Excel можно производить самые сложные математические вычисления.
В специальные ячейки файла нужно вносить не только данные и числа, но и формулы. При этом писать их нужно правильно, иначе промежуточные итоги будут некорректными.
С помощью программы пользователь может выполнять не только вычисления и подсчеты, но и логические проверки.
В программе можно вычислить целый комплекс показателей, в числе которых:
- максимальные и минимальные значения;
- средние показатели;
- проценты;
- критерий Стьюдента и многое другое.
Кроме того, в Excel отображаются различные текстовые сообщения, которые зависят непосредственно от результатов расчетов.
Главным преимуществом программы является способность преобразовывать числовые значения и создавать альтернативные варианты, сценарии, в которых осуществляется моментальный расчет результатов.
При этом необходимость вводить дополнительные данные и параметры отпадает.
Как применять простые формулы в программе?
Чтобы понять, как работают формулы в программе, можно сначала рассмотреть легкие примеры. Одним из таких примеров является сумма двух значений.
Для этого необходимо ввести в одну ячейку одно число, а во вторую – другое.
Например, В Ячейку А1 – число 5, а в ячейку В1 – 3. Для того чтобы в ячейке А3 появилось суммарное значение необходимо ввести формулу:
=СУММ(A1;B1).
Вычисление суммарного значения двух чисел
Определить сумму чисел 5 и 3 может каждый человек, но вводить число в ячейку С1 самостоятельно не нужно, так как в этом и замысел расчета формул.
После введения итог появляется автоматически.
При этом если выбрать ячейку С1, то в верхней строке видна формула расчета.
Если одно из значений изменить, то перерасчет происходит автоматически.
Например, при замене числа 5 в ячейке В1 на число 8, то менять формулу не нужно, программа сама просчитает окончательное значение.
На данном примере вычисление суммарных значений выглядит очень просто, но намного сложнее найти сумму дробных или больших чисел.
Сумма дробных чисел
В Excel можно производить любые арифметические операции: вычитание «-», деление «/», умножение «*» или сложение «+».
В формулы задается вид операции, координаты ячеек с исходными значениями, функция вычисления.
Любая формула должна начинаться знаком «=».
Если вначале не поставить «равно», то программа не сможет выдать необходимое значение, так как данные введены неправильно.
вернуться к меню ↑Создание формулы в Excel
В приведенном примере формула =СУММ(A1;B1) позволяет определить сумму двух чисел в ячейках, которые расположены по горизонтали.
Формула начинается со знака «=». Далее задана функция СУММ. Она указывает, что необходимо произвести суммирование заданных значений.
В скобках числятся координаты ячеек. Выбирая ячейки, следует не забывать разделять их знаком «;».
Если нужно найти сумму трех чисел, то формула будет выглядеть следующим образом:
=СУММ(A1;B1;C1).
Формула суммы трех заданных чисел
Если нужно сложить 10 и более чисел, то используется другой прием, который позволяет исключить выделение каждой ячейки. Для этого нужно просто указать их диапазон.
Например,
=СУММ(A1:A10). На рисунке арифметическая операция будет выглядеть следующим образом:
Определение диапазона ячеек для формулы сложения
Также можно определить произведение этих чисел. В формуле вместо функции СУММ необходимо выбрать функцию ПРОИЗВЕД и задать диапазон ячеек.
Формула произведения десяти чисел
Совет! Применяя формулу «ПРОИЗВЕД» для определения значения диапазона чисел, можно задать несколько колонок и столбцов. При выборе диапазона =ПРОИЗВЕД(А1:С10), программа выполнит умножение всех значений ячеек в выбранном прямоугольнике. Обозначение диапазона – (А1-А10, В1-В10, С1-С10).
вернуться к меню ↑Комбинированные формулы
Диапазон ячеек в программе указывается с помощью заданных координат первого и последнего значения. В формуле они разделяются знаком «:».
Кроме того, Excel имеет широкие возможности, поэтому функции здесь можно комбинировать любым способом.
Если нужно найти сумму трех чисел и умножить сумму на коэффициенты 1,4 или 1,5, исходя из того, меньше ли итог числа 90 или больше.
Задача решается в программе с помощью одной формулы, которая соединяет несколько функций и выглядит следующим образом:
=ЕСЛИ(СУММ(А1:С1)<90;СУММ(А1:С1)*1,4;СУММ(А1:С1)*1,5).
Решение задачи с помощью комбинированной формулы
В примере задействованы две функции – ЕСЛИ и СУММ. Первая обладает тремя аргументами:
- условие;
- верно;
- неверно.
В задаче – несколько условий.
Во-первых, сумма ячеек в диапазоне А1:С1 меньше 90.
В случае выполнения условия, что сумма диапазона ячеек будет составлять 88, то программа выполнит указанное действие во 2-ом аргументе функции «ЕСЛИ», а именно в СУММ(А1:С3)*1,4.
Если в данном случае происходит превышение числа 90, то программа вычислит третью функцию – СУММ(А1:С1)*1,5.
Комбинированные формулы активно применяются для вычисления сложных функций. При этом количество их в одной формуле может достигать 10 и более.
Чтобы научиться выполнять разнообразные расчеты и использовать программу Excel со всеми ее возможностями, можно использовать самоучитель, который можно приобрести или найти на интернет-ресурсах.
вернуться к меню ↑Встроенные функции программы
В Excel есть функции на все случаи жизни. Их использование необходимо для решения различных задач на работе, учебе.
Некоторыми из них можно воспользоваться всего один раз, а другие могут и не понадобиться. Но есть ряд функций, которые используются регулярно.
Если выбрать в главном меню раздел «формулы», то здесь сосредоточены все известные функции, в том числе финансовые, инженерные, аналитические.
Для того чтобы выбрать, следует выбрать пункт «вставить функцию».
Выбор функции из предлагаемого списка
Эту же операцию можно произвести с помощью комбинации на клавиатуре — Shift+F3 (раньше мы писали о горячих клавишах Excel).
Если поставить курсор мышки на любую ячейку и нажать на пункт «выбрать функцию», то появляется мастер функций.
С его помощью можно найти необходимую формулу максимально быстро. Для этого можно ввести ее название, воспользоваться категорией.
Мастер функций
Программа Excel очень удобна и проста в использовании. Все функции разделены по категориям. Если категория необходимой функции известна, то ее отбор осуществляется по ней.
В случае если функция неизвестна пользователю, то он может установить категорию «полный алфавитный перечень».
Например, дана задача, найти функцию СУММЕСЛИМН. Для этого нужно зайти в категорию математических функций и там найти нужную.
Выбор функции и заполнение полей
Далее нужно заполнить поля чисел и выбрать условие. Таким же способом можно найти самые различные функции, в том числе «СУММЕСЛИ», «СЧЕТЕСЛИ».
вернуться к меню ↑Функция ВПР
С помощью функции ВПР можно извлечь необходимую информацию из таблиц. Сущность вертикального просмотра заключается в поиске значения в крайнем левом столбце заданного диапазона.
После чего осуществляется возврат итогового значения из ячейки, которая располагается на пересечении выбранной строчки и столбца.
Вычисление ВПР можно проследить на примере, в котором приведен список из фамилий. Задача – по предложенному номеру найти фамилию.
Применение функции ВПР
Формула показывает, что первым аргументом функции является ячейка С1.
Второй аргумент А1:В10 – это диапазон, в котором осуществляется поиск.
Третий аргумент – это порядковый номер столбца, из которого следует возвратить результат.
Вычисление заданной фамилии с помощью функции ВПР
Кроме того, выполнить поиск фамилии можно даже в том случае, если некоторые порядковые номера пропущены.
Если попробовать найти фамилию из несуществующего номера, то формула не выдаст ошибку, а даст правильный результат.
Поиск фамилии с пропущенными номерами
Объясняется такое явление тем, что функция ВПР обладает четвертым аргументом, с помощью которого можно задать интервальный просмотр.
Он имеет только два значения – «ложь» или «истина». Если аргумент не задается, то он устанавливается по умолчанию в позиции «истина».
вернуться к меню ↑Округление чисел с помощью функций
Функции программы позволяют произвести точное округление любого дробного числа в большую или меньшую сторону.
А полученное значение можно использовать при расчетах в других формулах.
Округление числа осуществляется с помощью формулы «ОКРУГЛВВЕРХ». Для этого нужно заполнить ячейку.
Первый аргумент – 76,375, а второй – 0.
Округление числа с помощью формулы
В данном случае округление числа произошло в большую сторону. Чтобы округлить значение в меньшую сторону, следует выбрать функцию «ОКРУГЛВНИЗ».
Округление происходит до целого числа. В нашем случае до 77 или 76.
Функции и формулы в программе Excel помогают упростить любые вычисления. С помощью электронной таблицы можно выполнить задания по высшей математике.
Наиболее активно программу используют проектировщики, предприниматели, а также студенты.
Формулы EXCEL с примерами — Инструкция по применению
Проголосоватьgeek-nose.com
Какие есть формулы сокращенного умножения?
(a + b)2 = a2 + 2ab + b2.
(a – b)2 = a2 – 2ab + b2.
a2 – b2 = (a + b)(a – b).
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
(a – b)3 = a3 – 3a2b + 3ab2 – b3.
(a + b)(a2 – ab + b2) = a3
(a – b)(a2 + ab + b2) = a3 – b3.
Все формулы сокращенного умножения доказываются конкретным раскрытием скобок и приведением схожих слагаемых.
Пример 1. Докажите формулу a3 + b3 = (a + b)(a2 – ab + b2).
Решение. Раскрывая скобки и приводя подобные слагаемые, получаем:
(a + b)(a2 – ab + b2) = a3 – a2b + ab2 + ba2 – ab2 – b3 = a3 + b3,
что и обосновывает подходящую формулу.
Очень нередко приведение многочлена к стандартному виду есть возможность выполнить с помощью формул сокращенного умножения. Чтоб стремительно отыскивать требуемые преобразования, формулы сокращенного умножения необходимо знать назубок.
Пример 2. Упростите выражение (2×3 – 5z)(2×3 + 5z).
Решение. Пользуясь формулой разности квадратов, получаем:
(2x3 – 5z)(2x3 + 5z) = (2x3)2 – (5z)2 = 4x6 – 25z2.
Источники:
Глядеть также:
Источник материала Интернет-сайт www.genon.ru
new-best.com
100 формул / Все формулы по тригонометрии
Основные тригонометрические тождества
Формулы, связывающие тригонометрические функции одного и того же аргумента:
\(sin^2x+cos^2x=1\)
\(tgx= \frac{sinx}{cosx}\)
\(ctgx= \frac{cosx}{sinx}\)
\(tgxctgx=1\)
\(tg^2x+1= \frac{1}{cos^2x}\)
\(ctg^2x+1= \frac{1}{sin^2x}\)
Формулы двойного аргумента (угла)
\(sin2x=2cosxsinx\)
\(sin2x= \frac{2tgx}{1+tg^2x}= \frac{2ctgx}{1+ctg^2x} = \frac{2}{tgx+ctgx}\)
\(cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x\)
\(cos2x= \frac{1-tg^2x}{1+tg^2x}= \frac{ctg^2x-1}{ctg^2x+1}= \frac{ctgx-tgx}{ctgx+tgx} \)
\(tg2x= \frac{2tgx}{1-tg^2x}= \frac{2ctgx}{ctg^2x-1}= \frac{2}{ctgx-tgx}\)
\(ctg2x= \frac{ctg^2x-1}{2ctgx}= \frac{ctgx-tgx}{2}\)
Формулы тройного аргумента (угла)
\(sin3x=3sinx-4sin^3x\)
\(cos3x=4cos^3x-3cosx\)
\(tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}\)
\(ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}\)
Формулы половинного аргумента (угла)
\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\)
\(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\)
\(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\)
\(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\)
\(tg \frac{x}{2}= \frac{1-cosx}{sinx}= \frac{sinx}{1+cosx}\)
\(ctg \frac{x}{2}= \frac{1+cosx}{sinx}= \frac{sinx}{1-cosx}\)
Формулы квадратов тригонометрических функций
\(sin^2x= \frac{1-cos2x}{2}\)
\(cos^2x= \frac{1+cos2x}{2}\)
\(tg^2x= \frac{1-cos2x}{1+cos2x}\)
\(ctg^2x= \frac{1+cos2x}{1-cos2x}\)
\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\)
\(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\)
\(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\)
\(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\)
Формулы кубов тригонометрических функций
\(sin^3x= \frac{3sinx-sin3x}{4}\)
\(cos^3x= \frac{3cosx+cos3x}{4}\)
\(tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}\)
\(ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}\)
Формулы тригонометрических функций в четвертой степени
\(sin^4x= \frac{3-4cos2x+cos4x}{8}\)
\(cos^4x= \frac{3+4cos2x+cos4x}{8}\)
Формулы сложения аргументов
\(sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta\)
\(cos(\alpha + \beta) = cos \alpha cos \beta – sin \alpha sin \beta \)
\(tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 – tg \alpha tg \beta}\)
\(ctg(\alpha + \beta)= \frac{-1 + ctg \alpha ctg \beta }{ctg \alpha + ctg \beta}\)
\(sin(\alpha – \beta) = sin \alpha cos \beta – cos \alpha sin \beta\)
\(cos(\alpha – \beta) = cos \alpha cos \beta + sin \alpha sin \beta\)
\(tg(\alpha – \beta)= \frac{tg \alpha – tg \beta}{1 + tg \alpha tg \beta}\)
\(ctg(\alpha – \beta)= \frac{-1 – ctg \alpha ctg \beta }{ctg \alpha – ctg \beta}\)
Формулы суммы тригонометрических функций
\(sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha – \beta }{2}\)
\(cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha – \beta }{2}\)
\(tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta} \)
\(ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{sin \alpha sin \beta}\)
\((sin\alpha + cos\alpha)^2= 1+sin2\alpha \)
Формулы разности тригонометрических функций
\(sin\alpha – sin\beta = 2sin \frac{\alpha – \beta }{2} \cdot cos \frac{\alpha + \beta }{2}\)
\(cos\alpha – cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha – \beta }{2}\)
\(tg\alpha – tg\beta = \frac{sin(\alpha – \beta) }{cos \alpha cos \beta} \)
\(ctg\alpha – ctg\beta = – \frac{sin(\alpha – \beta) }{sin \alpha sin \beta}\)
\((sin\alpha – cos\alpha)^2= 1-sin2\alpha \)
Формулы произведения тригонометрических функций
\(sin\alpha \cdot sin\beta = \frac{cos(\alpha – \beta)-cos(\alpha + \beta)}{2}\)
\(sin\alpha \cdot cos\beta = \frac{sin(\alpha – \beta)+sin(\alpha + \beta)}{2}\)
\(cos\alpha \cdot cos\beta = \frac{cos(\alpha – \beta)+cos(\alpha + \beta)}{2}\)
\(tg\alpha \cdot tg\beta = \frac{cos(\alpha – \beta)-cos(\alpha + \beta)}{cos(\alpha – \beta)+cos(\alpha + \beta)} = \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta}\)
\(ctg\alpha \cdot ctg\beta = \frac{cos(\alpha – \beta)+cos(\alpha + \beta)}{cos(\alpha – \beta)-cos(\alpha + \beta)} = \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta}\)
\(tg\alpha \cdot ctg\beta = \frac{sin(\alpha – \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha – \beta)}\)
100formul.ru
Самые красивые физические и математические формулы.: lesovikov
Математик Анри Пуанкаре в книге «Наука и метод» писал: «Если бы природа не была прекрасна, она не стоила бы того, чтобы ее знать, жизнь не стоила бы того, чтобы ее переживать. Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».П.А.М. Дирак писал: “У теоретической физики есть еще один верный путь развития. Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой. Чтобы понять эту теорию, нужно обладать необычайно высокой математической квалификацией. Вы можете спросить: почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе”.
Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было. В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер. Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.
1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней “-1 представляет арифметику, i – алгебру, π – геометрию и e – анализ”.
2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.
3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе” темную энергию”). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.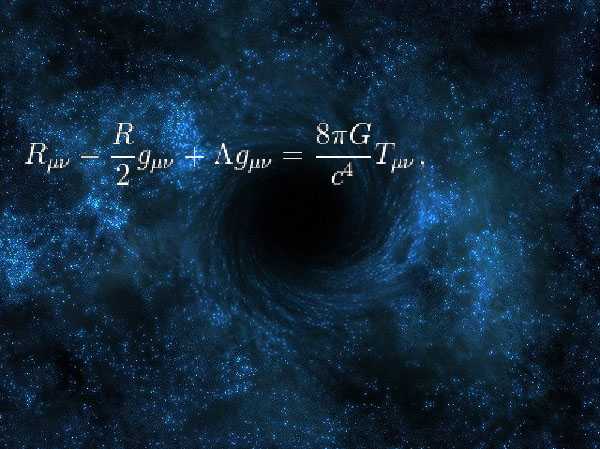
4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.
5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.
6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.
7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.
8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.
9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.
10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.
11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.
12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера – которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён – Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией – до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон – антиэлектрон, и предсказал наличие у электрона «спина» – вращения элементарной частицы.
13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»
14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.
lesovikov.livejournal.com
Какие есть формулы для расчета НДС (вычисление и выделение)?
Формула расчета НДС позволяет вычислить различные значения сумм, связанных с этим налогом. С помощью формул расчета НДС можно определить не только облагаемую налогом сумму, но и выделить его величину из суммарного значения. Об этих расчетах подробно говорится в настоящей статье.
Начисления НДС: основные требования
Как рассчитать НДС «сверху»?
Ставки налога, в том числе 18%, 10%, 0%
Как считать НДС: формулы вычисления и выделения НДС
Как вычислить НДС на онлайн-калькуляторе?
Начисления НДС: основные требования
Налог на добавленную стоимость был введен с 1992 года. Добавленная стоимость возникает на всех этапах производства продукции и при реализации облагается НДС. Этот налог позволяет государству изымать часть добавленной стоимости по утвержденным ставкам.
НДС оплачивают только в рублях. При использовании других валют НДС пересчитывается в рублях по курсу валюты на дату расчета. Фактической реализацией товара признается одна из более ранних дат: день отгрузки товара или день его оплаты.
Как рассчитать НДС «сверху»?
НДС рассчитывают как разницу стоимостей реализованной продукции и приобретенных для ее производства товаров, умноженную на ставку налога. По окончании налогового периода определяется сумма НДС для оплаты в бюджет. При этом фирмы используют право на вычеты согласно ст. 171 НК РФ.
Подробнее о вычетах по НДС читайте статью «Что такое налоговые вычеты по НДС?».
Как по формуле посчитать НДС по получаемым ТМЦ от продавца? Для этого достаточно стоимость товара умножить на коэффициент, полученный от деления ставки налога на 100.
Формула расчета НДС:
Нд = Ст * Нс / 100, где:
Нд — сумма НДС;
Ст — стоимость товара;
Нс — налоговая ставка.
Ставки налога, в том числе 18%, 10%, 0%
Согласно Налоговому кодексу к покупаемым товарам применяют следующие ставки: 0%, 10% и 18%.
Список реализуемых товаров с использованием ставки НДС 0% оговорен п. 1 ст. 164 НК. К ним относят драгметаллы и камни, товары космического назначения, экспортные товары и другие.
Подписывайтесь на наш бухгалтерский канал Яндекс.Дзен
ПодписатьсяК продукции, облагаемой по ставке 10%, принадлежат продовольственные, детские, медицинские и другие виды товаров, оговоренных в п. 2 ст. 164 НК РФ.
Вся остальная продукция облагается налогом по ставке 18%.
Как считать НДС: формулы вычисления и выделения НДС
Налог начисляют на стоимость продаваемого товара или услуги. Для этого берут их стоимость и увеличивают ее на сумму налога. Получается сумма для оплаты покупателем. Формула расчета стоимости с НДС такова:
См = Ст * (1 + Нс / 100), где:
См — стоимость при продаже товара.
Пример: при величинах Ст = 15 000, Нс = 18%
См = 15 000 * 1,18 = 17 700.
Для определения стоимости товара без налога используют следующую формулу:
Ст = См / (1 + Нс / 100).
Для выделения суммы НДС из стоимости товара нужно применить такую формулу расчета НДС:
Нд = См / (1 + Нс / 100).
Таким образом, данные формулы расчета НДС позволяют определить не только сумму НДС, но и стоимостные показатели сделки.
Как вычислить НДС на онлайн-калькуляторе?
Сами по себе расчеты налога не представляют сложности. Единственное, что может их осложнить, это количество.
Все приведенные выше формулы для расчета НДС можно использовать, если под рукой нет специального калькулятора для расчета НДС.
На нашем сайте представлен онлайн-калькулятор для расчета НДС — см. материал «Расчет НДС калькулятор онлайн».
Благодаря калькулятору удается максимально упростить подсчеты по НДС. Для этого в окно программы вводится сумма стоимости товара, а затем указывается ставка налога. Нажатием кнопки «Начислить НДС» можно найти стоимость товара с НДС. Кнопка «Выделить НДС» позволяет узнать НДС из введенной суммы. Нажав на кнопку «Сумма», вы сможете определить по значению НДС:
- стоимость товара;
- стоимость товара с налогом.
Использование калькулятора позволяет избежать вероятных ошибок при ручном подсчете НДС.
Вам также может быть полезен калькулятор для расчета взносов — см. материал «Онлайн-калькулятор страховых взносов и пеней по ним».
nalog-nalog.ru
Формула 1 на F1news.ru – все новости Формулы 1 2018

Отмар Сафнауэр прокомментировал столкновение Макса Ферстаппена и Эстебана Окона в Бразилии. Руководитель…

В Бразилии Льюис Хэмилтон одержал десятую победу в сезоне, но не ожидал такого успеха – инцидент между…

В Бразилии гонщики Haas F1 финишировали на восьмом и девятом местах, сократив отставание от Renault в…

Руководитель Mercedes Motorsport Тото Вольфф, комментируя итоги бразильской гонки, рассказал о том, что…

В Бразилии Red Bull Racing выглядела очень уверенно, но не добилась победы. Итоги уик-энда подвел руководитель…

Стартовав вторым, Себастьян Феттель финишировал шестым в Гран При Бразилии. После гонки пилот Ferrari…

Упустив победу в Гран При Бразилии из-за инцидента с Эстебаном Оконом, Макс Ферстаппен не скрывал недовольства…

После квалификации в Сан-Паулу Сергей Сироткин рассказал об инциденте, участниками которого были он и…

Единственным гонщиком Toro Rosso, вышедшим в финал квалификации в Бразилии, стал Пьер Гасли – француз…

Седьмое место на квалификации в Интерлагосе стало лучшим результатом в карьере Маркуса Эриксона. После…


Кими Райкконен прокомментировал итоги квалификации в Бразилии, где он показал четвёртый результат, и…
www.f1news.ru
