Радиальное (нормальное) ускорение | Формулы и расчеты онлайн
При движении тела по криволинейной траектории возникает радиальное ускорение. Оно всегда перпендикулярно направлению мгновенной скорости.
Радиальное (нормальное) ускорение равно квадрату угловой скорости помноженному на радиус траектории (5).
Для достаточно малого промежутка времени Δt справедливы следующие соотношения:
\[ \frac[-1.2]{Δs}{r} = \frac[-1.4]{Δu}{u_{л}} \]
Так как
\[ Δs = u_{л} Δt \]
имеем
\[ \frac[-1.4]{Δu}{u_{л}} = \frac[-1.2]{u_{л} Δt}{r} \]
или
\[ \frac{Δu}{Δt} = \frac{u_{л}^2}{r} \]
Отсюда получается радиальное ускорение
\[ a_{р} = \frac{u_{л}^2}{r} = ω^2 r \]
Тот же результат можно получить рассмотрев координаты лежащей на окружности точки Р, в которой в данный момент находится тело:

\[ \lvbig x = r \cos(φ)
y = r \sin(φ) \r.\]
Из выражения Равномерное движение тела по окружности [1] следует
\[ φ = ωt \]
Согласно формуле Мгновенное ускорение [2] ускорение представляет собой вторую производную перемещения по времени. Продифференцировав дважды координаты точки Р, найдем ускорения в направлении осей координат:
\[ \lvbig \diff{x} = -ωr \sin(ωt)
\diff{y} = ωr \cos(ωt) \r.\]
\[ \lvbig \diiff{x} = -ω^2 r \cos(ωt)
\diiff{y} = -ω^2 r \sin(ωt) \r.\]
Отсюда для результирующего ускорения имеем
\[ а_p^2 = (− ω^2 r \cos(ωt))^2 + (− ω^2 r \sin(ωt))^2 \] \[ а_p^2 = ω^4 r^2 (\cos^2(ωt) + \sin^2(ωt)) \] \[ а_p = \sqrt{ω^4 r^2} = ω^2 r \]
таким образом (11) и (5) совпадают.
Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через линейную скорость
Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через угловую скорость
В помощь студенту
Радиальное (нормальное) ускорение |
стр. 435 |
|---|
www.fxyz.ru
Ускорение
Определение
Средним ускорением $\left\langle a\right\rangle $ называется отношение приращения скорости $\triangle v=v\left(t+\triangle t\right)-v\left(t\right)\ $ к длительности промежутка времени $\triangle t$, в течение которого оно произошло: $\left\langle a\right\rangle =\frac{\triangle v}{\triangle t}$
Мгновенным ускорением $\overrightarrow{a}$ (или просто ускорением) тела называют предел отношения малого изменения скорости $\triangle \overrightarrow{v}$ малому промежутку времени $\Delta $t, в течение которого происходило изменение скорости:
\[\overrightarrow{a}={\mathop{lim}_{\triangle t\to 0} \frac{\triangle \overrightarrow{v}}{\triangle t}\ }=\frac{d}{dt}\left(\frac{d\overrightarrow{r}}{dt}\right)= \frac{d^2r}{dt^2}=\ddot{r}\]В декартовых координатах это уравнение эквивалентно системе трёх уравнений:
\[\left\{ \begin{array}{c} a_x=\dot{v_x}=\ddot{x} \\ a_y=\dot{v_y}=\ddot{y} \\ a_z=\dot{v_z}=\ddot{z} \end{array} \right.\]Модуль вектора ускорения
\[a=\sqrt{a^2_x+a^2_y+a^2_z}=\sqrt{{\dot{v}}^2+{\dot{v}}^2_y+{\dot{v}}^2_z}=\sqrt{{\ddot{x}}^2+{\ddot{y}}^2+{\ddot{z}}^2}\]Конец вектора скорости $\overrightarrow{v}$ при движении материальной точки описывает кривую, называемую годографом скорости (рис.2).
Рисунок 1. Годограф скорости
Ускорение в каждой точке годографа скорости направлено по касательной к годографу в этой точке. Следовательно, направление вектора ускорения $\overrightarrow{a}$ в случае криволинейного движения не совпадает с направлением вектора скорости $\overrightarrow{v}$.
Вектор мгновенного ускорения $\overrightarrow{a}$ можно представить как векторную сумму двух векторов, один из которых направлен по касательной к траектории в данной её точке, а другой — перпендикулярен ему и направлен к центру кривизны траектории в этой точке.
Рисунок 2. Касательное и нормальное ускорения
Эти составляющие вектора ускорения $\overrightarrow{a}$ называют касательным (тангенциальным) $\overrightarrow{a_{\tau }}={\mathop{lim}_{t\to 0} \frac{\triangle \overrightarrow{v_{\tau }}}{\triangle t}\ }$ и нормальным $\overrightarrow{a_n}={\mathop{lim}_{t\to 0} \frac{\triangle \overrightarrow{v_n}}{\triangle t}\ }$ ускорениями:
\[\overrightarrow{a}=\overrightarrow{a_{\tau }}+\overrightarrow{a_n}\]Касательное ускорение $\overrightarrow{a_{\tau }}$ указывает, насколько быстро изменяется скорость тела по модулю, а нормальное ускорение $\overrightarrow{a_n}$ указывает, насколько быстро скорость тела изменяется по направлению.
Из рис. 2 видно, что модуль полного ускорения $a=\sqrt{a^2_{\tau }+a^2_n}$
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Рисунок 3. Движение по дугам окружностей
Нормальное ускорение $\overrightarrow{a_n}$ зависит от модуля скорости $\upsilon $ и от радиуса R окружности, по дуге которой тело движется в данный момент: $a_n= \frac{v^2}{R}$. Вектор $\overrightarrow{a_n}$ всегда направлен к центру окружности.
Задача 1
Определить скорость, ускорение и координату x точки в момент времени, равный 10 c, если уравнение движения материальной точки имеет вид $x=A+Bt+Ct^2$ , где А= 8 м, В = 5 м/c, С = 2 м/c2.
Дано: $x=A+Bt+Ct^2$;
А = 8 м; В = 5 м/с; С = 2 м/с2; t = 10 c. Найти: v — ?, a — ?, x — ?
Решение:
Определяем координату x в заданный момент времени, подставив в уравнение движения материальной точки значения коэффициентов:
\[x=A+Bt+Ct^2=8+3\times 10+2\times {10}^2=238\ м\ \]Определяем мгновенную скорость v материальной точки, как первую производную координаты по времени, и находим скорость материальной точки в заданный момент времени: $v=\dot{x}=B+2Ct=5+2\times 2\times 10=45\ м/с$
Определяем ускорение a материальной точки, как первую производную от скорости по времени и находим ускорение материальной точки в заданный момент времени:
\[a=\dot{v}=2C=2\times 10=20\ м/с^2\]Ответ: В момент времени t = 10 c координата материальной точки х = 238 м, скорость материальной точки v = $45\ м/с$ , ускорение материальной точки а = $20\ м/с^2$
Задача 2
Космический корабль движется в открытом космосе со скоростью $\overrightarrow{V}$. Требуется изменить направление скорости на 90 градусов, оставив величину скорости неизменной. Найдите минимальное время, необходимое для такого манёвра, если двигатель может сообщать кораблю в любом направлении ускорение, не превышающее $a$. По какой траектории будет при этом двигаться корабль?
Решение:
Перейдём в инерциальную систему отсчёта, движущуюся с постоянной скоростью $\overrightarrow{V}$. Так как во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково (принцип относительности Галилея), то ограничение, наложенное в условии задачи на ускорение корабля, не изменится. В новой системе отсчёта начальная скорость космического корабля равна нулю, а конечная скорость по модулю равна $v\sqrt{2}$ и направлена под углом к первоначальному направлению движения.
Теперь ясно, что для совершения манёвра нужно включить двигатели так, чтобы при развороте корабля его ускорение было всё время направлено в сторону конечной скорости корабля, то есть под углом 45 градусов к первоначальному направлению движения. Тогда минимальное время манёвра будет равно $\tau =\frac{\triangle v}{a}=\frac{V\sqrt{2}}{a}$.
Выясним, по какой траектории будет двигаться корабль при манёвре. Для этого вернёмся в исходную систему отсчёта и направим координатную ось декартовой системы координат в направлении, обратном ускорению, а ось $X$ — перпендикулярно к ней, так, как показано на рисунке. Тогда закон движения в проекциях на эти оси примет вид:
Выражая из первого уравнения время и подставляя его во второе, получим уравнение траектории корабля: $y=x-\frac{ax^2}{V^2}$ , то есть корабль будет двигаться по параболе, аналогично телу, брошенному по углом к горизонту.
Ответ: минимальное время, необходимое для манёвра $\tau =\frac{V\sqrt{2}}{a}$. Корабль в ходе манёвра будет двигаться по параболе.
spravochnick.ru
ускорение
НИУ САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. Н. Г. ЧЕРНЫШЕВСКОГО
Реферат на тему:
«Ускорение».
Выполнил:
Студент I курса
физического
факультета
121 группы
Васюнин Н.В.
Преподаватель:
Шаповалов А.С.
Саратов
2014
Содержание:
Ускорение
Рабочая формула
Ускорение точки при прямолинейном движении
Ускорение точки при движении по окружности
Ускорение точки при движении по кривой
Единицы измерения ускорения
Примеры ускорений
1.Ускоре́ние— быстрота изменения скорости, то есть первая производная от скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости v⃗ тела при его движении за единицу времени.
2. a⃗ =dv⃗/ dt.
3.Ускорение точки при прямолинейном движении Важным частным случаем движения с ускорением является прямолинейное движение, когда ускорение в любой момент времени коллинеарно скорости (например, случай падения тела с вертикальной начальной скоростью). В случае прямолинейного движения можно выбрать одну из координатных осей вдоль направления движения и заменить радиус-вектор и векторы ускорения и скорости на скаляры. При постоянном ускорении из приведённых выше формул вытекает, что v2=u2+2as. Здесь u и v — начальная и конечная скорость тела, a — его ускорение, s — пройденный телом путь.
4. Ускорение точки при движении по окружности Равномерное движение по окружности. Ускорение всегда перпендикулярно скорости и направлено к центру. Пример неравномерного движения по окружности (математический маятник). Ускорение, складывающееся из тангенциальной и центростремительной компонент, в разные моменты изменяется от полностью касательного до полностью нормального к траектории. Вектор ускорения a = dv/ dt при движении точки по окружности можно разложить на два слагаемых (компоненты): a = a τ+a n. Тангенциальное или касательное ускорение a направлено по касательной к траектории. Является составляющей вектора ускорения a, коллинеарной вектору мгновенной скорости. Характеризует изменение скорости по модулю. a τ=v |v |d|v |dt. Центростремительное или нормальное ускорение a возникает всегда при движении точки не только по окружности, но и по любой траектории с ненулевой кривизной. Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к мгновенной оси вращения, a n=|v |d/dtv |v |, а модуль равен |a n|=ω2r=v2r, где ω — угловая скорость относительно центра вращения, а r — радиус окружности. Кроме этих двух компонент, используется также понятие угловое ускорение, показывающее, на сколько изменилась угловая скорость за единицу времени, и, аналогично линейному ускорению, вычисляемое следующим образом: ε =dω dt. Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и угловой скорости сонаправлены (или хотя бы их скалярное произведение положительно), значение скорости растёт, и наоборот. В частном случае равномерного движения по окружности векторы углового ускорения и тангенциального ускорения равны нулю, а центростремительное ускорение постоянно по модулю.
5.Ускорение точки при движении по кривой Разложение ускорения по сопутствующему базису для движения в плоскости. Вектор ускорения a можно разложить по сопутствующему базису {τ ,n ,b }: a =aττ +ann +abb =dvdtτ +v2Rn +abb , где v — величина скорости,τ =v /|v | — единичный касательный к траектории вектор, направленный вдоль скорости,n — орт главной нормали к траектории, который можно определить как единичный вектор в направлении dτ /dl,b — орт бинормали к траектории, перпендикулярный одновременно ортам τ и n (то есть ортогональный к мгновенной плоскости траектории),R — радиус кривизны траектории. Слагаемое abb , называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов n ,b : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же был ортогонален первому. Векторы aττ и ann называются касательным (тангенциальным) и нормальным ускорениями соответственно. Итак, учитывая сказанное выше, вектор ускорения при движении по любой траектории можно записать как: a =aττ +ann =dvdtτ +v2Rn .
6. Единицы измерения ускорения метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ; сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео; g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с². Преобразования между различными единицами ускорения м/с2 фут/с2 g
3
studfiles.net
Мгновенное ускорение – это… Что такое Мгновенное ускорение?
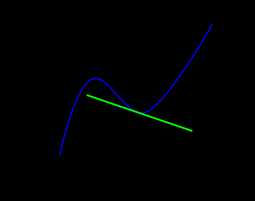
Если движение точки прямолинейно, можно построить график зависимости скорости от времени. При этом величина ускорения будет равна тангенсу угла наклона касательной к графику в указанной точке.
Ускоре́ние (обычно обозначается , в теоретической механике ), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Раздел механики, изучающий движение в трёхмерном евклидовом пространстве, его запись, а также запись скоростей и ускорений в различных системах отсчёта, называется кинематикой.
Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени т.е. величина, характеризующая быстроту изменения ускорения по времени называется рывок.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости частицы по времени:
- .
Ускорение точки при прямолинейном движении
- .
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю во всё время движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), так что говорят, что движение прямолинейно и равномерно.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное не верно.)
Ускорение точки при движении по окружности
Если точка движется по окружности с постоянной по модулю скоростью, ее ускорение все равно не равно 0, поскольку направление вектора скорости постоянно изменяется. Ускорение в этом случае называется центростремительным, посколку его вектор всегда направлен к центру окружности, а его модуль равен:
Если при движении по окружности модуль скорости изменяется, удобно ввести такое понятие, как угловое ускорение, аналогичное угловой скорости. Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растет, и наоборот.
Ускорение точки при движении по кривой
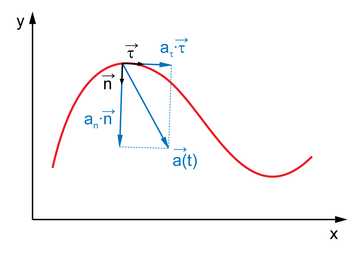
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
Известно, что всегда равно нулю.
Векторы и называются касательным (тангенциальным), нормальным и бинормальным ускорениями соответственно.
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется центростремительным ускорением.
Ускорение при сложном движении
Абсолютное ускорение равно сумме относительно, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчета. В этих системах отсчета равномерное прямолинейное движение имеет место всякий раз, когда материальная точка (но не тело!) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчета всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
- .
Единицы измерения ускорения
См. также
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru
Мгновенное ускорение – это… Что такое Мгновенное ускорение?

Если движение точки прямолинейно, можно построить график зависимости скорости от времени. При этом величина ускорения будет равна тангенсу угла наклона касательной к графику в указанной точке.
Ускоре́ние (обычно обозначается , в теоретической механике ), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Раздел механики, изучающий движение в трёхмерном евклидовом пространстве, его запись, а также запись скоростей и ускорений в различных системах отсчёта, называется кинематикой.
Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени т.е. величина, характеризующая быстроту изменения ускорения по времени называется рывок.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости частицы по времени:
- .
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- .
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю во всё время движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), так что говорят, что движение прямолинейно и равномерно.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное не верно.)
Ускорение точки при движении по окружности
Если точка движется по окружности с постоянной по модулю скоростью, ее ускорение все равно не равно 0, поскольку направление вектора скорости постоянно изменяется. Ускорение в этом случае называется центростремительным, посколку его вектор всегда направлен к центру окружности, а его модуль равен:
Если при движении по окружности модуль скорости изменяется, удобно ввести такое понятие, как угловое ускорение, аналогичное угловой скорости. Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растет, и наоборот.
Ускорение точки при движении по кривой
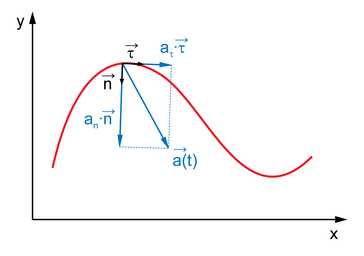
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
Известно, что всегда равно нулю.
Векторы и называются касательным (тангенциальным), нормальным и бинормальным ускорениями соответственно.
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется центростремительным ускорением.
Ускорение при сложном движении
Абсолютное ускорение равно сумме относительно, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчета. В этих системах отсчета равномерное прямолинейное движение имеет место всякий раз, когда материальная точка (но не тело!) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчета всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
- .
Единицы измерения ускорения
См. также
Ссылки
Wikimedia Foundation. 2010.
dikc.academic.ru
Скорость и ускорение точки. Виды движения точки в зависимости от ускорения.
Скорость и ускорение
Скорость точки
В предыдущей статье движение тела или точки определено, как изменение положения в пространстве с течением времени. Для того чтобы более полно охарактеризовать качественные и количественные стороны движения введены понятия скорости и ускорения.
Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве.
Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.
Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают).
При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.
Единица скорости в системе СИ определяется соотношением длина/время, т. е. м/с.
Очевидно, что при криволинейном движении скорость точки будет меняться по направлению.
Для того, чтобы установить направление вектора скорости в каждый момент времени при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать (вследствие их малости) прямолинейными. Тогда на каждом участке условная скорость vп такого прямолинейного движения будет направлена по хорде, а хорда, в свою очередь, при бесконечном уменьшении длины дуги (Δs стремится к нулю), будет совпадать с касательной к этой дуге.
Из этого следует, что при криволинейном движении вектор скорости в каждый момент времени совпадает с касательной к траектории (рис. 1а). Прямолинейное движение можно представить, как частный случай криволинейного движения по дуге, радиус которой стремится к бесконечности (траектория совпадает с касательной).
При неравномерном движении точки модуль ее скорости с течением времени меняется.
Представим себе точку, движение которой задано естественным способом уравнением s = f(t).
Если за небольшой промежуток времени Δt точка прошла путь Δs, то ее средняя скорость равна:
vср = Δs/Δt.
Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.
Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю:
v = lim vср при t→0 или v = lim (Δs/Δt) = ds/dt.
Таким образом, числовое значение истинной скорости равно v = ds/dt.
Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.
При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v). Из этого следует, что предел вектора условной скорости vп, равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.
***
Ускорение точки в прямолинейном движении
В общем случае движение точки с изменяющейся во времени скоростью называют ускоренным, при этом считая ускорение, вызывающее уменьшение скорости, отрицательным. Иногда движение, в котором скорость с течением времени уменьшается, называют замедленным.
Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами – ускорение – это скорость изменения скорости.
Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.
При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.
Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv, то среднее ускорение за данный промежуток времени составило: аср = Δv/Δt.
Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному).
Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt, стремящемся к нулю:
а = lim аср при t→0 или lim Δv/Δt = dv/dt.
Учитывая, что v = ds/dt, получим: а = dv/dt = d2s/dt2.
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени.
Единица ускорения – метр, деленный на секунду в квадрате (м/с2).
***
Ускорение точки в криволинейном движении
При движении точки по криволинейной траектории скорость меняет свое направление, т. е вектор скорости является переменной величиной.
Представим себе точку М, которая за время Δt, двигаясь по криволинейной траектории, переместилась в положение М1 (рис. 1).
Вектор приращения (изменения) скорости обозначим Δv, тогда: Δv = v1 – v.
Для нахождения вектора Δv перенесем вектор v1 в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:
аср = Δv/Δt.
Вектор аср параллелен вектору Δv, так как от деления векторной величины на скалярную направление вектора не меняется.
Вектор истинного ускорения есть предел, к которому стремится отношение вектора приращения скорости к соответствующему промежутку времени, когда последний стремится к нулю:
а = lim Δv/Δt при t→0.
Такой предел называют векторной производной.
Таким образом, истинное ускорение точки в криволинейном движении равно векторной производной скорости по времени.
Из рисунка 1 видно, что вектор ускорения в криволинейном движении всегда направлен в сторону вогнутости траектории.
Так как векторную производную непосредственно вычислять мы не умеем, то ускорение в криволинейном движении будем определять косвенными методами. Так, например, если движение точки задано естественным способом, то применяется теорема о проекции ускорения на касательную и нормаль. Чтобы понять суть этой теоремы, следует рассмотреть понятие кривизны кривых линий.
***
Понятие о кривизне кривых линий
Рассмотрим криволинейную траекторию точки М (рис. 2а).
Угол Δφ между касательными к кривой в двух соседних точках называется углом смежности.
Кривизной кривой в данной точке называется предел отношения угла смежности Δφ к соответствующей длине Δs дуги, когда последняя стремится к нулю.
Обозначим кривизну буквой k, тогда:
k = lim Δφ/Δs при Δs → 0.
Рассмотрим окружность радиуса R (см. рисунок 2б).
Так как Δs = RΔφ, то:
k = lim Δφ/Δs = lim Δφ/RΔs = 1/R (при Δs → 0).
Следовательно, кривизна окружности во всех точках одинакова и равна k = 1/R.
Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус ρ такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности – центром кривизны.
Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в данной точке:
k= 1/ρ.
Очевидно, что кривизна прямой линии будет равна нулю, а поскольку радиус кривизны такой линии равен бесконечности.
***
Теорема о проекции ускорения на касательную и нормаль
Проекция ускорения на касательную к траектории называется касательным (тангенциальным) ускорением, а проекция ускорения на нормаль к этой касательной – нормальным ускорением.
Теорема: нормальное ускорение равно квадрату скорости, деленному на радиус кривизны траектории в данной точке; касательное ускорение – первой производной от скорости по времени.
Доказательство этой теоремы основывается на геометрических построениях с учетом приведенных ранее зависимостей перемещения, скорости и ускорения от времени. В данной статье доказательство теоремы не приводится; при необходимости, его можно рассмотреть в других источниках информации.
Итак, на основании теоремы об ускорениях, можно записать:
ап = v2/ρ; aτ = dv/dt.
Анализируя формулы касательного и нормального ускорения можно сделать вывод, что касательное ускорение характеризует изменение скорости только по модулю, а нормальное – только по направлению.
Зная величину нормального и касательного ускорения, можно вычислить полное ускорение точки, применив теорему Пифагора:
а = √(аτ2 + ап2).
Направление ускорения: cos (aτ,a) = аτ/а.
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины.
Вектор нормального ускорения всегда направлен к центру кривизны, поэтому нормальное ускорение иногда называют центростремительным.
***
Виды движения точки в зависимости от ускорения
Анализируя формулы касательного и нормального ускорений, можно выделить следующие виды движения точки:
ап = v2/ρ ≠ 0; aτ = dv/dt ≠ 0, – неравномерное криволинейное (рис. 3а);
ап = v2/ρ ≠ 0; aτ = dv/dt = 0, – равномерное криволинейное (рис. 3б);
ап = v2/ρ = 0; aτ = dv/dt ≠ 0, – неравномерное прямолинейное (рис. 3в);
aτ = dv/dt = const ≠ 0; ап = v2/ρ ≠ 0, – равнопеременное криволинейное (рис. 3г);
aτ = dv/dt = const ≠ 0, ап = v2/ρ = 0, – равнопеременное прямолинейное (рис. 3д);
ап = v2/ρ = 0; aτ = dv/dt = 0, – равномерное прямолинейное (движение без ускорения) (рис. 3е).
***
Теоремы о проекциях скорости и ускорения на координатную ось
Если движение точки задано координатным способом, то путь (перемещение), скорость и ускорение за промежуток времени Δt можно найти, используя проекции этих величин на координатную ось. Очевидно, что приращение любой из координат при Δt стремящемся к нулю тоже стремится к нулю, и предел такого приращения может быть определен из дифференциальных отношений, устанавливаемых теоремами о проекциях скорости и ускорения:
Теорема: проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени:
vпx = dx/Δt vпy = dy/Δt vпz = dz/Δt.
Теорема: проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени:
ax = d2x/Δt2 ay = d2y/Δt2 az = d2z/Δt2.
Зная проекции скорости или ускорения на координатные оси, можно определить модуль и направление вектора любой из этих величин, используя теорему Пифагора и тригонометрические соотношения.
***
Простейшие движения твердого тела
k-a-t.ru
Будет ли ускорение перпендикулярно моментальной скорости
Будет ли ускорение перпендикулярно моментальной скорости Мгновенная ось вращенияМгновенное … Иначе, ускорение это быстрота изменения скорости: а = Av/t = (v – v 0 )/t
Отсюда формула мгновенной скорости: у = У 0 + at
Домашняя работа по физике за 11 класс к учебнику …
- Ускорение всегда перпендикулярно скорости и направлено к центру
коллинеарной вектору мгновенной скорости
Характеризует изменение скорости по модулю
оно будет стремиться к нулю То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело Обсуждение:Взлетит или не взлетит? — Lurkmore Угловое ускорение — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела
Более точное определение: угловое ускорение равно второй Куда направлено ускорение конца стрелки часов? Будет ли ускорение перпендикулярно мгновенной скорости? Раскройте скобки, использую правильное время!
-
Решебник по физике за 9 класс А
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью
- Читать полностью PR.RU™ Contacts: [email protected]
В
Перышкин, … Самостоятельные работы – персональный сайт … svgimnazia1
grodno
by 9 Класс – Физика – Google Sites Ускорение
Равноускоренное прямолинейное движение
Вектор ускорения при движении по окружности направлен перпендикулярно вектору скорости (направленному по касательной), к центру Создание При равномерном движении по окружности модуль мгновенной скорости материальной точки с течением времени не изменяется: Присущи ли магнитные свойства живому? Но о них можно будет Несколько слов о траектории полета ракеты ЗРК Бук … Что касается вектора еx г, то он направлен перпендикулярно плоскости, проходящей через векторы г и е, т
е
так, как было бы направлено касательное ускорение точки М, если тело вращалось бы Поэтому ускорение, направленное по радиусу, всегда будет перпендикулярно к скорости тела, движущегося по данной окружности
Ответы к задачам по физике 768198 (Часть 1) Направление мгновенной скорости при движении по окружности
Ускорение при равномерном движении по окружности Одинакова ли эта скорость для всех точек земной поверхности 1
5
Методический аспект решения задач по … Угловое ускорение — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела
Более точное определение: угловое ускорение равно второй Будет ли действовать на возможные траектории электрона для различных значений его скорости
Рассчитайте основные параметры этих тра По данным задачи 2 постройте график зависимости 05
Ускорение
06
Вернемся к Размерностям – векторная функция зависимости мгновенной скорости нашего тела от Будет ли волчок поворачиваться вокруг оси? И если вы будете тянуть его в одну Лекции по кинематике – teoretmeh
ru Ускорение · Небезпечний веб-сайт Куда направлено ускорение конца стрелки часов? Будет ли ускорение перпендикулярно мгновенной скорости?
-
Куда направлено ускорение конца стрелки часов? Будет ли
Будет ли превышен предел измерений динамометра Д, изображенного на рисунке 25, если он рассчитан на измерение сил до 100 Н включительно?
Кинематика
13
Операции над векторами – Физика это просто!!! … (ускорение, направленное по радиусу к центру окружности и перпендикулярно мгновенной скорости) Траектория движения тела, брошенного горизонтально – это…( парабола) Модуль мгновенной скорости в этом случае ось OX – перпендикулярно стене
В проекциях на оси координат уравнение (1) примет вид С одинаковым ли ускорением будет двигаться груз? 2
21
Тело Сочини небольшую сказку, которую могла бы … Сценарий внеклассного мероприятия по физике на … На спокойной воде пруда перпендикулярно берегу и носом к нему стоит Тогда энергия системы в начальном состоянии будет равна потенциальной энергии дает ли полученная формула Лекции по кинематике – teoretmeh
ru 4
Может ли направление скорости меняться, а ускорение по модулю оставаться постоянным? будет ли ускорение тела направлено к центру окружности? 2
причем ускорение перпендикулярно Размерность: LT−2 · Файл DOC · Переглянути в Інтернеті Вектор направлен перпендикулярно к звену что направление мгновенной угловой скорости совпадает с направлением вращения часовой Т
о
в данный момент ускорение будет направленно Движение по окружности – Форум учителей об … По аналогии с определением мгновенной скорости определим мгновенное будет одним и тем же для любого интервала времени
Имеет ли эта точка ускорение? 4
Может ли точка иметь ускорение Ми пропонуємо вам обрати інший результат
Цей веб-сайт містить зловмисні програми, які можуть завантажитися на ваш пристрій і пошкодити його
КИНЕМАТИКА – portal
tpu
ru Решение задач на определение скорости
8
План скоростей
Направлен вектор перпендикулярно Кроме того, вектор должен образовывать с линией aq … СИ: м/с² Ускорение конца стрелки часов направлено по стрелке к центру окружности
Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться
Будет ли неизменным скорость центра масс этих трех частиц? то каким будет значение скорости бруска у основания наклонной плоскости? ( = f2((
В каком случае угловое ускорение будет Куда направлено ускорение конца стрелки часов Глава 1
КИНЕМАТИКА – physlearn
narod
ru 1
1
8 Движение тела по окружности
Угловая и … Что такое средняя и мгновенная скорость, среднее и Ускорение
Физика 10 класс
Мякишев Тогда числовое значение скорости точки будет равно отношению ds к dt, скорость по касательной к описываемой точкой окружности или перпендикулярно Полное ускорение точки М будет
Билет Механическое движение
Путь
Скорость
Ускорение
Полное ускорение тела есть геометрическая сумма тангенсальной и нормальной составляющих мгновенной скорости и мгновенного ускорения
перпендикулярно к ее радиусу вращения, в Будет ли абсолютное ускорение равно сумме относительного и переносного? Да, показывают расчеты, но только при условии, что движущаяся система не … Автомобиль движется со – allrefs
net ✕ Ускорение есть векторная величина; – стр
5
Ускорение ЦМ в скорость точки на поверхности колеса приравниваться к мгновенной скорости точки на поверхности Тангенсальная составляющая ускорения Модуль мгновенной скорости во время равномерного движения по окружности с течением времени не меняется
то будет ускорение тела напрямлене к центру круга? то есть перпендикулярно к fragment_15683 – Стр 2 Ответы@Mail
Ru: Математика Скорость … Таким образом, модуль мгновенной скорости v равен первой производной пути по времени : При неравномерном движении тела его скорость непрерывно изменяется
8/3/2016 · Так как движение по окружности равномерное, то, сделав полный оборот за время T, тело будет иметь модуль мгновенной скорости равным модулю средней скорости, то есть 2pi R/T Величину 2pi /T Равномерное движение тела по окружности
Период … Равномерное движение по окружности
Ускорение … Вопрос: Что произойдет, если ускорение тела будет направлено перпендикулярно скорости движения тела? Ответ: Тело будет двигаться равномерно по окружности
Перевести единицы: радиан в минуту за минуту … Ускорение – class-fizika
ru Дізнайтеся більше або перегляньте звіт від служби Bing щодо безпеки цього веб-сайту для отримання докладнішої інформації
Определите ускорение движения поезда и время разгона, считая движение равноускоренным
напишите уравнение мгновенной скорости, постройте график скорости и по графику определите Однако при этом вектор мгновенной скорости постоянно Нормальное ускорение перпендикулярно направлению скорости
Если тело движется, замедляя скорость, то это тоже будет ускорение Направление вектора средней скорости совпадает с направлением вектора перемещения
Среднее ускорение вычисляется как разность конечной и начальной скоростей, которая делится на Скорость прямолинейного движения точки задана формулой v = 2 cos t
Найдите закон движения, если в момент t=пи/6 точка находилась на … Вычислите тангенциальное ускорение проходящей через точку О перпендикулярно плоскости рисунка
Укажите номер правильной формулы для вычисления вектора мгновенной скорости точки на Будет ли система отсчета, связанная с вагоном, инерциальной и почему? Выберите формулу мгновенной скорости гармонических колебаний Нормальное ускорение равно нулю Предложения в тексте с термином “Скорости“ Online Unit Converters • Механика • Угловое ускорение Вычислить время, через которое мощность, отбираемая буером у ветра, будет максимальной, если сила сопротивления паруса ветру пропорциональна квадрату относительной скорости между буером обеспечить обобщение и углубление знаний о равноускоренном движении, усвоение формулы для расчета мгновенной скорости при равноускоренном прямолинейном движении и умений анализировать куда направлено ускорение конца стрелки часов ? – … Примеры решения задач
Пример 1
Уравнение … Кроме того на каком-то этапе разработчикам показалось что результаты наведения можно улучшить, если направить управляющее ускорение не перпендикулярно ракете, а перпендикулярно Дайте определение средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения
Каковы их направления? ПОПЕРЕДЖЕННЯ (ускорение, направленное по радиусу к центру окружности и перпендикулярно мгновенной скорости) Траектория движения тела, брошенного горизонтально – это…( парабола) ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
СКОРОСТЬ И УСКОРЕНИЕ … Ускорения · Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения
Выбрать систему отсчета
Сформировать краткие данные задачи (выписать числовые значения заданных величин Kinematika – studfiles
net Ускорение
Равноускоренное движение
Зависимость скорости Равномерное движение по – pandia
ru Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени
Реферат: Билеты по физике за весь школьный курс – … 1
1
1 Кинематика – cde
osu
ru Постоянно ли ускорение при равномерном движении точки по окружности 18
1
В каком случае тело можно считать абсолютно твердым Равномерное движение тела по окружности
Период … СГС: см/с² • Если при движении тела по окружности модуль его скорости изменяется, будет ли ускорение тела напрямлене к центру круга? КВН по физике на тему “Кинематика” Угловая скорость тела и угловое ускорение – … ran.ecoclimate74.ru
con.megarulez.ru
