Криволінійний рух. Прискорення при криволінійному русі
Криволінійний рух – це рух, траєкторія якого представляє собою криву лінію (наприклад, окружність, еліпс, гіперболу, параболу). Прикладом криволінійного руху є рух планет, кінця стрілки годинника по циферблату і т. д. У загальному випадку швидкість при криволінійніному русі змінюється за величиною і по напрямку. Криволінійний рух матеріальної точки вважається рівномірним рухом, якщо модуль швидкості постійний (наприклад, рівномірний рух по колу), і є рівноприскореним, якщо модуль і напрям швидкості змінюється (наприклад, рух тіла, кинутого під кутом до горизонту).
Рис. 1.19. Траєкторія і вектор переміщення при криволінійному русі.
При русі по криволінійній траєкторії вектор переміщення направлений по хорді (рис. 1.19), а l – довжина траєкторії. Миттєва швидкість руху тіла (тобто швидкість тіла в даній точці траєкторії) спрямована по дотичній у точці траєкторії, де в даний момент знаходиться рухоме тіло (рис. 1.20).
Рис. 1.20. Миттєва швидкість при криволінійному русі.
Прискорення при криволінійному русі
Криволінійний рух – це завжди прискорений рух. Тобто прискорення при криволінійному русі є завжди, навіть якщо модуль швидкості не змінюється, а змінюється тільки напрям швидкості. Зміна величини швидкості за одиницю часу – це тангенціальне прискорення:
або
Де vτ, v0 – величини швидкостей
в момент часу t0 + Δt
t0 відповідно.
Тангенціальне прискорення в даній точці траєкторії за напрямом збігається з напрямком швидкості руху тіла або протилежне йому.
Нормальне прискорення – це зміна швидкості по напрямку за одиницю часу:
Нормальне прискорення спрямоване по радіусу кривизни траєкторії (до осі обертання). Нормальне прискорення перпендикулярно до напрямку швидкості.
Доцентрове прискорення – це нормальне прискорення при рівномірному русі по колу.
Повне прискорення при рівномірному криволінійному русі тіла дорівнює:
Рух тіла по криволінійній траєкторії можна наближено представити як рух по дугам деяких кіл (рис. 1.21).

Рис. 1.21. Рух тіла при криволінійному русі.
physic.cx.ua
Прямолінійний рівноприскорений рух. Прискорення
Тепер ми переходимо до розгляду нерівномірного руху. З усіх видів нерівномірного руху ми будемо вивчати найпростіше – прямолінійний рівноприскореному, при якому тіло рухається вздовж прямої лінії, а проекція вектора швидкості тіла за будь-які рівні проміжки часу змінюється однаково (при цьому модуль вектора швидкості може як збільшуватися, так і зменшуватися).
Наприклад, якщо швидкість рухомого по злітній смузі літака за будь-які 10 з збільшується на 15 м / с, за будь-які 5 с – на 7,5 м / с, в кожну секунду – на 1,5 м / с і т. Д., то літак рухається равноускоренно.
У даному випадку під швидкістю руху літака мається на увазі його так звана миттєва швидкість, т. Е. Швидкість в кожній конкретній точці траєкторії у відповідний момент часу (більш суворе визначення миттєвої швидкості буде дано в курсі фізики старших класів).
Миттєва швидкість тіл, що рухаються равноускоренно, може змінюватися по-різному: в одних випадках швидше, в інших – повільніше. Наприклад, швидкість звичайного пасажирського ліфта середньої потужності за кожну секунду розгону збільшується на 0,4 м / с, а швидкісного – на 1,2 м / с. У таких випадках кажуть, що тіла рухаються з різним прискоренням.
Розглянемо, яка фізична величина називається прискоренням.
Нехай швидкість деякого тіла, що рухається равноускоренно, за проміжок часу t змінилася від v0 до v. Під v0 мається на увазі початкова швидкість тіла, т. Е. Швидкість в момент t0 = О, прийнятий за початок відліку часу. А v – це швидкість, яку тіло мало до кінця проміжку часу t, який починається від t0 = 0. Тоді за кожну одиницю часу швидкість змінювалася на величину
Це відношення позначається символом а й називається прискоренням:
Прискоренням тіла при прямолінійному рівноприскореному русі називається векторна фізична величина, що дорівнює відношенню зміни швидкості до проміжку часу, за який ця зміна відбулася
Прискорення – векторна величина, яка характеризується не тільки модулем, але й напрямком.
Модуль вектора прискорення показує, на скільки змінюється модуль вектора швидкості в кожну одиницю часу. Чим більше прискорення, тим швидше змінюється швидкість тіла.
За одиницю прискорення в СІ приймається прискорення такого рівноприскореного руху, при якому за 1 с швидкість тіла змінюється на 1 м / с:
Таким чином, в СІ одиницею прискорення є метр на секунду в квадраті (м / с2).
Застосовуються й інші одиниці прискорення, наприклад 1 см / с2.
Обчислити прискорення тіла, що рухається прямолінійно і равноускоренно, можна за допомогою наступного рівняння, в яке входять проекції векторів прискорення і швидкості:
Покажемо на конкретних прикладах, як знаходиться прискорення. На малюнку 8, а зображені санки, які равноускоренно скочуються з гори.
Рівноприскореного руху санок
Рис. 8. Рівноприскорений рух санок, що скочуються з гори (АВ) і продовжують рух по рівнині (CD)
Відомо, що ділянка шляху АВ санки пройшли за 4 с. При цьому в точці А вони мали швидкість, рівну 0,4 м / с, а в точці В – швидкість, рівну 2 м / с (санки прийняті за матеріальну точку).
Визначимо, з яким прискоренням рухалися санки на ділянці АВ.
В даному випадку за початок відліку часу слід прийняти момент проходження санками точки А, оскільки згідно з умовою саме від цього моменту відраховується проміжок часу, за який модуль вектора швидкості змінився від 0,4 до 2 м / с.
Тепер проведемо вісь X, паралельну вектору швидкості руху санок і спрямовану в ту ж сторону. Спроеціруем на неї початку і кінці векторів v0 і v. Утворилися при цьому відрізки v0x і vx є проекціями векторів v0 і v на вісь X. Обидві ці проекції позитивні і рівні модулів відповідних векторів: v0x = 0,4 м / с, vx = 2 м / с.
Запишемо умову задачі і вирішимо її.
Проекція вектора прискорення на вісь X вийшла позитивною, значить, вектор прискорення сонаправлени з віссю X і зі швидкістю руху санок.
Якщо вектори швидкості і прискорення направлені в одну сторону, то швидкість зростає.
Тепер розглянемо інший приклад, в якому санки, скотившись з гори, рухаються по горизонтальній ділянці CD (рис. 8, б).
В результаті дії на санки сили тертя їх швидкість безперервно зменшується, і в точці D санки зупиняються, т. Е. Їх швидкість дорівнює нулю. Відомо, що в точці С санки мали швидкість 1,2 м / с, а ділянка CD був пройдений ними за 6 с.
Розрахуємо прискорення санок в цьому випадку, т. Е. Визначимо, на скільки змінювалася швидкість санок за кожну одиницю часу.
Початком відліку часу будемо вважати момент, коли санки проходять точку С. Тоді модуль вектора початкової швидкості дорівнює 1,2 м / с, а кінцевою – нулю.
Проведемо вісь X паралельно відрізку CD і сонаправім її зі швидкістю руху санок, як показано на малюнку. При цьому проекція вектора швидкості санок на вісь X в будь-який момент їх руху буде позитивна і дорівнює модулю вектора швидкості. Зокрема, при t0 = 0 v0x = 1,2 м / с, а при t = 6 з vx = 0.
Запишемо дані і обчислимо прискорення.
Проекція прискорення на вісь X негативна. Це означає, що вектор прискорення а спрямований протилежно осі X і відповідно протилежно швидкості руху. При цьому швидкість санок зменшувалася.
Таким чином, якщо вектори швидкості і прискорення рухомого тіла направлені в одну сторону, то модуль вектора швидкості тіла збільшується, а якщо в протилежні – зменшується.
питання
До якого виду руху – рівномірному або нерівномірного – відноситься прямолінійний рівноприскореному русі?
Що розуміють під миттєвою швидкістю нерівномірного руху?
Дайте визначення прискорення рівноприскореного руху. Яка одиниця прискорення?
Що таке рівноприскореного руху?
Що показує модуль вектора прискорення?
За якої умови модуль вектора швидкості рухомого тіла збільшується; зменшується?
Вправа 5
За один і той же проміжок часу t модуль вектора швидкості першого автомобіля змінився від vl до v ‘, а друга – від v2 до v’ (вектори швидкості зображені в однаковому масштабі на малюнку 9). Який з автомобілів рухався у вказаний проміжок з великим прискоренням? Швидкість якого з них зростала швидше?
moyaosvita.com.ua
Вектор прискорення точки
Прискорення характеризує зміну швидкості з плином часу. Миттєве прискорення точки в даний момент часу визначається
. (1.14)
Вектор
прискорення направлений по зміні вектора
швидкості  .
.
Коли рівняння руху точки задано в декартових координатах,то з формули (1.8), взявши похідну, отримуємо
, (1.15)
де 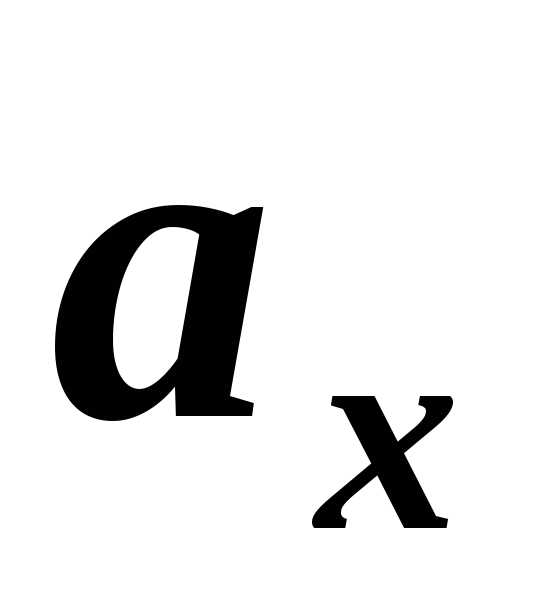 ,
, ,
, – алгебраїчні проекції прискорення на
декартові осі координат, які дорівнюють
другим похідним за часом від відповідних
координат точки або першим похідним за
часом від проекцій швидкості на відповідні
осі (рисунок аналогічний 1.6 зі зміною
– алгебраїчні проекції прискорення на
декартові осі координат, які дорівнюють
другим похідним за часом від відповідних
координат точки або першим похідним за
часом від проекцій швидкості на відповідні
осі (рисунок аналогічний 1.6 зі зміною на
на ).
Модуль вектора прискорення визначається
за формулою
).
Модуль вектора прискорення визначається
за формулою
. (1.16)
Якщо в процесі руху точки прискорення залишається сталим, рух називається рівнозмінним, і для вектора швидкості та радіус-вектора отримуємо формули:
, (1.17)
, (1.18)
де  та
та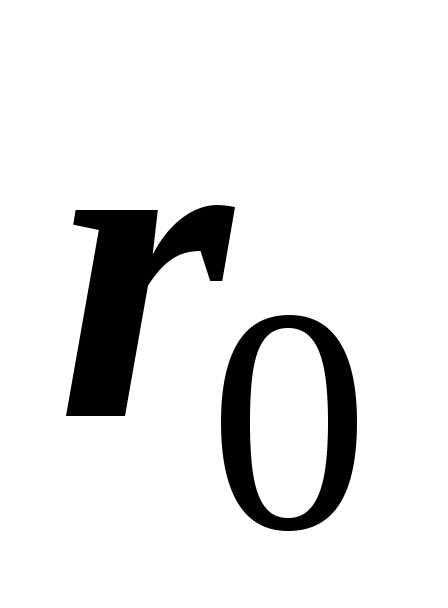 – значення швидкості та радіус-вектора
точки в момент часу
– значення швидкості та радіус-вектора
точки в момент часу = 0.
= 0.
У випадку натурального способудля вектора прискорення, після диференціювання (1.11) отримуємо вираз
. (1.19)
Отже, повне прискорення складається з двох взаємно перпендикулярних складових (рис. 1.8):
1) тангенціальногоприскорення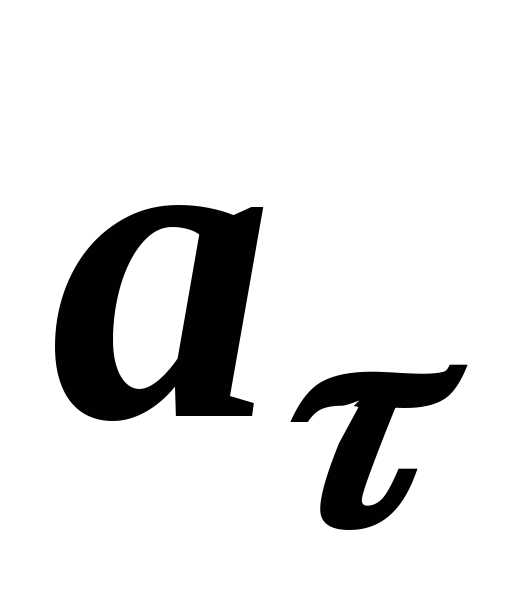 ,
яке спрямоване вздовж дотичної до
траєкторії і характеризує зміну швидкості
за модулем
,
яке спрямоване вздовж дотичної до
траєкторії і характеризує зміну швидкості
за модулем
 . (1.20)
. (1.20)
Якщо алгебраїчне значення швидкості
зростає ( ,
рис. 1.8, а), то напрями
,
рис. 1.8, а), то напрями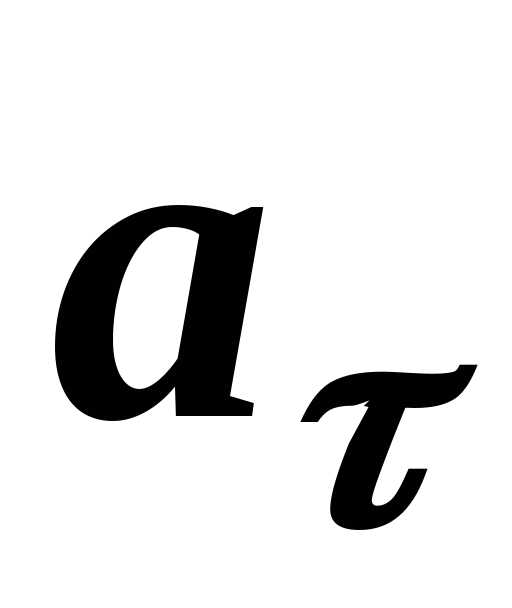 і
і співпадають, а коли алгебраїчне значення
швидкості зменшується, (
співпадають, а коли алгебраїчне значення
швидкості зменшується, ( ,
рис. 1.8, б) – напрями векторів
,
рис. 1.8, б) – напрями векторів і
і протилежні;
протилежні;
2) нормальногоприскорення, яке характеризує зміну швидкості за напрямом
, (1.21)
де
– орт, який перпендикулярний до вектора
швидкості і направлений у той бік, куди
повертається вектор швидкості (до центру
дуги, по якій рухається точка), – радіус кривизни траєкторії.
– радіус кривизни траєкторії.
Вектор повного прискорення направлений
по діагоналі прямокутника, побудованого
на векторах 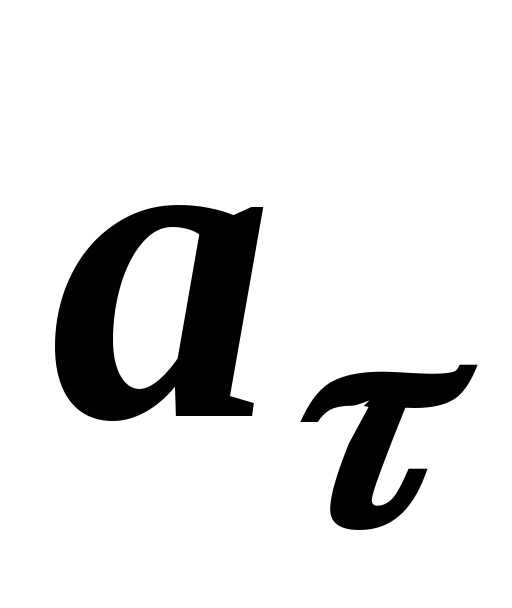 та
та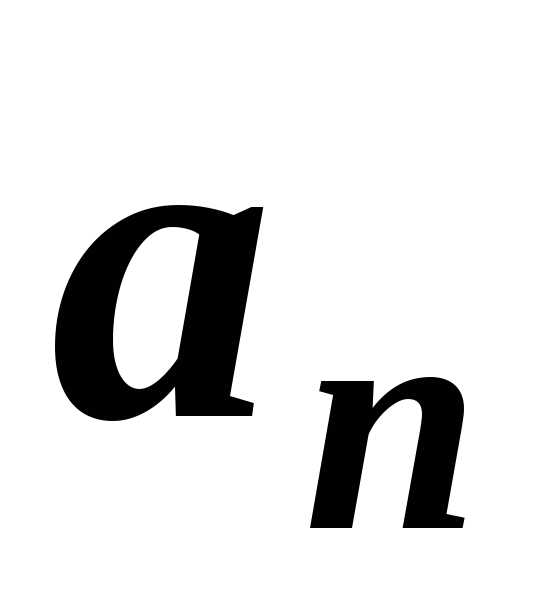 (рис. 1.8), а його модуль
(рис. 1.8), а його модуль
. (1.22)
Тангенціальне прискорення, яке є проекцією повного прискорення на вектор швидкості (рис. 1.8) можна визначити через скалярний добуток
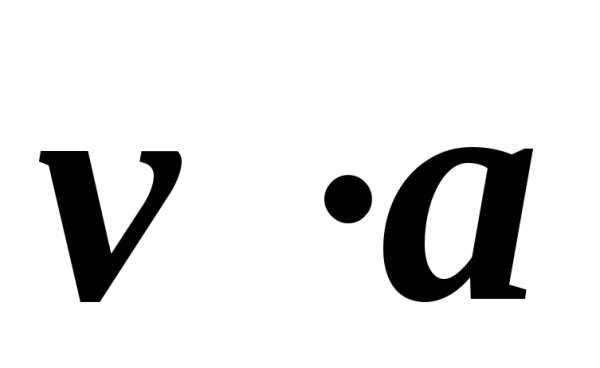 ==
== .
.
З останнього рівняння отримуємо формулу для обчислення тангенціального прискорення через компоненти векторів швидкості та прискорення
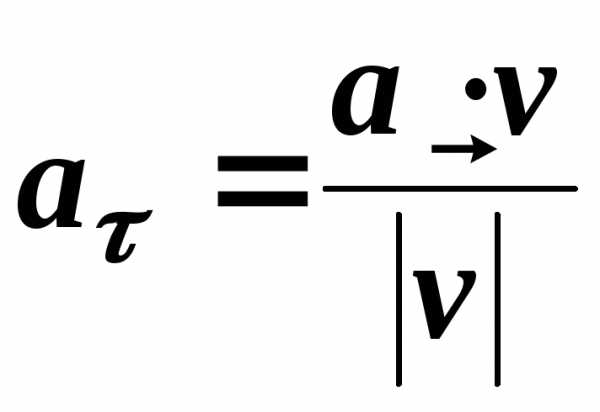 =
=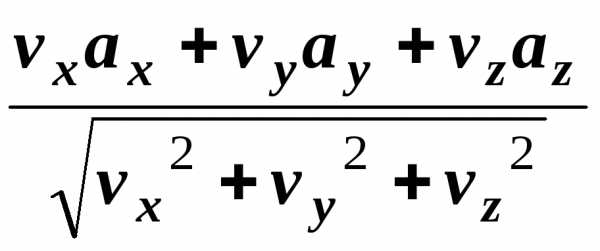 . (1.23)
. (1.23)
Якщо відомі величини повного  та
тангенціального
та
тангенціального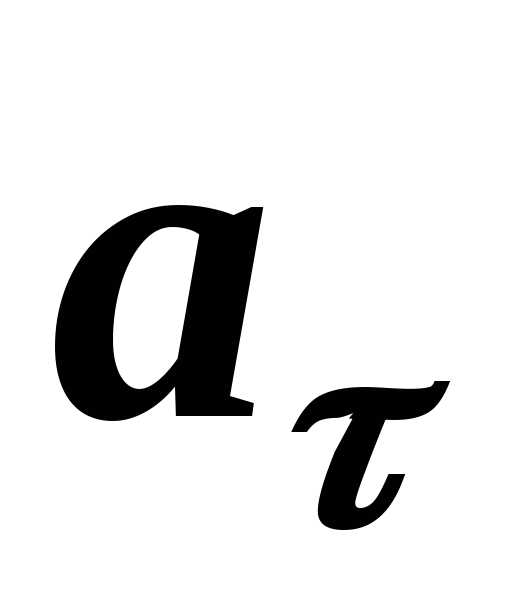 прискорень, то можна визначити нормальне
прискорення точки
прискорень, то можна визначити нормальне
прискорення точки
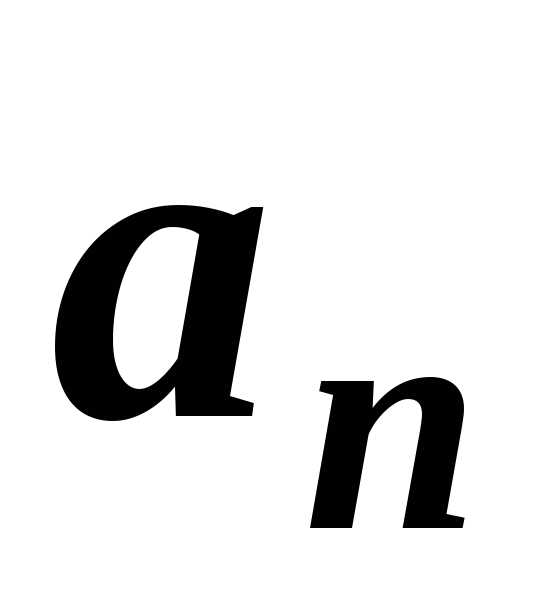 =
= =, (1.24)
=, (1.24)
та визначити радіус кривизни траєкторії
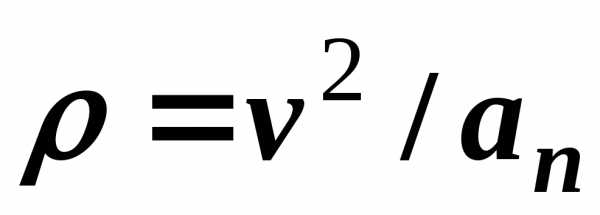 .
(1.25)
.
(1.25)
Розглянемо окремі випадки руху точки:
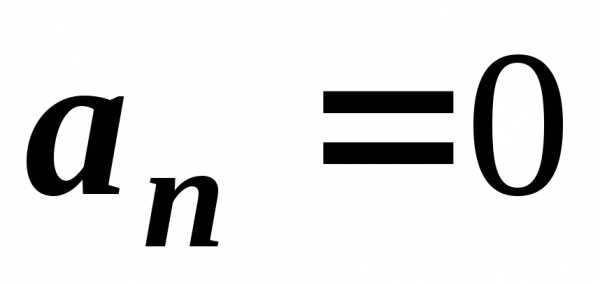 – коли точка рухається прямолінійно
(
– коли точка рухається прямолінійно
(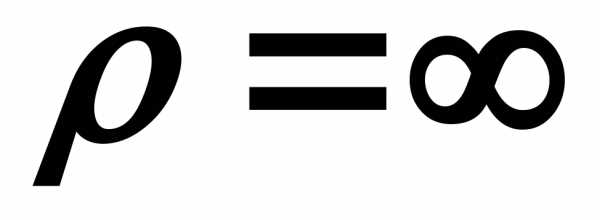 ),
а також у випадку криволінійного руху,
в момент часу, коли миттєве значення
швидкості
),
а також у випадку криволінійного руху,
в момент часу, коли миттєве значення
швидкості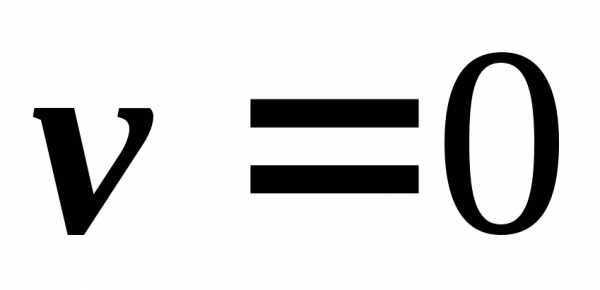 ,
в цих випадках має місце лише тангенціальне
прискорення, а вектор прискорення
направлений до дотичній до траєкторії;
,
в цих випадках має місце лише тангенціальне
прискорення, а вектор прискорення
направлений до дотичній до траєкторії;
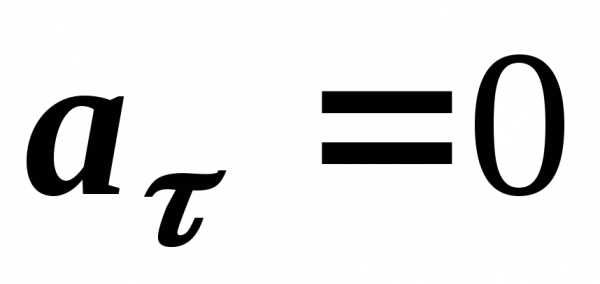 – коли величина швидкості стала, в цьому
випадку прискорення має лише нормальну
складову, і вектор прискорення
перпендикулярний вектору швидкості і
спрямований до центру кривизни траєкторії;
– коли величина швидкості стала, в цьому
випадку прискорення має лише нормальну
складову, і вектор прискорення
перпендикулярний вектору швидкості і
спрямований до центру кривизни траєкторії;
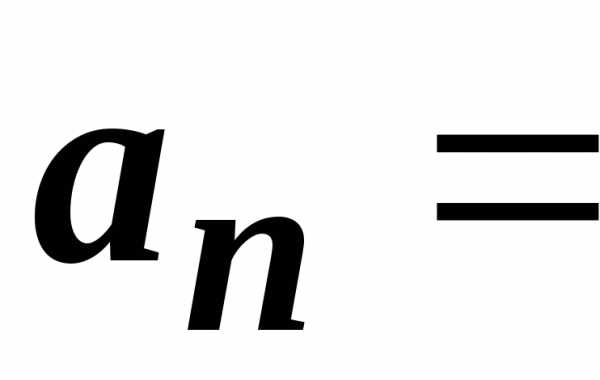
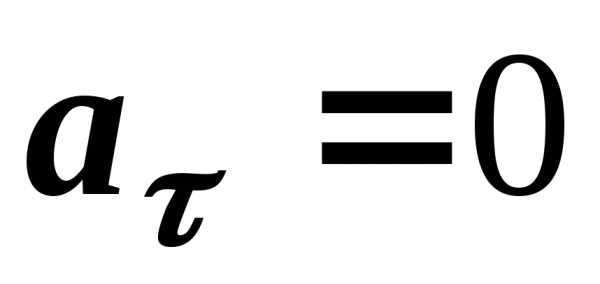 – коли точка рухається рівномірно та
прямолінійно.
– коли точка рухається рівномірно та
прямолінійно.
Контрольні запитання
Що вивчає кінематика?
В яких випадках тіло можна вважати точкою?
Які системи координат вам відомі? Запишіть формули перетворення координат від декартової до циліндричної, сферичної та навігаційної системи координат.
Що таке траєкторія руху точки? Які типи траєкторій вам відомі? Чи залежить форма траєкторії від системи відліку?
Які величини потрібно знати, щоб задати закон руху точки для векторного способу, координатного та природного способів описання?
Дайте означення вектора переміщення. Як знайти напрям та величину вектора миттєвої швидкості?
Як знайти компоненти вектора швидкості та його модуль у декартовій системі координат?
Як визначається миттєве прискорення точки? Як знайти напрям вектора миттєвого прискорення?
Який рух точки називається рівнозмінним? Запишіть формули для знаходження швидкості та положення точки при рівнозмінному прямолінійному русі.
Як за графіком залежності проекції швидкості від часу знайти значення відповідної проекції прискорення?
Як за графіком залежності проекції швидкості від часу знайти значення зміни відповідної координати точки?
Як знайти компоненти вектора прискорення та його модуль в декартовій системі координат?
Поясніть роль тангенціального прискорення у зміні швидкості.
Як знайти тангенціальне прискорення через компоненти швидкості та прискорення в декартовій системі координат?
Поясніть роль нормального прискорення у зміні швидкості.
Як знайти модуль повного прискорення?
Для якого руху точки по криволінійній траєкторії кут між векторами швидкості та прискорення: а) гострий? б) тупий? в) прямий?
Чи може повне прискорення точки у випадку криволінійного руху бути напрямленим по дотичній до траєкторії?
studfiles.net
траєкторія, переміщення, шлях, швидкість, прискорення. Зв’язок між ними.
Визначення. Кінематика – це розділ фізики, що вивчає руху фізичних тіл.
Визначення. Основним завданням кінематики є опис руху за допомогою математичного апарату без з’ясування причин, що викликають цей рух.
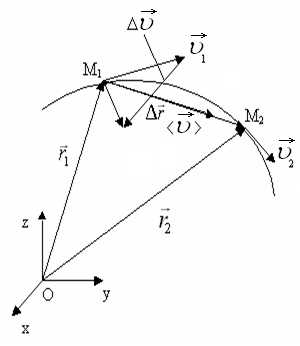
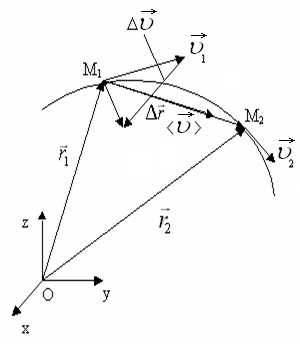
Основні кінематичні величини (рис. 1.1)
Траєкторія (червона лінія)
Радіус-вектори і вектор переміщення (чорні стрілки).
Вектори середньої і миттєвих швидкостей (Зелені стрілки).
Траєкторія
Визначення. Траєкторія – це уявна лінія, якиу описує кінець радіус-вектора в процесі руху.
Переміщення Δr
Визначення. Переміщення – це векторна фізична величина, що дорівнює різниці радіус-векторів в кінцевий і початковий моменти часу:
.
Середня швидкість
Визначення. Середня швидкість – це векторна фізична величина яка дорівнює відношенню вектора переміщення до проміжку часу, за який відбувається це переміщення:
.
Миттєва швидкість
1. Характеризує швидкість переміщення матеріальної точки.
2. Визначення. Миттєва швидкість – це векторна фізична величина, що дорівнює першій похідній від радіус-вектора за часом:
3. Миттєва швидкість завжди напрямлена по дотичній до траєкторії.
4. .
5. Одиниця вимірювання швидкості в системі СІ- [v] = м/с.
Не системна одиниця – км/год. 1 км/год= 1000м/3600с = 1/3, 6 м/с.
18 км/год = 5 м/с, 54 км/год = 15 м/с, 36 км/год = 10 м/с;
72 км/год = 20 м/с, 90 км/год = 25 м/с, 108 км/год = 30 м/с
6. Прилад для вимірювання – спідометр.
Миттєве прискорення
1. Характеризує швидкість зміни швидкості.
2. Визначення. Миттєве прискорення – це векторна фізична величина, що дорівнює другій похідній від радіус-вектора за часом і, відповідно, першій похідній від миттєвої швидкості за часом.
3. У випадку руху в площині вектор прискорення можна розкласти по супутньому базису: на вектор нормального і тангенціального прискорення.
4. .
5. Одиниця прискорення в системі СІ – [] = м/с2
6. Прилад для вимірювання – акселерометр.
2. Криволінійний рух. Нормальна та тангенціальна складові повного прискорення при криволінійному русі матеріальної точки
Криволінійний рух
Визначення. Криволінійним рухом називають рух тіла по траєкторії що не являє собою пряму лінію.
У випадку руху в площині вектор прискорення можна розкласти: на вектор нормального і тангенціального прискорення (рис. 1.2):
.
Де – одиничний вектор нормалі1,- одиничний вектор дотичної. Величинаназивається нормальним прискоренням Величинаназивається тангенціальним прискоренням.
Нормальне прискорення
1. Характеризує швидкість зміни напрямку руху.
2. Визначення. Нормальне прискорення – це прискорення, яке виникає в результаті зміни швидкості за напрямком.
3. Нормальне прискорення – це векторна величина, яка завжди напрямлена по нормалі до дотичної.
4. Нормальне прискорення виражається через миттєву швидкість і радіус кривизни траєкторії:.
5. [an] = м/с2
*При русі по колу з постійною швидкістю нормальне прискорення постійне по модулю і направлено до центру кола і називається доцентровим.
Тангенціальне прискорення aτ
1. Характеризує зміну модуля швидкості з часом.
2. Визначення. Тангенціальне прискорення дорівнює добутку одиничного вектора, напрямленого по швидкості руху, на похідну модуля швидкості за часом.
3. Це векторна величина що напрямлена в ту ж сторону, що і вектор швидкості при прискореному русі (позитивна похідна) і в протилежну при уповільненому (негативна похідна).
4. .
5. [aτ] = м/с2
studfiles.net
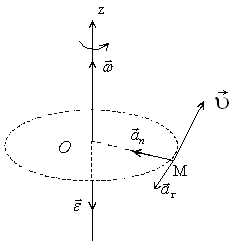
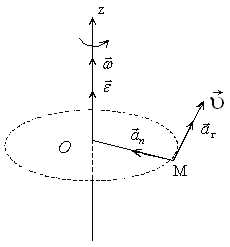
Вектори кутової швидкості і кутового прискорення.
Раніше
було
з’ясовано, що елементарне кутове
зміщення  можна розглядати як векторну величину.
можна розглядати як векторну величину.
Вектор
елементарного кутового зміщення  є напрямлений відрізок, що чисельно
дорівнює куту поворота, напрямлений по
осі обертання в сторону, яка вказуються
правилом правого гвинта. Як відомо, за
цим правилом напрям вектора повинен
збігатись з поступальним рухом гвинта,
якщо його, ручку повертати за напрямом
обертання.
є напрямлений відрізок, що чисельно
дорівнює куту поворота, напрямлений по
осі обертання в сторону, яка вказуються
правилом правого гвинта. Як відомо, за
цим правилом напрям вектора повинен
збігатись з поступальним рухом гвинта,
якщо його, ручку повертати за напрямом
обертання.
Таким чином, кутова швидкість і кутове прискорення – вектори, напрямлені по осі обертання.
Кутова швидкість – векторна фізична величина, що характеризує бистроту і напрям обертання.
Кутова швидкість – вектор, напрямлений вздовж осі обертання таким чином, щоб з його кінця було видно обертання, що здійснюється проти годинникової стрілки (правило правого гвинта).
Кутове прискорення – це вектор, що збігається з напрямом кутової швидкості при прискореному русі, або напрямлений проти кутової швидкості при сповільненому русі.
 ,
, 
На
відміну від розглянутих векторів 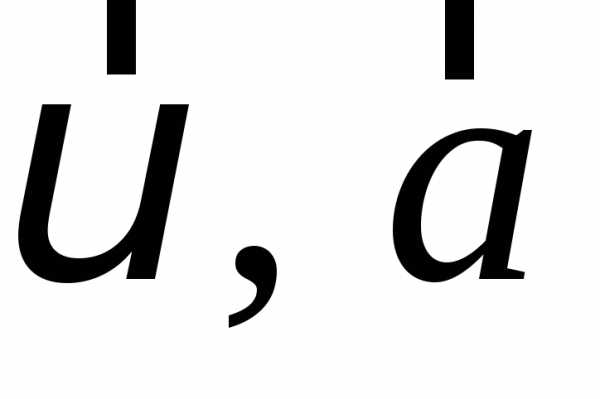 ,
напрями, яких очевидні, вважаються
істинними векторами; вектори
,
напрями, яких очевидні, вважаються
істинними векторами; вектори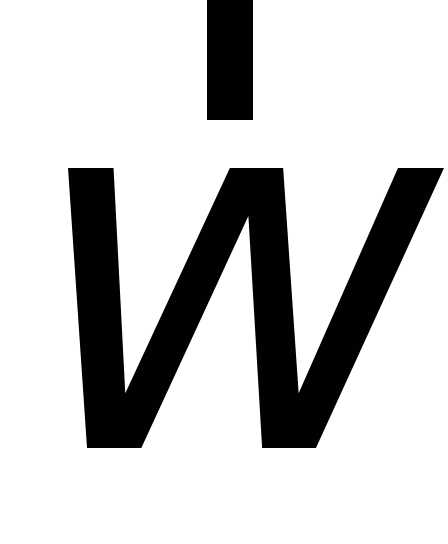 і
і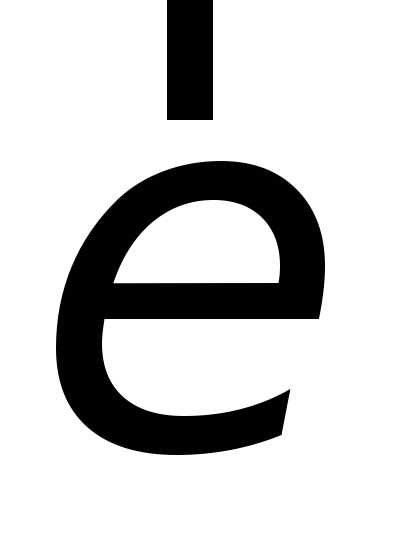 називаються псевдовекторами (рис. 1.12).
називаються псевдовекторами (рис. 1.12).
| |
Прискорене обертання | Сповільнене обертання |
Рис. 1.12. | |
Зв’язок лінійних і кутових величин
Рух
тіла (точки) по колу зручно описувати
сукупністю двох типів параметрів, що
називаються лінійним:
і кутовими: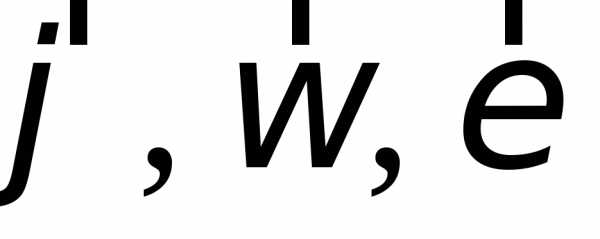 .
.
Встановимо зв’язок між ними.
Так
як
,
то взявши похідну за часом: ;
;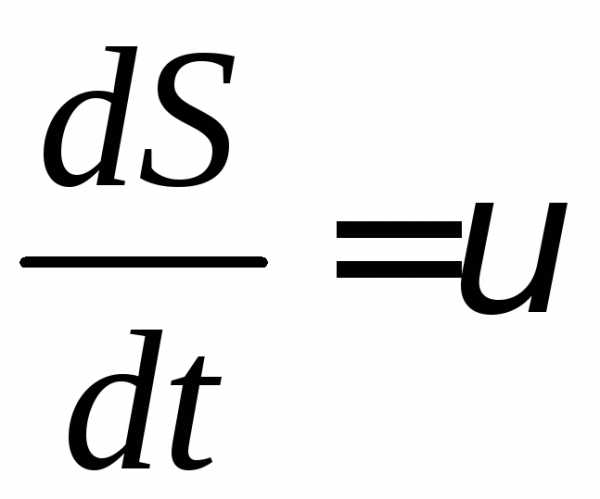 ;
;
(1-18)
 ;
; 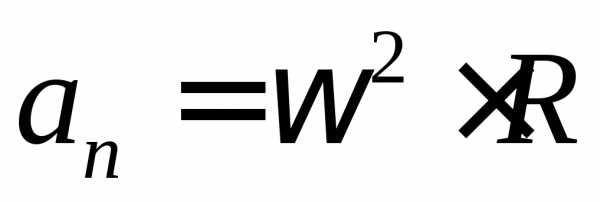 (1-19)
(1-19)
(1-20)
Рівняння рівномірного і рівнозмінного руху точки по колу.
а) Рівномірний рух по колу – це обертання точки з постійною кутовою швидкістю, або рух з постійним за модулем вектором лінійної швидкості:
; 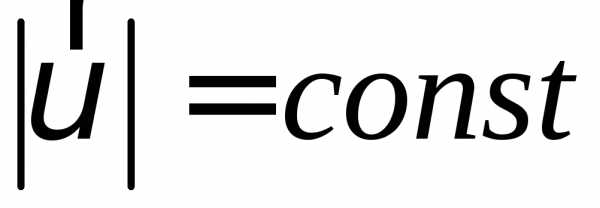
Виходячи з початкових умов, встановимо межі інтегрування:
При  ;
; 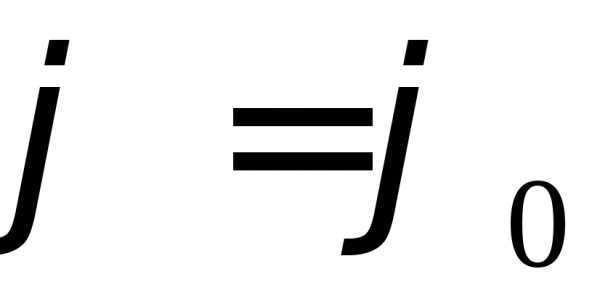 ;
; 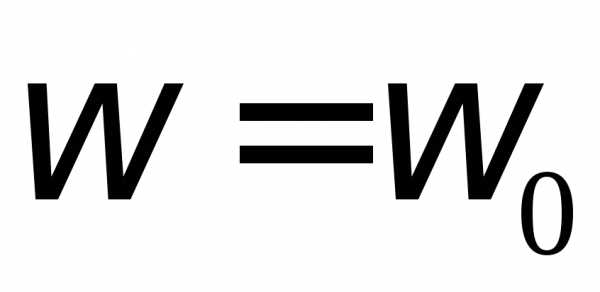 ;
;
при  ;
; 
Тоді:
;  ;
;
Інтегруючи, дістанемо закон рівномірного обертання:
; (1-21)
аналогія: з прямолінійним рівномірним рухом якщо:
; 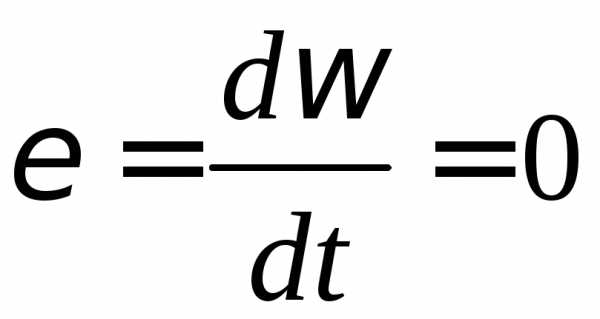 ;
;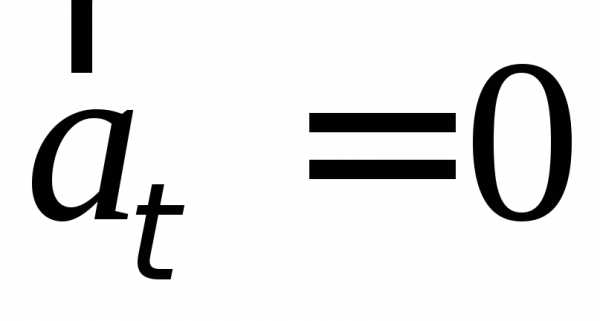 ;
;
Рівномірне обертання точки характеризується тільки однією складовою вектора прискорення – нормальним прискоренням.
б) Рівнозмінний рух по колу – це обертання точки з постійним кутовим прискоренням:
–прискорення;
–сповільнення.
Тоді:
Проводячи інтегрування дістанемо формулу кутової швидкості
 ;
;
;
;
(1-22)
аналогія: з прямолінійним рівнозмінним рухом
 ;
;
Проводячи інтегрування, отримаємо, закон рівнозмінного обертання.
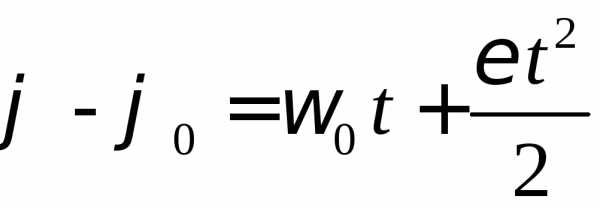 ;
; 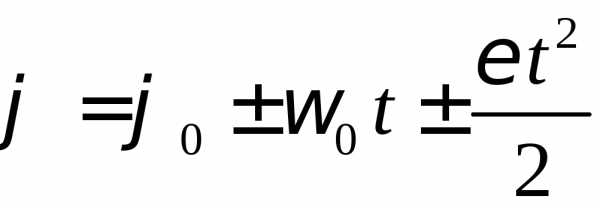 (1-23)
(1-23)
аналогія: 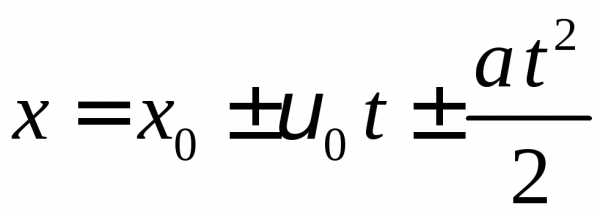 з прямолінійним рівнозмінним рухом.
з прямолінійним рівнозмінним рухом.
Практичне заняття 1.1 Тема: Кінематика прямолінійного руху матеріальної точки. Основні формули та методичні рекомендації
1. Кінематичні рівняння найпростіших механічних рухів матеріальної точки:
,
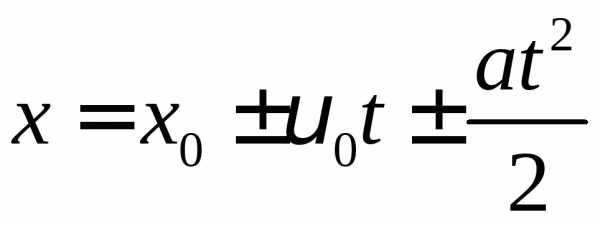 ,
.
,
.
2. Швидкість та прискорення прямолінійного руху матеріальної точки виражаються формулами:
3.
Ортогональні проекції 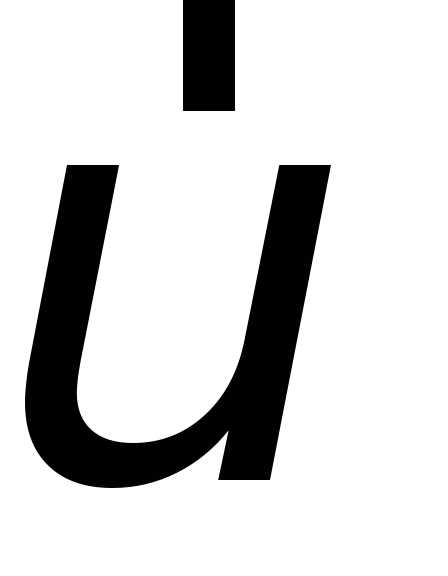 :
:  ;
; 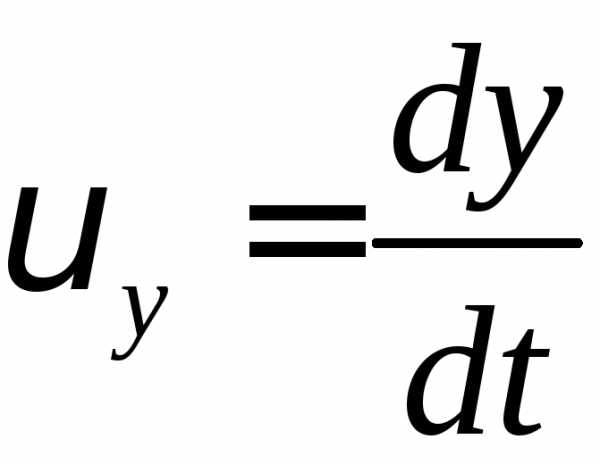 ;
; 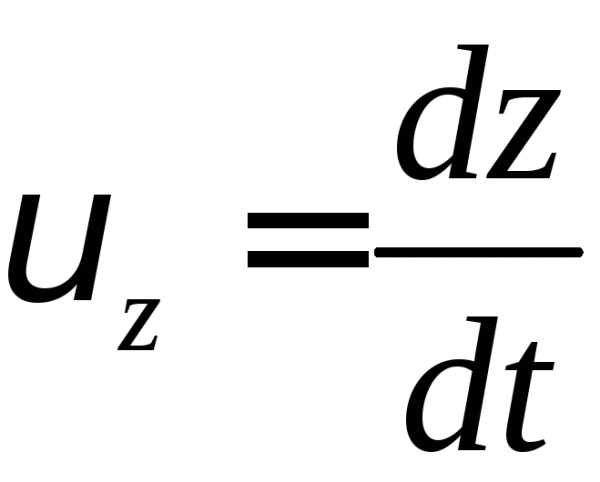
.
4. Класичні закони додавання швидкостей: .
Основна мета заняття: навчитися знаходити закон руху. Записати закон руху – це означає визначити положення тіла в деякій системі координат як функцію часу. Треба запам’ятати, що закон руху визначає положення тіла в даний момент часу, а не величину пройденого шляху. Як правило, запис закону руху проводиться в координатній формі. Вибір системи координат довільний; вибирати її необхідно кожного разу залежно від умов задачі так, щоб математичне рішення було спрощено. Наприклад, при розборі руху тіла, кинутого під кутом до горизонту, зручно вісь Оу направляти по горизонталі, вісь Ох – по вертикалі. Тоді рух уздовж осі Ох розглядається як рівномірний, уздовж осі Оу – рівнозмінний.
studfiles.net
вектори переміщення, швидкості і прискорення.
а)
Вектор переміщення 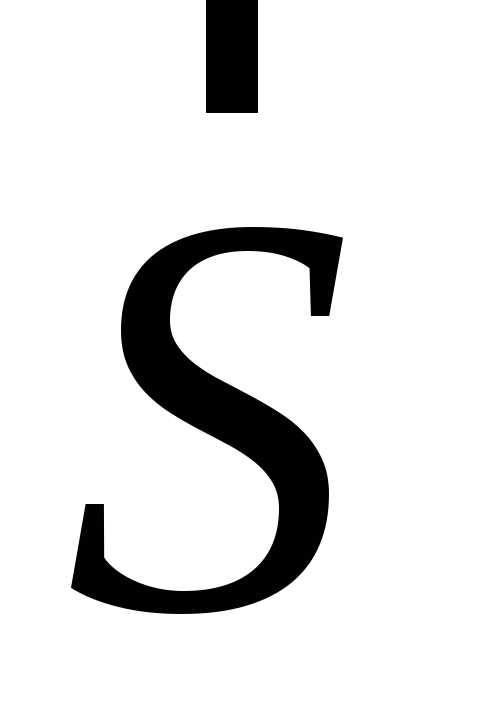 .
.
Задамо положення т. М векторним способом (рис. 1.3):
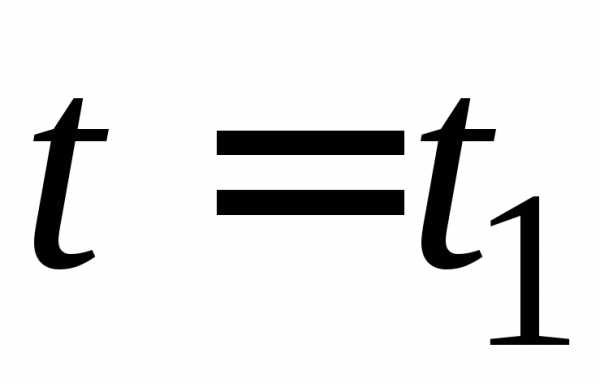 ;
т. М1 →
;
т. М1 → 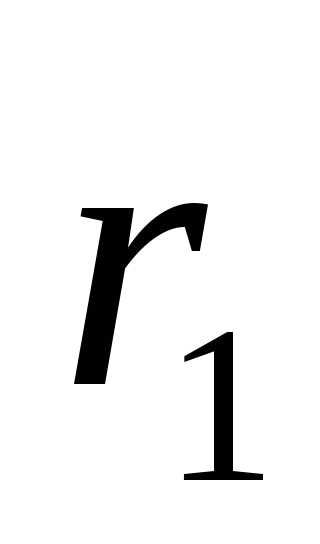
 ;
т. М2 →
;
т. М2 → 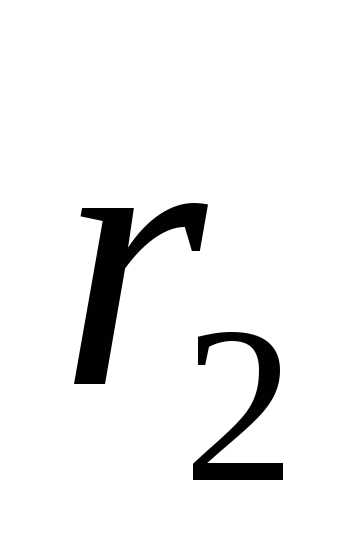
За проміжок часу , що відповідає зміні радіус-вектора
Вектор, що з’єднує положення матеріальної точки на початку даного проміжка часу з її положенням у кінці цього проміжкау називається вектором переміщення.
|
Рис. 1.3. |

Вектор переміщення дорівнює зміні (приросту) радіус-вектора точки за даний проміжок часу.
Переміщення – векторна фізична величина, що визначає, в якому напрямі та, на яку найкоротшу відстань зміститься матеріальна точка за даний проміжок часу.
Для
прямолінійного руху модуль вектора
переміщення дорівнює величині пройденого
шляху. 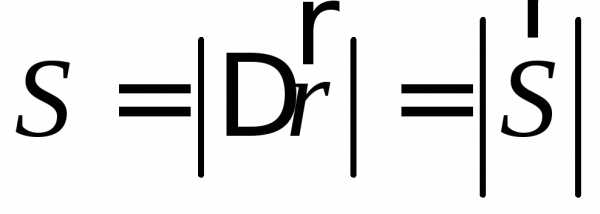
б)
Вектор швидкості  .
.
Для
визначення темпу руху (бистроти) та
напряму переміщення матеріальної точки
(тіла) в просторі вводиться поняття
вектора швидкості 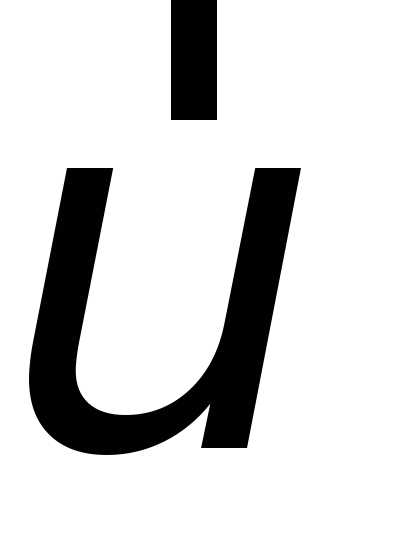 .
.
Нехай
матеріальна точка за певний проміжок
часу  здійснила переміщення
здійснила переміщення .
Тоді
.
Тоді – вектор середньої швидкості, який
характеризує бистроту переміщення
деякого фіктивного рівномірного руху,
що здійснюється не по дузі, а по хорді
(рис. 1.3).
– вектор середньої швидкості, який
характеризує бистроту переміщення
деякого фіктивного рівномірного руху,
що здійснюється не по дузі, а по хорді
(рис. 1.3).
Середня швидкість руху дорівнює такій швидкості рівномірного руху, при якому точка проходить за даний проміжок часу той відрізок траєкторії, який вона пройшла за той же час, рухаючись нерівномірно.
Вектор  характеризує середню бистроту переміщення
на даному відрізку траєкторії і
направлений по хорді.
характеризує середню бистроту переміщення
на даному відрізку траєкторії і
направлений по хорді.
 =
= 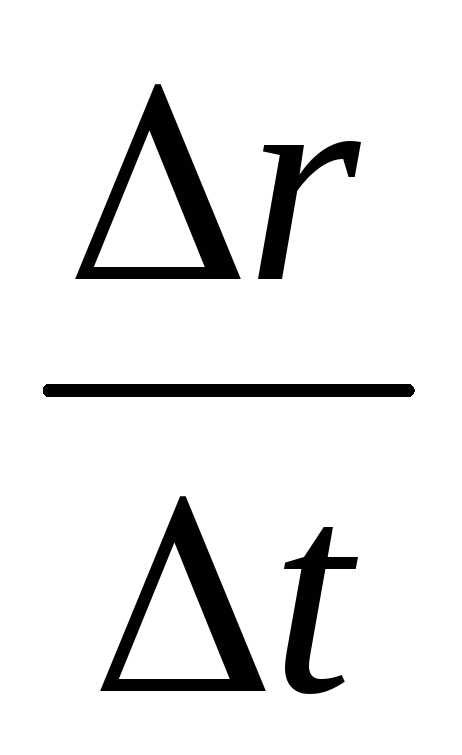 (1-3)
(1-3)
Для визначення дійсного (істинного) напряму і бистроти руху точки в будь-який момент часу вводять поняття вектора миттєвої швидкості.
Миттєва
швидкість – це векторна фізична величина, що
визначається границею, до якої наближається
середня швидкість, за умови, коли проміжок
часу  прямує до 0.
прямує до 0.
(1-4)
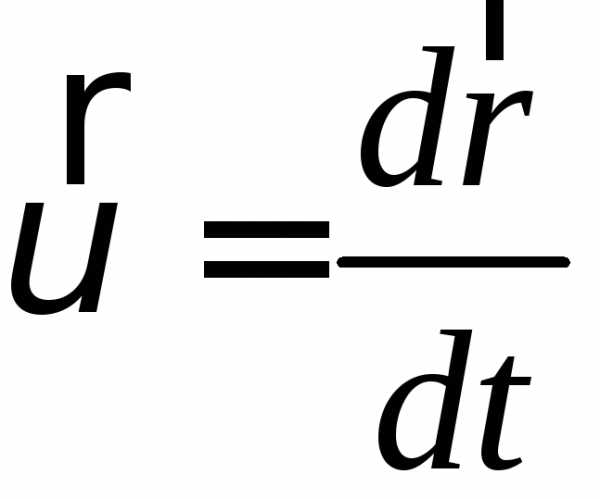 (1-4а)
(1-4а)
(1-4а) – формула швидкості при векторному способі задання руху.
Миттєва швидкість – це векторна величина, яка дорівнює першій похідній від радіус-вектора за часом і напрямлена по дотичній до траєкторії в бік руху.
Миттєва
швидкість – це швидкість точки в даний момент
часу або в даній точці траєкторії і
направлена по дотичній до траєкторії
в даній точці  ;
Привектор швидкості направлений по дотичній.
;
Привектор швидкості направлений по дотичній.
При координатному методі вводиться поняття ортогональних проекцій вектора швидкості .
;
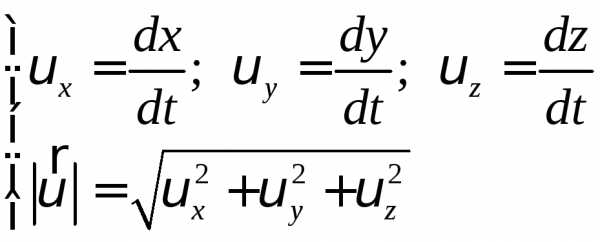 (1-5)
(1-5)
Проекції вектора швидкості на координатні осі визначаються першими похідними від відповідних координат за часом.
в)
Вектор прискорення 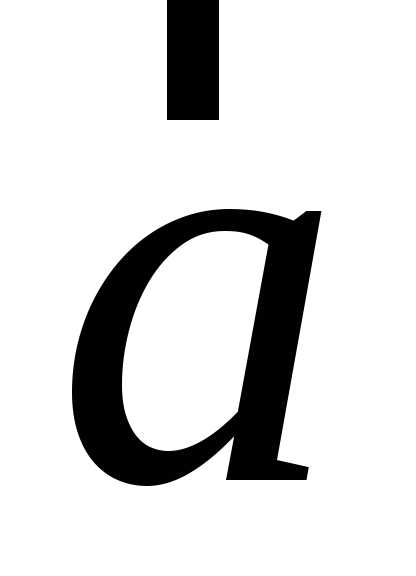 .
.
|
Рис. 1.3. |
Вектор
середнього приско-рення <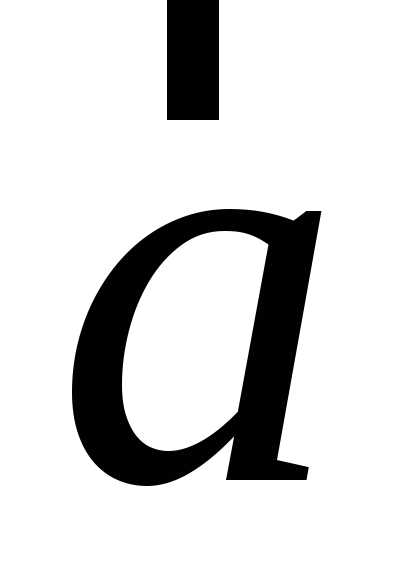 > – фізична величина, що характеризує
бистроту зміни швидкості на даному
відрізку траєкторії і визначається
> – фізична величина, що характеризує
бистроту зміни швидкості на даному
відрізку траєкторії і визначається 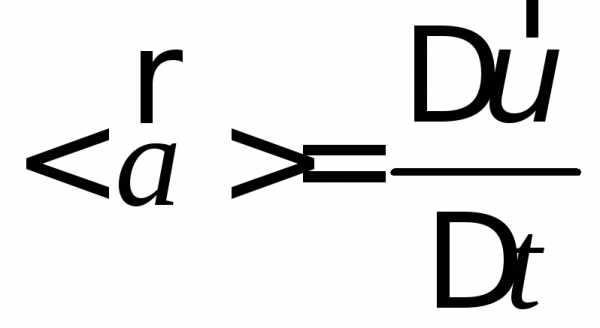 ,
де.
,
де.
На
(рис. 1.3) – т. М1:  ;
т.М2:
;
т.М2:  ;.
;.
Миттєве
прискорення, тобто прискорення в даний
момент часу або прискорення в даній
точці траєкторії визначається границею
до якої прямує відношення зміни вектора
швидкості до проміжку часу, протягом
якого вона здійснилась при 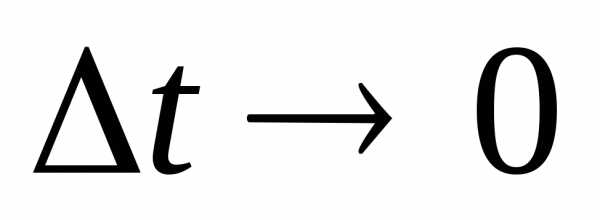 .
.
(1-6)
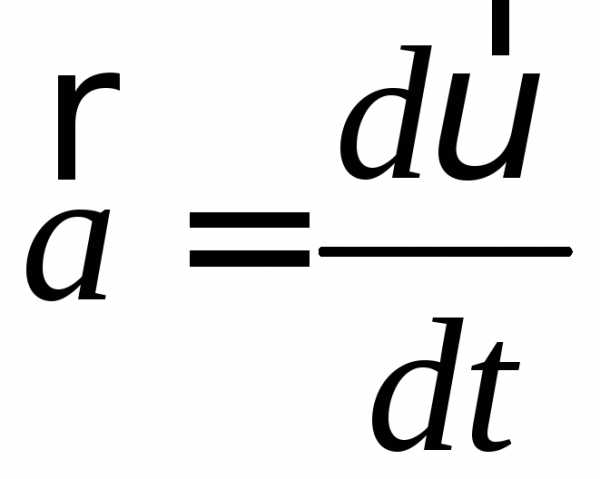 (1-6а)
(1-6а)
Вектор прискорення – фізична величина, яка дорівнює першій похідній вектора швидкості за часом, або другій похідній від радіус-вектора за часом.
Для
прямолінійного руху вектор прискорення
напрямлений у той бік, куди напрямлений
вектор зміни швидкості  .
.
для
прискореного руху: 
для
сповільненого руху: 
При
координатному методі: вводять ортогональні
проекції  :,
які визначаються першими похідними за
часом від відповідних ортогональних
проекцій вектора
:,
які визначаються першими похідними за
часом від відповідних ортогональних
проекцій вектора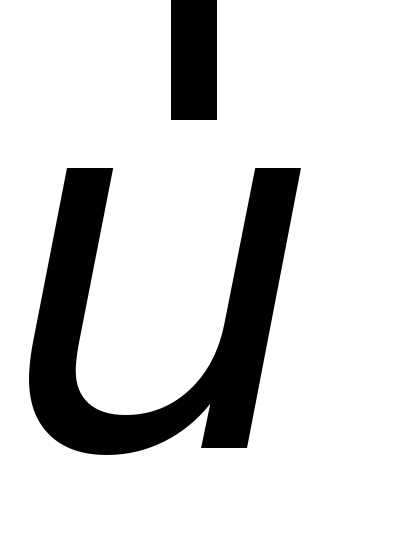 ,
або другими похідними за часом відповідних
координат так:
,
або другими похідними за часом відповідних
координат так:
(1-7)
studfiles.net
§ 5. Криволінійний рух
Швидкість у криволінійному русі. 0Прискорення у криволінійному русі.
Криволінійний рух – це рух по дугах кіл.
Досі ми розглядали рухи, коли тіло переміщувалось уздовж прямої лінії. І в природі, і в техніці часто зустрічаються рухи, траєкторії яких є не прямими, а кривими лініями. Такі рухи називають криволінійними. І зустрічаються вони значно частіше, ніж прямолінійні. По криволінійних траєкторіях рухаються в космічному просторі планети і штучні супутники, а на Землі – води річок, повітря атмосфери, автомобілі і літаки, деталі машин і механізмів. Криволінійним є рух тіла, кинутого під кутом до горизонту, рух по колу.
Завдання вивчення криволінійного руху, як і у випадку прямолінійного, полягає в тому, щоб за швидкістю тіла визначати його положення у будь-який момент часу. Складність полягає у тому, що вектор переміщення під час такого руху напрямлений не вздовж траєкторії, бо траєкторія у цьому випадку є кривою лінією. Напрям руху, тобто напрям вектора швидкості також увесь час змінюється; змінюється і вектор прискорення.
Оскільки для розв’язання основної задачі механіки важливо вміти обчислювати значення швидкості й прискорення, то ми насамперед повинні з’ясувати, як змінюються ці величини. Для спрощення обмежимося розглядом лише плоского руху, тобто такого, коли траєкторія тіла лежить у певній площині.
Швидкість
і прискорення у криволінійному русі. Під час криволінійного руху напрям
вектора швидкості змінюється від точки
до точки. Тому, коли кажуть про швидкість
криволінійного руху, то мають на увазі
миттєву швидкість. Який напрям швидкості
і переміщення у криволінійному русі?
Щоб відповісти на це запитання,
скористаємося тим самим прийомом, який
застосували, вивчаючи миттєву швидкість
для прямолінійного руху (див.
п.3, § 2 на с. … ….), коли елементи переміщення 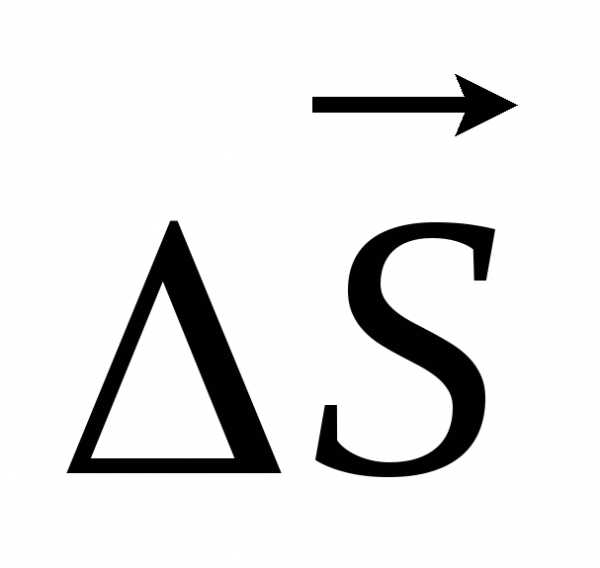 «стягують у точку». Нехай тіло рухається
вздовж деякої кривої від точки А до
точки В; його переміщення – вектор
«стягують у точку». Нехай тіло рухається
вздовж деякої кривої від точки А до
точки В; його переміщення – вектор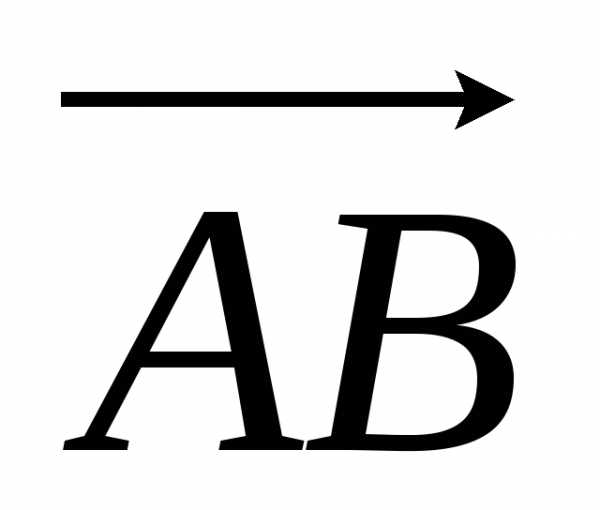 (мал. 1.39, а). Звичайно, не можна вважати, що швидкість
тіла під час цього руху напрямлено
вздовж вектора переміщення. Проведемо
між точками А та В хорди (мал.
1.39, б) і
вважатимемо, що на кожній з них тіло
рухається прямолінійно, а вектор
швидкості напрямлений уздовж хорди.
Скорочуватимемо ці прямолінійні ділянки
∆ S. Ця ламана лінія стане більш схожа
на плавну криву. Швидкість у кожній
точці цієї кривої буде напрямлена по
дотичній до кривої в цій точці (мал.
1.39, в).
(мал. 1.39, а). Звичайно, не можна вважати, що швидкість
тіла під час цього руху напрямлено
вздовж вектора переміщення. Проведемо
між точками А та В хорди (мал.
1.39, б) і
вважатимемо, що на кожній з них тіло
рухається прямолінійно, а вектор
швидкості напрямлений уздовж хорди.
Скорочуватимемо ці прямолінійні ділянки
∆ S. Ця ламана лінія стане більш схожа
на плавну криву. Швидкість у кожній
точці цієї кривої буде напрямлена по
дотичній до кривої в цій точці (мал.
1.39, в).
Ш
Мал.2.19
видкість криволінійного руху тіла вимірюється відношенням переміщення тіла ∆ S за інтервал часу ∆ t до цього інтервалу: .
.
Коли ∆ t → 0 і має бути малим, якщо тільки ми хочемо визначити не середню швидкість тіла за час ∆ t, а миттєву швидкість.
Ш
Мал.2.19
видкість руху тіла у будь-якій точці траєкторії напрямлена по дотичній до траєкторії у цій точці.Спостереження за заточуванням інструменту на шліфувальному диску (див. мал. 1.19, а на с. …) , бризок від колеса автомобіля, що буксує (мал. 1.19, б на с. …) переконують у тому, що швидкість тіла під час криволінійного руху спрямована по дотичній до кривої. Це є свідченням того, що криволінійний рух завжди прискорений і навіть тоді, коли модуль швидкості залишається сталим.
Прискорення
у криволінійному русі. Як і для руху тіла вздовж прямої, для
криволінійного руху прискорення
визначається відношенням приросту
швидкості 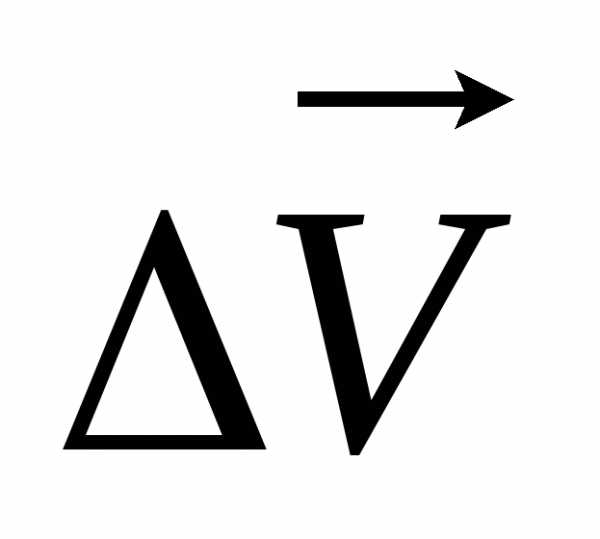 за інтервал часу ∆ t до цього інтервалу
∆ t:
за інтервал часу ∆ t до цього інтервалу
∆ t:
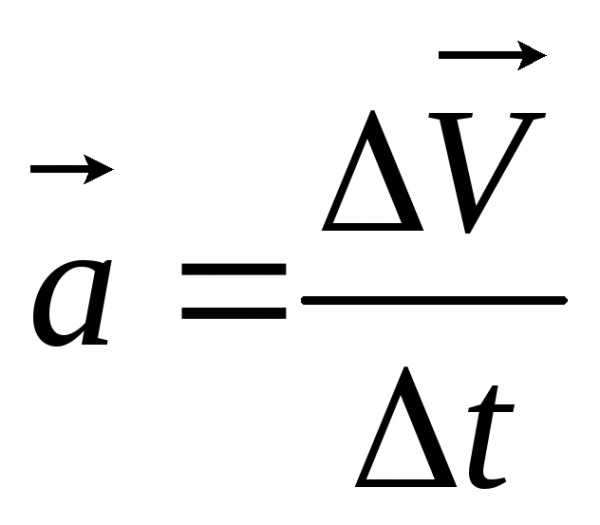 ,
коли ∆ t → 0.
,
коли ∆ t → 0.
На
відміну від випадку прямолінійного
руху тіла, у криволінійному русі напрям
вектора прискорення у певній точці
траєкторії може не збігатись із напрямом
вектора швидкості. Нехай тіло рухається
криволінійною траєкторією з точки А у
точку В за час ∆ t (мал.
1.40). Вектори
швидкості  та
та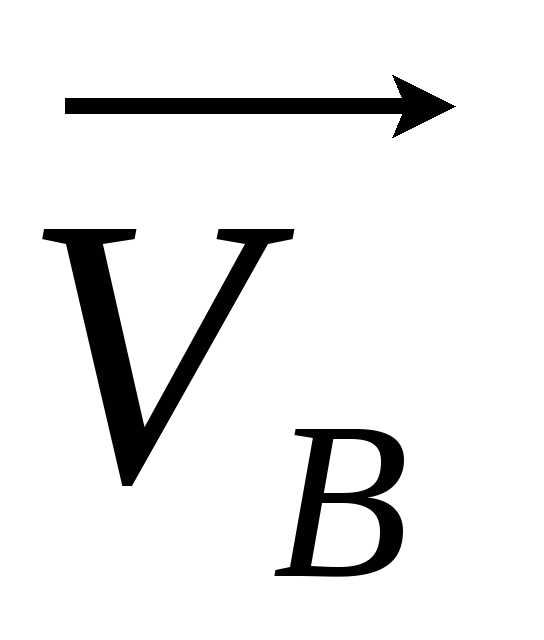 можуть відрізнятися як за напрямом, так
і за модулем. Знайдемо приріст ∆ V під
час переходу тіла з точки А у точку В за
правилом паралелограма. Для цього
перенесемо вектор
можуть відрізнятися як за напрямом, так
і за модулем. Знайдемо приріст ∆ V під
час переходу тіла з точки А у точку В за
правилом паралелограма. Для цього
перенесемо вектор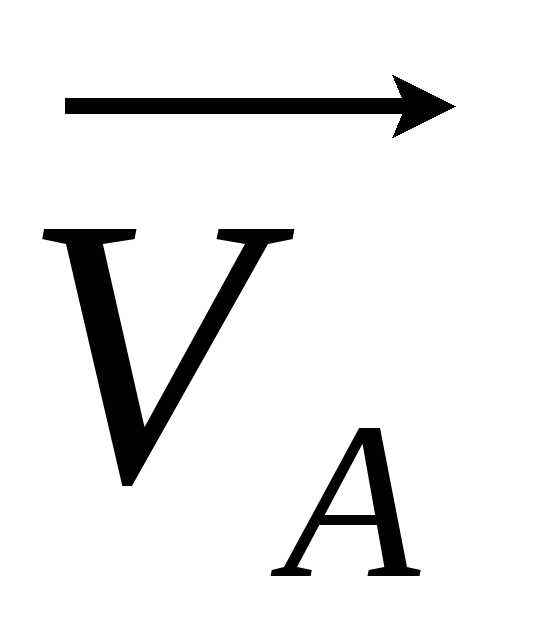 у точку В і побудуємо паралелограм на
цих векторах. Утворений вектор
у точку В і побудуємо паралелограм на
цих векторах. Утворений вектор і буде вектором приросту швидкості за
час ∆ t.
і буде вектором приросту швидкості за
час ∆ t.
Я

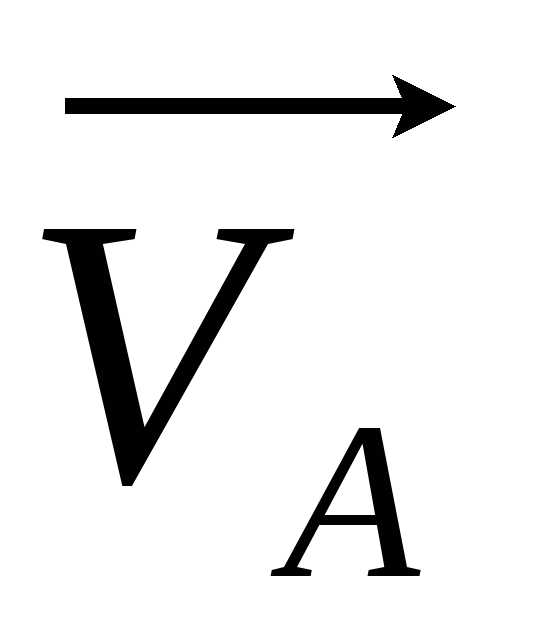 та
та 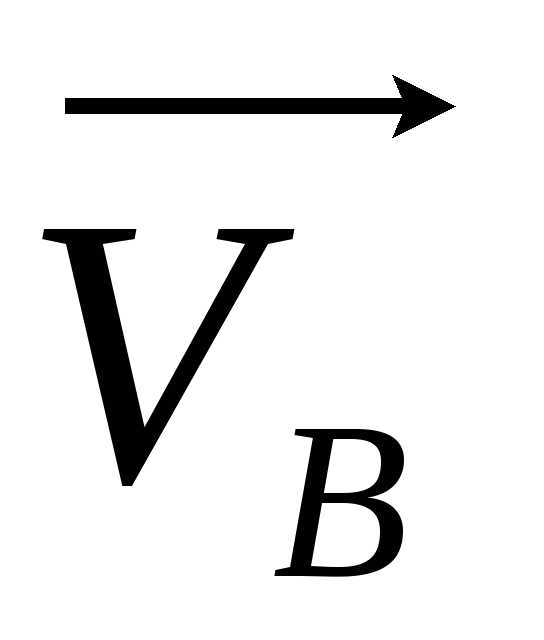 і прискорення збігались
у кожній точці траєкторії, то сама
траєкторія була б прямою лінією.
і прискорення збігались
у кожній точці траєкторії, то сама
траєкторія була б прямою лінією.3. Криволінійний рух – це рух по дугах кіл. На мал. 1.41 зображено складну траєкторію, уздовж якої рухається тіло. З малюнка видно, що деякі ділянки цієї траєкторії можна наближено подати як дуги деяких кіл, зображених штриховими лініями (ділянка KL – дуга кола радіуса r1; BM – радіуса r2; EF – радіуса r3).
Тому вивчення будь-якого криволінійного руху зводиться до вивчення руху тіла по колу.
? Запитання для самоперевірки
Як напрямлена миттєва швидкість у криволінійному русі?
Чим відрізняються зміни швидкості у криволінійному і прямолінійному рухах?
Чи може тіло рухатися по криволінійній траєкторії без прискорення?
Який зв’язок між криволінійним рухом і рухом по колу?
studfiles.net