Квантовая механика формулы – § 29. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ Основные формулы : РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО КУРСУ ОБЩЕЙ ФИЗИКИ : Экономико-правовая библиотека

4.2. Элементы квантовой механики Основные формулы и законы

,

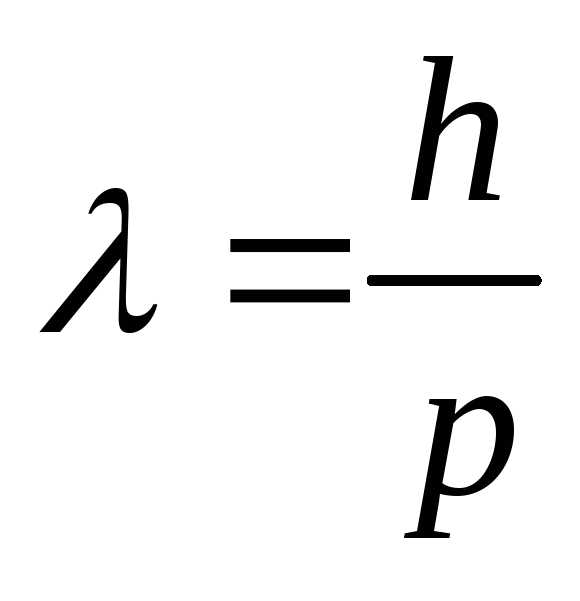где – постоянная Планка, p – импульс частицы.

,

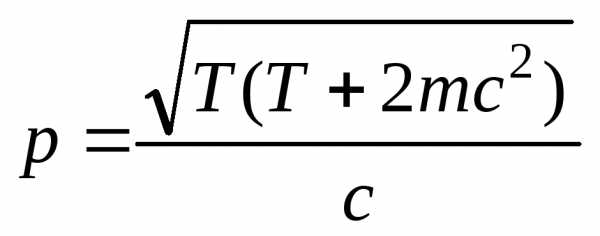где m – масса частицы. При малых скоростях .

,

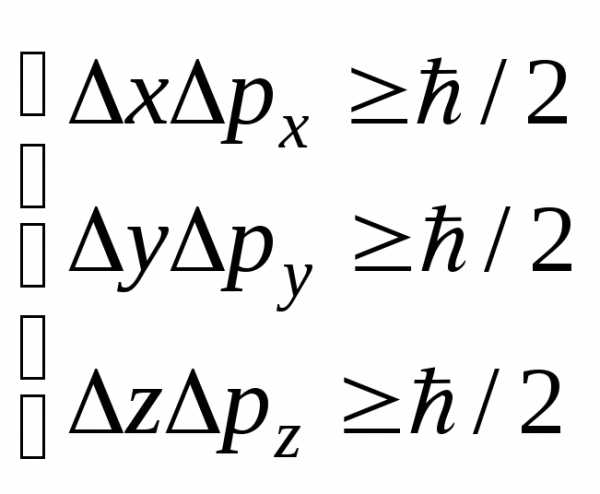где ,– соответственно неопределенности координаты, импульса, энергии и времени,ħ=h/.

.

,

где – волновая функция

микрочастицы, – полная энергия микрочастицы,=– потенциальная энергия частицы,– пространственная координата (=),t – время, ∆ = – оператор Лапласа (записан в декартовых координатах),m – масса микрочастицы, ћ – постоянная Планка,

= – мнимая единица.

.

.

,

где dW(x) –вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке dх.

.

• Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной (0 ≥ x ≥ )

(собственная нормированная волновая функция)

(собственное значение энергии),

где n – главное квантовое число ( n = 1, 2, 3,…). В области 0 ≥ x ≥

= ∞ и= 0.

,

где – коэффициент прозрачности барьера (коэффициент прохождения).

,

где n – главное квантовое число ( n = 0, 1, 2,…), – циклическая чачтота.

• Для частиц с целочисленными спинами (бозонов) справедлива статистика Бозе-Эйнштейна, а для частиц с полуцелыми спинами (фермионов) справедлива статистика Ферми-Дирака. Обобщенное уравнение для квантовых статистик

,

где – среднее число частиц в состоянии с номером,E_i – энергия частицы в этом состоянии; μ – так называемый химический потенциал, определяемый из условия

=N_i , т. е. сумма всех частиц равна полному числу N частиц в системе, знак минус (-) перед единицей в знаменателе соответствует статистике бозонов (распределению Бозе-Эйнштейна, а знак плюс (+) соответствует статистике фермионов (распределению Ферми -Дирака).

Задания

4.16. Вычислите длину волны де Бройля для протона, прошедшего разность потенциалов U = 10 В.

A. [9,1 пм] В. [91 пм] С. [0,91 пм] D. [4,55 нм]

4.17. При какой скорости электрона дебройлевская длина волны будет равна: а) 500 нм; б) 0,1 нм? (В случае электромагнитных волн первая длина волны соответствует видимой части спектра, вторая – рентгеновским лучам).

A. [1,46 ∙10³ м/с; 0,73 ∙10⁷ м/с] В. [0,73 ∙10³ м/с; 1,46∙10⁷ м/с]

С. [2,92 ∙10³ м/с; 1,46 ∙10⁷ м/с] D. [1,46 ∙10⁷ м/с; 2,92 ∙10³ м/с]

4.18. Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислите длину волны де Бройля для такого электрона.

A. [86 пм] В. [43 пм] С. [172 пм] D. [344 пм]

4.19. На грань кристалла никеля падает под углом 64^о к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Принимая расстояние между атомными плоскостями кристалла равным 200 пм, определите скорость электронов, если они испытывают дифракционное отражение первого порядка.

A. [2 Мм/с] В. [1 Мм/с] С. [0,5 Мм/с] [4 Мм/с]

4.20. Скорость протона составляет (8,880 ± 0,012)∙10⁵ м/с. С какой максимальной точностью можно измерить его положение?

A. [13 пм] В. [26 пм] С. [65 пм] D. [40 пм]

4.21. Исходя из того, что радиус атома имеет величину порядка 0,1 нм, оцените скорость движения электрона в атоме водорода.

A. [∆

= 5,8 ∙10⁵ м/с; ~10⁶ м/с] В. [∆ = 5,8 ∙10⁶ м/с; ~10⁷ м/с]

С. [∆= 5,8 ∙10⁴ м/с; ~10⁵ м/с] D. [∆

= 11,6 ∙10⁶ м/с;~10⁷ м/с]

4.22. Пуля массой 12 г вылетает из ружейного ствола со скоростью 450 м/с. Положение пули известно с точностью до 0,55 см (радиус ствола). Какая длина волны соответствует пуле и чему равна минимальная определенность ее скорости?

A. [ 1,2 ∙10^-34 м; 8∙10^-31 м/с] В. [ 1,2 ∙10^-31 м; 8∙10^-34 м/с]

С. [ 6 ∙10^-34 м; 1,6∙10^-31 м/с] D. [ 2,4 ∙10^-34 м; 10^-32 м/с]

4.23*. Длина волны излучаемого атомом водорода фотона равна 121,6 нм. Принимая время жизни возбужденного состояния ∆t = 10

-8 с, определите отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом.

A. [= 3∙10^-9] B. [= 3∙10^-7] C. [= 3∙10^-5] D. [= 5∙10^-6]

4.24. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид: , где

А – нормировочный коэффициент волновой функции, r – расстояние электрона от ядра, – первый боровский радиус. Определите наиболее вероятное расстояние электрона от ядра в основном состоянии.

А. [] В. [/2] С. [ 2]D. []

4.25*. Волновая функция, описывающая движение микрочастицы, имеет вид:

, где– нормировочный коэффициент волновой функции,r – расстояние этой частицы до силового центра, – некоторая постоянная, имеющая размерность длины. Определите среднее расстояние частицы от силового центра.

А. [= ] В. [=] С. [= 2] D. [=]

4.26. Запишите стационарное уравнение Шредингера для свободной частицы, которая движется вдоль оси, а также определите посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы?

А.[, спектр непрерывный] В.[, спектр дискретный]

С.[, спектр дискретный] D.[,спектр дискретный]

4.27. Электрон в бесконечно глубоком одномерном прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения электрона в средней трети ящика?

А. [0,609] В. [0,5] С. [0,195] D. [0,091]

4.28. Волновая функция описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной . Вычислите вероятность нахождения частицы в малом интервале ∆ = 0,2 в двух случаях: 1) вблизи стенки; 2) в средней части ящика.

А. [0,052; 0,4] В. [0,026; 0,2] С. [0,1; 0,4] D. [0,052; 0,8]

4.29. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной . Вычислите наименьшую разность энергий двух соседних энергетических уровней (в электронвольтах) электрона в двух случаях: 1) = 1 мкм; 2) = 0,1 нм.

A. [1,1∙10^-12 эВ; 110 эВ] В. [1,1∙10^-16 эВ; 1,1 эВ]

C. [0,55∙10^-13 эВ; 55 эВ] D. [5,5∙10^-12 эВ; 1,1 эВ]

4.30. Вероятность обнаружить частицу на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле . Если– функция имеет вид, указанный на рисунке справа, то вероятность обнаружить частицу на участке, где – ширина ящика, равна: A. [2/3] В. [1/3] С. [4/3] D. [5/6].

4.31. Пучок электронов с энергией Е = 15 эВ встречает на своем пути потенциальный барьер высотой U = 20 В и шириной = 0,1 нм. Определите коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1).

A. [D = 0,1; R = 0,9] В. [D = 0,9; R = 0,1]

С. [D = 0,5; R = 0,5] D. [D = 0,2; R = 0,8]

4.32. Частица массой m движется в одномерном потенциальном поле =(гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид, где– нормировочный коэффициент;– положительная постоянная. Используя уравнение Шредингера, определите: 1) постоянную; 2) энергию частицы в этом состоянии.

А. [; ] В. [; ]

С. [; ]D. [; ]

4.33. Покажите, что при kT >> E_i (малом параметре вырождения) квантовые распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла – Больцмана, то есть бозонный и фермионный газы приобретают свойства классического идеального газа.

А. [<< 1; ]

4.34. Для каких квантовых частиц характерна знаковая неоднозначность волновой функции и какие значения спина имеют эти частицы?

А. [фермионов; имеют полуцелые значения спина]

В. [бозонов; имеют целые значения спина]

4.35. Для каких квантовых частиц характерна знаковая однозначность волновой функции и какие значения спина имеют эти частицы?

А. [бозонов; имеют целочисленные значения спина]

В. [фермионов; имеют полуцелочисленные значения спина]

studfiles.net

Квантовая механика (волновая).

1. Гипотеза Луи де Бройля. 1924 г.

Известно, что фотон обладает свойствами волны и частицы. Луи де Бройль выдвигает гипотезу, что любая частица вещества (электрон, например) также обладает свойствами волны и частицы, то есть наличие волновых и квантовых свойств является общим универсальным свойством всей материи.

Для электрона можно записать формулу фотона:

; p=mV

Момент импульса есть вектор!

;

В обычных электронных приборах напряжение меняется от 1 до 10⁴ В. следовательно =(12-0,12).

Для проведения опытов по дифракции с электронным пучком, в качестве дифракционной решетки надо взять кристаллическую решетку, в которой расстояние между узлами соизмеримо с несколькими ангстремами (6-8).

Опыт Тартаковской. Рис.1.6.

Так как распределение электронов на экране, соответствующее ходу кривой интенсивности при дифракции, устанавливается только при большом числе прошедших электронов, то волновые свойства электронов следует объяснять статистически: интенсивность волны де Бройля пропорциональна вероятности обнаружения электрона в данном месте пространства. Поэтому волны де Бройля – есть волны вероятности, ибо они дают ответ на вопрос: какова вероятность того, что в данный момент времени частица находится в данном объеме пространства (волновые свойства света – это реальное поле определенной длины волны).

Энергия частицы отрицательна, волны дискретны.

2. Тот факт, что электрон, ударяясь об экран, вызывает вспышку только в одной точке, указывает на то, то электрон частица.

3. Частицы, которые явно обладают волновыми и квантовыми свойствами, называются микрочастицами. Наличие у них волновых свойств приводит к тому, что поведение их носит вероятностный характер.

4. Если говорить о пуле, вылетевшей из ружья, то в силу ее большой массы, , связанная с движением пули, будет очень маленькой (). Следовательно, будет мала вероятность того, что пуля отклонится от траектории, рассчитанной для нее по законам Ньютона (макрочастица). Поведение пули носит достоверный характер.

5. Так как микрочастицы обладают волновыми свойствами и поведение их носит вероятностный характер, то, следовательно, основным уравнением их движения не может быть уравнение Ньютона.

Принцип неопределенности.

Постановка задачи. Классическая механика.

Эти характеристики достоверно известны одновременно в данный момент времени.

, px -проекция момта импульса на ось Х. сопряженные параметры

Можно ли таким же образом описывать поведение микрочастиц? Нет, так как природа процессов различная.

Ответ находят, рассматривая опыт по дифракции электронов на щели. Рис.1.7.

AB=x- ширина щели (расстояние между узлами кристаллической решетки).

Если на экране появилась вспышка, то можно утверждать, что электрон прошел щель. При этом ширина щели () есть неопределенность местонахождения электрона в момент прохождения щели.

Если сужать щель () то получим достоверное значение координаты х электрона в момент прохождения щели.

Благодаря волновым свойствам электрона можно утверждать, что электрон, пройдя щель, дальше движется внутри конуса с углом раствора .

-неопределенность p_x электрона при прохождении через щель. .

– угол первого дифракционного минимума на щели.

Итак.

1. Если , то естьх.

–возрастает, -возрастает.

2. Если , то естьp_х.

.

Следовательно, координата и спряженный импульс не могут быть одновременно неопределены не в силу технических невозможностей, а в силу того, что эти две величины не являются характеристиками микрочастицы потому что микрочастица, в отличие от классической частицы, обладает еще и волновыми свойствами. Как только мы хотим применить к микрочастице характеристики классической часитцы, возникает неопределенность.

Если все же хотим описать поведение микрочастицы с помощью координаты и сопряженного импульса, то это можно сделать только в следующих пределах:

С учетом дифракционных минимумов большего порядка соотношение будет следующим: – соотношение неопределенностей. Является следствием волновых свойств микрочастиц.

Соотношение неопределенностей поставили последнюю точку в споре о том, можно ли использовать законы Ньютона в микромире. Нет.

studfiles.net

16. Понятие о квантовой механике.

Доминирующей современной теорией поведения электронов и других микрообъектов, обладающих очень малой массой, является квантовая механика. Квантовая волновая механика изучает законы движения микрообъектов в силовых полях. Главной особенностью квантовой механики является ее вероятностный статистический характер: она дает возможность находить вероятность того или иного значения некоторой физической величины. В отличии от классической физики в квантовой механике все объекты микромира (электроны, атомы, молекулы и др.) выступают как носители и корпускулярных и волновых свойств (волново-корпускулярный дуализм), которые не исключают, а дополняют друг друга. Не представляет труда обосновать объективность волново-корпускулярного дуализма для световых квантов – фотонов. Так, фотоэффект Столетова (это испускание электронов веществом под действием света ) и эффект Комптона (явление изменения длины волны электромагнитного излучения вследствие рассеивания его электронами) доказывают корпускулярную природу видимого и рентгеновского излучений, а интерференция (изменение в характере звуковых, тепловых, световых и электрических явлений, объясняемое колебательным движением: в первом случае частиц звучащего тела, в остальных трех — колебанием) и дифракция (волн, явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием) – волновую природу света.

В 20-е годы прошлого столетия активно развивалась квантовая механика (Шрёдингер, Гейзенберг, Эйнштейн и др.). Квантовая механика исследует поведение микрочастиц ( электронов, фотонов и др.) в микрополях атомов, молекул и кристаллов, т.е. каких-либо комплексов. Ее выводы носят статистический характер. Микрочастицы движутся по своим законам, их природа носит двойной характер – волново-корпускулярный дуализм («корпускула» – частица и одновременно имеет ЭМ волны). Шрёдингер вывел волновое уравнение, которое описывает поведение электрона в атоме. Из решения уравнения Шрёдингера вытекает понятие «орбиталь» (собственная функция), т.е. квантовая механика отвергает существование в атоме стационарных орбит. Орбиталь – отражает вероятность нахождения электрона в какой-то части атомного пространства. Из уравнения вытекают и некоторые числа, носящие названия квантовых, которые характеризуются определенными значениями и задают форму орбитали, ее энергию ориентацию в пространстве.

Квантовая механика адекватно описывает основные св-ва и поведение атомов, ионов, молекул, конденсированных сред, и др. систем с электронно-ядерным строением. Квантовая механика также способна описывать поведение электронов, фотонов, а также др.элементарных частиц.

Квантовые числа.

n– главное квантовое число (=1,2,3…+∞) – за полный запас электронов в атоме.

е – (0 до n=-1) отвечает за форму атомной орбитали (е 0 1 2 3

spdf

s²p⁶d¹⁰f¹⁴

m_e– магнитное квантовое число (-l; 0; +l)- характеризует ориентацию орбитали в пространстве(нарисовать из тетради)

m_s– спиновое квантовое число – отвечает за вращение электронов вокруг своей оси (-1/2; +1/2)

s²p⁶d⁹f¹⁴

Квантовая формула отражает характер распределения электронов по орбиталям и квантовым слоям.

Закономерности распределения.

1. Принцип Паули. В атоме не может быть двух электронов с одинаковыми значениями всех четырех квантовых чисел.

2. Принцип наименьшей энергии.В атоме электроны в первую очередь занимают орбитали с наименьшей энергией (т.е. располагаются ближе к ядру).

3. Правило Гунда.На вырожденных орбиталях электроны располагаются так, чтобы суммарное спиновое квантовое вещество было максимальным. (вырожденная – орбиталь, характеризующаяся одной и той же энергией).

Из написания квантовых формул бросается в глаза, что систематически повторяются строение наружного электронного слоя у атомов элементов разной химической природы (т.е. разных элементов). В этом состоит главный физический смысл периодического закона. Физическое свойство периодического закона состоит в периодическом повторении строения наружных атомных орбиталей элементов с ростом числа электронных слоев (главного квантового числа)

Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.

Некоторые квантовые числа связаны с движением в пространстве и характеризуют пространственное распределение волновой функции частицы. Это, например, радиальное (главное) ( ), орбитальное ( ) и магнитное ( ) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.

Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция.

Главное (радиальное) квантовое число — целое число, обозначающее номер энергетического уровня. Характеризует энергию электронов, занимающих данный энергетический уровень. Является первым в ряду квантовых чисел, который включает в себя главное, орбитальное и магнитное квантовые числа, а также спин. Эти четыре квантовых числа определяют уникальное состояние электрона в атоме (его волновую функцию). Главное квантовое число обозначается как . При увеличении главного квантового числа возрастают радиус орбиты и энергия электрона.Главное квантовое число равно номеру периода элемента.

Наибольшее число электронов на энергетическом уровне с учетом спина электрона определяется по формуле N = 2n2.

Орбитальное квантовое число — в квантовой физике квантовое число ℓ, определяющее форму распределения амплитуды волновой функции электрона в атоме, то есть форму электронного облака. Определяет подуровень энергетического уровня, задаваемого главным (радиальным) квантовым числом n и может принимать значения

l = 0; 1; 2; …; n-1.

Магни́тное ква́нтовое число́ — параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы). Магнитное квантовое число (m) характеризует ориентацию в пространстве орбитального момента количества движения электрона или пространственное расположение атомной орбитали. магнитное квантовое число, в частности, определяет проекцию орбитального магнитного момента водородоподобного атома на направление магнитного поля и служит причиной расщепления спектральных линий атома в магнитном поле (см. Эффект Зеемана).

Спиновое квантовое число s принимает два значения: +1/2; -1/2. Характеризует собственное вращательное движение электрона (по часовой и против часовой стрелки)

studfiles.net

Основные формулы и методические рекомендации по решению задач на квантовую механику

Данная тема посвящена посвятим тому, что вспомним некоторые важные определения, понятия и формулы, относящиеся к квантовой механике, а также дадим общие рекомендации по решению задач на данную тему.

И так, как же возникло учение о квантах? Из курса электродинамики известно, что теоретические исследования Джеймса Клерка Максвелла показали, что свет есть электромагнитные волны определенного диапазона, что позже подтвердил Генрих Герц в своих опытах. Электромагнитная теория смогла объяснить многие наблюдаемые явления, в том числе, давление, интерференцию и дифракцию света. Но такое явление, как дисперсия, теория Максвелла объяснить не смогла. Это было сделано голландским ученым Хендриком Лоренцем, создавшим электронную теорию взаимодействия света с веществом.

Но и дополненная теория Максвелла нуждалась в уточнениях. Ведь такие явления, как, например, распределение мощности излучения в спектре абсолютно черного тела или возникновение линейчатых спектров и законы фотоэффекта, она объяснить не могла.

Нова теория была выдвинута в одна тысяча девятисотом году Максом Планком. Согласно его гипотезе, электроны атомов излучают свет не непрерывно, а отдельными порциями — квантами. При этом энергия кванта пропорциональна частоте колебаний электрона в веществе.

Квантовые представления о свете, введенные в науку Планком, развил далее Альберт Эйнштейн. Он пришел к выводу о том, что свет не только излучается, но и распространяется в пространстве, и поглощается веществом в виде квантов.

Вот таким вот образом и возникло учение о квантах и, собственно, квантовая физика, которая смогла объяснить ряд явлений, наблюдаемых при взаимодействии света с веществом.

В 1887 году Генрих Герц открыл явление внешнего фотоэффекта, которое было изучено русским ученым Александром Григорьевичем Столетовым.

Внешний фотоэффект возникает при взаимодействии вещества с поглощаемым электромагнитным излучением, при этом происходит вырывание электронов с поверхности вещества.

Проводя свои эксперименты, Столетов установил следующий закономерности фотоэффекта:

1) При отсутствии напряжения между электродами фототок отличен от нуля, что можно объяснить наличием у фотоэлектронов при вылете кинетической энергии.

2) При некотором значении напряжения между электродами сила фототока перестает зависеть от напряжения, то есть достигает насыщения.

3) Если поменять местами полярности катода и анода, то в электростатическом поле между электродами фотоэлектроны будут тормозится и, при некотором значении этого отрицательного напряжения, фототок полностью прекратится.

На основании этих экспериментальных данных были сформулированы законы фотоэффекта.

Первый закон фотоэффекта звучит следующим образом: сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени.

Второй закон формулируется так: при увеличении частоты падающего света максимальная кинетическая энергия линейно возрастает. При этом кинетическая энергия не зависит от интенсивности падающего света.

Третий закон говорит о том, что красная граница фотоэффекта зависит только от рода вещества катода. Напомним, что красная граница — это минимальная частота (или максимальная длина волны), при которой еще возможен фотоэффект.

А четвертый закон утверждает, что фотоэффект практически безинерционен, так как с момента облучения металла светом, до вылета электрона проходит время порядка миллиардной доли секунды.

В 1905 году для объяснения экспериментальных законов фотоэффекта Эйнштейн использовал квантовые представления о свете, введенные Планком, и применил их к поглощению света веществом.

И так фотон, обладающей энергией hν, падая на поверхность металла, поглощается электроном поверхностного слоя металла. И если энергия фотона равна или превышает работу выхода, то электрон вылетает из металла. При этом часть энергии фотона тратится на совершение работы выхода, а остальная часть переходит в кинетическую энергию фотоэлектрона.

Таким образом, было установлено, что свету присущи и корпускулярные свойства. В настоящее время принято считать, что свет обладает двойственной корпускулярно-волновой природой. Двойственность свойств света находит свое выражение в формулах, которые вы сейчас видите на экране. В них корпускулярные характеристики фотона (энергия, масса и импульс) связаны с волновой характеристикой — частотой.

В 1927 году Нильс Бор сформулировал принцип дополнительности. Звучит он следующим образом: для полного понимания природы света необходимо учитывать, как волновые, так и корпускулярные свойства света: они взаимно дополняют друг друга. Однако следует помнить, что для объяснения какого-либо эксперимента следует использовать либо волновые, либо корпускулярные представления о природе света, но не те и другие одновременно.

Теперь немного поговорим о физике атома и атомного ядра.

Bзвестно, что атомы представляют собой очень прочные системы, несоизмеримо более устойчивые, чем составленные из атомов молекулы. Поэтому до конца 19 века атомы считались простейшими неделимыми частицами вещества. Однако последующее развитие науки опровергло эту точку зрения. Было установлено, что атомы представляют собой достаточно сложные образования. Одним из таких фактов стали опыты Резерфорда по рассеиванию альфа-частиц.

На основании проделанных опытов Резерфорд предложил ядерную (или планетарную) модель атома. Согласно модели, в центре атома находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома. А вокруг неподвижного ядра по замкнутым орбитам вращаются электроны, число которых совпадает с порядковым номером элемента в таблице Менделеева.

Однако некоторое время и эта модель считалась не состоятельной, так как согласно расчетам, в этой модели атом должен быть неустойчивым. Противоречия возникли из-за того, что к электронам в атомах применяли законы классической физики, а в микромире действуют свои законы.

Первым, кто признал невозможность применения классических законов физики к атомам, был датский ученый Нильс Бор, который в 1913 году ввел элементы квантовой теории в модель атома Резерфорда и создал неклассическую теорию атома. В основе этой теории лежит три постулата.

Первый постулат (его еще называют постулатом стационарных состояний), говорит о том, что существуют особые, стационарные состояния атома, находясь в которых, атом не излучает энергию, при этом, электроны в атоме движутся с ускорением.

Второй постулат Бора еще называют правилом частот. Согласно ему, атом, при переходе из одного стационарного состояния в другое, излучает или поглощает квант энергии.

В третьем постулате (правило квантования орбит) говорится о том, что в стационарном состоянии атома электрон, движущийся по круговой орбите, должен иметь квантованные (дискретные) значения момента импульса.

Исходя из этих постулатов и используя планетарную модель строения атома, Бор разработал количественную теорию атома водорода. Данная модель была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. С ее помощью удалось объяснить основные закономерности в спектрах атомов водорода и водородоподобных систем и вычислить частоты спектральных линий.

Оставалось, однако, неясным, от чего зависит интенсивность излучений тех или иных частот. Остался без ответа и вопрос, почему совершаются те или иные переходы. И, самое главное, с помощью модели атома Бора невозможно было описать атом гелия — один из простейших атомов, непосредственно следующий за водородом.

Поэтому в 1925 — 1927 годах на смену модели атома Бора пришла квантовая механика, которая явилась строгой непротиворечивой теорией и имела свой собственный математический аппарат.

Сведём в таблицу основные формулы на световые кванты, действие света.

Формула	Описание формулы
	Энергия фотона, где h = 6,63 ∙ 10−34 Дж ∙ с — постоянная Планка, v — частота, c = 3 ∙ 108 м/с — скорость света в вакууме, λ — длина волны.
	Импульс фотона.
	Уравнение Эйнштейна для внешнего фотоэффекта, где Авых — работа выхода электрона, m — масса электрона, υmax — максимальная скорость фотоэлектрона.
	Максимальная кинетическая энергия фотоэлектрона, где е — заряд электрона, Uз — задерживающее напряжение.
	Красная граница фотоэффекта.
	Световое давление, где I — интенсивность света, ρ — коэффициент отражения света.

Теперь сведём в таблицу основные формулы физики атома.

Формула	Описание формулы
	Энергия электрона, находящегося на стационарной орбите в атоме водорода, где е — заряд электрона, ε0 — электрическая постоянная, r — радиус боровской орбиты электрона.
	Энергия, излученная или поглощенная атомом водорода, где W1 и W2 — энергии атома в соответствующих стационарных состояниях.
	Обобщенная формула Бальмера, где R — постоянная Ридберга, n — номер орбиты, на которую переходит электрон, k — номер орбиты, с которой переходит электрон.
	Условие квантования стационарных орбит, где m — масса электрона, υn —скорость электрона на n-ой орбите, rn— радиус n-ой орбиты.
	Радиус n-ой стационарной орбиты электрона в атоме водорода.

Сведём в таблицу основные формулы для элементов квантовой механики.

Формулы	Описание формулы
	Формула де Бройля, где λБ — длина волны де Бройля, h — постоянная Планка, m — масса частицы, υ — скорость частицы.
	Соотношение неопределенностей Гейзенберга, где Δх — неопределенность координаты, Δрх— неопределенность проекции импульса, ћ = h/2π.
	Соотношение неопределенностей, где ΔW — неопределенность значения энергии системы, Δt — неопределенность промежутка времени пребывания системы в данном состоянии

Методические рекомендации по решению задач по квантовой физике.

1) Необходимо всегда помнить о взаимосвязи между волновыми и квантовыми характеристиками частиц.

2) Помните, что взаимодействие фотонов с веществом подчиняется законам сохранения импульса и энергии (законы фотоэффекта следуют из закона сохранения энергии, а формула для расчета светового давления является следствием из закона сохранения импульса).

3) Следует помнить и основные положения ядерной модели атома с точки зрения классической электродинамики для расчета характеристик движения электрона в атоме.

4) Необходимо учитывать то, что, согласно положениям квантовой физики, радиус орбиты электрона, энергия атома, энергия излученного или поглощенного кванта могут иметь только определенные дискретные значения.

videouroki.net

Квантовая механика

Квантовая механика

Quantum mechanics

Квантовая механика – фундаментальная физическая теория, устанавливающая способ описания и законы движения микрочастиц (молекул, атомов, атомных ядер, частиц) во внешних полях. Более формально квантовая механика – это физическая теория систем, у которых физические величины, имеющие размерность углового момента (момента количества движения) сравнимы с постоянной Планка ћ (ћ = h/2π,

h = 6.6.10-34 Дж.с = 4.1.10-15эВ.с). Этому условию, как правило, удовлетворяют микрочастицы. Квантовая механика включает в себя классическую механику как частный случай, реализующийся для макрообъектов. Обычно в нерелятивистской квантовой механике рассматривается движение микрочастиц, для которых скорость v << с, где с – скорость света.

Квантовая механика в основном была создана в течение первых трёх десятилетий 20-го века благодаря работам М. Планка, А. Эйнштейна, Н. Бора, А. Комптона,

Л. де Бройля, В. Паули, М. Борна, В. Гейзенберга, Э. Шрёдингера и П. Дирака.

Физической основой квантовой механики является корпускулярно-волновой дуализм, согласно которому любому материальному объекту – частице или волне – присущи как волновые, так и корпускулярные свойства. Корпускулярно-волновой дуализм наиболее ярко проявляется у микрообъектов. Его следствием является необходимость отказа от некоторых классических представлений, возникших в результате наблюдений за движением макроскопических тел. В частности волновые свойства частиц несовместимы с представлением об их движении по определённым классическим траекториям.

Волновые свойства частицы, например, электрона, требуют и соответствующего “волнового” её описания. В квантовой механике частица описывается комплексной функцией ψ(x,t), называемой волновой функцией, амплитуда которой зависит от пространственных координат х (х – совокупность координат) и времени t. Волновая функция ψ(x,t) полностью определяет состояние частицы. Как известно интенсивность любой волны определяется квадратом её амплитуды. Интенсивность волны, связанной с материальной частицей, определяется квадратом модуля волновой функции, т.е. величиной |ψ|2 = ψ*ψ. Однако, в отличие от классической волны, величина |ψ(х,t)|2 есть вероятность обнаружить частицу в момент времени t в единичном объеме вокруг точки пространства с координатами x. Этот вероятностный характер поведения частицы, во-первых, позволяет отразить волновые свойства объектов при их корпускулярном описании и, во-вторых, принципиально отличает квантовую систему от классической. В классической физике знание положения и импульса частицы в начальный момент и сил, действующих на неё, полностью и однозначно определяет её положение и импульс во все последующие моменты. Т.е. движение классических объектов полностью предопределено (детерминировано). В квантовой механике можно говорить лишь о вероятности обнаружить частицу в каком-то месте пространства, даже при полном знании её начальных кинематических характеристик и всех внешних полей, действующих на неё. И это не связано с какой-то неполнотой квантовых законов, а заложено в природе микрообъектов. Об этом свидетельствуют и соотношения неопределённостей, например, (x,t) Δx·Δp ≈ ћ (Δx – неопределённость в координате, а Δp – неопределённость в импульсе системы). Если потребовать чёткой локализации частицы в пространстве в какой-то момент, т.е. потребовать Δx ≈ 0, то в этот же момент у неё будет полностью неопределённым импульс (Δp ≈ ∞). Таким образом, в следующий момент частица может неконтролируемо переместиться куда угодно и ни о каком предопределённом (детерминированном) движении частицы не может быть и речи.

Состояния в классической и квантовой физике

Классическая физика

Квантовая физика

1. Описание состояния

(x,y,z,px,py,pz)

ψ(x,y,z)

2. Изменение состояния во времени

=∂H/∂p, = -∂H/∂t,

3. Измерения

x, y, z, px, py, pz

ΔхΔpx ~ splank.gif (65 bytes)

ΔyΔpy ~ splank.gif (65 bytes)

ΔzΔpz ~ splank.gif (65 bytes)

4. Детерминизм. Статистическая теория

Динамическое

(не статистическое) описание

|ψ(x,y,z)|2

5. Гамильтониан

H = p2/2m + U(r) op_h = 2/2m + U(r)

В квантовой механике для нахождения всего набора (спектра) возможных значений какой-либо физической величины обычно решаются дифференциальные уравнения, в которых каждой наблюдаемой физической величине (энергии, импульсу, угловому моменту, координате и так далее) сопоставляется оператор (обычно дифференциальный). Во многих случаях этот спектр является дискретным (квантованным), что принципиально отличает квантовую механику от классической.

Эволюция квантовой системы в нерелятивистском случае описывается волновой функцией, удовлетворяющей уравнению Шредингера

где ψ(х,y,z,t) – волновая функция, op_h – оператор Гамильтона (оператор полной энергии системы). В нерелятивистском случае

где m – масса частицы, op_p – оператор импульса, op_U(x,y,z) – оператор потенциальной энергии частицы. Задать закон движения частицы в квантовой механике – это значит, определить значение волновой функции в каждый момент времени в каждой точке пространства. Уравнение Шредингера играет в квантовой механике такую же роль, как и второй закон Ньютона в классической механике. Знание волновой функции квантовой системы и операторов физических величин позволяет вычислить все физические величины, характеризующие данную квантовую систему. В силу недетерминированности квантово-механических предсказаний эти вычисляемые (и наблюдаемые) физические величины носят вероятностный характер, т. е. являются статистическими средними. В результате реализации такой программы можно получить исчерпывающее квантово-механическое описание поведения частицы (системы) в изолированном состоянии или во внешних полях. Так квантово-механическая задача для атома водорода сводится к решению уравнения Шрёдингера для электрона в кулоновском поле протона, с которым он связан. Решением этой задачи является дискретный (квантованный) спектр энергетических состояний (уровней) электрона, квантовые числа, характеризующие электрон в каждом из этих состояний, и, конечно, сами волновые функции электрона в каждом состоянии. Если электрон в атоме водорода не находится в самом нижнем энергетическом состоянии, то атом неустойчив и будет претерпевать эволюцию, вызванную переходами электрона на более низкие энергетические уровни. Вероятности этих переходов также вычисляются методами квантовой механики.

Волновая функция

Волнова́я фу́нкция (функция состояния, пси-функция, амплитуда вероятности) — комплексная функция, используемая в квантовой механике для вероятностного описания состояния квантовомеханической системы. В широком смысле — то же самое, что и вектор состояния.

Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы (или физической системы) в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния.

Физический смысл квадрата модуля волновой функции Править

Волновая функция

\! \Psi(x_1, x_2, \ldots , x_n)

зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля

\! \left|\Psi(x_1, x_2, \ldots , x_n)\right|^2

представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами

\! x_1=x_{01}, x_2=x_{02}, \ldots , x_n=x_{0n}.

Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока

Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.

Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями \! \Psi_1 и \! \Psi_2, то она может пребывать и в состоянии, описываемом волновой функцией

\! \Psi_\Sigma = c_1 \Psi_1 + c_2 \Psi_2

при любых комплексных \! c_1 и \! c_2. См. также Квантовая суперпозиция.

Матричная и векторная формулировки

Любая функция может быть представлена, как бесконечная таблица из её значений, соответствующих каждому аргументу. Если представить в таком виде волновую функцию, то она станет столбцом координат бесконечномерного вектора в Гильбертовом пространстве, то есть, матрицей.

Одна и та же волновая функция в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов.

Функциональная (волновая), матричная и векторная формулировки математически эквивалентны.

Философский смысл волновой функции

Волновая функция представляет собой наиболее полное возможное описание квантовомеханической системы, за исключением, быть может, матрицы плотности, предложенной Л.Д.Ландау, с помощью которой можно описывать системы систем, что невозможно при использовании волновой функции (в случае обычной системы матрица плотности есть тот же квадрат модуля волновой фукнции) скоростей всех её частиц и это описание позволяло описать всё будущее и прошлое системы, то в квантовой механике некоторые параметры описать принципиально невозможно. Согласно квантовой механике, описание системы заканчивается на уровне волновой функции (и матрицы плотности) и только на уровне волновой функции (и матрицы плотности) возможно описать будущее и прошлое системы. Более подробное описание системы, например, с точностью до указания местоположений и скоростей всех её частиц — невозможно, и значения этих параметров оказываются более или менее случайными.

Таким образом, создав квантовую механику, наука дошла до состояния, когда она смогла положить конец многовековому противопоставлению детерминизма и индетерминизма. Современная наука утверждает, в мире сочетаются детерминизм и индетерминизм, и границей между ними служит… матрица плотности или волновая функция?..

Следует понимать, что проблема, которую решает квантовая механика, — это проблема самой сути научного метода познания мира. Если представить себе бильярдный стол, закрытый непроницаемой крышкой, и единственным способом исследования вопроса, есть ли на нём бильярдные шары, предположить закатывание в стол других шаров, то мы и получаем ту самую проблему, для решения которой привлечён метод квантовой механики. Пока вброшенный шар проходит сквозь стол без изменения траектории, предсказуемо, мы можем сделать вывод о том, что на траектории шара других шаров нет. Если в результате взаимодействия шаров на столе мы получаем выкатившиеся несколько шаров с различными конечными импульсами и точками, в которых шары покинули стол, то мы можем лишь предполагать о том, каким образом происходило взаимодействие в системе. Если же лузы в бильярдном столе ограничивают возможность шаров покидать стол (энергетический барьер), то система запутывается ещё больше.

Подобный пример с бильярдом очень наглядно демонстрирует те трудности, с которыми сталкиваются исследователи, разрабатывая инструменты квантовой механики.

Смешанное состояние

Смешанное состояние (смесь состояний) — состояние квантовомеханической системы, в котором не задан максимально полный набор независимых физических величин, определяющих состояние системы, а определены лишь вероятности w_1,w_2,\ldots (\sum w_i=1) нахождения системы в различных квантовых состояниях, описываемых волновыми функциями \psi_1,\psi_2,\ldots. Таким образом, в отличие от чистого состояния, смешанное состояние не описывается одной волновой функцией, а описывается матрицей плотности.

Примерами смешанных состояний могут служить:

неполяризованный пучок частиц;

газ в термостате.

Среднее значение какой-либо физической величины A (которой соответствует оператор) в смешанном состоянии определяется следующим образом:

\bar{A}=\sum_i w_i A_i,\ \ A_i=\int \psi_i^*(x)~\hat{A}~\psi_i(x)dx

В смешанном состоянии, в отличие от суперпозиции состояний, различные квантовые состояния не интерферируют между собой, так как при определении среднего складываются не волновые функции, а средние значения.

СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ

СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ — математически формулируемый принцип квантовой теории, согласно которому запрещается существование таких состояний физической системы, в которых две динамические переменные (далее обозначаемые в общем виде А и В) имели бы вполне определенное значение, если эти переменные являются канонически сопряженными величинами. Поскольку может иметь место несколько различных пар канонически сопряженных величин, постольку можно говорить во множественном числе о соотношениях неопределенностей. Хотя соотношения неопределенностей рассматриваются в качестве принципа квантовой механики, однако его действие может быть прослежено на основе понятий классической механики. Канонически сопряженные величины представляют собою математические переменные, входящие в т. н. канонические уравнения механики (уравнения Гамильтона) и определяющие состояние механической системы в любой момент времени. В качестве канонически сопряженных переменных величин выбирают обычно обобщенные координаты q и обобщенные импульсы/”. С помощью т. н. канонических преобразований можно перейти от q тир к другим канонически сопряженным величинам Q и Р, которые могут иметь другой физический смысл.

Если две переменные А и В канонически сопряжены друг с другом в смысле гамильтонова формализма, то никакой эксперимент не может привести к одновременному точному измерению таких переменных. Неточность измерения связана при этом не с несовершенством измерительной техники, а с объективными свойствами исследуемой системы. Математически соотношения неопределенностей записываются в общем виде следующим образом: ΛΑ-ΔΒ >h. Эта запись означает, что произведение погрешностей измерения канонически сопряженных величин не может быть по порядку величины меньше постоянной Планка h. Чем точнее определено значение одной из входящих в соотношение величин, тем менее определенно значение другой величины: при попытке предельно точно определить значение одной из величин неопределенность значения другой оказывается в области бесконечных значений. Учитывая чрезвычайную малость постоянной Планка h в сравнении с макроскопическими величинами той же физической размерности, приходится делать заключение, что соотношения неопределенностей существенны лишь дри изучении явлений атомного масштаба.

Математическое выражение соотношений неопределенностей было впервые сформулировано В. Гейзенбергом в 1927 в контексте проблемы парадоксального соединения волновых и корпускулярных свойств у микрочастиц. Обсуждая с ним эту проблему, Н. Бор настойчиво искал способ рационального объединения корпускулярных и волновых свойств в объектах микромира. Размышляя о теоретико-познавательных проблемах, Бор пришел тогда к идее дополнительности — корпускулярные и волновые свойства не исключают друг друга, но находятся во взаимнодополнительном отношении. Иногда принцип дополнительности Бора представляется в качестве некоего обобщения соотношений неопределенностей. Однако первоначально Гейзенберг решительно отрицал возможность такого построения новой теории, в которой учитывались бы волновые свойства частиц. Он был тогда убежден, что можно построить новую теорию исключительно на основе идеи дискретности. Конкретное же соотношение неопределенностей между координатой и импульсом частицы было сформулировано им под влиянием Бора, который полагал необходимым найти выражение для характеристики связей между корпускулярными и волновыми свойствами микрочастиц. В соотношениях неопределенностей различные дополнительные свойства частиц своеобразно объединены в одной формуле — на основе методологического принципа был построен специальный математический аппарат.

Отличительная особенность атомных процессов заключается в их корпускулярно-волновой природе, что проявляется в экспериментах. Движение частицы связано с распространением специфической волны, а сама частица может быть обнаружена в любой точке этой волны. В результате движение микрочастицы имеет вероятностный характер. Напр., в эксперименте, где изучается явление дифракции электронов, частица определенной энергии падает на дифракционную решетку; процесс падения электрона многократно повторяется. При этом возникает характерная дифракционная картина, свидетельствующая о волновых свойствах электрона, ибо явление дифракции заключается именно в отклонении от прямолинейного движения, присущего законам геометрической оптики, которая отвлекается от волнового характера физического процесса. Сама картина дифракции электрона показывает, что в акте взаимодействия электрона с дифракционной решеткой участвуют все ее ячейки. Это означает, что невозможно предсказать траекторию движения электрона при его падении на решетку, иначе говоря, невозможно узнать, в каком направлении будет двигаться электрон. Наблюдаемое явление дифракции электронов подтверждает волновую природу микрочастиц и вместе с тем указывает на вероятностный характер их поведения. В квантовой теории состояние частицы в описанной ситуации выражается волновой функцией и не может быть представлено с точностью, характерной для классических понятий. Т. о., к микроскопическим объектам неприменимы классические понятия импульса и координаты. При описании поведения микрочастиц возникает необходимость учета их квантовых свойства, что и проявляется в соотношениях неопределенностей.

Концепции квантовой механики

Квантовая механика изучает законы поведения микрочастиц (атомов, элементарных частиц)

М.Планк (изучая тепловое движение тел, 1900г.): атомы излучающего тела отдают электромагнитную энергию порциями (квантами), причем энергия одного кванта пропорциональна частоте излучения : (Джс – постоянная Планка).

А.Эйнштейн (изучая явления фотоэффекта, 1905г): свет не только излучается, но распространяется и поглощается квантами (кванты света – фотоны, существуют только в движении).

А.Эйнштейн (1909г): свет одновременно обладает и корпускулярными (квантовыми) и волновыми (электромагнитными) свойствами. Т.е. свету присущ корпускулярно-волновой дуализм (двойственность).

Л де Бройль (1924г) сформулировал универсальный корпускулярно-волновой дуализм:

каждый микрообъект проявляет себя одновременно и как частица (имеющая импульс и энергию) и как волна (с частотой и длинй волны).

Де Бройлю удалось сформулировать соотношение, связывающее импульс квантовой частицы с длиной волны, которая ее описывает ( или ).

Экспериментальное подтверждение наличия волновых свойств микрочастиц (К.Дэвиссон, Л.Джермер, 1927г) привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. Однако, волновые свойства макротел (и в частности, человеческого тела) не могут быть экспериментально обнаружены. Это объясняется тем, что длина волны (обратно пропорциональная массе объекта, согласно отношению Де Бройля) при большой массе столь мала, что ее обнаружение лежит за пределами возможности экспериментальной техники.

Мысленный эксперимент «микроскоп Гейзенберга»

В классической физике, построенной на ньютоновских принципах и применяемой к объектам макромира, принимается, что процесс измерения не влияет на измеряемые свойства объекта. Однако, так ли обстоит дело в микромире, позволяет понять следующий мысленный эксперимент: чтобы точно определить положение электрона в пространстве, необходимо направить на него электромагнитную волну, «осветить» его и посмотреть в некий сверхсильный «микроскоп». Но при этом сам микрообъект (например, электрон), являющийся объектом излучения, в результате взаимодействия, с направленным на него другим микрообъектом (квантом света – фотоном), изменит свое положение в пространстве. Таким образом, сам факт замера приводит к изменению положения измеряемого объекта, и неточность измерения обуславливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора.

Этот мысленный эксперимент, отражающий тот факт, что измерение невозможно без взаимодействия, взаимодействие – без воздействия на измеряемый объект и, как следствие, искажение результатов измерения, позволил В.Гейзенбергу (1927г) сформулировать принцип неопределенности (соотношение неопределенности):

( т.к. ) здесь – неопределенность (погрешность измерения) пространственной координаты микрочастицы, (или ) – неопределенность импульса (или скорости) частицы, – масса частицы, – постоянная Планка.

Принцип неопределенностей касается и других характеристик микрочастиц. Еще одна такая взаимосвязанная пара – это энергия и время протекании квантовых процессов.

Принцип Гейзенберга играет в квантовой механике ключевую роль, хотя бы потому, что достаточно наглядно объясняет, как и почему микромир отличается от знакомого нам макромира. Принцип неопределенности говорит о том, что если бы нам удалось абсолютно точно установить местоположение квантовой частицы, о ее скорости мы бы не имели ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы не имели понятия, где она находится.

Однако, принцип неопределенности не утверждает, что у квантовых частиц отсутствуют определенные координаты и скорости (или что эти величины абсолютно непознаваемы) – он утверждает лишь, что мы не в состоянии достоверно узнать и то и другое одновременно.

Принцип дополнительности Бора (1927г)

Соотношение неопределенностей является конкретным выражением более общего положения – принципа дополнительности Бора.

Квантовомеханический принцип дополнительности:

результаты, полученные в разных экспериментах, не могут быть связаны в единую картину, но они необходимы для исчерпывающего описания квантового объекта.

В дальнейшем Бор придал принципу дополнительности широкий философский смысл: полное понимание свойств любого объекта исследования требует дополняющих взглядов на него с разных, несовместимых между собой, точек зрения.

Статистический характер квантового описания природы.

Из-за принципа неопределенностей, описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми привыкли описывать механическое движение, в квантовой механике объекты описываются, так называемой, волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам, как изменяется со временем состояние квантовой системы.

Принципиальные отличия квантовой механики от классической механики заключаются прежде всего в том, что:

– ее законы являются статистическими по своей природе

– ее предсказания имеют вероятностный характер

Резюмируем все вышесказанное:

– в классической механике можно точно вычислить значения координат и скорости объекта

– в квантовой механике можно вычислить лишь вероятность того или иного значения координат, скорости и энергии частицы в заданный момент времени

– состояние системы в классической механике задается координатами и скоростями всех материальных точек системы

– состояние объекта (или системы объектов) в квантовой механике задается волновой функцией объекта (или системы объектов)

– корпускулярные свойства света легче наблюдать, когда его длина волны достаточно мала

– волновые свойства человеческого тела затруднительно наблюдать ввиду его большой массы покоя

– если в данном квантовом состоянии физические величина Х не имеет определенного значения, это означает, что можно предсказать лишь вероятность того или иного результата измерения Х

– при взаимодействии макроскопического измерительного прибора с квантовым объектом, в процессе измерения изменяется состояние измеряемого квантового объекта.

Принцип дополнительности Бора (в узком квантовомеханическом смысле):

– результаты, полученные в разных экспериментах, не могут быть связаны в единую картину, но они необходимы для исчерпывающего описания квантового объекта

– все величины, характеризующие объект, можно разделить на такие группы, что измерение величин из одной группы делает невозможным или неточным измерение соответствующих величин из другой группы

– дополнительные физические величины всегда связаны тем или иным соотношением неопределенности

– дополнительными величинами являются: координаты и импульс; энергия и время

– при точном измерении физической величины невозможно измерить точно дополнительную ей величину (это следует из принципа неопределенности)

– принцип дополнительности отражает невозможность невозмущенных измерений (это следует из принципа неопределенности).

Принцип дополнительности Бора (в широком философском смысле):

– полное понимание свойств любого объекта исследования требует взгляда на него с разных, несовместимых, дополняющих друг друга точек зрения

– исследование реальности всегда сопровождается ее изменением, а результат исследования зависит от того как оно выполняется

– значение принципа дополнительности состоит в том, что он подчеркивает равноценность разных, в том числе несовместимых точек зрения

– однозначно, одним методом невозможно описать явление, объект или субъект – необходимо привлечь дополнительные представления

– никакое отдельное знание о предмете не может быть самодостаточным, требуется дополнение в лице других наук.

Примеры проявления принципа дополнительности (в широком смысле):

– культура как цельность ее научной и гуманитарно-художественной составляющей

– человек как цельность его биологического и социального начал

– естественнонаучная и гуманитарная культуры – это два, взаимодополняющих друг друга, способа постижения мира человека

– взаимоотношения между объектом исследования и исследователем являются одним из примеров принципа дополнительности

– биологическая и социальная сущности в человеке – это две, дополняющие друг друга, характеристики

– соотношения между хаосом и порядком в процессе самоорганизации материи являются одним из примеров действия принципа дополнительности

– анализ и синтез – два метода научного познания, которые связаны друг с другом по принципу дополнительности.

Квантово-механическое описание физических явлений микромира считается единственно верным и наиболее полно отвечающим реальности. Объекты макромира подчиняются законам другой, классической механики. Граница между макро- и микромиром размыта, а это вызывает целый ряд парадоксов и противоречий. Попытки их ликвидировать приводят к появлению других взглядов на квантовую механику и физику микромира. Видимо, наилучшим образом выразить их удалось американскому теоретику Дэвиду Джозефу Бому (1917-1992).

studfiles.net

Квантовая механика. Парадоксы микромира

«Если квантовая механика не потрясла вас до глубины души — вы ее не поняли.»
Нильс Бор

На первый взгляд кажется, что квантовая механика противоречит здравому смыслу. На самом деле она противоречит лишь законам макромира, где действует механика Ньютона. А мир элементарных частиц живет по своим правилам.

Граница между мирами

Макс Планк (1858–1947) — физик-теоретик, основоположник квантовой физики

У квантовой теории есть точная дата рождения — 14 декабря 1900 года. В этот день проходило заседание Немецкого физического общества, на котором Макс Планк зачитал свой доклад, где впервые прозвучал термин «квант». Этим словом ученый обозначил порцию энергии, излучаемой атомами. Он вывел формулу, при помощи которой можно рассчитать количество энергии, соответствующей одному кванту. Эту величину назвали постоянной Планка.

Сам Планк не считал кванты реальной вещью, для него это была всего лишь удобная математическая модель, позволяющая объяснить взаимодействие между электромагнитными волнами и атомами. Но предположение Планка, что атомы излучают энергию порциями, позже было подтверждено экспериментально.

Постоянная Планка есть во всех формулах квантовой механики. Ее присутствие означает, что речь идет о бесконечно малых величинах, гораздо меньше обычной песчинки. Можно сказать, что эта величина в физике проводит границу между микромиром и макромиром.

В микромире, изучением которого занимается квантовая механика, работают совсем не те физические законы, к которым мы привыкли в мире обыденном. Можно даже сказать, что квантовая механика противоречит здравому смыслу. В чем же заключается это противоречие? В первую очередь в том, что в микромире невозможно произвести какие-либо измерения, не повлияв на объект этих измерений.

Квантовая механика на заре своего существования называлась атомной, потому что эта наука изучает движение электронов в атоме

Все очень неопределенно

В обыденной жизни мы живем среди предметов, размеры которых сопоставимы с нашими. Здесь с измерениями проблем нет. Мы можем взять рулетку и узнать высоту и ширину окна в своей комнате — наше присутствие и воздействие рулетки никак не повлияет на размеры окна. В микромире все гораздо сложнее. Мы не можем увидеть электрон невооруженным глазом, более того, у нас нет измерительных инструментов такого микроскопического масштаба. Чтобы узнать какой-либо из параметров электрона (например, его координаты), физики направляют на него другую элементарную частицу и замеряют отклонения, которые возникли в результате их столкновения.

Таким образом, факт измерения, изучения частицы воздействует на нее. И результаты, естественно, искажаются. Это неразрешимое противоречие квантовой механики: изучение законов элементарных частиц невозможно без воздействия на них, но это воздействие искажает результаты.

Эффект воздействия инструментов на объекты измерения, существующий в квантовом мире, впервые описал немецкий физик Вернер Гейзенберг. Поэтому он был назван принципом неопределенности Гейзенберга. Согласно этому принципу, чем меньше неопределенность одной величины, тем больше неопределенность другой. Если бы этот закон действовал в нашем мире, то, измерив ширину окна, мы не могли бы точно узнать его высоту. Это кажется странным, но только для макромира.

Представьте, что в ходе опыта измеряется пространственное положение квантовой частицы. С некоторой погрешностью, возникшей из-за измерения, его удалось установить. Но если мы захотим измерить еще и скорость этой частицы, сделать это будет гораздо сложнее, ведь из-за того, что мы направили к ней электрон, ее скорость изменилась. То есть неопределенность второй измеряемой величины гораздо выше, чем первой. В этом и заключается принцип Гейзенберга.

«В науке головоломку тебе задает не кто иной, как Господь. Он придумал и саму игру, и ее правила, которые к тому же ты можешь и не знать полностью» (Э. Шрёдингер)

Поделиться ссылкой

sitekid.ru

Квантовая механика — Юнциклопедия

В 1900 г. М. Планк обнаружил, что имеется единственная возможность объяснить распределение по частотам излучения из отверстия в ящике с нагретыми стенками (см. Физические парадоксы): частицы, излучающие волны частоты со, могут изменять свою энергию только скачкообразно, порциями ħω. Коэффициент ħ называют постоянной Планка.

Основываясь на этом, Планк получил свою знаменитую формулу, с огромной точностью описавшую экспериментальное распределение интенсивности излучения для всех частот и при всех температурах стенок. Классическая физика не знала такой скачкообразности — скачки энергии так малы из-за малости Я, что изменения кажутся непрерывными.

В 1905 г. скачкообразность подтвердилась работой А. Эйнштейна по теории фотоэффекта. Фотоэффект можно объяснить, только предположив, что свет — это набор частиц — фотонов у которые, взаимодействуя с электроном, выбрасывают его из атома. Представление о свете как о классической электромагнитной волне не могло объяснить концентрации энергии на одном электроне, необходимой для его вырывания. Эйнштейн показал, что фотон с энергией е имеет импульс р = ε/с = ħω/c = 2πħ/с. Энергия волны заданной частоты может изменяться только скачкообразно, порциями ħω, подобно энергии излучателей в рассуждении Планка. Скачкообразность распространилась и на электромагнитные волны.

В некотором смысле точка зрения Эйнштейна означала возврат к ньютоновской теории корпускул (см. Оптика, Фотон). Опять возник вопрос, на который не смог ответить И. Ньютон: как объединить волновую природу света, доказанную опытами по интерференции и дифракции, с корпускулярной, необходимой для объяснения фотоэффекта?

В 1913 г. Н. Бор распространил на атом идею о дискретности возможных значений энергий излучателей: допустимы не все орбиты, а лишь некоторые. Бор установил правила для нахождения этих допустимых орбит. С классической точки зрения электрон, вращающийся вокруг ядра, должен излучать электромагнитные волны. Он движется с ускорением, а по законам классической электродинамики не излучает только заряд, движущийся по прямой с постоянной скоростью. Почему же электрон не падает на ядро, излучая свет?

Согласно правилам Бора, электрон может излучать свет только при переходе с одной орбиты на другую порциями с частотой со, равной ω = (Еn—Еm)/ħ, где Еn и Еm — значения энергии электрона на n-той и m-той орбитах. На орбите с наименьшей возможной энергией электрон живет неограниченно долго — ему некуда переходить. Так была объяснена стабильность атомов.

Теория Бора описывала все главнейшие свойства атомов, но смысл правил квантования оставался загадочным. Бор назвал их постулатами — недоказанными предположениями. Их смысл стал ясен только после создания квантовой механики.

Правила квантования Бора — одно из удивительных явлений в истории науки. Только гениальным озарением можно объяснить появление этой теории до того, как выяснились волновые свойства частиц. Эйнштейн сказал по этому поводу: «Это высшая музыкальность в области теоретической мысли».

В 1924 г. французский ученый Л. де Бройль предположил, что поведение частиц, например электронов, должно описываться волновым процессом с длиной волны λ, связанной с количеством движения р так же, как связана длина волны фотонов с их импульсом: К = 2πħ/р. Уже через три года это предсказание подтвердилось опытом: американские физики К. Дэвиссон и Л. Джермер открыли дифракцию электронов на кристаллах — электрон, действительно, ведет себя как волна. По расположению дифракционных пятен после прохождения кристалла можно было найти длину волны, связанной с электроном данной энергии. Она совпала с предсказанием де Бройля.

Следующее важное событие произошло в 1926 г. Э. Шрёдингер обобщил догадку де Бройля на случай, когда электрон движется не в свободном пространстве, а во внешнем поле, например в кулоновском поле ядра. Он получил уравнение для функции, описывающей волновые свойства частиц. В свободном пространстве решение этого уравнения переходит в функцию, описывающую волновой процесс с длиной волны де Бройля. Во внешнем поле длина волны изменяется от точки к точке. Стационарное состояние электрона в атоме водорода на языке уравнения Шрёдингера означает, что получилась стоячая волна. Для этого в области движения электрона должно уложиться целое число волн де Бройля. В этом и состоит смысл правил квантования Бора. Стоячие волны могут образоваться только при дискретных значениях энергии электрона, когда укладываются 1, 2 и т. д. волн.

Вот простой пример того, как получаются дискретные уровни энергии. Предположим, что частица движется в одном направлении внутри интервала длины l, или, иными словами, внутри потенциальной ямы длины l с бесконечными стенками. Волновая функция на краях ямы должна обращаться в нуль. Стационарное состояние получается из условия, что на длине l должно уложиться целое число полуволн 2l/λ = n. Теперь используем формулу, связывающую длину волны де Бройля с импульсом частицы: р = 2πħ/λ = πħn/l. Найдем энергию Е = р²/2m. Нетрудно получить такую формулу: E=π²ħ²n²/2ml². Аналогично можно найти и уровни энергии в более сложных случаях.

Вот как выглядит уравнение Шрёдингера для одномерного движения в потенциале V(x):

d²ψ/(d²x²ψ) + 2m/ħ² • (E-V)ψ = 0

Первое слагаемое — вторая производная ψ по х. Если первая производная характеризует скорость изменения ψ с х, то вторая производная дает скорость изменения этой скорости.

Решения этого уравнения для V = 0 очень легко найти. Их два: ψ₁ = a₁ sin kx и ψ₁ = a₂ cos kx. Они и описывают волны де Бройля: k = 2πħ/λ = p/ħ = √(2mE)/ħ.

Для частицы, колеблющейся около положения равновесия, когда возвращающая сила пропорциональна величине отклонения х, потенциал V(x) имеет вид: V(x) = γх²/2. Точное решение уравнения Шрёдингера для подобного потенциала непростая задача; приведем только результат. Возможные значения энергии такого осциллятора Еn = (n + 1/2)ħω. В наинизшем состоянии (n = 0), в отличие от классического осциллятора, ни кинетическая, ни потенциальная энергии не равны нулю. Сумма их равняется ħω/2. Частица колеблется около положения равновесия, так что среднее значение кинетической энергии равняется среднему значению потенциальной и равняется ħω/4.

Опыты по дифракции электронов тоже описываются уравнением Шрёдингера, если предположить, что интенсивность пучка электронов после рассеяния пропорциональна квадрату модуля волновой функции. Там, где волны, рассеянные атомами кристаллической решетки, складываются, получается максимальная интенсивность электронного пучка.

При уменьшении интенсивности пучка обнаруживается, что дифракционная картина не изменяется, даже если пролетает, скажем, один электрон в минуту. Значит, уже одному электрону нужно приписать вероятность попасть в то или иное место фотопластинки, стоящей за кристаллом.

В 1926 г. немецкий физик М. Борн предположил, что вероятность найти электрон в том или ином месте равняется квадрату модуля волновой функции. Что же помогло прийти к такому заключению?

Вспомним, что теория волновых явлений света — интерференции и дифракции — была разработана задолго до уравнения Максвелла, т. е. до понимания электромагнитной природы света. Предполагалось только, что источник света испускает волны неизвестной природы, а интенсивность света пропорциональна квадрату той величины, которая колеблется. В современном представлении колеблются во времени и пространстве электрические и магнитные поля, и интенсивность света пропорциональна их квадрату. Но почти все волновые проявления объясняются независимо от природы света.

Было естественно и для волн, связанных с частицами, считать, что есть некий волновой процесс, а интенсивность — в нашем случае вероятность — пропорциональна квадрату модуля волновой функции.

Сначала предполагали, что волновым свойствам частицы соответствует некое реальное физическое поле, подобное электромагнитному Полю в световой волне. Но тогда уже один электрон давал бы в одном акте всю дифракционную картину, а он чернит только одно зерно фотопластинки. И это не единственный довод против такого взгляда на природу волнового процесса.

Итак, волновая функция частицы не есть какое-либо физическое поле; она описывает потенциальные возможности исхода того или иного последующего наблюдения.

Истинный смысл волновой функции выяснился после того, как В. Гейзенберг получил соотношение неопределенностей (1927), и особенно в многолетних спорах Н. Бора с А. Эйнштейном.

Квантовая механика не дает однозначного ответа на некоторые вопросы, а лишь, вероятность того или иного результата. Главное открытие квантовой механики — вероятностный характер предсказаний — следствие того, что мы пользуемся классическими понятиями, не имеющими точно определенного смысла (см. Соотношение неопределенностей).

Дальнейшее развитие квантовая механика получила в работах английского физика П. Дирака, обобщившего уравнение Шрёдингера на случай частиц со спином 1/2, движущихся со скоростями, сравнимыми со скоростью света. Основное следствие уравнения Дирака состоит в том, что наряду с частицами должны существовать античастицы (например, наряду с электроном — позитрон), отличающиеся от частиц только знаком заряда.

В 1930 г. Э. Ферми применил квантовую механику к электромагнитному полю. Волна с волновым вектором k представляет собой осциллятор, в котором колеблются электрическое и магнитное поля. Энергия магнитного поля играет роль потенциальной энергии осциллятора, а энергия электрического поля — роль кинетической. Но применение квантовой механики к осциллятору приводит к тому, что энергия осциллятора может изменяться порциями величины ħω и, кроме того, в состоянии с наинизшей энергией кинетическая и потенциальная энергии не равны нулю. В вакууме, где нет ни одной частицы, ни одного кванта, электрическое и магнитное поля для каждого волнового вектора колеблются около нулевого значения. В пустоте существуют нулевые колебания электромагнитного поля. Если для какого-нибудь волнового вектора энергия переходит из самого нижнего значения в первое возбужденное, говорят, что в пространстве появился один кванте волновым вектором k, энергией ε = ħkc, импульсом р = ħk. Это и есть фотон, предсказанный Эйнштейном в 1905 г.

Согласно уравнению Шрёдингера, атом должен был бы неограниченно долго находиться в любом возбужденном состоянии. Именно нулевые колебания заставляют электрон переходить на более низкую орбиту с испусканием кванта света — фотона.

Применение квантовой механики к другим полям, например к описывающим электроны и позитроны, приводит к аналогичному результату — в вакууме существуют нулевые колебания электрон-позитронного поля, непрерывно рождаются и исчезают всевозможные частицы. Такие временно образующиеся частицы называют виртуальными (см. Вакуум физический).

yunc.org