Примеры решения задач по квантовой механике
Задача 6. Найдите частоту красной границы фотоэффекта для металла, если при энергии падающих фотонов 6,6 эВ максимальная кинетическая энергия фотоэлектронов составляла 4,2 эВ. Постоянная Планка h = 6,61034 Джс, е = 1,61019 Кл. Ответ: 5,81014 Гц.
Решение.
Чтобы найти частоту красной границы фотоэффекта, нежно знать работу выхода электронов из металла. Работу выхода найдем из уравнения Эйнштейна:
Приравняв работу выхода к минимальной энергии фотонов, получим
Задача 9. Найдите максимальную скорость фотоэлектронов, вылетающих из металла с работой выхода 5 эВ под действием излучения с энергией квантов 10 эВ. Масса электрона
Решение.
Сначала найдем максимальную кинетическую энергию фотоэлектронов из уравнения Эйнштейна:
а потом по классической формуле кинетической энергии найдем максимальную скорость.
Задача 15. Микрочастица находится в квантовом состоянии, энергия которого с точностью до 0,01% равна 6,6 эВ. Оцените среднее время жизни частицы в этом состоянии. Постоянная Планка
Решение.
Согласно условию неопределенность значения энергии
Используем соотношение неопределенностей
Задача 22. Рассмотрите все способы распределения двух частиц по двум состояниям для случаев: а) частицы квантовые с целочисленным спином; б) частицы квантовые с полуцелым спином. Ответ: 3 способа, 1 способ.
Решение.
Сначала будем их размещать по одной частице в ячейке. Имеем один способ.
Теперь по две частицы в ячейке. Сначала в одной, потом в другой. Имеем еще два способа.
Квантовые частицы с полуцелым спином являются фермионами, и в любом квантовом состоянии могут находиться только в единственном числе.
Их можно разместить только по одной частице в ячейке. Имеем один способ.
Итак, две квантовые частицы с целочисленным спином по двум состояниям можно разместить тремя способами, а две квантовые частицы с полуцелым спином – одним способом.
Задачи по термодинамике
Задача. Посчитайте среднюю энергию молекулы данного газа.
Решение.
Средняя энергия молекулы газа зависит только от температуры газа и вычисляется по формуле
где – число степеней свободы молекулы данного газа. Это число зависит от количества атомов в молекуле газа.
Число атомов | 1 | 2 | 3 |
3 | 5 | 6 |
Задача. Посчитайте внутреннюю энергию некоторого количества данного газа.
Решение.
Внутренняя энергия заданного числа молей газа зависит только от температуры газа и вычисляется по формуле
Решение.
Изменение внутренней энергии заданного числа молей газа зависит только от температуры газа и вычисляется по формуле
Задача на вычисление работы газа , количества подведенного к нему теплаи изменения его внутренней энергии.
Решение.
Эта задача предполагает применение уравнения первого начала термодинамики
Все величины в этом уравнении могут быть как положительными, так и отрицательными.
Если газ нагревается, , если газостывает, . Визотермическом процессе .
Если газ расширяется, , если газсжимается, . Визохорическом процессе .
При адиабатном расширении газ остывает, а при адиабатном сжатии газ нагревается.
Задача 35. Двум киломолям водяного пара сообщили количество теплоты, равное Q = 80000 Дж. Найдите изменение температуры, внутренней энергии и совершенную работу, если процесс изохорический. Газовая постоянная равна 8,31 Дж/мольК. Ответ: 1,6 К, 80000 Дж, 0.
Решение.
Так как по условию процесс изохорический, имеем . Тогда из уравненияпервого начала термодинамики
Следовательно, изменение внутренней энергии газа равно 80000 Дж. Остается найти изменение температуры по формуле
studfiles.net
Решение задач по квантовой механике
Для многих студентов квантовая механика — все равно что китайская грамота. Почему данная наука вызывает непонимание, а каждое домашнее или контрольное задание становится труднопреодолимым испытанием?
Причины бывают самые разные в зависимости от того, к какому виду относится тот или иной студент. Без лукавства можно сказать, что самой распространенной из них является элементарная лень. Большинство студентов не имеют желания тратить время и усилия на освоение науки, сильно отличной от всех и потому требующей большего внимания. Другие страдают от нехватки базовых знаний в области математики и физики, ведь, согласитесь, сложно решать квантовомеханические дифференциальные уравнения, не имея хороших навыков дифференцирования и интегрирования. Вызван дефицит знаний ленью или “плохой школой” — уже другая история.
Конечно, бывает и такoй фактор, как преподавание предмета плохим лектором, неспособным грамотно, логически структурированно пояснить фундаментальные основы квантовой механики.
Квантовая механика не является чем-то недоступным для человеческого понимания. На самом деле, при наличии желания понять данный предмет и должном усердии можно достичь больших успехов (что справедливо, впрочем, и для любого другого предмета).
Желающим приложить усилия и изучить квантовую механику как следует можем дать следующие рекомендации. Итак, краткая инструкция:
- Восполните пробелы в своих знаниях по линейной алгебре: линейные пространства, базисы, детерминанты, матрицы. Без этих знаний вам будет сложной понять математический аппарат квантовой механики. Рекомендую доступную в плане изложения книгу —
- Вспомните, как решать дифференциальные уравнения. Если не умеете, научитесь!
- К сожалению, хороших русскоязычных учебников по квантовой механике мало. Традиционно, для курса квантовой механики используют следующий учебник: Л.Д. Ландау и Е. М. Лифшица «Квантовая механика». Можно воспользоваться такими книгами, как Мессиа А. « Квантовая механика». Если есть возможность, то лучше ознакомиться с хорошим западным учебником, например, Claude Cohen-Tannoudji, Bernard Diu , Frank Laloe «Quantum
- Читать хорошо, но надо и практиковаться, решать задачки и выполнять некие математические выкладки для понимания того, что и откуда выводится. Для этих целей хорошо подходят следующие задачники:
- В.М.Галицкий, Б.М.Карнаков, В.И.Коган. «Задачи по квантовой механике».
- З. Флюгге . «Задачи по квантовой механике» (содержит и теорию).
Для желающих заработать хорошую оценку при меньших усилиях, есть хорошая новость. За исключением отдельных физических специализаций на отдельных факультетах, большинство проходит неполный курс ознакомительного характера. А это значит, что круг тем для вас значительно сужается и вам достаточно освоить фундаментальные принципы квантовой механики, которые не являются очень сложными, но требуют некоторого осмысления. К книжкам надо обращаться, но вам потребуются лишь первые главы.
Квантовый мир устроен немного иначе. И вам надо понять основные различия между квантовой механикой и теоретической: получить представление о вероятностном характере движения электрона, уяснить принцип неопределенности Гейзенберга и его последствия, и т.д.
Типичные вопросы, на которых ловят нерадивых студентов:
- Почему движущийся с ускорением электрон не падает на ядро, теряя энергию при излучении электромагнитных волн?
- Схоже ли движение электрона вокруг ядра с движением Луны вокруг солнца (нет, поймите почему)?
- Может ли частица проскочить через барьер с энергией меньшей, чем высота барьера (вероятность туннелирования маленькая, но не нулевая)?
- В чем отличие квантового гармонического осциллятора от классического гармоническом осцилляторе из курса теоретической механики (обязательно поясните для себя, в чем состоит различие между двумя этими задачами)?
Решение квантовой механики на заказ
Для тех, кому изучение квантовой механики кажется слишком сложным путем, есть мы, решатели. У нас можно заказать подробное решение задач по квантам. Нужно только прикрепить задание и указать сроки.
УЗНАТЬ СТОИМОСТЬ РЕШЕНИЯ
reshatel.org
Решение задач по квантовой механике
Квантовая механика раздел теоретической физики, которому уже сотня лет, и у истоков которой стояли выдающиеся ученые. Они разработали основные уравнения квантовой механики, которые тесно связаны со многими разделами математики. И в решении задач по этой дисциплине необходимы только твердые знания.
Задача – цель, задача – решение
Со старта обучения в вузе студенту предстоят нелегкие испытания в виде решения задач. Главная из них – успешно завершить учебу и получить диплом. Но перед этим придется решать задачи очень разные. Это и чисто житейские, но больше, конкретные, по различным дисциплинам. Не исключаются и задачи по квантовой механике. Вот только далеко не все готовы к этим испытаниям. Особенно новички из младших курсов. За советом и опытом им, естественно, стоит обратиться к старшим коллегам. Уверены, что совет прозвучит, как твердая необходимость использовать услуги нашей компании.
Неспроста у нас такая репутация
Наша уверенность в своих силах имеет много оснований, которые за 8 лет нашей деятельности на рынке услуг в помощь при написании студенческих работ, только окрепли. За эти годы сложился костяк из настоящих профессионалов, представляющих различные отрасли и области науки, техники и социальной сферы. Научно-производственный и жизненный опыт, высокий уровень образования позволяет им:
- все работы, поступившие на заказ, готовить в оригинальном варианте, с отлично раскрытой тематикой, обозначением акцентов на главных направлениях, четкости решений с подробным расписанием формул, при необходимости, с анализами и выводами;
- все работы сдавать в том виде, который соответствует их характеру и требованиям к техническому оформлению;
- все работы сдавать в срок, с особым вниманием к пометке срочно, и в соответствии с остальными параметрами, оговоренными в договоре с клиентами.
Такие договора, которые используем с момента основания фирмы, являются обоюдным стимулом. Для наших специалистов выполнение каждого пункта – это подтверждение имиджа фирмы и их собственного мастерства, а для клиентов – весомый стимул обращения к нашим услугам. Ведь наличие договора – это фактическая гарантия того, что работа будет исполнена в срок и в соответствии с теми требованиями, которые выдвинул заказчик.
Далее, договор фиксирует важный пункт, где обозначена цена написания работы. А это, согласитесь, не последняя составляющая при балансировании заказчика между необходимостью обратиться к нам или воспользоваться бесплатными услугами Интернета.
Вольному воля
Разумеется, каждый волен выбирать сам свою судьбу. Поверьте, что в этом контексте это не высокопарность, а реальное отображение того, что может ожидать студента. То, что работы из Интернета качественные, правильные во всех отношениях – подтверждений нет. Более того, везде ведется работа по выявлению плагиата из мировой Сети, за чем следуют жесткие санкции к тем, кто воспользовался услугами анонимных сайтов и беспризорных научных работ. Если даже избежать участи отчисления, то все оставшееся время студент будет под постоянным подозрением, постоянно его работы будут проверяться с особенной тщательностью.
Работы, заказанные у нас, все оригинальные, на то он и индивидуальный заказ, ведь мы не можем предугадать тему и вид работы. Поэтому написание уже происходит по факту. Ведь не можем мы знать тему курсовой или дипломного проекта. А такие солидные работы наиболее часто попадают в руки наших специалистов. Особенно, от студентов-заочников, у которых всегда нет времени, но зато есть деньги.
В отношении оплаты не переживают и остальные наши заказчики, ибо работы у нас выполняются недорого. Это одна из основных составляющих в нашей деятельности. Ценообразование целиком доходчивое для каждого. Берется сложность работы по виду и предмету, по срокам и объему, и от этого договариваемся с заказчиком, Как правило, наша цена устраивает даже безденежное студенчество. И оно предпочитает спокойствие и уверенность за небольшую плату нам, чем тревогу и волнения бесплатно из Интернета.
fiziku5.ru
Демонстрация решения простейших задач квантовой механики с помощью компьютерных моделей системы Wolfram Mathematica
Рассмотрена возможность применения компьютерных моделей системы Wolfram Mathematica для демонстрации законов квантовой механики.
Ключевые слова: квантовая механика, интерактивная демонстрация, компьютерная модель.
Квантовая механика — один из самых сложных разделов в лекционном курсе общей физики. Для его понимания нужны хорошие знания не только физики, но и высшей математики, например, надо знать теорию решения дифференциальных уравнений. К сожалению, количество часов, отведенных на лекции по физике, уменьшается, а знания студентов не становятся лучше. Наглядная демонстрация решения простейших задач квантовой механики значительно улучшает понимание ее законов. В сети Интернет существует большое количество различных материалов, созданных с помощью разнообразных программных продуктов. Их создание требует специальных знаний в области программирования, разработки достаточно сложны и недешевы. Например, многие интерактивные моделирующие программы используют технологии Java [1]. Часто используются также Flash-технологии [2]. Разработки компании Wolfram Research созданы на основе CDF-технологии (Computable Document Format) с помощью системы Wolfram Mathematica. Сайт компании имеет раздел «Demonstration project», материалы этого раздела находятся в открытом доступе.
Система Wolfram Mathematica — это постоянно совершенствующаяся система, фактически ставшая самой мощной вычислительной системой мира. С помощью этой системы можно создавать интерактивные лекции-презентации, используя уже имеющиеся компьютерные модели или создавая свои.
Покажем, как продемонстрировать решение простейших одномерных задач квантовой механики с помощью таких интерактивных моделей.
На рис.1а и 2б изображены волновые функции частицы в одномерной прямоугольной потенциальной яме. Интерактивная анимация позволяет изменять ширину и глубину ямы, при этом меняется вид волновых функций и расстояние между энергетическими уровнями. Видно, что энергия частицы может принимать только определенные дискретные значения, то есть находиться только на определенных уровнях энергии.
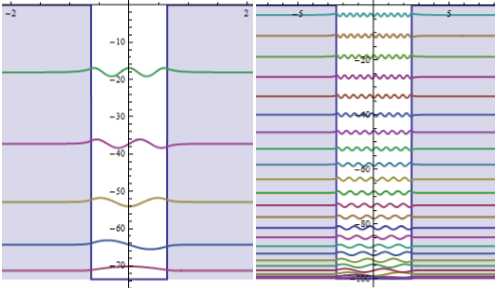
Рис.1. а, б
Если размеры ямы малы (рис.1а), то уровни энергии заметно дискретны. Если же размеры ямы увеличить (рис.1б), то расстояние между уровнями сильно уменьшается и при очень широкой яме энергетический спектр становится непрерывным. На этом примере хорошо виден переход от законов квантовой механики к классической физике.
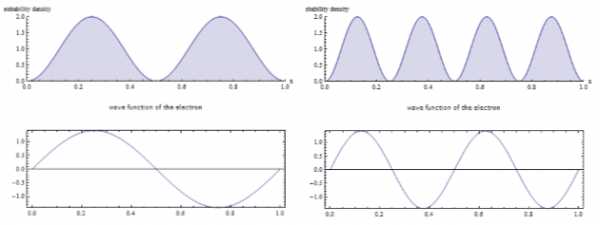
Рис. 2. а, б
Более подробно волновые функции и плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы можно показать на примере следующей демонстрации. Анимированные графики позволяют менять главное квантовое число n от 1 до 10, показывая, как при этом меняется вид волновой функции. На рис.2 приведены волновые функции ψn (x) (нижние кривые) и плотностивероятности │ψn (x)│2 (верхние кривые) для n=2 (рис.2а) и n=4 (рис.2б). При n=2 частица не может находиться в середине ямы, а с одинаковой вероятностью может находиться в ее левой и правой части. При n=3 вероятность также в разных местах ямы различна.. Модель показывает, что в квантовой механике нельзя говорить о траектории частицы.
Еще один характерный пример — прохождение частицы через потенциальный барьер (туннельный эффект). Компьютерная модель позволяет менять ширину и высоту барьера, и энергию частицы. На рис.3а изображен широкий потенциальный барьер. Энергия частицы меньше высоты барьера (штриховые линии). Нижний рисунок — волновые функции частицы (действительная и мнимая части). Это классический случай — частица отражается от такого барьера. Рис3б. — узкий барьер, энергия частицы меньше высоты барьера. В этом случае наблюдается туннельный эффект- проникновение частицы за барьер. Наконец, рис.3в. показывает, что даже если энергия частицы больше высоты барьера, частица может и отразиться от него, что в классической механике невозможно.
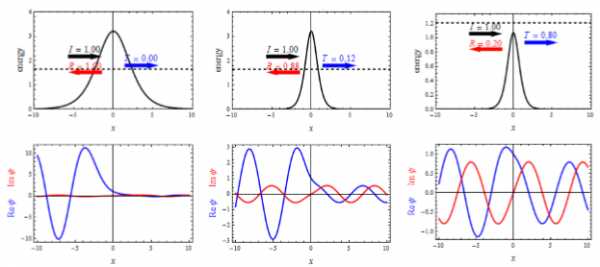
Рис.3. а, б, в
Раздел «Demonstration project» содержит большое количество примеров решения различных задач квантовой механики средствами Wolfram Mathematica. Содержание каждой демонстрации проверено экспертами компании. Компьютерная анимация сопровождается пояснительным текстом и необходимыми формулами.
Применение компьютерных анимационных моделей и графиков сокращает время изложения сложных разделов квантовой механики и улучшает их понимание, что повышает эффективность усвоения лекционного материала.
Литература:
1. Постникова Е. И., В. В. Ларионов. Лекционные занятия по физике в условиях информатизации образования в ВУЗе // Изв.Томского политехнического университета. 2007, т.310, № 2. — С.249–253.
2. Бутиков Е. И. Компьютерные модели для изучения динамики твердого тела // XIII Всероссийская научно-методическая конференция «Телематика’2006», Санкт-Петербург, 5–8 июня 2006 г. С. 350–351.
moluch.ru
КВАНТОВАЯ МЕХАНИКА Решение задач по теме 7:
Documents войти Загрузить ×- Математика
Related documents

Адаптивные линейные измерения амплитуды и фазы

21 – Sanish2.ru

28 – Sanish2.ru

Исследование проявлений квантового хаоса для семейства
Когерентное состояние

Копцов Д.В.
Лекция24

О.В.Алифанов Термодинамические свойства осциллятора с

Lekciya9

Программа курса (pdf

Нелинейный осциллятор

Зависимость гашения звука от частоты.

Основы единой теории физики.

Осцилляторы вакуума и эффект Унру.

Нелинейный осциллятор

(OBV) История осциллятора On Balance Volume или
studydoc.ru
Решение типичных задач в курсе квантовой механики
страница 1 страница 2Министерство образования Украины
НТУУ “КПИ”
Решение типичных задач в курсе квантовой механики
часть 2
Киев 2002
Рецензенты
Д-р ф.-м. наук Олейник В.П.
Канд. ф.-м. наук Гусева О.А.
Терентьева Ю.Г.
Решение типичных задач в курсе квантовой механики.
НТУУ «КПИ» 2002
Содержание
Часть 2. Типичные задачи.
Частица в одномерной прямоугольной потенциальной яме с
бесконечными стенками. …..…………………….…………….…4
Частица в сферической потенциальной яме………………………14
Туннельный эффект………………………………………………..19
Самостоятельная расчетная работа «Определение коэффици-
ента туннелирования частицы через потенциальный барьер»….23
Раздел 2. Типичные задачи
Частица в одномерной прямоугольной потенциальной яме
Постановка задачи
Пусть частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы l. Найти:
-
Нормированные волновые функции стационарных состояний и энергетический спектр частицы, используя уравнение Шредингера. -
Возможные значения энергии частицы, исходя из того, что реализуются лишь такие ее состояния, при которых в пределах данной ямы укладывается целое число полуволн де Бройля. -
Плотность уровней (dN/dE) (т.е. число уровней на единичный интервал энергии), как функцию Е, при условии, что ширина ямы такова, что уровни расположены весьма густо. Вычислить (dN/dE) для электрона при Е = 1,0 ЭВ, и ширине ямы l = 1,0 см. -
С помощью соотношения неопределенностей Гейзенберга силу давления частицы на стенки этой ямы при минимально возможной ее энергии. Для оценок массу частицы взять равной массе электрона. -
Вероятность пребывания частицы в области l/3xl/3, если она находится в основном энергетическом состоянии. -
Среднее значение координаты частицы x> и проекции импульса px> если частица находится в основном состоянии.
Анализ условия
-
“частица массы m“ означает, что по условию считается известной масса частицы. Этой частицей может быть любой микрообъект: электрон, протон, нейтрон или, например, -частица. -
“находится в потенциальной яме” – этот термин не является чисто квантовым. Применительно к системе, описываемой классической механикой, это означает, что частица находится в такой области пространства, в которой действуют потенциальные силы. Причем эти силы направлены так, чтобы удерживать частицу в данной области. В квантовой механике понятие «силы» не существует. Квантовая механика вообще не ищет ответа на вопрос – какая причина приводит к изменению в состоянии частицы?, она рассматривает вероятность того, что состояние будет именно таким. Поэтому под потенциальной ямой подразумевается область пространства, в которой потенциальная энергия частицы задается некоторой функцией координат – потенциалом.
-
” потенциальная яма одномерна “ – следовательно, потенциальная энергия частицы зависит только от одной-единственной координаты. Этот термин тоже не является чисто квантовым. Если этой координатой является одна из декартовых осей, говорят о прямоугольной потенциальной яме (для сравнения – в классической механике – потенциальная энергия силы тяготения вблизи поверхности Земли, которая зависит только от высоты h расположения тела над землей U(h)=mgh). Если же этой координатой является r – расстояние до центра поля, говорят о сферической потенциальной яме (в электростатике – потенциальная энергия поля точечного заряда U(r)=kq/r, она зависит только от расстояния до источника поля). -
“бесконечно высокие стенки “ в потенциальной яме – означает, что в ограниченной области пространства потенциальная энергия принимает конечные значения (в частном случае – ноль), а за пределами этой области – потенциальная энергия бесконечно велика. Последнее утверждение означает, что чтобы попасть в область бесконечно большого потенциала частица должна вначале получить откуда-нибудь дополнительную энергию, равную бесконечно большой величине. Эта ситуация математически возможна, а физически – нет, поэтому становится очевидно, что находиться в области бесконечно большого потенциала частица не может вообще. Если графически изобразить аналитическую зависимость потенциала от координаты
получится следующая картинка:
U(x)
const
0 l x
Рис.2
В точках х=0 и х=l имеется скачкообразное изменение потенциала, который, таким образом, графически имеет форму незамкнутого прямоугольника. Отсюда и термин “прямоугольная” потенциальная яма. Поскольку потенциал по своей природе есть величина, определенная с точностью до постоянной, а аналитический вид решения принципиально не зависит от величины const, то обычно выбирают const = 0. В этом случае расчеты упрощаются.
Решение
Задание I
Найти нормированные волновые функции стационарных состояний и энергетический спектр частицы, используя уравнение Шредингера.
Для начала запишем стационарное уравнение Шредингера в общем виде,
а теперь посмотрим, какой вид оно примет с учетом условия нашей задачи. Поскольку наша задача одномерна (потенциал зависит только от одной координаты), то волновая функция частицы, находящейся в таком пространстве, тоже зависит только от этой одной координаты. В таком случае от оператора Лапласа, который в декартовой системе координат представляет собой сумму вторых частных производных по всем координатам, остается только вторая производная по единственной координате х
Учитывая вид потенциала, разобьем пространство (в данном случае ось ОХ) на три области: область I : х є (-,0), где потенциал равен бесконечно большой величине, область II : х є (0,l), где потенциал равен константе (мы договорились, что константа равна нулю), и область III :
х є (l ,) – где потенциал снова равен бесконечности. Далее следует решить уравнение Шредингера в каждой области отдельно и, наконец, пользуясь непрерывностью волновой функции во всем пространстве, сшить полученные решения между собой на границах областей.
Уравнения Шредингера для каждой области выглядят следующим образом:
область I: (1)
область II: (2)
область III: (3)
Тот факт, что результирующая волновая функция должна быть непрерывна во всем пространстве, означает, что ее куски непрерывны каждый в своей области и, кроме того, в пограничных точках, где стыкуются области, значения соответствующих кусков волновой функции слева и справа должны совпадать. Поэтому граничными условиями в точках х = 0 и х = l являют-ся следующие соотношения
(4)
В уравнениях (1) и (3) в качестве второго слагаемого входит бесконечно большая величина. Уравнение Шредингера, выражая универсальный закон сохранения энергии, должно выполняться в любой части пространства. Единственный путь удовлетворить уравнение Шредингера в этих областях – предположить, что волновая функция здесь тождественно равна нулю
(5)
и считать неопределенности равными нулю. Поскольку в дальнейшем это предположение к противоречию не приводит, то оно является допустимым. Иными словами, в областях I и II частицы нет.
Осталось найти волновую функцию в области II. Уравнение (2) представляет собой хорошо известное дифференциальное уравнение второго порядка, решение которого – гармоническая функция
где (6)
А и В – константы интегрирования, найти которые нам предстоит дальше. Кроме того, как только в процессе решения задачи будет определена величина k, автоматически в соответствии с (6), это даст нам численное значение полной энергии частицы Е.
Воспользовавшись первым из граничных условий – в точке х=0, получаем
,
первое слагаемое равно нулю при любом значении А ( из-за синуса), а второе равно нулю только если . Тогда
(7)
Второе граничное условие – в точке x=l дает
(8)
или
, где n-целые числа (8а)
Следует отметить, что формально равенство (8) будет выполняться и при А=0. Тогда волновая функция II тождественно равна нулю. А если учесть, что и I иIII тоже равны нулю, то выходит, что во всем пространстве частицы нет. Таким образом, вариант А=0 соответствует тривиальной ситуации.
Возвращаясь к соотношению (8а), записываем
или, выражая Е, (9)
Это есть искомое выражение для энергетического спектра частицы. Как уже отмечалось (формула (8а)), n принимает значения целых чисел. Таким образом, энергия частицы не непрерывна, а дискретна, то есть может принимать ряд четко определенных значений, а квантовое число n соответствует номеру энергетического уровня частицы.
Может ли число n быть равным нулю? Если да, тогда это означало бы, что в области II находится частица, имеющая одновременно нулевую потенциальную энергию (по условию) и равную нулю полную энергию (согласно(9)), а,следовательно, нулевую кинетическую энергию. В то же время k=0 (согласно(7)), означает, что и волновая функция частицы в области II тоже тождественно равна нулю. Таким образом, очевидно, значение n = 0 описывает тривиальную ситуацию – отсутствие объекта исследования. Посему n = 0 включать в рассмотрение нет смысла, и будем считать, что n=1,2,…
Волновая функция частицы равна
(10)
Остается найти нормировочный множитель А. Эта процедура является простым математическим упражнением по вычислению интеграла. Вспомнив, что волновая функция, будучи возведеной в квадрат, даст плотность вероятности нахождения частицы в данной области, а после интегрирования по всей области – полную вероятность нахождения частицы во всей области, а также считая факт нахождения частицы хоть где-нибудь внутри области достоверным, то есть таким, вероятность которого равна единице, получаем равенства,
(11)
откуда
Окончательно, волновая функция, описывающая нахождение частицы в бесконечно глубокой потенциальной яме,
(12)
Задание 2.
Де Бройль предположил, что всякому микрообъекту можно поставить в соответствие волну, длина которой обратно пропорциональна импульсу частицы
(13)
(очевидно, что p2=2mE , Е – кинетическая энергия частицы). Если рассматривать эту волну, заключенную в некоторой части пространства, то логично сделать вывод, что стационарному (или неизменному во времени ) состоянию должна соответствовать стоячая волна. Такое состояние может реализоваться совсем не всегда, а только когда на краях области (в нашем случае – на краях ямы) будут узлы. И, следовательно, на ширине ямы будет укладываться целое число полуволн де Бройля.
(14)
Подставив (13) в (14) легко получаем выражение для энергии частицы Е
(15)
Последнее выражение (15) тождественно результату (9), полученному в задании 1.
Вычислим несколько значений энергии на соседних энергетических уровнях и оценим, как изменяется “расстояние” между ними по мере роста номера уровня n.
Таб.1
| n | En | E=|En – En-1| | = E/En |
1 | | ||
2 | | | 3/4 |
3 | | | 5/9 |
4 | | | 7/16 |
Из приведенной выше таблицы видно, что абсолютное “расстояние“ между уровнями E увеличивается с ростом номера уровня, в то время, как относительное расстояние уменьшается, стремясь к нулю как 1/n согласно формуле:
Lim n= Lim n(n2-(n-1)2)/n21/n0
Задание 3
Плотность уровней легко получим, взяв дифференциал от обеих частей равенства (15)
и воспользовавшись еще раз соотношением (15) только в немного измененной форме
Окончательный результат выглядит так
(16)
Для электрона при Е=1,0 эв и l=1,0 см
(эв-1)
Задание 4
Соотношение неопределенностей Гейзенберга служит для описания системы, которая находятся в пограничном состоянии между макро- и микромиром и проявляет себя и как классический и как квантовый объект. Поэтому понятие «сила», которое вводится в классической механике и уже не имеющее смысла в квантовой физике, еще может быть использовано для проведения оценочных расчетов.
Если частицу рассматривать как классический объект, то сила давления, как и любая сила, согласно второму закону Ньютона, может быть вычислена как отношение приращения импульса частицы к промежутку времени, за который это приращение произошло,
Приращение импульса имеет место вследствие его неопределенности, поскольку наша частица проявляет и волновые свойства. Тогда для оценки силы давления можно использовать приближенные (или оценочные) значения для px и t, полученные из оотношения неопределенностей Гейзенберга, которое связывает между собой кординату с проекцией импульса, и время с энергией
.
(17)
Здесь для простоты считаем, что частица находится в основном энергетическом состоянии. Тогда, разделив почленно равенства (17) одно на другое и пренебрегая несущественны множителем 2/2 получим
(18)
Еще раз напомним, что соотношение Гейзенберга само по себе оценочное, поэтому точность ответа в пределах одного порядка является приемлемой.
Задание 5
Вероятность того, что частица находится где-то внутри области 0хl, равна единице, поскольку мы исходим из того, что, во-первых, частица существует и, во-вторых, «живет» внутри этой области. Математическим выражением этого факта является условие нормировки
Чтобы определить вероятность нахождения частицы в какой-то части этой области достаточно в приведенном выше интеграле указать координаты этой области
Дальнейшие вычисления зависят от того, на каком энергетическом уровне находится частица. По условию задания она находится в основном состоянии, то есть n=1.
Таким образом, вероятность того, что частица находится в средней трети области, равна 0,61.
Задание 6
Связь между операторами и измеряемыми физическими величинами в квантовой механике устанавливается с помощью формулы для среднего значения величины m в состоянии, описываемом волновой функцией
(19)
Это соотношение является почти тривиальным, если принять во внимание следующие рассуждения.
Пусть путем экспериментального измерения некоторой физической величины мы убеждаемся, что получаем одно и то же численное значение (разумеется, в пределах погрешности эксперимента), сколько бы измерений мы ни проводили. Это значит, что данная величина имеет точное значение, которое может быть получено как среднее по всем измерениям. С точки зрения квантовой механики, существование точного значения физической величины означает, что для оператора этой физической величины волновая функция системы, находящейся в данном состоянии, является собственной, а значит,
(20)
где М – собственное число. Напомним, что собственное число по своей сути как раз и является точным значением измеряемой величины. Теперь умножим выражение (20) слева на ψ* :
Поскольку в правой части равенства содержится число М – множитель, то его запросто можно поставить на первое место, после чего проинтегрировать равенство по всему фазовому объему
Таким образом, точное значение физической величины, если таковое существует, с одной стороны, является собственным значением соответствующего оператора, а с другой – средним значением измеряемой величины, разумеется, при достаточно большом количестве измерений.
Вернемся к частице в потенциальной яме и определим среднее значение ее координаты и проекции импульса на ось х. Воспользовавшись уравнением (19), явным видом волновой функции частицы (12), которая находится в потенциальном ящике в основном состоянии ( n = 1 ), а также тем фактом, что оператор координаты это умножение на координату, запишем
Итак, среднее значение координаты частицы в яме равно l/2. Среднее значение импульса частицы равно нулю, что видно из
Приведенные результаты оказываются почти очевидными, если подойти к данному вопросу с классической точки зрения и принять во внимание, что, внутри ямы координата частицы может быть любой, а среднее значение координаты, естесственно, это середина ямы, то есть точка l/2. Проекция же скорости (и импульса) – это величина векторная колеблется вокруг положения равновесия, как у маятника, изменяясь и по модулю, и по направлению. Поэтому среднее значение проекции скорости (и импульса) равно нулю.
Следует отметить, что интерпретировать результаты квантовомеханических расчетов с помощью классических аналогий можно в очень редких случаях, поскольку квантовая механика, как теория описания физических процессов вступает в свои права тогда, когда классическая теория себя исчерпывает и не в состоянии адекватно объяснять явления. Это происходит, например, на границе макро и микромира. Что касается данной конкретной задачи, то ее можно в какой-то мере рассматривать как пограничную, которая еще как-то подчиняется классическим законам, но в то же время квантование (дискретность) энергии не может быть объяснено только классической теорией. Очевидно, здесь требуется принципиально новый, квантовомеханический подход.
Частица в сферически-симметричной потенциальной яме.
Потенциал, как известно, это универсальная функция координат, характеризующая потенциальную энергию частицы в любой точке пространства. Обычно используют прямоугольную систему координат, тогда потенциал есть функция декартовых координат U(x,y,z). В предыдущем разделе мы рассмотрели подробно частный случай, когда потенциал зависит не от всех трех декартовых координат, а лишь от одной; таким образом, «жизнь» частицы, процессы – все происходит вдоль одного-единственного, выделенного направления. Вообще говоря, в качестве системы координат можно использовать любую, вариантов можно предложить более десятка, например, хорошо известную цилиндрическую или сферическую. Однако, бывают такие задачи, в которых удобно использовать совершенно конкретную систему координат, это приводит к резкому упрощению расчетов и анализа результатов. В первую очередь выбор системы координат диктуется симметрией потенциала. В этом случае говорят, что симметрия задачи совпадает с его симметрией.
Чаще всего (возможно, даже чаще, чем прямоугольная) в задачах встречается сферическая симметрия. Продиктовано это тем, что в квантовой механике существует класс задач, посвященных описанию поведения элементарных частиц (к примеру, электронов), входящих в состав атомов, а, значит, находящихся в кулоновском поле ядра. А ведь хорошо известно, что потенциальная энергия частицы в кулоновском поле зависит не от абсолютного положения частицы в пространстве, а от того, насколько далеко она находится от источника поля. Поэтому говорят, что такая задача имеет сферическую симметрию. Другими словами, потенциальная энергия частицы имеет одно и то же значение для всех точек, принадлежащих сферической поверхности радиуса r : U=U(r).
Что же представляет собой бесконечно глубокая сферическая яма? В действительности она является почти полностью придуманным, идеализированным объектом, как, впрочем, и одномерная потенциальная яма с бесконечными стенками. Проще всего представить ее себе, если вообразить некую точку, окруженную на некотором расстоянии R0 абсолютно непроницаемой сферической поверхностью. Тогда если внутри этой поверхности находится частица, ей очень не повезло – она никогда не сможет вырваться за пределы сферы. Тот факт, что для того, чтобы покинуть пространство в пределах сферы R0 она должна получить бесконечно большую энергию, и означает, что она находится в бесконечно глубокой потенциальной яме.
Потенциал внутри ямы может быть не обязательно кулоновским, в зависимости от условия задачи он может иметь любой другой аналитический вид. Очевидно, это повлияет на состояние частицы внутри ямы. Теперь для того, чтобы начать изучать поведение частицы в такой потенциальной яме рассмотрим конкретное условие задачи.
Постановка задачи
Частица массы m находится в сферически-симметричной потенциальной яме, в которой потенциал определяется, как
Для случая, когда волновая функция зависит только от r
найти:
-
Нормированные волновые функции частицы -
Возможные значения энергии частицы -
Для основного состояния частицы наиболее вероятное значение расстояния rвер , а также вероятность нахождения частицы в области r rвер
Решение
Задания 1 и 2
Возможные значения энергии частицы находим, решая операторное уравнение
Поскольку потенциал имеет сферическую симметрию, то оператор Лапласа разумно будет записать также в сферических координатах
Кроме того, волновая функция частицы в потенциале, который зависит только от одной координаты r , будет также зависеть только от этой одной координа-ты. Тогда дифференцирование волновой функции по остальным переменным будет давать нуль, а значит, в выражении для оператора Лапласа можно оста-вить только те слагаемые, которые содержат производные только по r
Следуя форме потенциала, разделим пространство на две области – первая область внутри сферы радиуса R0, а вторая – за пределами этой сферы. Для каждой из этих областей составим и решим уравнение Шредингера, а потом «сошьем» решения на границе областей. Итак, уравнения
в чем-то похожи на те, что мы детально исследовали в разделе 1. Второе уравнение содержит бесконечно большое слагаемое, поэтому его решение – волновая функция, тождественно равная нулю.
Первое уравнение отличается от того, что мы анализировали в разделе 1, тем, что содержит в операторе Лапласа дополнительное слагаемое. Такое уравнение решается стандартным методом подстановки
,
где функция (r) является неизвестной. После подстановки волновой функции в таком виде в уравнение Шредингера, выполнения всех необходимых операций дифференцирования и всех возможных сокращений приходим к уравнению для (r)
которое является хорошо изученным и до боли знакомым уравнением гармонических колебаний. Его решение
Возвращаемся к подстановке ( ). Тогда волновая функция принимает вид
Для нахождения констант интегрирования А и В воспользуемся следующими соображениями. Вследствие деления на r , в волновой функции в точке r =0 имеется сингулярность, или, проще говоря, возрастание к бесконечно большой величине. Волновая функция, однако, не имеет права быть неограниченной, поэтому, чтобы избавиться от этой неприятности нам остается только потребовать, чтобы числитель также стремился к нулю. Тогда неопределенность типа легко раскрывается (хотябы по правилу Лопиталя) и приводит к конечной величине (r) . Тогда условие
дает В=0 и волновая функция принимает вид
Далее воспользуемся граничным условием. Волновая функция на границе областей должна совпадать. Так как в области r>R0 она равна нулю, то и на границе ( то есть в точках с r=R0) тоже должна принимать нулевое значение
Автоматически это дает
Таким образом, энергетический спектр частицы нами уже получен.
Последнюю неизвестную константу интегрирования А находим из условия нормировки, которое состоит в том, что волновая функция, после интегрирования в квадрате по объему dV=4 r2 d r должна дать единицу
тогда , и искомое выражение для волновой функции приобретает вид
Задание 3.
Для нахождения наиболее вероятного значения rвер необходимо исследовать на предмет наличия экстремума функцию , которая является плотностью вероятности нахождения частицы в сферическом слое толщины dr. Дифференцирование по r дает нам условие экстремума
или, с учетом соотношения ( ), а также того, что, по условию, частица находится в основном энергетическом состоянии (т.е. n=1 ), определяем значения rextr, соответствующие экстремумам функции :
rextr1 = 0, rextr2 = R0
соответствуют минимумам функции , в чем легко убедиться прямой подстановкой.
rextr3 = R0/2 = rвер соответствует максимуму функции плотности вероятности и как раз является искомым наиболее вероятным значением.
страница 1 страница 2
pora.zavantag.com
Задача – квантовая механика – Большая Энциклопедия Нефти и Газа, статья, страница 1
Задача – квантовая механика
Cтраница 1
Задачи квантовой механики, приводящие к классическим ортогональным полиномам. Проиллюстрируем применение доказанной теоремы для решения ряда задач – квантовой механики, когда уравнение Шредипгера может быть приведено к обобщенному уравнению гипергеометрического типа. [1]
Задачей квантовой механики является нахождение собственных значений Е, при которых можно найти собственные функции у, удовлетворяющие уравнению Шредингера при заданном значении потенциальной энергии. [2]
Задачей квантовой механики является нахождение собственных значений Е, при которых возможно решение уравнения Шредингера. [3]
Вторая задача квантовой механики, которую мы рассмотрим, относится к жесткому ротатору. [4]
Рассмотрение задач квантовой механики многоэлектронных систем в формализме матрицы плотности приводит к существенным упрощениям по сравнению с обычным языком волновых функций. Как известно, волновые функции квантовомеханической системы должны обладать определенными свойствами симметрии. [5]
Далеко не все задачи квантовой механики могут быть решены современными математическими методами точно. Более того, в подавляющем большинстве случаев как для энергии, так и для волновых функций удается найти лишь приближенные решения. При этом приходится прибегать к различного рода приближенным методам вычислений. Одним из таких методов является получивший наиболее широкое распространение метод теории возмущений, пришедший в квантовую механику из небесной механики, где он был впервые развит. [6]
Лишь незначительное число задач квантовой механики, которые относятся к простым системам, может быть решено с помощью точных аналитических методов. [7]
Эффективным методом решения многих задач квантовой механики является теория возмущений. Поэтому естественно так называемое приближение слабо связанных электронов, когда периодический потенциал W ( r) считается малым и рассматривается как возмущение. [8]
Другой метод приближенного решения задач квантовой механики носит название теории возмущений. Постановка задачи здесь весьма проста: по известным решениям некоторой исходной задачи восстановить решения другой, слабо отличающейся от нее задачи. Существует довольно большое число различных вариантов теории возмущений, из которых мы ограничимся в существенной степени лишь одним для стационарных задач и одним – для задач, в которых учитывается явная зависимость от времени. В настоящем параграфе будут рассмотрены стационарные задачи. [9]
АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ – метод приближенного решения задач квантовой механики, применяемый для описания квантовых систем, в к-рых можно выделить быструю и медленную подсистемы. Исходная задача решается в два этапа: сначала рассматривается движение быстрой подсистемы при фик-сир. [10]
В чем заключается вариационный принцип и какую задачу квантовой механики он позволяет решать. [11]
Классические компьютеры испытывают огромные трудности, решая такие задачи квантовой механики. Но квантовые могли бы сделать то легко. Именно такая возможность вдохновила позднего Ричарда Фейнмана рассуждать о том, могут ли квантовые компьютеры быть действительно построены. [12]
Математический аппарат квантовой механики должен соответствовать физической постановке задач квантовой механики. Оказалось, что в математике был уже разработан соответствующий математический аппарат – теория линейных операторов. Мы рассмотрим сперва основы этой теории, а в дальнейшем покажем, как аппарат теории линейных операторов может быть связан с задачами квантовой механики. [13]
Это свойство классических ортогональных полиномов широко используется при решении задач квантовой механики, связанных с нахождением уровней энергии и волновых функций частицы, движущейся в стационарном силовом поле. Если внешние силы удерживают частицу в ограниченной области пространства, так что она не может уйти на бесконечность, то говорят о связанных состояниях частицы. [14]
Наиболее детальньш описанием элементарного акта катализа явилось бы его рассмотрение как задачи квантовой механики. Однако в полной мере сейчас это неосуществимо по двум причинам. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
