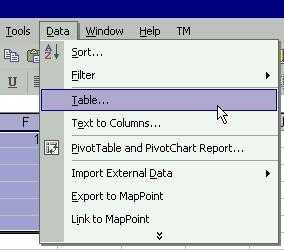
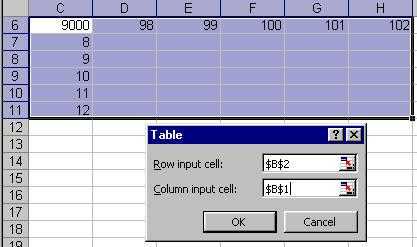
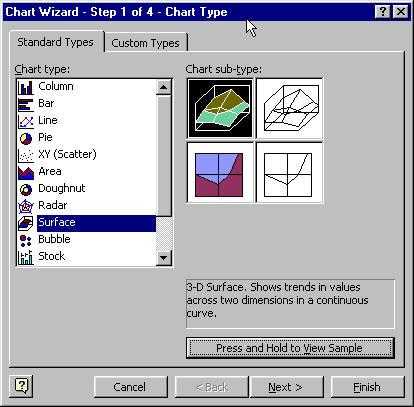
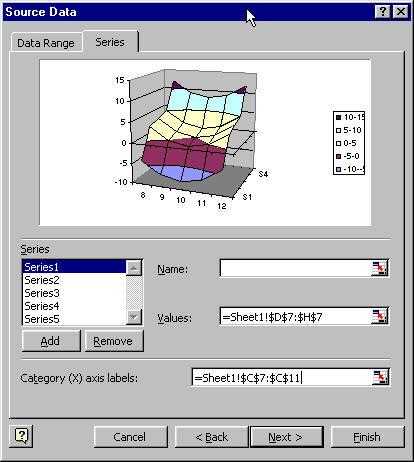
Линейная экстраполяция в excel – Иллюстрированный самоучитель по Microsoft Excel › Диаграммы и графики › Дополнительные возможности при построении диаграммы [страница - 77] | Самоучители по офисным пакетам - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Экстраполяция в Excel

Существуют случаи, когда требуется узнать результаты вычисления функции за пределами известной области. Особенно актуален данный вопрос для процедуры прогнозирования. В Экселе есть несколько способов, с помощью которых можно совершить данную операцию. Давайте рассмотрим их на конкретных примерах.

Использование экстраполяции

В отличие от интерполяции, задачей которой является нахождения значения функции между двумя известными аргументами, экстраполяция подразумевает поиск решения за пределами известной области. Именно поэтому данный метод столь востребован для прогнозирования.

В Экселе можно применять экстраполяцию, как для табличных значений, так и для графиков.

Способ 1: экстраполяция для табличных данных

Прежде всего, применим метод экстраполяции к содержимому табличного диапазона. Для примера возьмем таблицу, в которой имеется ряд аргументов (X) от 5 до 50 и ряд соответствующих им значений функции

(f(x)). Нам нужно найти значение функции для аргумента 55, который находится за пределом указанного массива данных. Для этих целей используем функцию ПРЕДСКАЗ.

Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.

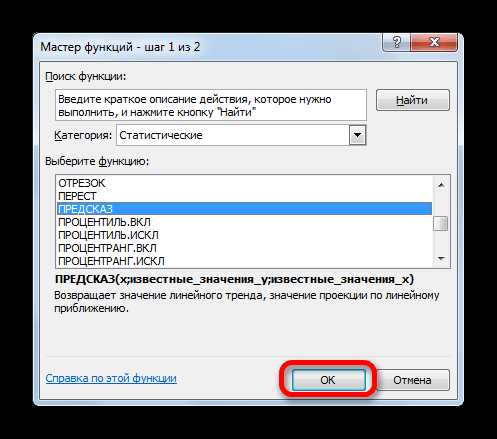
Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования
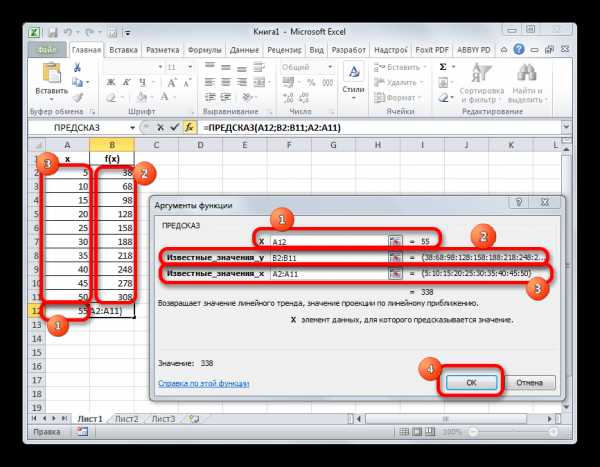
«ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.

Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.
В поле «X» следует указать значение аргумента, функцию от которого нам следует вычислить. Можно просто вбить с клавиатуры нужное число, а можно указать координаты ячейки, если аргумент записан на листе. Второй вариант даже предпочтительнее. Если мы произведем внесение именно таким способом, то для того, чтобы просмотреть значение функции для другого аргумента нам не придется менять формулу, а достаточно будет изменить вводную в соответствующей ячейке. Для того, чтобы указать координаты этой ячейки, если был выбран все-таки второй вариант, достаточно установить курсор в соответствующее поле и выделить эту ячейку. Её адрес тут же отобразится в окне аргументов.

В поле «Известные значения y» следует указать весь имеющийся у нас диапазон значений функции. Он отображается в колонке «f(x)». Следовательно, устанавливаем курсор в соответствующее поле и выделяем всю эту колонку без её наименования.
В поле «Известные значения x» следует указать все значения аргумента, которым соответствуют внесенные нами выше значения функции. Эти данные находятся в столбце
«x». Точно так же, как и в предыдущий раз выделяем нужную нам колонку, предварительно установив курсор в поле окна аргументов.
После того, как все данные внесены, жмем на кнопку «OK».

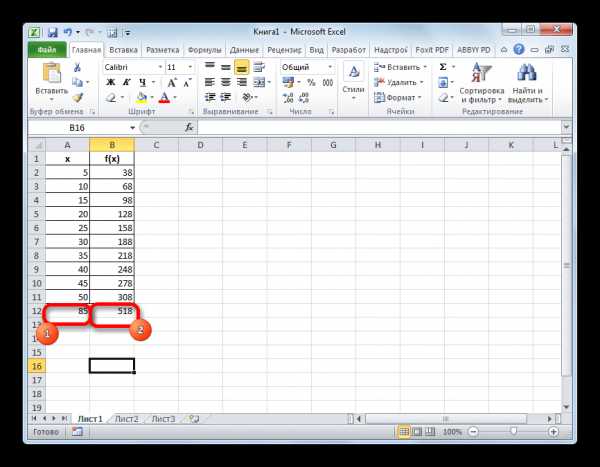
После этих действий результат вычисления путем экстраполяции будет выведен в ячейку, которая была выделена в первом пункте данной инструкции перед запуском Мастера функций. В данном случае значение функции для аргумента 55 равно 338.

Если все-таки был выбран вариант с добавлением ссылки на ячейку, в которой содержится искомый аргумент, то мы легко сможем его поменять и просмотреть значение функции для любого другого числа. Например, искомое значение для аргумента 85 буде равно 518.

Урок: Мастер функций в Excel

Способ 2: экстраполяция для графика

Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.

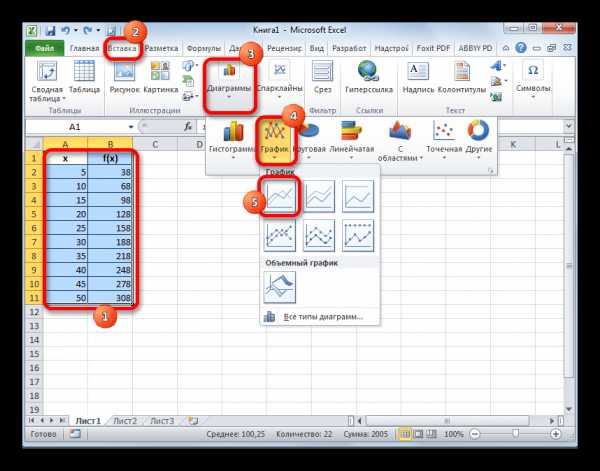
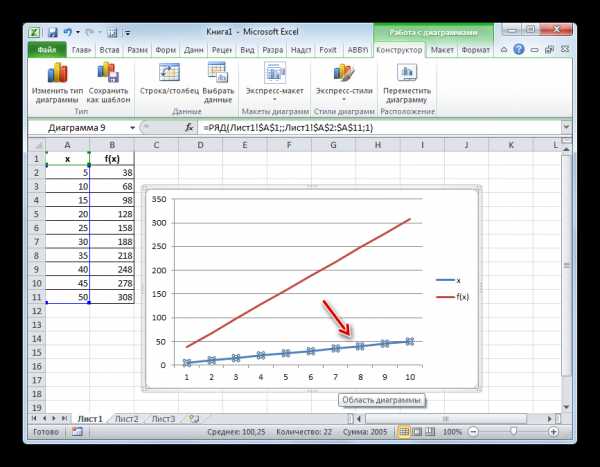
Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка» , кликаем по кнопке «График». Этот значок расположен в блоке «Диаграммы» на ленте инструментов. Появляется перечень доступных вариантов графиков. Выбираем наиболее подходящий из них на свое усмотрение.

После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete на клавиатуре компьютера.

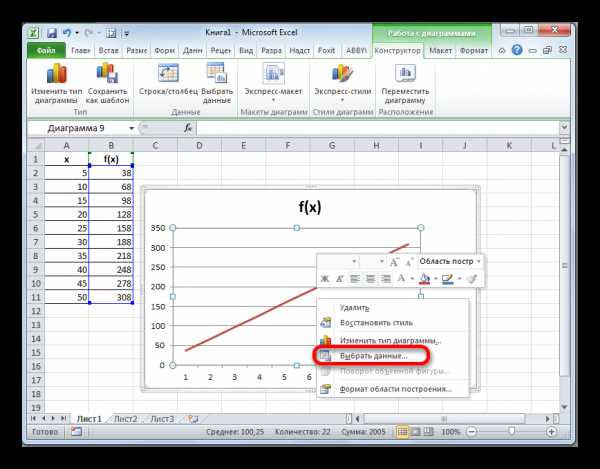
Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении
«Выбрать данные».

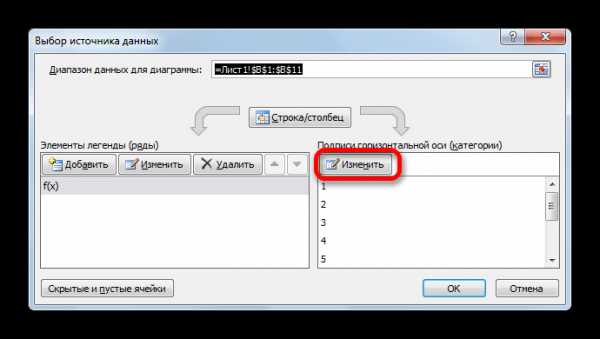
В запустившемся окне выбора источника данных кликаем по кнопке «Изменить» в блоке редактирования подписи горизонтальной оси.

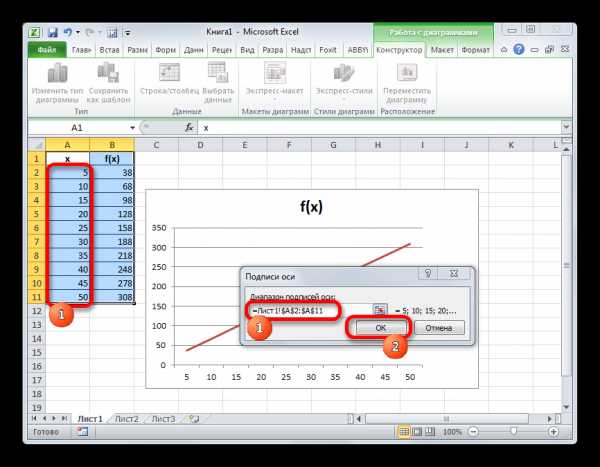
Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X» без его наименования. Затем жмем на кнопку «OK».

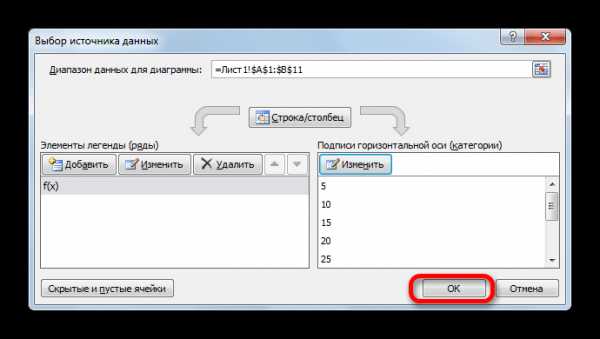
После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK».

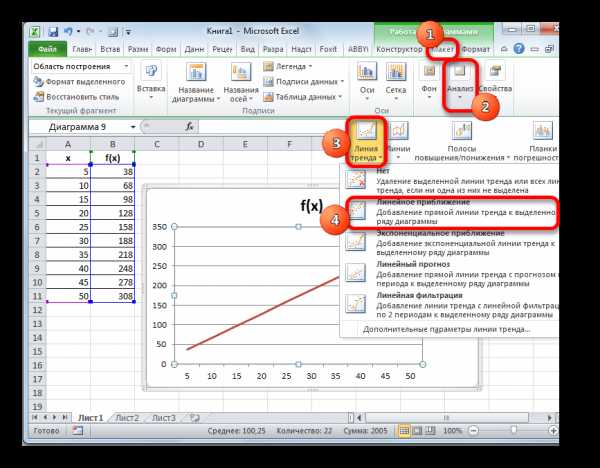
Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда. Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами». Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ». Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение».

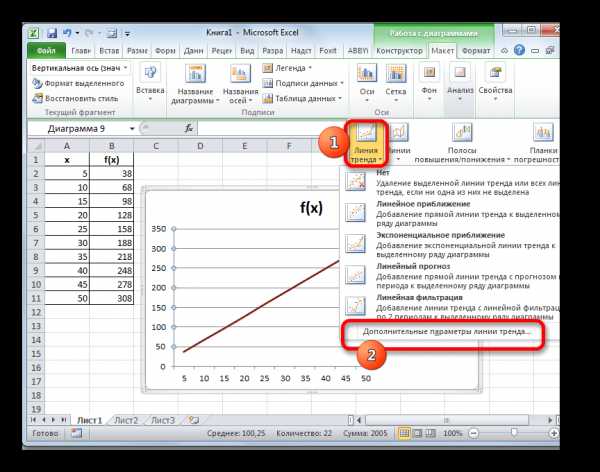
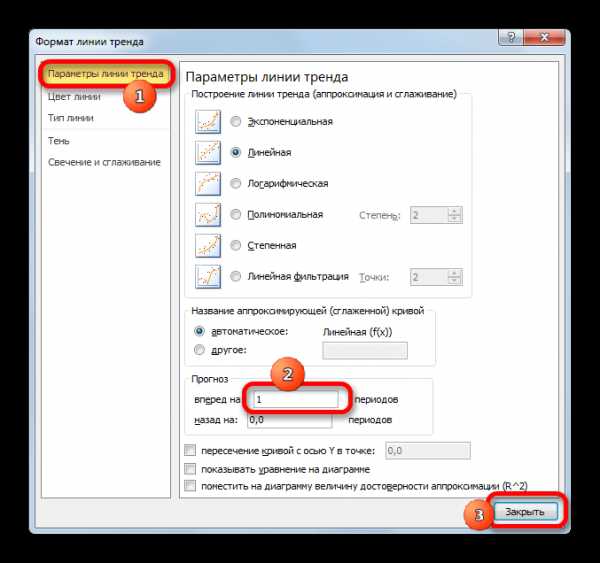
Линия тренда добавлена, но она полностью находится под линией самого графика, так как мы не указали значение аргумента, к которому она должна стремиться. Чтобы это сделать опять последовательно кликаем по кнопке «Линия тренда», но теперь выбираем пункт «Дополнительные параметры линии тренда».

Запускается окно формата линии тренда. В разделе «Параметры линии тренда» есть блок настроек «Прогноз». Как и в предыдущем способе, давайте для экстраполяции возьмем аргумент 55. Как видим, пока что график имеет длину до аргумента 50 включительно. Получается, нам нужно будет его продлить ещё на 5 единиц. На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. 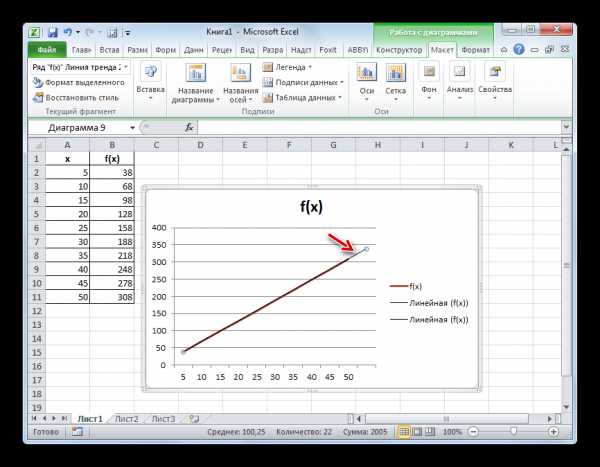В поле «Вперед на» вписываем значение «1». Жмем на кнопку «Закрыть» в нижнем правом углу окна.

Как видим, график был продлен на указанную длину с помощью линии тренда.

Урок: Как построить линию тренда в Excel

Итак, мы рассмотрели простейшие примеры экстраполяции для таблиц и для графиков. В первом случае используется функция ПРЕДСКАЗ, а во втором – линия тренда. Но на основе этих примеров можно решать и гораздо более сложные задачи прогнозирования.

Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

lumpics.ru

Прогнозирование значений в рядах – Excel

Когда необходимо оценить затраты следующего года или предсказать ожидаемые результаты серии научных экспериментов, можно использовать Microsoft Office Excel для автоматической генерации будущих значений, которые будут базироваться на существующих данных или для автоматического вычисления экстраполированных значений, базирующихся на вычислениях по линейной или экспоненциальной зависимости.

В Microsoft Excel можно заполнить ячейки рядом значений, соответствующих простому линейному или экспоненциальному тренду, с помощью маркер заполнения или команды Прогрессия. Для экстраполяции сложных и нелинейных данных можно применять функции или средство регрессионный анализ из надстройки “Пакет анализа”.

В арифметической прогрессии шаг или различие между начальным и следующим значением в ряде добавляется к каждому следующему члену прогрессии.

Начальное значение	Продолжение ряда (арифметическая прогрессия)
1, 2	3, 4, 5…
1, 3	5, 7, 9
100, 95	90, 85

Для прогнозирования линейной зависимости выполните следующие действия.

Укажите не менее двух ячеек, содержащих начальные значения.

Если требуется повысить точность прогноза, укажите дополнительные начальные значения.
Перетащите маркер заполнения в нужном направлении, чтобы заполнить ячейки возрастающими или убывающими значениями.

Например, если ячейки C1:E1 содержат начальные значения 3, 5 и 8, то при протаскивании вправо значения будут возрастать, влево — убывать.

Совет: Чтобы управлять созданием ряда вручную или заполнять ряд значений с помощью клавиатуры, воспользуйтесь командой Прогрессия (вкладка Главная, группа Редактирование, кнопка Заполнить).

В экспоненциальных рядах начальное значение умножается на шаг для получения следующего значения в ряде. Получившийся результат и каждый последующий результат умножаются на шаг.

Начальное значение	Продолжение ряда (геометрическая прогрессия)
1, 2	4, 8, 16
1, 3	9, 27, 81
2, 3	4.5, 6.75, 10.125

Для прогнозирования экспоненциальной зависимости выполните следующие действия.

Укажите не менее двух ячеек, содержащих начальные значения.

Если требуется повысить точность прогноза, укажите дополнительные начальные значения.
Удерживая правую кнопку мыши, перетащите маркер заполнения в нужном направлении для заполнения ячеек возрастающими или убывающими значениями, отпустите правую кнопку, а затем щелкните Экспоненциальное приближение в контекстное меню.

Например, если ячейки C1:E1 содержат начальные значения 3, 5 и 8, то при протаскивании вправо значения будут возрастать, влево — убывать.

С помощью команды Прогрессия можно вручную управлять созданием линейной или экспоненциальной зависимости, а также вводить значения с клавиатуры.

Для получения линейного тренда к начальным значениям применяется метод наименьших квадратов (y=mx+b).
Для получения экспоненциального тренда к начальным значениям применяется алгоритм расчета экспоненциальной кривой (y=b*m^x).

В обоих случаях не учитывается шаг прогрессии. При создании этих прогрессий получаются те же значения, которые вычисляются с помощью функций ТЕНДЕНЦИЯ и РОСТ.

Для заполнения значений вручную выполните следующие действия.

Выделите ячейку, в которой находится первое значение создаваемой прогрессии.

Команда Прогрессия удаляет из ячеек прежние данные, заменяя их новыми. Если необходимо сохранить прежние данные, скопируйте их в другую строку или другой столбец, а затем приступайте к созданию прогрессии.
На вкладке Главная в группе Правка нажмите кнопку Заполнить и выберите пункт Прогрессия.
Выполните одно из указанных ниже действий.
- Если необходимо заполнить значениями ряда часть столбца, выберите вариант по столбцам.
- Если необходимо заполнить значениями ряда часть строки, выберите вариант по строкам.
В поле Шаг введите число, которое определит значение шага прогрессии.

Тип прогрессии	Результат шага
Арифметическая	Шаг — это число, добавляемое к каждому следующему члену прогрессии.
Геометрическая	Начальное значение умножается на шаг. Получившийся результат и каждый последующий результат умножаются на шаг.

В разделе Тип выберите тип прогрессии: арифметическая или геометрическая.
В поле Предельное значение введите значение, на котором нужно остановить прогрессию.

Примечание: Если в ячейках уже содержатся первые члены прогрессии и требуется, чтобы приложение Microsoft Excel создало прогрессию автоматически, установите флажок Автоматическое определение шага.

Если имеются существующие данные, для которых следует спрогнозировать тренд, можно создать на диаграмме линия тренда. Например, если имеется созданная в Excel диаграмма, на которой приведены данные о продажах за первые несколько месяцев года, можно добавить к ней линию тренда, которая представит общие тенденции продаж (рост, снижение или стабилизацию) продемонстрирует предполагаемую тенденцию на ближайшие месяцы.

Эта процедура предполагает, что диаграмма, основанная на существующих данных, уже создана. Если это еще не сделано, просмотрите раздел Создание диаграмм.

Щелкните диаграмму.
Выберите ряд данных, к которому нужно добавить линия тренда или скользящее среднее.
На вкладке Макет в группе Анализ нажмите кнопку Линия тренда и выберите нужный тип регрессионной линии тренда или скользящего среднего.
Для определения параметров и форматирования регрессионной линии тренда или скользящего среднего щелкните линию тренда правой клавишей мыши и выберите пункт Формат линии тренда.
Выберите параметры линии тренда, тип линий и эффекты.
- При выборе типа Полиномиальная введите в поле Степень наибольшую степень для независимой переменной.
- При выборе типа Скользящее среднее введите в поле Период число периодов, используемых для расчета скользящего среднего.

Примечания:

В поле Построен на ряде перечислены все ряды данных диаграммы, поддерживающих линии тренда. Для добавления линии тренда к другим рядам выберите нужное имя в поле, а затем выберите нужные параметры.
Если к двумерной диаграмме (диаграмме распределения) добавляется скользящее среднее, то это скользящее среднее базируется на порядке расположения значений X в диаграмме. Для получения нужного результата перед добавлением скользящего среднего, возможно, потребуется отсортировать значения X.

Использование функции ПРЕДСКАЗ . Функция ПРЕДСКАЗ вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это y-значение, соответствующее заданному x-значению. Известные значения — это существующие x- и y-значения; новое значение предсказывается с использованием линейной регрессии. Этой функцией можно воспользоваться для прогнозирования будущих продаж, потребностей в складских запасах или тенденций потребления.

Использование функций ТЕНДЕНЦИЯ и РОСТ . Функции ТЕНДЕНЦИЯ и РОСТ позволяют экстраполировать будущие y-значения, продолжающие прямую линию или экспоненциальную кривую, наилучшим образом описывающую существующие данные. Эти функции могут возвращать y-значения, соответствующие заданным x-значениям, на базе линейной или экспоненциальной зависимости. Используя существующие x-значения и y-значения, возвращаемые этими функциями, можно построить прямую или кривую, описывающую существующие данные.

Использование функций ЛИНЕЙН и ЛГРФПРИБЛ . Функции ЛИНЕЙН и ЛГРФПРИБЛ позволяют вычислить прямую линию или экспоненциальную кривую для имеющихся данных. Функции ЛИНЕЙН и ЛГРФПРИБЛ возвращают различные данные регрессионного анализа, включая наклон и точку пересечения линии с осью.

Следующая таблица содержит ссылки на дополнительные сведения об этих функциях.

Функция	Описание
ПРЕДСКАЗ	Прогнозирование значений
тенденция	Прогнозирование линейной зависимости.
РОСТ	Прогнозирование экспоненциальной зависимости.
линейн	Построение линейного приближения.
лгрфприбл	Построение экспоненциального приближения.

При необходимости выполнить более сложный регрессионный анализ — включая вычисление и отображение остатков — можно использовать средство регрессионного анализа в надстройке “Пакет анализа”. Дополнительные сведения см. в статье Загрузка пакета статистического анализа.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.

К началу страницы

support.office.com

Интерполяция в Excel

Бывает ситуация, когда в массиве известных значений нужно найти промежуточные результаты. В математике это называется интерполяцией. В Excel данный метод можно применять как для табличных данных, так и для построения графиков. Разберем каждый из этих способов.

Использование интерполяции

Главное условие, при котором можно применять интерполяцию – это то, что искомое значение должно быть внутри массива данных, а не выходить за его предел. Например, если мы имеем набор аргументов 15, 21 и 29, то при нахождении функции для аргумента 25 мы можем использовать интерполяцию. А для поиска соответствующего значения для аргумента 30 – уже нет. В этом и является главное отличие этой процедуры от экстраполяции.

Способ 1: интерполяция для табличных данных

Прежде всего, рассмотрим применения интерполяции для данных, которые расположены в таблице. Для примера возьмем массив аргументов и соответствующих им значений функции, соотношение которых можно описать линейным уравнением. Эти данные размещены в таблице ниже. Нам нужно найти соответствующую функцию для аргумента 28. Сделать это проще всего с помощью оператора ПРЕДСКАЗ.

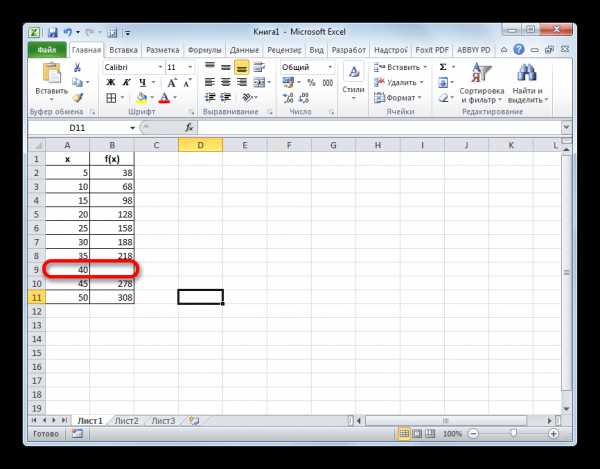
Выделяем любую пустую ячейку на листе, куда пользователь планирует выводить результат от проведенных действий. Далее следует щелкнуть по кнопке «Вставить функцию», которая размещена слева от строки формул.

Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».

Запускается окно аргументов функции ПРЕДСКАЗ. В нем имеется три поля:
- X;
- Известные значения y;
- Известные значения x.
В первое поле нам просто нужно вручную с клавиатуры вбить значения аргумента, функцию которого следует отыскать. В нашем случае это 28.
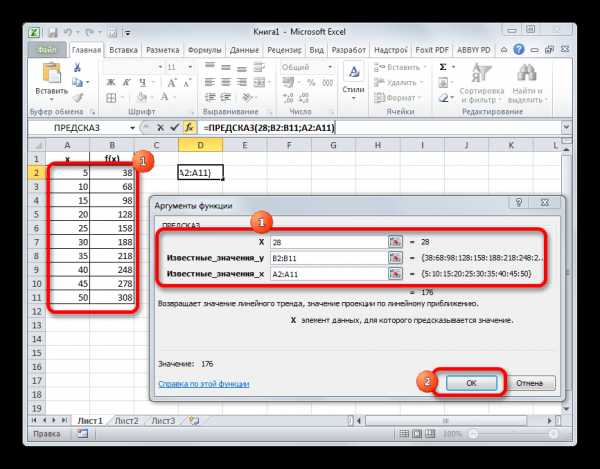
В поле «Известные значения y» нужно указать координаты диапазона таблицы, в котором содержатся значения функции. Это можно сделать вручную, но гораздо проще и удобнее установить курсор в поле и выделить соответствующую область на листе.
Аналогичным образом устанавливаем в поле «Известные значения x» координаты диапазона с аргументами.
После того, как все нужные данные введены, жмем на кнопку «OK».

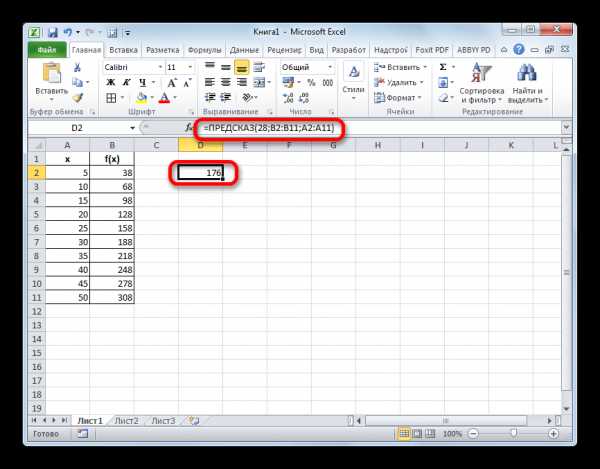
Искомое значение функции будет отображено в той ячейке, которую мы выделили ещё в первом шаге данного способа. В результате получилось число 176. Именно оно и будет итогом проведения процедуры интерполяции.

Урок: Мастер функций в Экселе

Способ 2: интерполяция графика с помощью его настроек

Процедуру интерполяции можно применять и при построении графиков функции. Актуальна она в том случае, если в таблице, на основе которой построен график, к одному из аргументов не указано соответствующее значение функции, как на изображении ниже.

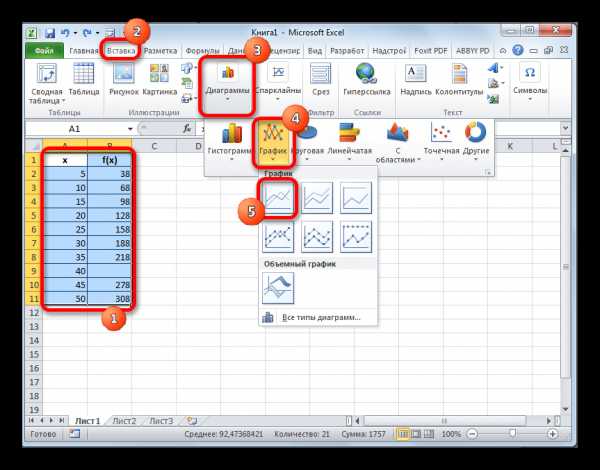
Выполняем построение графика обычным методом. То есть, находясь во вкладке «Вставка», выделяем табличный диапазон, на основе которого будет проводиться построение. Щелкаем по значку «График», размещенному в блоке инструментов «Диаграммы». Из появившегося списка графиков выбираем тот, который считаем более уместным в данной ситуации.

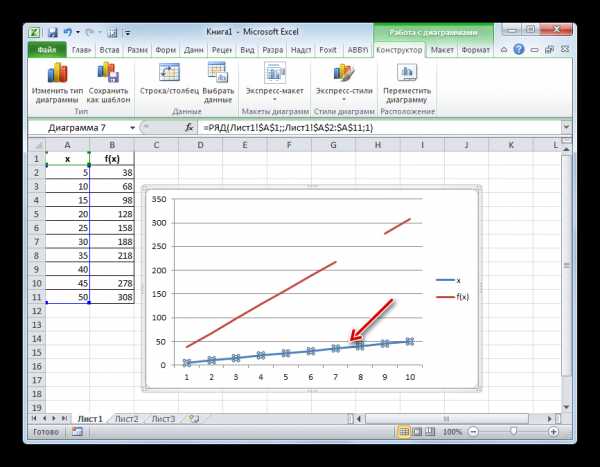
Как видим, график построен, но не совсем в таком виде, как нам нужно. Во-первых, он разорван, так как для одного аргумента не нашлась соответствующая функция. Во вторых, на нем присутствует дополнительная линия X, которая в данном случае не нужна, а также на горизонтальной оси указаны просто пункты по порядку, а не значения аргумента. Попробуем исправить все это.
Для начала выделяем сплошную синюю линию, которую нужно удалить и жмем на кнопку Delete на клавиатуре.

Выделяем всю плоскость, на которой размещен график. В появившемся контекстном меню щелкаем по кнопке «Выбрать данные…».

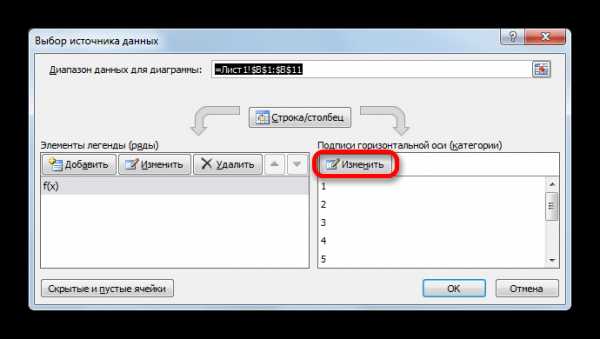
Запускается окно выбора источника данных. В правом блоке «Подписи горизонтальной оси» жмем на кнопку «Изменить».

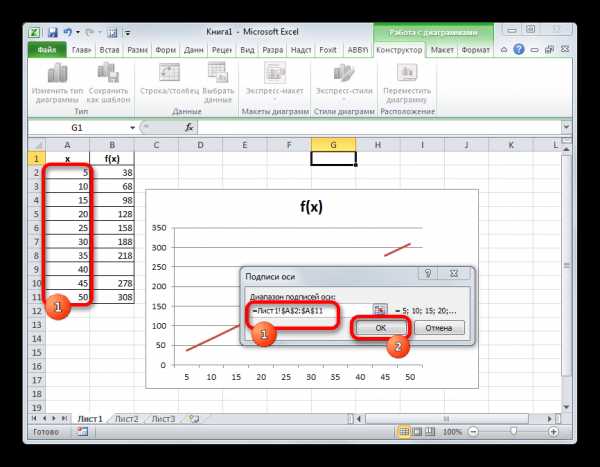
Открывается небольшое окошко, где нужно указать координаты диапазона, значения из которого будут отображаться на шкале горизонтальной оси. Устанавливаем курсор в поле «Диапазон подписей осей» и просто выделяем соответствующую область на листе, в которой содержаться аргументы функции. Жмем на кнопку «OK».

Теперь нам осталось выполнить основную задачу: с помощью интерполяции устранить разрыв. Вернувшись в окно выбора диапазона данных жмем на кнопку «Скрытые и пустые ячейки», расположенную в нижнем левом углу.

Открывается окно настройки скрытых и пустых ячеек. В параметре «Показывать пустые ячейки» выставляем переключатель в позицию «Линию». Жмем на кнопку «OK».

После возвращения в окно выбора источника подтверждаем все сделанные изменения, щелкнув по кнопке «OK».

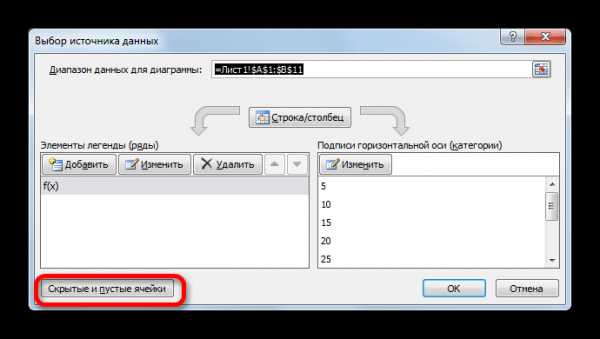
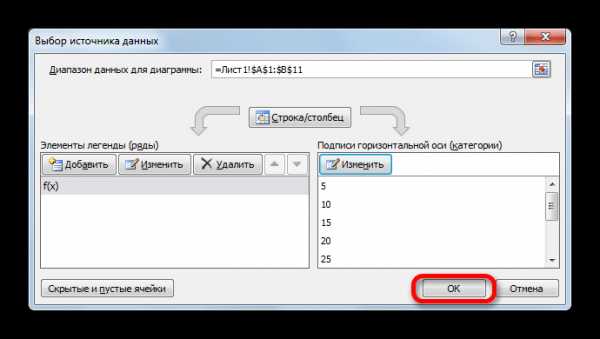
Как видим, график скорректирован, а разрыв с помощью интерполяции удален.

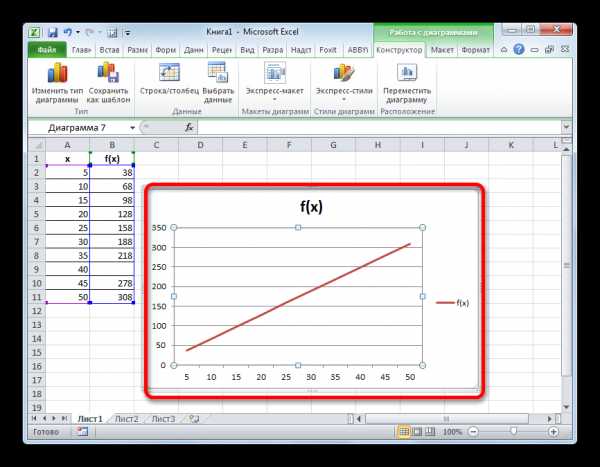
Урок: Как построить график в Excel

Способ 3: интерполяция графика с помощью функции

Произвести интерполяцию графика можно также с помощью специальной функции НД. Она возвращает неопределенные значения в указанную ячейку.

После того, как график построен и отредактирован, так как вам нужно, включая правильную расстановку подписи шкалы, остается только ликвидировать разрыв. Выделяем пустую ячейку в таблице, из которой подтягиваются данные. Жмем на уже знакомый нам значок «Вставить функцию».

Открывается Мастер функций. В категории «Проверка свойств и значений» или «Полный алфавитный перечень» находим и выделяем запись «НД». Жмем на кнопку «OK».

У данной функции нет аргумента, о чем и сообщает появившееся информационное окошко. Чтобы закрыть его просто жмем на кнопку «OK».

После этого действия в выбранной ячейке появилось значение ошибки «#Н/Д», но зато, как можно наблюдать, обрыв графика был автоматически устранен.

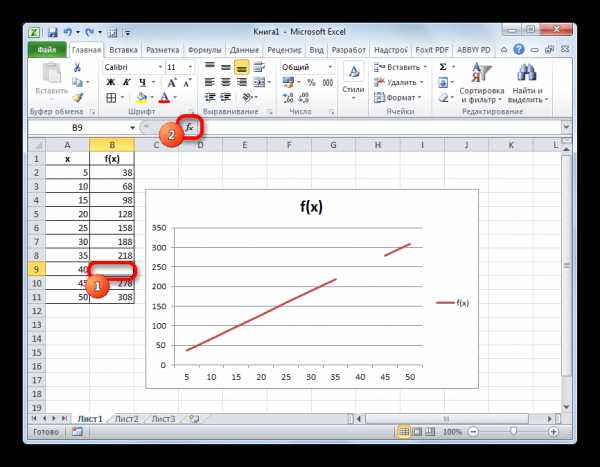
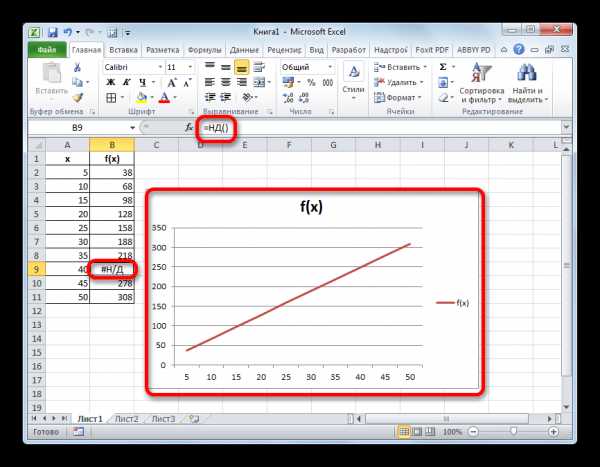
Можно сделать даже проще, не запуская Мастер функций, а просто с клавиатуры вбить в пустую ячейку значение «#Н/Д» без кавычек. Но это уже зависит от того, как какому пользователю удобнее.

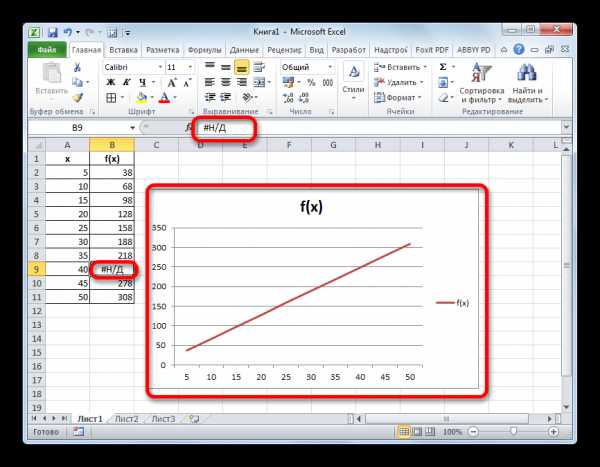
Как видим, в программе Эксель можно выполнить интерполяцию, как табличных данных, используя функцию ПРЕДСКАЗ, так и графика. В последнем случае это осуществимо с помощью настроек графика или применения функции НД, вызывающей ошибку «#Н/Д». Выбор того, какой именно метод использовать, зависит от постановки задачи, а также от личных предпочтений пользователя.

Помогла ли вам эта статья?

Да Нет

lumpics.ru

4. Построение прогнозов в Excel

Прогнозирование– это метод научного исследования, ставящей своей целью предусмотреть возможные варианты тех процессов и явлений, которые выбраны в качестве предмета анализа.

Одним из методов прогнозирования является метод экстраполяции. Метод экстраполяции заключается в нахождении значений, лежащих за пределами данного статистического ряда: по известным значениям статистического ряда находятся другие значения, лежащие за пределами этого ряда.

При экстраполяции переносится выводы, сделанные при изучении тенденций развития явления в прошлом и настоящем, на будущее, т.е. в основе экстраполяции лежит предположение об определенной стабильности факторных признаков, влияющих на развитие данного явления.

Чем более устойчивый характер носит прогнозируемые процессы и тенденции, тем дальше может быть отодвинут горизонт прогнозирования. Как показывает практика, интервал наблюдения должен быть в три и более раз длиннее интервала упреждения. Как правило, этот период – довольно короткий. Метод экстраполирования не работает при скачкообразных процессах.

Метод экстраполяции легко реализуется на персональном компьютере. Использование современных табличных процессоров, таких как MSExcelпозволяет оперативно проводить прогнозирование различных процессов с использованием экстраполяционного метода.

Для повышения точности прогноза, необходимо учитывать зависимость прогнозируемой величины Y, от внешних факторов Х.Совокупность изучаемых величин подвержена, как правило, воздействию случайных факторов. В связи с этим зависимость прогнозируемой величины Y, от внешних факторов Х чаще всего статистическая, или – корреляционная.

Статистическойназывается зависимость случайных величин, при которой каждому значению одной их них соответствует закон распределения другой, то есть изменение одной из величин влечет изменение распределения другой.

Корреляционнойназывается статистическая зависимость случайных величин, при которой изменение одной из величин влечет изменение среднего значения другой.

Мерой корреляционной зависимости двух случайных величин Х и Y служит коэффициент корреляции r, который является безразмерной величиной, и поэтому он не зависит от выбора единиц измерения изучаемых величин.

Свойства коэффициента корреляции:

1) Если две случайные величины Х и Y независимы, то их коэффициент корреляции равен нулю, т.е. r=0.

2) Модуль коэффициента корреляции не превышает единицы, т.е. |r|1, что эквивалентно двойному неравенству:1r1.

3) Равенство коэффициента -1 или +1 показывает наличие функциональной (прямой) связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «-» – на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).

После определения наиболее существенных факторных признаков влияющих прогнозируемую величину, не менее важно установить их математическое описание (уравнение), дающее возможность численно оценивать результативный показатель через факторные признаки.

Уравнение, выражающее изменение средней величины результативного показателя в зависимости от значений факторных признаков, называется уравнение регрессии.

Линии на координатной плоскости, соответствующие уравнениям регрессии называются линиями регрессии.

Корреляционные зависимости могут выражаться уравнениями регрессии различных видов: линейной, параболической, гиперболической, показательной и т.д.

Линейная регрессия

Уравнением линейной регрессии(выборочным)YнаХназывается зависимость от наблюдаемых значений величины Х, выраженная линейной функцией: , где величина называется коэффициентом линейной регрессии YнаХ, b– константа.

Линейная аппроксимация хорошо описывает изменение величин, происходящее с постоянной скоростью.

Если коэффициент корреляции двух величин ХиYравенr=1, то эти величины связаны линейной зависимостью. Коэффициент корреляции служит мерой силы (тесноты) линейной зависимости измеряемых величин. На практике, если коэффициент корреляции двух величинХиY|r|>0.5, то считают, что есть основания предполагать наличие линейной зависимости между этими величинами. Однако ориентироваться при выборе типа линии регрессии (линейной или нелинейной) лучше по виду эмпирической зависимости величинХиY.

Параболическая и полиномиальная регрессии.

Параболическойзависимостью величиныYот величиныХназывается зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):_.Это уравнение называетсяуравнением параболической регрессииYнаХ. Параметрыа,b,сназываютсякоэффициентами параболической регрессии.

Уравнение параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальнойзависимостью величиныYот величиныХназывается зависимость, выраженная полиномомn-ого порядка: ,где числаа_i(i=0,1,…,n) называютсякоэффициентами полиномиальной регрессии.

Полиномиальная аппроксимация используется для описания величин, попеременно возрастающих и убывающих.

Степенная регрессия.

Степеннойзависимостью величиныYот величиныХназывается зависимость вида: . Это уравнение называетсяуравнением степенной регрессииYнаХ. Параметрыаиbназываютсякоэффициентами степенной регрессии.

Степенная аппроксимация полезна для описания монотонно возрастающей либо монотонно убывающей величины, например расстояния, пройденного разгоняющимся автомобилем. Использование степенной аппроксимации невозможно, если данные содержат нулевые или отрицательные значения.

Показательная регрессия.

Показательной(илиэкспоненциальной) зависимостью величиныYот величиныХназывается зависимость вида: (или )

Это уравнение называется уравнениемпоказательной(илиэкспоненциальной)регрессииYнаХ. Параметрыа(илиk) иbназываютсякоэффициентами показательной(илиэкспоненциальной)регрессии.

Экспоненциальная аппроксимация полезна в том случае, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, этот вид приближения неприменим.

Логарифмическая регрессия.

Логарифмическойзависимостью величиныYот величиныХназывается зависимость вида:_.Это уравнение называетсяуравнением логарифмической регрессииYнаХ. Параметрыаиbназываютсякоэффициентами логарифмической регрессии.

Логарифмическая аппроксимация полезна для описания величины, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Логарифмическая аппроксимация использует как отрицательные, так и положительные величины.

Гиперболическая регрессия.

Гиперболическойзависимостью величиныYот величиныХназывается зависимость вида: . Это уравнение называетсяуравнением гиперболической регрессии YнаХ. Параметрыаиbназываютсякоэффициентами гиперболической регрессии.

Проведение регрессионного анализа можно разделить на три этапа: выбор формы зависимости (вида уравнения) на основе статистических данных, вычисление коэффициентов выбранного уравнения, оценка достоверности выбранного уравнения.

Использование табличного процессора позволяет легко выполнить все этапы регрессионного анализа.

Использование функции ТЕНДЕНЦИЯ

Для прогнозирования процессов, изменение которых носит линейный характер можно использовать функцию ТЕНДЕНЦИЯ.

Эта функция позволяет находить значения в соответствии с линейным трендом. Она аппроксимирует прямой линией (по методу наименьших квадратов) массивы известных значений Yи известных значения Х. Находит новые значенияY, в соответствии с этой прямой для новых значений Х. Например, если у нас есть данные изменения цены на энергоносители за несколько последних лет, то с помощью функции ТЕНДЕНЦИЯ мы можем получить прогноз на цену на энергоносители на будущий год. При этом если зависимость цены от времени близка к линейной, то результат будет удовлетворительным.

Предварительно, перед использованием функции ТЕНДЕНЦИЯ необходимо ввести (в столбец или в строку) массивы XиY, взаимосвязанных величин, а также значенияXдля которых будет спрогнозирована величинаY.

Затем, вызываем статистическую функцию ТЕНДЕНЦИЯ. Для этого необходимо вызвать Мастер функций, щелкнув на кнопке строки формул или отдав команду Вставка/Функция.В окне Мастера функций выберите категориюСтатистическиеи в полеВыберите функцию выберите из списка функцию ТЕНДЕНЦИЯ. В появившемся диалоговом окнеАргументы функции (рис.5.8) в соответствующие поля внесите ссылки на диапазоны ячеек в которых хранятся известные значения величинYиX, новые значения Х, для которых ТЕНДЕНЦИЯ возвращает соответствующие значенияY. С помощью поляКонст можно указать вычислять ли константу b или принять равной 0. Если это поле имеет значение ИСТИНА или опущено, то b вычисляется обычным образом, если ЛОЖЬ – то b полагается равным 0, и значенияподбираются таким образом, чтобы выполнялось соотношениеy = x.

Рис. 8. Фрагмент диалогового окна Аргументы функции.

После ввода всех необходимых аргументов функции необходимо нажать на кнопке ОК.

Быстрое построение линий регрессии в Excel: линия тренда.

В Excel имеется быстрый и удобный способ построить график линейной регрессии, а также основных видов нелинейных регрессий. Это можно сделать следующим образом:

Выделить столбцы с данными X и Y (они должны располагаться именно в таком порядке!).

Вызвать Мастер диаграмм (используя инструмент или команду Вставка/Диаграмма) и в открывшемся окне Мастер диаграмм выбрать в группе Тип – Точечная и сразу нажать Готово.

Не сбрасывая выделения с диаграммы, выбрать появившейся пункт основного меню Диаграмма, в котором следует выбрать пункт Добавить линию тренда.

В открывшемся диалоговом окне Линия тренда во вкладке Тип выбрать тип. Можно выбрать одну из шести зависимостей: линейная, степенная, логарифмическая, экспоненциальная, полиномиальная и линейная фильтрация. Для полиномиальной аппроксимации можно указать степень. При линейной фильтрации (скользящее среднее) элементы данных усредняются, и полученный результат используется в качестве среднего значения для приближения. Так, если шаг линейной фильтрации равен 2, первая точка сглаживающей кривой определяется как среднее значение первых двух элементов данных, вторая точка – как среднее следующих двух элементов и так далее.

Рис.5.9. Вкладка Линия тренда.

studfiles.net

Графики в Excel – Стр 2

Дополнительные возможности при построении диаграммы

Обработка результатов наблюдений является важной частью анализа. Проводите ли Вы лабораторные исследования или изучаете результаты продаж, у вас всегда присутствует номер опыта и количественная величина того, что Вы измеряете, будь то число популяций или количество проданных компьютеров.

XY-точечная диаграмма – наиболее подходящее средство для обработки результатов исследований такого рода.

При обработке результатов измерений достаточно часто возникает вопрос о тенденции развития или изменения. В Excel этот вопрос решается при помощи определения тренда. Линии тренда графически иллюстрируют тенденцию изменения рядов данных. Они обычно используются в тех случаях, когда нужно построить диаграммы для задач прогнозирования и экстраполяции (так называемых задач регрессионного анализа). С помощью регрессионного анализа можно продолжить линию тренда вперед или назад, экстраполировать ее за пределы, в которых данные уже известны, и показать тенденцию их изменения. Для построения линии тренда активизируйте ряд данных, после чего нажмите правую клавишу мыши. В появившемся списке команд выберите Добавить линию тренда, а затем в соответствующем окне диалога – рисунок с линейным трендом.

Линии тренда можно проводить на гистограммах, графиках, линейчатых и XY-точечных диаграммах. Нельзя строить линии тренда для рядов данных на объемных, круговых и кольцевых диаграммах. Если Вы измените тип представления группы рядов на один из вышеперечисленных, то соответствующие этим рядам данных линии тренда будут потеряны.

В Excel можно выбрать один из пяти типов экстраполяции: линейный, полиномиальный, логарифмический, экспоненциальный или степенной. Тип выбранной экстраполяции задает способ вычислений линии тренда. В зависимости от используемых данных некоторые типы экстраполяции могут оказаться надежнее других с точки зрения оценки результатов сделанных прогнозов. Таким образом, может оказаться полезным проделать несколько различных экстраполяции, чтобы посмотреть, какой из типов лучше всего подходит в данной ситуации.

В Excel можно рисовать диаграммы не только столбцами, линиями и точками, но и произвольными рисунками. Причем Вы можете вместо одного столбца изобразить один рисунок, тогда он будет растянут в соответствии с размерами столбцов, или заполнить столбец рисунками одинакового размера.

Чтобы вставить вместо столбца на диаграмме рисунок, выполните следующие действия.

Активизируйте ряд данных на диаграмме.
Выберите команду Рисунок из меню Вставка. Excel предложит Вам выбрать нужный рисунок из файла, автофигуру или объект WordArt.
Выберите необходимый пункт и нажмите клавишу Enter или кнопку ОК в окне. Вместо столбца на диаграмме появится изображение.

Если Вы хотите использовать какое-либо изображение, то Вам нужно позаботиться о том, чтобы поместить его в графический файл до того, как Вы будете вставлять его в диаграмму.

Текст является неотъемлемой частью диаграммы. Он присутствует в названии диаграммы, в надписях к осям, в легенде, в метках строк и столбцов.

После того как диаграмма построена, Вы всегда можете внести изменения и добавления в ее текст. Для этого нужно в режиме редактирования диаграммы нажать левую клавишу мыши на панели инструментов для вызова диалога форматирования необходимого объекта, где можно добавить необходимые надписи.

На самом деле в диаграмму можно ввести любой текст в произвольном месте. Для этого достаточно сделать активным любой, не относящийся к тексту, элемент диаграммы и просто ввести текст. При вводе он будет отображаться в строке формул. Если Вы нажмете левую клавишу мыши на диаграмме, то текст, введенный вами в строке формул, будет заключен на диаграмме в рамку, после чего Вы сможете обращаться с ним, как с любым объектом диаграммы.

Графики математических функций

При построении графиков элементарных математических функций значения функций задаются в конечном числе точек. Если просто соединить эти точки отрезками прямых линий, то полученная ломаная совсем не будет похожа на истинный график функции.

Если Вы начнете увеличивать число точек, в которых вычисляются значения функции, то это потребует введения большого количества данных, и построение графика потеряет наглядность.

Мы не будем увеличивать число точек, в которых вычисляются значения функций, а воспользуемся при построении графиков интерполяционными многочленами, при помощи которых реализован процесс построения гладких кривых в формате диаграмм График.

Этот режим построения можно задать при выборе типа и формата диаграммы.

В результате графики будут иметь вид гладких кривых, проходящих через заданные точки. Построим графики двумерных функций у=х*х/8, y=sin(x) и у=1n(1+х) и расположим их на одном рисунке, и трехмерной функции – гиперболического параболоида, который описывается уравнением вида z=(x/a)2 -(у/Ь)2.

При построении графиков часто возникает проблема отображения на ограниченном экране широкого диапазона изменения данных. Одним из способов решения этой проблемы является введение логарифмической шкалы для области значений.

Excel поддерживает при построении графиков логарифмическую шкалу как для обычных типов графиков, так и для смешанных, то есть на одной оси Вы можете ввести логарифмическую шкалу, а на другой – линейную.

Перейти на Главную страницу

Перейти на Сайт: www.shans–i.narod.ru

You are on the Home/Excel/Charts/3D Surface page

Share Your Comments

About this site

Начало формы

Web This Site

Конец формы

TM Plot Create a chart from any cell with a formula

TM Calendar An easy-to-use calendar with reminder capability for Microsoft Excel

TM AutoChart Link chart axis values to worksheet cells

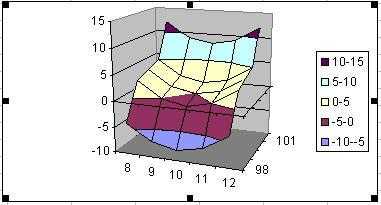
What does the final graph look like?

Enter the function to be graphed

Create a table of data for the chart

Create the chart

What Excel really does and why a 3-D surface chart is not a ‘true’ 3-D chart

The goal Plot z=(x-10)³ + (y-100)² as in the chart on the right

Enter the function to be graphed

To ease understanding of how Excel creates a 3-D surface chart, we will start by naming the cells that will contain the x, y, and z values. Enter the text x, y, and z in cells A1:A3 as on the right. Then, select A1:B3 and select the menu item Insert | Name > Create…

Accept Excel’s default choice of ‘Left column’ by clicking the OK button.

Now, enter the function in cell B3 as shown on the right. Note that the formula uses the names of the cells, rather than the cell addresses. If we had not named the cells, the formula might have looked like =(B1-10)^3+(B2-100)^2

Create the data table for the chart

Create the chart

Step 1: Create the basic chart

Step 2: Specify the ‘x-values’

Step 3: Specify the ‘y-values’

Step 4: The result

Step 1: The basic chart

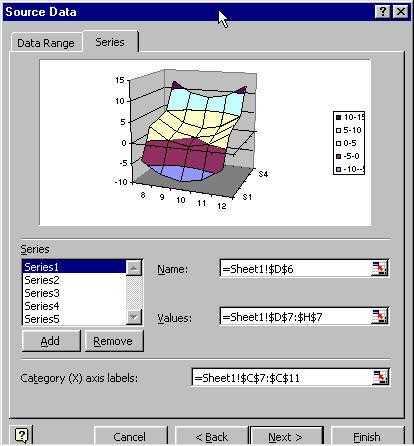
Step 2: Specify the ‘x-values’

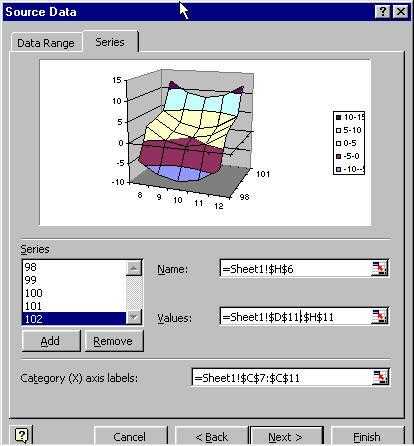
Step 3: Specify the ‘y-values’

Step 4: The result

What’s the limitation on creating a 3-D chart?

In creating the chart above, the x-values were entered not a real numeric values but as ‘category labels.’ This was done in Step 2 of the Chart Wizard. Excel does not attach any numerical significance to these labels. All the labels are arranged so that they are next to each other at equal distances.

Similarly, the y-values are not real values. Excel draws a 3-D chart by charting multiple series and overlaying a surface across all the series. What looks like y-values of 98, 99, etc., are nothing but series names specified in Step 2 of the Chart Wizard.

This example deliberately picked x-values such that the difference between adjacent values was the same (1 in this case). The y-values have the same characteristic, with each being 1 more than the previous one.

Any category chart which contains equidistant x-values will look OK. However, consider the case where the x values are 8, 9, 10, 15, and 20. The chart corresponding to this data set is shown on the right.

studfiles.net

Иллюстрированный самоучитель по Microsoft Excel › Диаграммы и графики › Дополнительные возможности при построении диаграммы [страница – 77] | Самоучители по офисным пакетам

Дополнительные возможности при построении диаграммы

XY-точечная диаграмма – наиболее подходящее средство для обработки результатов исследований такого рода.

С помощью регрессионного анализа можно продолжить линию тренда вперед или назад, экстраполировать ее за пределы, в которых данные уже известны, и показать тенденцию их изменения. Для построения линии тренда активизируйте ряд данных, после чего нажмите правую клавишу мыши. В появившемся списке команд выберите Добавить линию тренда, а затем в соответствующем окне диалога – рисунок с линейным трендом.

В Excel можно выбрать один из пяти типов экстраполяции: линейный, полиномиальный, логарифмический, экспоненциальный или степенной. Тип выбранной экстраполяции задает способ вычислений линии тренда. В зависимости от используемых данных некоторые типы экстраполяции могут оказаться надежнее других с точки зрения оценки результатов сделанных прогнозов. Таким образом, может оказаться полезным проделать несколько различных экстраполяции, чтобы посмотреть, какой из типов лучше всего подходит в данной ситуации.

Чтобы вставить вместо столбца на диаграмме рисунок, выполните следующие действия.

Активизируйте ряд данных на диаграмме.
Выберите команду Рисунок из меню Вставка. Excel предложит Вам выбрать нужный рисунок из файла, автофигуру или объект WordArt.
Выберите необходимый пункт и нажмите клавишу Enter или кнопку ОК в окне. Вместо столбца на диаграмме появится изображение.

samoychiteli.ru

Линейная экстраполяция онлайн с решением и графиком

Подробности: Обновлено: 01.06.2018 11:10; Опубликовано: 31.03.2016 15:11

Калькулятор линейной экстраполяции позволяет вычислить значение линейной функции если абсцисса (Х) искомой точки лежит за пределами отрезка интерполяции [X₁, X₂].

Дано:

округление до 12345знаков после запятой

Решение:

Формула линейной экстраполяции

расчет линейной экстраполяции по двум точкам

Помощь на развитие проекта CAE-CUBE.ru

Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали – обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен – подари проекту CAE-CUBE.ru всего 2 ₽ и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при расчете линейной экстраполяции онлайн калькулятором:

Для проведения экстраполяции требуется ввести значения координат 2 точек ([X₁, Y₁]; [X₂, Y₂]) и абсциссу (Х) той точки, значение которой необходимо вычислить.
График справа позволяет визуализировать полученный линейной экстраполяцией результат.

II. Для справки:

интерполяция: — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
линейная интерполяция: — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними).
квадратичная интерполяция: — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка – парабола).
экстраполяция: — способ нахождения значений функции по уже известным нескольким ее значениям.

cae-cube.ru

Экстраполяция в Excel

Использование экстраполяции

Способ 1: экстраполяция для табличных данных

Способ 2: экстраполяция для графика

Помогла ли вам эта статья?

Прогнозирование значений в рядах – Excel

Дополнительные сведения

Интерполяция в Excel

Использование интерполяции

Способ 1: интерполяция для табличных данных

Способ 2: интерполяция графика с помощью его настроек

Способ 3: интерполяция графика с помощью функции

Помогла ли вам эта статья?

4. Построение прогнозов в Excel

Графики в Excel – Стр 2

Дополнительные возможности при построении диаграммы

Линейная экстраполяция онлайн с решением и графиком

Формула линейной экстраполяции

Оставить комментарий Отменить ответ